2. 上海交通大学 海洋工程国家重点实验室, 上海 200240;
3. 上海交通大学 高新船舶与深海开发装备协同创新中心, 上海 200240
2. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;
3. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China
移动粒子半隐式法(moving particle semi-implicit, MPS)是一种基于Lagrangian系统描述流场的无网格粒子类方法,采用任意分布的粒子对流场进行空间离散,基于预估-修正(半隐式)的方式来求解流体控制方程,通过核函数表征的相互作用模型实现粒子间质量、动量、压力等信息的传递。相对于网格类计算方法,MPS方法在船舶海洋工程水动力学问题中具有独特的优势。例如,该方法不需要离散N-S方程的对流项,因此可以有效地避免对流项离散而引起的数值发散问题;计算流程简洁,易于针对具体问题实现程序化并推广应用;自由面形状由流体域的边界粒子表示,不需要使用额外的数值手段来描述,故而易于模拟复杂的强非线性自由面流动现象,如波浪破碎、翻卷、液体飞溅等;计算过程不需要使用网格,省去了网格生成与重构的繁杂过程;物体边界采用粒子表达,通过移动粒子即可方便地模拟边界的运动或变形。鉴于这些显著特点,越来越多的研究人员采用MPS方法开展复杂流动问题的数值仿真工作。由于船舶与海洋工程领域的流动问题多存在复杂强非线性变化的自由面,故而在过去的二十年期间,MPS方法在该领域的应用研究中发挥着日益重要的作用。例如,该方法已成功应用于溃坝、破波、液舱晃荡、波浪和结构物相互作用、甲板上浪、入水砰击、流固耦合等问题。
从目前的应用成果来看,MPS方法在处理船舶与海洋工程中的自由面大变形流动问题具有很大的潜力和优势,但是为适用于更广泛和更大规模的流体计算问题,该方法仍有广阔的发展空间。
首先,该方法虽然能够很好地模拟流动中剧烈变化的自由面形状,但流场计算存在较为严重的压力震荡现象。为保证MPS方法的计算精度和稳定性,有必要对数值模型进行改进。在以往的研究中,学者们主要从梯度模型、拉普拉斯模型、引入源项的泊松方程、核函数选取等方面着手对MPS方法进行了大量的改进。研究成果表明,改进的MPS方法虽然能够获得合理的压力场,但并不能完全避免压力震荡现象,并且采用单一的改进手段往往难以获得满意的结果,而多种改进方式结合虽然可能获得较好的效果,但大幅增加了计算流程的复杂性,各种改进方法的普适性也需要进一步研究考证。
其次,除了上述数值模型关系到MPS方法的计算精度之外,计算边界条件的设置对该方法的应用范围、计算结果的可靠性及效率也具有重要的影响作用。对于自由面边界,流体粒子的压力将被指定为零,作为边值条件代入压力泊松方程的求解中。一旦有流体内部粒子被误判为自由面粒子,将导致该粒子所在位置及周围区域的压力场失真。为避免自由面粒子的误判,一些学者通过提出新的判断策略结合粒子间碰撞模型来提高流场的计算精度和稳定性。对于物面边界,目前常见的处理策略是在边界上及边界外布置多层边界粒子。该策略虽然能够保证边界粒子的作用域完整,避免壁面粒子穿透的现象,但用于离散壁面的边界粒子数量通常较多,既不利于实现物体的运动、变形等,也一定程度上增加了计算量。因此,有必要发展更新型的壁面边界处理方法。
此外,目前基于MPS方法的研究主要集中在二维问题上,但船舶与海洋工程领域的许多问题具有明显的三维特征,例如船在水中的兴波、波浪在结构物上的绕射、几何形状复杂的物体入水过程等。为实现MPS方法在这些三维流动问题上的应用,首先要解决的问题是提高MPS方法的计算效率。目前,计算流体力学中常用的技术是通过将数个甚至数百个CPU联合并行求解流动问题,此类技术虽然已在网格类方法中得到了广泛的应用,但在MPS粒子类方法中应用时仍存在较大挑战。通常在并行计算时,程序需要通过对流场划分子区域的方式将计算量分配于各个计算线程,保证各线程的计算负载平衡的同时,协调进程间的信息交换。由于采用MPS方法计算时,流动特征是由粒子的运动来表现,在流场的运动变化过程中,难以保持各线程的负载均衡。因此有必要结合硬件条件及程序算法综合发展新的并行策略,提高计算效率。
本文对MPS方法的最新研究进展及其在船舶与海洋工程水动力学问题中的应用展开讨论。回顾了MPS方法在计算精度方面的最新成果,包括核函数的选取、梯度模型、拉普拉斯模型、泊松方程的源项格式等影响因素。从计算机硬件资源的利用和算法改进方面,概述了提高MPS方法计算效率的主要技术手段。介绍了MPS方法在自由面、物面、出入口边界条件等方面的改进,以及在多相流、流固耦合及其他工程应用问题中的发展现状。最后,对MPS方法在今后需要进一步深入研究的方面进行了展望。
1 数值方法最新进展 1.1 计算精度MPS方法在数值模拟带自由面的流动问题中具有明显的优势和可观的前景,然而该方法仍然具有一些缺点,限制了其在实际工程问题中的应用。其中,首先需要解决的问题是计算过程中常见的非物理压力震荡现象。近年来,越来越多的学者在该方面提出了新的见解,使得MPS方法的计算精度和稳定性逐步提高。本节将从核函数、梯度模型、拉普拉斯算子及高阶源项等方面介绍,对MPS方法的主要改进技术进行总结。
1.1.1 核函数核函数作为粒子间相互作用的权重函数,在MPS方法中有重要作用。目前,使用最广泛的核函数(式(1))由Koshizuka[1]提出,该核函数的主要特点是当两个粒子之间距离逐步减小时,权重函数W(r)的值为无穷大,基于该核函数的粒子间排斥力亦为一个较大值。由此可知,采用该核函数可避免粒子在相互作用过程中出现局部聚集的现象。
然而,对于剧烈的流动问题,可能发生相邻粒子的瞬时间距较小的情况,进而导致相邻粒子间出现过大的排斥力,对流体粒子的运动方向产生不利扰动,影响数值计算的精度和稳定性。针对此问题,张雨新等[2]提出了一种与原核函数形式相似但无奇点的核函数(式(2)),其数值验证结果表明,采用该新式核函数能有效提高MPS方法的精度和稳定性。
由于MPS方法中的核函数仅代表粒子间相互作用物理量的权重,故而存在多种表达式形式。Ataie-Ashtiani等[3]比较了6种不同的核函数对于MPS方法模拟溃坝问题的数值精度和稳定性的影响。在其研究中考察了SPH方法中Belytschko等[4]使用的指数核函数、三次样条核函数、四次样条核函数、Shao等[5]使用的B样条核函数,以及在MPS方法中Koshizuka[1, 6]提出的两种核函数。数值结果认为在溃坝模拟中,Shao等使用的核函数具有更好的精度和稳定性。
| $ w\left( r \right) = \left\{ \begin{array}{l} \frac{{{r_e}}}{r} - 1,\;\;\;\;0 \le r < {r_e}\\ 0,\;\;\;\;\;\;\;\;\;\;{r_e} \le r \end{array} \right. $ | (1) |
| $ w\left( r \right) = \left\{ \begin{array}{l} \frac{{{r_e}}}{{0.85r + 0.15{r_e}}} - 1,\;\;\;\;0 \le r < {r_e}\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{r_e} \le r \end{array} \right. $ | (2) |
梯度模型是MPS方法中一个重要的粒子模型,控制方程中压力梯度的离散是基于梯度模型完成的。在原始的MPS方法中,压力梯度模型如式(3)所示。该模型的缺点是粒子间作用力并非都为排斥力,整个粒子系统的动量不守恒,计算容易发散。为改善计算的稳定性,Koshizuka等[6]提出将式(3)中第i个粒子的压力换成i作用域内所有粒子的最小压力值(如式(4)所示),从而保证了粒子间始终存在排斥力。此后,研究人员又提出了多种压力梯度模型。Khayyer等[7]通过在两个相邻粒子中心构建一个虚构的点,推导了一个完全反对称(大小相同,方向相反)的梯度模型(式(5))。该模型是在式(4)模型的基础上进行了改进,既保证了粒子间始终相互排斥,也保证了整个粒子系统的动量守恒性。随后,Tanaka等[8]提出了一种与前式相似的压力梯度模型,如式(6)所示。通过二维溃坝问题的数值模拟表明,该式相对式(5)更为简洁,且能够一定程度上缓解流场的压力震荡现象。最近,Tsuruta等[9]鉴于粒子瞬时运动的方向不定性可能对流场的稳定产生不利影响,提出了一种考虑了动态稳定的梯度模型(式(7))。
| $ {\left\langle {\nabla P} \right\rangle _i} = \frac{d}{{{n_0}}}\sum\limits_{j \ne i} {\left[ {\frac{{{P_j} - {P_i}}}{{{{\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|}^2}}}\left( {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right)w\left( {\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|} \right)} \right]} $ | (3) |
| $ {\left\langle {\nabla P} \right\rangle _i} = \frac{d}{{{n_0}}}\sum\limits_{j \ne i} {\left[ {\frac{{{P_j} - {P_{i\min }}}}{{{{\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|}^2}}}\left( {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right)w\left( {\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|} \right)} \right]} $ | (4) |
| $ \begin{array}{*{20}{c}} {{{\left\langle {\nabla P} \right\rangle }_i} = \frac{d}{{{n_0}}}\sum\limits_{j \ne i} \cdot }\\ {\left[ {\frac{{\left( {{P_i} + {P_j}} \right) - \left( {{P_{i\min }} + {P_{j\min }}} \right)}}{{{{\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|}^2}}}\left( {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right)w\left( {\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|} \right)} \right]} \end{array} $ | (5) |
| $ {\left\langle {\nabla P} \right\rangle _i} = \frac{d}{{{n_0}}}\sum\limits_{j \ne i} {\left[ {\frac{{{P_i} + {P_j}}}{{{{\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|}^2}}}\left( {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right)w\left( {\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|} \right)} \right]} $ | (6) |
| $ \begin{array}{*{20}{c}} {{{\left\langle {\nabla P} \right\rangle }_i} = \frac{d}{{{n_0}}}\sum\limits_{j \ne i} {\left[ {\frac{{{P_j} - {P_i}}}{{{{\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|}^2}}}\left( {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right)w\left( {\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|} \right)} \right]} + }\\ {\frac{1}{{{n_0}}}\sum\limits_{j \ne i} {\left[ {F_{ij}^{DS}w\left( {\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|} \right)} \right]} } \end{array} $ | (7) |
由于MPS方法中流体压力场是通过求解泊松方程而得到,故而该方程模型的构建方法及求解方式关系到压力场计算的精确性。截止目前,不断有学者分别从泊松方程的左端即拉普拉斯算子和右端源项出发,提出了关于压力泊松方程的多种形式。
在标准的MPS方法中,基于流场的瞬时扩散思想可得到粒子模型形式的拉普拉斯模型。为了进一步提高流场压力计算的稳定性,研究者们对拉普拉斯模型进行了一些改进。Zhang等[10]综合散度模型和梯度模型,提出了一种适用于热传导问题的拉普拉斯模型(式(8))。Khayyer等[11-12]根据SPH梯度模型的离散方式和原始MPS核函数,推导了高阶的拉普拉斯模型(式(9)),并将其扩展到三维问题。考虑修正的梯度模型,Ikari等[13]得到了一个修正的高阶拉普拉斯模型(式(10))。
| $ {\left\langle {{\nabla ^2}\mathit{\Phi }} \right\rangle _i} = \frac{{2d}}{{{n_0}}}\sum\limits_{j \ne i} {\frac{{{\mathit{\Phi }_j} - {\mathit{\Phi }_i}}}{{{{\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|}^2}}}\left( {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right)w\left( {\left| {{\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}} \right|} \right)} $ | (8) |
| $ {\left\langle {{\nabla ^2}\mathit{\Phi }} \right\rangle _i} = \frac{1}{{{n_0}}}\sum\limits_{j \ne i} {\left( {{\mathit{\Phi }_{ij}}\frac{{{\partial ^2}{w_{ij}}}}{{\partial r_{ij}^2}}} \right)} $ | (9) |
| $ {\left\langle {{\nabla ^2}\mathit{\Phi }} \right\rangle _i} = \frac{1}{{{n_0}}}\sum\limits_{j \ne i} {\left( {{\mathit{\Phi }_{ij}}\frac{{{\partial ^2}{w_{ij}}}}{{\partial r_{ij}^2}} - \frac{{{\mathit{\Phi }_{ij}}}}{{{r_{ij}}}}\frac{{\partial {w_{ij}}}}{{\partial {r_{ij}}}}} \right)} $ | (10) |
在压力泊松方程的源项方面,传统的MPS方法中该项完全由粒子数密度构成,即通过粒子数密度的不变条件来表达流体的不可压缩性。然而,实际计算过程中,剧烈流动时粒子数密度场并不光滑,这必然导致压力场的不光滑。因此,一些学者从泊松方程源项出发,着力于改善压力场的光顺性。例如,Khayyer等[14]将泊松方程中的源项用随时间变化的粒子数密度代替,并通过核函数表达粒子数密度时间变量。进而,通过计算核函数对时间的物质导数,得到了一个高阶的源项表达式。通过溃坝问题的数值模拟表明,该高阶源项法相对传统的源项能够更好地缓解压力震荡现象,但该方法在壁面附近还存在局部压力不光顺的问题。此后,Khayyer等[11]通过对源项进行误差补偿,提出了一种改进的源项表达式,如式(12)、(13)。该式是在高阶源项的基础之上增加了两项误差缓解项,其中一项代表粒子数密度的瞬时变化量,另一项代表粒子数密度相对理论值的偏差。
| $ {\left\langle {{\nabla ^2}{P_{k + 1}}} \right\rangle _i} = - \frac{\rho }{{{n_0}\Delta t}}\sum\limits_{j \ne i} {\frac{{{r_e}}}{{r_{ij}^3}}\left( {{x_{ij}}u_{ij}^ * + {y_{ij}}v_{ij}^ * } \right)} $ | (11) |
| $ {\left\langle {{\nabla ^2}{P_{k + 1}}} \right\rangle _i} = - \frac{\rho }{{{n_0}\mathit{\Delta }t}}\sum\limits_{j \ne i} {\left( {\frac{{{\rm{D}}n}}{{{\rm{D}}t}}} \right)_i^*} + {\mathit{\Lambda }_{{\rm{ECS}}}} $ | (12) |
| $ \begin{array}{*{20}{c}} {{\mathit{\Lambda }_{{\rm{ECS}}}} = \frac{\rho }{{\Delta t}}\left\{ {\frac{\alpha }{{{n_0}}}\left( {\frac{{{\rm{D}}n}}{{{\rm{D}}t}}} \right)_i^k + \frac{\beta }{{\Delta t}}\frac{{n_i^k - {n_0}}}{{{n_0}}}} \right\},}\\ {\alpha = \left| {\frac{{n_i^k - {n_0}}}{{{n_0}}}} \right|,\beta = \left| {\frac{{\Delta t}}{{{n_0}}}\left( {\frac{{{\rm{D}}n}}{{{\rm{D}}t}}} \right)_i^k} \right|} \end{array} $ | (13) |
对于不可压问题,由于速度的散度为零,故而可用速度的散度项代表泊松方程的源项。在数值仿真过程中,如此处理源项虽然能够得到光顺的压力场结果,但速度的散度存在计算误差,该误差会累积从而造成流体体积的不守恒。为结合粒子数密度不变条件所具有的体积守恒性质,以及速度无散度条件能够获得光滑压力场的特点,Tanaka等[8]提出了一个混合源项法,该方法经过Lee等[15]改进为式(14)更合理的形式。此外,Tanaka等[8]在泊松方程中提出了一个准不可压缩项(式(15)),用来提高数值模拟的稳定性。Kondo等[16]将混合源项中的密度项离散成了一个主要部分和两个误差补偿部分:
| $ {\nabla ^2}P = \frac{\rho }{{\Delta t}}\nabla \cdot {V^ * } + \gamma \frac{\rho }{{\Delta {t^2}}}\frac{{{n^0} - {n^k}}}{{{n^0}}} $ | (14) |
| $ {\nabla ^2}P = \frac{\rho }{{\Delta {t^2}}}\left( {\frac{{{n^0} - {n^k}}}{{{n^0}}} + \alpha P_i^{k + 1}} \right) $ | (15) |
| $ \begin{array}{*{20}{c}} {\frac{1}{{{\rho ^0}}}\left( {\frac{{{{\rm{D}}^2}\rho }}{{{\rm{D}}{t^2}}}} \right) = \frac{{1 - \beta }}{{\Delta {t^2}}}\frac{{n_i^ * - 2n_i^k + n_i^{k - 1}}}{{{n^0}}} + }\\ {\frac{{\beta - \gamma }}{{\Delta {t^2}}}\frac{{n_i^ * - n_i^k}}{{{n^0}}} + \frac{\gamma }{{\Delta {t^2}}}\frac{{n_i^ * - {n^0}}}{{{n^0}}}} \end{array} $ | (16) |
MPS方法虽然在带自由面的问题中展现了明显的潜力和优势,但实际工程问题多具有三维特性,例如船艏破波、甲板上浪、艏艉的入水砰击等现象已不适用二维MPS方法进行模拟,因此将二维MPS方法扩展到三维的研究工作是很有必要的。然而,三维问题首先面临的挑战是计算量巨大。以船艏破波问题[17]为例,为了能够比较精细地描述船体附近破波的形状,船体附近的初始粒子间距不能太大,对计算域离散需要的粒子总数要达到千万级以上。此外,由于MPS方法在二维和三维空间下粒子的作用域范围分别为圆形和球形域,这意味着三维计算模型中每个粒子所对应的邻居粒子数是二维模型的N=1.33×r倍(其中r为作用域半径)。对于泊松方程的求解,r通常取值为4.01。故而,即使采用相同的粒子数计算模型,三维模型的计算量也将为二维模型的N=5.33倍。
针对MPS方法计算量大的问题,研究人员从多个角度提出了一些解决方案。一种是通过直接增加计算资源(如GPU或CPU)来分担传统单CPU的计算负荷,从而提高计算效率;另一种是开发局部流场的精细化技术,减少粒子法数值模拟所需要的总粒子数,降低整体的计算负荷并将计算资源主要集中在重点关注的局部区域内。
1.2.1 CPU并行加速技术由于单个CPU核心性能的提升有严重的瓶颈问题,随着计算机硬件条件的发展,普通计算机上也配置着多个计算核心,并且核心数目会越来越多。因此,如何有效调用多个CPU核心,合理分配MPS计算任务,对大规模问题拥有可观的计算效率,已有不少学者对此展开了研究。对MPS采用多CPU加速最为普遍的并行策略可以分为两大类,一是粒子分解法,二是区域分解法。
粒子分解法是将粒子按编号分配给各个进程,每个进程负责一组固定的粒子。粒子分解法容易实现负载平衡,但在做计算粒子积分时需要知道邻居粒子的信息,而邻居粒子可能不在本进程内,因此需要进程间进行大量的信息传递,这会很大程度地影响计算效率。针对这一问题,Iribe等[18]对每一次计算步内的粒子编号进行了重新排序,将粒子按照一个方向的坐标进行统一编号。这样既可以保证将来分解的子计算域内粒子编号连续,减小传入各核心邻居粒子搜寻表的长度,加快邻居粒子搜寻速度,还可以使压力泊松方程系数矩阵中非零元素更加集中,减少带宽加快求解速度。通过对一百万粒子的计算,采用重新编号技术同时提高了邻居粒子搜索和压力泊松方程求解速度,并且随着核心数的增加,也能保持较为理想的加速比。
在区域分解法中,计算域被分成多个子域,子域的数量等于参加计算的进程数,每个进程负责一个子域。区域分解法的进程间通信量很小,大部分内部粒子积分可以从子域信息中得到,只有在子域边界处需要进行部分粒子信息的交换。Ikari等[19]分析了粒子分解法和区域分解法两种并行策略的优缺点,结果显示区域分解法能够获得更好的并行效率。但对于区域分解法,由于粒子的位置在计算中发生变化,粒子可能会从一个进程进入另一个进程,因此,使用区域分解法容易出现负载的不平衡现象。基于MPI并行库,张雨新[20]采用动态负载平衡技术,即每间隔一定的时间步按照顺序,对一纵列背景网格内的粒子个数进行判断,当区域内粒子个数接近于理论平均值时,则将选中的纵列背景网格作为一个子域分配给一个计算核心,如不满足则对背景网格的框选范围进行扩大或缩小,以满足每个核心中计算的粒子个数基本相同。
1.2.2 GPU并行加速技术上述研究表明,采用CPU并行加速技术,增加CPU计算核心数,可以有效地提高MPS方法模拟大规模问题的计算效率。一般而言,随着核数的增加,计算时间也会逐步减少。因此,如果有足够多计算核心同时进行计算,可以得到非常可观的计算效率。图像处理器(GPU)最初被用来做图像运算工作,但由于其硬件构架与CPU不同,在相同芯片面积情况下划分了更多的算术逻辑单元(ALU),天然的众核构架形式决定了GPU十分适合大规模并行科学计算。目前GPU已经应用在深度学习、大气监测等领域。关于将GPU并行加速技术应用到MPS方法中的研究,近几年来也在逐步推进中。Hori等[21]基于CUDA平台对MPS方法的GPU改造进行了阐述,分析了GPU与CPU的编程方式的不同性,如何充分发挥GPU众核同时处理数据的能力。他还采用ELLPACK-R形式存储压力泊松方程系数矩阵,并将带宽更大的纹理存储器用于压力泊松方程迭代过程中的向量相乘,对于二维溃坝问题模拟,GPU加速比达到3~7倍。
GPU的内存是分层的存储形式,布置着六种存储:本地内存(local memory)、寄存器(registers)、共享内存(shared memory)、全局内存(global memory)、常量内存(constant memory)和纹理内存(texture memory)。每种内存的大小和访问速度都不同,合理利用各种内存也是GPU加速的一种方式。朱小松[22]针对不同类型GPU内存的使用情况进行了研究,并发现合理使用共享内存、常量内存和纹理内存可以提高计算速度。但是由于共享内存、常量内存和纹理内存的内存容量很小,对于大规模计算问题适用性不强。
众所周知,MPS方法中压力泊松方程求解占据整个计算时间的80%以上,因此如何在GPU上加速求解该方程是提高计算效率的关键。此外,很多公司针对GPU构架,开发了各种加速函数库,以方便用户进行数组处理。张雨新[20]采用Photonics公司开发的CULA Sparse线性矩阵库求解压力泊松方程离散后的大型稀疏代数方程组,对不同粒子数的三维溃坝问题进行了模拟,随着粒子数的增加,GPU的加速比也会逐渐增大,证明了GPU是非常适合MPS方法大规模问题计算的。李海洲[23]也采用CULA Sparse线性矩阵库对压力泊松方程进行求解,模拟了三维带障碍物溃坝和晃荡问题,仅压力泊松方程一项加速比可达到10倍。
此外,随着计算问题规模的增大,单块GPU对某些问题无法满足计算需求,采用多块GPU进行并行加速计算成为一个新的趋势。Ovaysi等[24]将MPI通信技术用于多块GPU之间的数据交换。与多CPU并行相似,Ovaysi等[24]也采用区域分解法将计算域等分成若干个子域,并通过MPI分配给各GPU,并将子域交界处的粒子信息传递给相邻GPU。同时每次压力泊松方程的迭代都需要各GPU之间交互两次信息,所以必须要提前确定好相邻GPU之间的邻居粒子,以减少数据交互时间。Ovaysi等[24]还采用了无阻塞MPI通信,同时进行数据计算和交换,并对四千万粒子的孔隙尺度流动问题进行了多GPU的模拟。
1.2.3 多分辨率粒子技术粒子局部加密技术算法基本是基于压力显式求解的SPH方法来进行研究和开发的。相比于SPH方法,MPS方法在这方面所开展的工作比较少,目前已经报道的主要有重叠粒子技术(overlapping particle technique)及多分辨率粒子技术(multi-resolution particle technique)。
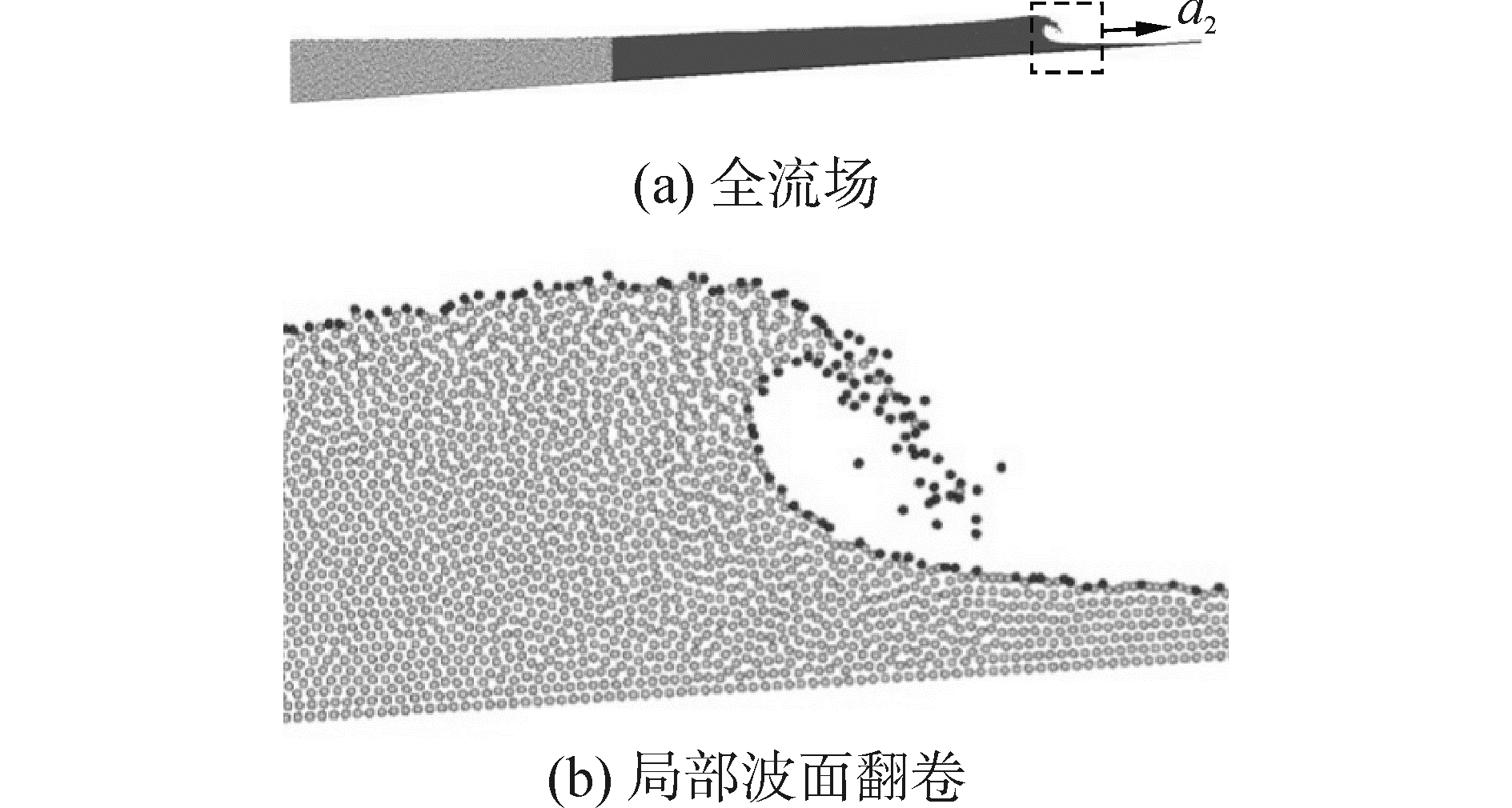
Tanaka等[25]是最早基于MPS方法开展Multi-resolution粒子技术研究工作的。在Multi-resolution粒子技术中,不同分辨率粒子直接参与粒子作用模型的计算及进行压力泊松方程的求解。Multi-resolution粒子技术能够较好地满足粒子系统质量的守恒。考虑到原始MPS方法主要基于全流场采用相同大小粒子来表征,Multi-resolution粒子技术采用原始的粒子作用模型时往往需要进行修正。Tanaka等[25]引入粒子直径对粒子作用模型进行修正,并通过一系列的数值试验来确定核函数的修正系数。同时,为了避免不同分辨率粒子对应的粒子数密度的不准确性,对不同分辨率粒子界面附近粒子的泊松方程的源项采用全散度源项。在该文献中,Multi-resolution算法的研究工作都是基于传统的MPS开展的;其次,在Multi-resolution仿真中自由面判断不准确也可能导致压力场的空间震荡。Tang等[26]采用Multi-resolution粒子技术模拟了二维溃坝问题,壁面砰击压力和水头高度的演化与实验和统一分辨率粒子的结果吻合较好,并且相较统一分辨率粒子,粒子数量减少一半,计算时间减少了60%(图 1)。Tang等[27]还进一步模拟了三维溃坝和圆柱入水问题,所得计算结果也都与实验值相吻合(图 2)。

|
Download:
|
| 图 1 多分辨率粒子技术在溃坝问题中的应用 Fig. 1 Applications of multi-resolution particle technique on dambreak problem | |
|
Download:
|
| 图 2 `重叠粒子技术在波浪爬坡问题上的应用 Fig. 2 Applications of overlapping particle technique on wave run-up problems | |
与Tanaka等[25]的处理方式不同,Yoon等[28-30]将MPS方法与MAFL(meshless advection using flow-directional local-grid)方法结合并在MPS方法中实现了Variable-size技术。在MPS-MAFL中,流体的不可压缩性将不再采用粒子数密度为常数而是采用速度散度为零条件来表征。具体地,压力泊松方程中右端源项将全部采用速度散度来表征,这样可以放开对粒子数密度的限制,从而容许粒子在局部区域内聚集,实现局部区域采用高分辨率粒子来进行数值模拟。此后,Heo等[31]、Tian[32]、Chen等[33]、陈荣华等[34-36]、左娟莉等[37]将Variable-size技术用于气泡的上升行为及融合等特性的研究,这样可以比较精细的描述气泡的形状变化。
1.2.4 重叠粒子技术在压力隐式求解方案的无网格粒子法中实现Multi-resolution的仿真比压力显式求解方案的粒子法中要困难的多。在MPS方法中流体是完全不可压缩的,不同分辨率的粒子相互作用时往往容易导致计算的发散。如果不同分辨率粒子的直径比比较大时,不同分辨率的粒子直接采用原始的粒子作用模型来计算粒子间的相互作用容易造成计算的不稳定。其次,粒子分裂后会造成局部区域内粒子数密度的突变,从而导致计算发散。
为了克服这个问题,Shibata[38]提出了重叠粒子技术(overlapping particle technique, OPT),避免不同分辨率的粒子直接进行相互作用。它的主要思想是:在整个计算域(含重叠区域)内布置大粒子,在局部重点关注的空间(重叠区域)内布置小粒子。在一个时间步内,首先通过低分辨率粒子获得整个流场信息,然后把重叠区域截断边界处的压力和速度信息传递给高分辨率粒子,继而高分辨率粒子再重新计算一次局部流场。也就是说,大粒子作为一个整体进行计算,小粒子作为一个整体进行计算。
在整个过程中,高分辨率粒子和低分辨率粒子之间的耦合是一种单向的关系,即:低分辨率粒子传递必要的信息给高分辨率粒子,但高分辨率粒子不需要传递任何信息给低分辨率粒子。将重叠粒子技术和传统的MPS方法结合,Shibata等[39]通过一个二维甲板上浪的算例验证了重叠粒子算法在计算效率方面的优势。Tang等[40]基于万德成教授课题组在改进的MPS方法上自主开发的无网格粒子法MLParticle-SJTU求解器中开发了重叠粒子模块,并将Overlapping粒子技术应用到溃坝流及孤立波的破碎问题中。Tang等[41]进一步将Overlapping技术应用到三维带障碍物的溃坝问题中,水头波高和压力变化与实验结果基本一致,并且计算时间相比全部高分辨率粒子减少了40%。通过Shibata等[39]、Tang等[40]的数值结果,可以发现Overlapping粒子技术能够避免不同大小粒子之间的直接作用,并提高数值仿真的计算效率。
1.3 计算边界条件在基于MPS方法的数值模拟中,为了保证流体力学方程组的封闭,需要结合考虑计算的初始和边界条件的影响。目前,有关MPS方法在计算边界条件方面的研究成果虽然少于SPH方法,但由于两种方法本质上的相似性,SPH方法的边界条件处理方法亦可推广应用于MPS方法,故而本节将综合介绍两种方法中常用的自由面、物体壁面、流场的进出口等边界条件。
1.3.1 自由面条件在包括MPS方法的投影类粒子方法中,被判定为自由面的粒子所携带的压力将被指定为零,作为边值条件带入到压力泊松方程的求解中。一旦有流体内部粒子被误判为自由面粒子将导致压力泊松方程不能得到准确的解,进而表现为该粒子所在位置及周围区域的压力场失真。因此,准确地判断自由面粒子并将动力学边界条件施加于此类粒子之上,对计算精度有重要影响作用。
在原始的MPS方法中,通过粒子数密度的变化实现对自由面粒子的判断[1]。由于自由面处,粒子的积分域被截断,相应的粒子数密度积分值较小。该判断方法数学格式简单,且具有一定的合理性,故而被众多学者采纳。然而,在剧烈流动时,计算域内部流体粒子的邻居粒子数量可能瞬时有所降低或距离较远,此时该内部粒子将因粒子数密度积分值较小而被误判为自由面粒子。近年来,研究人员不断提出新的自由面粒子判断方式以降低自由面的误判可能性。由于自由面上的粒子具有邻居粒子不对称性分布的特征,即邻居粒子多集中于积分域的一侧而流体内部粒子其邻居粒子分布近似对称。Tanaka等[8]基于该特征提出一种对称型函数,自由面粒子对应的函数值通常为小量。与之相似,Khayyer等[14]也提出了一种与原始判断方法相结合的反对称型函数;Ma等[42]在其基于Rankine源的无网格局部彼得洛夫-伽辽金方法上提出了粒子数密度与辅助函数混合的方法;Park等[43]提出了一种自由面弧度判断方法。以上方法虽然都考虑了自由面粒子分布的不对称性特征,但其不对称性仍然是基于粒子数密度的相关函数进行表达。为减小剧烈流动时内部流体粒子数密度的变化而造成的自由面误判,Zhang等[44]基于粒子及其邻居粒子的相对位置矢量函数来判定自由面粒子,其数值试验结果表明该方法能显著提高自由面粒子判断的准确度,进而改善压力场。
1.3.2 壁面边界条件粒子类方法对物面边界的处理方式通常可分为三类,其中应用最为广泛的是采用多层虚粒子(或称镜像粒子)对物体壁面进行离散。此类物面处理方式能够保证边界粒子影响域的完整性,进而有效避免粒子的穿透现象,但付出的代价是计算量的增加,且对于具有复杂形状的边界难以采用虚粒子进行模型的描述。
近年来,研究人员不断探索新的技术,期望能够保证物面抗穿透性的同时降低流场的计算时间。其中,通过在壁面粒子及其邻居粒子上施加排斥力的方法可视为第二类壁面边界处理技术,例如Monaghan等[45]通过在单层壁面粒子和流体粒子间施加了辐射力,修正了近壁面处流体粒子的运动,避免了粒子穿透现象的发生。虽然此类方法能够适用于复杂的壁面形状且简单易行,但由于排斥力是由人为确定,不能代表实际的物理特征,故而并未推广应用。近年来,Kulasegaram[46]及Ferrand[47]等提出的统一半解析边界模型可被视为第三类壁面边界处理技术。Leroy等[48]通过在ISPH的泊松方程中考虑非均匀的Neumann压力边界条件,实现了ISPH与统一半解析边界模型的结合,在其数值验证算例中,仅采用单层边界便避免了物面粒子的穿透。
1.3.3 进出口边界条件在对实际工程问题进行数值模拟时,进出口边界条件是最常见的边界类型之一。与网格类方法不同,在MPS方法中流动现象是通过粒子的运动来描述,故而采用特定的技术使流体粒子进入或流出计算域范围便可实现流动的进出口边界条件。
截止目前,常用的进出口边界处理技术是在流场分别划分进口区域、流动区域、出口区域。在进口区域中,基于进口边界条件设定粒子的运动速度,基于流动区域中邻居粒子的压力插值设定进口区域粒子的压力。粒子由进口区域进入流动区域后,粒子的运动由流场计算得到的粒子间相互作用力来驱动。由于粒子通常是由进口区域向流动区域单向运动,故而需要根据离开的粒子数量多少在进口区域新增粒子。相对进口边界条件而言,出口边界条件更易实现,因为流动过程中没必要在出口区域新增粒子[49]。
上述进出口边界处理技术虽然简单易行,但由于进出流场粒子数量的变化及而难以保证流场的质量守恒,并可能使压力场的震荡更为剧烈。近年来,研究人员不断开发新的出入口边界处理技术。例如,Hosseini等[50]提出了一种压力修改策略,使得压力在入口处满足Neumann条件,出口处满足Dirichlet条件。Leroy等[51]在半解析物面条件理论的基础上提出了一种新的出入口边界模型并成功应用于三维流动问题。数值结果表明,该模型能够保证流场及出入口边界上获得足够精确的速度、压力、温度物理信息。当粒子法应用与波浪相关的问题时,出口边界条件还需要额外的处理技术,以避免出口处出现波浪的反射等问题。为此,Shibata等[52]提出了透射边界条件,既能够实现波浪在传递至出口边界时保持理想的波形,也能减少波浪模拟所需的计算域尺寸,进而降低计算资源的需求。
1.4 多相流多相流问题广泛存在于各种尺度和流态下的工程和工业过程中。但由于多相流包含复杂的内部物理现象,对它进行数值模拟仍是计算流体力学中最具挑战性的研究之一。多相流模拟中存在的主要难点包括:相界面处密度和粘度的突变,大变形移动边界以及拓扑转换,比如界面的合并。考虑到粒子法在处理大变形边界上的优势,将粒子法引入到多相流的数值模拟中后,最主要的难点只有相界面处密度的突变。
利用粒子法模拟多相流时,相界面处密度变化急剧且突然,造成密度场的不连续,从而使压力梯度场不连续。因此,即使在压力梯度计算中出现了很小的误差,也会带来严重的数值不稳定问题。如何处理好密度不连续问题,是将粒子法应用于多相流模拟,尤其是相间密度差别比较大的多相流模拟的关键挑战。
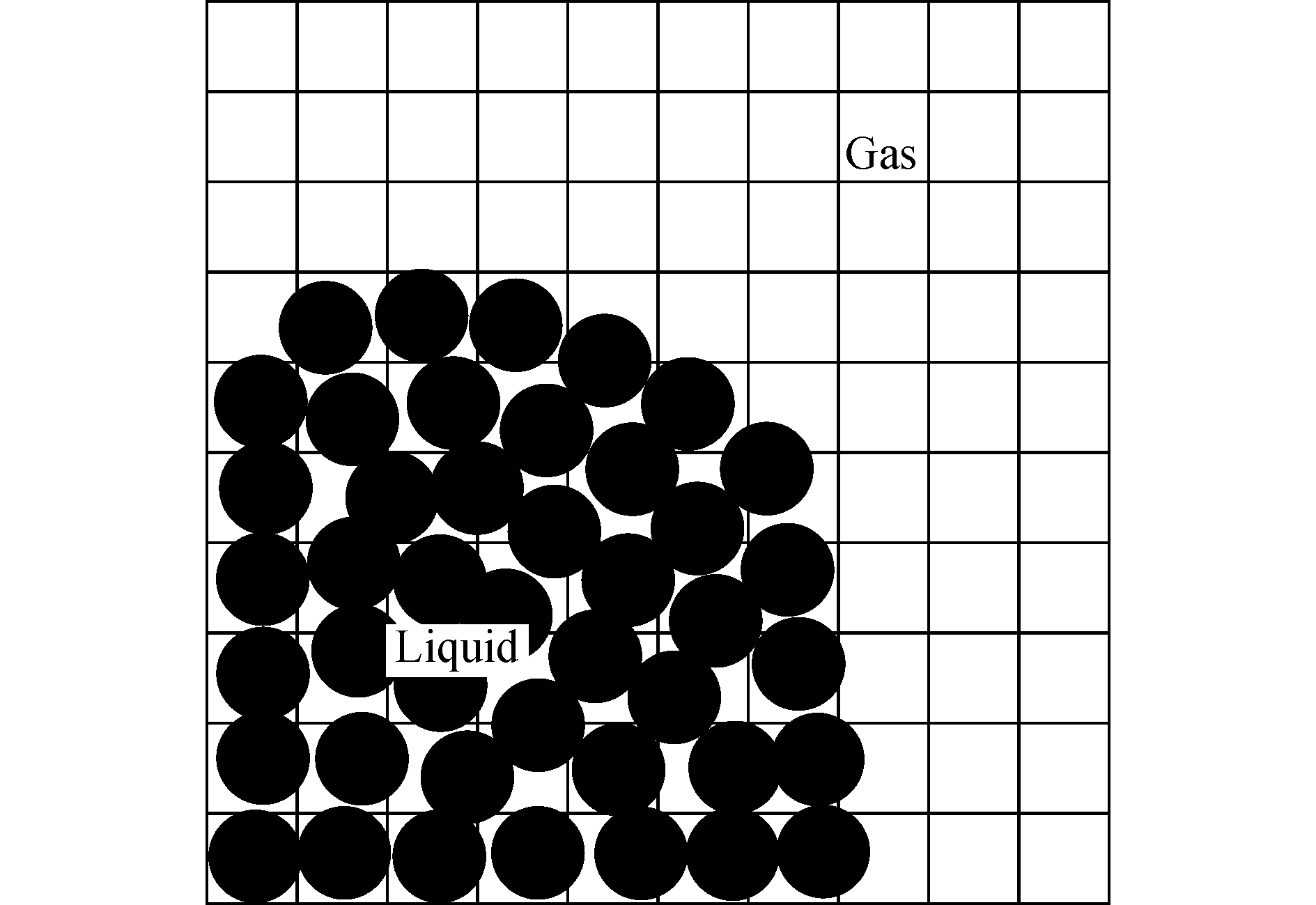
Gotoh等[53]发展了固-液两相流MPS方法,这是第一个两相流MPS方法,其中液体和固体具有不同的控制方程,模拟结果得到了将沙土倒入水中的沉积和扩散过程。Liu等[54]提出了一种粒子法与网格法结合的MPS-FVM方法,用粒子代表密度较大的流体,而密度较小的流体用网格计算(图 3)。通过将界面粒子的密度和粘度外推插值到网格,解决了不连续问题,并计算得到了瑞利-泰勒不稳定问题等两相流问题(图 4)。
|
Download:
|
| 图 3 粒子与网格分布 Fig. 3 Distribution of particle and mesh | |

|
Download:
|
| 图 4 瑞利-泰勒不稳定问题 Fig. 4 Rayleigh-Taylor instability | |
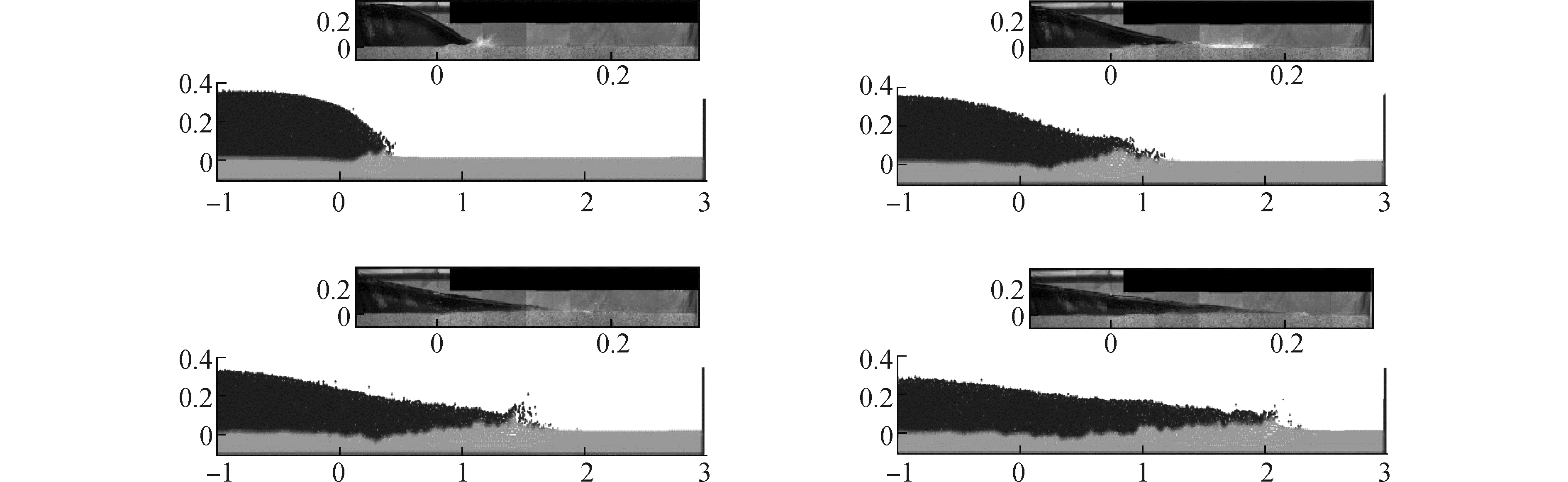
为模拟动床溃坝流动,Shakibaeinia等[55]提出了包含非牛顿基本模型的两相流MPS方法,充分考虑了沉积相(固相)的非牛顿性质,证明了MPS方法在模拟流动结构和沉积相运输方面的适用性(图 5)。Shakibaeinia等[56]采用弱可压缩MPS方法,模拟了低密度比的两相流。在该方法中对密度进行了空间平均,粘度则采用了调和平均数,但这会带来非物理耗散,无法表示两相界面处真实的密度变化,并且也会带来两相粒子的非物理扩散,密度较大的流体会穿透到密度较小的流体中去。
|
Download:
|
| 图 5 动床溃坝的MPS模拟与实验对比 Fig. 5 Numerical and experimental result of dambreak flow on movable bed | |
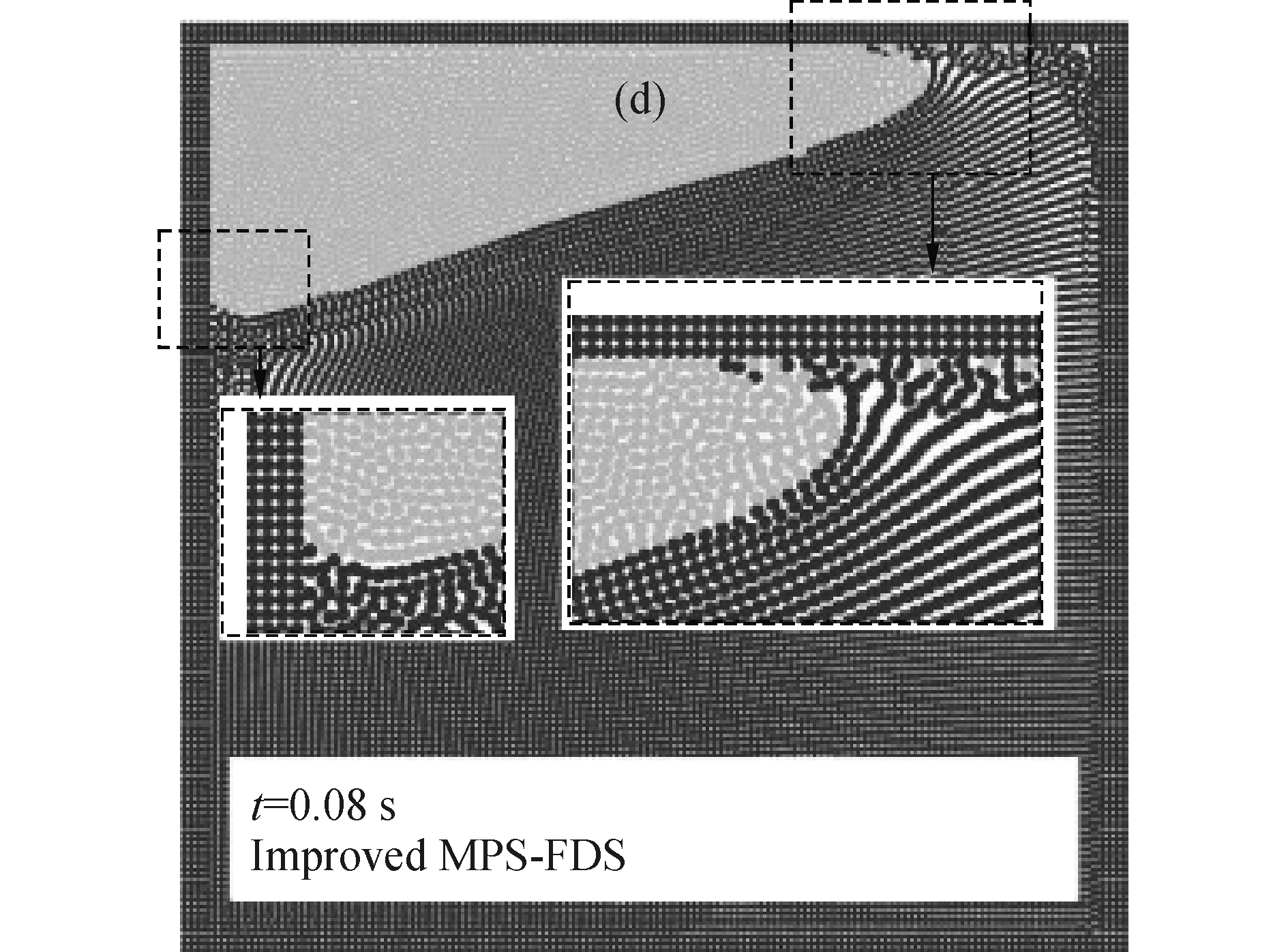
Khayyer等[57]提出了一种更稳定的MPS两相流方法,该方法包括了四种已有的改进格式,以及一种专门为准确模拟两相界面处密度而提出的光滑格式,该格式是基于泰勒级数展开,可以认为是SPH中常用的零阶密度光滑格式的扩展,通过这一扩展,可明显改善MPS对高密度比多相流模拟的准确性,特别是在保持界面处密度变化清晰、提供连续密度场、减少非物理穿透等方面有很大提高,改善了数值稳定性,并在两相流液舱晃荡问题中得到了应用(图 6)。他们指出,单相流MPS方法中使用的反对称压力梯度模型在多相流模拟,尤其是高密度比多相流模拟中会带来数值不稳定的问题。
|
Download:
|
| 图 6 剧烈液舱晃荡的MPS模拟 Fig. 6 Simulation of violent tank sloshing using MPS method | |
液舱晃荡是指在外部激励作用下部分装载的液舱内液体所产生的波动现象。当部分装载的液货船在海上航行时,在波浪作用下,往往会发生船舶的横摇、纵摇、垂荡等激励运动,导致液舱内液体产生晃荡现象。网格类方法在液舱晃荡问题中已经取得了很多成果,但是在处理复杂自由液面的问题时仍具有一定的困难。剧烈的晃荡往往伴随着水跃、冲顶、波浪破碎、自由面翻卷等强非线性现象,这就要求网格类方法划分更加精细的网格,对网格和计算的要求更加苛刻。而无网格粒子方法基于拉格朗日方法,能够很好地处理此类自由面大变形及强非线性问题。目前,MPS方法已广泛应用于液舱晃荡问题中,成为分析研究该问题不可或缺的技术途径。
潘徐杰等[58-59]基于改进MPS法分析了液舱晃荡现象,比较了在横摇激励下不同自由面条件、核函数对模拟结果的影响。Hwan等[60]通过对传统MPS方法的核函数和压力泊松方程进行改进,将其应用到二维液舱晃荡问题中,减缓了压力震荡现象,得到了理想的砰击压力结果。张雨新等[61-65]对传统的MPS方法进行了多方面的改进,将其应用于二维和三维液舱晃荡问题模拟,MPS计算的壁面砰击压力和自由面波形与实验和其他方法结果吻合。由于晃荡产生的瞬时巨大的砰击压力会对液舱结构和载体稳性造成危害,在液舱内布置隔板以减少晃荡幅度是常用的方法。Tsukamoto等[66]在二维液舱中间布置了一个与舱壁之间用弹簧连接的浮体,并用MPS方法研究了在不同充液率和激励频率下,流体对浮体和舱壁的作用力,结果表明浮体能有效地减小流体对舱壁的砰击力。Yang等[67-69]及杨亚强等[70-74]应用改进MPS方法对晃荡问题进行了一系列的数值模拟,研究包括激励频率和充液率对晃荡幅度的影响、不同自由度和多自由度激励下的晃荡特征、二维三维矩形或菱形液舱的晃荡,以及水平或垂直隔板对砰击压力和自由面破碎的抑制作用等,该系列的模拟从数值角度深刻地揭示了不同情况下的晃荡特征和流场细节(图 7)。Chen等[75-77]在杨亚强等[70-74]的基础上,主要研究了不同类型隔板对晃荡的抑制作用,其中包括三维环形隔板、T型隔板、不同布置位置的水平和垂直隔板,研究表明隔板能有效地阻碍流场的运动,减小壁面砰击压力,抑制自由面大变形,并且不同隔板布置形式对晃荡的抑制作用也有区别。

|
Download:
|
| 图 7 摇动激励下液舱内流场分布图 Fig. 7 Snapshots of the tank sloshing under roll motion | |
目前MPS方法对晃荡的研究还集中在简化模型和晃荡机理的研究上,忽略了一些真实情况,如剧烈晃荡过程中会卷入空气的两相流问题,真实的液舱并不是简单的强迫正弦激励,而是真实船舶在波浪中的运动激励。对于这些方面,随着MPS计算精度的提高和更多数学模型的开发,也逐步开展了研究工作。Rueda等[78]应用MPS方法模拟了在波浪环境中液舱的运动情况,并从计算结果的运动响应中得到了液舱的幅值响应算子(RAO),与实验比对吻合。Lee等[79]用MPS方法模拟了在外流作用下带流体液舱的运动响应,并与无流体液舱的运动响应进行了对比,结果表明液舱内的流体能有效地减小液舱的运动幅度。Kim等[80]开发了多相流MPS方法,并将该方法应用到多层流体的晃荡问题中,在不同的激励频率和幅值下,对不同流体间的交界面变形演化进行了研究,并与实验结果吻合较好。
此外,针对实尺度的大规模晃荡问题,也有学者进行了初步探讨,但由于传统MPS方法泊松方程求解十分耗时,研究者参照SPH方法,开发了显式MPS方法。Hashimoto等[81]基于大阪海域地震引起的地面振动,采用显式MPS方法模拟了近海储油罐内的液舱晃荡情况。Kawamura等[82]采用同样的方法研究了在地震激励下的储油罐内液舱晃荡溢油情况。
2.2 波-物相互作用在船舶与海洋工程领域,波浪与结构物的相互作用是最普遍的自然现象,而此现象对于岸基结构物以及船舶、海洋平台等大型海上结构系统的安全性是一种巨大的挑战。因此,在最近的一个世纪里,学者提出各种科学方法对波物相互作用问题进行不断探索研究。但是由于在该相互作用问题中通常涉及波浪自由面的翻卷、破碎、飞溅、融合以及结构的复杂运动响应等非线性现象,此问题远未得到完善的解决。幸运的是,随着无网格粒子类方法的提出,人们对此类非线性现象的研究取得了大量成果。
对于波物相互作用问题的研究通常可分为数值波浪水池的构建、波浪与固定式结构物的相互作用、波浪与浮式结构物的相互作用三部分。对于数值波浪水池的构建,通常包括造波和消波功能。其中采用MPS方法为代表的粒子法进行造波的方式可参考物理造波机的工作原理,常采用的方式包括推板式、摇版式以及活塞式等。Khayyer等[83]采用了推板式造波数值模拟了波浪在斜坡上的翻卷破碎现象,一方面显示了MPS方法能够很真实地再现波面的非线性演化过程,另一方面验证了其提出的修正的MPS方法相对原始MPS方法在自由面判断方面的改进效果。由于采用MPS方法在波浪问题的数值模拟时计算量较大,为节省计算资源的消耗,Shibata等[84]采用摇板造波的方式实现了在小尺寸水槽内的造波。为避免水槽壁面处产生反射干扰波,通常的处理技术是在壁面处设置一定长度的消波区,而该作者独辟蹊径,提出了在壁面处设置透射边界的思想,即实现波浪在到达壁面处将能继续保持理论波形。Sueyoshi等[85]通过一种楔形活塞,实现了线性规则波的生成,值得注意的是,在其研究中提出了一种MPS与BEM相结合的方法。该方法结合了MPS方法能够模拟复杂波面的能力以及BEM方法能够在广域空间问题的模拟中具有较高效率的优势,为MPS方法对波浪的数值模拟研究提供了新的思路。
波浪与固定式结构物的相互作用问题在近岸工程中较为常见。由于近岸处通常布置有破波结构或波浪能发电设备,这些结构通常可视为多孔介质,采用传统网格类方法对此类问题难以获取直观精确的结果,于是有学者考虑采用MPS方法对波浪与岸基多孔介质的相互作用问题进行了研究[86]。Zhang等[87]研究了固定的FPSO模型在规则波、孤立波下的上浪问题,分析了流体的自由液面以及甲板的砰击压力。Rao等[88]研究了三维水平平板受到孤立波砰击的问题,分析发现波浪引起的竖直方向上的合力在孤立波波峰到达平板前缘瞬时达到最大值。
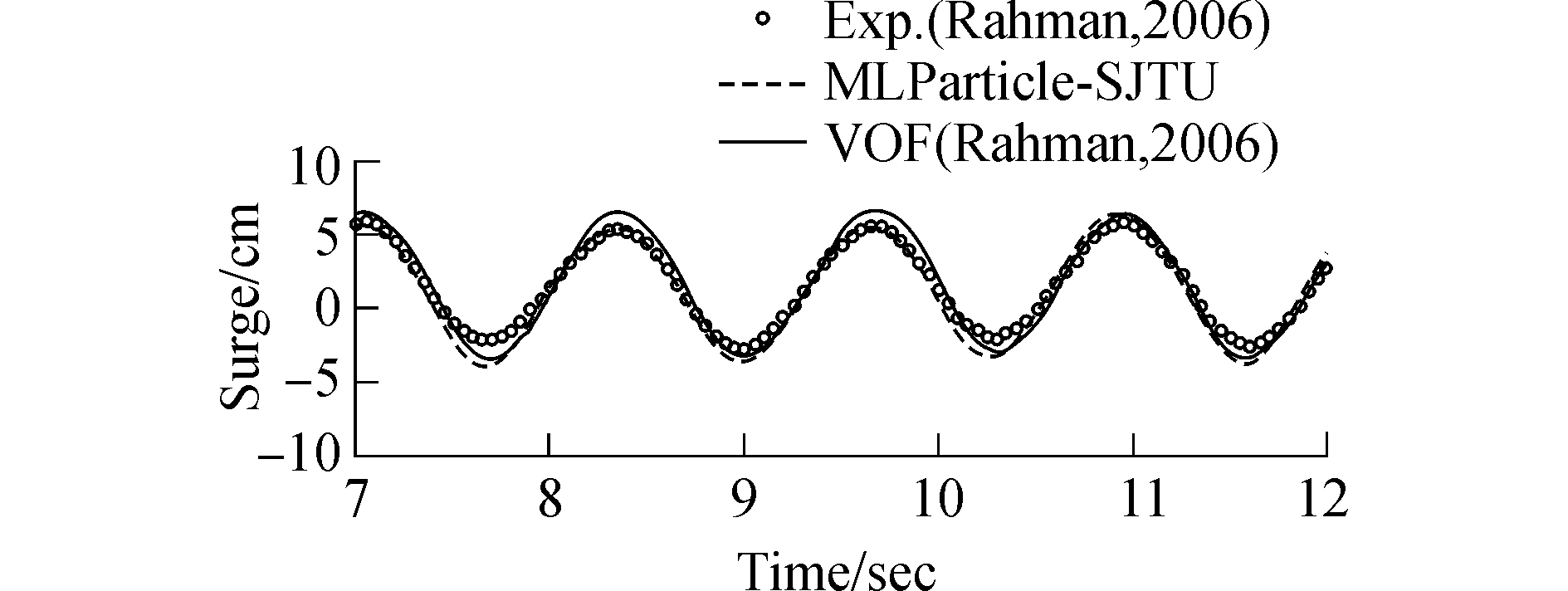
随着人类逐步实现对深远海资源的利用和开发,波浪与浮式结构物的相互作用问题将成为船舶与海洋工程面临的主要水动力学问题,MPS方法在该问题的研究中扮演越来越重要的作用。例如,Sueyoshi等[89]基于MPS方法研究了二维带甲板的浮体在规则波下的运动。Zhang等[90]基于MPS方法研究了二维箱式浮体在不同频率规则波下的横摇运动,并将获得的横摇幅值响应算子与试验进行比较,取得了较好的结果。张雨新[20]对二维规则波与防波堤的相互作用进行了研究,结构表明MPS方法不单能够获得较好的自由面变化,并与VOF以及试验结果吻合较好(图 8、9)。此后,张雨新将该求解器进行了并行扩展,研究了三维Wigley船的甲板上浪问题(图 10)。
|
Download:
|
| 图 9 防波堤纵荡运动历程 Fig. 9 Surge motion of the floating wave breaker | |

|
Download:
|
| 图 10 船在波浪中的运动瞬间[20] Fig. 10 Snapshot of the ship motion under regular wave | |
物体的入水砰击问题在船舶与海洋实际工程中普遍存在,例如当船舶航行于恶劣海况时,船体随波浪发生升沉及纵摇运动,进而将导致艏艉部与水面发生瞬时高速砰击现象。当船体长时间处于这种周期性的上下砰击环境中可能会造成结构的破损,故而针对入水砰击问题的研究对船舶与海洋结构物的设计制造有重要指导意义。
对于船体入水问题,人们往往将船体模型简化成楔形体结构,基于数值模拟的手段能方便地考察结构可能遭受的砰击压力特征。在过去的二十年中,虽然针对入水问题开展了广泛的数值研究,但MPS方法在该问题上的应用则起步稍晚。例如,Lee等[91]通过MPS方法研究了平板在一定横倾角姿态下的入水过程。Shibata等[92]对三维救生艇的入水过程进行了数值模拟,艇体的加速度运动结果与试验结果趋势一致(图 11)。但在该文的工作中,虽然采用了较多的粒子数量,仍难以实现对艇体结构进行精细的构建。Yokoyama等[93]数值模拟了球形体的入水问题,并探讨了球体表面滑移系数等对入水后飞溅现象的影响。Sun等[94]提出了一种MPS结合模态分析的方法研究了入水过程中楔形体二维剖面的振动响应。余谦等[95]基于大涡模拟的改进MPS,模拟了二维矩形体的入水砰击压力,与实验对比证明了该方法的正确性,然后模拟了不同斜升角的楔形体的匀速入水,并与实验结果进行了对比,验证了大涡模拟改进MPS法在砰击问题中的适用性。Khayyer等[96]采用可压缩多相流的MPS方法,将模拟的入水冲击压力与实验值和单相流数值进行了对比,计算结果比单相流模拟更加接近实验值。Zhang等[97]对不同入水角姿态下楔形体的入水过程进行了数值模拟,得到的楔形体入水运动状态与实验吻合良好,在倾斜姿态下楔形两侧弦边所受砰击压力幅值远大于正浮姿态(图 12)。Tang等[98]分别采用MPS方法和重叠网格法模拟了带倾角的三维圆柱入水,将圆柱的重心位置变化与SPH方法、重叠网格法和实验进行了对比,得到了较好的一致性(图 13)。

|
Download:
|
| 图 11 救生艇入水过程 Fig. 11 Water entry of the lifeboat | |

|
Download:
|
| 图 12 不同姿态角楔形体入水 Fig. 12 Water entry of wedge with various entry angles | |

|
Download:
|
| 图 13 三维带倾角圆柱体入水过程 Fig. 13 Water entry of inclined 3D cylinder | |
随着船舶与海洋工程向大型化、深远海方向的发展,越来越多的船海结构物将运营于复杂的海洋波浪环境中,为结构安全带来的挑战也越来越严峻。例如,船舶在大波浪中的艏部砰击、甲板上浪、液舱晃荡等问题都可能引起结构的变形、振动,甚至破坏。这些问题的共性特征是自由面的变化复杂剧烈,流体对壁面产生瞬时砰击力,结构的响应与流体的演化过程相互耦合。
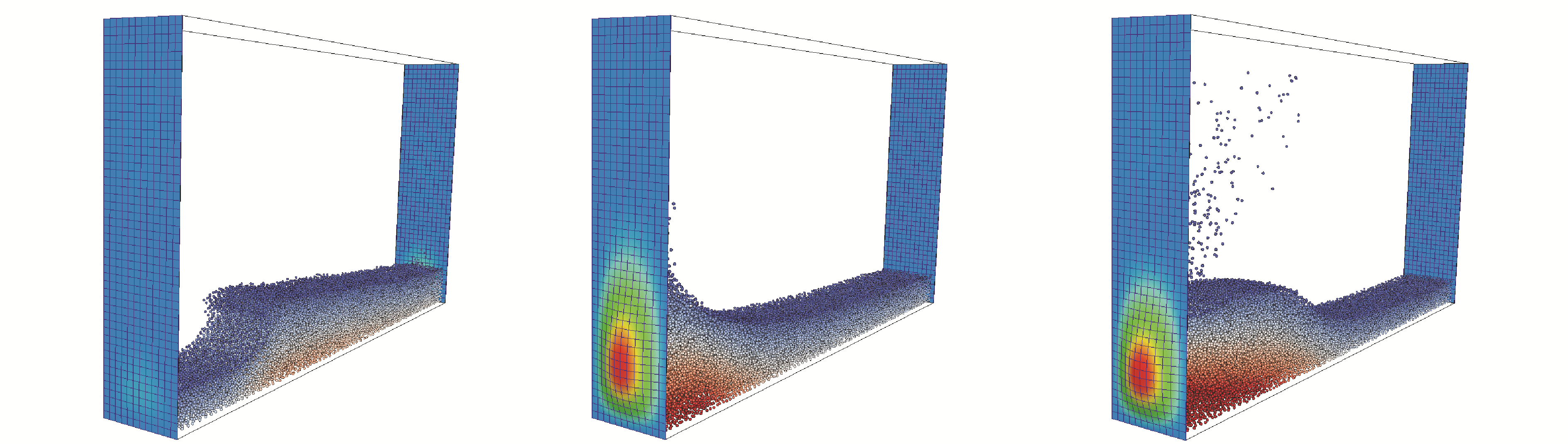
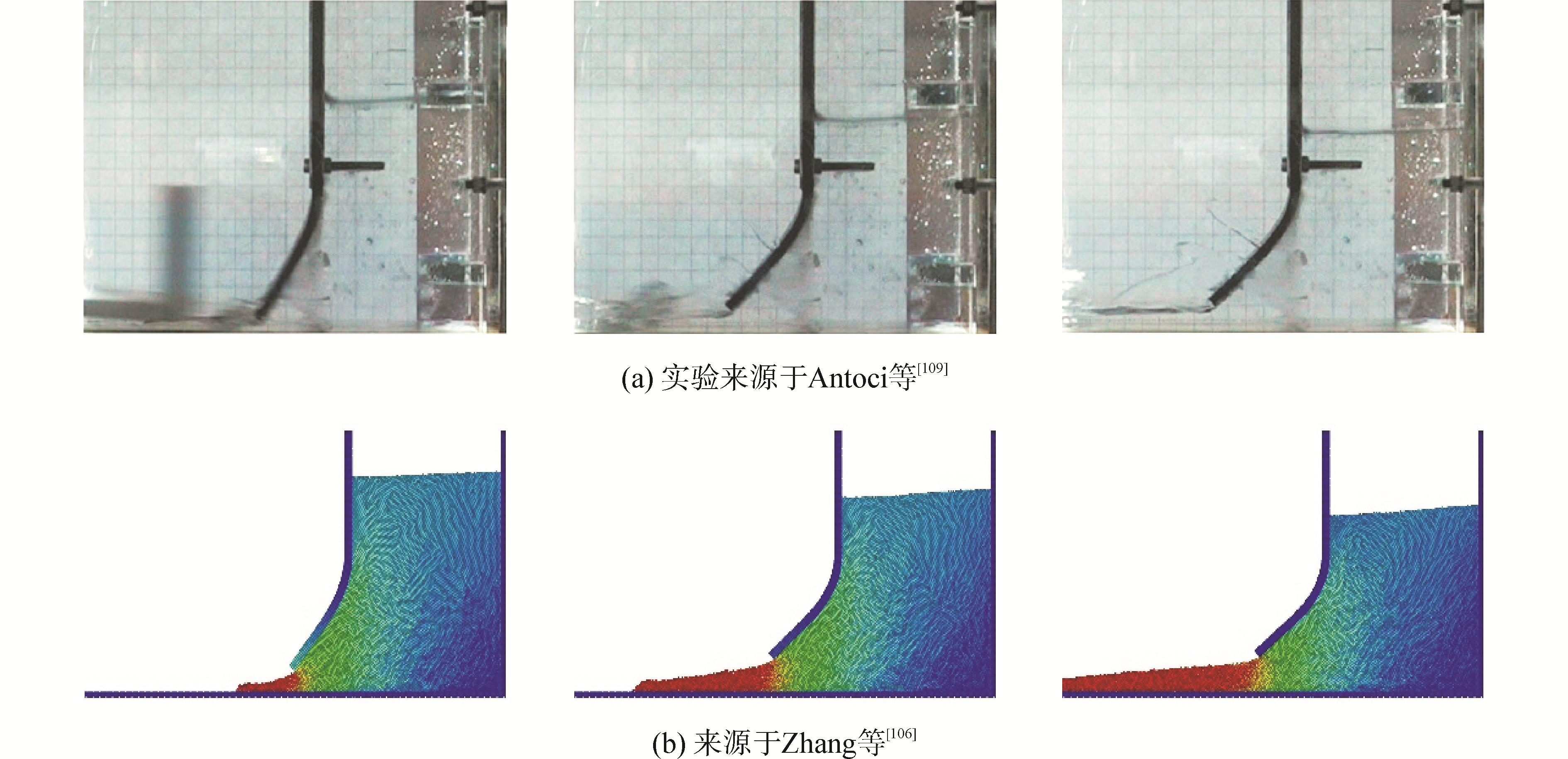
随着人们对船舶与海洋工程领域流固耦合问题的日益重视,研究人员对此开展了深入研究。例如,Liu等[99]将BEM与FEM结合,其中BEM被用来计算流体运动而FEM被用来计算结构变形,研究了二维弹性板在波浪载荷下的响应。Liao等[100]采用FDM-FEM耦合方法研究了弹性结构与自由面流体的耦合问题。上述是两个有代表性的基于网格方法的流固耦合研究,尽管网格类的方法计算效率高,但在流固耦合计算中为了协调流体、结构边界,通常需要对网格进行变形调整、网格重构等处理。近年来,一些新涌现的无网格粒子方法,如MPS、SPH等,能够很好地解决网格带来的问题,它们对大变形或者剧烈流动问题表现出了很好的适应性,被学者们用来研究流固耦合问题。Lee等[101]采用了MPS-FEM耦合方法,并将其运用于流体与弹性结构物的耦合问题。Hwang等[102]基于改进的MPS方法研究了液舱晃荡问题,其中流体、结构域均采用粒子表示,该方法不需要引入任何人工修正项(如人工粘性项、人工应力项和碰撞模型)来解决流体、结构计算中存在的张力不稳定问题(tensile instability)。Khayyer等[103]在此基础上进一步改进,在流体计算中采用了ECS和DS格式,并在结构计算中采用Wendland核函数计算流体力,对弹性结构物入水问题进行了研究。Zhang等[104]采用MPS-FEM耦合方法,研究了带弹性隔板、考虑侧壁弹性的液舱晃荡[105](图 14、15),溃坝流与弹性板相互作用问题[106](图 16)。Rao等[107-108]采用MPS-FEM耦合方法研究了孤立波对弹性板的砰击作用。

|
Download:
|
| 图 14 考虑侧壁弹性的二维液舱晃荡 Fig. 14 Sloshing flow in a 2D tank with flexible bulkheads | |
|
Download:
|
| 图 15 考虑侧壁弹性的三维液舱晃荡 Fig. 15 Sloshing flow in a 3D tank with flexible bulkheads | |
|
Download:
|
| 图 16 溃坝流与弹性板相互作用 Fig. 16 Interaction between dambreak flow and elastic plate | |
MPS方法提出至今有很大程度的改进,并逐步在船舶与海洋工程的实际问题上得到应用。在计算精度方面,研究人员从核函数模型、梯度模型、拉普拉斯算子及泊松方程的源项模型等方面提出了多种改进的数学格式。但相对于网格类方法,其压力的非物理震荡现象仍未完全消除。对于船舶与海洋工程问题,除了复杂的自由面演化现象之外,结构物的受力也是实际工程最为关心的物理量,而压力的震荡严重影响了数值仿真中结构物受力的计算精确度。故而,对压力场的非物理震荡问题仍是学者对MPS方法改进的最重要方向。
在计算效率方面,虽然近年研究人员提出了重叠粒子技术、多分辨率粒子技术等,但是目前粒子类方法仍主要采用在大部分流体空间内均匀布置粒子的方式对计算域进行离散。相对于网格类方法中采用的可变尺度空间网格离散方式以及自适应网格技术,粒子类方法在对计算空间的粒子离散方面仍有很大的改进空间。由于粒子在空间上无固定的拓扑关系,且具有运动随意性的特点,故而很难采用网格类方法相似的空间离散技术。近年来,研究人员通过MPS方法与势流或者网格类方法的结合,有效提高了对实际问题数值模拟时的计算效率。例如,Shibata等[52]提出了一种MPS与BEM相结合的方法模拟了波浪与浮式结构物的相互作用,相较全流场采用均匀粒子离散能够大量节省计算时间。Erkan等[110]在OpenFOAM平台的基础上实现了VOF方法与MPS方法的结合实现了三维雾滴的落水模拟,为MPS方法应用于船舶与海洋工程大范围长时间历程的实际问题提供了新的途径。此外,随着计算机硬件水平的快速发展,近年来采用GPU或众核架构的CPU进行数值仿真的加速计算为MPS方法计算效率的提高提供了新的技术途径。
在计算边界条件方面,由于船舶与海洋工程中通常同时存在复杂的波面变化和流动的现象,为使MPS方法适用于此类实际问题,需要对该方法进行更深入的改进,发展自由面边界、固壁边界、进出口边界、对称边界等多种条件的数学模型。
既往的研究成果表明,MPS方法作为一种拉格朗日无网格粒子法,在处理自由面大变形流动问题、多自由度物体大幅运动问题、流固耦合产生的结构物柔性变形等问题具有很好的灵活性。虽然目前该方法在三维实际工程问题中的应用仍较少,但是随着其计算精度和效率等问题逐步解决,可逐步将之扩展到船舶与海洋工程中更复杂的流动问题,如实际船型在恶劣海况下的操纵性、耐波性问题,带锚链的海洋平台运动响应等问题。由于这些流动问题通常比较剧烈,甚至会带有砰击等现象,更能发挥MPS方法的优势。
4 结论本文对MPS方法的最新进展及其在船舶与海洋工程问题中的应用进行了回顾。从计算精度的角度,介绍了研究人员对多种粒子间相互作用模型的改进成果;分析了为扩展MPS方法的应用范围,近年来研究人员开发的适用于粒子类方法的边界条件以及多相流模型;从提高MPS方法计算效率的角度,介绍了主要的加速算法以及提高硬件资源利用率的技术途径;回顾了MPS方法在液舱晃荡、波浪与结构物相互作用、入水砰击、流固耦合等典型的船舶与海洋工程问题中的应用成果。最后,对MPS方法的发展方向及其应用前景进行了展望。
| [1] |
KOSHIZUKA S, OKA Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid[J]. Nuclear science and engineering, 1996, 123(3): 421-434. DOI:10.13182/NSE96-A24205 (  0) 0)
|
| [2] |
ZHANG Yuxin, WAN Decheng, HINO T. Comparative study of MPS method and level-set method for sloshing flows[J]. Journal of hydrodynamics, Ser. B, 2014, 26(4): 577-585. DOI:10.1016/S1001-6058(14)60065-2 (  0) 0)
|
| [3] |
ATAIE-ASHTIANI B, FARHADI L. A stable moving-particle semi-implicit method for free surface flows[J]. Fluid dynamics research, 2006, 38(4): 241-256. DOI:10.1016/j.fluiddyn.2005.12.002 (  0) 0)
|
| [4] |
BELYTSCHKO T, KRONGAUZ Y, ORGAN D, et al. Meshless methods:an overview and recent developments[J]. Computer methods in applied mechanics and engineering, 1996, 139(1/2/3/4): 3-47. (  0) 0)
|
| [5] |
SHAO Songdong, LO E Y M. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface[J]. Advances in water resources, 2003, 26(7): 787-800. DOI:10.1016/S0309-1708(03)00030-7 (  0) 0)
|
| [6] |
KOSHIZUKA S, NOBE A, OKA Y. Numerical analysis of breaking waves using the moving particle semi-implicit method[J]. International journal for numerical methods in fluids, 1998, 26(7): 751-769. DOI:10.1002/(ISSN)1097-0363 (  0) 0)
|
| [7] |
KHAYYER A, GOTOH H. Development of CMPS method for accurate water-surface tracking in breaking waves[J]. Coastal engineering journal, 2008, 50(2): 179-207. DOI:10.1142/S0578563408001788 (  0) 0)
|
| [8] |
TANAKA M, MASUNAGA T. Stabilization and smoothing of pressure in MPS method by quasi-compressibility[J]. Journal of computational physics, 2010, 229(11): 4279-4290. DOI:10.1016/j.jcp.2010.02.011 (  0) 0)
|
| [9] |
TSURUTA N, KHAYYER A, GOTOH H. A short note on dynamic stabilization of moving particle semi-implicit method[J]. Computers & fluids, 2013, 82: 158-164. (  0) 0)
|
| [10] |
ZHANG Shuai, MORITA K, FUKUDA K, et al. An improved MPS method for numerical simulations of convective heat transfer problems[J]. International journal for numerical methods in fluids, 2006, 51(1): 31-47. DOI:10.1002/(ISSN)1097-0363 (  0) 0)
|
| [11] |
KHAYYER A, GOTOH H. A higher order Laplacian model for enhancement and stabilization of pressure calculation by the MPS method[J]. Applied ocean research, 2010, 32(1): 124-131. DOI:10.1016/j.apor.2010.01.001 (  0) 0)
|
| [12] |
KHAYYER A, GOTOH H. A 3D higher order Laplacian model for enhancement and stabilization of pressure calculation in 3D MPS-based simulations[J]. Applied ocean research, 2012, 37: 120-126. DOI:10.1016/j.apor.2012.05.003 (  0) 0)
|
| [13] |
IKARI H, KHAYYER A, GOTOH H. Corrected higher order Laplacian for enhancement of pressure calculation by projection-based particle methods with applications in ocean engineering[J]. Journal of ocean engineering and marine energy, 2015, 1(4): 361-376. DOI:10.1007/s40722-015-0026-2 (  0) 0)
|
| [14] |
KHAYYER A, GOTOH H. Modified moving particle semi-implicit methods for the prediction of 2D wave impact pressure[J]. Coastal engineering, 2009, 56(4): 419-440. DOI:10.1016/j.coastaleng.2008.10.004 (  0) 0)
|
| [15] |
LEE B H, PARK J C, KIM M H, et al. Step-by-step improvement of MPS method in simulating violent free-surface motions and impact-loads[J]. Computer methods in applied mechanics and engineering, 2011, 200(9/10/11/12): 1113-1125. (  0) 0)
|
| [16] |
KONDO M, KOSHIZUKA S. Improvement of stability in moving particle semi-implicit method[J]. International journal for numerical methods in fluids, 2011, 65(6): 638-654. DOI:10.1002/fld.v65.6 (  0) 0)
|
| [17] |
GOTOH H, KHAYYER A, IKARI H, et al. Refined reproduction of a plunging breaking wave and resultant splash-up by 3D-CMPS method[C]//Proceedings of the Nineteenth International Offshore and Polar Engineering Conference. Osaka, Japan, 2009: 518-524.
(  0) 0)
|
| [18] |
IRIBE T, FUJISAWA T, KOSHIZUKA S. Reduction of communication in parallel computing of particle method for flow simulation of seaside areas[J]. Coastal engineering journal, 2010, 52(4): 287-304. DOI:10.1142/S0578563410002221 (  0) 0)
|
| [19] |
IKARI H, GOTOH H. Parallelization of MPS method for 3D wave analysis[C]//Proceedings of the 8th International Conference on Hydro-science and Engineering (ICHE). Nagoya, Japan, 2008.
(  0) 0)
|
| [20] |
张雨新. 改进的MPS方法及其三维并行计算研究[D]. 上海: 上海交通大学, 2014. ZHANG Yuxin. Improved MPS method and its 3D parallel computation[D]. Shanghai: Shanghai Jiao Tong University, 2014. (  0) 0)
|
| [21] |
HORI C, GOTOH H, IKARI H, et al. GPU-acceleration for moving particle semi-implicit method[J]. Computers & fluids, 2011, 51(1): 174-183. (  0) 0)
|
| [22] |
朱小松. 粒子法的并行加速及在液体晃荡研究中的应用[D]. 大连: 大连理工大学, 2011. ZHU Xiaosong. Parallel acceleration of particle method and its application on the study of liquid sloshing[D]. Dalian: Dalian University of Technology, 2011. (  0) 0)
|
| [23] |
李海州. 三维MPS法的GPU并行加速研究[D]. 上海: 上海交通大学, 2016. LI Haizhou. A study of parallel acceleration of GPU in 3-D MPS method[D]. Shanghai: Shanghai Jiao Tong University, 2016. (  0) 0)
|
| [24] |
OVAYSI S, PIRI M. Multi-GPU acceleration of direct pore-scale modeling of fluid flow in natural porous media[J]. Computer physics communications, 2012, 183(9): 1890-1898. DOI:10.1016/j.cpc.2012.04.007 (  0) 0)
|
| [25] |
TANAKA M, CARDOSO R, BAHAI H. Multi-resolution MPS method[J]. Journal of computational physics, 2018, 359: 106-136. DOI:10.1016/j.jcp.2017.12.042 (  0) 0)
|
| [26] |
TANG Zhenyuan, ZHANG Youlin, WAN Decheng. Multi-resolution MPS method for free surface flows[J]. International journal of computational methods, 2016, 13(4): 1641018. DOI:10.1142/S0219876216410188 (  0) 0)
|
| [27] |
TANG Zhenyuan, WAN Decheng, CHEN Gang, et al. Numerical simulation of 3D violent free-surface flows by multi-resolution MPS method[J]. Journal of ocean engineering and marine energy, 2016, 2(3): 355-364. DOI:10.1007/s40722-016-0062-6 (  0) 0)
|
| [28] |
YOON H Y, KOSHIZUKA S, OKA Y. Mesh-free numerical method for direct simulation of gas-liquid phase interface[J]. Nuclear science and engineering, 1999, 133(2): 192-200. DOI:10.13182/NSE99-A2081 (  0) 0)
|
| [29] |
YOON H Y, KOSHIZUKA S, OKA Y. A particle-gridless hybrid method for incompressible flows[J]. International journal for numerical methods in fluids, 1999, 30(4): 407-424. DOI:10.1002/(ISSN)1097-0363 (  0) 0)
|
| [30] |
YOON H Y, KOSHIZUKA S, OKA Y. Direct calculation of bubble growth, departure, and rise in nucleate pool boiling[J]. International journal of multiphase flow, 2001, 27(2): 277-298. DOI:10.1016/S0301-9322(00)00023-9 (  0) 0)
|
| [31] |
HEO S, KOSHIZUKA S, OKA Y. Numerical analysis of boiling on high heat-flux and high subcooling condition using MPS-MAFL[J]. International journal of heat and mass transfer, 2002, 45(13): 2633-2642. DOI:10.1016/S0017-9310(02)00011-X (  0) 0)
|
| [32] |
TIAN Wenxi, ISHIWATARI Y, IKEJIRI S, et al. Numerical simulation on void bubble dynamics using moving particle semi-implicit method[J]. Nuclear engineering and design, 2009, 239(11): 2382-2390. DOI:10.1016/j.nucengdes.2009.06.018 (  0) 0)
|
| [33] |
CHEN Ronghua, TIAN Wenxi, SU Guanghui, et al. Numerical investigation on bubble dynamics during flow boiling using moving particle semi-implicit method[J]. Nuclear engineering and design, 2010, 240(11): 3830-3840. DOI:10.1016/j.nucengdes.2010.08.008 (  0) 0)
|
| [34] |
陈荣华, 田文喜, 苏光辉, 等. 流动泡核沸腾中汽泡行为的MPS数值模拟[J]. 原子能科学技术, 2011, 45(9): 1051-1055. CHEN Ronghua, TIAN Wenxi, SU Guanghui, et al. Numerical simulation on bubble growth and departure by MPS[J]. Atomic energy science and technology, 2011, 45(9): 1051-1055. (  0) 0)
|
| [35] |
陈荣华, 田文喜, 左娟莉, 等. 基于MPS方法的汽泡冷凝与融合特性研究[J]. 工程热物理学报, 2011, 32(11): 1876-1880. CHEN Ronghua, TIAN Wenxi, ZUO Juanli, et al. Numerical investigation on bubble condensation and coalescence of bubble pairs using moving particle semi-implicit method[J]. Journal of engineering thermophysics, 2011, 32(11): 1876-1880. (  0) 0)
|
| [36] |
陈荣华, 田文喜, 左娟莉, 等. 基于MPS方法的液态铅铋合金内气泡上升流数值模拟[J]. 核动力工程, 2011, 32(5): 96-99. CHEN Ronghua, TIAN Wenxi, ZUO Juanli, et al. Numerical analysis of bubble rising behavior in a liquid metal using MPS[J]. Nuclear power engineering, 2011, 32(5): 96-99. (  0) 0)
|
| [37] |
左娟莉, 田文喜, 秋穗正, 等. 液态金属内单个气泡上升行为的MPS法数值模拟[J]. 原子能科学技术, 2011, 45(12): 1449-1455. ZUO Juanli, TIAN Wenxi, QIU Suizheng, et al. Numerical simulation on single bubble rising behavior in liquid metal using moving particle semi-implicit method[J]. Atomic energy science and technology, 2011, 45(12): 1449-1455. (  0) 0)
|
| [38] |
SHIBATA K, KOSHIZUKA S, SAKAI M, et al. Lagrangian simulations of ship-wave interactions in rough seas[J]. Ocean engineering, 2012, 42: 13-25. DOI:10.1016/j.oceaneng.2012.01.016 (  0) 0)
|
| [39] |
SHIBATA K, KOSHIZUKA S, TAMAI T. Overlapping particle technique and application to green water on deck[C]//Proceedings of the 2nd International Conference on Violent Flows. Nantes, France, 2012: 106-111.
(  0) 0)
|
| [40] |
TANG Zhenyuan, ZHANG Yuxing, LI Haizhou, et al. Overlapping MPS method for 2D free surface flows[C]//Proceedings of the Twenty-Fourth International Ocean and Polar Engineering Conference. Busan, Korea, 2014: 411-419.
(  0) 0)
|
| [41] |
TANG Zhenyuan, ZHANG Youlin, WAN Decheng. Numerical simulation of 3-D free surface flows by overlapping MPS[J]. Journal of hydrodynamics, Ser. B, 2016, 28(2): 306-312. DOI:10.1016/S1001-6058(16)60632-7 (  0) 0)
|
| [42] |
MA Q W, ZHOU J T. MLPG_R method for numerical simulation of 2D breaking waves[J]. Computer modeling in engineering & sciences, 2009, 43(3): 277-303. (  0) 0)
|
| [43] |
PARK J I, PARK J C, HWANG S C, et al. Two-dimensional particle simulation for behaviors of floating body near quaywall during tsunami[J]. Journal of ocean engineering and technology, 2014, 28(1): 12-19. DOI:10.5574/KSOE.2014.28.1.012 (  0) 0)
|
| [44] |
ZHANG Y X, WAN D C. Apply MPS method to simulate liquid sloshing in LNG tank[J]. Phytotherapy research, 2012, 29(12): 843-1857. (  0) 0)
|
| [45] |
MONAGHAN J J, KAJTAR J B. SPH particle boundary forces for arbitrary boundaries[J]. Computer physics communications, 2009, 180(10): 1811-1820. DOI:10.1016/j.cpc.2009.05.008 (  0) 0)
|
| [46] |
KULASEGARAM S, BONET J, LEWIS R W, et al. A variational formulation based contact algorithm for rigid boundaries in two-dimensional SPH applications[J]. Computational mechanics, 2004, 33(4): 316-325. DOI:10.1007/s00466-003-0534-0 (  0) 0)
|
| [47] |
FERRAND M, LAURENCE D R, ROGERS B D, et al. Unified semi-analytical wall boundary conditions for inviscid, laminar or turbulent flows in the meshless SPH method[J]. International journal for numerical methods in fluids, 2013, 71(4): 446-472. DOI:10.1002/fld.v71.4 (  0) 0)
|
| [48] |
LEROY A, VIOLEAU D, FERRAND M, et al. Unified semi-analytical wall boundary conditions applied to 2-D incompressible SPH[J]. Journal of computational physics, 2014, 261: 106-129. DOI:10.1016/j.jcp.2013.12.035 (  0) 0)
|
| [49] |
LASTIWKA M, BASA M, QUINLAN N J. Permeable and non-reflecting boundary conditions in SPH[J]. International journal for numerical methods in fluids, 2010, 61(7): 709-724. (  0) 0)
|
| [50] |
HOSSEINI S M, FENG J J. Pressure boundary conditions for computing incompressible flows with SPH[J]. Journal of computational physics, 2011, 230(19): 7473-7487. DOI:10.1016/j.jcp.2011.06.013 (  0) 0)
|
| [51] |
LEROY A, VIOLEAU D, FERRAND M, et al. A new open boundary formulation for incompressible SPH[J]. Computers & mathematics with applications, 2016, 72(9): 2417-2432. (  0) 0)
|
| [52] |
SHIBATA K, KOSHIZUKA S, SAKAI M, et al. Transparent boundary condition for simulating nonlinear water waves by a particle method[J]. Ocean engineering, 2011, 38(16): 1839-1848. DOI:10.1016/j.oceaneng.2011.09.012 (  0) 0)
|
| [53] |
GOTOH H, FREDSØE J. Lagrangian two-phase flow model of the settling behavior of fine sediment dumped into water[C]//Proceedings of the 27th International Conference on Coastal Engineering. Sydney, Australia, 2000: 3906-3919.
(  0) 0)
|
| [54] |
LIU J, KOSHIZUKA S, OKA Y. A hybrid particle-mesh method for viscous, incompressible, multiphase flows[J]. Journal of computational physics, 2005, 202(1): 65-93. DOI:10.1016/j.jcp.2004.07.002 (  0) 0)
|
| [55] |
SHAKIBAEINIA A, JIN Y C. A mesh-free particle model for simulation of mobile-bed dam break[J]. Advances in water resources, 2011, 34(6): 794-807. DOI:10.1016/j.advwatres.2011.04.011 (  0) 0)
|
| [56] |
SHAKIBAEINIA A, JIN Y C. MPS mesh-free particle method for multiphase flows[J]. Computer methods in applied mechanics and engineering, 2012, 229-232: 13-26. DOI:10.1016/j.cma.2012.03.013 (  0) 0)
|
| [57] |
KHAYYER A, GOTOH H. Enhancement of performance and stability of MPS mesh-free particle method for multiphase flows characterized by high density ratios[J]. Journal of computational physics, 2013, 242: 211-233. DOI:10.1016/j.jcp.2013.02.002 (  0) 0)
|
| [58] |
潘徐杰, 张怀新. 用移动粒子半隐式法模拟液舱横摇晃荡现象[J]. 上海交通大学学报, 2008, 42(11): 1904-1907. PAN Xujie, ZHANG Huaixin. Moving-particle semi-implicit method for simulation of liquid sloshing on roll motion[J]. Journal of Shanghai Jiao Tong University, 2008, 42(11): 1904-1907. DOI:10.3321/j.issn:1006-2467.2008.11.034 (  0) 0)
|
| [59] |
潘徐杰, 张怀新. 移动粒子半隐式法晃荡模拟中的压力震荡现象研究[J]. 水动力学研究与进展, 2008, 23(4): 453-463. PAN Xujie, ZHANG Huaixin. A study on the oscillations appearing in pressure calculation for sloshing simulation by using moving-particle semi-implicit method[J]. Chinese journal of hydrodynamics, 2008, 23(4): 453-463. (  0) 0)
|
| [60] |
HWAN S C, LEE B H, PARK J C. Numerical simulation of violent sloshing motion in rectangular tank using improved MPS method[C]//Proceedings of the Ninth ISOPE Pacific/Asia Offshore Mechanics Symposium. Busan, Korea, 2010: 10-14.
(  0) 0)
|
| [61] |
张雨新, 万德成. 用MPS方法数值模拟低充水液舱的晃荡[J]. 水动力学研究与进展, 2012, 27(1): 100-107. ZHANG Yuxin, WAN Decheng. Numerical simulation of liquid sloshing in low-filling tank by MPS[J]. Chinese journal of hydrodynamics, 2012, 27(1): 100-107. (  0) 0)
|
| [62] |
张雨新, 万德成, 日野孝则. 基于MPS方法数值模拟三维液舱晃荡[C]//第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会并周培源诞辰110周年纪念大会文集. 无锡, 中国, 2012: 310-318. ZHANG Yuxin, WAN Decheng, HINO Takanori. 3D simulation of liquid sloshing based on MPS method[C]//Proceedings of the 11th National Congress on Hydrodynamics & 24th National Conference on Hydrodynamics and Commemoration of the 110th Anniversary of Zhou Pei-yuan's Birth. Wuxi, China, 2012: 310-318. (  0) 0)
|
| [63] |
张雨新, 万德成. MPS方法在二维液舱晃荡中的应用[J]. 复旦学报(自然科学版), 2013, 52(5): 618-626, 634. ZHANG Yuxin, WAN Decheng. Application of MPS method for 2D liquid sloshing[J]. Journal of Fudan university (nature science), 2013, 52(5): 618-626, 634. (  0) 0)
|
| [64] |
张雨新, 万德成, 日野孝则. MPS方法数值模拟液舱晃荡问题[J]. 海洋工程, 2014, 32(4): 24-32. ZHANG Yuxin, WAN Decheng, HINO Takanori. Application of MPS method in liquid sloshing[J]. The ocean engineering, 2014, 32(4): 24-32. (  0) 0)
|
| [65] |
ZHANG Yuxin, YANG Yaqiang, TANG Zhenyuan, et al. Parallel MPS method for three-dimensional liquid sloshing[C]//Proceedings of the Twenty-fourth International Ocean and Polar Engineering Conference. Busan, Korea, 2014: 257-264.
(  0) 0)
|
| [66] |
TSUKAMOTO M M, CHENG L Y, NISHIMOTO K. Analytical and numerical study of the effects of an elastically-linked body on sloshing[J]. Computers & fluids, 2011, 49(1): 1-21. (  0) 0)
|
| [67] |
YANG Yaqiang, TANG Zhenyuan, WAN Decheng. Numerical simulations of 3D liquid sloshing flows by MPS method[C]//Proceedings of the Eleventh ISOPE Pacific/Asia Offshore Mechanics Symposium. Shanghai, China, 2014: 192-197.
(  0) 0)
|
| [68] |
YANG Yaqiang, TANG Zhenyuan, ZHANG Youlin, et al. Investigation of excitation period effects on 2D liquid sloshing by MPS method[C]//Proceedings of the Twenty-Fifth International Ocean and Polar Engineering Conference. Kona, Hawaii, USA, 2015: 891-897.
(  0) 0)
|
| [69] |
YANG Yaqiang, TANG Zhenyuan, WAN Decheng. Numerical simulation of 3D sloshing flows in a rectangular tank by MPS method[C]//Proceedings of the 9th International Workshop on Ship and Marine Hydrodynamics. Glasgow, UK, 2015.
(  0) 0)
|
| [70] |
杨亚强, 唐振远, 万德成. 基于MPS方法模拟带水平隔板的液舱晃荡[J]. 水动力学研究与进展A辑, 2015, 30(2): 146-153. YANG Yaqiang, TANG Zhenyuan, WAN Decheng. Numerical study on liquid sloshing in horizontal baffled tank by MPS method[J]. Chinese journal of hydrodynamics, 2015, 30(2): 146-153. (  0) 0)
|
| [71] |
杨亚强, 唐振远, 万德成. 基于MPS方法模拟薄膜型液舱晃荡问题[C]//第二十七届全国水动力学研讨会文集. 南京, 中国, 2015: 318-324. YANG Yaqiang, TANG Zhenyuan, WAN Decheng. Numerical study on liquid sloshing in membrane tank by MPS method[C]//Proceedings of the 27th National Conference on Hydrodynamics. Nanjing, China, 2015: 318-324. (  0) 0)
|
| [72] |
肖武, 杨亚强, 万德成. 基于MPS方法数值模拟三维LNG液舱的晃荡问题[J]. 水动力学研究与进展A辑, 2016, 31(6): 697-705. XIAO Wu, YANG Yaqiang, WAN Decheng. Numerical study on liquid sloshing in 3D LNG tank by MPS method[J]. Chinese journal of hydrodynamics, 2016, 31(6): 697-705. (  0) 0)
|
| [73] |
BULIAN G, SOUTO-IGLESIAS A, DELORME L, et al. Smoothed particle hydrodynamics (SPH) simulation of a tuned liquid damper[J]. Journal of hydraulic research, 2010, 48(S1): 28-39. (  0) 0)
|
| [74] |
杨亚强. 基于MPS方法的液舱晃荡数值模拟与分析[D]. 上海: 上海交通大学, 2016. YANG Yaqiang. Numerical investigation of liquid sloshing by MPS method[D]. Shanghai: Shanghai Jiao Tong University, 2016. (  0) 0)
|
| [75] |
CHEN Xiang, TANG Zhenyuan, WAN Decheng. The effects of T type baffle on liquid sloshing by MPS method[C]//Proceedings of 3rd International Conference on Violent Flows (VF-2016). Osaka, Japan, 2016: 25.
(  0) 0)
|
| [76] |
CHEN Xiang, WAN Decheng, HUANG Wenhua. Numerical simulation of effects of two different baffles on liquid sloshing by MPS method[C]//Proceedings of the Twenty-sixth International Ocean and Polar Engineering Conference. Rhodes, Greece, 2016: 931-938.
(  0) 0)
|
| [77] |
CHEN X, ZHANG Y L, WAN D C. Effects of the location of horizontal baffle on liquid sloshing by MPS method[C]//Proceedings of the Second Conference of Global Chinese Scholars on Hydrodynamics. Wuxi, China, 2016: 448-454.
(  0) 0)
|
| [78] |
RUEDA G E, TSUKAMOTO M M, MEDEIROS H F, et al. Validation study of MPS (Moving Particle Semi-Implicit Method) for sloshing and damage stability analysis[C]//Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering. Estoril, Portugal, 2008: 483-489.
(  0) 0)
|
| [79] |
LEE B H, PARK J C, KIM M H. Two-dimensional vessel-motion/liquid-sloshing interactions and impact loads by using a particle method[C]//Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, China, 2010: 679-686.
(  0) 0)
|
| [80] |
KIM K S, KIM M H, PARK J C. Development of Moving Particle Simulation method for multiliquid-layer sloshing[J]. Mathematical problems in engineering, 2014, 2014: 350165. (  0) 0)
|
| [81] |
HASHIMOTO H, HATA Y, KAWAMURA K. Estimation of oil overflow due to sloshing from oil storage tanks subjected to a possible Nankai trough earthquake in Osaka bay area[J]. Journal of loss prevention in the process industries, 2017, 50: 337-346. DOI:10.1016/j.jlp.2016.10.008 (  0) 0)
|
| [82] |
KAWAMURA K, HASHIMOTO H, ONODERA N, et al. GPGPU simulation of oil tank sloshing based on explicit MPS method[C]//Proceedings of 3rd International Conference on Violent Flows (VF-2016). Osaka, Japan, 2016.
(  0) 0)
|
| [83] |
KHAYYER A, GOTOH H, SHAO Songdong. Enhanced predictions of wave impact pressure by improved incompressible SPH methods[J]. Applied ocean research, 2009, 31(2): 111-131. DOI:10.1016/j.apor.2009.06.003 (  0) 0)
|
| [84] |
SHIBATA K, MASAIE I, KONDO M, et al. Improved pressure calculation for the moving particle semi-implicit method[J]. Computational particle mechanics, 2015, 2(1): 91-108. DOI:10.1007/s40571-015-0039-6 (  0) 0)
|
| [85] |
SUEYOSHI M, KIHARA H, KASHIWAGI M. A hybrid technique using particle and boundary-element methods for wave-body interaction problems[C]//Proceedings of the 9th International Conference on Numerical Ship Hydrodynamics. Michigan, USA, 2007: 241-252.
(  0) 0)
|
| [86] |
AKBARI H. Modified moving particle method for modeling wave interaction with multi layered porous structures[J]. Coastal engineering, 2014, 89: 1-19. DOI:10.1016/j.coastaleng.2014.03.004 (  0) 0)
|
| [87] |
ZHANG Yuxin, WANG Xuyang, TANG Zhenyuan, et al. Numerical simulation of green water incidents based on parallel MPS method[C]//Proceedings of the Twenty-third International Offshore and Polar Engineering Conference. Anchorage, Alaska, 2013: 931-938.
(  0) 0)
|
| [88] |
RAO Chengping, ZHANG Youlin, WAN Decheng. FSI analysis of solitary wave interacting with horizontal flexible plate by MPS-FEM method[C]//Proceedings of the Twenty-Seventh International Ocean and Polar Engineering Conference. San Francisco, California, USA, 2017.
(  0) 0)
|
| [89] |
SUEYOSHI M, KASHIWAGI M, NAITO S. Numerical simulation of wave-induced nonlinear motions of a two-dimensional floating body by the moving particle semi-implicit method[J]. Journal of marine science and technology, 2008, 13(2): 85-94. DOI:10.1007/s00773-007-0260-y (  0) 0)
|
| [90] |
ZHANG Youlin, WAN Decheng. Numerical study of interactions between waves and free rolling body by IMPS method[J]. Computers & fluids, 2017, 155: 124-133. (  0) 0)
|
| [91] |
LEE B H, PARK J C, KIM M H, et al. Numerical simulation of impact loads using a particle method[J]. Ocean engineering, 2010, 37(2/3): 164-173. (  0) 0)
|
| [92] |
SHIBATA K, KOSHIZUKA S, SAKAI M, et al. Numerical analysis of acceleration of a free-fall lifeboat using the MPS method[J]. International journal of offshore and polar engineering, 2010, 23(4): 279-285. (  0) 0)
|
| [93] |
YOKOYAMA M, KUBOTA Y, KIKUCHI K, et al. Some remarks on surface conditions of solid body plunging into water with particle method[J]. Advanced modeling and simulation in engineering sciences, 2014, 1: 9. DOI:10.1186/2213-7467-1-9 (  0) 0)
|
| [94] |
SUN Zhe, XING J T, DJIDJELI K, et al. Coupling MPS and modal superposition method for flexible wedge dropping simulation[C]//Proceedings of the 25th International Ocean and Polar Engineering Conference. Hawaii, USA, 2015: 144-151.
(  0) 0)
|
| [95] |
余谦, 张怀新. 改进的移动粒子半隐式法模拟楔形体入水砰击[J]. 海洋工程, 2013, 31(6): 9-15, 90. YU Qian, ZHANG Huaixin. Research on water entry of wedge based on the improved MPS method with large eddy simulation[J]. The ocean engineering, 2013, 31(6): 9-15, 90. (  0) 0)
|
| [96] |
KHAYYER A, GOTOH H. A multi-phase compressible-incompressible particle method for water slamming[C]//Proceedings of the Twenty-Fifth International Ocean and Polar Engineering Conference. Hawaii, USA, 2015.
(  0) 0)
|
| [97] |
ZHANG Youlin, TANG Zhenyuan, WAN Decheng. Simulation of water entry of a free-falling wedge by improved MPS method[C]//Proceedings of the Twenty-sixth International Ocean and Polar Engineering Conference. Rhodes, Greece, 2016: 220-227.
(  0) 0)
|
| [98] |
TANG Zhenyuan, WANG Jianhua, ZHANG Youlin, et al. Numerical investigation of 3D water entry based on IMPS method and overset method[C]//Proceedings of 3rd International Conference on Violent Flows. Osaka, Japan, 2016.
(  0) 0)
|
| [99] |
LIU Xiaodong, SAKAI S. Time domain analysis on the dynamic response of a flexible floating structure to waves[J]. Journal of engineering mechanics, 2002, 128(1): 48-56. DOI:10.1061/(ASCE)0733-9399(2002)128:1(48) (  0) 0)
|
| [100] |
LIAO Kangping, HU Changhong. A coupled FDM-FEM method for free surface flow interaction with thin elastic plate[J]. Journal of marine science and technology, 2013, 18(1): 1-11. DOI:10.1007/s00773-012-0191-0 (  0) 0)
|
| [101] |
LEE C J K, NOGUCHI H, KOSHIZUKA S. Fluid-shell structure interaction analysis by coupled particle and finite element method[J]. Computers & structures, 2007, 85(11/12/13/14): 688-697. (  0) 0)
|
| [102] |
HWANG S C, PARK J C, GOTOH H, et al. Numerical simulations of sloshing flows with elastic baffles by using a particle-based fluid-structure interaction analysis method[J]. Ocean engineering, 2016, 118: 227-241. DOI:10.1016/j.oceaneng.2016.04.006 (  0) 0)
|
| [103] |
KHAYYER A, GOTOH H, FALAHATY H, et al. Towards development of enhanced fully-Lagrangian mesh-free computational methods for fluid-structure interaction[J]. Journal of hydrodynamics, 2018, 30(1): 49-61. DOI:10.1007/s42241-018-0005-x (  0) 0)
|
| [104] |
ZHANG Youlin, WAN Decheng. MPS-FEM coupled method for sloshing flows in an elastic tank[J]. Ocean engineering, 2018, 152: 416-427. DOI:10.1016/j.oceaneng.2017.12.008 (  0) 0)
|
| [105] |
ZHANG Youlin, CHEN Xiang, WAN Decheng, et al. Sloshing flows in an elastic tank with high filling liquid by MPS-FEM coupled method[C]//Proceedings of the Twenty-seventh International Ocean and Polar Engineering Conference. San Francisco, California, USA, 2017.
(  0) 0)
|
| [106] |
ZHANG Youlin, CHEN Xiang, WAN Decheng. An MPS-FEM coupled method for the comparative study of liquid sloshing flows interacting with rigid and elastic baffles[J]. Applied mathematics and mechanics, 2016, 37(12): 1359-1377. (  0) 0)
|
| [107] |
RAO Chengping, ZHANG Youlin, WAN Decheng. Numerical simulation of the solitary wave interacting with an elastic structure using MPS-FEM coupled method[J]. Journal of marine science and application, 2017, 16(4): 395-404. DOI:10.1007/s11804-017-1430-x (  0) 0)
|
| [108] |
RAO Chengping, WAN Decheng. Numerical study of the wave-induced slamming force on the elastic plate based on MPS-FEM coupled method[J]. Journal of hydrodynamics, 2018, 30(1): 70-78. DOI:10.1007/s42241-018-0007-8 (  0) 0)
|
| [109] |
ANTOCI C, GALLATI M, SIBILLA S. Numerical simulation of fluid-structure interaction by SPH[J]. Computers & structures, 2007, 85(11/12/13/14): 879-890. (  0) 0)
|
| [110] |
ERKAN N, KAWAKAMI T, MADOKORO H, et al. Numerical simulation of droplet deposition onto a liquid film by VOF-MPS hybrid method[J]. Journal of visualization, 2015, 18(2): 381-391. DOI:10.1007/s12650-014-0241-2 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39



