半潜式海洋平台一般由上甲板、立柱、横撑及下浮体组成,具有甲板面积大、可变载荷大、抗风浪能力强、适用水深范围较广等特点[1],已广泛应用于海上生产[2]、海上火箭发射[3]、钻探和海上原油处理[4-5]。
平台运动性能直接影响平台的有效工作时间、工作人员舒适度及其结构安全。对于Spar和TLP平台,通过在平台底部安装垂荡板,增大垂荡运动模态下的附加质量,提高平台垂荡固有周期,使其远离波浪谱中能量集中的部分,同时垂荡板又增加了垂荡运动模态下的粘性阻尼,进一步降低结构物的垂荡运动响应[6-8]。另外Cozijn等[9]实验研究装有裙板的CALM浮筒的垂荡、横摇和纵摇阻尼问题。Li等[10]实验研究了KC数、振荡频率β、垂荡板深度、垂荡板厚宽比、垂荡板边缘的形状、开孔率和开孔的大小对单一垂荡板的水动力特性的影响。刘鲲等[11-12]提出一种新型可调节垂荡板系统并将其应用于半潜式平台上,起到垂荡抑制及能量收集作用。关于降低半潜式平台横摇和纵摇运动幅值的研究较少,因此本文提出一种自控式可收放阻尼板。在半潜式平台航行时收放到下附体中,在其处于零航速实施采油、钻井及其他功能时,阻尼板从下附体水平伸展出。采用CFD方法对半潜式平台自由衰减运动进行数值模拟并与实验值对比验证。在此基础上,系统地研究阻尼板几何特性和平台运动初始衰减位置对平台粘性阻尼的影响,并对阻尼板附近流场进行分析,以此揭示其作用机理。
1 数值模拟概况 1.1 雷诺平均控制方程本文数值模拟利用了流体的雷诺平均质量守恒方程和动量守恒方程,表达如下
| $ \frac{\partial \rho }{\partial t}+\frac{\partial }{\partial {{x}_{i}}}(\mathit{\boldsymbol{ }}\!\!\rho\!\!\text{ }{{\mathit{\boldsymbol{u}}}_{i}})=\text{ }0 $ | (1) |
| $ \rho \left[\frac{\partial {{\mathit{\boldsymbol{u}}}_{i}}}{\partial t}+\frac{\partial ({{\mathit{\boldsymbol{u}}}_{i}}{{\mathit{\boldsymbol{u}}}_{j}})}{\partial {{x}_{j}}} \right]=\text{ }-\frac{\partial \mathit{\boldsymbol{p}}}{\partial {{x}_{i}}}+\mu {{\nabla }^{2}}{{\mathit{\boldsymbol{u}}}_{i}}+\frac{\partial }{\partial {{x}_{j}}}(-\rho {{\mathit{\boldsymbol{{u}'}}}_{i}}{{\mathit{\boldsymbol{{u}'}}}_{j}}) $ | (2) |
式中:ui表示笛卡尔坐标系中xi(i=1, 2, 3)方向的时均速度,ρ是流体密度,t是时间,ρ是时均压力;u′i是笛卡尔坐标中xi方向的脉动速度;-ρu′iu′j是雷诺应力。另外为使上述方程组封闭,计算过程中采用k-ω SST湍流模型[13]。
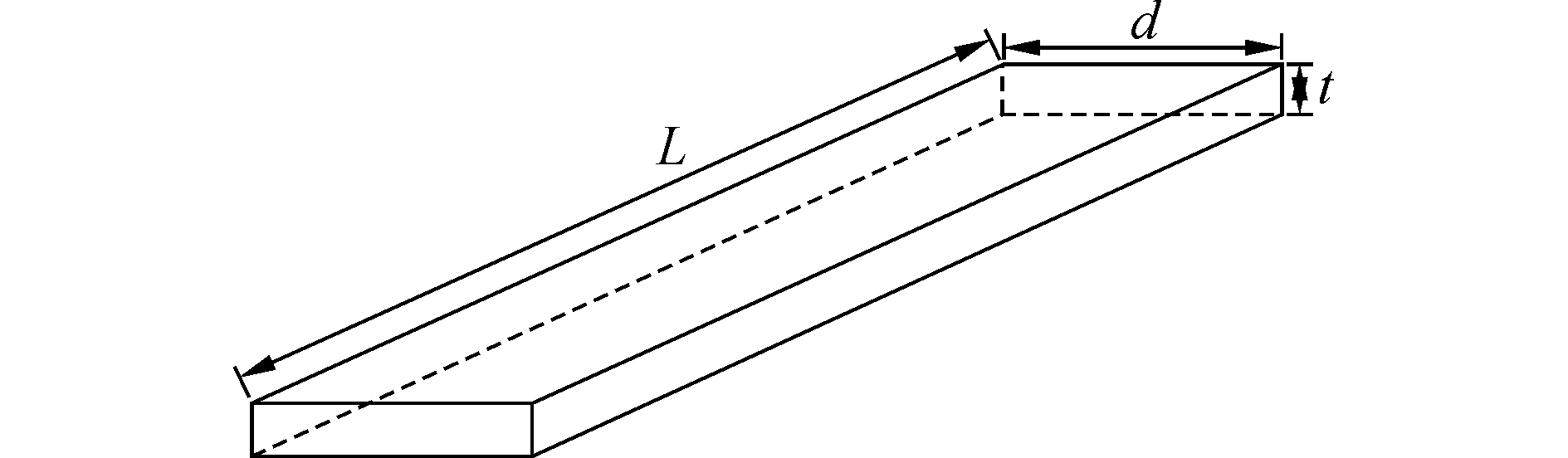
1.2 模型尺寸选用文献[5]中半潜式平台实验模型作为算例进行数值模拟。自控式阻尼板长度l为1.5 m,宽度d分别为0.025、0.05、0.075、0.1 m,厚度t分别为0.002、0.004、0.006、0.008、0.01 m,其几何示意图如图 1所示。
|
Download:
|
| 图 1 自控式阻尼板示意图 Fig. 1 Sketch of automatic damping plate | |
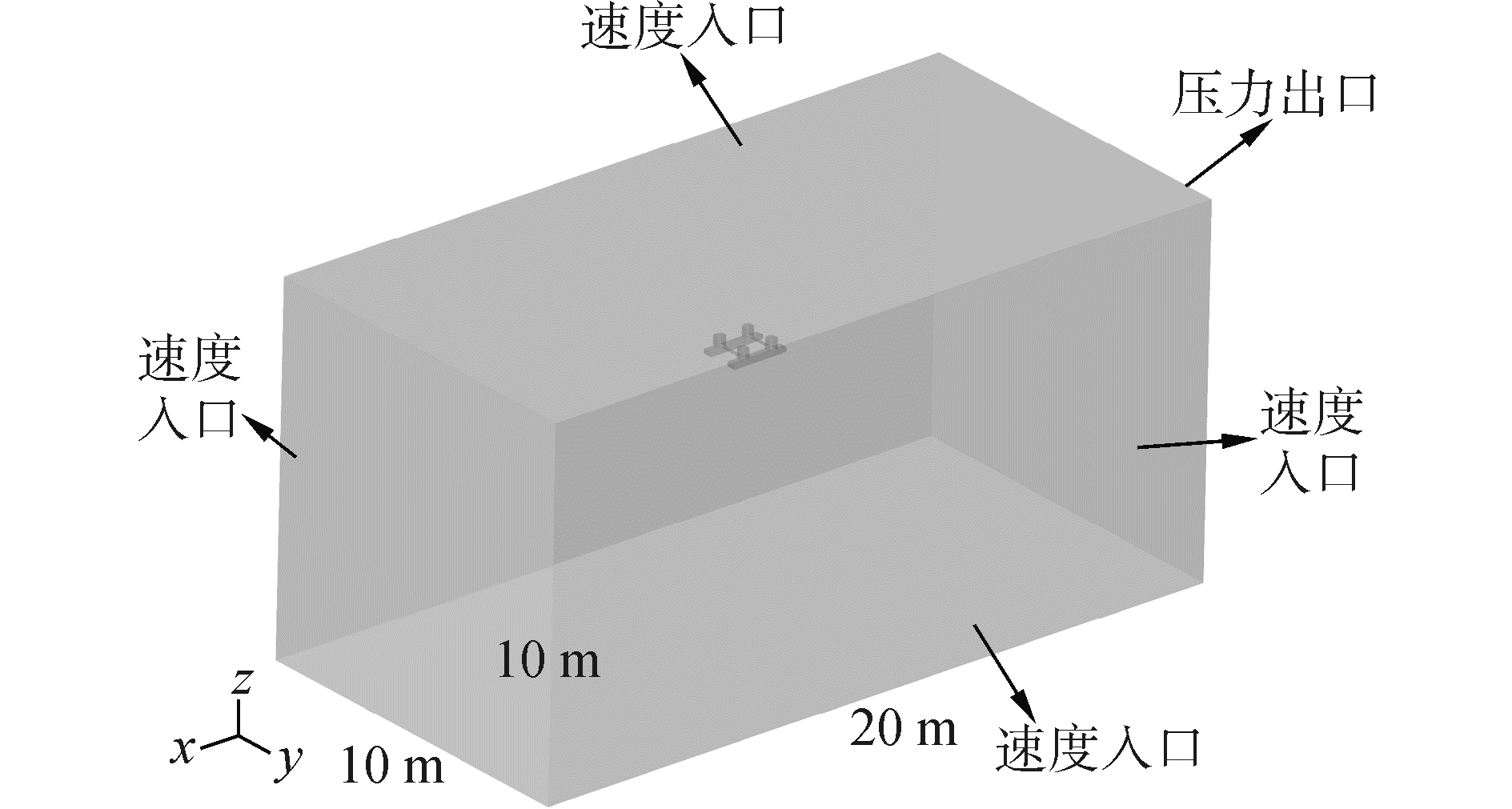
本文采用计算流体力学软件STAR-CCM+对半潜式平台自由衰减运动进行数值模拟。整个计算域分为含半潜式平台的重叠区域与外部的背景区域,如图 2、3所示。计算中采用笛卡尔坐标系,坐标系原点位于平台的重心,背景计算域尺度在x、y、z方向长度分别为20、10、10 m,平台在x、y、z方向尺度分别为1.9、1.3、0.4 m。半潜式平台边界层的厚度为10 cm,在边界层中生成了6层网格,边界层网格增长因子为1.2。
|
Download:
|
| 图 2 计算域和边界条件 Fig. 2 Computational domain and boundary conditions | |

|
Download:
|
| 图 3 计算域网格结构图 Fig. 3 The grid structure of computational domain | |
背景域的边界条件如图 2所示。速度入口边界上ui初始条件为零,压强法向梯度为零。在压力出口边界,流动方向上无梯度变化,速度和压强的梯度为零。背景域两侧面的边界上,其速度和压强为对称边界条件。半潜式平台及阻尼板表面为无滑移不可穿透边界条件ui为零,压强法向梯度为零。另外利用多相流体域体积模型来模拟半潜式平台的气液两相混合流场,运用流体域体积(volume of fluid, VOF)方法捕捉自由液面。流场的湍流强度取为0.01,湍流粘性比取为10。
1.5 控制方程离散与求解动量方程对流项采用二阶QUICK格式离散,QUICK格式为对流运动的二次迎风格式,是一种改进的离散方程截断方法。湍流模型对流项采用二阶迎风格式进行离散,分离流对流项采用二阶迎风离散。求解器中隐式不定常临时离散项采用Crank-Nicolson格式,理论上Crank-Nicolson格式时无条件稳定的,而且在采用同样的网格时比显示格式要更精确,另外各项的亚松弛因子采用0.1,计算采用固定时间步长0.01 s。由于PISO算法计算速度快,总体效率高,并且对于瞬态问题有明显优势,因次最后利用PISO算法对整个计算域离散后的控制方程组进行求解。
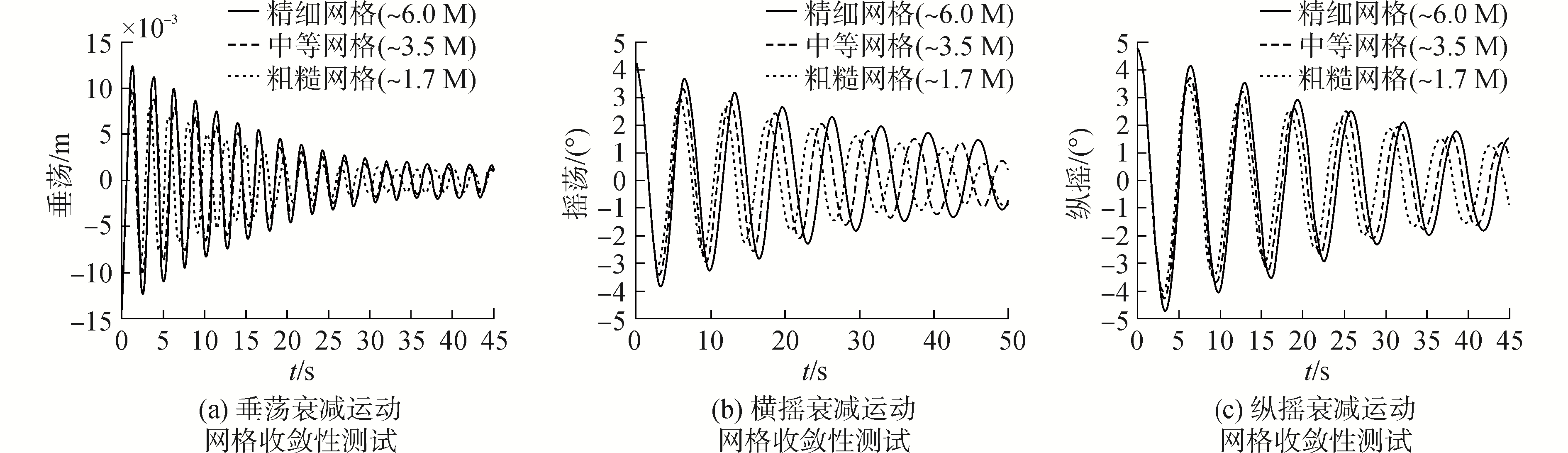
2 数值方法验证在对网格大小进行收敛性分析过程中,根据平台边界到网格增长区域的增长率和背景域网格大小的不同生成了三种不同数量类型网格,分别为粗糙网格(Coarse grid)、中等网格(Medium grid)和精细网格(Fine grid),其中网格数量分别约为170万、350万、600万。图 3以精细化网格为例,显示了数值模拟中计算域、y=0剖面及平台附近网格的加密情况。
图 4显示了不同网格数量下得到的纵摇、横摇和垂荡衰减曲线。不同运动模态的自由衰减受网格数量的影响不同,随着时间的累计,计算过程中的错误积累越来越大。显然网格数量较少时,离散引起的误差较大,衰减过程中能量被耗散,平台运动衰减相对较快,导致固有周期偏小,粘性阻尼偏大。
|
Download:
|
| 图 4 网格收敛性测试 Fig. 4 Grid convergence test | |
表 1为精细网格条件下数值模拟与实验值对比,数值模拟得到的固有周期和阻尼系数与实验值吻合较好。考虑到采用精细网格计算时有较好的精度,因此在之后数值研究过程中,采用该种类型的网格划分形式。
| 表 1 数值模型验证 Tab.1 Numerical model validation |
本文讨论半潜式平台在不同初始衰减位置[14],对阻尼板宽度、厚度对其垂荡、横摇和纵摇阻尼的影响规律。各运动模态初始衰减位置如表 2所示。为分析阻尼板作用机理,同时考虑到阻尼板对垂荡、横摇和纵摇阻尼影响的相似性,故仅分析不同时刻下垂荡衰减过程中阻尼板周围流场涡量变化规律。
| 表 2 各运动模态初始衰减位置 Tab.2 Initial cycle amplitude of different motion |
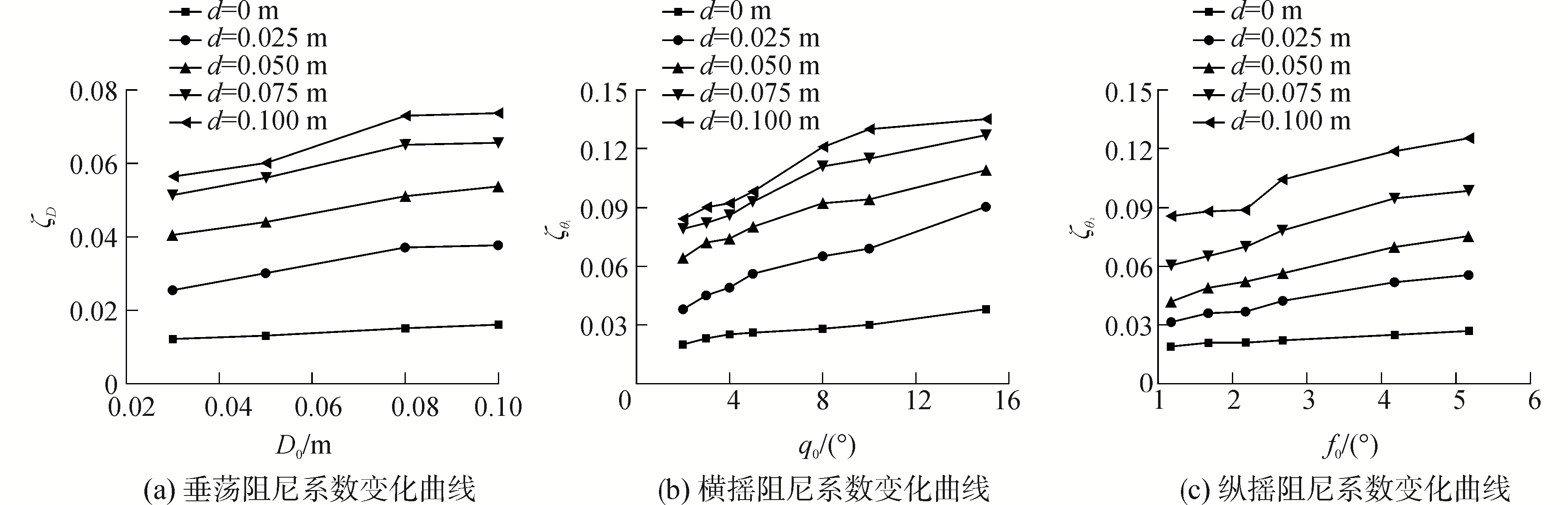
图 5为阻尼板厚度t=0.1 m时,垂荡、横摇和纵摇阻尼系数δp、δθ1、δθ2随初始衰减位置和阻尼板宽度的变化曲线。可以看出:在相同初始衰减位置下,装有阻尼板的半潜式平台与不装阻尼板(d=0)相比,阻尼增幅明显;垂荡、横摇和纵摇阻尼系数随着初始衰减位置的增加呈整体上升趋势。其原因是随着初始衰减位置的增加,平台垂荡、横摇和纵摇恢复力(矩)变大,使阻尼板与周围流体之间产生较高的相对速度,导致阻尼板周围涡量增大、涡泄增强。同时随初始衰减位置增加,不同阻尼板宽度对各运动模态下的阻尼系数影响程度不同。阻尼板宽度d为0.025 m时,横摇阻尼系数增幅最大,达到137.37%;d为0.05 m时,纵摇阻尼系数增幅最大,达到83.74%;d为0.025 m时,垂荡阻尼系数增幅最大,达到32.5%,另外随着阻尼板宽度的增加,对三个自由度方向上的阻尼系数影响程度不同。对于垂荡阻尼,在当阻尼板厚度d在0.02~0.075 m时增幅较为均匀,当d大于0.075 m时,增幅程度减小趋势变缓。对于横摇阻尼,随着阻尼板板宽的增加,其增幅程度呈非线性变化。例如,初始衰减位置q0=5°时,增幅程度分别为115.38%、42.86%、16.25%、5.38%。对于纵摇阻尼,其增幅呈较为均为呈线性变化,同样当初始衰减位置f0=5°时增加幅值分别为0.020、0.014、0.033、0.026。
|
Download:
|
| 图 5 阻尼系数随初始衰减位置和阻尼板宽度变化曲线 Fig. 5 The curve of damping coefficient under different initial cycle amplitude and width of damping plate | |
图 6为阻尼板宽度d=0.75 m时,垂荡、横摇和纵摇阻尼系数随初始衰减位置和阻尼板厚度的变化曲线。可以看出:在相同初始衰减位置下,装有阻尼板的半潜式平台与不装阻尼板(t=0 m)相比,阻尼增幅明显;垂荡、横摇和纵摇阻尼系数随着初始衰减位置的增加呈整体上升趋势,但是在初始衰减位置范围为0.03~0.05 m时,垂荡和纵摇阻尼系数呈下降趋势。参考文献[10, 15],分析其主要原因可能是在初始衰减位置和阻尼板的厚度较小时,阻尼板自身阻尼系数随着初始衰减位置的增加而减小。同时随初始衰减位置增加,不同阻尼板厚度对各运动模态下的阻尼系数影响程度不同。d为0.01 m时,横摇阻尼系数增幅最大,达到60.76%;d为0.01 m时,纵摇阻尼系数增幅最大,达到63.76%;d为0.008 m,垂荡阻尼系数增幅最大,达到38.94%;另外阻尼板厚度对三个自由度方向上的阻尼系数影响呈负相关,并且初始衰减位置在较小的范围内更为明显,这与文献[15-17]结论相似。对于垂荡阻尼,初始衰减位置D0小于0.05 m时,板厚对影响程度呈明显的非线性关系,当初始衰减位置D0大于0.05 m时,板厚对影响程度接近于线性关系。对于横摇阻尼,随着阻尼板板厚d的均匀减小,其阻尼增幅呈非线性变化,例如当初始衰减位置q0为4°时,增幅程度分别为6%、13.2%、12.5%、18.5%。而对于纵摇阻尼,其增幅变化不规律,同样当f0为4°时增加幅值分别为0.002 8、0.019 3、-0.000 69、0.006 21。

|
Download:
|
| 图 6 阻尼系数随初始衰减位置和阻尼板厚度变化曲线 Fig. 6 The curve of damping coefficient under different initial cycle amplitude and thickness of damping plate | |
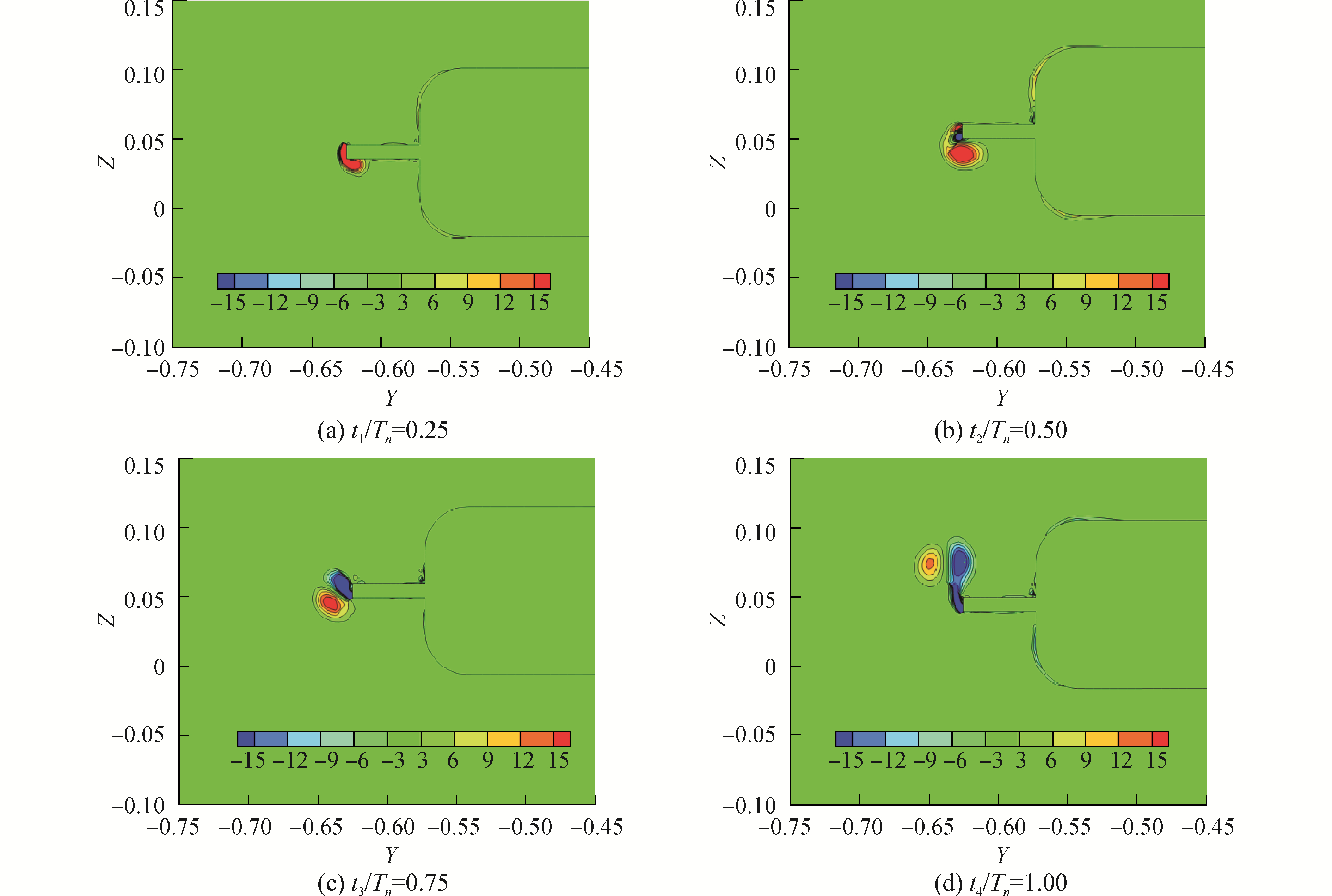
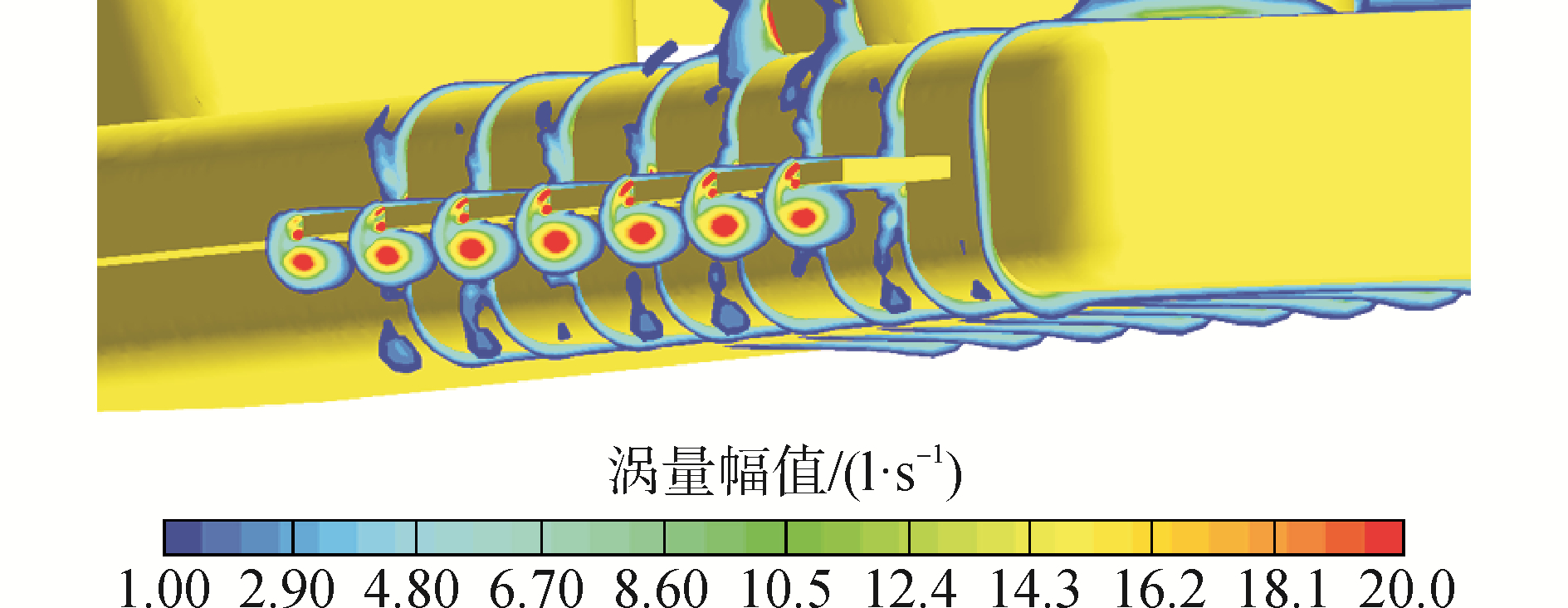
图 7显示了阻尼板厚度t为0.01 m、宽度d为0.05 m、垂荡初始衰减位置D0为-0.03 m时,垂荡自由衰减第一个周期下x轴方向上的涡量场。可以看出:四个时刻相比,在t1/Tn为0.25时刻,由于阻尼板与流体之间的局部相对速度最大,此时诱导产生的涡量中心处最大。此时,半潜式平台从初始衰减位置D0为-0.03 m继续向上移动,在阻尼板周围可以观察到逆时针方向的涡。在t2/Tn为0.5时刻,涡开始向外扩散,并且与阻尼板产生分离,同时在平台向下移动之前,可以观察到顺时针方向的涡已经形成。为更加直观表示此时刻平台与阻尼板周围流场,通过设置等间距切面,建立了涡量幅值分布图,如图 8所示。在t3/Tn为0.75时刻,之前形成顺时针方向的涡开始从阻尼板边缘发生脱落。在t4/Tn为1时刻,一对顺时针和逆时针的涡完全从阻尼板边缘脱落,并且逆时针方向上的漩涡沿45°轨迹向自由液面扩散,但是由于流体之间的内摩擦阻力,使漩涡的能量转变成了热能,导致其强度减小。当然随着垂荡衰减周期的增加,阻尼板诱导形成的涡的强度会变的越来越小。
|
Download:
|
| 图 7 x轴向阻尼板周围涡量分布(t=0.01 m、d=0.05 m) Fig. 7 The distribution of vortices around damping plate in x-axis(t=0.01 m、d=0.05 m) | |
|
Download:
|
| 图 8 平台与阻尼板周围流场涡量幅值(t=0.01 m、d=0.05 m、t2/Tn=0.5) Fig. 8 The vorticity amplitude of flow field around platform and damping plate(t=0.01 m、d=0.05 m、t2/Tn=0.5) | |
1) 装有阻尼板的半潜式平台与原型相比,阻尼板运动过程中,其边缘处诱导了旋涡的生成,并发生流动分离,增加了平台垂荡、横摇和纵摇阻尼,降低运动幅值。
2) 在阻尼板相同宽度和厚度条件下,随着自由衰减初始衰减位置的增加,半潜式平台的阻尼呈整体上升趋势。显然平台运动幅度越大,阻尼板起到的抑制作用越强。
3) 在阻尼板相同厚度条件下,阻尼板宽度与垂荡、横摇及纵摇阻尼呈正相关,并且随着其宽度的增加,横摇阻尼呈非线性变化。纵摇呈线性变化,即随着阻尼板宽度的增加,纵摇阻尼均匀增加。而垂荡阻尼呈阶段式变化,即阻尼板宽度d≤0.075 m时,随着阻尼板宽度增加,垂荡阻尼增幅明显,当d>0.075 m时,随着阻尼板宽度增加,垂荡阻尼增幅较小。
4) 在阻尼板相同宽度在下,阻尼板厚度与垂荡、横摇及纵摇阻尼呈负相关,并且随着其厚度的增加,横摇阻尼呈非线性变化。垂荡阻尼同样呈阶段式变化,阻尼板厚度t=0.01 m相对于t=0时,即阻尼板的出现使得垂荡阻尼增幅明显,但是随着阻尼板厚度的减小,垂荡阻尼增幅较小。而纵摇阻尼与阻尼板厚度整体呈负相关,但是当t为0.01 m和t为0.008 m时,阻尼板对纵摇阻尼的影响比较接近,当t为0.006 m和t为0.004 m时,同样阻尼板对纵摇阻尼的影响比较接近。
| [1] |
王俊荣, 谢彬. 半潜式平台水动力性能及运动响应研究综述[J]. 中国造船, 2009, 50(S): 255-261. WANG Junrong, XIE Bin. Review of hydrodynamic performance and global motion prediction of semi-submersibles[J]. Shipbuilding of China, 2009, 50(S): 255-261. (  0) 0)
|
| [2] |
SARAVANAN R, BHATTACHARYYA S K, SELVAM R P, et al. Hydrodynamic analysis of semisubmersibles for a large Scale desalination plant[C]//Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering. Rotterdam, The Netherlands, 2011: 663-669.
(  0) 0)
|
| [3] |
KONYUKHOV S N. Applied mechanics problems accompanying spacecraft launches from a floating platform and their resolution by the sea launch project[J]. International applied mechanics, 2004, 40(2): 115-139. DOI:10.1023/B:INAM.0000028591.66544.e4 (  0) 0)
|
| [4] |
胡志强. 多学科设计优化技术在深水半潜式钻井平台概念设计中的应用研究[D]. 上海: 上海交通大学, 2008. HU Zhiqiang. Application of multidisciplinary design optimization technique on the conceptual design of deep-water semi-submersible drilling unit[D]. Shanghai: Shanghai Jiao Tong University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10248-2010113118.htm (  0) 0)
|
| [5] |
史琪琪. 深水锚泊半潜式钻井平台运动及动力特性研究[D]. 上海: 上海交通大学, 2011. SHI Qiqi. Research on kinetic and dynamic characteristics of a deepwater drilling semi-submersible platform[D]. Shanghai: Shanghai Jiao Tong University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10248-1011267918.htm (  0) 0)
|
| [6] |
SRINIVASAN N, CHAKRABARTI S, RADHA R. Damping-controlled response of a truss-pontoon semi-submersible with heave-plates[C]//Proceedings of the 24th International Conference on Offshore Mechanics and Arctic Engineering. Halkidiki, Greece, 2005: 1007-1020.
(  0) 0)
|
| [7] |
DOWNIE M J, GRAHAM J M R, HALL C, et al. An experimental investigation of motion control devices for truss spars[J]. Marine structures, 2000, 13(2): 75-90. DOI:10.1016/S0951-8339(00)00010-1 (  0) 0)
|
| [8] |
SUBBULAKSHMI A, SUNDARAVADIVELU R. Heave damping of spar platform for offshore wind turbine with heave plate[J]. Ocean engineering, 2016, 121: 24-36. DOI:10.1016/j.oceaneng.2016.05.009 (  0) 0)
|
| [9] |
COZIJN H, UITTENBOGAARD R, TER B E. Heave, roll and pitch damping of a deepwater CALM buoy with a skirt[C]//Proceedings of the 15th International Offshore and Polar Engineering Conference. Seoul, Korea, 2005: 388-395.
(  0) 0)
|
| [10] |
LI Jinxuan, LIU Shuxue, ZHAO Min, et al. Experimental investigation of the hydrodynamic characteristics of heave plates using forced oscillation[J]. Ocean engineering, 2013, 66: 82-91. DOI:10.1016/j.oceaneng.2013.04.012 (  0) 0)
|
| [11] |
刘鲲. 深海半潜式平台浪激响应分析及垂荡响应控制[D]. 哈尔滨: 哈尔滨工业大学, 2010. LIU Kun. Wave induced response analysis and heave motion control of a semi-submersible platform[D]. Harbin: Harbin Institute of Technology, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10213-1011262044.htm (  0) 0)
|
| [12] |
LIU Kuan, OU Jinping. A novel tuned heave plate system for heave motion suppression and energy harvesting on semi-submersible platforms[J]. Science China technological sciences, 2016, 59(6): 897-912. DOI:10.1007/s11431-016-6055-9 (  0) 0)
|
| [13] |
BLAZEK J. Computational fluid dynamics:principles and applications[M]. 3rd ed. Sankt Augustin, Germany: Butterworth-Heinemann, 2015.
(  0) 0)
|
| [14] |
FALTINSEN O M. Sea loads on ships and offshore structures[M]. Britain: Cambridge University Press, 1993.
(  0) 0)
|
| [15] |
HE Haiping. Hydrodynamics of thin plates[M]. Ann Arbor, Michigan: University of Michigan, 2003.
(  0) 0)
|
| [16] |
TAO Longbin, THIAGARAJAN K. Low KC flow regimes of oscillating sharp edges Ⅰ. Vortex shedding observation[J]. Applied ocean research, 2003, 25(1): 21-35. DOI:10.1016/S0141-1187(03)00031-2 (  0) 0)
|
| [17] |
TAO Longbin, THIAGARAJAN K. Low KC flow regimes of oscillating sharp edges. Ⅱ:Hydrodynamic forces[J]. Applied ocean research, 2003, 25(2): 533-62. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


