涡激振动现象广泛存在于许多工程领域中,例如海洋油气勘探中的立管、桥梁悬索、天线等。涡激振动的现实意义重大,目前国内外有许多学者致力于研究其发生机理、振动特性等[1-2]。
Khalak等[3]在雷诺数为2 000~12 000测量了圆柱体涡激振动的幅值响应和频率,发现在低质量阻尼比条件下的幅值响应存在两个分支。Guilmineau[4]参照Williamson等[5]的单自由度低质量比试验,利用数值模拟分析了圆柱体单自由度涡激振动,其在计算中把初始条件设为匀加速,由此得到的最大振动幅值能够与Williamson的试验值保持一致,但是却无法准确模拟试验值中的上端分支形状。
涡激振动数值模拟中一个关键之处是湍流模型的选取。Celik等[6]在数值模拟中利用标准k-ε模型计算了定常流中的圆柱体绕流问题,发现计算结果与试验结果存在较大差别。Menter[7]通过结合标准k-ε模型和k-ω模型,提出了SST k-ω湍流模型,该湍流模型在模拟圆柱绕流方面有了一定的改善,但由于其在尾流区采用标准k-ε模型,而标准k-ε模型在有大量漩涡存在时计算效果较差,因此将SST k-w湍流模型应用到圆柱体涡激振动数值模拟中仍具有改进的空间。
为利用CFD数值模拟来分析圆柱体涡激振动特性,本文对SST k-ε湍流模型进行了改进,利用开源软件OpenFOAM在圆柱绕流中验证其有效性。然后分别采用匀速、匀加速及匀减速三种初始条件对质量比为2.6的圆柱双自由度涡激振动进行数值模拟,分析三种初始条件下圆柱振动幅值、锁定区间、流体力特性、运动轨迹以及漩涡脱落特点,并对涡激振动的迟滞机理进行讨论,阐述了不同初始条件下漩涡脱落模式与迟滞现象的内在联系。
1 湍流模型的改进 1.1 SST k-ω湍流模型介绍Menter将Wilcox[8]提出的k-ω湍流模型和Launder等[9]提出的k-ε湍流模型通过混合函数结合在一起,提出了SST k-ω湍流模型,其表达式为
| $ \frac{{D\rho k}}{{Dt}} = {P_k} - {\beta ^ * }\rho wk + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _k}{\mu _t}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] $ | (1) |
| $ \begin{array}{*{20}{c}} {\frac{{D\rho \omega }}{{Dt}} = {P_\omega } - \beta \rho {\omega ^2} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _\omega }{\mu _t}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right] + }\\ {2\rho \left( {1 - {F_1}} \right){\sigma _{{\omega _2}}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}}} \end{array} $ | (2) |
湍动粘度系数μt为
| $ {\mu _t} = \frac{{\rho {a_1}k}}{{\max \left( {{a_1}\omega ,S{F_2}} \right)}} $ | (3) |
式中:a1=0.31,
| $ {P_k} = {\tau _{ij}}\frac{{\partial {u_i}}}{{\partial {x_j}}},{P_\omega } = \frac{{\rho \gamma {P_k}}}{{{\mu _t}}} $ | (4) |
| $ {\tau _{ij}} = 2{\mu _t}\left( {{S_{ij}} - \frac{1}{3}\frac{{\partial {u_k}}}{{\partial {x_k}}}{\delta _{ij}}} \right) - \frac{2}{3}\rho k{\delta _{ij}} $ | (5) |
设ϕ1为标准k-ω模型经验参数(σk1,σω1,…,γ1),ϕ2为转化为k-ω形式的k-ε模型经验参数(σk2,σω2,…,γ2),ϕ为SST k-ω模型经验参数(σk,σω,…,γ),其关系为
| $ \phi = {F_1}{\phi _1} + \left( {1 - {F_1}} \right){\phi _2} $ | (6) |
ϕ1系列参数为标准k-ω参数:σk1=0.85,σω1=0.5,β1=0.075,β*=0.09,κ=0.41,γ1=β1/β*-σw1κ2/
ϕ2系列参数为标准k-ε参数:σk2=1.0,σω2=0.856,β2=0.082 8,β*=0.09,κ=0.41,γ2=β2/β*-σw2κ2/
F1为混合函数,其计算公式为
| $ {F_1} = \tanh \left\{ {{{\left\{ {\min \left[ {\max \left( {\frac{{\sqrt k }}{{{\beta ^ * }\omega y}},\frac{{500\nu }}{{{y^2}\omega }}} \right),\frac{{4\rho {\sigma _{{\omega _2}}}k}}{{{D_{k\omega }}{y^2}}}} \right]} \right\}}^4}} \right\} $ | (7) |
| $ {D_{k\omega }} = \max \left( {2\rho {\sigma _{{\omega _2}}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_j}}},{{10}^{ - 20}}} \right) $ | (8) |
圆柱体发生涡激振动时其尾流区域会存在大量漩涡,使得流场的流线产生一定的曲率变化和局部旋转。标准SST k-ω湍流模型虽然在近壁区采用k-ω模型,可以较好地模拟圆柱表面存在逆压梯度的层流,但采用标准k-ε模型来处理远离壁面的流场,计算结果往往不太理想[10]。另外,由于标准SST k-ω湍流模型在模化时未能计入强逆压梯度下的湍流非平衡特性[11],仍然采用湍流生产和耗散的平衡关系,因此其分离区流动的湍动能生成过小。
为改善标准SST k-ω湍流模型在圆柱涡激振动数值模拟的精确度,需要对其进行改进。
首先结合RNG k-ε模型对标准k-ε模型的改进原理,在标准SST k-ε湍流模型中的k-ε模型部分中增加附加生成项R项以反映主流时均应变率,提升弯曲壁面模拟和强旋流模拟的能力:
| $ {R_\omega } = \frac{{\eta \left( {1 - \eta /{\eta _0}} \right)\omega }}{{1 + \beta {\eta ^3}k}}{P_k} $ | (9) |
式中:η=S/ω,η0=4.38。
另一方面,为模拟边界层分离过程中湍流生成项与耗散项的不平衡关系,对耗散方程中pω进行修正,本文结合Gan等[12]的流动分离修正方法,对其进行修正。具体方法如下
| $ {P_{rkw}} = \frac{{{P_k}}}{{{\beta ^ * }\rho k\omega }} $ | (10) |
| $ {f_5} = 4{P_{rkw}} - 5 $ | (11) |
| $ {f_5} = \min \left( {\max \left( {{f_5},1} \right),12} \right) $ | (12) |
| $ {r_d} = \frac{{{\mu _t} + \mu }}{{\rho \sqrt {{S_{ij}}{S_{ij}} + {\Omega _{ij}}{\Omega _{ij}}} {\kappa ^2}{d^2}}} $ | (13) |
| $ {f_d} = 1.0 - \tanh \left( {{{\left( {8{r_d}} \right)}^3}} \right) $ | (14) |
| $ {f_5} = {f_5}{f_d} + \left( {1.0 - {f_d}} \right) $ | (15) |
| $ {{\bar P}_\omega } = {f_5}{P_\omega } $ | (16) |
式中:Prkw、f5及rd均为中间迭代变量,Pω为修正结果。
结合以上修正方法对标准SST k-ω湍流模型进行改进,得到的新湍流模型如下
| $ \frac{{D\rho k}}{{Dt}} = {{\bar P}_k} - {\beta ^ * }\rho wk + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _k}{\mu _t}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] $ | (17) |
| $ \begin{array}{*{20}{c}} {\frac{{D\rho \omega }}{{Dt}} = {{\bar P}_\omega } - \beta \rho {\omega ^2} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _\omega }{\mu _t}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right] + }\\ {2\rho \left( {1 - {F_1}} \right){\sigma _{{\omega _2}}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}} - }\\ {\left( {1 - {F_1}} \right)\frac{{\eta \left( {1 - \eta /{\eta _0}} \right)\omega }}{{1 + {\beta _3}{\eta ^3}k}}{P_k}} \end{array} $ | (18) |
其中模型的各项经验参数确定方法与标准SST k-ω模型中的参数确定方法类似,不同的是这里需要将ϕ2系列标准k-ε参数改为RNG k-ε模型参数。
1.3 改进模型的验证为验证改进湍流模型的正确性,在圆柱绕流中与标准SST k-ω模型进行对比。
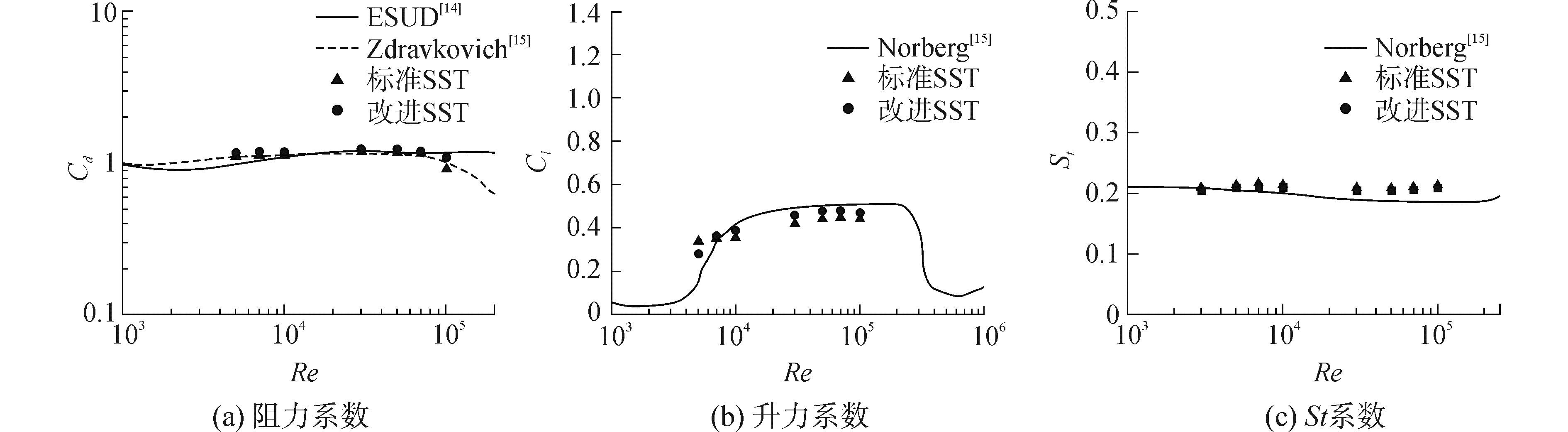
图 1所示为两种湍流模型计算得到的阻力系数以及Zdravkoyich[13]和ESDU[14]得到的圆柱绕流阻力系数曲线。通过对比可以发现:在Re范围为[5×103,7×105],两种湍流模型计算的阻力系数都与试验结果吻合良好,在Re为105时,两种模型都与Zdravkoyich的结果趋势一致,但改进模型的精度要更高。
|
Download:
|
| 图 1 不同雷诺数下流体力系数与St数比较 Fig. 1 Comparison of the fluid force coefficients and the Strouhal number under different Renolds numbers | |
图 1(b)所示为两种模型计算得到的升力系数与Norberg[15]得到试验结果对比图。通过对比发现:在Re范围为5×103~3×104,改进湍流模型与Norberg的结果一致,而标准SST k-ω湍流模型则存在一定的差别,这是由于改进模型进行了边界层分离修正,对边界层分离和漩涡脱落更加敏感。随着雷诺数的增大,由于标准SST k-ω模型的湍动能生成过低和对涡脱落抑制的缺点越发明显,得到的升力系数明显偏小,而改进模型通过引入附加生成项,修正了湍动能耗散率,能有效提高其对涡致升力的模拟精度。
图 1(c)所示为两种湍流模型计算得到的St数与Norberg[15]结果的比较图。可以发现两种湍流模型得到的结果差别不大,这是由于改进模型主要改变的是生成项与耗散项的关系,并未改变泄涡频率,因此两种模型的St数差异不大。
图 2所示为Re为104时两种模型得到的x向速度云图。通过对比可知:两种模型均模拟出了回流区,但改进模型的回流区范围要更大,并且改进模型的漩涡强度更大。

|
Download:
|
| 图 2 x向速度云图对比 Fig. 2 Comparison of the velocity contour in x direction | |
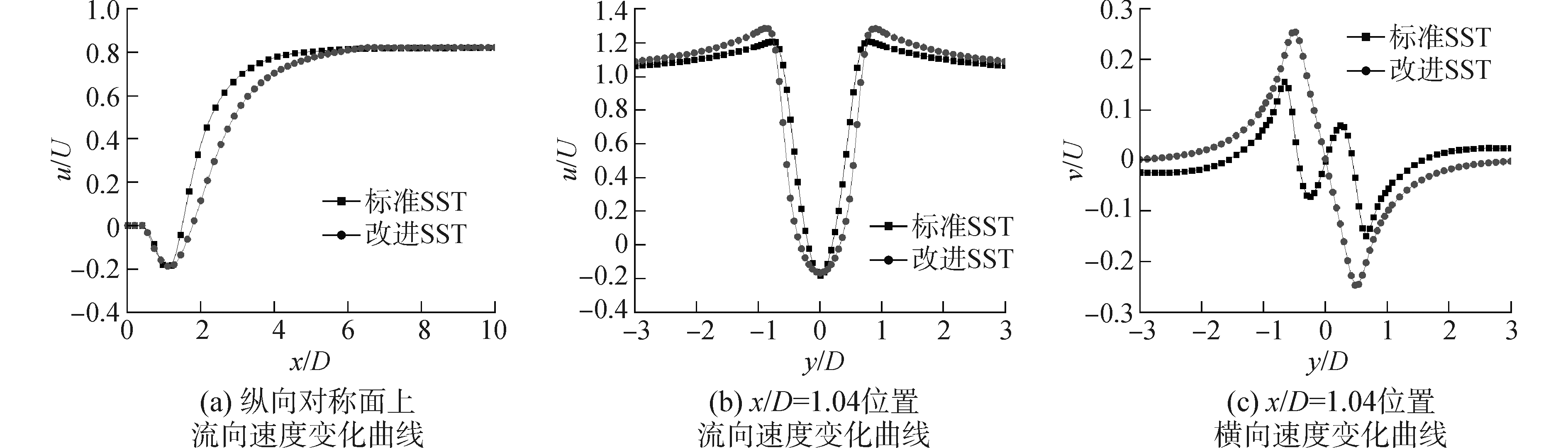
为了更加清晰地观察两种模型的回流区范围,在图 3(a)中给出了Re为104时圆柱纵向对称面上流向速度随x/D的变化曲线,可以发现标准SST k-ω模型的回流区间长度为0.95D,而改进模型为1.3D;在(b)和(c)中给出了尾流区x/D为1.04处流向和横向速度随y/D的变化曲线,发现改进模型的回流区间宽度也更大,并且改进模型的速度最大值与最小值之差更大,表明其漩涡强度也更大。
|
Download:
|
| 图 3 纵向对称面和x/D=1.04位置的速度变化曲线 Fig. 3 Velocity curves on longitudinal symmetry plane and the position of x/D=1.04 | |
总的来说,改进的湍流模型的回流区域更大,可以更有效地模拟漩涡,计算得到的涡致升力精度比标准SST k-ω模型更高,可以将其应用到涡激振动数值模拟的研究中。
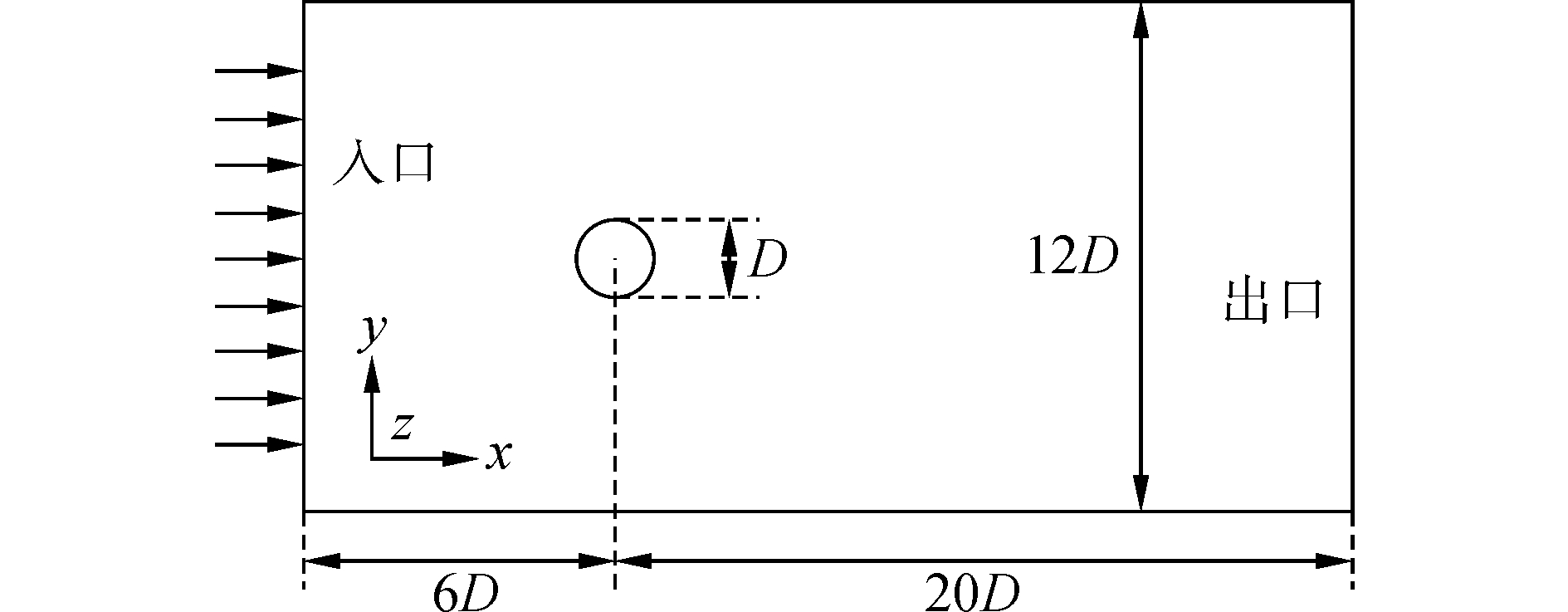
2 涡激振动数值模拟 2.1 计算模型利用OpenFOAM自编程序PimpleDyMFoam求解器求解,计算区域与边界条件见图 1,工况选取为Re为5×103、7×103、104,3×104、5×104、7×104和105,库朗数(Courant number)控制在0.2以下,其计算域如图 4所示。
|
Download:
|
| 图 4 计算域示意图 Fig. 4 Schematic diagram of the computational domain | |
为保证计算精度的同时减少计算时间,在网格划分时,圆柱周围4D的范围内采用O型网格,远场区域采用结构网格,如图 5所示。

|
Download:
|
| 图 5 计算区域网格划分示意图 Fig. 5 Schematic diagram of the computing grid | |
数值模拟中采用改进的SST k-ω湍流模型和非稳态一阶隐式进行求解,动量方程的压力速度耦合采用PIMPLE算法。
2.2 时间步长控制时间步长影响着收敛速度和稳定性。库朗数指的是时间步长和物理空间尺度的对应关系,其计算公式如下
| $ {\rm{Courant}}\;{\rm{number}} = u\Delta t/\Delta x $ | (19) |
式中:u为来流速度,Δt为时间步长,Δx为网格尺寸。为满足Courant-Friedrichs-Lewy条件,必须要求库朗数足够小,设定库朗数最大值小于0.50,时间步长取为Δt=0.000 1。
2.3 模拟工况选取Williamson等[5]的质量比为2.6的圆柱双自由度涡激振动试验作为参考,圆柱直径为0.038 1 m,质量阻力比为0.013,固有频率为0.4 Hz,约化速度范围为2~14,约化速度间隔为0.2。数值过程中,采取3种不同的初始条件:
1) 匀加速:约化速度从2增加,加速度为0.025,增加至目标速度后保持30个周期,上一流速模拟结束的物理场是下一流速模拟的初始条件;
2) 匀减速:约化速度从14减少,加速度为-0.025,到达目标速度后模拟30个周期,上一流速模拟结束的物理场是下一流速模拟的初始条件;
3) 匀速:在数值模拟开始时,约化速度直接给定为目标约化速度,随后保持该约化速度30个周期。
3 计算结果对比与分析 3.1 幅值响应分析图 6(a)为3种初始条件下的圆柱双自由度涡激振动横向振幅随约化速度的变化曲线。通过对比可以发现,匀速和匀减速条件只能模拟出幅值响应中的初始分支与下端分支,而最重要的上端分支却无法得到;匀加速条件下得到了初始分支、下端分支和上端分支,其结果已经与试验结果较为接近。另外,匀加速与匀减速条件结合起来可以模拟出迟滞现象,其迟滞区间Ur范围为6~6.8,而Williamson试验的迟滞区间Ur范围为7.8~8.6,数值模拟的迟滞要提前于试验结果,但其迟滞区间的大小一致,都为0.8。

|
Download:
|
| 图 6 不同初始条件下的圆柱幅值与频率响应对比 Fig. 6 Comparison of the amplitude and frequency responses under different intial conditions | |
图 6(b)为相应的圆柱流向振幅随约化速度的变化曲线。可以发现匀速与匀减速条件都只能模拟出初始分支和下端分支,而匀加速条件可以将初始分支、下端分支和上端分支都模拟出来,但得到的最大幅值仍与试验值存在一定差别。匀加速与匀减速结合同样模拟出了迟滞区间,但迟滞区间较为提前。
3.2 无因次振动频率分析图 6(c)为不同初始条件下的圆柱横向无因次振动频率随约化速度的变化曲线与Williamson试验数据的对比。通过分析可以发现,匀速和匀减速条件下的锁定频率在1.25附近,匀加速条件下的锁定频率在1.33附近。对于锁定区间的范围,三种初始条件有较大的不同。匀速条件下,涡激振动的锁定区间范围为3.8~14;匀减速条件下,锁定区范围为4.2~12.8,其中4.2~6属于上端分支,6~12.8属于下端分支;匀加速条件下,锁定区范围也为4.2~12.8,但4.2~6.8属于上端分支,6.8~12.8属于下端分支。匀加速与匀减速条件得到的迟滞区间6~6.8提前于试验值的7.8~8.6,这与幅值响应分析相一致。
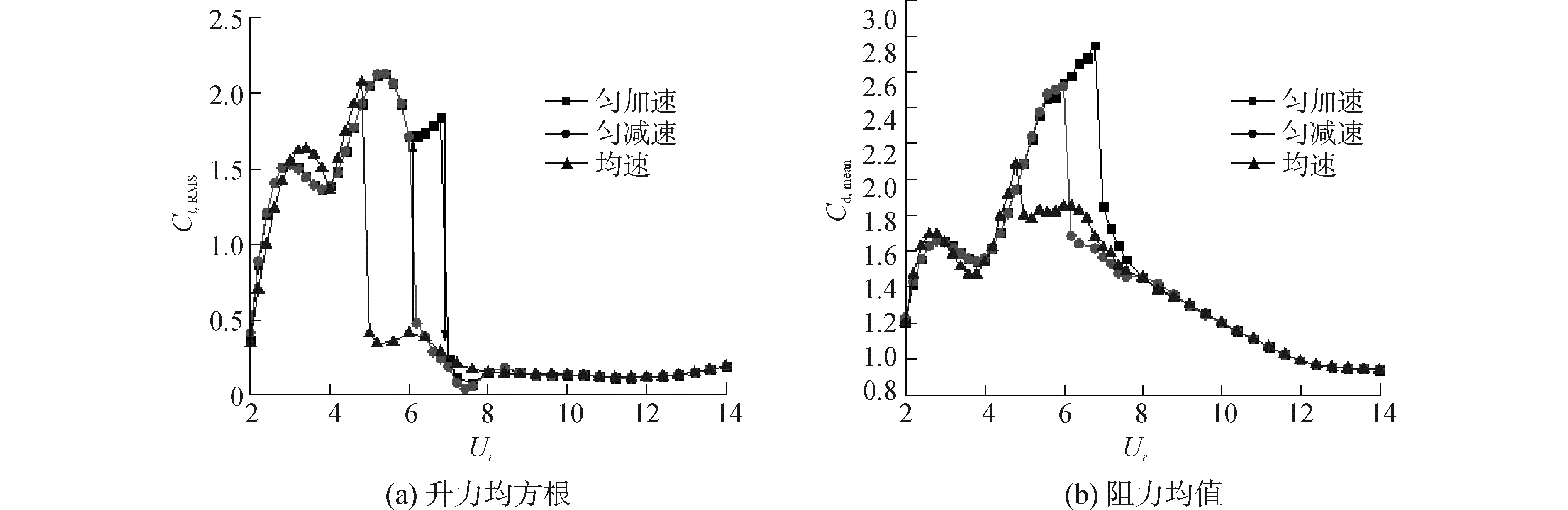
3.3 流体力分析图 7所示为三种初始条件下的升力均方根Cl, RMS和阻力均值Cd, mean曲线。对于升力,匀减速和匀加速条件下的趋势一致,但是其发生突变的Ur值不同。对于阻力,匀减速和匀加速条件在Ur范围内6~8结果出现一定的差别,匀速条件下的结果要明显偏小,无法模拟阻力峰值。另外,可以发现作用在圆柱表面的水动力系数也存在迟滞区域,并且迟滞区间与其振幅的幅值响应迟滞区间一致。
|
Download:
|
| 图 7 三种初始条件下升力均方根和阻力均值曲线对比 Fig. 7 Comparison of the curves of lift RMS and mean drag | |
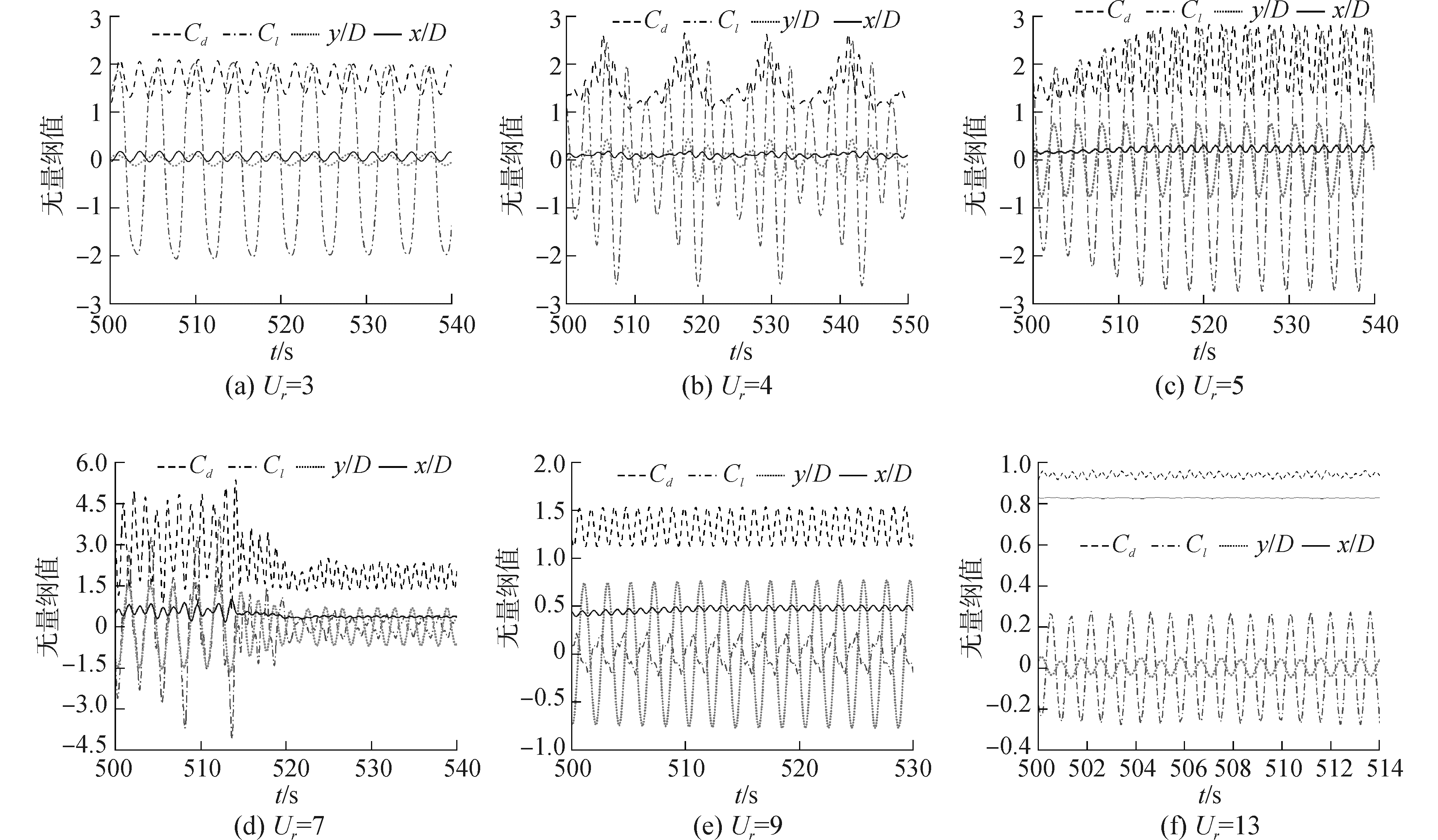
为系统分析流体力在各Ur下的特征,在图 8中给出了匀加速条件下的无量纲位移y/D、x/D、升力系数Cl以及阻力系数Cd曲线。可以发现,Ur=3时,y/D与Cl,x/D与Cd分别为同相位形式;Ur=4时,y/D、x/D、Cl及Cd曲线均出现了“拍”现象,这是由于此时由“初始分支”向“上端分支”过渡,存在两个相近的振动频率;Ur=5时,振动完全进入“上端分支”,此时y/D与Cl,x/D与Cd分别为同相位形式;Ur=7时,y/D与Cl,x/D与Cd均大幅减小并出现了“相位切换”现象。Ur=9时,升力系数曲线出现了“双峰”现象,这是由锁定区域的三倍频率分量导致的。Ur=13时,y/D、x/D、Cl及Cd均减小到很小的值,并且分别为反相位状态。
|
Download:
|
| 图 8 匀加速条件下的y/D、x/D、Cl及Cd随时间变化曲线 Fig. 8 Time dependent curves of y/D, x/D, Cl and Cd under the condition of acceleration | |
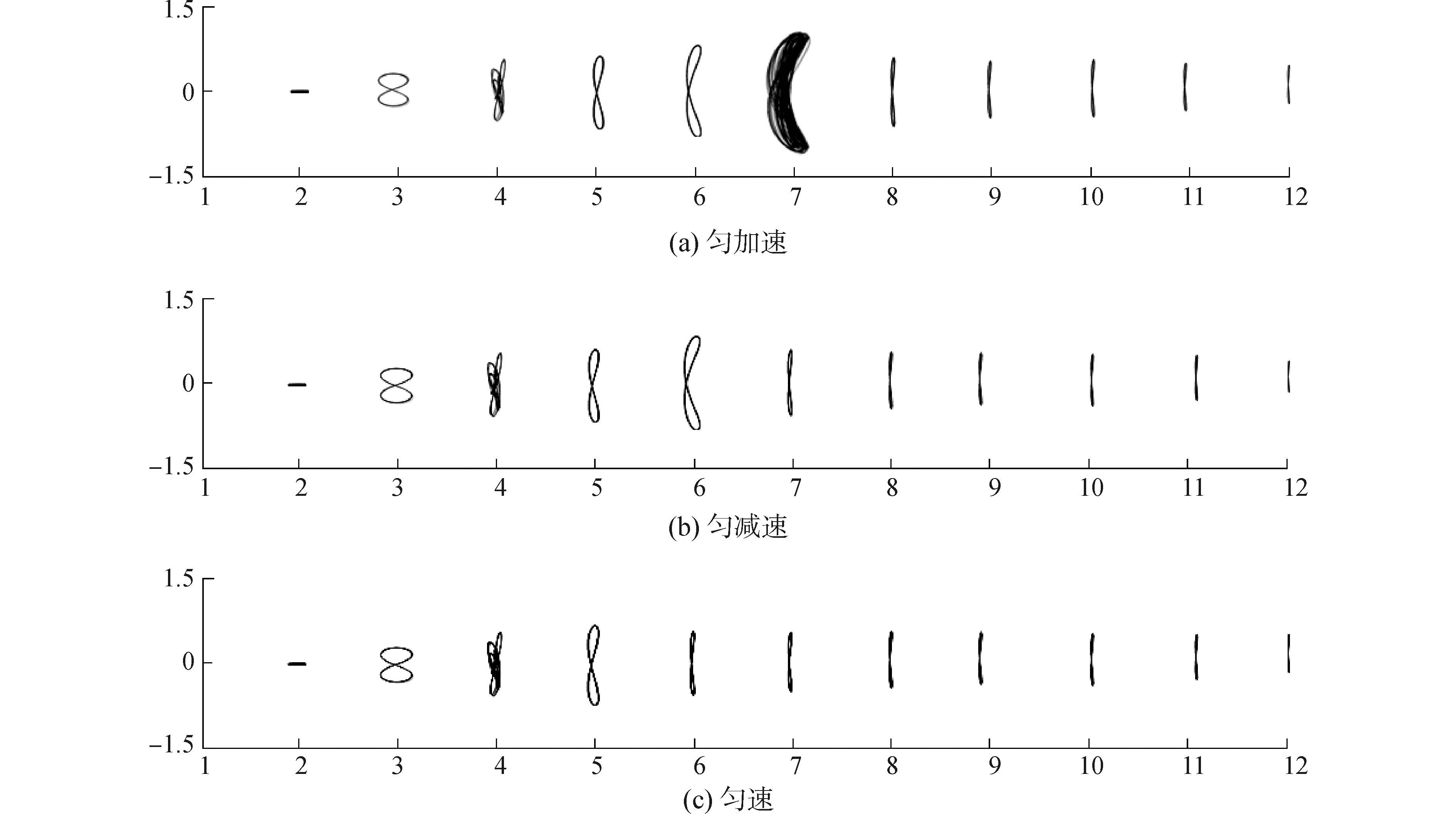
图 9给出了3种初始条件下的圆柱运动轨迹,匀加速条件下,Ur=2时,流向振幅大于横向振幅,呈现为一条横线;随着Ur的增加,横向振动幅值增大,呈现出标准“8”字形与瘦长“8”字形;Ur=7时,横向振幅达到最大,其轨迹被拉扯呈现为月牙形;Ur=8时,轨迹为极瘦长的“8”字形;Ur>9后,流向幅值较微弱,轨迹近似为一条竖线。
|
Download:
|
| 图 9 三种初始条件下的圆柱运动轨迹对比 Fig. 9 Comparison of the cylinder trajectories under three initial conditions | |
匀减速与匀速条件下其轨迹经历了近似横线、标准“8”字形、瘦长“8”字形、近似竖线的变化过程,匀减速条件缺少了月牙形,匀速条件则缺少了瘦长“8”字形和月牙形。
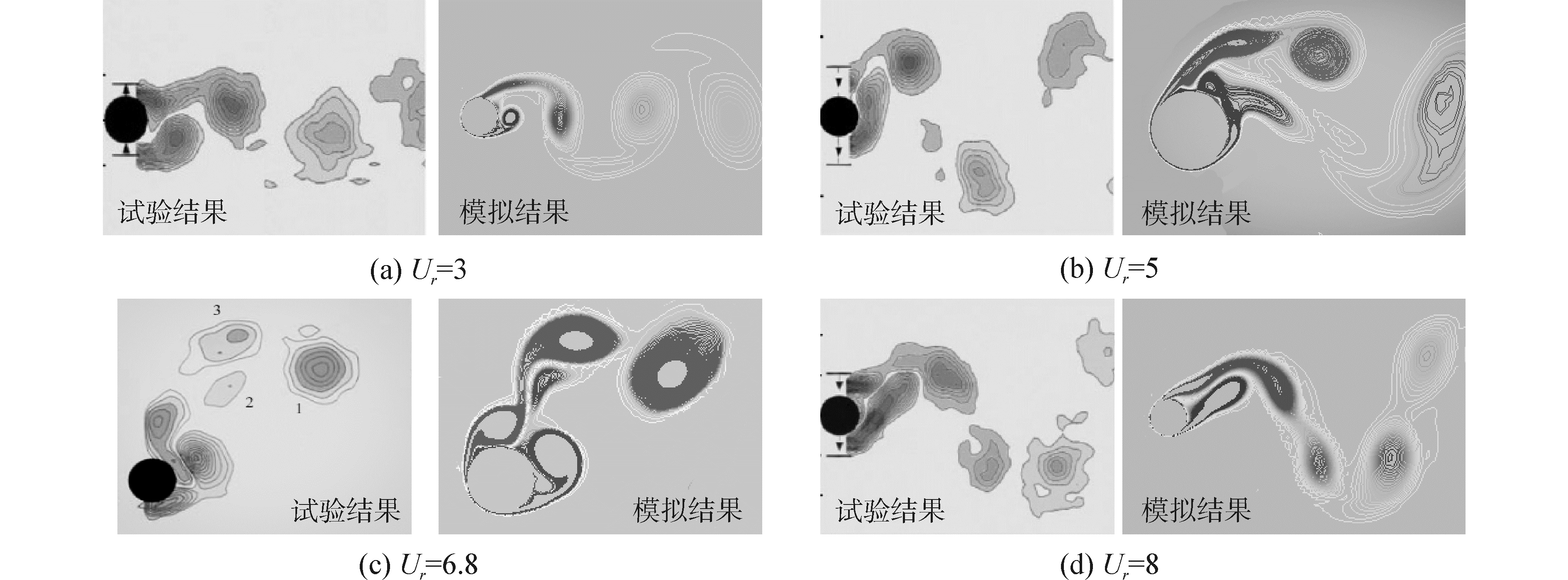
3.5 漩涡脱落分析图 10为匀加速条件下的数值模拟涡量等值云图与Williamson[5]试验结果的对比图。可以发现在各约化速度下匀加速条件的结果与试验结果保持一致,Ur=3时,对应初始分支,涡脱落模式为“2S”模式;Ur=5时,对应上端分支,涡脱落模式为“2P”模式;Ur=6.8时,对应超上端分支,涡脱落模式为“2T”模式;Ur=8时,对应下端分支,涡脱落模式变为“2P”模式,并且每个涡对中的两个涡强度相当。
|
Download:
|
| 图 10 匀加速条件下的圆柱泄涡等值云图 Fig. 10 Vortex cloud of the cylinder under the condition of acceleration | |
从上述分析中可以发现每个分支的变化都对应着涡脱落模式的变化,为观察匀速和匀减速条件在每个分支突变处的涡脱落变化,分别给出了两种初始条件的泄涡等值云图,如图 11、12所示。

|
Download:
|
| 图 11 匀速条件下的圆柱泄涡等值云图 Fig. 11 Vortex cloud under the condition of constant velocity | |

|
Download:
|
| 图 12 匀减速条件下的圆柱泄涡等值云图 Fig. 12 Vortex cloud under the condition of deceleration | |
分析图 11可以发现,Ur=5和Ur=6.8时涡脱落模式都为“2P”模式,该模式无法提供较大的脉动升力和阻力,因此得到的横向和顺向振幅中都缺失了上端分支。分析图 12可以发现,Ur=6.8时涡脱落模式为“2P”模式,随着Ur的降低,其所能提供的作用会逐渐超出维持“2P”模式的范围,Ur=6时,漩涡脱落模式变成了“2T”模式,该泄涡模式产生了较大脉动升力与阻力,使振幅显著增加。
总的来说,匀加速和匀减速条件的漩涡脱落模式的突变导致了幅值分支之间的突变,并且可以发现锁定区的涡脱落模式体现出“惯性”的性质,涡脱落模式总有着维持原脱落模式的趋势,当Ur提供的作用超出了维持原漩涡脱落模式的承受范围后,其脱落模式将出现突变,匀加速和匀减速的区别在于,匀加速条件是从“2T”模式突变为“2P”模式,其需要超出维持“2T”模式的承受范围,而匀减速条件则是从“2P”模式突变为“2T”模式,需要超出维持“2P”模式的承受范围,二者要超出的承受范围不同,因此发生突变的Ur不同,这也就产生了“迟滞现象”。
4 结论1) 与标准SST k-ω湍流模型相比,本文改进的湍流模型在圆柱绕流中的得到的结果更接近试验结果,并且其模拟的回流范围和漩涡强度更大,表明该改进湍流模型可以改善标准SST k-ω模型湍动能生成过低和对涡脱落抑制的缺点,进而有效提高计算精度。
2) 在三种初始条件下模拟得到的圆柱涡激振动幅值、频率、流体力、运动轨迹及漩涡脱落特点等有所区别,相比之下,匀加速条件下的结果最为准确,匀减速条件次之,匀速条件最差,表明涡激振动数值模拟中初始条件的设定对模拟结果有较大影响,并且本文改进的湍流模型在圆柱涡激振动中得到了进一步的验证,这对于准确预报结构物涡激振动特性具有较大的参考价值。
3) 通过对漩涡脱落模式进行分析,发现漩涡脱落模式的突变导致了流体力的突变进而使幅值分支发生突变,并且漩涡脱落模式体现出了“惯性”的性质,这是产生“迟滞现象”的内在原因之一。这些成果对涡激振动诸多现象的内在产生机理与特性等研究具有一定的推动作用。
| [1] |
KANG Zhuang, NI Wenchi, SUN Liping. An experimental investigation of two-degrees-of-freedom VIV trajectories of a cylinder at different scales and natural frequency ratios[J]. Ocean engineering, 2016, 126: 187-202. DOI:10.1016/j.oceaneng.2016.08.020 (  0) 0)
|
| [2] |
KANG Zhuang, NI Wenchi, SUN Liping. A numerical investigation on capturing the maximum transverse amplitude in vortex induced vibration for low mass ratio[J]. Marine structures, 2017, 52: 94-107. DOI:10.1016/j.marstruc.2016.11.006 (  0) 0)
|
| [3] |
KHALAK A, WILLIAMSON C H K. Dynamics of a hydroelastic cylinder with very low mass and damping[J]. Journal of fluids and structures, 1996, 10(5): 455-472. DOI:10.1006/jfls.1996.0031 (  0) 0)
|
| [4] |
GUILMINEAU E, QUEUTEY P. Numerical simulation of vortex-induced vibration of a circular cylinder with low mass-damping in a turbulent flow[J]. Journal of fluids and structures, 2004, 19(4): 449-466. DOI:10.1016/j.jfluidstructs.2004.02.004 (  0) 0)
|
| [5] |
JAUVTIS N, WILLIAMSON C. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping[J]. Journal of fluid mechanics, 2004, 509(509): 23-62. (  0) 0)
|
| [6] |
CELIK I, SHAFFER F D. Long time-averaged solutions of turbulent flow past a circular cylinder[J]. Journal of wind engineering and industrial aerodynamics, 1995, 56(2/3): 185-212. (  0) 0)
|
| [7] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 (  0) 0)
|
| [8] |
WILCOX D C. Turbulence modeling for CFD[M]. 3rd ed. Palm Drive, La Caada: DCW Industries, 2006.
(  0) 0)
|
| [9] |
JONES W P, LAUNDER B E. The calculation of low-Reynolds-number phenomena with a two-equation model of turbulence[J]. International journal of heat and mass transfer, 1973, 16(6): 1119-1130. DOI:10.1016/0017-9310(73)90125-7 (  0) 0)
|
| [10] |
FRANKE R, RODI W. Calculation of vortex shedding past a square cylinder with various turbulence models[M]//DURST F, FRIEDRICH R, LAUNDER B E, et al. Turbulent Shear Flows 8. Berlin Heidelberg: Springer, 1993: 189-204.
(  0) 0)
|
| [11] |
STRINGER R M, ZANG J, HILLIS A J. Unsteady RANS computations of flow around a circular cylinder for a wide range of Reynolds numbers[J]. Ocean engineering, 2014, 87: 1-9. DOI:10.1016/j.oceaneng.2014.04.017 (  0) 0)
|
| [12] |
甘文彪, 周洲, 许晓平, 等. 基于改进SST模型的分离流动数值模拟[J]. 推进技术, 2013, 34(5): 595-602. GAN Wenbiao, ZHOU Zhou, XU Xiaoping, et al. Investigation on improving the capability of predicting separation in modified SST turbulence model[J]. Journal of propulsion technology, 2013, 34(5): 595-602. (  0) 0)
|
| [13] |
ZDRAVKOVICH M M. Conceptual overview of laminar and turbulent flows past smooth and rough circular cylinders[J]. Journal of wind engineering and industrial aerodynamics, 1990, 33(1/2): 53-62. (  0) 0)
|
| [14] |
ESDU. ESDU 80025 Mean forces, pressures and flow field velocities for circular cylindrical structures: Single cylinder with two-dimensional flow[S]. London: ESDU International, 1986: 1-66.
(  0) 0)
|
| [15] |
NORBERG C. Fluctuating lift on a circular cylinder:review and new measurements[J]. Journal of fluids and structures, 2003, 17(1): 57-96. DOI:10.1016/S0889-9746(02)00099-3 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


