地磁场是地球的一个基本物理场,以地磁场为基础的地磁导航具有无源、无辐射、隐蔽性强、误差不随时间累积等众多优点,具有重要的军事意义[1-3]。因此地磁导航可为其他导航系统提供辅助手段实现载体的导航定位[4-6]。地磁匹配导航是指载体在运动过程中,利用磁传感器实时测定地磁场的有关特征值信息,并根据惯性导航系统输出的参考轨迹形状,与预先存储的地磁数据库在计算机中进行线图匹配,从而实现对载体的导航定位。
轮廓线匹配方法是目前常规的地磁匹配算法,通过在预先存储的地磁数据库中寻找与实际测量序列之间相关性指标最优的轨迹作为对真实轨迹的估计结果[7]。地磁轮廓线匹配方法具有原理简单、适用范围广、对初始误差要求低等优点,而且有均方差,平均绝对差、Hausdorff距离等多种相关性指标函数,可根据不同的应用条件予以选择。
然而,轮廓线匹配方法要求根据惯性导航系统输出的参考轨迹形状进行遍历求解,实时性难以保证。因此为了实现在线匹配,传统的轮廓线匹配方法只考虑惯性导航系统的初始位置误差,即遍历所有平行于参考轨迹的序列,匹配精度无法得到保证[8]。为了提高平行搜索的实时性,文献[9-10]提出一种基于等值线约束的地磁匹配算法,把不确定域转换为不确定曲线,减小了匹配计算量。文献[11]将平行搜索转化为一种迭代计算以提高匹配效率。文献[12]采用迭代评价匹配算法,根据惯导输出和实测地磁数据自适应调整匹配数据序列长度和迭代步数,具有较好的实时性。此外,文献[13]考虑了惯导系统的初始位置和初始航向两种误差,并以迭代方法求解匹配结果,保证了算法实时性的同时又提高了匹配定位精度。文献[14]则考虑了惯导系统的初始位置、初始航向和初始速度三种误差,并以粗精二级匹配缩短遍历搜索的计算时间。
为了更好地解决地磁匹配精度和匹配算法实时性相互制约的问题,本文将综合文献[13-14]两种算法的优点,在文献[13]的基础上额外考虑了惯导系统的初始速度误差,并以迭代计算替代了文献[14]的遍历求解手段,进而提出一种匹配精度高、实时性好的基于仿射参数估计的地磁匹配导航算法。
1 地磁匹配仿射模型地磁轮廓线匹配要求根据惯性导航系统输出的参考轨迹形状搜索地磁数据库信息进行匹配运算。因此需要对参考轨迹与真实轨迹之间的关系建立数学模型。根据惯性导航系统的解算要求,分别考虑如下3种误差[14]:
1) 在地磁匹配开始前,惯性导航系统存在初始位置误差,计为(Δx, Δy),其中Δx为初始经度误差,Δy为初始纬度误差。
2) 地磁匹配导航定位过程中,惯性导航系统的解算速度v为
| $ v = {v_r} + {\mathit{\Delta } _v} + {\varepsilon _v} $ | (1) |
式中:vr为载体的真实速度,Δv为地磁匹配导航定位前载体速度累积误差(即地磁匹配前惯性导航系统的初始速度误差),εv为地磁匹配导航定位过程中速度误差的变化量。由于地磁匹配导航定位历时短,地磁匹配导航定位过程中速度误差变化量εv远远小于地磁匹配导航定位前载体速度累积误差Δv,因此式(1)可以简化为
| $ v = {v_r} + {\mathit{\Delta } _v} $ | (2) |
3) 地磁匹配导航定位过程中,惯性导航系统的解算航向d为
| $ d = {d_r} + {\mathit{\Delta } _d} + {\varepsilon _d} $ | (3) |
式中:dr为载体的真实航向,Δd为地磁匹配导航定位前载体航向累积误差(即地磁匹配前惯性导航系统的初始航向误差),εd为地磁匹配导航定位过程中航向误差的变化量。由于地磁匹配导航定位历时短,地磁匹配导航定位过程中航向误差变化量εd远远小于地磁匹配导航定位前载体航向累积误差Δd,因此式(3)可以简化为
| $ d = {d_r} + {\mathit{\Delta } _d} $ | (4) |
由以上分析可知,在地磁匹配导航定位的这段时间内,惯性导航系统输出的参考轨迹和载体的真实轨迹之间可以简化为一个曲线间的仿射变换。而惯性导航系统的初始位置误差对应着仿射变换的平移参数,惯性导航系统的初始航向误差对应着仿射变换的旋转参数以及惯性导航系统的初始速度误差对应着仿射变换的伸缩误差。因此可以建立一个简单的仿射变换模型:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} u\\ w \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{k_1}}&0\\ 0&{{k_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{\sin \alpha }\\ { - \sin \alpha }&{\cos \alpha } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {a - {a_1}}\\ {b - {b_1}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{a_1}}\\ {{b_1}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y} \end{array}} \right]} \end{array} $ | (5) |
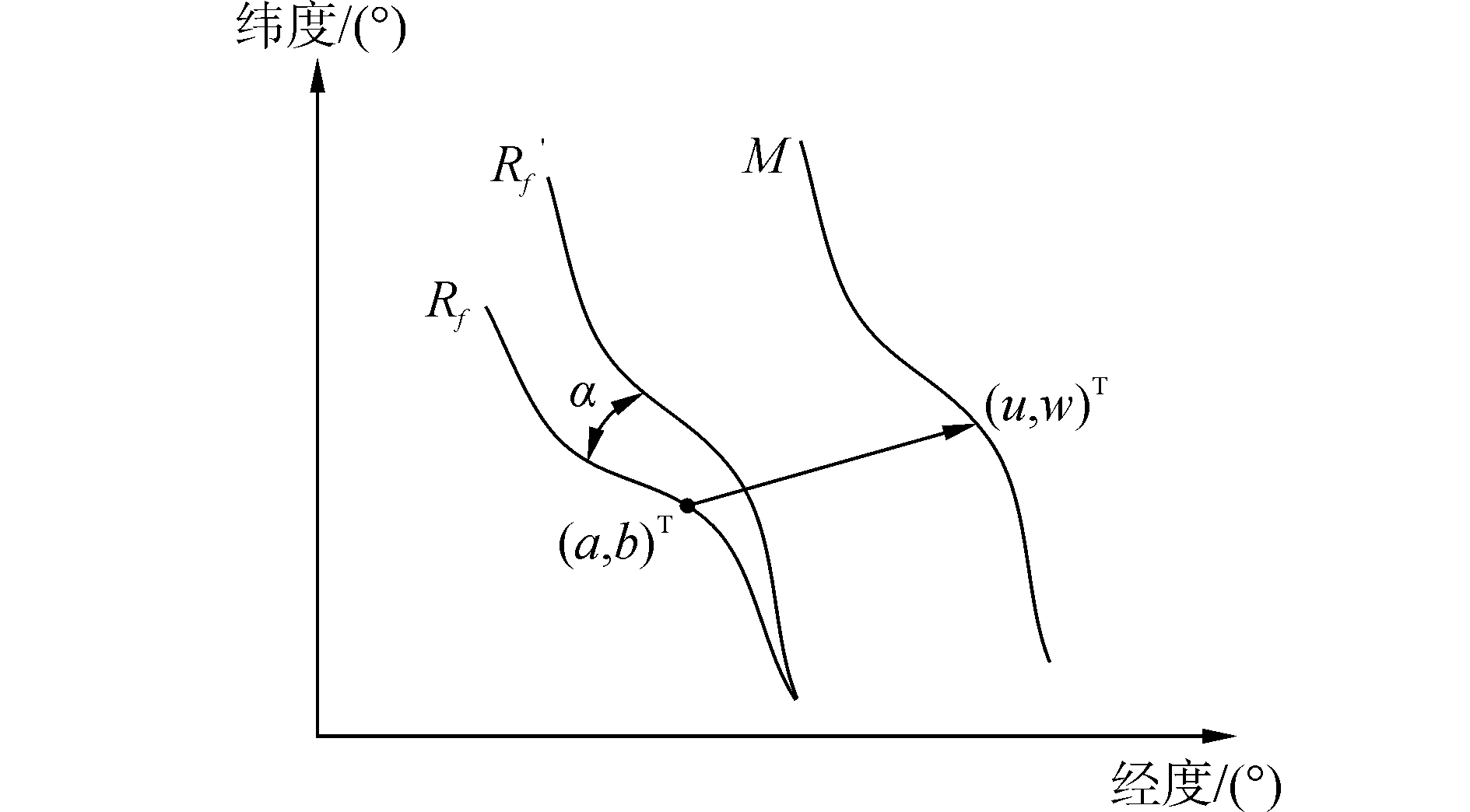
式中:(a, b)T表示惯性导航系统输出的参考轨迹的坐标,a表示经度,b表示纬度,(a1, b1)T表示匹配开始时惯性导航系统解算的初始点坐标,(u, w)T表示载体真实轨迹的坐标,u表示经度,w表示纬度,Δx和Δy分别表示惯性导航系统的初始经度误差和纬度误差,α表示惯性导航系统初始航向误差导致的仿射模型旋转参数,k1和k2表示惯性导航系统初始速度误差导致的仿射模型的伸缩参数。
图 1给出了上述的地磁匹配仿射模型示意图。其中曲线Rf为惯导系统输出的轨迹曲线,即参考轨迹;曲线M为真实轨迹;曲线Rf′与真实轨迹平行。从图中可以看出,参考轨迹和真实轨迹之间存在着平移、旋转和伸缩。
|
Download:
|
| 图 1 地磁匹配仿射模型示意图 Fig. 1 Description of geomagnetic matching affine model | |
采用MSD计算曲线的相关性,即计算匹配轨迹序列上各点的地磁场特征值与真实测量所得的地磁场特征值之差的平方和的平均值,该值最小对应的轨迹序列就是最优的匹配位置。
分别用I(ai, bi)、I(ui, wi)表示点(ai, bi)T和点(ui, wi)T所在位置对应的地磁图库中地球磁场特征值,下标i表示相应轨迹序列点的第i点。用Ir(ai, bi)表示载体在参考点(ai, bi)T时,磁强计实时测量得到的地磁场特征值,则MSD相关性指标函数可以表示为
| $ E = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {I\left( {{u_i},{w_i}} \right) - {I_r}\left( {{a_i},{b_i}} \right)} \right]}^2}} $ | (6) |
式中N为参考轨迹序列点的总个数。
传统的地磁轮廓线匹配方法采用遍历的手段求解匹配轨迹,为了提高匹配搜索速度,往往仅考虑惯导系统的初始位置误差,即仅遍历所有平行于参考轨迹的序列。若加入航向误差和速度误差进行搜索,计算量急剧增大,难以在线计算。
本文在匹配曲线的形状约束中(式(5))引入MSD相关性指标函数(式(6)),从而将地磁匹配问题转化为仿射参数的估计问题,通过仿射模型参数的反复迭代完成地磁匹配,提高匹配算法的实时性。
考虑到真实轨迹在参考轨迹附近,即可将I(ui, wi)在参考点(ai, bi)T处泰勒展开:
| $ \begin{array}{*{20}{c}} {I\left( {{u_i},{w_i}} \right) = I\left( {{a_i},{b_i}} \right) + \frac{{\partial I\left( {{a_i},{b_i}} \right)}}{{\partial x}}\left( {{u_i} - {a_i}} \right) + }\\ {\frac{{\partial I\left( {{a_i},{b_i}} \right)}}{{\partial y}}\left( {{w_i} - {b_i}} \right) + {O_2}} \end{array} $ | (7) |
式中:∂I(ai, bi)/∂x表示地磁场特征值对经度方向的梯度在点(ai, bi)T上的取值,∂I(ai, bi)/∂y表示地磁场特征值对纬度方向的梯度在点(ai, bi)T上的取值,O2为泰勒展开后的二阶及二阶以上高阶小项。
将式(7)代入式(6),并忽略二阶及二阶以上高阶小项可得
| $ \begin{array}{*{20}{c}} {E = \frac{1}{N}\sum\limits_{i = 1}^N {\left[ {\frac{{\partial I\left( {{a_i},{b_i}} \right)}}{{\partial x}}\left( {{u_i} - {a_i}} \right) + \frac{{\partial I\left( {{a_i},{b_i}} \right)}}{{\partial y}}\left( {{w_i} - {b_i}} \right) + } \right.} }\\ {{{\left. {\left( {I\left( {{a_i},{b_i}} \right) - {I_r}\left( {{a_i},{b_i}} \right)} \right)} \right]}^2}} \end{array} $ | (8) |
在不引起混淆的情况下,将式(8)写成如下简化形式:
| $ E = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {{I_{x,i}}\left( {{u_i} - {a_i}} \right){I_{y,i}}\left( {{w_i} - {b_i}} \right) + {I_{z,i}}} \right]}^2}} $ | (9) |
其中
| $ {I_{x,i}} = \frac{{\partial I\left( {{a_i},{b_i}} \right)}}{{\partial x}} $ | (10) |
| $ {I_{y,i}} = \frac{{\partial I\left( {{a_i},{b_i}} \right)}}{{\partial y}} $ | (11) |
| $ {I_{z,i}} = I\left( {{a_i},{b_i}} \right) - {I_r}\left( {{a_i},{b_i}} \right) $ | (12) |
将仿射变换模型(5)代入MSD相关性指标函数(9)可得
| $ \begin{array}{*{20}{c}} {E = \frac{1}{N}\sum\limits_{i = 1}^N {\left[ {{I_{x,i}}\left( {{k_1}{{a'}_i}\cos \alpha + {k_1}{{b'}_i}\sin \alpha - {{a'}_i} + \Delta x} \right) + } \right.} }\\ {{{\left. {{I_{y,i}}\left( { - {k_2}{{a'}_i}\sin \alpha + {k_2}{{b'}_i}\cos \alpha - {{b'}_i} + \Delta y} \right) + {I_{z,i}}} \right]}^2}} \end{array} $ | (13) |
其中
| $ {{a'}_i} = {a_i} - {a_1} $ | (14) |
| $ {{b'}_i} = {b_i} - {b_1} $ | (15) |
因此地磁匹配问题可以转化为寻求仿射模型参数Δx、Δy、α、k1和k2,使式(13)取极小值。可将式(13)对仿射模型参数Δx、Δy、α、k1和k2求一阶偏导数,并令其为零,即
| $ \frac{{\partial E}}{{\partial \Delta x}} = 0,\frac{{\partial E}}{{\partial \Delta y}} = 0,\frac{{\partial E}}{{\partial \alpha }} = 0,\frac{{\partial E}}{{\partial {k_1}}} = 0,\frac{{\partial E}}{{\partial {k_2}}} = 0 $ | (16) |
将MSD相关性指标函数式(13)代入式(16)可得
| $ \begin{array}{*{20}{c}} {{g_1}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right) = \frac{N}{2}\frac{{\partial E}}{{\partial \Delta x}} = }\\ {\sum\limits_{i = 1}^N {\left[ {I_{x,i}^2\left( {{k_1}{{a'}_i}\cos \alpha + {k_1}{{b'}_i}\sin \alpha - {{a'}_i} + \Delta x} \right) + } \right.} }\\ {\left. {{I_{x,i}}{I_{y,i}}\left( {{k_2}{{b'}_i}\cos \alpha - {k_2}{{a'}_i}\sin \alpha - {{b'}_i} + \Delta y} \right) + {I_{x,i}}{I_{z,i}}} \right]} \end{array} $ | (17) |
| $ \begin{array}{*{20}{c}} {{g_2}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right) = \frac{N}{2}\frac{{\partial E}}{{\partial \Delta y}} = }\\ {\sum\limits_{i = 1}^N {\left[ {{I_{x,i}}{I_{y,i}}\left( {{k_1}{{a'}_i}\cos \alpha + {k_1}{{b'}_i}\sin \alpha - {{a'}_i} + \Delta x} \right) + } \right.} }\\ {\left. {I_{y,i}^2\left( {{k_2}{{b'}_i}\cos \alpha - {k_2}{{a'}_i}\sin \alpha - {{b'}_i} + \Delta y} \right) + {I_{y,i}}{I_{z,i}}} \right]} \end{array} $ | (18) |
| $ \begin{array}{*{20}{c}} {{g_3}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right) = \frac{N}{2}\frac{{\partial E}}{{\partial \alpha }} = }\\ {\sum\limits_{i = 1}^N {\left\{ {\left[ {{I_{x,i}}\left( {{k_1}{{a'}_i}\cos \alpha + {k_1}{{b'}_i}\sin \alpha - {{a'}_i} + \Delta x} \right) + } \right.} \right.} }\\ {\left. {{I_{y,i}}\left( {{k_2}{{b'}_i}\cos \alpha - {k_2}{{a'}_i}\sin \alpha - {{b'}_i} + \Delta y} \right) + {I_{z,i}}} \right] \times }\\ {\left[ {{I_{x,i}}{k_1}\left( {{{b'}_i}\cos \alpha - {{a'}_i}\sin \alpha } \right) - } \right.}\\ {\left. {\left. {{I_{y,i}}{k_2}\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)} \right]} \right\}} \end{array} $ | (19) |
| $ \begin{array}{*{20}{c}} {{g_4}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right) = \frac{N}{2}\frac{{\partial E}}{{\partial {k_1}}} = }\\ {\sum\limits_{i = 1}^N {\left\{ {\left[ {{I_{x,i}}\left( {{k_1}{{a'}_i}\cos \alpha + {k_1}{{b'}_i}\sin \alpha - {{a'}_i} + \Delta x} \right) + } \right.} \right.} }\\ {\left. {{I_{y,i}}\left( {{k_2}{{b'}_i}\cos \alpha - {k_2}{{a'}_i}\sin \alpha - {{b'}_i} + \Delta y} \right) + {I_{z,i}}} \right] \times }\\ {\left. {\left( {{I_{x,i}}{{\alpha '}_i}\cos \alpha + {I_{x,i}}{{b'}_i}\sin \alpha } \right)} \right\}} \end{array} $ | (20) |
| $ \begin{array}{*{20}{c}} {{g_5}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right) = \frac{N}{2}\frac{{\partial E}}{{\partial {k_2}}} = }\\ {\sum\limits_{i = 1}^N {\left\{ {\left[ {{I_{x,i}}\left( {{k_1}{{a'}_i}\cos \alpha + {k_1}{{b'}_i}\sin \alpha - {{a'}_i} + \Delta x} \right) + } \right.} \right.} }\\ {\left. {{I_{y,i}}\left( {{k_2}{{b'}_i}\cos \alpha - {k_2}{{a'}_i}\sin \alpha - {{b'}_i} + \Delta y} \right) + {I_{z,i}}} \right] \times }\\ {\left. {\left( { - {I_{y,i}}{{\alpha '}_i}\sin \alpha + {I_{y,i}}{{b'}_i}\cos \alpha } \right)} \right\}} \end{array} $ | (21) |
因此地磁匹配问题可转化为由仿射模型参数Δx、Δy、α、k1和k2组成的非线性方程组
| $ \left\{ \begin{array}{l} {g_1}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right) = 0\\ {g_2}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right) = 0\\ {g_3}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right) = 0\\ {g_4}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right) = 0\\ {g_5}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right) = 0 \end{array} \right. $ | (22) |
求解问题。匹配结果可以根据非线性方程组(22)的解和式(5)计算得到。
3 地磁匹配迭代求解非线性方程组(22)可以采用Broyden迭代方法求解。求解时,(ai, bi)T由惯导系统给出,Ir(ai, bi)由与载体捷联的磁强计得到; I(ai, bi)根据惯导系统指示的位置,在地磁数据库中检索得到; Ix, i和Iy, i可以通过检索地磁数据库中的地磁特征值信息在线计算得到,也可将匹配区域的地磁特征值的梯度信息事先存入导航计算机,匹配计算时直接在导航计算机中检索得到。
基于仿射参数估计的地磁匹配导航算法的实现步骤如下:
1) 从惯导系统得到N个待匹配点的参考坐标(ai, bi)T;从磁强计得到载体在这N个待匹配点的地磁特征信息的实时测量值Ir(ai, bi)。
2) 根据惯导系统指示的N个待匹配点的坐标,从预先存储的地磁数据库中检索得到相应的地磁特征值I(ai, bi),并计算或检索得到地磁特征值的梯度信息Ix, i和Iy, i。
3) 引入并初始化匹配位置偏移量、航向偏移量和伸缩系数:
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {\Delta x}&{\Delta y}&\alpha &{{k_1}}&{{k_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&0&1&1 \end{array}} \right] $ | (23) |
4) 根据式(24)~(26)计算迭代参数G、F和H:
| $ \mathit{\boldsymbol{G}} = g\left( \mathit{\boldsymbol{M}} \right) $ | (24) |
| $ \mathit{\boldsymbol{F}} = f\left( \mathit{\boldsymbol{M}} \right) $ | (25) |
| $ \mathit{\boldsymbol{H}} = {\mathit{\boldsymbol{F}}^{ - 1}} $ | (26) |
其中
| $ g\left( \mathit{\boldsymbol{M}} \right) = \left[ {\begin{array}{*{20}{c}} {{g_1}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right)}\\ {{g_2}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right)}\\ {{g_3}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right)}\\ {{g_4}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right)}\\ {{g_5}\left( {\Delta x,\Delta y,\alpha ,{k_1},{k_2}} \right)} \end{array}} \right] $ |
| $ f\left( \mathit{\boldsymbol{M}} \right) = \left[ {\begin{array}{*{20}{c}} {{f_{11}}}&{{f_{12}}}&{{f_{13}}}&{{f_{14}}}&{{f_{15}}}\\ {{f_{12}}}&{{f_{22}}}&{{f_{23}}}&{{f_{24}}}&{{f_{25}}}\\ {{f_{13}}}&{{f_{23}}}&{{f_{33}}}&{{f_{34}}}&{{f_{35}}}\\ {{f_{14}}}&{{f_{24}}}&{{f_{34}}}&{{f_{44}}}&{{f_{45}}}\\ {{f_{15}}}&{{f_{25}}}&{{f_{35}}}&{{f_{45}}}&{{f_{55}}} \end{array}} \right] $ |
| $ {f_{11}} = \sum\limits_{i = 1}^N {I_{x,i}^2} $ |
| $ {f_{12}} = \sum\limits_{i = 1}^N {{I_{x,i}}{I_{y,i}}} $ |
| $ \begin{array}{*{20}{c}} {{f_{13}} = \sum\limits_{i = 1}^N {\left[ {I_{x,i}^2{k_1}\left( {{{b'}_i}\cos \alpha - {{a'}_i}\sin \alpha } \right) - } \right.} }\\ {\left. {{I_{x,i}}{I_{y,i}}{k_2}\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)} \right]} \end{array} $ |
| $ {f_{14}} = \sum\limits_{i = 1}^N {I_{x,i}^2\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)} $ |
| $ {f_{15}} = \sum\limits_{i = 1}^N {{I_{x,i}}{I_{y,i}}\left( {{{b'}_i}\cos \alpha - {{a'}_i}\sin \alpha } \right)} $ |
| $ {f_{22}} = \sum\limits_{i = 1}^N {I_{y,i}^2} $ |
| $ \begin{array}{*{20}{c}} {{f_{23}} = \sum\limits_{i = 1}^N {\left[ {{I_{x,i}}{I_{y,i}}{k_1}\left( {{{b'}_i}\cos \alpha - {{a'}_i}\sin \alpha } \right) - } \right.} }\\ {\left. {I_{y,i}^2{k_2}\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)} \right]} \end{array} $ |
| $ {f_{24}} = \sum\limits_{i = 1}^N {{I_{x,i}}{I_{y,i}}\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)} $ |
| $ {f_{25}} = \sum\limits_{i = 1}^N {I_{y,i}^2\left( {{{b'}_i}\cos \alpha - {{a'}_i}\sin \alpha } \right)} $ |
| $ \begin{array}{*{20}{c}} {{f_{33}} = \sum\limits_{i = 1}^N {\left\{ {\left( {{I_{x,i}}{k_1}\left( {{{b'}_i}\cos \alpha - {{a'}_i}\sin \alpha } \right)} \right) - } \right.} }\\ {{{\left. {{I_{y,i}}{k_2}\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)} \right]}^2} + }\\ {\left[ {{I_{x,i}}\left( {{k_1}{{a'}_i}\cos \alpha + {k_1}{{b'}_i}\sin \alpha - {{a'}_i} + \Delta x} \right) + } \right.}\\ {\left. {{I_{y,i}}\left( { - {k_2}{{a'}_i}\sin \alpha + {k_2}{{b'}_i}\cos \alpha - {{b'}_i} + \Delta y} \right) + {I_{z,i}}} \right] \times }\\ {\left[ {{I_{y,i}}{k_2}\left( {{{a'}_i}\sin \alpha + {{b'}_i}\cos \alpha } \right) - } \right.}\\ {\left. {\left. {{I_{x,i}}{k_1}\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)} \right]} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{f_{34}} = \sum\limits_{i = 1}^N {\left\{ {\left[ {{I_{x,i}}{k_1}\left( {{{b'}_i}\cos \alpha - {{\alpha '}_i}\sin \alpha } \right) - } \right.} \right.} }\\ {\left. {{I_{y,i}}{k_2}\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)} \right] \times }\\ {\left[ {{I_{x,i}}\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)} \right] + }\\ {\left[ {{I_{x,i}}\left( {{k_1}{{a'}_i}\cos \alpha + {k_1}{{b'}_i}\sin \alpha - {{a'}_i} + \Delta x} \right) + } \right.}\\ {\left. {{I_{y,i}}\left( { - {k_2}{{a'}_i}\sin \alpha + {k_2}{{b'}_i}\cos \alpha - {{b'}_i} + \Delta y} \right) + {I_{z,i}}} \right] \times }\\ {\left. {\left( { - {I_{x,i}}{{a'}_i}\sin \alpha + {I_{x,i}}{{b'}_i}\cos \alpha } \right)} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{f_{35}} = \sum\limits_{i = 1}^N {\left\{ {\left[ {{I_{x,i}}{k_1}\left( {{{b'}_i}\cos \alpha - {{\alpha '}_i}\sin \alpha } \right) - } \right.} \right.} }\\ {\left. {{I_{y,i}}{k_2}\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)} \right] \times }\\ {\left[ {{I_{y,i}}\left( {{{b'}_i}\cos \alpha - {{a'}_i}\sin \alpha } \right)} \right] + }\\ {\left[ {{I_{x,i}}\left( {{k_1}{{a'}_i}\cos \alpha + {k_1}{{b'}_i}\sin \alpha - {{a'}_i} + \Delta x} \right) + } \right.}\\ {\left. {{I_{y,i}}\left( { - {k_2}{{a'}_i}\sin \alpha + {k_2}{{b'}_i}\cos \alpha - {{b'}_i} + \Delta y} \right) + {I_{z,i}}} \right] \times }\\ {\left. {\left( { - {I_{y,i}}{{a'}_i}\cos \alpha - {I_{y,i}}{{b'}_i}\sin \alpha } \right)} \right\}} \end{array} $ |
| $ {f_{44}} = \sum\limits_{i = 1}^N {I_{x,i}^2{{\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)}^2}} $ |
| $ {f_{45}} = \sum\limits_{i = 1}^N {{I_{x,i}}{I_{y,i}}\left( {{{a'}_i}\cos \alpha + {{b'}_i}\sin \alpha } \right)\left( {{{b'}_i}\cos \alpha - {{a'}_i}\sin \alpha } \right)} $ |
| $ {f_{55}} = \sum\limits_{i = 1}^N {I_{y,i}^2{{\left( {{{b'}_i}\cos \alpha - {{a'}_i}\sin \alpha } \right)}^2}} $ |
5) 计算匹配位置偏移量、航向偏移量和伸缩系数的增量:
| $ \delta \mathit{\boldsymbol{M}} = - \mathit{\boldsymbol{H}} \times \mathit{\boldsymbol{G}} $ | (27) |
6) 更新匹配位置偏移量、航向偏移量和伸缩系数:
| $ \mathit{\boldsymbol{M}} = \mathit{\boldsymbol{M}} + \delta \mathit{\boldsymbol{M}} $ | (28) |
7) 判断是否满足终止迭代条件,若满足则停止迭代并跳到10),否则跳到8)。
终止迭代条件为以下(a)、(b)中的任意一个:(a)迭代次数达到预设的最大迭代次数;(b)匹配位置偏移量的增量、航向偏移量的增量和伸缩系数的增量δM的2范数小于预先给定的迭代最小误差,即
| $ {\left\| {\delta \mathit{\boldsymbol{M}}} \right\|_2} < \varepsilon $ | (29) |
式中ε为预先给定的迭代最小误差。
8) 根据更新后的M计算参数N和δN:
| $ \mathit{\boldsymbol{N}} = g\left( \mathit{\boldsymbol{M}} \right) $ | (30) |
| $ \delta \mathit{\boldsymbol{N}} = \mathit{\boldsymbol{N}} - \mathit{\boldsymbol{G}} $ | (31) |
9) 根据式(32)~(33)计算迭代变量H和G,并跳到5)。
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}} = \mathit{\boldsymbol{H}} + \left[ {\left( {\delta \mathit{\boldsymbol{M}}} \right) - \mathit{\boldsymbol{H}}\left( {\delta \mathit{\boldsymbol{N}}} \right)} \right]{{\left( {\delta \mathit{\boldsymbol{M}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{H}}/}\\ {\left[ {{{\left( {\delta \mathit{\boldsymbol{M}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{H}}\left( {\delta \mathit{\boldsymbol{N}}} \right)} \right]} \end{array} $ | (32) |
| $ \mathit{\boldsymbol{G}} = \mathit{\boldsymbol{N}} $ | (33) |
10)根据迭代计算得到的匹配位置偏移量、航向偏移量和伸缩系数M,按式(34)计算输出匹配结果。
| $ \left[ {\begin{array}{*{20}{c}} {{u_i}}\\ {{w_i}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{k_1}}&0\\ 0&{{k_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{\sin \alpha }\\ { - \sin \alpha }&{\cos \alpha } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{a'}_i}}\\ {{{b'}_i}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{a_i}}\\ {{b_i}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y} \end{array}} \right] $ | (34) |
需要指出的是,基于仿射参数估计的地磁匹配导航算法将真实轨迹序列的地磁特征值函数在相应参考点进行泰勒展开,忽略了二阶及二阶以上高阶小项,以一阶差分形式近似MSD相关性指标函数。当惯导系统初始误差较大时,忽略二阶及二阶以上高阶小项会对相关性指标函数产生较大误差,影响算法精度。因此可采用多次迭代的方式克服上述影响,提高算法的匹配精度。多次迭代时,用上次迭代得到的匹配结果作为下次迭代的参考轨迹序列。由于迭代算法可以补偿大部分惯导系统的初始误差,因此上次迭代的结果较为接近真实轨迹,以其作为下次迭代的参考轨迹,可以降低二阶及二阶以上高阶小项对相关性指标函数的影响,提高匹配精度。
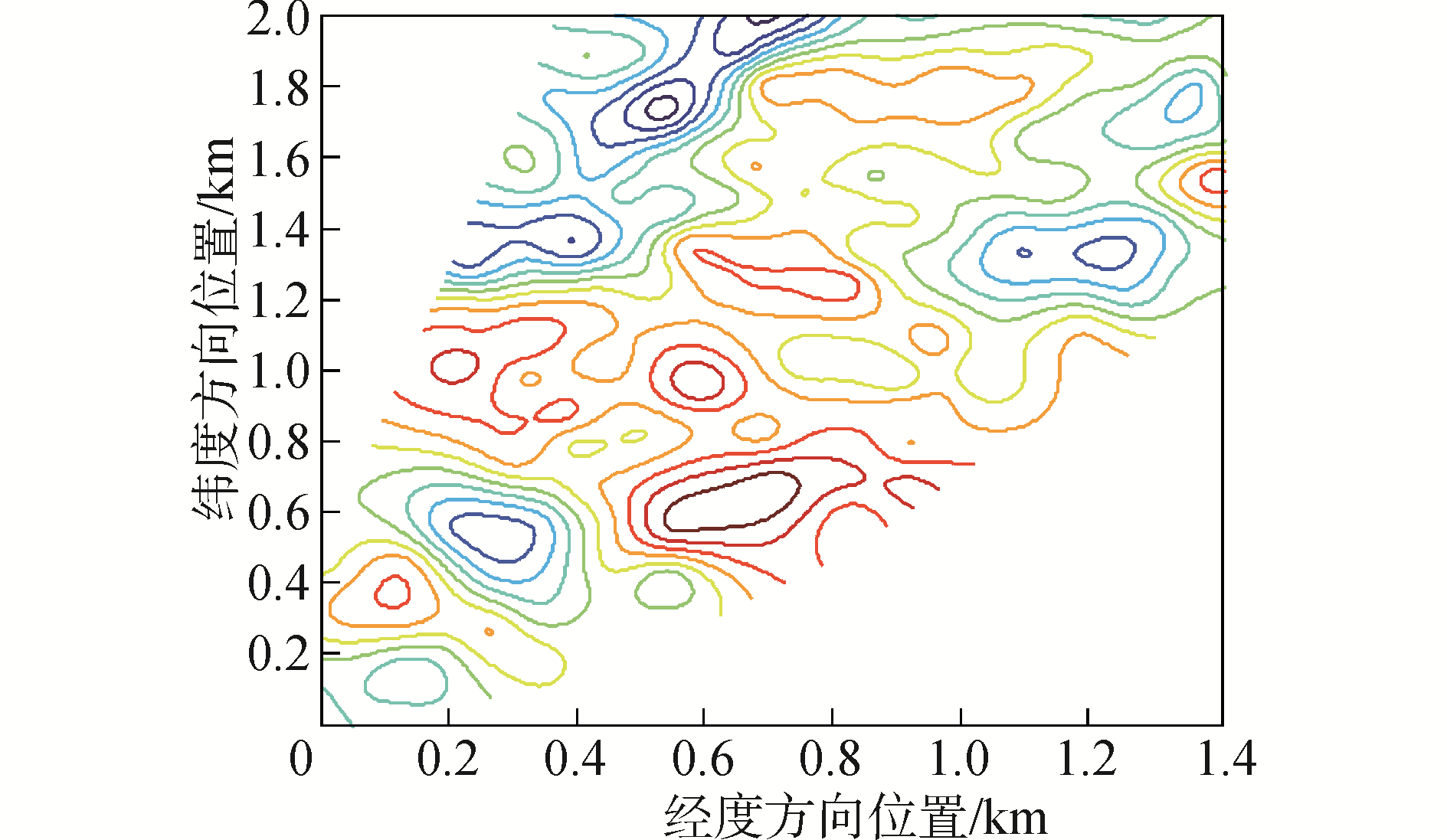
4 地磁匹配试验验证采用外场试验验证算法的有效性。试验区域选择哈尔滨周边某地磁异常场变换较为剧烈的区域。地磁图的测量采用加拿大GEM公司生产的GSM-19T高精度质子磁力仪。该磁力仪测量值为地磁总场,同时根据2015年推出的第12代国际地磁场模型(IGRF12)计算主磁场,由两者相减得到试验区域的地磁异常数据,图 2给出了该区域地磁异常场等值线图。
|
Download:
|
| 图 2 试验区域地磁异常场等值线图 Fig. 2 Geomagnetic contour map of the experiment region | |
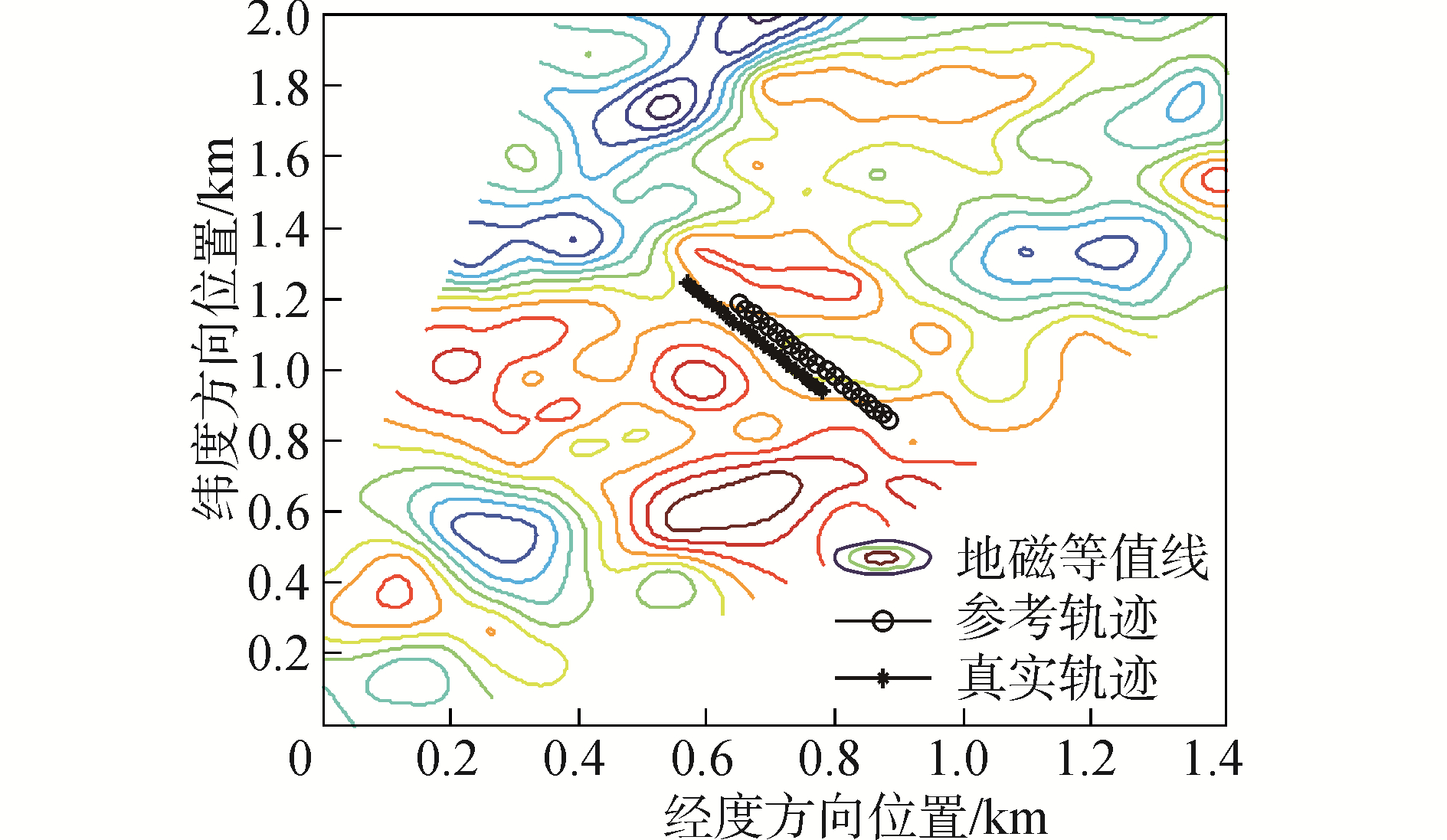
惯性导航系统中的陀螺漂移为0.5(°)/h,加表零偏为0.05 mg。试验中,以GPS信号作为试验载体的真实位置。由于匹配区域较小、历时较短,故地磁日变采用常值补偿。设置惯导系统的初始位置误差为(82 m, 57 m),初始航向误差为3°,初始速度误差为(1 m/s, 2 m/s)。载体的真实位置轨迹和由惯导系统计算得到的参考轨迹如图 3所示。
|
Download:
|
| 图 3 参考轨迹和真实轨迹 Fig. 3 The reference track and the real track | |
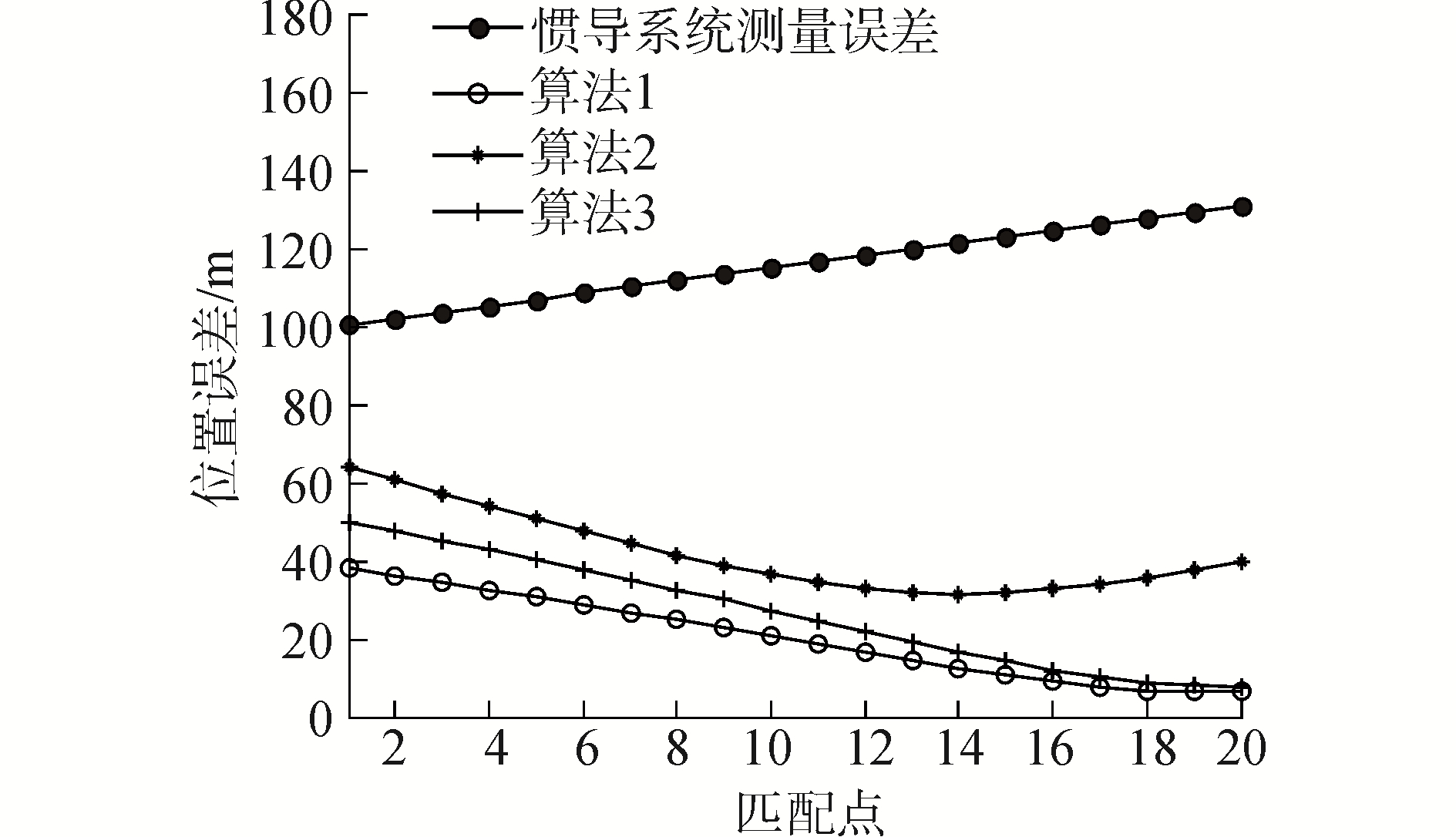
分别采用上述基于仿射参数估计的地磁匹配导航算法以及文献[13-14]中的算法计算匹配结果,并与真实轨迹做差得到匹配误差。图 4给出了误差曲线,其中算法1为本文所提出的基于仿射参数估计的地磁匹配导航算法;算法2为文献[13]所提出的匹配算法;算法3为文献[14]所提出的匹配算法。试验时,地磁特征值的梯度信息事先存入导航计算机,匹配实现过程中该信息直接在导航计算机中检索得到。利用Matlab中的tic和toc语句计算匹配算法在计算机中的运行时间。各匹配算法的匹配精度与算法耗时如表 1所示。
|
Download:
|
| 图 4 误差曲线 Fig. 4 The error curves | |
| 表 1 匹配误差和匹配耗时 Tab.1 Maximum error and matching time |
根据理论分析与试验比较可知,与文献[13]相比,本文所提出的算法额外考虑了惯导系统的初始速度误差,所以匹配精度有较大提升;同时由于考虑的误差源较多,匹配迭代耗时有所增加,但仍能满足匹配导航实时性的要求。与文献[14]相比,本文提出的算法采用了经度方向和纬度方向不同的伸缩系数,对应着不同的经度方向初始速度误差和纬度方向初始速度误差,所以匹配精度较高;而且以迭代计算替代了遍历的搜索方式,算法耗时大幅度减小。
根据试验结果可以看出,本文所提出的基于仿射参数估计的地磁匹配导航算法具有较高的匹配精度,可以修正惯导系统的初始位置误差、初始航向误差和初始速度误差。此外,在保证匹配精度的同时算法耗时较少,可以满足地磁匹配对算法实时性的要求。
5 结论1) 通过分析惯导系统初始位置误差、初始航向误差和初始速度误差对参考轨迹形状的影响,建立了地磁匹配仿射模型,提高了地磁匹配算法的定位精度。
2) 通过泰勒展开将相关性指标函数转化为仿射参数的表达式,进而以迭代计算替代了遍历求解手段,提高了地磁匹配算法的实时性。
3) 试验验证结果表明,与传统方法相比,本文所提出算法在保证匹配精度的同时可以有效地改善地磁匹配导航的实时性。
| [1] |
LIU Zhongyan, PANG Hongfeng, PAN Mengchun, et al. Calibration and compensation of geomagnetic vector measurement system and improvement of magnetic anomaly detection[J]. IEEE geoscience and remote sensing letters, 2016, 13(3): 447-451. (  0) 0)
|
| [2] |
解伟男, 李清华, 屈桢深, 等. 地磁日变影响下的地磁匹配算法[J]. 中国惯性技术学报, 2017, 25(6): 776-781. XIE Weinan, LI Qinghua, QU Zhenshen, et al. Geomagnetic matching algorithm under geomagnetic diurnal variation influence[J]. Journal of Chinese inertial technology, 2017, 25(6): 776-781. (  0) 0)
|
| [3] |
BATISTA P, PETIT N, SILVESTRE C, et al. Further results on the observability in magneto-inertial navigation[C]//Proceedings of the American Control Conference. Washington, USA, 2013: 2503-2508. http: //www. researchgate. net/publication/259197846_Further_results_on_the_observability_in_magneto-inertial_navigation
(  0) 0)
|
| [4] |
唐会林. SINS/DVL/UTP/VP组合导航系统在UUV回收中的应用[J]. 应用科技, 2016, 43(3): 1-7. TANG Huilin. Application of SINS/DVL/UTP/VP integrated navigation system to UUV underwater docking[J]. Applied science and technology, 2016, 43(3): 1-7. (  0) 0)
|
| [5] |
阮帅, 张文旭, 孙家骥, 等. GPS/BDⅡ双模导航接收机设计与实现[J]. 应用科技, 2016, 43(4): 50-56. RUAN Shuai, ZHANG Wenxu, SUN Jiaji, et al. Design and implementation of GPS/BDⅡ dual mode navigation receiver[J]. Applied science and technology, 2016, 43(4): 50-56. (  0) 0)
|
| [6] |
闫保中, 李英帅. 室内Wi-Fi定位系统设计及组合算法[J]. 应用科技, 2017, 44(3): 72-77. YAN Baozhong, LI Yingshuai. Design and combined location algorithm on indoor Wi-Fi positioning system[J]. Applied science and technology, 2017, 44(3): 72-77. (  0) 0)
|
| [7] |
郭才发, 胡正东, 张士峰, 等. 地磁导航综述[J]. 宇航学报, 2009, 30(4): 1314-1319, 1389. GUO Caifa, HU Zhengdong, ZHANG Shifeng, et al. A survey of geomagnetic navigation[J]. Journal of astronautics, 2009, 30(4): 1314-1319, 1389. DOI:10.3873/j.issn.1000-1328.2009.04.002 (  0) 0)
|
| [8] |
赵建虎, 王胜平, 王爱学. 一种改进型TERCOM水下地磁匹配导航算法[J]. 武汉大学学报(信息科学版), 2009, 34(11): 1320-1323. ZHAO Jianhu, WANG Shengping, WANG Aixue. An improved TERCOM algorithm for underwater geomagnetic matching navigation[J]. Geomatics and information science of Wuhan university, 2009, 34(11): 1320-1323. (  0) 0)
|
| [9] |
刘颖, 吴美平, 谢红卫. 地磁匹配算法研究框架和组合匹配策略[J]. 国防科技大学学报, 2010, 32(6): 171-176. LIU Ying, WU Meiping, XIE Hongwei. A framework for magnetic matching study and an integrated matching method[J]. Journal of National University of Defense Technology, 2010, 32(6): 171-176. DOI:10.3969/j.issn.1001-2486.2010.06.030 (  0) 0)
|
| [10] |
LIU Ying, WU Meiping, HU Xiaoping, et al. Research on geomagnetic matching method[C]//2nd IEEE Conference on Industrial Electronics and Applications. Harbin, China, 2007: 2707-2711. Research on geomagnetic matching metho
(  0) 0)
|
| [11] |
XIE Weinan, QU Zhenshen, LI Qinghua. A fast algorithm of the geomagnetic correlation matching based on MSD[C]//The 3rd International Conference on Control, Automation and Systems Engineering. 2013: 59-62. https: //www. researchgate. net/publication/266643004_A_Fast_Algorithm_of_the_Geomagnetic_Correlation_Matching_Based_on_MSD
(  0) 0)
|
| [12] |
黄斌, 孙永荣, 王丽娜, 等. 地磁导航的迭代评价匹配算法[J]. 南京航空航天大学学报, 2012, 44(4): 565-569. HUANG Bin, SUN Yongrong, WANG Li'na, et al. Iterative evaluation matching algorithm for geomagnetic navigation[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(4): 565-569. DOI:10.3969/j.issn.1005-2615.2012.04.022 (  0) 0)
|
| [13] |
解伟男, 李清华, 奚伯齐, 等. 基于迭代计算的地磁轮廓线匹配算法[J]. 中国惯性技术学报, 2015, 23(5): 631-635. XIE Weinan, LI Qinghua, XI Boqi, et al. Geomagnetic contour matching algorithm based on iterative method[J]. Journal of Chinese inertial technology, 2015, 23(5): 631-635. (  0) 0)
|
| [14] |
罗诗途, 任治新. 基于仿射模型变换的地磁匹配导航算法[J]. 中国惯性技术学报, 2010, 18(4): 462-465. LUO Shitu, REN Zhixin. Geomagnetic matching algorithms based on affine model[J]. Journal of Chinese inertial technology, 2010, 18(4): 462-465. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


