2. 中国科学院 可再生能源重点实验室, 广东 广州 510640;
3. 广东省新能源和可再生能源研究开发与应用重点实验室, 广东 广州 510640;
4. 中国科学院大学, 北京 100049
2. Key Laboratory of Renewable Energy, Chinese Academy of Sciences, Guangzhou 510640, China;
3. Guangdong Provincial Key Laboratory of New and Renewable Energy Research and Development, Guangzhou 510640, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China
有机朗肯循环(organic Rankine cycle, ORC)作为一种先进的能量转换技术,在开发利用太阳能、地热能、生物质能以及工业余热等低品位能源方面优势明显[1]。在过去的几十年里,研究人员针对ORC开展了大量的工作,总体上看,研究主要集中在有机工质遴选[2]、循环流程优化[3]以及动力部件设计[4]等方面。虽然目前关于ORC的研究已取得了丰硕的成果,但是由于ORC系统发电成本较高,目前尚未达到规模化应用的程度。
在ORC系统中,当冷热源的温差较小时,换热器包括蒸发器和冷凝器所占的投资成本最大,其所占比例有时甚至高达80%~90%[5-7],因此,在设计ORC系统时,必须考虑换热器的传热面积。对一特定规模的ORC系统来说,换热器的传热能力UA(总传热系数U与传热面积A的乘积)是其传热面积的反映,因而可以利用换热器的UA值来反映ORC系统的技术经济性[7]。换热器的UA值对热力系统的性能影响很大,针对换热器的UA值进行参数化分析,可以兼顾系统的热力性能和技术经济性。如Rameshkumar等[8]研究了换热器UA值对压缩吸收式制冷系统性能系数的影响,结果表明系统存在最优的换热器UA值,使性能系数达1.185。对于ORC系统,现有的研究大多将换热器的UA值作为一个性能指标参数[9-11],未见关于换热器UA值对ORC系统热力性能和技术经济性影响的详细报导。
本文以R1233zd(E)作为工质,利用EES软件建立了低温亚临界ORC数学模型,研究蒸发器和冷凝器的UA值对系统净输出功、热效率、不可逆损失、第二定律效率的影响规律。此外,以管壳式换热器为例,分析换热器的UA值对系统比初始总投资的影响规律。
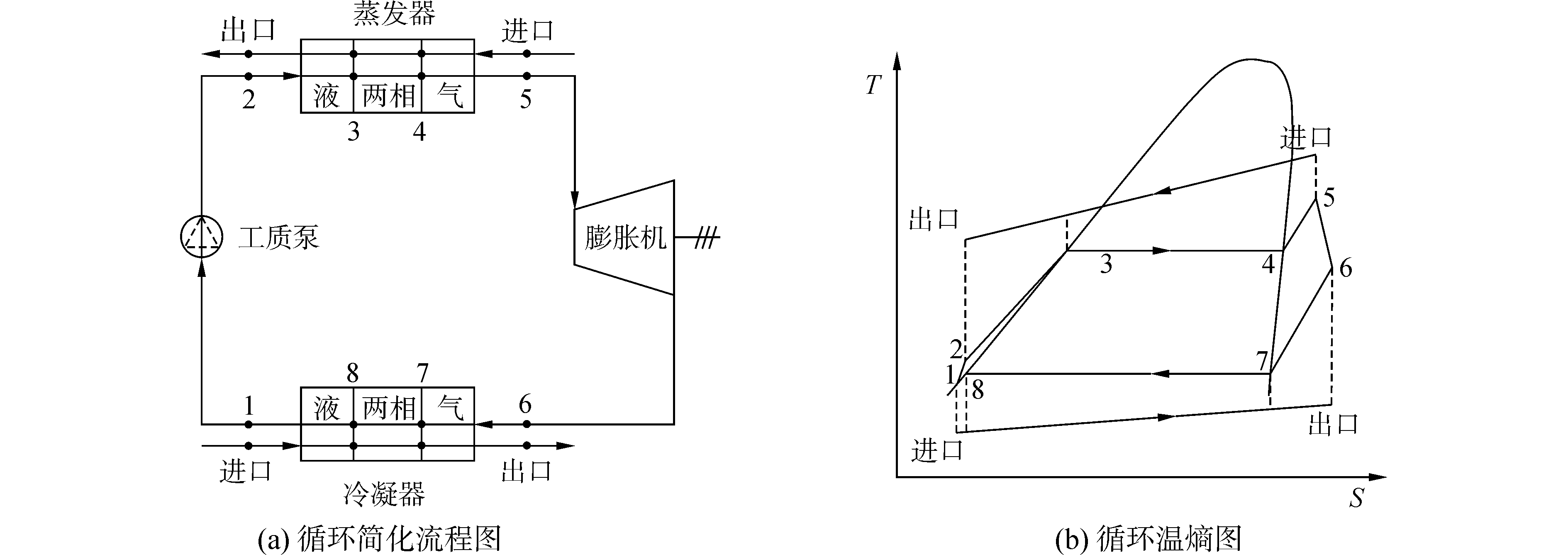
1 ORC数学模型ORC系统主要由蒸发器、膨胀机、冷凝器和工质泵4个部件组成,其基本流程和热力过程如图 1所示。从图 1可以看出,ORC一般由4个热力过程组成:2→3→4→5定压吸热过程,5→6绝热膨胀过程,6→7→8→1定压放热过程,1→2绝热压缩过程。
|
Download:
|
| 图 1 有机朗肯循环简化流程与温熵图 Fig. 1 Simplified schematic and T-s diagram of organic Rankine cycle | |
为了简化计算,本文数学建模过程做如下假设[12]:1)系统处于稳定流动状态;2)忽略系统散热损失;3)不计工质流动阻力损失;4)工质泵和膨胀机的等熵效率在不同工况下保持不变;5)蒸发器和冷凝器的UA基准值保持不变。
1.1 换热器传热模型 1.1.1 蒸发器模型有机工质与热源流体在蒸发器中一般以逆流形式进行热交换,热源流体放热,温度不断降低,有机工质吸热逐步从过冷状态变为饱和蒸汽或过热气体流出蒸发器。根据换热器传热方程式,蒸发器热负荷为
| $ {Q_{{\rm{eva}}}} = {U_{A,{\rm{eva}}}}\Delta {T_{\ln ,{\rm{eva}}}} = \left( {{U_{{\rm{eva}}}}{A_{{\rm{eva}}}}} \right)\Delta {T_{\ln ,{\rm{eva}}}} $ | (1) |
同时,根据能量守恒定律,蒸发器中热源提供的热量与循环工质吸收的热量相等,则有
| $ {Q_{{\rm{eva}}}} = {m_{hf}}{c_{{\rm{p}},{\rm{hf}}}}\left( {{T_{{\rm{hf}},{\rm{in}}}} - {T_{{\rm{hf}},{\rm{out}}}}} \right) = {m_{wf}}\left( {{h_5} - {h_2}} \right) $ | (2) |
式中:Q为热负荷,kW;UA为传热能力,kW/K;ΔTln为对数平均温差,K;U为传热系数,W/(m2·K);A为传热面积,m2;m为质量流量,kg/s;cp为定压比热容,kJ/(kg·K);T为温度,K;h为比焓,kJ/kg;下标“eva”、“hf”、“wf”分别表示蒸发器、热源流体和工质;下标“in”与“out”分别表示进出设备;下标“2”和“5”对应图 1中的状态点。
1.1.2 冷凝器模型冷却介质与有机工质在冷凝器中一般亦是以逆流形式进行热交换,冷却介质吸热,温度不断升高,有机工质放热逐步从过热蒸汽或饱和蒸汽变为饱和液体或过冷液体流出冷凝器。根据换热器传热方程式,冷凝器热负荷为
| $ {Q_{{\rm{con}}}} = {U_{A,{\rm{con}}}}\Delta {T_{\ln ,{\rm{con}}}} = \left( {{U_{{\rm{con}}}}{A_{{\rm{con}}}}} \right)\Delta {T_{\ln ,{\rm{con}}}} $ | (3) |
同时,根据能量守恒定律,冷凝器中冷却介质吸收的热量与循环工质释放的热量相等,则有
| $ {Q_{{\rm{con}}}} = {m_{cf}}{c_{{\rm{p}},{\rm{cf}}}}\left( {{T_{{\rm{cf}},{\rm{out}}}} - {T_{{\rm{cf}},{\rm{in}}}}} \right) = {m_{wf}}\left( {{h_6} - {h_1}} \right) $ | (4) |
式中:下标“con”和“cf”分别表示冷凝器和冷却介质,下标“1”和“6”对应图 1中的状态点。
式(1)、(3)中,换热器的对数平均温差由下式计算:
| $ \begin{array}{*{20}{c}} {\Delta {T_{{\rm{ln}}}} = {Q_{{\rm{liq}}}}/\left( {{Q_{{\rm{tot}}}}\Delta {T_{{\rm{liq}}}}} \right) + {Q_{tp}}/\left( {{Q_{{\rm{tot}}}}\Delta {T_{{\rm{tp}}}}} \right) + }\\ {{Q_{{\rm{gas}}}}/\left( {{Q_{{\rm{tot}}}}\Delta {T_{{\rm{gas}}}}} \right)} \end{array} $ | (5) |
ORC运行过程中,工质泵的耗功为
| $ {W_{{\rm{pup}}}} = {m_{{\rm{wf}}}}\left( {{h_2} - {h_1}} \right) = {m_{{\rm{wf}}}}\left( {{h_{2,{\rm{s}}}} - {h_1}} \right)/{\varepsilon _{{\rm{pup}}}} $ | (6) |
式中:W为功率,kW;ε为等熵效率;下标“pup”表示工质泵;下标“s”表示等熵过程。
1.3 膨胀机模型膨胀机的输出功为
| $ {W_{{\rm{exp}}}} = {m_{{\rm{wf}}}}\left( {{h_5} - {h_6}} \right) = {m_{{\rm{wf}}}}\left( {{h_5} - {h_{6,{\rm{s}}}}} \right)/{\varepsilon _{{\rm{exp}}}} $ | (7) |
式中下标“exp”表示膨胀机。
1.4 设备投资模型忽略管道、阀门等辅助设施,ORC系统的初始总投资主要由蒸发器、冷凝器、膨胀机和工质泵的成本构成,即
| $ {C_{{\rm{tot}}}} = {C_{{\rm{eva}}}} + {C_{{\rm{con}}}} + {C_{\exp }} + {C_{{\rm{pup}}}} $ | (8) |
根据文献[13],蒸发器、冷凝器、膨胀机和工质泵的投资成本可以分别用式(9)~(12)估算:
| $ {C_{{\rm{eva}}}} = 6.228\left( {285 + 465{A_{{\rm{eva}}}}} \right) $ | (9) |
| $ {C_{{\rm{con}}}} = 6.228\left( {285 + 465{A_{{\rm{con}}}}} \right) $ | (10) |
| $ {C_{\exp }} = 6.228\left( {506.25 + 382.5{V_{{\rm{exp,in}}}}} \right) $ | (11) |
| $ {C_{{\rm{pup}}}} = 8408{\left( {{W_{{\rm{pup}}}}/300} \right)^{0.25}} $ | (12) |
式中:C为投资成本,元;V为体积流量,m3/s。
1.5 性能参数净输出功、热效率、不可逆损失、第二定律效率以及比初始总投资(系统初始总投资成本与净输出功之比)常被用来表征ORC系统的性能,如文献[13-16],分别计算如下:
| $ {W_{{\rm{net}}}} = {W_{{\rm{exp}}}} - {W_{{\rm{pup}}}} $ | (13) |
| $ {\eta _{\rm{I}}} = {W_{{\rm{net}}}}/{Q_{{\rm{eva}}}} $ | (14) |
| $ \begin{array}{*{20}{c}} {{E_{{\rm{D}},{\rm{tot}}}} = {m_{{\rm{wf}}}}{T_0}\left( {{h_5} - {h_2}} \right)/{T_{{\rm{hf}},{\rm{m}}}} + }\\ {{m_{{\rm{wf}}}}{T_0}\left( {{h_1} - {h_6}} \right)/{T_{{\rm{cf}},{\rm{m}}}}} \end{array} $ | (15) |
| $ {\eta _{{\rm{II}}}} = {W_{{\rm{net}}}}/{Q_{{\rm{eva}}}}\left( {1 - {T_0}/{T_{{\rm{hf}},{\rm{m}}}}} \right) $ | (16) |
| $ {R_{{\rm{C}},{\rm{ini}}}} = {C_{{\rm{tot}}}}/{W_{{\rm{net}}}} $ | (17) |
式中:Thf, m与Tcf, m分别为热冷源的平均传热温差,K,计算如下:
| $ {T_{\rm{m}}} = \frac{{\max \left( {{T_{{\rm{in}}}},{T_{{\rm{out}}}}} \right) - \min \left( {{T_{{\rm{in}}}},{T_{{\rm{out}}}}} \right)}}{{\ln \left[ {\max \left( {{T_{{\rm{in}}}},{T_{{\rm{out}}}}} \right)/\min \left( {{T_{{\rm{in}}}},{T_{{\rm{out}}}}} \right)} \right]}} $ | (18) |
式中:ηⅠ和ηⅡ分别为热效率和第二定律效率;ED, tot为总不可逆损失,kW;T0为环境温度,K;RC, ini为比初始总投资,元/kW。
2 计算结果与分析 2.1 模型验证本文中的数值模拟计算通过EES软件来完成,其中有机工质的物性参数来自该软件的内嵌函数。为了检验所建的ORC系统数学模型的准确性,以R245fa为工质,将文献[17]中的计算工况(热水温度363.15 K,热水流量mhf=1 kg/s,换热器夹点温差5 K,膨胀机等熵效率0.8,工质泵等熵效率0.75)代入本文所建模型,并将计算结果与文献[17]中的实验数据进行对比,其结果如表 1所示。从表 1可以看出,本文计算所得的系统热效率和第二定律效率与文献[17]的计算结果吻合的很好,最大相对误差均不超过1%,验证了本文所建模型的准确性。
| 表 1 系统热效率和第二定律效率随热源温度的变化 Tab.1 Comparison between present work and Ref. [17] of thermal efficiency and exergy efficiency of ORC system versus heat source temperature |
采用典型的太阳能热水(温度373.15 K)作为热源流体,水作为冷却介质。由于热源流体流量对ORC循环热力性能几乎无影响,故热源流体的质量流量设为1.0 kg/s[15]。其他计算工况参数如下:
1) 蒸发器:过热度5.0 K,热水进口温度373.15 K,热水流量1.0 kg/s,UA基准值(UA, eva, ref)10.0 kW/K;
2) 冷凝器:过冷度3.0 K,冷却水进口温度293.15 K,冷却水流量5.0 kg/s,UA基准值(UA, con, ref)20.0 kW/K;
3) 膨胀机:等熵效率0.8;
4) 工质泵:等熵效率0.8;
5) 环境:温度293.15 K。
在上述给定的参数下,本文在两种不同约束条件即蒸发器热负荷恒定(热水出口温度固定为333.15 K)和系统净输出功最大(最优工况)的工况下对ORC系统进行模拟计算,两种约束条件下ORC系统的热力性能如表 2所示。
| 表 2 计算工况下ORC系统的性能参数 Tab.2 Performance parameters of ORC system under calculation conditions |
从表 2中可以看出,最优工况下的ORC系统热效率、第二定律效率和膨胀机输出功均大于热水出口温度固定为333.15 K时的工况,且蒸发器和冷凝器的热负荷和不可逆损失均小于热水出口温度固定时的工况。
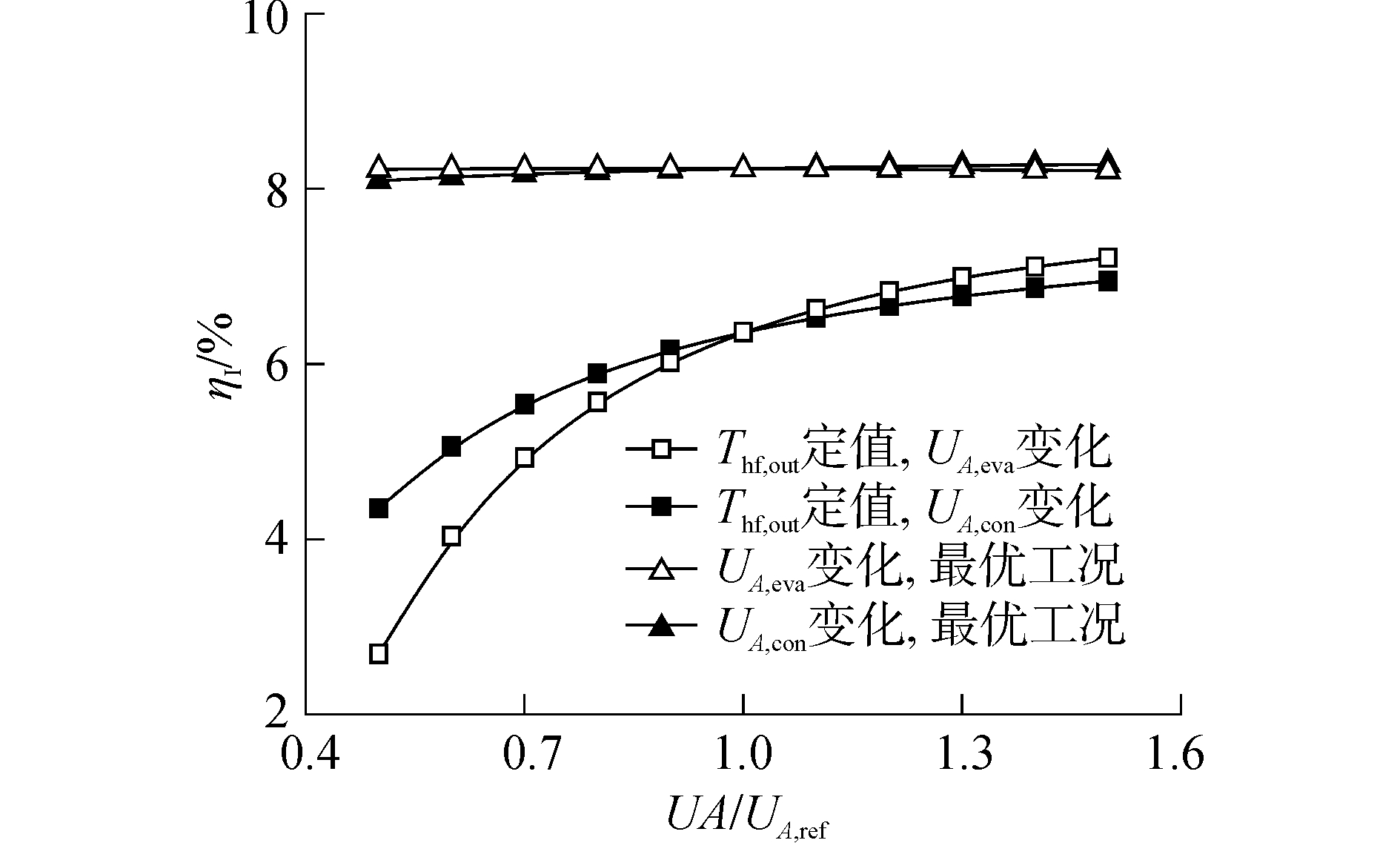
2.2 换热器UA值对ORC系统热力性能的影响换热器UA值的变化对ORC系统热效率的影响如图 2所示。当热水出口温度固定为333.15 K时,随着换热器UA值的增大,ORC系统热效率逐渐升高,增幅逐渐减小。当UA, eva/UA, eva, ref从0.5增大至1.5时,系统热效率从2.7%升高到7.2%,增幅达168%;当UA, con/UA, con, ref从0.5增大至1.5时,系统热效率从4.4%升高至6.9%,增幅达60%。
|
Download:
|
| 图 2 ORC系统热效率随蒸发器与冷凝器UA值的变化 Fig. 2 Thermal efficiency of ORC system versus UA of evaporator and condenser | |
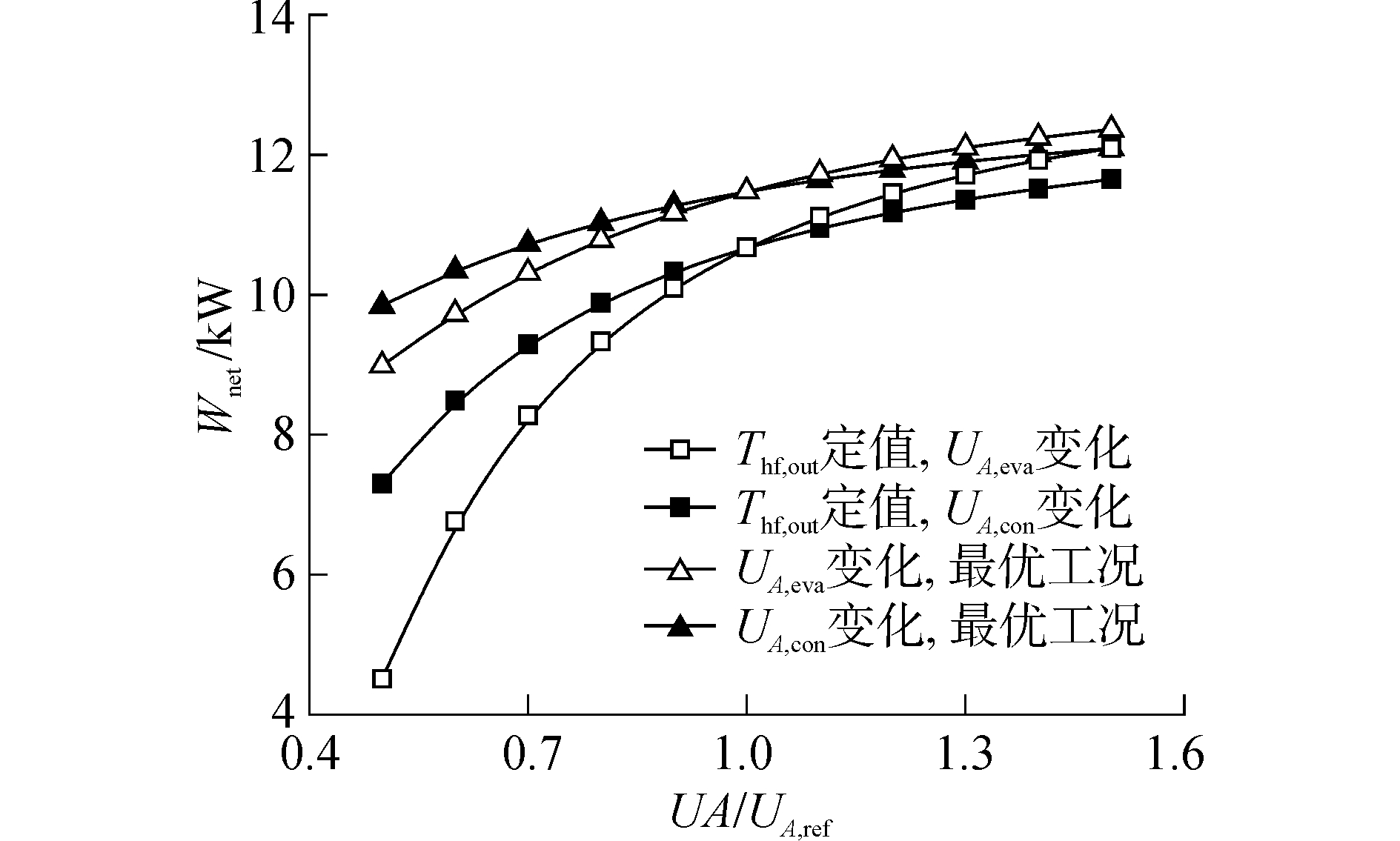
当蒸发器热负荷一定时,ORC系统的净输出功与热效率成正比[14],因此,如图 3所示,系统的净输出功也随蒸发器和冷凝器UA值的增大而增大,增幅同样逐渐变小。这是由于随着蒸发器与冷凝器UA值的增大,蒸发温度逐渐增大,冷凝温度降低,二者皆有利于提高系统的热力性能,但受传热温差限制,蒸发温度与冷凝温度均存在极值,因而随换热器UA值的增大系统热力性能的增幅逐渐降低。
|
Download:
|
| 图 3 ORC系统净输出功随蒸发器与冷凝器UA值的变化 Fig. 3 Net power output of ORC system versus UA of evaporator and condenser | |
从图 2和图 3可以看出,尽管最优工况下ORC系统净输出功随换热器UA值的增大呈持续增大的趋势,但是其热效率却基本保持不变,在给定的工况范围内,稳定在8.2%左右。此外,最优工况下系统热效率与净输出功较热水出口温度固定时的对应值具有很大的提高。当UA, eva/UA, eva, ref为0.5时,最优工况下ORC系统的热效率与净输出功比热水出口温度固定为333.15 K时分别高出约206%和99%,而当UA, eva/UA, eva, ref升高至1.5时,仅分别高出14%和2%左右;当UA, con/UA, con, ref为0.5时,最优工况下ORC系统的热效率与净输出功比热水出口温度固定为333.15 K时的对应值分别高出约86%和35%,而当UA, con/UA, con, ref升高至1.5时,仅分别高出19%和4%左右。
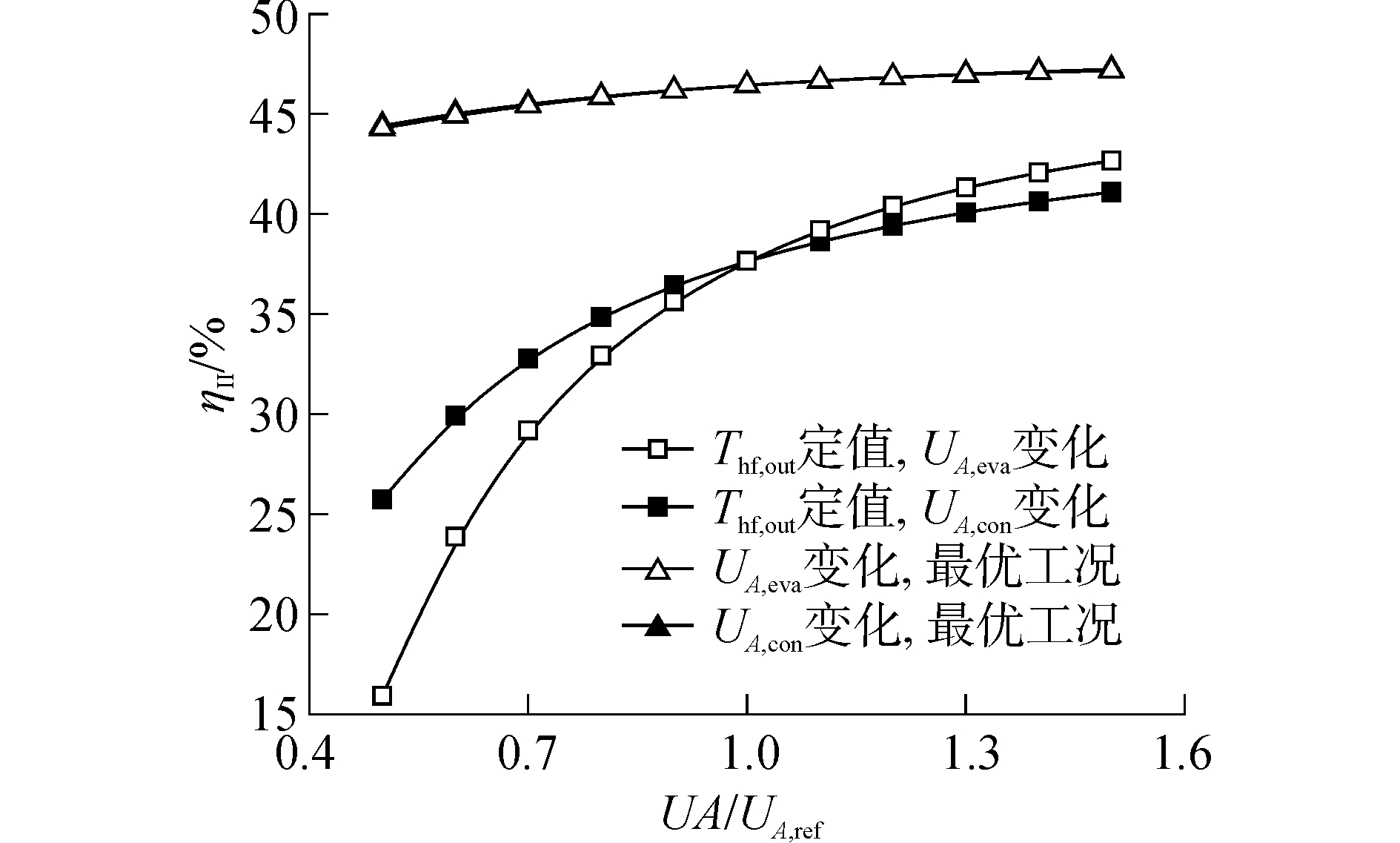
换热器UA值的变化对ORC系统第二定律效率的影响如图 4所示。当热水出口温度固定为333.15 K时,随着换热器UA值的增大,ORC系统第二定律效率逐步升高,增幅越来越小。当UA, eva/UA, eva, ref从0.5增大至1.5时,系统第二定律效率从15.9%增加到42.7%,增幅达168%。当UA, con/UA, con, ref从0.5增大至1.5时,系统第二定律效率从25.8%增加到41.1%,增幅约60%。与预料的一样,如图 5所示,对应的系统总不可逆损失随着换热器UA值的增大而逐渐降低,且降幅亦是越来越小,逐步趋于平缓。
|
Download:
|
| 图 4 ORC系统第二定律效率随蒸发器与冷凝器UA值的变化 Fig. 4 Second law efficiency of ORC system versus UA of evaporator and condenser | |
|
Download:
|
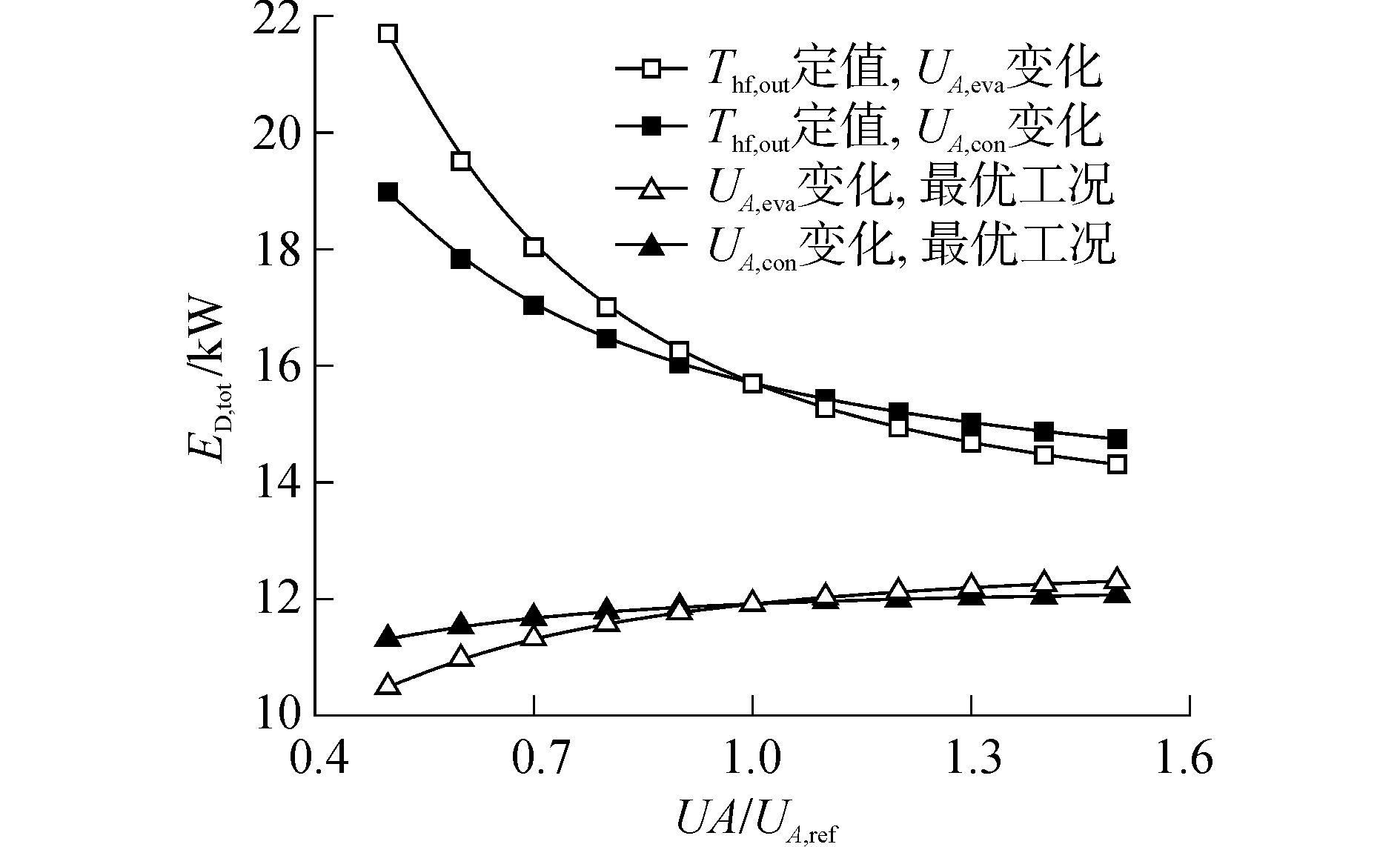
| 图 5 ORC系统不可逆损失随蒸发器与冷凝器UA值的变化 Fig. 5 Irreversible loss of ORC system versus UA of evaporator and condenser | |
从图 4、5可以看出,在最优工况下,随着换热器UA值的增大,尽管ORC系统总不可逆损失呈上升趋势,但是系统第二定律效率仍然有小幅升高。当UA, eva/UA, eva, ref从0.5增大至1.5时,系统总不可逆损失由10.5 kW增大至12.3 kW;当UA, con/UA, con, ref从0.5增大至1.5时,系统总不可逆损失由11.3 kW增大至12.1 kW,两者对应的第二定律效率增幅均为6.3%左右。此外,最优工况下系统第二定律效率与总不可逆损失较热水出口温度固定为333.15 K时的对应值具有很大的改善。当UA, eva/UA, eva, ref为0.5时,与热水出口温度固定时的工况相比较,最优工况下ORC系统的第二定律效率提高了约178%,总不可逆损失降低了52%左右,但当UA, eva/UA, eva, ref升高至1.5时,第二定律效率仅提高约11%,总不可逆损失降低14%左右;当UA, con/UA, con, ref为0.5时,与热水出口温度固定时的工况相比较,最优工况下ORC系统的第二定律效率提高了约72%,总不可逆损失降低了40%左右,但当UA, con/UA, con, ref升高至1.5时,第二定律效率仅提高约15%,总不可逆损失降低18%左右。
2.3 换热器UA值对ORC系统技术经济性的影响传热系数的计算较为复杂,涉及换热器结构、流体物性等多个方面。GIMELLI等[18]指出,当换热器的类型和传热介质确定时,在操作温度变化不大的情况下,换热器的总传热系数可以视为常数。本文以管壳式换热器为例,取Ueva=0.263 kW/(m2·K)和冷凝器传热系数Ucon=0.836 kW/(m2·K)[19]。
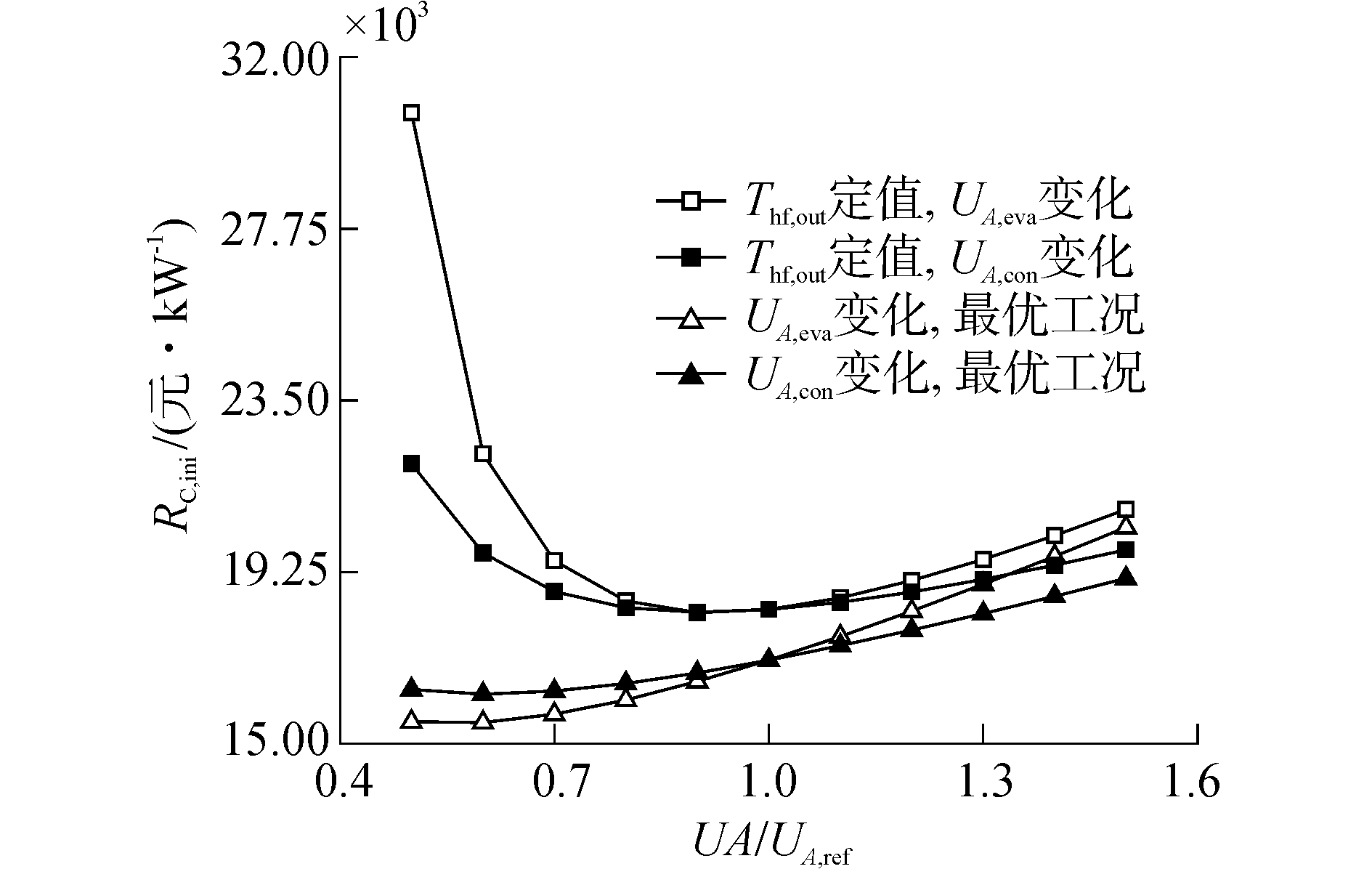
换热器UA值的变化对ORC系统比初始总投资的影响如图 6所示。当热水出口温度固定为333.15 K时,随着换热器UA值的增大,ORC系统比初始总投资先减小后增大,存在最小值。UA, eva/UA, eva, ref从0.5增大至1.5时,比初始总投资从30 330元/kW先下降至最小值18 067元/kW然后再增大到20 596元/kW,当UA, eva/UA, eva, ref等于0.9时,比初始总投资取得最小值;而当UA, con/UA, con, ref等于0.9时,比初始总投资同样取得最小值约为18 080元/kW。在最优工况下,随着换热器UA值的增大,ORC系统的比初始总投资亦呈先减小后增大的趋势。UA, eva/UA, eva, ref从0.5增大至1.5时,ORC系统比初始总投资从15 389元/kW先下降至最小值15 371元/kW然后再增大到20 160元/kW,当UA, eva/UA, eva, ref等于0.6时,比初始总投资取得最小值;而当UA, con/UA, con, ref等于0.6时,比初始总投资同样取得最小值,约为16 068元/kW。
|
Download:
|
| 图 6 ORC系统比初始总投资随蒸发器与冷凝器UA值的变化 Fig. 6 Specific investment cost of ORC system versus UA of evaporator and condenser | |
1) 在蒸发器热负荷恒定的条件下,换热器UA值的增大都能有效地提高ORC系统的热效率、净输出功和第二定律效率,并能降低ORC系统的总不可逆损失。
2) 在系统净输出功最大的条件下,蒸发器和冷凝器UA值的增大对ORC系统热力学效率的影响都不大,但都将使ORC系统的净输出功得到明显的提高。
3) 在两种约束工况下,相对而言,蒸发器UA值较冷凝器UA值对ORC系统热力性能的影响更为显著。当UA, eva/UA, eva, ref从0.5增大至1.5时,系统热效率和第二定律效率增幅均高达168%左右,而当UA, con/UA, con, ref从0.5增大至1.5时,系统热效率增幅约60%,第二定律效率增幅仅为6.3%。
4) 受传热温差的限制,提高蒸发器和冷凝器的UA值对改善ORC系统热力性能的作用随其UA值的增大而逐渐降低。可以预见,当蒸发器和冷凝器UA值增大到一定值后,进一步增大将无助于ORC系统热力性能的提高。
5) 在两种约束工况下,随着蒸发器和冷凝器UA值的增大,存在最佳的UA值使得比初始总投资最小;且两者相比,蒸发器UA值变化较冷凝器UA值对ORC系统比初始总投资的影响更为显著。
6) 此外,随着蒸发器和冷凝器UA值的增大,ORC系统的最大热力性能与最优技术经济性并不重叠,因此在工程设计中应当开展多目标协同优化来确定最佳的换热器UA值。
| [1] |
马新灵, 孟祥睿, 魏新利, 等. 有机朗肯循环低品位热能发电系统向心透平的设计与性能研究[J]. 中国电机工程学报, 2014, 34(14): 2289-2296. MA Xinling, MENG Xiangrui, WEI Xinli, et al. Design and performance study of radial inflow turbine used on organic Rankine cycle waste heat power generation system[J]. Proceedings of the CSEE, 2014, 34(14): 2289-2296. (  0) 0)
|
| [2] |
BAO Junjiang, ZHAO Li. A review of working fluid and expander selections for organic Rankine cycle[J]. Renewable and sustainable energy reviews, 2013, 24: 325-342. DOI:10.1016/j.rser.2013.03.040 (  0) 0)
|
| [3] |
LECOMPTE S, HUISSEUNE H, VAN DEN BROEK M, et al. Review of organic Rankine cycle (ORC) architectures for waste heat recovery[J]. Renewable and sustainable energy reviews, 2015, 47: 448-461. DOI:10.1016/j.rser.2015.03.089 (  0) 0)
|
| [4] |
ZYWICA G, KACZMARCZYK T Z, IHNATOWICZ E. A review of expanders for power generation in small-scale organic Rankine cycle systems:Performance and operational aspects[J]. Proceedings of the institution of mechanical engineers, part A:journal of power and energy, 2016, 230(7): 669-684. DOI:10.1177/0957650916661465 (  0) 0)
|
| [5] |
QUOILIN S, VAN DEN BROEK M, DECLAYE S, et al. Techno-economic survey of Organic Rankine Cycle (ORC) systems[J]. Renewable and sustainable energy reviews, 2013, 22: 168-186. DOI:10.1016/j.rser.2013.01.028 (  0) 0)
|
| [6] |
PAPADOPOULOS A I, STIJEPOVIC M, LINKE P. On the systematic design and selection of optimal working fluids for Organic Rankine Cycles[J]. Applied thermal engineering, 2010, 30(6/7): 760-769. (  0) 0)
|
| [7] |
贺超, 刘朝, 焦有宙, 等. 超临界ORC系统综合性能优化[J]. 工程热物理学报, 2015, 36(10): 2111-2116. HE Chao, LIU Chao, JIAO Youzhou, et al. Comprehensive performance optimization of supercritical organic Rankine cycle (ORC) system[J]. Journal of engineering thermophysics, 2015, 36(10): 2111-2116. (  0) 0)
|
| [8] |
RAMESHKUMAR A, UDAYAKUMAR M, SARAVANAN R. Heat transfer studies on a GAXAC (generator-absorber-exchange absorption compression) cooler[J]. Applied energy, 2009, 86(10): 2056-2064. DOI:10.1016/j.apenergy.2009.01.024 (  0) 0)
|
| [9] |
GUO Tao, WANG Huaixin, ZHANG Shengjun. Comparative analysis of CO2-based transcritical Rankine cycle and HFC245fa-based subcritical organic Rankine cycle using low-temperature geothermal source[J]. Science China technological sciences, 2010, 53(6): 1638-1646. DOI:10.1007/s11431-010-3123-4 (  0) 0)
|
| [10] |
HE Chao, LIU Chao, GAO Hong, et al. The optimal evaporation temperature and working fluids for subcritical organic Rankine cycle[J]. Energy, 2012, 38(1): 136-143. (  0) 0)
|
| [11] |
WU Yuandan, ZHU Yadong, YU Lijun. Thermal and economic performance analysis of zeotropic mixtures for Organic Rankine Cycles[J]. Applied thermal engineering, 2016, 96: 57-63. DOI:10.1016/j.applthermaleng.2015.11.083 (  0) 0)
|
| [12] |
王娟丽, 何雅玲, 程泽东, 等. 基于模拟退火算法的有机朗肯循环的性能优化[J]. 工程热物理学报, 2013, 34(9): 1606-1610. WANG Juanli, HE Yaling, CHENG Zedong, et al. Performance optimization of organic Rankine cycle based on simulated annealing algorithm[J]. Journal of engineering thermophysics, 2013, 34(9): 1606-1610. (  0) 0)
|
| [13] |
WU Dan, AYE L, NGO T, et al. Optimisation and financial analysis of an organic Rankine cycle cooling system driven by facade integrated solar collectors[J]. Applied energy, 2017, 185: 172-182. DOI:10.1016/j.apenergy.2016.10.071 (  0) 0)
|
| [14] |
刘超, 徐进良, 陈奇成, 等. 低温跨临界有机朗肯循环工质筛选[J]. 中国电机工程学报, 2013, 33(23): 37-43. LIU Chao, XU Jinliang, CHEN Qicheng, et al. Working fluid selection for low temperature transcritical organic Rankine cycle[J]. Proceedings of the CSEE, 2013, 33(23): 37-43. (  0) 0)
|
| [15] |
倪渊, 赵良举, 刘朝, 等. 非共沸混合工质ORC对低焓地热能的深度利用[J]. 太阳能学报, 2014, 35(9): 1670-1676. NI Yuan, ZHAO Liangju, LIU Chao, et al. Deeply recovery of low-enthalpy geothermal resources by organic Rankine cycles with non-azeotropic mixtures[J]. Acta energiae solaris sinica, 2014, 35(9): 1670-1676. DOI:10.3969/j.issn.0254-0096.2014.09.018 (  0) 0)
|
| [16] |
孙志强, 易思阳, 郭美茹, 等. 利用中低温余热的回热有机朗肯循环性能分析[J]. 热能动力工程, 2015, 30(1): 24-30. SUN Zhiqiang, YI Siyang, GUO Meiru, et al. Analysis of the performance of recuperative organic Rankine cycles utilizing a medium and low temperature waste heat[J]. Journal of engineering for thermal energy and power, 2015, 30(1): 24-30. (  0) 0)
|
| [17] |
ZHANG Shengjun, WANG Huaixin, GUO Tao. Performance comparison and parametric optimization of subcritical Organic Rankine Cycle (ORC) and transcritical power cycle system for low-temperature geothermal power generation[J]. Applied energy, 2011, 88(8): 2740-2754. DOI:10.1016/j.apenergy.2011.02.034 (  0) 0)
|
| [18] |
GIMELLI A, LUONGO A, MUCCILLO M. Efficiency and cost optimization of a regenerative Organic Rankine Cycle power plant through the multi-objective approach[J]. Applied thermal engineering, 2017, 114: 601-610. DOI:10.1016/j.applthermaleng.2016.12.009 (  0) 0)
|
| [19] |
GÓMEZ ALÁEZ S L, BOMBARDA P, INVERNIZZI C M, et al. Evaluation of ORC modules performance adopting commercial plastic heat exchangers[J]. Applied energy, 2015, 154: 882-890. DOI:10.1016/j.apenergy.2015.05.080 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


