2. 中船重工集团第719研究所, 湖北 武汉 430064
2. 719 Institute, China Shipbuilding Industry Corporation, Wuhan 430064, China
对转桨在减小桨叶负载、提高推进效率、降低振动噪声以及平衡扭矩等方面有明显的优势,已广泛应用于水下航行器。无论是舰艇自身隐蔽性需要,还是减小海底噪声污染,均要求对转桨噪声低。特别是低频无空泡噪声,由于不易耗散且传播距离远,因而易于被声呐接受和识别。准确预报对转桨无空泡噪声对于指导其低噪声设计和性能评估是非常重要的。由于前后桨的相互干扰,使得对转桨无空泡噪声数值预报问题的研究比普通螺旋桨复杂很多,仍有许多问题亟待解决。
目前,对转桨数值预报可采用的方法有势流理论和粘流理论。由于计算机和数值预报技术的发展,使得近些年来基于粘流理论CFD技术预报对转桨无空泡噪声的研究逐渐增多。吴文辉等[1]基于不可压缩流体雷诺时均方程和RSM湍流模型计算了大侧斜对转桨线谱噪声特性,证明大侧斜对转桨的水动力性能及线谱噪声要优于普通对转桨。杨琼方等[2]采用雷诺时均方程、尺度适应模拟和分离涡模拟三种方法,结合声类比方程开展伴流场中对转桨辐射噪声预报。侯知音等[3]基于CFD技术预报了对转桨的无空泡噪声,并对其声指向性进行分析。曾赛等[4]基于CFD技术计算的对转桨非空泡线谱噪声及其声压指向性与理论结果非常吻合。虽然CFD技术预报对转桨无空泡噪声的准确性有优势,但是需要复杂的建模和网格划分过程,且计算速度较慢。而基于势流面元法理论预报对转桨无空泡噪声,计算速度能够大幅度提升,可自动完成建模和网格划分,使用方便。面元法预报普通螺旋桨无空泡噪声的研究很早开始了,从最开始的Lighthill理论[5],到近期FW-H方程[6-7],使得面元法预报普通螺旋桨的无空泡噪声已经较为成熟[8-11]。与普通螺旋桨相比,对转桨由于两个桨之间相互干扰,需要考虑多方面的因素,使得面元法预报对转桨无空泡噪声问题比较复杂,目前还未见相关文献中开展此类研究。
然而,基于面元法理论预报对转桨无空泡噪声是一种简便而又高效的方法。为此,本文以面元法为基础,引入噪声预报理论与声学理论,建立对转桨无空泡噪声性能理论预报方法,并分析桨叶数、直径、前后桨间距以及伴流场对对转桨无空泡噪声计算结果的影响。
1 对转桨无空泡噪声预报方法与普通单桨的噪声计算理论方法类似[12],本文在计算过程中,把对转桨也以声源模型来处理,在其检测点上进行不相干声源的处理,为噪声的预报提供一定的依据。
对转桨的两个桨所处的环境不同,实际旋转的情况完全不一样,所发射出来的声波产生相干波的可能性很小,所以采用不相干声波的叠加方法。处于声场中某一点,有两列声波[13]:
| $ \left\{ \begin{array}{l} {p_1} = {p_{1a}}{\rm{cos}}\left( {{\omega _1}t-{\varphi _1}} \right)\\ {p_2} = {p_{2a}}{\rm{cos}}({\omega _2}t-{\varphi _2}) \end{array} \right. $ | (1) |
式中:p1、p2分别为前桨和后桨的声压,p1a、p2a分别为前桨和后桨的声压幅值,ω1、ω2分别为前桨和后桨的声压振动圆频率。那就可以推算出总声场的平均声密度ε为
| $ \bar \varepsilon = {{\bar \varepsilon }_1} + {{\bar \varepsilon }_2} + {\rm{ }}\frac{{2{p_{1a}}{p_{2a}}}}{{{\rho _0}c_0^2}}\overline {{\rm{cos}}({\omega _1}t-{\varphi _1}){\rm{cos}}({\omega _2}t-{\varphi _2})} $ | (2) |
式中:ε1、ε2分别为前桨和后桨的平均声密度,ρ0为水的密度,c0为声速。式(2)右侧第三项上面的横线表示对时间的平均,由理论可知此项平均结果为零,所以平均声密度可简化为
| $ \bar \varepsilon = {{\bar \varepsilon }_1} + {{\bar \varepsilon }_2} $ | (3) |
对于没有关联的声波而言,其合成的平均声能量密度,等于两个声波独自存在时,自身所产生出平均声能量密度之和。也就是说两列声波所合成的声压振幅平方为两列声波自身声压振幅平方的和,用有效声压pe可表示:
| $ p_{\rm{e}}^2 = p_{{\rm{1e}}}^2 + p_{{\rm{2e}}}^2 $ | (4) |
式中p1e、p2e分别为前桨和后桨的有效声压。
假如说有n个声源,在某一点分别产生的有效声压为pi,声压级为Li,那么可得合成有效声压p平方为
| $ {p^2} = \sum\limits_{i = 1}^n {p_i^2} {\rm{, }}\;\;\;\;i = 1, 2, \ldots, n $ | (5) |
按照声压级的定义处理,总声压级Lp表示为
| $ {L_p} = 10{\rm{lg}}\sum\limits_{i = 1}^n {\frac{{p_i^2}}{{p_0^2}}} $ | (6) |
式(6)就是所需要求出的噪声声压级叠加公式,p0 为参考声压。
2 预报方法验证 2.1 验证模型本次算例采用ITTC已公布DTMB4381桨[13]来进行程序运算和验证。把每个桨叶表面网格划分为15×15个面元网格,此外尾涡网格划分选用线性尾涡模型,每一个尾涡条带的划分网格数为30,均为2个周期数,网格模型如图 1所示。

|
Download:
|
| 图 1 螺旋桨模型 Fig. 1 Propeller model | |
为了确保程序的准确性,在进速系数J=0.8下,计算DTMB4381桨的推力和转矩系数分别为Kt=0.250、Kq=0.048 5。而文献[13]测得的推力系数和转矩系数分别为Kt=0.254、Kq=0.048 0。由此计算得到,推力和转矩系数的误差分别为1.6%、1.0%。可见,两者误差较小,验证了本文面元法程序的正确性。
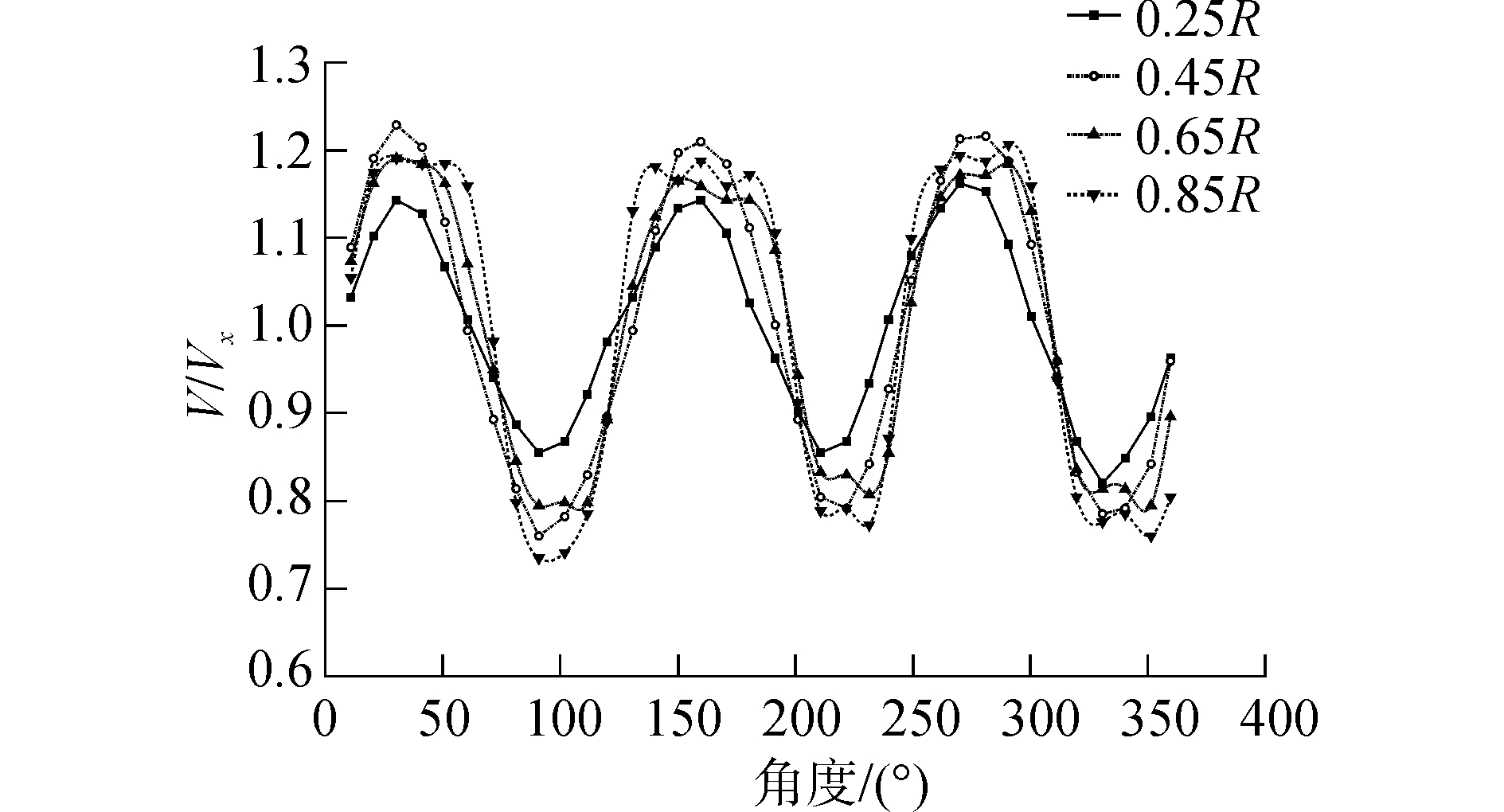
非定常计算时角度步长4°,以来流平均速度计算的进速系数为0.8,伴流分布采用给出的3-cycle伴流,不同半径处的轴向伴流随角度变化情况如图 2,给出了在0.25R、0.45R、0.65R、0.85R半径处的3-cycle伴流分布结果。
|
Download:
|
| 图 2 各半径处伴流的分布情况 Fig. 2 Distribution of flow at each radius | |
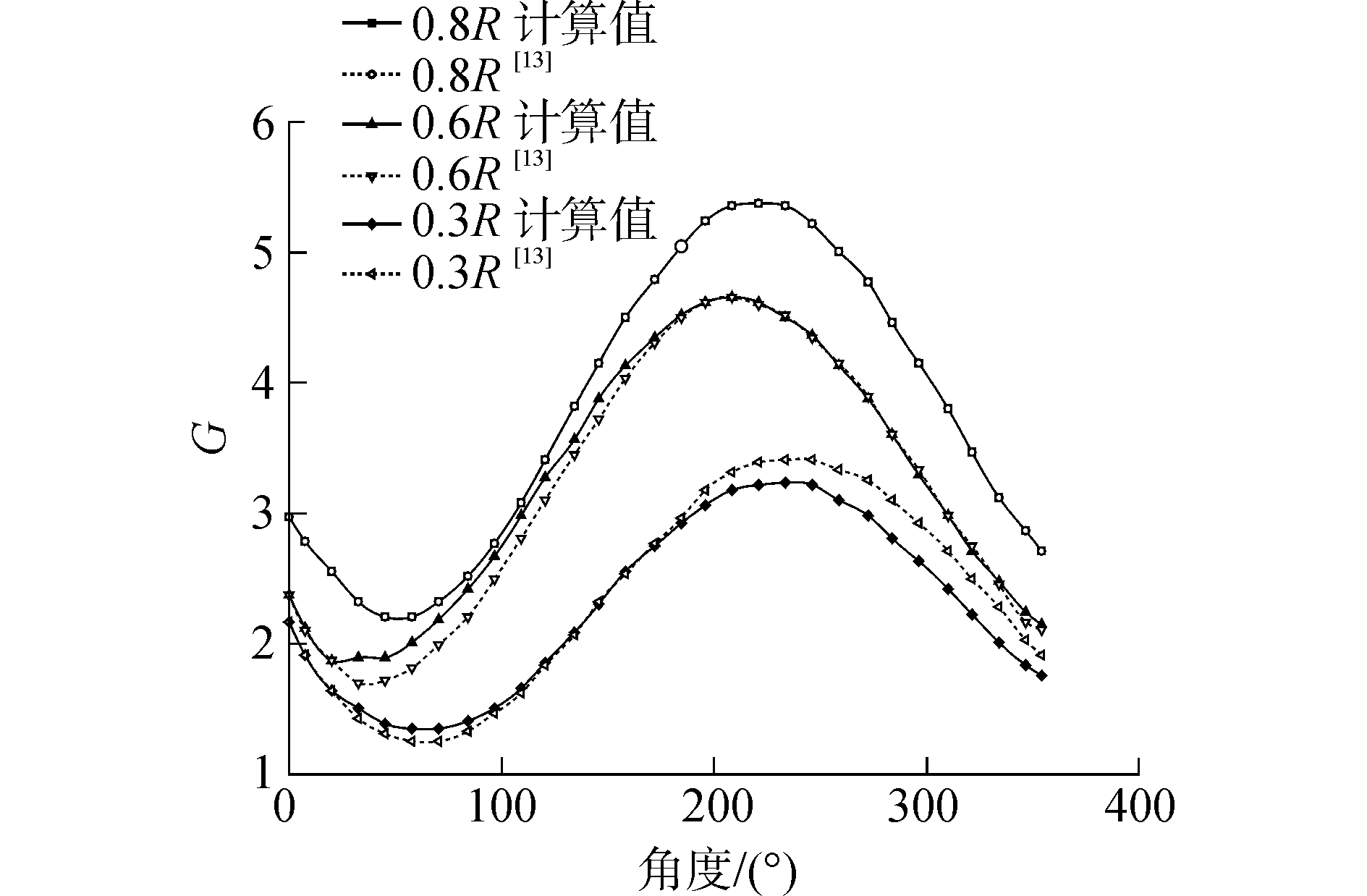
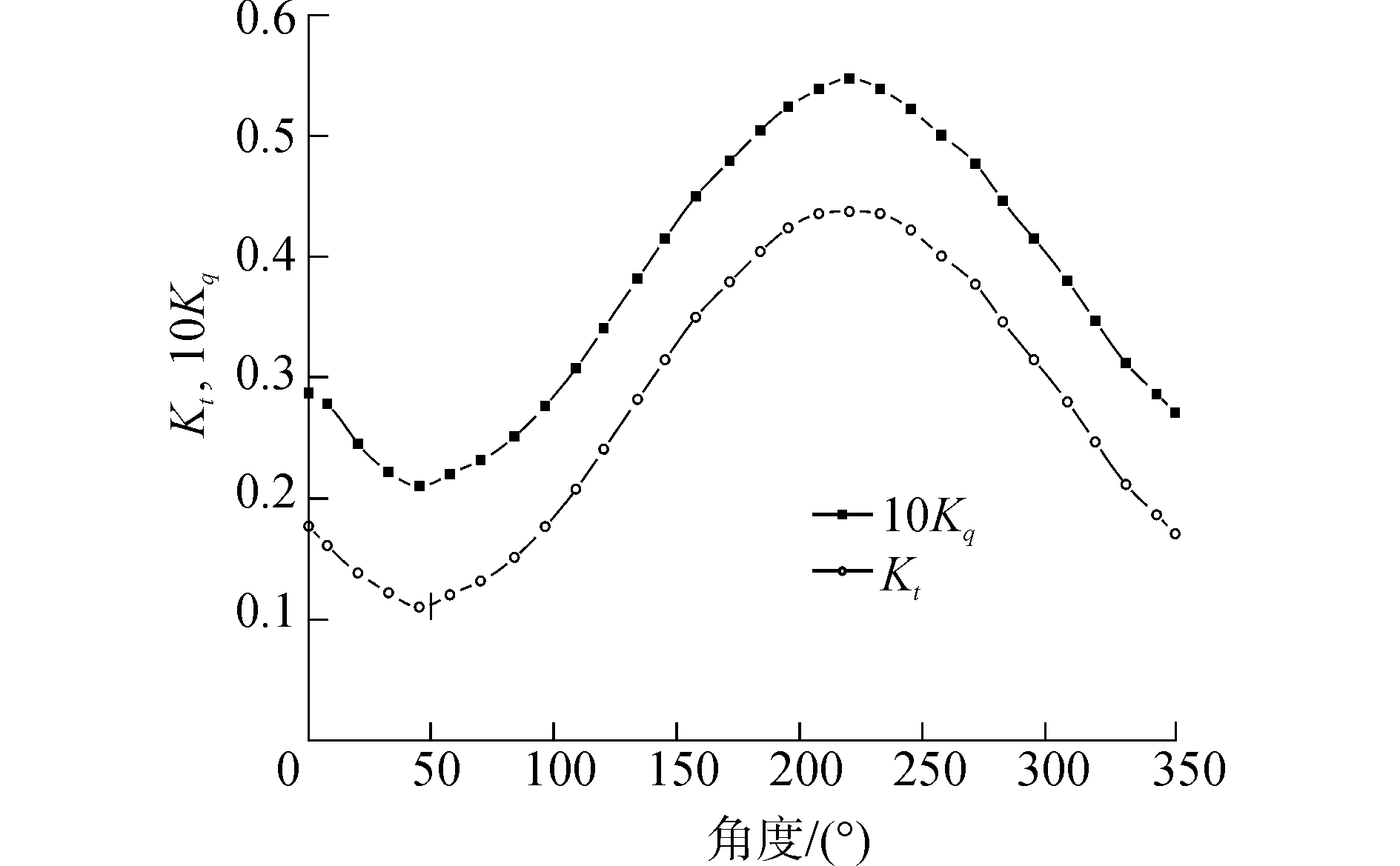
主桨叶半径处的环量值如图 3,并与Hisn[13]所计算的值相比较,整体计算结果非常一致:在此伴流条件下也有一峰值,存在明显的周期性。进而得出了螺旋桨推力系数和扭矩系数变化如图 4,也具有一定的周期性,旋转过程中会产生较为剧烈的波动。
|
Download:
|
| 图 3 不同半径处的环量 Fig. 3 The circulation at different radius | |
|
Download:
|
| 图 4 螺旋桨推力与扭矩系数 Fig. 4 The thrust and torque coefficient of the propeller | |
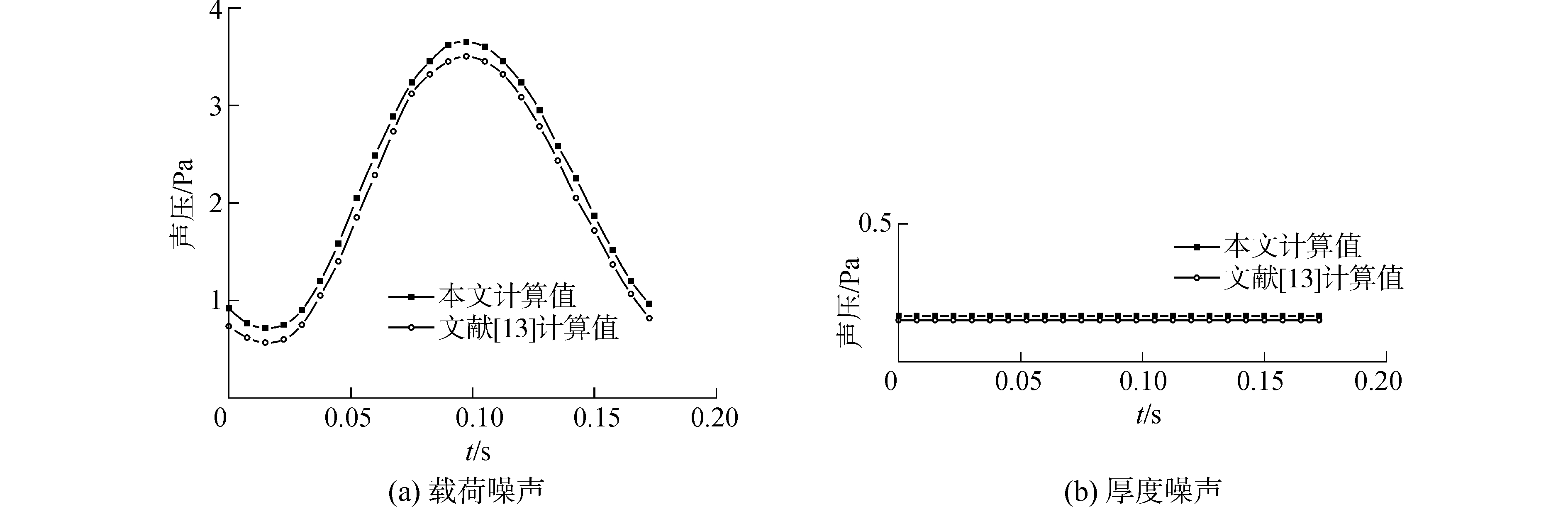
基于非定常面元法来进行普通桨的无空泡噪声预报,时间间隔取0.007 5 s,分别计算了与桨轴夹角θ=0°和θ=90°处的载荷噪声与厚度噪声的时域变化值,如图 5、6,与文献[13]计算值进行比较,走势一致,最大误差不超过4%,初步验证算法的可靠性。
|
Download:
|
| 图 5 θ=0°载荷噪声和厚度噪声 Fig. 5 Load noise and thickness noise at θ=0° | |

|
Download:
|
| 图 6 θ=90°载荷噪声和厚度噪声 Fig. 6 Load noise and thickness noise when θ=90° | |
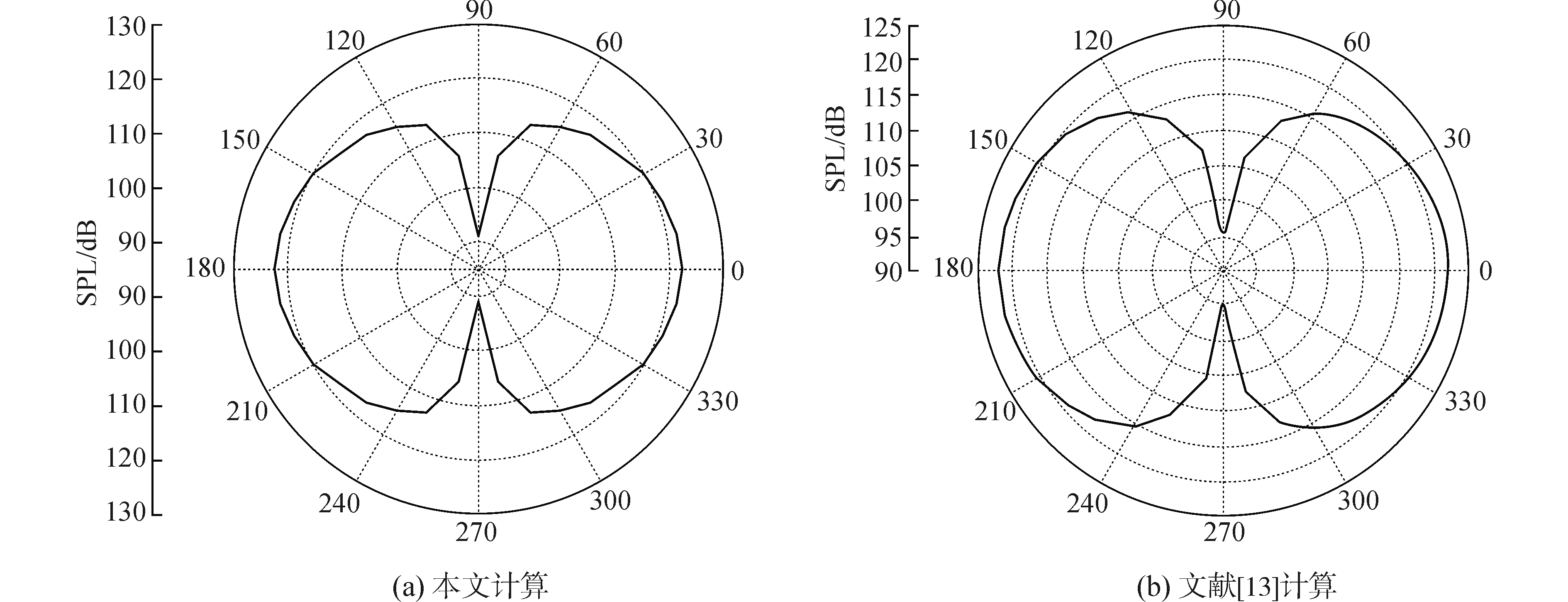
为更加全面地分析螺旋桨噪声,距离桨轴中心10D的一个圆周上布置测点,并计算出其声压分贝值,绘制出螺旋桨的噪声指向性图,如图 7。
|
Download:
|
| 图 7 声压级指向性 Fig. 7 Directivity of sound pressure level | |
通过声压级指向性图可以看出,所计算的结果与文献[13]所得的基本一致,在计算噪声值以及走势方面均较为吻合,进一步证实了本文所编写的噪声预报程序的正确性,而且在垂直于桨盘面的平面所预报噪声的指向性曲线,成一个横向的“8字形”分布,可以知道处于90°方向的噪声辐射较低,而处于0°方向噪声辐射较高,这是因为在计算非均匀流中的螺旋桨噪声时,其中的载荷噪声为最主要的组成部分,而偶极子声源能够呈现出这一分布特点,因此在总噪声曲线分布具有偶极子声源的指向性特点。
3 对转桨无空泡噪声性能预报计算模型选用CRP4-4桨(前桨为DTMB3686,后桨为DTMB3687 A),各桨叶具体参数见表 1。前后桨间距为0.141 5倍前桨直径。
| 表 1 各桨参数 Tab.1 Main parameters of each propellers |
非定常计算采用的步长为10°,来流的平均进速系数选取0.9,伴流分布采用3-cycle伴流,非定常力和转矩如图 8。由图 8计算得到CRP4-4非定常推力和转矩的系数均值,分别为Kt=0.286、Kq=0.064 5。而推力和转矩的系数实验值分别为Kt=0.275、Kq=0.062 9。由此计算得到,推力和转矩系数的误差不超过4%。

|
Download:
|
| 图 8 CRP4-4前桨和后桨非定常系数 Fig. 8 The unsteady coefficient of the front and back propeller of CRP4-4 | |
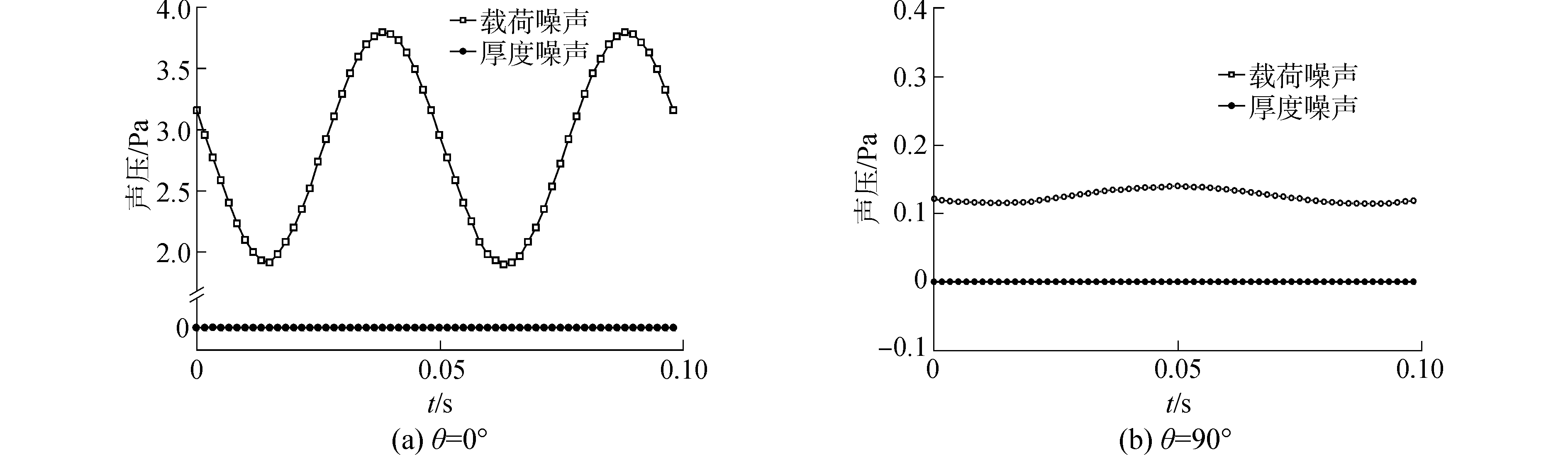
时间间隔取0.007 5 s,以桨轴旋转中心为中心,距离10R的位置为测量点,分别测量出θ=0°和θ=90°的载荷噪声与厚度噪声如图 9。
|
Download:
|
| 图 9 θ=0°和θ=90°方向的载荷噪声与厚度噪声 Fig. 9 Load noise and thickness noise at θ=0° and θ=90° | |
在3-cycle伴流情况下,无论是桨轴方向还是桨盘面方向,载荷噪声占据整体噪声的主要部分,桨轴方向的要比桨盘面方向的噪声大的多,这是因为非均匀流中桨叶面载荷变化较大,起主要作用的是载荷噪声;θ=90°方向由于处于螺旋桨的旋转平面上因此受到螺旋桨周期性旋转的影响很大,所以噪声也表现出周期性变化。
在计算得出声压时域值后,可以进行傅里叶变换而使结果更为直观,就是把连续的信号转换为离散的时域化,采用傅里叶变化时一定要把握好采样与分析这两种频率。傅里叶的变化公式为
| $ X\left( f \right) = \int_{-\infty }^\infty {x\left( t \right){\rm{exp}}(-2j2{\rm{ \mathsf{ π} }}ft){\rm{d}}t} $ | (7) |
进行离散化处理,如果在时间t内总共需采集N个点,则式(7)的频率可变为f=kΔf,离散化的傅里叶公式为
| $ X(k\Delta f) = \sum\limits_{n = 0}^{N-1} {x(n{t_s}){\rm{exp}}\left( {-j2{\rm{ \mathsf{ π} }}\frac{{nk}}{N}} \right){t_s}} $ | (8) |
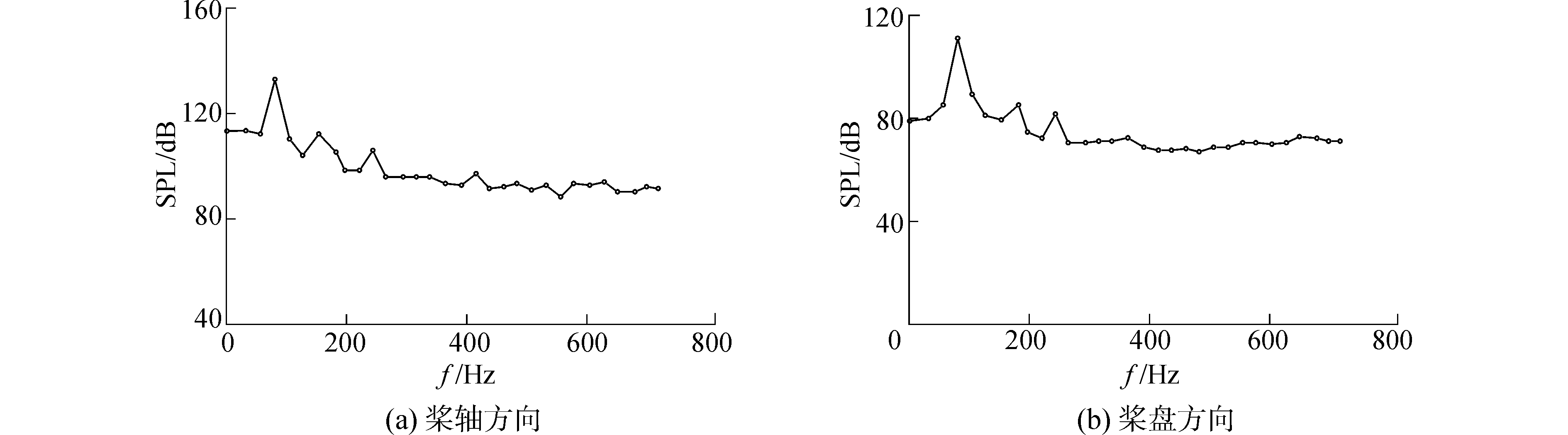
利用此理论进行Matlab编程,因为快速傅里叶变化的结果具有对称性,为了方便计算,只取其值得一半。在计算噪声时,每6°算一次,共60步,共取30个点,经过程序处理噪声的时域信号可以得到桨轴方向与桨盘面方向的噪声频谱图,如图 10所示,可以看出1倍频程处噪声级最大,随后迅速下降;比较叶频处的声压值,进一步证实了桨轴方向的噪声要远大于桨盘面的噪声。
|
Download:
|
| 图 10 桨轴方向和桨盘面方向噪声频谱 Fig. 10 Noise spectrum of the direction of the shaft and disk | |
几何参数及运动条件的改变,都会引起对转桨水动力性能的变化,从而非定常力也会受到影响,对转桨的噪声也随之发生一定的变化。尽量保持其他条件不变,只改变其的某一个因素,得出其声压级趋势图,分析其对噪声所产生的影响,为设计对转桨提供一定的参考。对转桨的几何参数众多,无法一一进行分析,这里选择对转桨设计中重点关注的几个参数进行分析,包括桨叶数、直径、前后桨间距以及伴流分布进行分析。由于之前分析在θ°=90°所产生的噪声相比θ=0°处不明显,同时为了简捷,只测量在θ=0方向的噪声足以说明问题了,下文计算分析时Δ为一固定值。
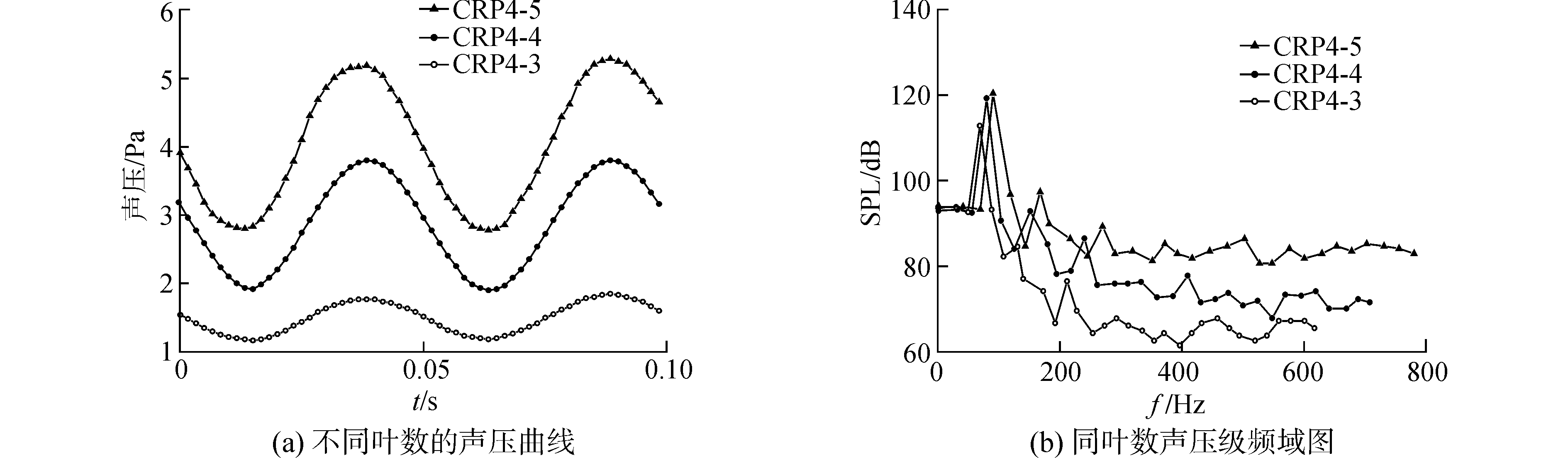
4.1 桨叶数模型桨为CRP4-4组(前桨为DTMB3686,后桨为DTMB3687A),改变其后桨的叶数,变为CRP4-3(后桨单个桨叶参数不变)和CRP4-5(后桨变为DTMB3849),分别测量距桨轴中心10R,处于θ=0°方向的测量点的噪声声压变化,见图 11(a),其频谱见图 11(b),桨叶数量对噪声的具体影响见表 3。
|
Download:
|
| 图 11 不同桨叶数的声压曲线和频域图 Fig. 11 The sound pressure curves and frequency chart of different number of blades | |
| 表 3 桨直径对噪声的影响 Tab.3 The influence of different propeller diameter |
由于桨叶的减少,两桨之间的扰动不激烈,产生的非定常力也较为稳定,同时叶数的减少,与流场之间的接触面积也相对减少,以致产生的噪声减小,由表 2可看出,桨叶减少则噪声声压明显降低。但桨叶过少不仅保证不了最小推力满足要求,还会导致强度不够的问题。而且,有可能导致整个对转桨的转矩增加,带来结构不平衡,设计时需均衡考虑。
| 表 2 叶数对噪声的影响 Tab.2 The influence of different number of blades on noise |
保持其他参数不变,分别改变其后桨的直径为原来直径的1.02和0.98倍,并测量距桨轴线中心10R,处于θ=0°方向的测量点的噪声声压变化,声压曲线见图 12(a),其频谱见图 12(b),具体影响值见表 3。

|
Download:
|
| 图 12 不同桨直径的声压曲线和频域图 Fig. 12 The sound pressure curves and frequency chart of different propeller diameter | |
一般情况下,尾流具有收缩作用,如果后桨的直径大于前桨直径,那么会产生更为剧烈的干扰,同时,流场与桨之间的相互作用也会更加剧烈,这就进一步增大了噪声;反之,小于前桨直径,后桨处于尾流之中,将减少额外的流体作用而减少噪声。因此,在保证对转桨总推力和结构强度满足条件的前提下,适当减小后桨直径可以提升对转桨的噪声性能。
4.3 前后桨间距原桨前后桨间距为0.141 5倍的前桨直径,现改变前后两桨间的距离,分别是0.16倍和0.12倍的前桨直径,并分别测量距桨轴中心为10R,处于θ=0°方向的测量点的噪声声压变化,见图 13(a)表示,其声压频谱见图 13(b),具体影响值见表 4。

|
Download:
|
| 图 13 不同间距的声压曲线和频谱图 Fig. 13 The sound pressure curves and frequency chart of different distance | |
| 表 4 间距对噪声的影响 Tab.4 The influence of different propeller distance on noise |
间距的增大,意味着后桨距前桨更远,由于尾流进一步收缩,将会产生与改变后桨直径等同的效果,在尾流收缩的有效范围内,间距增大噪声也随之增大,反之减小;但是当两桨间距过小时,两桨之间剧烈的扰动对噪声的影响会超过尾流的收缩作用,而且间距对后桨推力影响也很大,所以设计对转桨前后桨间距时,往往需要分析多种因素,统筹优化。
4.4 伴流场的影响 4.4.1 伴流场对噪声声压的影响仍选择CRP4-4桨,其条件也一样,分别有敞水与4-clcye伴流的流场条件。在桨轴方向与桨盘面方向的10R处分别设置测量点,得出其声压曲线,来分析比较伴流场对噪声声压的影响,并得出其噪声频谱图,分析伴流所造成的影响。
首先比较轴向方向,从图 14(a)中的曲线可以看出,在均匀流场下,轴向的声压几乎没有变化,厚度噪声占据主要部分,虽然存在两桨之间的扰动,但在远场处衰减较为厉害。在均匀流中螺旋桨的表面脉动相对比较稳定,再者,厚度噪声的源汇在桨轴方向有一定抵消,因此总噪声变小,而非均匀伴流的扰动加大,声压脉动幅度也较大。

|
Download:
|
| 图 14 桨轴方向和桨盘面方向的声压脉动 Fig. 14 The pressure fluctuation diagram of shaft direction and disk direction | |
在桨盘面方向的声压脉动曲线,如图 14(b),均匀流中以厚度噪声为主,由于两桨的干扰也会增加载荷噪声的比重,4-cycle伴流加大了载荷噪声的影响,使得总噪声增大。
对比图 14(a)和图 14(b),可以发现在4-cycle伴流中,桨轴方向噪声声压比桨盘面方向大得多,这是因为4-cycle伴流中4阶谐波占主要成分,而谐波阶数为螺旋桨桨叶数的倍数的来流谐波对非定常力的轴向分量有重要作用,其他来流谐波螺旋桨各单个桨叶上产生的非定常力的各谐波分量相互抵消,也就是螺旋桨对来流不均匀性的“过滤”性能。
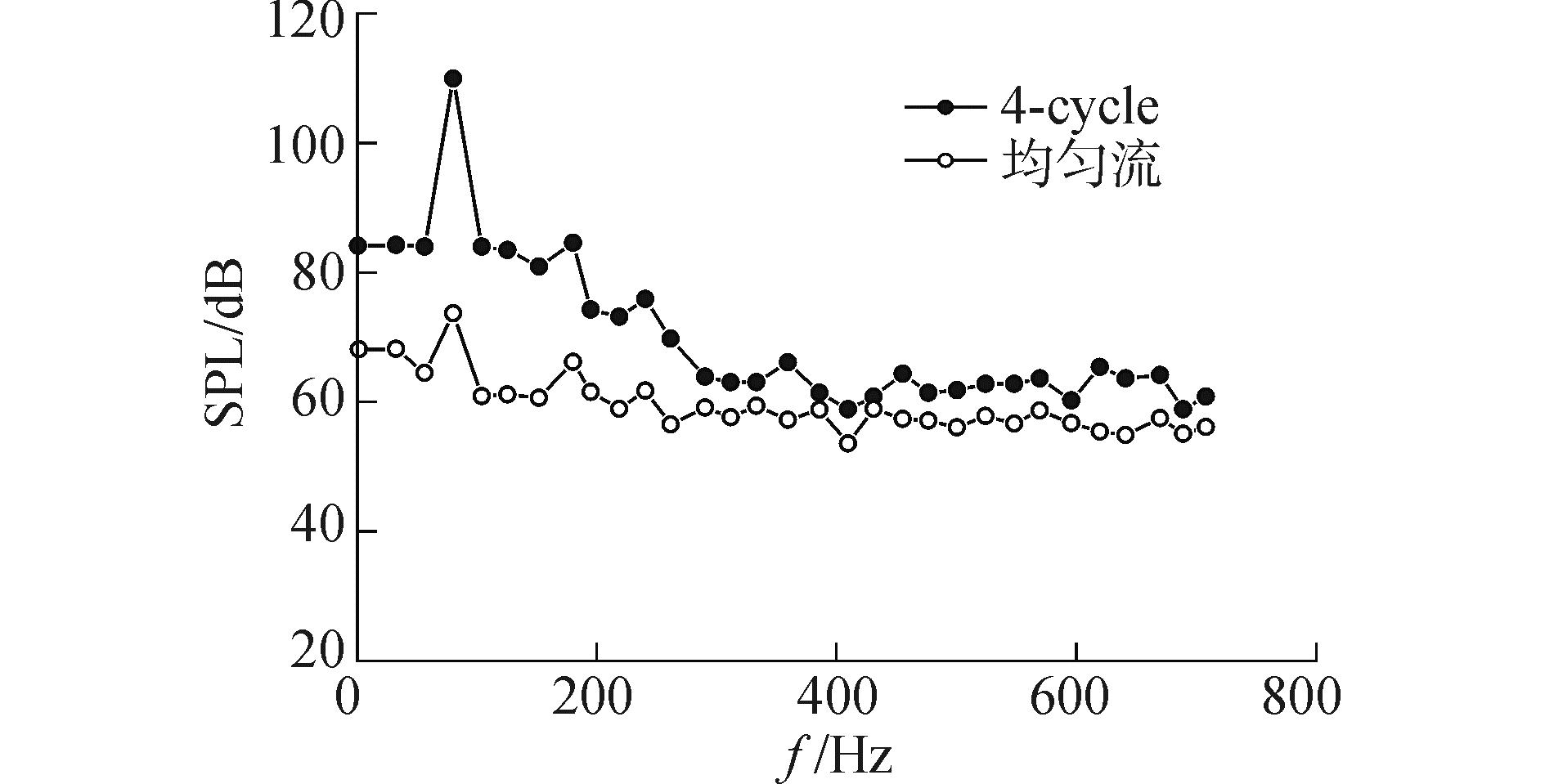
由图 15可以更加明显地看出,伴流对噪声声压的影响非常大,尤其是桨轴方向,主要是因为该方向正好处于螺旋桨旋转尾流后,螺旋桨的运动噪声要比桨轴方向上的大得多。另外,可以看出呈现的声压脉动曲线趋势相一致,而且均是处于均匀流中的噪声值要小。
|
Download:
|
| 图 15 不同流场中的声压频谱 Fig. 15 The sound pressure spectrum in different flow fields | |
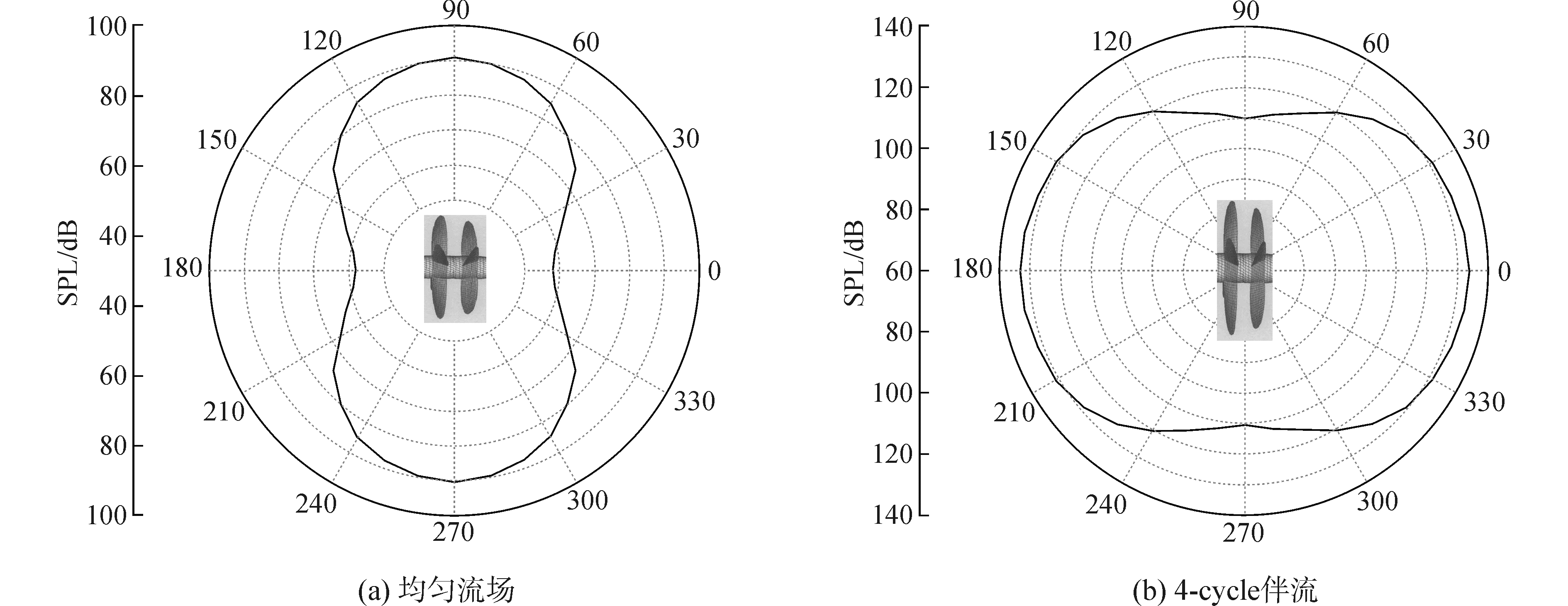
在程序计算过程中,取0°指向螺旋桨桨轴方向的下游,每相隔10°为一测量点,距桨轴中心均为10R,总共测量了36个点,将整桨作为研究对象,经过频域方法处理,得出桨的一叶频噪声声压值,然后得出其指向性,图 16(a)给出了均匀流场下的噪声指向性图。
|
Download:
|
| 图 16 均匀流场和4-cycle伴流下的指向性图 Fig. 16 Directivity pattern in uniform flow field and 4-cycle flow field | |
从图 16(a)可知,在均匀流场情况下,螺旋桨的厚度噪声占主要部分,噪声在桨盘面处最大,在桨轴方向最小,对转桨相对的表面非定常力较稳定,产生的载荷噪声相对于厚度噪声要小,呈现单极子指向性的特性,这是因为厚度噪声是由螺旋桨旋转对流体的周期性挤压或膨胀产生的,具有单极子的特点。但由于两桨之间存在干扰问题,载荷噪声仍有一定的影响,故同对转桨的两桨不完全相同,前桨比后桨直径大,所以在桨盘面上不完全对称,每个测量点都会有不同的差别,前桨产生的噪声比后桨的稍大。另外,并不是将整桨看作一个单极子声源,而是在桨叶的表面分布单极子声源,所以,整个螺旋桨在垂直于桨盘面上的圆周上的指向性,并不是一个均匀的圆,应在桨盘面方向上最大,桨轴方向最小,这是由于桨叶上布置的单极子声源在沿弦长的分布,恰好使它们在桨轴方向的声压相互抵消,从而使桨轴方向的厚度噪声的数值最小,所以噪声指向性图呈现出“8字形”。
而在伴流条件下,如图 16(b),由于复杂的流场环境,对转桨桨叶表面的非定常力显著增大,但在4-cycle伴流下,叶数为4的桨,产生的指向性图也呈现出“8字形”,这是因为螺旋桨的“过滤”性能;一阶叶频下桨轴方向的非定常力由于各桨叶的叠加而显著增大,导致噪声在0°和180°时(桨轴方向)最大,而在90°和180°(桨盘面)方向最小,从而使“8字形”噪声指向图偏转。
同时,两桨的情况不同,所以每个相对称的位置产生的噪声声压级也基本不同,是由于对转桨的情况复杂,以及两桨的声源模型不完全相同所造成的。
5 结论1) 基于非定常面元法来进行DTMB4381桨的验证计算,所得非定常水动力性能与实验值一致,桨轴夹角θ=0°和θ=90°处的载荷噪声与厚度噪声的时域变化值与文献值一致,验证本文计算方法的可行性。
2) 保持其他参数不变,改变对转桨后桨参数,发现桨叶数量和桨直径对对转桨噪声影响类似,在保证推力满足的情况下,减少桨叶数量和桨直径能够提升对转桨噪声性能。在尾流收缩的有效范围内,前后桨间距增大,噪声也随之增大,但是当两桨间距过小时,两桨之间的剧烈扰动对噪声的影响会超过尾流的收缩作用;
3) 伴流分布对螺旋桨的噪声声压级和指向性有重要的影响。当来流的主要谐波阶数等于螺旋桨桨叶数目时,轴向的噪声由于各桨叶贡献的叠加显著增强,指向性呈现典型的“8”字形,方向关于桨轴方向和桨盘面方向对称。而在均匀流场中,螺旋桨的厚度噪声占主要部分,噪声在桨盘面处最大,在桨轴方向最小,呈现单极子指向性的特性。
由于本文只是对螺旋桨噪声进行了初步的预报,并仅对转桨的噪声影响因素进行了分析,并没有考虑到声波反射等能量损耗的作用,而且计算是基于Lighthill声类比理论,来处理各种声源模型,没有考虑流噪声机理相关的涡流噪声,算法仍有很大的改进空间。
| [1] |
吴文辉, 郭敏, 李兵. 大侧斜对转桨水动力及线谱噪声特性分析[J]. 四川兵工学报, 2013, 34(4): 141-145. WU Wenhui, GUO Min, LI Bing. Features of hydrodynamics performance and tone noise for high-skewed contra-rotating propeller[J]. Journal of Sichuan ordnance, 2013, 34(4): 141-145. (  0) 0)
|
| [2] |
杨琼方, 王永生, 张志宏, 等. 伴流场中对转桨空化初生的判定与辐射噪声预报和校验[J]. 声学学报, 2014, 39(5): 589-604. YANG Qiongfang, WANG Yongsheng, ZHANG Zhihong, et al. Numerical prediction of cavitation inception radiated noise of contra-rotating propeller with non-uniform inflow[J]. Acta acustica, 2014, 39(5): 589-604. (  0) 0)
|
| [3] |
侯知音, 王超, 白雪夫. 基于CFD的对转桨无空泡噪声的仿真预报[J]. 船海工程, 2015, 44(4): 37-40. HOU Zhiyin, WANG Chao, BAI Xuefu. Noise characteristics without cavitation prediction simulation of contra-rotating propeller based on CFD[J]. Ship & ocean engineering, 2015, 44(4): 37-40. (  0) 0)
|
| [4] |
曾赛, 杜选民, 范威. 水下对转桨非空化线谱噪声分析与数值研究[J]. 兵工学报, 2015, 36(6): 1052-1060. ZENG Sai, DU Xuanmin, FAN Wei. Numerical simulation and analysis of non-cavitation noise line-spectrum frequency of underwater counter-rotation propeller[J]. Acta armamentarii, 2015, 36(6): 1052-1060. (  0) 0)
|
| [5] |
LIGHTHILL M J. On sound generated aerodynamically I. general theory[J]. Proceedings of the royal society A:mathematical, physical and engineering sciences, 1952, 211(1107): 564-587. DOI:10.1098/rspa.1952.0060 (  0) 0)
|
| [6] |
FARASSAT F, NYSTROM P A, BROWN T J. Bounds on Thickness and loading noise of rotating blades and the favorable effect of blade sweep on noise reduction[C]//United States: NASA, 1987.
(  0) 0)
|
| [7] |
FARASSAT F. Linear acoustic formulas for calculation of rotating blade noise[J]. AIAA journal, 1981, 19(9): 1122-1130. DOI:10.2514/3.60051 (  0) 0)
|
| [8] |
汤渭霖. 螺旋桨涡旋噪声预报[J]. 船舶力学, 1999, 3(2): 49-57. TANG Weilin. Prediction of propeller vortex noise[J]. Journal of ship mechanics, 1999, 3(2): 49-57. (  0) 0)
|
| [9] |
朱锡清, 吴武生. 螺旋桨负荷噪声研究[J]. 船舶力学, 1998, 2(3): 62-71. ZHU Xiqing, WU Wusheng. Study of marine propeller loading noise[J]. Journal of ship mechanics, 1998, 2(3): 62-71. (  0) 0)
|
| [10] |
孙红星, 朱锡清. 螺旋桨离散谱噪声计算研究[J]. 船舶力学, 2003, 7(4): 105-109. SUN Hongxing, ZHU Xiqing. Study on discrete noise induced by marine propeller[J]. Journal of ship mechanics, 2003, 7(4): 105-109. (  0) 0)
|
| [11] |
朱锡清, 李亚, 孙红星. 船舶螺旋桨叶片与艉部湍流场互作用噪声的预报研究[J]. 声学技术, 2006, 25(4): 361-364. ZHU Xiqing, LI Ya, SUN Hongxing. Prediction of noise induced by interaction between turbulent flow and propeller blades[J]. Technical acoustics, 2006, 25(4): 361-364. (  0) 0)
|
| [12] |
王超, 张立新, 郑小龙, 等. LES和无限元耦合方法预报螺旋桨均匀流噪声[J]. 哈尔滨工程大学学报, 2015, 36(1): 91-97. WANG Chao, ZHANG Lixin, ZHENG Xiaolong, et al. Prediction of propeller noise in steady flow based on combining LES and I-FEM[J]. Journal of Harbin Engineering University, 2015, 36(1): 91-97. (  0) 0)
|
| [13] |
SEOL H, SUH J C, LEE S. Development of hybrid method for the prediction of underwater propeller noise[J]. Journal of sound and vibration, 2005, 288(1/2): 345-360. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


