2. 浙江大学 建筑工程学院, 浙江 杭州 310058
2. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
风力发电无污染且可持续供给,是继水力发电之后技术最成熟、最具规模化开发和商业化发展前景的可再生能源[1]。随着风电产业的蓬勃发展,陆上风电占地面积大、噪音大、风能密度低等缺陷逐渐显现,海上风电将成为未来风能发展的主要方向[2]。高成本是限制海上风电大规模商业化发展的一个关键因素,而风机基础结构是导致海上风电高成本的重要原因之一,海上风机基础投入可占到风电场成本的20%~30%左右。在中等水深海域,四腿桁架式结构是目前使用较多、适用范围较广的一种风机基础结构型式。这种结构型式与用于海上油气开采的导管架平台结构相近,但不同的功能需求造成两类结构的不同承载特征,从而形成不同的结构特点和设计要求。为降低基础结构造价,需对其进行有效的优化设计。目前,学术界和工程界已对风机基础结构的优化策略和方法进行了一些研究[3-5]。T Ashuri等[6]基于多参数优化设计(MDO)方法对海上单立柱式风电结构进行了优化工作,优化主要针对风机叶片部分,对风机基础结构的关注较少。M Tahani等[7]以发电效率为目标参数,利用BEM和CFD工具对风电结构叶片部分进行了优化设计。A Z Dhunny等[8]同样基于CFD分析对风电结构转子部分进行了风-电能量转化效率计算,并对其进行了优化设计工作。Ertong Hao等[9]以靠船冲击力为目标参数,分别对高桩承台式、单柱三桩式和桁架式风机基础型式进行对比和拓扑优化设计,最终得出桁架式基础型式抵抗冲击性能最优。Daniel Zwick等[10]将结构疲劳寿命作为主要优化准则,通过敏感性分析简化优化过程,对四腿桁架式风机基础结构进行了优化设计。优化过程中仅对各构件壁厚进行调整,保持结构型式和构件直径不变。Y S Lee等[11]应用拓扑优化技术对海上风机基础过渡段进行了FEA整体优化设计。已有的针对四腿桁架式海上风电结构优化设计方法的研究工作主要关注风机叶片等局部结构,或对部分构件进行尺寸优化,尚没有对风机基础整体结构包含拓扑优化和尺寸优化的系统优化策略研究工作。本文即在上述各研究工作基础上,针对完整风机基础结构,分别对整体结构和过渡段、甲板等局部构件,开展系统性拓扑优化与尺寸优化工作,从而形成多准则多参数风机基础结构优化策略和方法。
1 多准则多参数结构优化策略多准则多参数结构优化策略是针对包含多目标和多参数的优化系统,通过数值技术进行结构优化设计工作的方法。在多参数优化设计理论中,通常将一个具体的结构优化设计问题抽象为目标函数、设计参数和约束条件。结构优化过程就是寻找一组设计参数,在满足约束条件的情况下,使得目标函数最小。这组设计参数构成的结构型式就是最优的设计方案。目标函数、设计参数和约束条件的表达式如下
| $ \left\{ \begin{array}{l} 目标函数:f({x_1}, {x_2}, \ldots, {x_n}) = {\rm{min}}\\ 设计参数:x = \{ {x_1}, {x_2}, \ldots, {x_n}\} \\ 约束条件:{g_i}({x_i}) \ge 0;{h_k}({x_k}) = 0 \end{array} \right. $ | (1) |
式中:f(x)是与结构各设计参数相关的目标函数;x1, x2, …, xn是一系列结构设计参数,包含拓扑参数和尺寸参数;约束条件可以分为两类:等式条件和不等式条件,分别表示设计参数的建议值和取值范围。
1.1 多准则控制算法在结构设计中,希望设计方案能够同时满足安全性、使用性和经济性要求。对于四腿桁架式海上风机基础结构,上述三项基本设计原则体现为结构完整性、动力特征、耐久性和经济性等要求。在优化设计过程中,优化方案必须同时满足上述各项设计目标,并控制建造成本最低。因此,式(1)中目标函数的表达式可以替换为
| $ F\{ {f_1}[{g_1}\left( x \right)], {f_2}[{g_2}\left( x \right)], \ldots, {f_n}[{g_n}\left( x \right)]\} = {\rm{min}} $ | (2) |
式中:f1[g1(x)], f2[g2(x)], …, fn[gn(x)]即为四腿桁架式风机基础结构优化设计中需遵循的控制准则。
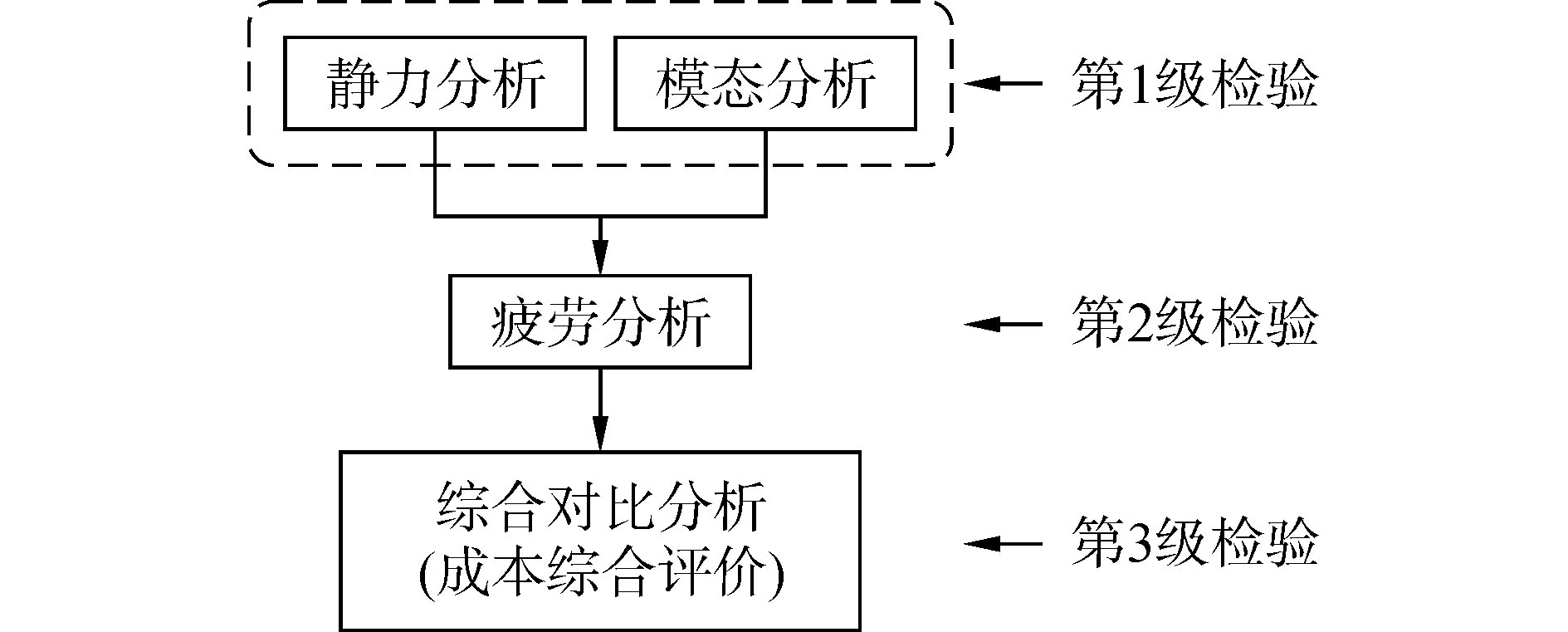
影响结构整体性能的各控制准则并不是相互独立的,而是彼此联系的。为提高设计参数的搜索效率,首先需对控制准则进行分级。在海上风机基础结构设计中,一般应进行静力分析、模态分析、疲劳分析和地震分析等工作,从而保证结构具备满足设计要求的完整性、动力特征、耐久性和经济性。控制准则的分级依据是重要程度和敏感性,即直接影响海上风电结构功能性的控制准则,以及对结构整体性能敏感性高的控制准则具有更高的优先级。而敏感性较低的控制准则,或在满足其他要求情况下即可满足的控制准则分级靠后,或不作为控制准则进行考虑。对于应用于中等水深海域(20~50 m)的四腿桁架式风机基础结构,根据环境载荷特征和相关工程经验,可将各控制准则分为3级(如图 1)。由一系列设计参数组成的优化方案经过三级控制准则检验和评价,最终得到最优的结构设计方案。
|
Download:
|
| 图 1 控制准则分级 Fig. 1 Classification of control criterions | |
在控制准则分级中,静力分析和模态分析并列作为第1级检验标准。其中,静力分析的目的是检验优化方案是否满足规范中的强度要求和变形要求,即杆件应力UC值和管节点应力IR值是否小于1.0,风机基础结构的转角是否小于允许值。模态分析的目的是检验优化方案的1阶固有频率是否在允许的频率范围内,即介于风机振动频率1P和3P之间。其中,1P是单个叶片旋转一周频率,3P是3个叶片旋转至上一位置频率。静力分析是结构设计中的基本要求,结构的疲劳分析和地震分析结果与静力分析结果直接相关。根据工程经验,满足规范中静力分析要求的优化方案,一般较易满足疲劳分析和地震分析要求。因此,将静力分析作为第1级控制准则,各优化方案首先要通过静力分析检验。频率要求是海上风电结构特有的一种控制准则,风机基础结构只有介于风机振动频率1P和3P之间,才能保证风机正常运行。四腿桁架式风电结构的动力特性要求十分严苛,结构动力性能对模态分析十分敏感。因此,将模态分析与静力分析并列,也作为第1级控制准则。优化方案在第1级检验中必须同时满足静力分析和模态分析要求,才能通过第1级检验。
第2级控制准则是疲劳分析,包括风激疲劳分析和波浪疲劳分析。如果风电结构位于寒冷有冰海域,还应包含冰激疲劳分析。疲劳分析主要检验优化方案结构的耐久性,即优化方案的疲劳寿命需大于设计寿命,才能通过第2级检验。第3级控制准则是综合对比分析,即对所有通过前两级检验的优化方案进行成本综合评价。在第3级检验中,并不是以结构用钢量作为单一评价指标,而是综合考虑优化方案结构的加工和安装难度、工期、整体静力性能、动力性能以及疲劳性能等因素,在各优化方案中筛选出最优的四腿桁架式风机基础型式。
1.1.1 第1级控制准则第1级检验包括静力分析和模态分析,优化方案必须同时满足静力强度要求、静力变形要求和频率要求。
1) 静力分析。
在静力分析中,需要校核优化方案是否满足强度要求和变形要求。对于四腿桁架式基础结构,变形要求一般是指基础环顶处的转角。转角一般可以参考风机厂商提出的控制标准。
静力分析中的强度要求一般是检验结构杆件和管节点的应力是否满足规范要求。在分析中,依据API RP 2 A-WSD (2007)[12]规范确定杆件强度校核准则,主要评价各单项应力和组合应力。在规范中将各种应力计算结果与许用应力的比值定义为UC值,从而用一个统一的比例参数表征实际作用应力与许用应力间的关系。当某杆件的UC值大于1时,说明该杆件不满足规范的强度要求。在静力分析中,依据规范确定风机基础结构管节点强度校核准则。在规范中定义管节点相互作用比IR值,作为评价管节点强度的重要参数。当各管节点最大IR值均小于1.0时,可以认为风机基础结构满足规范的管节点强度要求。
2) 模态分析。
在模态分析中,需要检验优化方案的1阶固有频率是否满足风机厂商提出的频率范围。风机系统中转子的转动是其最明显的激励。转子引起的激励能量有很高的频率成分,但一般仅考虑1P和3P,因为这两个激励频率的能量最为集中。为避免共振,风机系统的1阶固有频率需要避开1P和3P。对于刚度非常大的结构,自振频率将高于3P,称为“超刚度”结构,这种情况下会造成结构很大的冗余度,经济性较低。对于刚度非常小的结构,自振频率将低于1P,称为“超柔度”结构,这种情况下结构的固有频率会落入波浪频率范围,易与波浪发生共振。因此,结构最适宜的刚度情况应为介于1P和3P之间(如图 2)。一般情况下,在工程设计中不会让结构正好介于1P和3P之间,在这两个频率阈值两侧各设置至少10%的安全裕量,令结构频率介于更窄的一个频率范围内。

|
Download:
|
| 图 2 1P和3P频率分隔的结构刚度区间 Fig. 2 Structural stiffness regions divided by 1P and 3P | |
第2级检验是对优化方案进行疲劳分析,校核结构的抗疲劳性能。对于一般海域,疲劳分析包括风激疲劳分析和波浪疲劳分析。其中,风激疲劳分析可以采用风激疲劳载荷谱法,波浪疲劳分析可以使用波浪谱疲劳分析方法,将两者得到的疲劳损伤通过Miners准则线性叠加,即得到总疲劳损伤和疲劳寿命。对于寒区有冰海域,还需进行冰激疲劳分析。
1) 波浪疲劳分析方法。
在波浪谱疲劳分析方法中,首先根据工程场址的波高、波周期联合概率分布和波浪玫瑰图,确定波浪疲劳分析工况。在各波浪疲劳分析工况中,选取适当波浪谱描述波浪能在频域内的分布情况,如P-M谱:
| $ {S_{\eta \eta }}\left( f \right) = \frac{{H_s^2{T_z}}}{{{\rm{4 \mathsf{ π} }}}}{({T_z}f)^{- 5}}{\rm{exp}}\left[{-\frac{1}{{\rm{ \mathsf{ π} }}}{{({T_z}f)}^{-4}}} \right] $ | (3) |
式中:Hs和Tz是所选疲劳分析工况对应的有效波高和平均波周期,f是频率,Sηη(f)是波高功率密度函数。将波高谱通过传递函数转换,可以得到结构各管节点应力波动范围响应谱:
| $ {S_{\sigma \sigma }}\left( f \right) = {\left| {T\left( f \right)} \right|^2}{S_{\eta \eta }}\left( f \right) $ | (4) |
式中:T(f)是应力范围传递函数,应力范围传递函数可通过对结构进行有限元数值模拟得到。
管节点上的应力范围历程可假定是一个窄带高斯过程,其峰值服从瑞利分布。瑞利分布概率密度函数p(σr):
| $ p({\sigma _r}) = \frac{{{\sigma _r}}}{{{m_0}}}{\rm{exp}}\left[{-\frac{{\sigma _r^2}}{{2{m_0}}}} \right] $ | (5) |
式中:σr是应力范围标准差,m0是应力范围响应谱的0阶谱矩,该函数曲线所围总面积为1。其中,对于大于5倍标准差的应力范围,其出现概率可以忽略;对于5倍标准差以内的应力范围,可将其划分为更小的应力范围区域,用各分块应力范围均值代表该区域内的应力范围值。各区域的出现概率与曲线下所围频带面积相对应。
将各波浪疲劳分析工况下各应力范围区域的热点应力范围和年循环次数代入S-N曲线中,即可求得该应力范围区域的年疲劳损伤。应力范围区域的年循环次数可通过该区域出现概率和应力响应有效频率计算得到。将不同疲劳工况下各应力范围区域的年疲劳损伤线性叠加,可以得到结构各管节点的年累积疲劳损伤,进而得到疲劳寿命。
2) 风激疲劳分析方法。
使用风激疲劳载荷谱法对结构进行风激疲劳分析,应考虑各级风激疲劳荷载的方向分布特性。将各级风机疲劳载荷与风向组合,形成风激疲劳分析工况。在风激疲劳分析中,各疲劳分析工况下结构损伤和结构年累积疲劳损伤的计算方法与波浪谱疲劳分析中相同,同样选取规范推荐的管节点S-N曲线计算各工况下的临界应力循环次数。计算各工况下结构疲劳损伤,需要确定风激疲劳荷载作用下结构内各管节点应力波动范围和应力循环次数这两个关键参数。其中,各疲劳分析工况下的年应力循环次数,可由风激疲劳载荷谱中给出的年循环次数乘以风向概率得到。应力波动范围则需通过风激载荷谱与应力波动的换算关系确定。
1.1.3 第3级控制准则经过前两级控制准则检验之后,如果还有至少两个以上的优化方案能够通过,则对所有这些优化方案进行第3级检验,即综合对比分析。在这一级检验中,并不是针对某一项指标的单纯比较,而是将所有指标,包括强度、变形、频率、疲劳、用钢量、加工安装难度、建造周期等因素综合在一起,进行成本综合评价,最终筛选出一个最优的四腿桁架式风机基础结构设计方案。
1.2 交叉式优化算法对于复杂工程结构,影响结构安全性、使用性和经济性的设计参数较多,包括装机功率、作业水深、环境特征、地质参数、结构拓扑和尺寸等。其中,装机功率、作业水深、环境特征和地质参数随前期规划和选址完成即可确定,不作为结构优化设计中需要考虑的变量。因此,这些设计参数作为结构优化的设计条件,是开展优化工作的前提和基础。另一方面,结构拓扑参数和尺寸参数直接决定结构整体力学性能,将作为结构优化过程中的设计变量,基于交叉式优化算法进行搜索,组合成一系列优化方案通过多准则控制算法的检验和筛选。
为提高设计变量的搜索效率,按照优化顺序对各设计变量进行分级,形成逐级搜索策略。在设计变量搜索过程中,必须依据可能性、合理性和全面性等搜索原则。其中,四腿桁架式风机基础结构各设计参数取值范围必须满足约束条件的限制,从而保证设计参数搜索的可能性。风机基础结构各构件的尺寸参数并不是连续变化的,应根据构件型值表选择标准型材,尽量避免使用异型构件造成成本升高,从而保证设计参数搜索的合理性。对设计参数的搜索必须完全覆盖所有可能出现的取值,避免遗漏最优的设计参数组合,从而保证设计参数搜索的全面性。
将各优化设计变量按照优化顺序分级(如图 3),包括过渡段拓扑变量、甲板尺寸变量、桁架结构拓扑变量和整体模型。其中,过渡段拓扑变量包括过渡段斜撑表观倾角和桁架腿甲板处间距,根据这两项设计参数可以确定过渡段的拓扑形式。甲板尺寸设计变量为甲板梁尺寸。桁架结构拓扑形式设计变量包括:主腿斜度s和拓扑宽高比α,由这两个设计变量可以明确桁架式基础结构的拓扑形式。上述各级设计变量汇集于整体模型中,同时包含设计变量:过渡段斜撑尺寸、桁架腿尺寸和撑杆尺寸,共同形成优化设计方案。

|
Download:
|
| 图 3 设计参数逐级搜索策略 Fig. 3 Sequential search strategy of design parameters | |
约束条件是四腿桁架式风机基础结构优化设计中的关键环节。一方面,约束条件限制设计参数取值范围或给出建议取值,是设计参数必须满足的边界条件;另一方面,约束条件指引设计参数搜索方向,可以提高搜索效率。因此,约束条件设置是否全面、合理,直接影响结构优化策略的准确性和效率。
1.3.1 过渡段拓扑形式过渡段的主要功能是连接上部塔筒与下部基础结构。一方面,过渡段是塔筒的基础,具有约束风机和塔筒位移、控制结构固有频率的作用;另一方面,过渡段起到将上部风机载荷传递至下部基础结构的作用。鉴于过渡段结构的上述功能,在设计过渡段结构时应遵循以下原则:1)过渡段应具备足够的强度,从而有效支撑和约束上部风电模块;2)过渡段应具备极佳的载荷重新分配与传递能力;3)过渡段设计通常是支撑结构设计的原点,其拓扑形式直接决定了下部支撑结构的拓扑发展方向。
过渡段拓扑形式设计参数包括:过渡段斜撑表观倾角和桁架腿甲板处间距。根据对已有工程实例的调研,桁架腿甲板处间距应介于主筒体直径的2~3倍:
| $ 2{D_t} \le {L_d} \le 3{D_t} $ | (6) |
式中:Ld为桁架腿甲板处间距,Dt为主筒体直径。过渡段高度,即基础环顶至甲板高度Ht,一般设置在1~2倍主筒体直径:
| $ {D_t} \le {H_t} \le 2{D_t} $ | (7) |
另一方面,过渡段斜撑表观倾角直接影响过渡段结构刚度,是拓扑优化过程中的重要设计参数。为了确定过渡段斜撑表观倾角的约束条件(取值范围),建立过渡段局部结构模型进行数值模拟分析。基于过渡段结构设计原则,在设计中应保证结构具有较大刚度。用一个等效刚度k同时表征过渡段结构的水平刚度和旋转刚度:
| $ k = \frac{F}{{{D_x}}} + \frac{M}{{L \times {D_x}}} $ | (8) |
式中:F是基础环顶处风机剪力,M是基础环顶处风机弯矩,L是过渡段高度,Dx是基础环顶处水平位移。在数值计算过程中,将不同级别的风机载荷分别施加在基础环顶位置,过渡段结构无量纲刚度k随斜撑表观倾角的变化情况如图 4所示。图中15条曲线分别代表了15种典型工况风机载荷作用下过渡段等效刚度的变化情况。

|
Download:
|
| 图 4 过渡段结构等效刚度随斜撑表观倾角变化曲线 Fig. 4 Equivalent stiffness curves with apparent angles of diagonal braces in the transition section | |
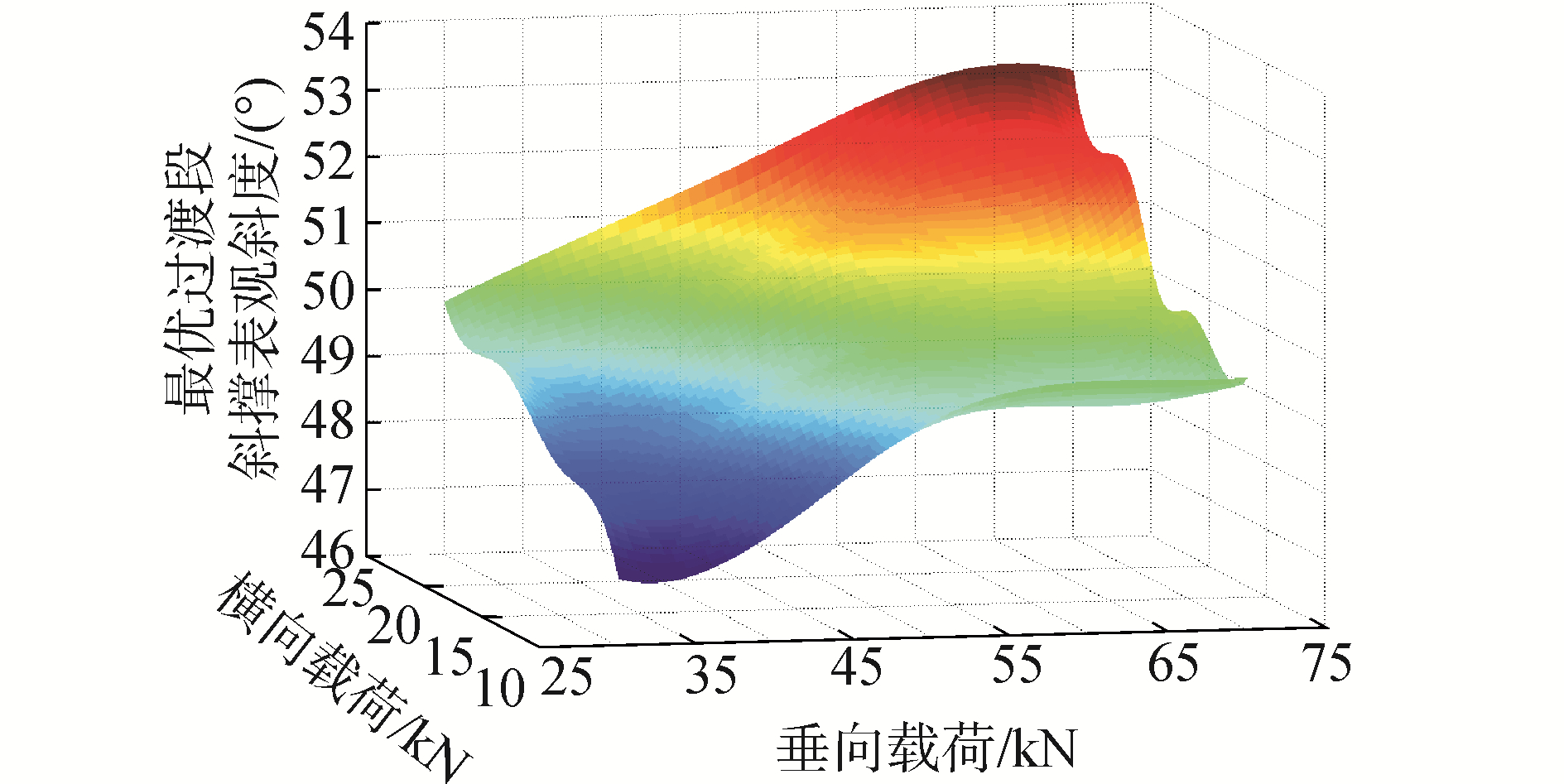
由图 4中变化趋势,可将等效刚度的平稳段划定为最优角度范围。根据设计和工程经验,为保证风电结构满足风机厂商提出的频率要求,桁架式风机基础应尽量设计为细长型构型。因此,在最优斜撑表观倾角范围内,可选取上限值作为最优过渡段斜撑表观倾角。据此,可得到上述各级载荷所对应的最优过渡段斜撑表观倾角,如图 5所示。可以看到,图中的曲面即为过渡段拓扑形式的优化算法。
|
Download:
|
| 图 5 最优过渡段斜撑表观倾角随风机载荷变化曲面 Fig. 5 Optimum apparent angles of diagonal braces surface with wind turbine loads in the transition section | |
四腿桁架结构是连接过渡段结构与桩基础的关键部分。桁架结构拓扑形式设计参数包括:主腿斜度s和拓扑宽高比α。一般地,桁架结构都可以看作是由两个或更多平面框架组成(如图 6(a)),平面框架通过水平撑杆和斜撑相互连接。平面框架本身也可以看作是由单跨框架模块组成的,如图 6(b)所示,再相互叠加而成。平面框架结构拓扑宽高比α定义为
| $ \alpha = \frac{{\left( {a + b} \right)}}{{2h}} $ | (9) |

|
Download:
|
| 图 6 平面框架和单跨框架单元 Fig. 6 Plane frame and single span frame unit | |
式中:a是框架上部宽度,b是框架底部宽度,h是框架高度。工程界已经在钢桁架结构的设计建造中积累了丰富的经验,这些经验表明,拓扑宽高比α的取值在0.7~1.4时桁架结构具备最佳的横向载荷抵抗能力[14]。
1.3.3 整体模型除了上述各级设计参数外,还有以下尺寸设计参数需要考虑:包括过渡段斜撑尺寸、桁架腿尺寸和撑杆尺寸。这些设计参数中还存在以下约束条件:过渡段斜撑与甲板连接位置的底部一般与桁架腿相连,因此,过渡段斜撑与甲板连接一端的横截面尺寸通常设置为与桁架腿相同。过渡段斜撑常进行变径处理,即距离基础环顶越近,横截面尺寸越大,从而增大斜撑与主筒体之间的焊接面积。基础环顶一端过渡段斜撑的直径与甲板一端常保持2:1的关系。据此,在尺寸优化中,甲板斜撑尺寸随桁架腿尺寸变化,共同组成相应的结构优化方案。
不仅是过渡段斜撑尺寸,整体模型是将四腿桁架式风机基础结构所有设计参数组合起来,共同形成优化方案。组成优化方案的各设计参数均应满足相应约束条件的要求,各设计参数均在取值范围内,将各尺寸设计参数按照设定步长变化,每形成一个优化方案即代入多准则控制算法。如果能够通过前两级优化检验,则进入第3级作为最优方案备选;如果不能通过前两级优化检验,则返回整体模型,按步长变化设计参数,形成新的优化方案再进行多级检验。
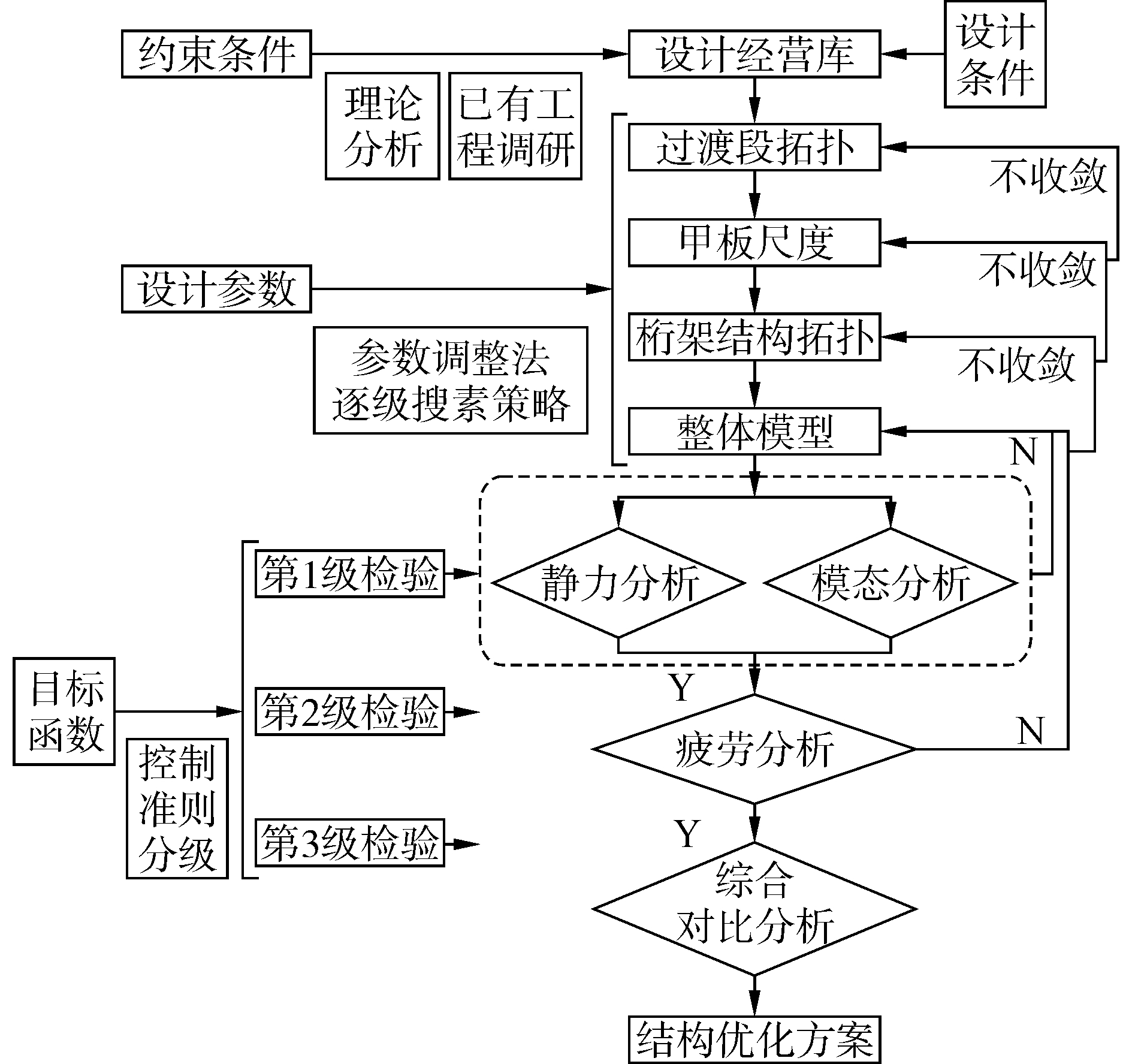
综上,多准则多参数结构优化策略具体流程如图 7所示。为提高优化效率,在各控制准则的结构分析中分别使用Ansys和SCAS有限元软件进行计算,使用VB语言分别编译相应的程序包完成设计参数交叉式搜索、结构分析程序调用、分析结果比对和设计参数自动调整等工作。
|
Download:
|
| 图 7 多准则多参数结构优化策略流程 Fig. 7 Procedure of multi-criteria and multi-parameter structure optimized strategy | |
基于上述针对四腿桁架式风机基础结构的多准则多参数优化策略,对我国某海域风电结构进行优化设计,从而验证该结构优化策略与方法的实际效果。
2.1 设计条件设计目标工程场址水深21 m,50年一遇极端高潮位为+4.56 m,50年一遇H1%为12.90 m,平均波周期为10.29 s。该海域不同水深位置潮流可能最大流速分别为:表层流速0.89 m/s,底层流速0.52 m/s。风电机组设计装机功率为4 MW,轮毂高程为+90 m,在+10 m高程处50年一遇风机极限载荷列于表 1。
| 表 1 风机极限载荷 Tab.1 Ultimate load of the wind turbine |
在进行结构优化设计之前,首先对风电结构的桩基承载力进行分析。该结构基础型式为预埋桩基础,安装时将桁架式基础直接与预埋桩连接。桩基承载力与预埋桩的桩径和打桩深度相关,经分析发现,该结构承载力对桩径变化并不敏感,主要随打桩深度的增加而增大。因此,调整打桩深度即可满足桩基承载力的要求,在结构优化设计中可以暂不考虑桩基承载力这一目标函数。
依据结构优化策略,将各设计参数组合成一系列优化方案,分别对各方案进行第1级检验。在设计参数搜索过程中,按照逐级搜索策略,当优化方案无法通过控制准则检验时,整体模型中的桁架腿直径、撑杆直径和过渡段斜撑直径作为首先调整的设计参数,调整步长设为50 mm。当改变整体结构设计参数仍无法使控制准则收敛时,进而调整桁架结构拓扑形式中的主腿斜度s和拓扑宽高比α,斜度调整步长设为2,宽高比调整步长随X型立面斜撑跨数变化。当改变桁架结构拓扑形式设计参数仍不能令控制准则收敛时,继续返回调整甲板尺寸中的梁尺寸,根据型钢表选择适当构件尺寸。当改变甲板尺寸设计参数也不能使控制准则收敛时,最后调整过渡段拓扑形式中的斜撑表观倾角和桁架腿在甲板处间距,表观倾角的调整步长设为1°,桁架腿间距的调整步长设为0.5 m。
根据型钢表选择适当构件尺寸。设计参数,调整步长随型钢表增强/减弱一个型号确定。
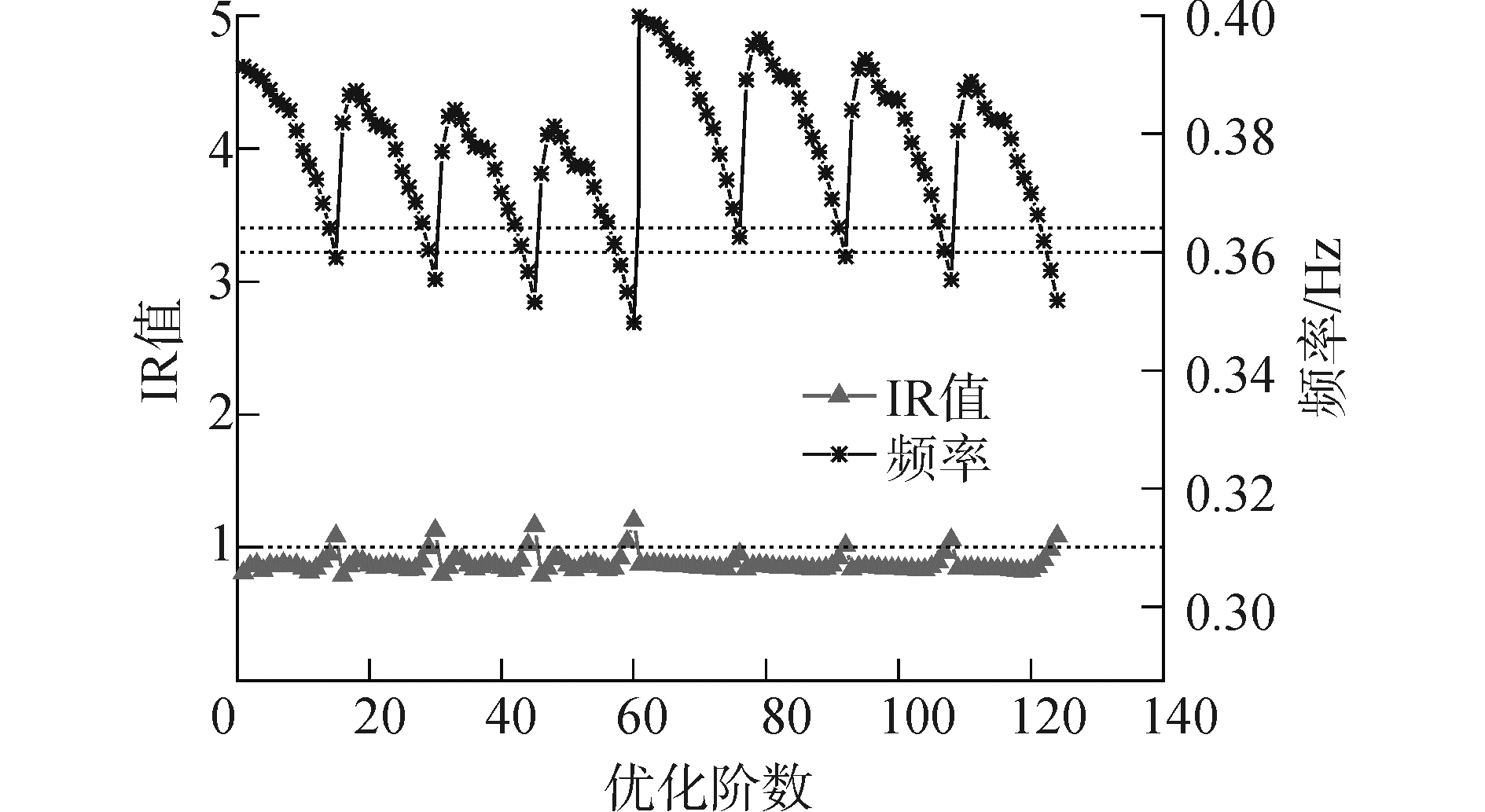
在静力分析中,选取50年一遇极端风机载荷工况进行检验,该工况计算条件为:50年一遇极端高潮位下,遭遇风机极限荷载、50年一遇H1%波浪力和分层潮流力,各环境载荷沿四腿桁架结构对角线方向入射。将静力分析中的主要检验指标最大位移比(基础环顶处水平位移与允许位移之比)、管节点最大应力IR值和杆件最大应力UC值,分别与模态分析得到的结构1阶固有频率结果组合,如图 8~10所示。

|
Download:
|
| 图 8 第1级检验位移比与频率计算结果 Fig. 8 Displacement ratio and frequency results in the first order check | |
|
Download:
|
| 图 9 第1级检验管节点IR值与频率计算结果 Fig. 9 IR of tubular joints and frequency results in the first order check | |
|
Download:
|
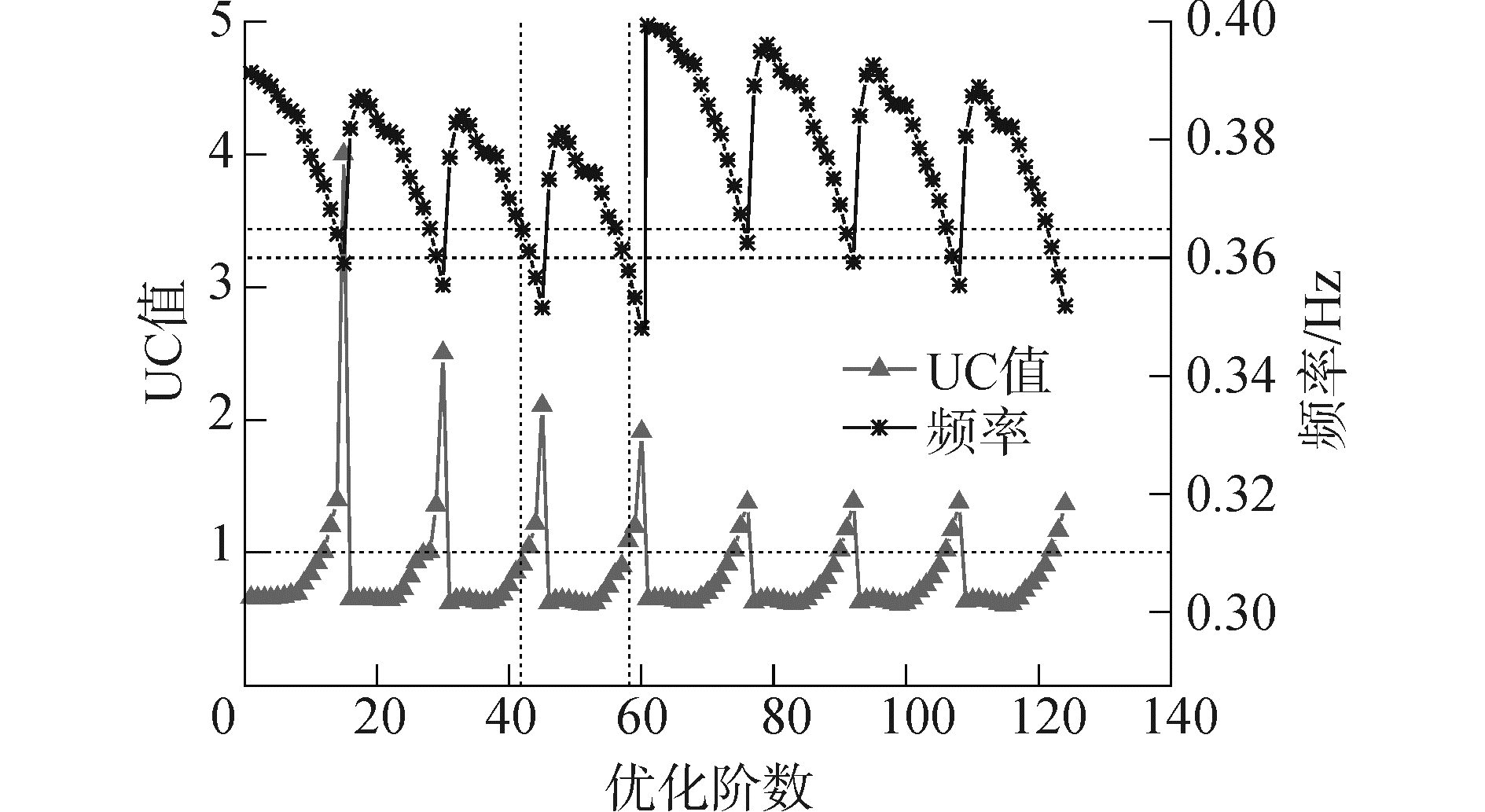
| 图 10 第1级检验杆件UC值与频率计算结果 Fig. 10 UC of members and frequency results in the first order check | |
在图 8~10中,横坐标是优化阶数,即进行第1级检验的优化方案的序号。右侧纵坐标是优化方案的1阶固有频率,左侧纵坐标是静力分析检验指标。为避免曲线过于混杂,这3个检验指标是从同一个优化方案得出后分别表示在3个图中。因此,第1级控制准则就要求这3项检验指标与1阶固有频率同时满足规范和风机厂商要求,即优化方案应取3张图分别选取的优化方案的交集。
该风电工程拟选风机的允许频率范围为0.31~0.365 Hz,用两条虚线在图中表示。优化方案整体结构的1阶固有频率落于这两条虚线之间,同时各项静力检验指标落于1.0虚线以下,则该方案可以满足第1级控制准则的要求。由图可见,优化方案最大位移比和管节点最大应力IR值均与1阶固有频率存在较多收敛方案,在图 10中杆件最大应力UC值与1阶固有频率之间有两个优化方案可以令控制准则收敛。取三者交集,即共有2个优化方案通过了第1级检验。这两个优化方案具有十分相近的结构型式,如图 11所示。两优化方案过渡段均采用变径斜撑与甲板相组合的型式,桁架结构设置两跨X型斜撑,未设置水平撑杆。两优化方案各杆件尺寸完全相同,只有桁架腿斜度存在差异,方案1主腿斜度为10,方案2主腿斜度为12。

|
Download:
|
| 图 11 第1级检验优化方案结构模型 Fig. 11 Structure model of optimized schemes in the first order check | |
依据多准则多参数结构优化策略,第2级检验是对通过第1级检验的优化方案进行疲劳分析。对于该风电工程场址海域,风电结构主要经历风激疲劳和波浪疲劳作用,在第2级控制准则检验中分别对两个优化方案进行风激疲劳分析和波浪疲劳分析。
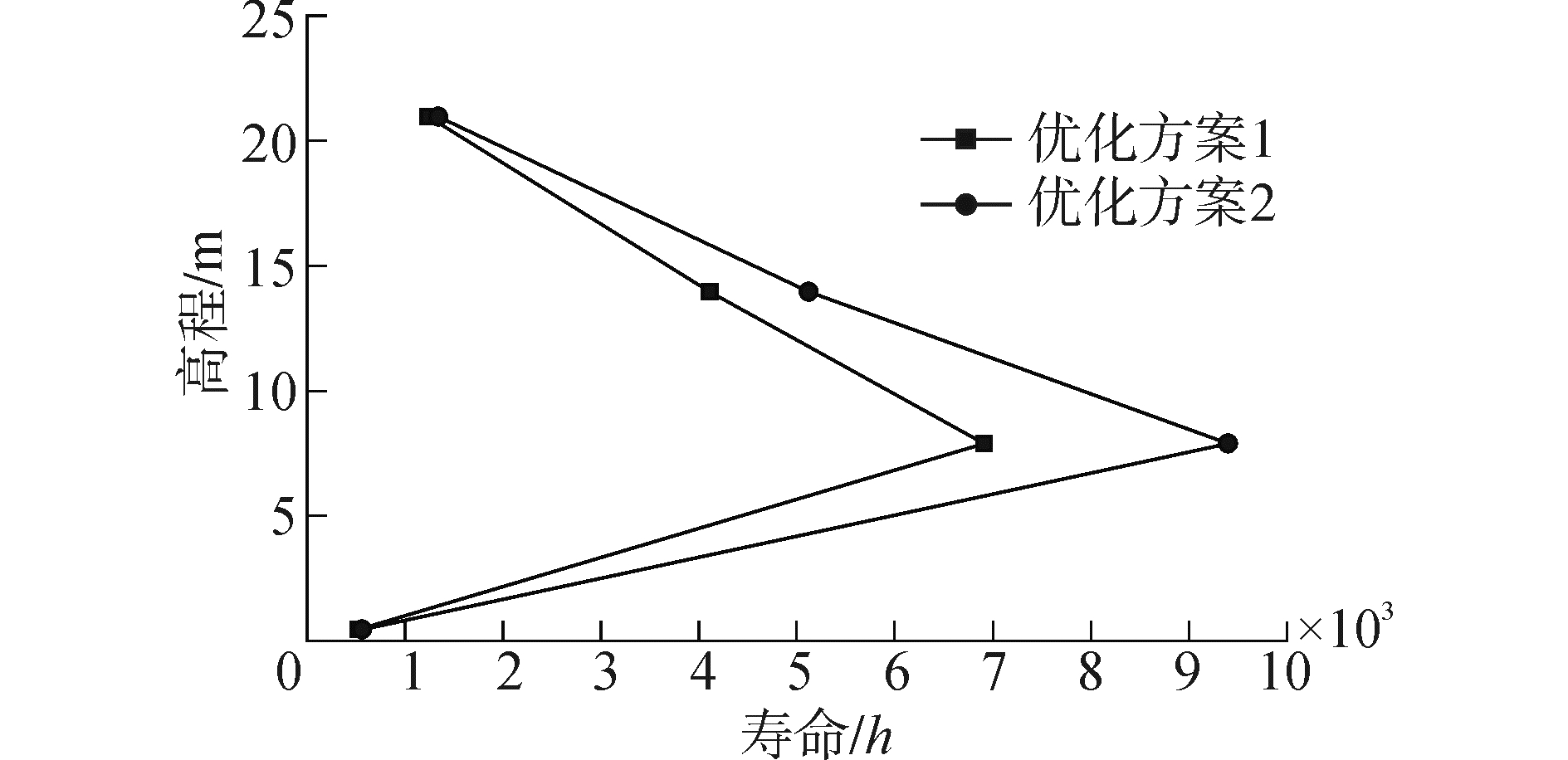
在风激疲劳分析中,优化方案1结构的最小风激疲劳寿命为525年,优化方案2结构的最小风激疲劳寿命为562年,远大于设计要求50年,可以满足风激疲劳校核要求。在波浪谱疲劳分析中,使用P-M谱描述波浪,使用S-N曲线法计算波浪疲劳损伤和疲劳寿命。优化方案1结构在波浪载荷作用下最小疲劳寿命为2.20×1011年,可见波浪疲劳损伤与风相比很小,几乎可以忽略,结构的疲劳寿命主要受风激疲劳控制。将风激疲劳与波浪疲劳损伤线性叠加,得到优化方案1结构最小疲劳寿命为525年,优化方案2结构最小疲劳寿命为562年,均满足疲劳寿命要求,可以通过第2级检验。将两方案结构沿高度方向上管节点的疲劳寿命共同列于同一图中(如图 12所示)。
|
Download:
|
| 图 12 两优化方案管节点疲劳寿命沿高度分布 Fig. 12 Fatigue lives of tubular joints along the height in these two optimized schemes | |
两个优化方案1和2均可以通过前两级控制准则检验,将两优化方案的各项指标列于表 2中,同时将该结构原经验设计方案指标列于表中作为对照。对这两个优化方案进行综合比较,从而确定最优的四腿桁架式风机基础结构优化方案。
| 表 2 优化方案综合对比分析 Tab.2 Comprehensive comparison of optimized schemes |
两优化方案结构型式十分接近,这一特点清晰反映在表 2的优化方案综合对比分析中。优化方案结构各项指标均满足规范及设计要求。细致对比两方案,方案1在控制基础环顶水平位移方面更为突出,其余各项指标均相差很小,因此推荐优化方案1为该海域风机基础结构型式。
3 结论1) 结构优化控制准则使用多准则控制算法分为3级。将对结构安全和性能起关键性作用的目标函数分为3级,逐级形成优化方案并进行检验,提高了优化方案的组合和筛选效率。
2) 结构优化设计参数使用交叉式优化算法逐级搜索和调整。在每一级检验中,通过交叉式优化算法进行变量搜索,保证了设计参数组合的完备性,不致遗漏优化方案。
3) 引入约束条件限制设计参数的取值范围。根据工程设计经验和理论分析结果建立约束条件,限制各设计参数的取值范围,从而提高了交叉式优化算法的搜索效率。
4) 将该多准则多参数结构优化策略应用于我国某海域一实际风电工程中,经过实际优化设计可得,该方法筛选出的优化方案与经验设计方案相比材料利用率显著提高,结构用钢量明显减少,特别是结构疲劳寿命大幅提高,由不满足设计要求提高至留有足够安全裕量。这种多准则多参数结构优化方法并不是针对某一结构得出的,在中等水深海域四腿桁架式风机基础结构的优化设计中具有一定范围的适用性。
在目标函数筛选时未将地震分析和基础承载力分析等纳入优化策略,对于特定环境,地震分析、基础承载力分析或其他结构分析内容可能成为控制因素。在今后工作中,还需对该优化策略的适用范围进行更多的应用和分析,并对该方法持续补充和完善。
| [1] |
何祚庥. 解决中国能源短缺问题的重要途径[J]. 福州大学学报(哲学社会科学版), 2005(1): 5-7, 112. HE Zuoxiu. Solutions to china's energy shortage[J]. Journal of Fuzhou University (philosophy and social sciences), 2005(1): 5-7, 112. (  0) 0)
|
| [2] |
张国伟, 龚光彩, 吴治. 风能利用的现状及展望[J]. 节能技术, 2007, 25(1): 71-76. ZHANG Guowei, GONG Guangcai, WU Zhi. State of the art and prospects on wind energy[J]. Energy conservation technology, 2007, 25(1): 71-76. (  0) 0)
|
| [3] |
ACHMUS M, KUO Y S, ABDEL-RAHMAN K. Behavior of monopile foundations under cyclic lateral load[J]. Computers and geotechnics, 2009, 36(5): 725-735. DOI:10.1016/j.compgeo.2008.12.003 (  0) 0)
|
| [4] |
CLOUGH R W, PENZIEN J. Dynamics of structures[M]. Berkeley: Computers and Structures, 2003: 133-134.
(  0) 0)
|
| [5] |
PANTALEO A, PELLERANO A, RUGGIERO F, et al. Feasibility study of off-shore wind farms:an application to Puglia region[J]. Solar energy, 2005, 79(3): 321-331. DOI:10.1016/j.solener.2004.08.030 (  0) 0)
|
| [6] |
ASHURI T, ZAAIJER M B, MARTINS J R R A, et al. Multidisciplinary design optimization of offshore wind turbines for minimum levelized cost of energy[J]. Renewable energy, 2014, 68: 893-905. DOI:10.1016/j.renene.2014.02.045 (  0) 0)
|
| [7] |
TAHANI M, MAEDA T, BABAYAN N, et al. Investigating the effect of geometrical parameters of an optimized wind turbine blade in turbulent flow[J]. Energy conversion and management, 2017, 153: 71-82. DOI:10.1016/j.enconman.2017.09.073 (  0) 0)
|
| [8] |
DHUNNY A Z, LOLLCHUND M R, RUGHOOPUTH S D D V. Wind energy evaluation for a highly complex terrain using Computational Fluid Dynamics (CFD)[J]. Renewable energy, 2017, 101: 1-9. DOI:10.1016/j.renene.2016.08.032 (  0) 0)
|
| [9] |
HAO Ertong, LIU Chunguang. Evaluation and comparison of anti-impact performance to offshore wind turbine foundations:Monopile, tripod, and jacket[J]. Ocean engineering, 2017, 130: 218-227. DOI:10.1016/j.oceaneng.2016.12.008 (  0) 0)
|
| [10] |
ZWICK D, MUSKULUS M, MOE G. Iterative optimization approach for the design of full-height lattice towers for offshore wind turbines[J]. Energy procedia, 2012, 24: 297-304. DOI:10.1016/j.egypro.2012.06.112 (  0) 0)
|
| [11] |
LEE Y S, GONZÁLEZ J A, LEE J H, et al. Structural topology optimization of the transition piece for an offshore wind turbine with jacket foundation[J]. Renewable energy, 2016, 85: 1214-1225. DOI:10.1016/j.renene.2015.07.052 (  0) 0)
|
| [12] |
API RP 2A-WSD-2007. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design[S]. [S. l. ], 2007.
(  0) 0)
|
| [13] |
KARSAN D I. Design of jackets in deeper Gulf of Mexico waters[J]. Journal of waterway, port, coastal, and ocean engineering, 1986, 112(3): 427-446. DOI:10.1061/(ASCE)0733-950X(1986)112:3(427) (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


