2. 南华大学 机械工程学院, 湖南 衡阳 421001
2. School of Mechanical Engineering, University of South China, Hengyang 421001, China
弹性变形和热变形是齿轮在传动过程中产生振动与噪声的主要原因,齿廓修形是解决该问题的有效方法[1-2]。目前齿廓修形的方法及加工技术已基本成熟[3-7],修形对齿轮传动系统静态和动态特性的影响研究颇多[8-15],但其修形仅考虑了轮齿在啮合过程中的弹性变形。孙月海等[16]对含误差的直齿轮的齿廓修形进行了研究。程愿应等[17]对直齿轮的弹性变形,热变形及齿廓修形进行了研究。任素波等[18]对烧结机星轮齿形的热变形进行了研究。陶燕光等[19]对高速齿轮的热变形修形进行了实验研究。本文综合考虑齿轮啮合过程中轮齿的弹性变形及热变形,分别采用分段修形和连续修形两种不同的修形方式,推导两种方式下的修形量表达式,并对两种方式下修形对齿间载荷分配系数及传动误差进行分析。
1 齿轮热变形分析轮齿热变形是由齿轮在啮合过程中产生的摩擦热导致的。齿轮的摩擦热量随时间的推移以两种方式存在,一是齿面闪温,二是齿轮的本体温度即稳态温度。齿轮的稳态温度是影响轮齿热变形的主要因素。齿轮基圆内稳态温度分布的计算公式可表示为[20]
| $ t\left( r \right) = {t_n} + \frac{{{t_b} - {t_n}}}{{\ln \frac{{{r_b}}}{{{r_n}}}}}\ln \frac{r}{{{r_n}}} $ | (1) |
式中:t为基圆内任一点的稳态温度,tb为基圆稳态温度,tn为齿轮轴孔稳态温度,rb为基圆半径,rn为轴孔半径,r为基圆内任一点的半径。
由式(1)可知,齿轮基圆内的稳态温仅为半径的一元函数,且在齿宽方向上没有变化。因此在不考虑外力和残余应力的情况下,可将齿轮基圆柱内的热变形问题简化为轴对称的平面应力或平面应变问题来求解。当齿宽b与分度圆齿厚s的比值b/s≥5时为平面应变问题,反之为平面应力问题[20]。
1.1 齿轮热变形的解析法如图 1所示,在圆柱坐标系下,将轮齿齿廓上任意一点K的热变形量分为径向热变形Δrk和周向热变形Δsk两个分量。其中Δsk是轮齿渐开线上任意一点齿厚热变形量的一半:

|
Download:
|
| 图 1 齿廓热变形示意图 Fig. 1 The sketch map of thermal deformation of tooth profile | |
| $ \Delta {s_k} = \Delta {t_k}\lambda {s_k}/2 $ | (2) |
式中:Δtk为啮合点K的温升,即稳态温度t(rk)与环境温度t0的差值,sk为K点的齿厚,λ为齿轮材料的热膨胀系数。
Δrk可将其进一步分解为基圆热变形量Δrb和渐开线上K点半径rk与基圆半径rb差值的热变形量之和:
| $ \Delta {r_k} = \Delta {r_b} + \Delta {t_k}\lambda ({r_k} - {r_b}) $ | (3) |
齿轮基圆的物理方程:
| $ \left[ \begin{array}{l} {\varepsilon _r}\\ {\varepsilon _\theta }\\ {\varepsilon _z} \end{array} \right] = \frac{1}{E}\left[ {\begin{array}{*{20}{c}} 1&{ - \mu }&{ - \mu }\\ { - \mu }&1&{ - \mu }\\ { - \mu }&{ - \mu }&1 \end{array}} \right]\left[ \begin{array}{l} {\sigma _r}\\ {\sigma _\theta }\\ {\sigma _z} \end{array} \right] + \lambda \Delta T $ | (4) |
式中:E为材料的弹性模量,μ为泊松比,ΔT为基圆内任意点的温升。
对于平面应力问题,σz=0,代入式(4)得到平面应力状态下的径向和周向应变:
| $ \left[ \begin{array}{l} {\varepsilon _r}\\ {\varepsilon _\theta } \end{array} \right] = \frac{1}{E}\left[ {\begin{array}{*{20}{c}} 1&{ - \mu }\\ { - \mu }&1 \end{array}} \right]\left[ \begin{array}{l} {\sigma _r}\\ {\sigma _\theta } \end{array} \right] + \lambda \Delta T $ | (5) |
将几何方程εr=∂u/∂r,εθ=u/r代入式(5),求得应力与位移之间的关系:
| $ \left[ \begin{array}{l} {\sigma _r}\\ {\sigma _\theta } \end{array} \right] = \frac{E}{{1 - {\mu ^2}}}1\left[ {\begin{array}{*{20}{c}} 1&\mu \\ \mu &1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\rm{d}}u/{\rm{d}}r}\\ {u/r} \end{array}} \right] - \left( {1 + \mu } \right)\lambda \Delta T $ | (6) |
将式(6)代入平衡方程:du/dr+(σr-σθ)/r=0,得到
| $ \frac{{{{\rm{d}}^{\rm{2}}}u}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\frac{{{\rm{d}}u}}{{{\rm{d}}r}} - \frac{u}{{{r^2}}} = \frac{{\rm{d}}}{{{\rm{d}}r}}\left[ {\frac{1}{r}\frac{{\rm{d}}}{{{\rm{d}}r}}\left( {ru} \right)} \right] = \left( {1 + \mu } \right)\lambda \frac{{{\rm{d}}T}}{{{\rm{d}}r}} $ | (7) |
对式(7)进行两次积分,得到
| $ u = \frac{{\left( {1 + \mu } \right)\lambda }}{r}\int_{{r_n}}^r {Tr{\rm{d}}r + \frac{{{C_1}}}{2}r + \frac{{{C_2}}}{r}} $ | (8) |
式中:C1、C2为积分待定系数,由边界条件确定。将式(8)代入式(6)得到
| $ {\sigma _r} = \frac{{ - E\lambda }}{{{r^2}}}\int_{{r_n}}^r {Tr{\rm{d}}r + \frac{{E{C_1}}}{{2\left( {1 - \mu } \right)}} + \frac{{E{C_2}}}{{\left( {1 + \mu } \right){r^2}}}} $ | (9) |
齿轮在自由膨胀状态下,σr|r=rn=0,σr|r=rb=0,将以上边界条件代入式(9),确定积分待定系数C1、C2,并将其代入式(8)得到基圆内任一点的径向变形与半径之间的关系:
| $ \begin{array}{l} u = \frac{{\left( {1 + \mu } \right)\lambda }}{r}\int_{{r_{\rm{n}}}}^r {Tr{\rm{d}}r + \frac{{r\lambda \left( {1 - \mu } \right)}}{{(r_b^2 - r_n^2)}}\int_{{r_n}}^{{r_b}} {Tr{\rm{d}}r + } } \\ \;\;\;\;\;\;\;\frac{{\lambda \left( {1 + \mu } \right)r_n^2}}{{r(r_b^2 - r_n^2)}}\int_{{r_n}}^{{r_b}} {Tr{\rm{d}}r} \end{array} $ | (10) |
将r=rb代入式(10)得到齿轮基圆的热变形量:
| $ \Delta {r_b} = {u_b} = {r_b}\lambda {t_n} + \frac{{\lambda r_b^3({t_b} - {t_n})}}{{r_b^2 - r_n^2}} - \frac{{\lambda {r_b}({t_b} - {t_n})}}{{2(\ln {r_b} - \ln {r_n})}} $ | (11) |
对于平面应力问题,εz=0,σz=μ(σr+σθ)-EλT,同理得到平面应变状态下基圆内任意点的径向热变形及基圆热变形量:
| $ \begin{array}{l} u = \frac{{\left( {1 + \mu } \right)\lambda }}{{\left( {1 - \mu } \right)}}\frac{1}{r}\left[ {\int_{{r_n}}^r {Tr{\rm{d}}r + \frac{{\left( {1 - 2\mu } \right){r^2} + r_n^2}}{{r(r_b^2 - r_n^2)}}\int_{{r_n}}^{{r_b}} {Tr{\rm{d}}r} } } \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2\mu \lambda r}}{{r_b^2 - r_n^2}}\int_{{r_n}}^{{r_b}} {Tr{\rm{d}}r} \end{array} $ | (12) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\Delta {r_b} = {u_b} = {r_b}\lambda {t_n} + \\ \frac{{\lambda \left( {1 + \mu } \right){r_b}[r_b^2\left( {1 - 2\mu } \right) - r_n^2]({t_b} - {t_n})}}{{\left( {1 - \mu } \right){r_n}(r_b^2 - r_n^2)}} \end{array} $ | (13) |
工作侧齿廓上任意点K热变形后对应的K'点半径rk'为rk'=rk+Δrk。rk'与y轴的夹角φk'=φk+Δφk。其中φk和Δφk分别表示为
| $ {\varphi _k} = \frac{{{s_k}}}{{2R}} - ({\rm{inv}}{\alpha _k} - {\rm{inv}}\alpha ) $ | (14) |
| $ \Delta {\varphi _k} = \frac{{\Delta {s_k}}}{{{r_{k1}}}} $ | (15) |
式中:φk为工作侧渐开线上任意点K的半径与y轴夹角,R为齿轮分度圆半径,αk为K点压力角,α为分度圆压力角。
在直角坐标系下,K'点热变形沿坐标轴的分量分别为
| $ \left\{ \begin{array}{l} {\Delta _x} = {r_{k'}}\sin {\varphi _{k'}} - {r_k}\sin {\varphi _k}\\ {\Delta _y} = {r_{k'}}\cos {\varphi _{k'}} - {r_k}\cos {\varphi _k} \end{array} \right. $ | (16) |
K'点啮合线法向的热变形量ΔΓ为
| $ {\Delta _\mathit{\Gamma }} = {\Delta _x}\cos {\omega _k} + {\Delta _y}\sin {\omega _k} $ | (17) |
式中ωk为K点的载荷角。
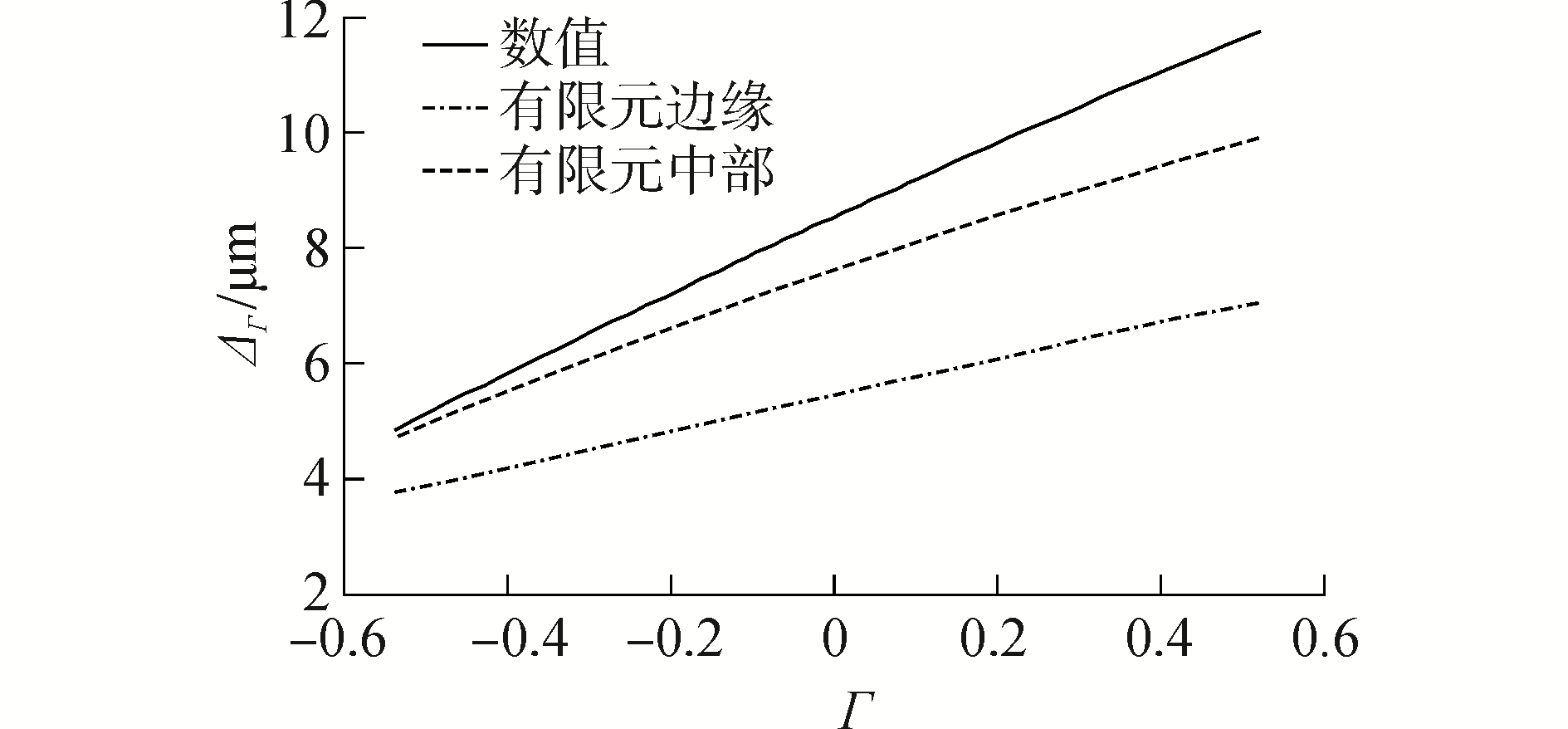
1.2 轮齿热变形的有限元仿真利用有限元热弹耦合的间接方法,进行单齿自由状态下的热膨胀分析。先利用有限元求解齿轮稳态温度场,再将稳态温度场以载荷形式加载到单齿结构分析的模型中,约束内孔圆柱面的所有自由度以及在圆柱坐标系下两个侧面的轴向和周向(即X、Z方向),并给定材料的热膨胀系数λ=1.13×10-5,求解便可得到单齿在自由状态下的热变形。本文研究对象的基本参数如表 1所示,仿真结果如图 2所示(放大50倍效果图)。啮合线法向热变形如图 3所示。
| 表 1 研究对象基本参数 Tab.1 Basic parameters of the research object |

|
Download:
|
| 图 2 单齿热膨胀有限元结果 Fig. 2 The thermal expansion result of FEA | |
|
Download:
|
| 图 3 齿廓啮合线法向变形 Fig. 3 Thermal deformation along the direction of meshing line | |
当传动齿轮的重合度在1~2时,在齿轮啮合的过程中将交替出现单、双齿啮合区。在双齿啮合区将由两对齿轮参与啮合并共同承担齿轮系统传递的载荷。仅考虑齿轮热变形时,其齿轮对间的载荷分配系数及传动误差可表示为
| $ \left\{ \begin{array}{l} {\zeta _1} = \frac{{{k_1}}}{{{k_1} + {k_2}}}\left( {1 + \frac{{{k_2}({\Delta _{{{\rm{t}}_1}}} - {\Delta _{{{\rm{t}}_{\rm{2}}}}})}}{w}} \right)\\ {\zeta _2} = \frac{{{k_2}}}{{{k_1} + {k_2}}}\left( {1 + \frac{{{k_1}({\Delta _{{{\rm{t}}_2}}} - {\Delta _{{{\rm{t}}_{\rm{1}}}}})}}{w}} \right) \end{array} \right. $ | (18) |
| $ \begin{array}{l} {\rm{TE}} = \left\{ \begin{array}{l} (w - {k_1}{\Delta _{{{\rm{t}}_{\rm{1}}}}} - {k_2}{\Delta _{{{\rm{t}}_{\rm{2}}}}})/({k_1} + {k_2})\\ w/{k_1} - {\Delta _{{{\rm{t}}_{\rm{1}}}}}\\ w/{k_2} - {\Delta _{{{\rm{t}}_2}}} \end{array} \right.\\ \left\{ \begin{array}{l} {\Delta _{{{\rm{t}}_1}}} - {\Delta _{{{\rm{t}}_2}}} \le \min (w/{k_1}, w/{k_2})\\ {\Delta _{{{\rm{t}}_1}}} - {\Delta _{{{\rm{t}}_2}}} > w/{k_1}\\ {\Delta _{{{\rm{t}}_2}}} - {\Delta _{{{\rm{t}}_1}}} > w/{k_2} \end{array} \right. \end{array} $ | (19) |
式中:ζ1、ζ2为啮合齿轮对1、2的载荷分配系数,k1、k2为啮合齿轮对1、2的啮合刚度,Δt1、Δt2为啮合齿轮对1、2的总热变形量,w为齿轮传递的单位线载荷,TE为齿轮的传动误差。
针对本文研究对象,在有足够齿侧间隙的条件下,热变形后系统齿间载荷分配系数及传动误差如图 4所示。由图 4可知,热变形对齿间载荷分配系数的影响很小,在啮入端双齿啮合区载荷分配系数变小,在啮出端双齿啮合区载荷分配系数增大,但总的变化量很小,载荷仍然存在突变。对于齿轮的传动误差,热变形仅改变了传动误差的绝对大小,改变量为啮合齿轮对的热变形之和,但传动误差的波动没有改变。

|
Download:
|
| 图 4 热变形条件下的载荷分配系数及传动误差 Fig. 4 Load-sharing ratio and transmission error after thermal deformation | |
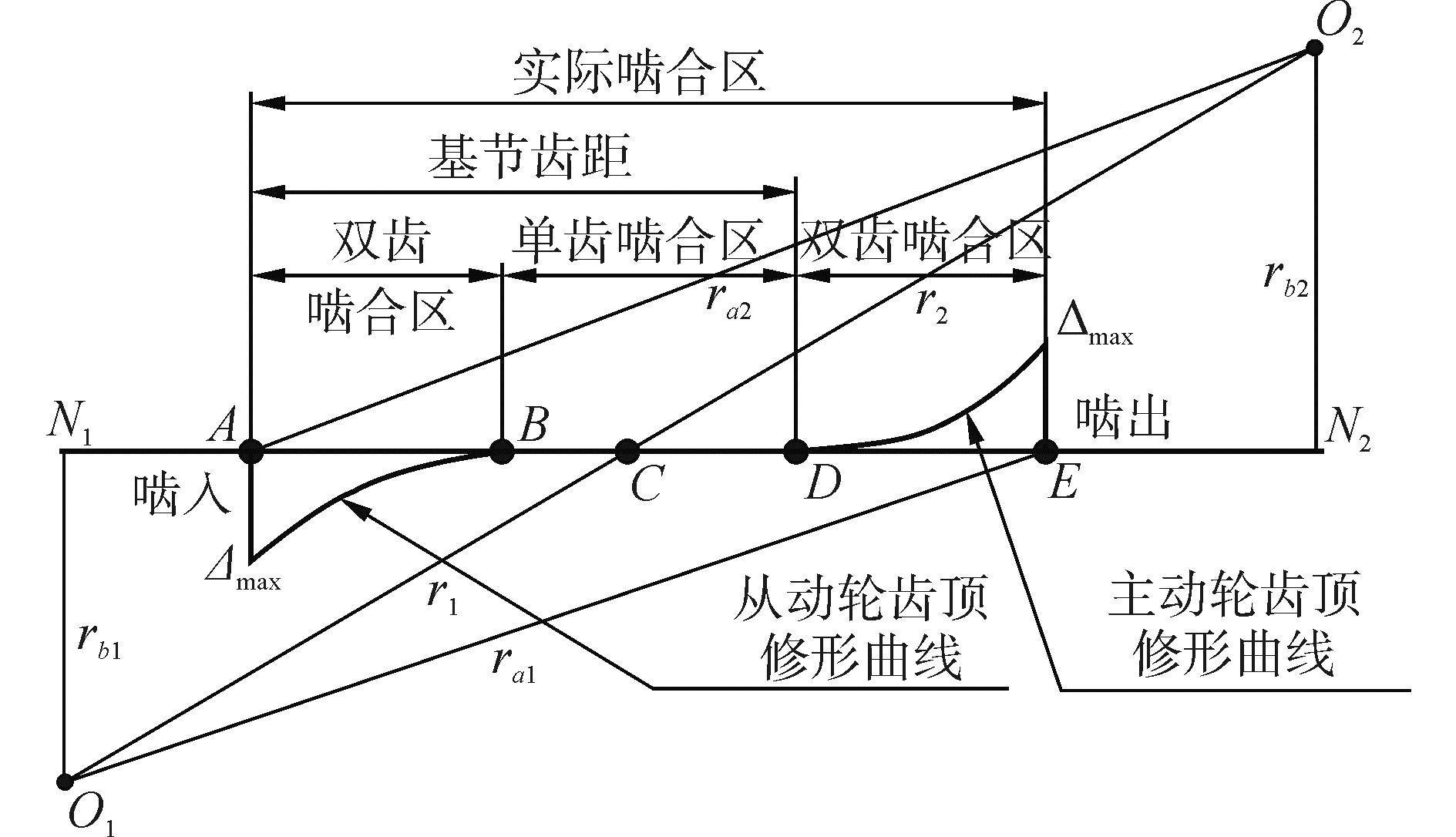
齿廓修形可以有效消除齿间载荷分配系数的突变和减小传动误差的波动,从而达到减振降噪的目的。本文采用主动轮和从动轮齿顶同时进行修形的方式,修形量沿啮合线的分布如图 5所示,其修形量为
|
Download:
|
| 图 5 修形量沿啮合线的分布 Fig. 5 The distribution of modification amount along the meshing line | |
| $ {\Delta _e} = {\Delta _{\max }}{\left( {x/L} \right)^{{\beta _c}}} $ | (20) |
式中:Δmax为最大修形量,取单双齿交替处B、D点的变形量;x为啮合线上双齿啮合区内任一点K到单齿啮合区的下界点B或上界点D的距离;L为啮合线上双齿啮合区的长度, ;βc为修形指数,取值1.43。
齿廓修形后传动系统的齿间载荷分配系数及传动误差仍由式(18)、(19)确定。只需将式中的热变形量Δt用修形量Δe替代,同时规定热变形量取正值,修形量取负值。修形后载荷分配系数及传动误差沿啮合线的分布如图 6所示。

|
Download:
|
| 图 6 弹性修形后的载荷分配系数及传动误差 Fig. 6 The load-sharing ratio and transmission error after the elastic modification | |
由图 6可知,修形后双齿啮合区的载荷分配系数在区间[0, 1]连续变化,载荷突变消除;绝对误差并未改变,但误差的相对波动大幅减小,在整个啮合过程中绝对误差趋于恒定。
4 考虑热弹耦合变形的齿廓修形 4.1 具有足够齿侧间隙的热修形齿廓热变形的方向与齿廓修形方向相反,因此热变形后齿廓的实际修形量为Δ=Δe-Δt,热变形后,齿廓的实际修形曲线如图 7中虚线所示。

|
Download:
|
| 图 7 齿廓修形曲线 Fig. 7 The tooth profile modification curves | |
在有足够齿侧间隙的条件下,传动系统的载荷分配系数及传动误差如图 8所示。

|
Download:
|
| 图 8 足够齿侧间隙时热修形后的载荷分配系数及传动误差 Fig. 8 The load-sharing ratio and transmission error after thermal modification with enough gear backlash | |
由图 8可知,在有足够齿侧间隙的情况下,热变形对修形后的载荷分配系数分布影响很小,双齿啮合区分配系数的连续性没有改变,但A、D点稍有后移,即单齿啮合区增大,双齿啮合区减小。对于传动误差,绝对误差减小,但仍趋于恒定,即误差波动没有变化。因此,在有足够齿侧间隙的条件下,热变形对于修形后的传动误差分布是有利的。
4.2 齿侧间隙不足的热修形在实际工况中,齿侧间隙是有限的,轮齿的热膨胀变形将对传动系统产生不良影响,降低传动精度,产生振动噪声,甚至产生卡齿使传动失效。因此在齿廓修形时必须消除热变形的影响。由图 7可知,热变形后理论修形曲线上移,实际修形量减小,因此要使热变形后的实际修形量达到理论修形量,在修形初期必须增大修形量,同时修形长度应该扩展到单齿啮合区,如图 5中AD或EB段。
4.2.1 分段修形分段修形是将整个修形区间分为双齿啮合区和单齿啮合区两段,在不同修形区间段采用不同的修形函数。在双齿啮合区采用指数修形函数,同时加上啮合齿轮对在AB段的热变形量。在单齿啮合区段采用线性修形函数,使B点的修形量等于该点的热变形量,D点的修形量为0。主、从动轮修形量沿啮合线的分布分别表示为
| $ {\Delta _1} = \left\{ \begin{array}{l} {\Delta _{\max }}{\left( {\frac{{{\mathit{\Gamma }_x} - {\mathit{\Gamma }_D}}}{{{\mathit{\Gamma }_E} - {\mathit{\Gamma }_D}}}} \right)^{{\beta _c}}} + {\Delta _t}\;\;\;\;{\mathit{\Gamma }_x} \in \left[ {E, D} \right]\\ \frac{{{\mathit{\Gamma }_B} - {\mathit{\Gamma }_x}}}{{{\mathit{\Gamma }_B} - {\mathit{\Gamma }_D}}}{\Delta _{tD}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\Gamma }_x} \in \left[ {D, B} \right] \end{array} \right. $ | (21) |
| $ {\Delta _2} = \left\{ \begin{array}{l} {\Delta _{\max }}{\left( {\frac{{{\mathit{\Gamma }_x} - {\mathit{\Gamma }_B}}}{{{\mathit{\Gamma }_A} - {\mathit{\Gamma }_B}}}} \right)^{{\beta _c}}} + {\Delta _t}\;\;\;\;\mathit{\Gamma }x \in \left[ {A, B} \right]\\ \frac{{{\mathit{\Gamma }_D} - {\mathit{\Gamma }_x}}}{{{\mathit{\Gamma }_D} - {\mathit{\Gamma }_B}}}{\Delta _{tB}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\Gamma }_x} \in \left[ {B, D} \right] \end{array} \right. $ | (22) |
式中:Δi为齿廓上任一点的修形量,下标i=1, 2,分别表示主、从动轮,Γx为啮合线上任一点的归一化坐标,ΓA、ΓB、ΓD、ΓE分别为啮合线上对应点的归一化坐标,Δt为Γx对应点的热变形量,ΔtB、ΔtD分别为B、D点的热变形量。
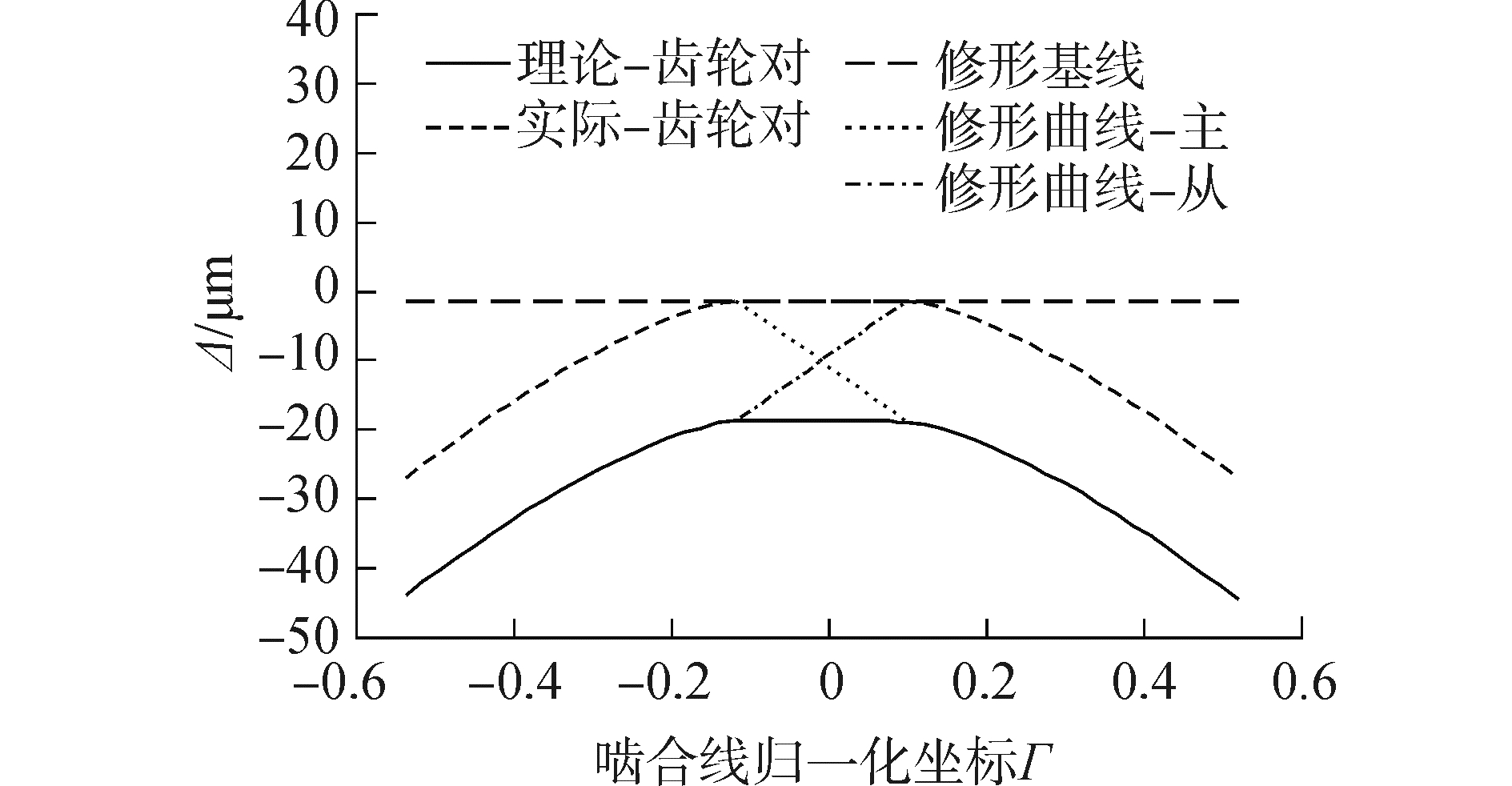
分段修形后,理论修形量及热变形后的实际修形量沿啮合线的分布如图 9所示。
|
Download:
|
| 图 9 分段修形曲线 Fig. 9 The modification curves in the piecewise way | |
对比图 9中的热变形后的实际修形曲线与图 7中仅考虑弹性变形的修形曲线,两者完全吻合。因此,采用分段修形的方式,齿廓热变形后传动系统的载荷分布系数和传动误差与仅考虑弹性变形时的载荷分配系数和传动误差相同,如图 8所示。
4.2.2 连续修形分段修形可以很好的达到弹性变形时的修形效果,但分段节点不好识别,且修形曲线在分段节点处不光滑,使得齿轮的实际修形加工过程变得十分复杂。为了改善分段修形的制造工艺性,本文对分段修形曲线进行二次拟合,得到了连续光滑的拟合修形曲线。修形量的通用表达式为
| $ \Delta = {a_2}\Delta {'_{\max }}{\left( {\frac{{x'}}{{L'}}} \right)^2} + {a_1}\Delta {'_{\max }}\left( {\frac{{x'}}{{L'}}} \right) $ | (23) |
式中:Δ'max为考虑热变形后的最大修形量,取弹性修形的最大修形量Δmax与A(或E)点的热变形量ΔtA(或ΔtE)之和,x'为啮合线上任意一点到D(或B)点的距离,L'为基圆节距,a1、a2为拟合待定系数,由分段修形曲线上的数据点采用最小二乘法拟合确定。
针对本文研究对象,采用连续修形函数得到的修形曲线如图 10所示。

|
Download:
|
| 图 10 连续修形曲线 Fig. 10 The modification curves in the continuous way | |
图 10中点实线表示的是热变形后的实际修形曲线。在连续修形曲线下,系统的载荷分配系数及传动误差如图 11所示。由图 11可知,采用连续修形曲线得到的载荷分配系数在双齿啮合区的连续性得到保留,载荷不存在突变,修形后单齿啮合区增大,双齿啮合区小,但变化量较小。对于传动误差,单齿啮合区的绝对误差减小,双齿啮合区的误差波动增大;其主要的原因在于:修形后单齿啮合区的实际修形量偏小,使得热变形后单齿啮合区的绝对误差减小,相对波动增加。在双齿啮合区,采用连续修形函数修形后,修形曲线的非线性程度发生了变化,从而导致双齿啮合区的误差波动增大。

|
Download:
|
| 图 11 热弹耦合连续修形后的载荷分配系数及传动误差 Fig. 11 The load-sharing ratio and transmission error after thermo-elastic coupling modification in the continuous way | |
从总体上看,采用连续修形方式修形后的系统载荷分配系数及传动误差相对于未修形状态有很大的改善。载荷分配系数的突变消失,误差波动显著减小,同时齿廓修形的工艺性得到保证。
5 结论1) 将齿轮简化为平面应力或应变模型后,通过推导得到了齿廓热变形的计算公式,表明tb、tn、Δtk及基圆内的温度部分是影响热变形的主要因素。
2) 在齿侧间隙足够时,齿廓热变形可以改变双齿啮合区的齿间载荷分配系数,但改变量较小;同时热变形可以减小系统传动误差的绝对大小,且不改变误差的波动。此时,热变形对于修形后的传动误差分布是有利的。
3) 在齿侧间隙不足时,分段修形可以很好的保持啮合过程载荷分配系数的连续性,消除载荷突变,减小传动误差的波动,使误绝对差趋于恒定,但修形的制造工艺性较差。连续修形后载荷分配系数仍然连续,突变消失,其制造工艺也较好,但单齿啮合区域增大;单齿啮合区绝对误差减小,误差波动较分段修形增大。
| [1] |
SIMON V. Optimal tooth modifications for spur and helical gears[J]. Journal of mechanisms, transmissions, and automation in design, 1989, 111(4): 611-615. DOI:10.1115/1.3259044 (  0) 0)
|
| [2] |
LITVIN F L, FUENTES A. Gear geometry and applied theory[M]. New York: Cambridge University Press, 2004.
(  0) 0)
|
| [3] |
朱传敏, 宋孔杰, 田志仁. 齿轮修形的优化设计与试验研究[J]. 机械工程学报, 1998, 34(4): 63-68. ZHU Chuanmin, SONG Kongjie, TIAN Zhiren. Optimum design and experiment study on the gear profile modification[J]. Chinese journal of mechanical engineering, 1998, 34(4): 63-68. (  0) 0)
|
| [4] |
SACHIDANANDA H K, RAGHUNANDANA K, GONSALVIS J. Design of spur gears using profile modification[J]. Tribology transactions, 2015, 58(4): 736-744. DOI:10.1080/10402004.2015.1010762 (  0) 0)
|
| [5] |
李润方. 齿轮传动的刚度分析和修形方法[M]. 重庆: 重庆大学出版社, 1998.
(  0) 0)
|
| [6] |
MEI Wenjie, NA Jingzhou, YANG Fan, et al. The optimal design method and standardized mathematical model of tooth profile modification of spur gear[J]. Mathematical problems in engineering, 2016, 2016: 6347987. (  0) 0)
|
| [7] |
LI Zheng, MAO K. The tooth profile modification in gear manufacture[J]. Applied mechanics and materials, 2008, 10-12: 317-321. (  0) 0)
|
| [8] |
PRAMONO A S. Experimental study of the influence of tooth profile modifications on spur gear dynamic strain and vibration[J]. Key engineering materials, 2006, 306-308: 79-84. DOI:10.4028/www.scientific.net/KEM.306-308 (  0) 0)
|
| [9] |
BAHK C J, PARKER R G. A study on planetary gear dynamics with tooth profile modification[C]//ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Washington, DC, 2011: 365-377. http://www.researchgate.net/publication/267489265_A_Study_on_Planetary_Gear_Dynamics_With_Tooth_Profile_Modification
(  0) 0)
|
| [10] |
WU Yongjun, WANG jianjun, HAN Qinkai. Static/dynamic contact FEA and experimental study for tooth profile modification of helical gears[J]. Journal of mechanical science and technology, 2012, 26(5): 1409-1417. DOI:10.1007/s12206-011-1028-1 (  0) 0)
|
| [11] |
马辉, 逄旭, 宋溶泽, 等. 考虑齿轮-转子系统振动响应的最佳修形曲线研究[J]. 振动与冲击, 2015, 34(11): 17-22. MA Hui, PANG Xu, SONG Rongze, et al. Optimal profile modification curves for spur gears considering vibration responses of a gear-rotor system[J]. Journal of vibration and shock, 2015, 34(11): 17-22. (  0) 0)
|
| [12] |
WAGAJ P, KAHRAMAN A. Influence of tooth profile modification on helical gear durability[J]. Journal of mechanical design, 2002, 124(3): 501-510. DOI:10.1115/1.1485289 (  0) 0)
|
| [13] |
YUE Huijun, LIU Yanfang, XU Xiangyang, et al. Study on vibration characteristics and tooth profile modification of a plus planetary gear set[J]. Journal of vibroengineering, 2014, 16(2): 954-964. (  0) 0)
|
| [14] |
薛建华, 李威. 齿廓修形机理及其对温度场的影响[J]. 东北大学学报(自然科学版), 2013, 34(12): 1763-1767. XUE Jianhua, LI Wei. Tooth profile modification mechanism and its influence on temperature fields[J]. Journal of northeastern university (natural science), 2013, 34(12): 1763-1767. DOI:10.3969/j.issn.1005-3026.2013.12.022 (  0) 0)
|
| [15] |
罗彪, 李威, 于静. 基于模糊综合决策的直齿圆柱齿轮齿廓最佳修形[J]. 工程科学学报, 2016, 38(10): 1458-1466. LUO Biao, LI Wei, YU Jing. Tooth profile modification of the spur gear based on fuzzy comprehensive decision[J]. Chinese journal of engineering, 2016, 38(10): 1458-1466. (  0) 0)
|
| [16] |
孙月海, 张策, 葛楠. 含误差的直齿轮的齿廓修形[J]. 机械工程学报, 2003, 39(12): 91-94. SUN Yuehai, ZHANG Ce, GE Nan. Tooth profile modification for spur gears with manufacturing error[J]. Chinese journal of mechanical engineering, 2003, 39(12): 91-94. DOI:10.3321/j.issn:0577-6686.2003.12.017 (  0) 0)
|
| [17] |
程愿应, 杨元山, 罗铭佑. 直齿轮弹性变形、热变形及齿廓修形[J]. 华中理工大学学报, 1990, 18(S3): 261-267. CHENG Yuanying, YANG Yuanshan, LUO Mingyou. Elastic deformation, thermal deformation and profile modification of spur gears[J]. Journal of Huazhong University of Science and Technology, 1990, 18(S3): 261-267. (  0) 0)
|
| [18] |
任素波, 白明华. 偶数齿烧结机星轮齿形的热变形研究与误差分析[J]. 机械工程学报, 2011, 47(22): 55-60. REN Subo, BAI Minghua. Hot deformation and error analysis of sprocket wheel tooth profile for even tooth sintering machine[J]. Journal of mechanical engineering, 2011, 47(22): 55-60. (  0) 0)
|
| [19] |
陶燕光, 黎上威, 马宪本, 等. 高速齿轮热变形修形的试验研究[J]. 齿轮, 1988, 12(2): 25-28. TAO Yanguang, LI Shangwei, MA Xianben, et al. Experimental study on thermal deformation modification of high speed gear[J]. Gear, 1988, 12(2): 25-28. (  0) 0)
|
| [20] |
李桂华. 复杂规则曲面机械零件的热变形理论及应用研究[D]. 合肥: 合肥工业大学, 2006. LI Guihua. Theoretical and applied research of thermal deformation of complicated machine components with regular camber[D]. Hefei: Hefei University of Technology, 2006. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1015515 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


