2. 审计署计算机技术中心, 北京 100073
2. Audit Research Institute of Chinese National Audit Office, Beijing 100073, China
近年来,随着例如传感器网络、RFID网络、面向轨迹的服务等新兴应用的出现,不确定数据的管理受到了更多的关注和重视[1-5],面向解决不确定性问题的方法以及管理手段的需求更加迫切。在不确定数据管理中,不确定对象的相似性查询是一个重要的研究方向,已有非常多的不确定管理项目对其开展了研究并建立了例如Trio[6-7]、CONQUER[8]、MystiQ[9]、URank[10]等复杂的系统。
常用的不确定数据相似性查询方法有Sky-line[11]、Top-K[12]以及Nearest-Neighbor[13]等。Sky-line采用多目标优化算法解决原始的多目标问题,返回的结果集是一组互相不可直接比较优劣的解,每个解中起码有一维优于其他对象,而其他维又不劣于其他对象。而Top-K是通过对不确定对象集合中的每个对象的多个属性进行聚集,计算得到一个Score值,并将对象按照Score值排序,选取出前k个对象作为解。Nearest-Neighbor方法则是计算k个距离查询对象最近的可能性最高的不确定对象。然而这些查询方法更多关注的是不确定对象间的相似性问题(例如距离问题),却忽视了不确定对象本身的模型准确性与复杂性,本质上讲,不确定对象的建模方法决定了不确定信息的完整性以及不确定对象的相关计算问题。
数据流是一种动态、流式的数据序列,对数据流的处理是动态、顺序的以及一次或有限次的[14]。构成数据流对象的取值是唯一的,但可能是不精确的,即使当数据流中的对象具有较多属性时,这些属性的取值依然是唯一的,这种数据流常称之为确定数据流。然而当观测数据流中的确定对象,却得到更多不唯一的信息时,例如在数据流中的对象的同一属性可以由多个取值表示时,由这种取值不唯一的对象构成的数据流序列,称之为不确定数据流。
在确定数据流的相似性查询问题中,一般研究的对象是两个数据流的距离或者其间的相似性问题,并且这些问题的解都是确定的取值。在不确定数据流的查询问题中,待解决的问题同样是其间的距离或者相似性,但结果不是唯一或确定的值,而是符合某种概率分布的随机数[15-16]。
解决不确定数据流相似性问题大致分为两种思路,一种类似穷举的方法,计算所有不确定对象间的距离,这种方法的好处是模型客观且容易理解,但时间复杂性非常高。另一种是降低维度的方法,这类方法一般假设不确定对象符合某种分布,利用统计信息表示不确定对象,将不确定问题转换为确定的问题求解,其复杂性较低但准确性较差。
但在现实情况中,由于系统的复杂性,导致可收集到的信息并不遵循任意模型明确且固定不变的分布,统计信息随之不断变化,假设的模型也随之失效。
针对上述问题,本文提出一种基于频繁模式挖掘方法的不确定数据流查询方法,方法主要利用非参数估计的思想对不确定对象建模,意在不假设对象符合任何确定或理论密度分布,这种研究方法不受模型和参数的限制而具有良好的灵活性,同时还具有较低的维度使得模型和运算的复杂性均较小。同时,为了满足相似性查询时效的要求,方法结合了模糊语义表述方法以及高阶Markov模型作为提高检索速度的手段。
1 不确定数据流相似性查询方法本文提出的面向不确定数据流相似性查询方法——HB-UTS, 其核心思想是基于非参数密度估计方法的不确定对象建模以及不确定数据流中的固定长度的数据序列间的相似性匹配问题。方法首先利用直方图密度估计对不确定数据流中的对象建模,然后利用聚类方法对得到的直方图密度分布进行模式挖掘,再通过模糊语义表述方法对聚类结果进行抽象,此时可将原本的数值序列转换为语义序列,最后通过高阶Markov构建不确定数据流语义序列的状态转移矩阵,即不确定数据流的索引矩阵。在查询阶段,采用固定滑动窗口的方式处理不确定数据流,对窗口内固定长度的序列数据进行相似性计算,并根据计算条件以及匹配程度返回查询结果。HB-UTS算法主要由不确定数据流的密度分布模型、密度分布模式挖掘、模糊语义表述以及查询方法几个核心部分构成,各部分的具体步骤如下文所述。
1.1 不确定数据流的密度分布模型不确定性问题分为存在的不确定性与属性的不确定性,本文所讨论的是属性的不确定性,即一个对象具有不唯一的取值。属性的不确定会导致观测对象由于大量的取值而具有较高的维度,增加了建模的难度,并且由于观测值数量的不确定,对象维度规模的动态变化也会使对象的模型难于确定。为了解决上述问题,本文选择以密度分布的形式表示不确定对象,一方面降低了属性的维度,另一方面模型本身不会受样本规模而出现较大变化。但在实际问题中,不确定数据流中的对象一般不符合理论分布(正态分布、均匀分布等),不能借用简单的典型分布模型对不确定对象建模,因此本文在不假设对象样本符合任何理论分布的前提下,运用非参数估计方法对不确定对象建模,此时,不确定对象的密度分布的形式主要依赖于样本的实际取值,当样本的取值发生较大变化时,模型本身也会随之改变。
为了可以更有效的对密度分布模式挖掘,本文选择基于直方图的非参数估计方法,如图 1所示。直方图经常用来描述数据的频率,结果直观且容易理解,并且在模式挖掘的实施过程中,可以有效地降低计算的复杂性。

|
Download:
|
| 图 1 不确定数据流的非参数建模方法示意图 Fig. 1 Non-parametric estimation modeling for uncertain data stream | |
假设不确定数据流集合UTS,其中的不确定数据流,ui中的第j个不确定对象可表示为,l是不确定对象的样本数量,ui, jl的密度估计函数为
在直方图密度函数估计中,核函数定义为
| $ {{\hat f}_h}\left( x \right) = \left\{ \begin{array}{l} \frac{{{v_i}}}{{nh}}, \;\;\;\;I\left( {x \in B} \right)\\ 0, \;\;\;\;\;\;\;{\rm{others}} \end{array} \right. $ | (1) |
因此可以通过上述方法确定不确定对象ui, jl的密度函数估计为
结合上述理论,不确定对象的直方图密度估计的方法步骤如下:
1) 给定一个不确定对象的样本ui, jl,大小为l,对其排序并设x1=min(ui, jl)以及xn=max(ui, jl)分别为最大和最小样本,确定最小下届a0≤x1;
2) 估计组距h,可得组分的界点a0, a1, …, ak,其中ai+1-ai=h,i=0, 1, …, k-1,xn≤ak≤xn+h;
3) 计算落在每组区间Ai=(ai, ai+1],i=0, 1, …, k-1中的样本频数:v1, v2, …, vk;
4) 以h为带宽,v1, v2, …, vk为高作直方图;
5) 由直方图估计样本对应总体的密度分布可得
构建直方图密度估计的关键就是确定组距h,组距的选择决定了密度函数的性质和总体分布特征,若取值不合理,估计的密度函数相对真实的情况就会有较大的偏差,这里假设不确定对象u的真实密度函数u(x)以及直方图的估计密度为
平方损失风险常用于获取近似的估计密度函数,该值越小,估计的密度函数与真实密度函数越接近。因此本文通过平方损失风险求得合理的组距h值。首先定义平方损失风险:
| $ R\left( {\hat u, u} \right) = \smallint {\left( {\hat u\left( x \right) - u\left( x \right)} \right)^2}{\rm{d}}x $ | (2) |
此时,考察如式(3)所示的平方损失风险的期望,并经过式(4)的计算,将该损失风险转换为
| $ R\left( {\hat u, u} \right) = {\rm{E}}\smallint {\left( {\hat u\left( x \right) - u\left( x \right)} \right)^2}{\rm{d}}x $ | (3) |
| $ \begin{array}{l} R, \left( {\hat u, u} \right) = \smallint {\left( {{\rm{E}}\hat u\left( x \right) - u\left( x \right)} \right)^2}{\rm{d}}x + \\ \;\;\;\;\;{\rm{E}}\smallint {\left( {\hat u\left( x \right) - u\left( x \right)} \right)^2}{\rm{d}}x \end{array} $ | (4) |
| $ R\left( {\hat u, u} \right) = \smallint {\rm{Bia}}{{\rm{s}}^2}\left( x \right){\rm{d}}x + \smallint V\left( x \right){\rm{d}}x $ | (5) |
式(5)中的损失风险包括两项内容:偏差Bias(x)和方差V(x),偏差用于评估估计密度的精准度,而方差则用于测量估计量的波动变化。其中偏差Bias(x)计算可表示为
| $ \begin{array}{l} \smallint {\rm{Bia}}{{\rm{s}}^2}\left( x \right){\rm{d}}x = \smallint {\left( {u'\left( x \right)} \right)^2}\left( {\frac{h}{2} - {x^2}} \right){\rm{d}}x\\ \;\;\;\smallint {\rm{Bia}}{{\rm{s}}^2}\left( x \right){\rm{d}}x \approx \frac{{{h^2}}}{{12}}\smallint u'{\left( x \right)^2}{\rm{d}}x \end{array} $ | (6) |
而方差V(x)可表示为
| $ V\left( x \right) = \frac{{{u_j}}}{{n{h^2}}} \approx u\left( x \right)/nh, $ | (7) |
式中n为样本个数。
将式(6)、(7)代入式(3),可得损失风险:
| $ R\left( {\hat u, u} \right) \approx \frac{{{h^2}}}{{12}}\smallint {\left( {u'\left( x \right)} \right)^2}{\rm{d}}x + \frac{1}{{nh}} $ | (8) |
那么极小化式(10)后可得最佳的带宽h*:
| $ {h^*} = \frac{1}{{{n^{\frac{1}{3}}}}}{\left( {\frac{6}{{\smallint u'{{\left( x \right)}^2}{\rm{d}}x}}} \right)^{1/3}} $ | (9) |
在确定带宽时,一般假设u(x)为正态分布,可得hopt=3.5n-1/3。
1.2 不确定对象的频繁密度分布模式挖掘通过上述非参数的密度估计方法,得到了不确定数据流的密度分布模型,使不确定对象的复杂性大大降低。为了进一步优化不确定数据流的表示形式,提高不确定数据流的查询效率,本文通过频繁模式挖掘的方法对数据流中的不确定对象进行挖掘分析,使具有相同密度分布模式的不确定对象进行聚集,然后用聚簇的中心作为不确定对象的代表和索引。
聚类是频繁模式发现的重要手段,主要有DBSCAN、KMEANS、KNN等算法。由于本文的查询方法只对查询过程要求较高的响应速度,对历史数据建模的时间复杂性要求较低,所以选择了聚类效果较好的谱聚类方法。该方法是一种非无督学习过程,相对于其他聚类算法,它能够有效解决数据分布复杂的情况,且收敛于全局最优解。当前部分关于谱聚类的研究集中于利用拉普拉斯矩阵的性质,其中较典型的是基于矩阵摄动理论的谱聚类算法。基于摄动理论的谱聚类算法,相较于传统谱聚类算法,具有自适应的能力,可自动确定聚簇个数。
已知不确定数据流i的对象j的密度分布三元组
根据谱聚类方法过程,不确定数据流集合UTS={u1, u2, …, un},不确定对象的直方图密度集合S={
1) 计算S的相似矩阵Q,根据高斯相似性有qij=exp(-‖
2) 构造拉普拉斯矩阵L=D-Q,其中D为对角矩阵, 且
3) 计算拉普拉斯矩阵L的特征值,将其升序排列0<λ1≤λ2≤…≤λn;
4) 计算特征值序列的差分,当差分的方差明显变化时得k个特征值及其对应的特征向量;
5) 利用前k个特征向量构成矩阵,再通过k-means聚类方法聚类;
6) 最后,得到k个聚簇的聚类结果。
该方法仍以遵循谱聚类的基本算法程序,不同之处在于它对拉普拉斯矩阵的特征值序列进行了判断,即当矩阵的第i+1个特征值相对于其前一个第i个特征值变化较大时,则由前i个特征向量所构成的特征矩阵所代表的元素间的关系越稳定,因此可利用特征值的差值来确定聚簇的个数,但多大程度的差值可以得到最佳的聚簇个数需要通过计算特征值的方差来判断。此时,可得k个聚簇中心V={v1, v2, …, vk},并标记不确定对象
为了能够高效地对不确定数据流进行查询,就需要对不确定数据流序列进行简约的存储以及构建高效的索引结构。因此本节首先利用语义对不确定数据流进行抽象表示及存储,然后再通过索引优化的方法实现高效的不确定数据流查询策略。
1.3.1 不确定数据流的模糊语义关系表示通过谱聚类方法,得到不确定数据流中不确定对象的抽象,即各聚簇的中心集合V,每一个聚簇中心代表了属于这个聚簇的不确定对象。现假设语义集A1, A2, …, Ak,为V={v1, v2, …, vk}赋予语义,使A1→v1, A2→v2, …, Ak→vk。由于V是UTS的一个抽象,所以UTS同样可利用语义集合进行表示。
例如,一个不确定数据流ui包含的不确定对象序列为{ui, 1, ui, 2, …, ui, n},已知其中各不确定对象所属的聚簇,可将其表示为{v1, v2, v5, v1, v4, v7, …, v3},并可根据语义进一步抽象的为A1, A1, A5, A1, A4, A7, …, A3。此时,该语义序列的一阶模糊关系为A1→A1, A1→A5,二阶模糊关系为A1A1→A5, A1A5→A1,高阶关系以此类推。
1.3.2 不确定数据流查询方法不确定数据流查询的核心问题查询效率以及查询准确性,查询效率指面对大规模不确定数据时能够在有限且较短的时间内返回查询结果,查询准确性则是指查询的结果不仅是准确的,而且在概率统计上是有意义的。为了解决这两方面问题,本文选择了基于高阶Markov模型的索引结构。根据Markov理论,Markov的状态转移矩阵描述了状态之间的概率转移关系,具有概率统计意义,并且在高阶关系中,高阶状态转移矩阵还可以描述状态之间的复杂对应关系,所以高阶Markov模型作为不确定数据流索引具有好的适用性。
状态转移矩阵中,各元素都是非负数,且各行元素之和为1,各元素用概率表示,状态之间在一定条件下是可以互相转移的。假设矩阵P,其中各元素表示为pi, j,根据上述定义有,0≤pi, j≤1,且
现以二阶Markov状态转移矩阵为例说明,已知语义集A1, A2, …, Ak,则有对应状态集A1, A2, …, Ak,可构建转移矩阵为
| $ \begin{array}{l} \begin{array}{*{20}{c}} {}&{{A_1}}&{{A_2}}& \cdots &{{A_k}} \end{array}\\ \begin{array}{*{20}{c}} {{A_1}, {A_1}}\\ {{A_1}, {A_2}}\\ \vdots \\ {{A_k}, {A_k}} \end{array}\left[ {\begin{array}{*{20}{c}} {{a_{1, 1, 1}}}&{{a_{1, 1, 2}}}& \cdots &{{a_{1, 1, k}}}\\ {{a_{1, 2, 1}}}&{{a_{1, 2, 2}}}& \cdots&\vdots \\ \vdots&\vdots&\ddots &{{a_{\left( {k - 1} \right), \left( {k - 1} \right), k}}}\\ {{a_{k, k, 1}}}& \cdots &{{a_{k, k, (k - 1)}}}&{{a_{k, k, k}}} \end{array}} \right] \end{array} $ |
若a1, 1, 1是语义关系的一种统计,则可进行归一化处理使
另外,作为Markov状态转移矩阵的扩展,aijh可以同时记录以Ai→Aj→Ah为序列开始的所有不确定数据流序列的地址,在查询时即可同时返回不同概率下所对应不同序列集合。
如图 2所示,状态转移矩阵中(a)A1、A2行记录了以A1, A2起始的数据流序列,(b)列表示A1、A2的子序列A1、A2、A3与A1、A2、A2,其中以A1、A2、A3起始的序列占60%,A1、A2、A2起始的数据流序列占40%。

|
Download:
|
| 图 2 二阶Markov状态转移矩阵 Fig. 2 Second order Markov transition matrix | |
高阶Markov状态转移矩阵的行列组合代表了不同的语义序列,阶数则代表了所管理索引结构的大小,二阶矩阵只保留了样本语义序列的前三位信息,而其他部分则由概率表示,阶数越高可表示更精准的语义序列。矩阵中的元素除了存储了语义序列的可能概率,还管理着以该语义序列为起始的语义序列的地址信息,查询算法会优先遍历概率较高的地址信息中的子序列,匹配成功则返回结果,若失败则遍历概率相对较小的地址信息中的子序列。
2 实验分析本节将通过实验方法对提出的数据流查询算法进行验证,首先本节将阐述验证本算法有效的实验思路,包括数据集的选择、实验的设置、对比的算法以及指标的选择,然后是对实验结果的相关分析和结论的阐述。
2.1 实验思路类似于相关不确定数据流的研究方法中对数据集的选择[16],本文同样选择UCR数据集作为基础数据。其中,本文选择了12个数据集作为实验样本:50words、Adiac、Beef、CBF、Coffee、ECG200、Lighting2、Wafer、OliveOil、SwedLeaf、Trace、Yoga,基本覆盖各个领域的数据流形式,数据的规模如表 1所示。
| 表 1 数据流数据集 Tab.1 Data stream datasets |
对于不确定数据流研究方法有效性的验证,由于诸多因素的限制使得真实不确定数据较难获得也难于处理。因此,实验仿真时,常用的方法是对确定的数据流对象增加不确定性,例如使数据流对象中的元素转化为均值和方差稳定不变的符合某种理论分布的随机数,若需增加随机的程度,可同时混合多种理论分布。
一般的做法是以确定数据流中的对象为均值,然后选择某密度分布作为分布特征,然后生成一定数量的随机样本,经常使用的密度分布为指数分布、正态分布和均匀分布,但是这种单一分布特征的不确定化方法往往使数据过于规律,而且在实际问题中数据的分布特征也是比较复杂,并不趋向某一种特定的纯分布,所以本文采用的随机化方法是在确保均值不变的前提下,将某两种密度分布组合,例如指数分布与正态分布或均匀分布与正态分布。
2.2 实验结果分析首先,为了分析本方法在处理不同形式的不确定数据时的效果,本文对数据集的样本进行随机化处理。对数据集样本中的任意数据流,取数据流中的每个对象,以方差为参数,分别生成符合正态分布以及均匀分布的样本规模为50、100以及500的不确定数据流。随机化方法的本质是将一维的数据流随机化为50、100以及500的高维数据流,并且使样本具有符合理论分布的随机性。
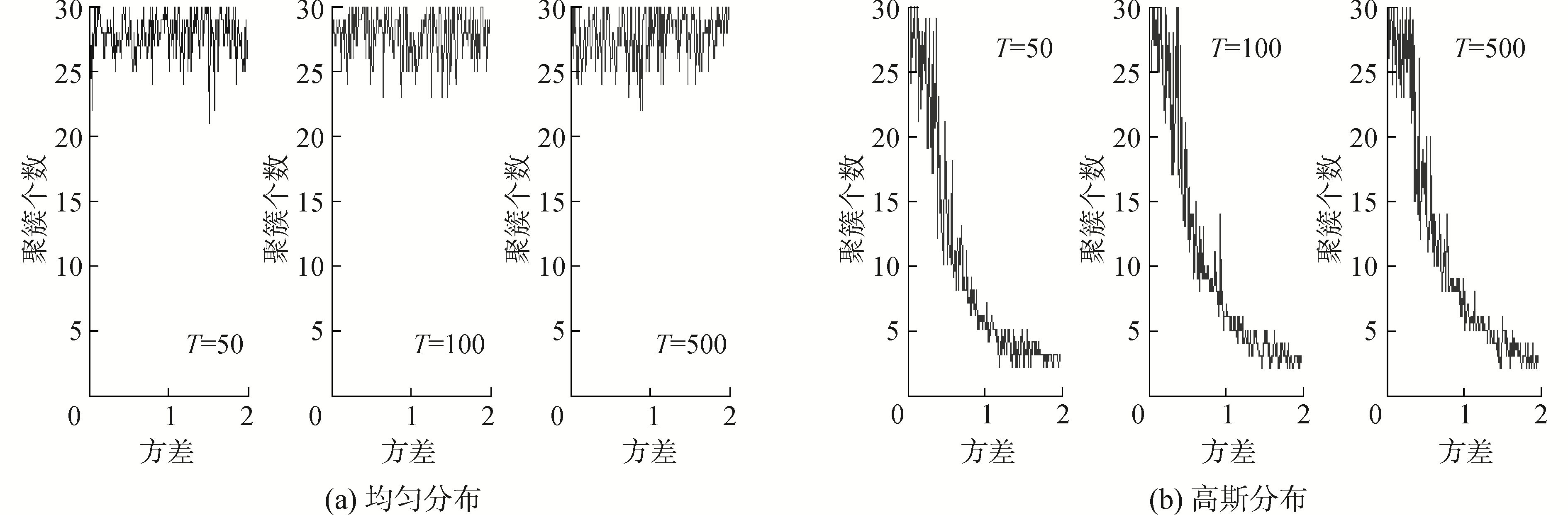
然后,根据上文所述谱聚类的摄动理论,分析不确定数据流样本在不同规模以及方差在[0.01,2]区间变化时,模型拟合效果最佳条件下的聚簇个数变化情况。通过实验可以发现,在均匀分布的随机性条件下,如图 3(a),HB-UTS方法并不受样本规模的影响,在T=50、T=100以及T=300时的最佳聚簇个数基本稳定在25~30。在高斯分布的随机性条件下,如图 3(b),HB-UTS方法同样也不受样本规模的影响,T=50、T=100以及T=500时的聚簇变化曲线基本相同。所以本方法在处理大规模不确定数据对象时,依然可以保持模型的稳定性。另外,在均匀分布的随机性条件下,样本虽然具有不确定性,但不确定性的分布较为均匀,模型可以在样本方差为[1, 2]时依然保持较好的拟合能力。然而在高斯分布的随机性条件下,随着样本方差的增加,样本取值密度的复杂性随之增加,使得模型所需聚簇个数随方差的增加而减少,在方差为2时聚簇个数仅有2~3个,HB-UTS方法的建模效果随之下降。
|
Download:
|
| 图 3 不同不确定性条件下的聚簇个数变化 Fig. 3 Cluster numbers with different uncertainty | |
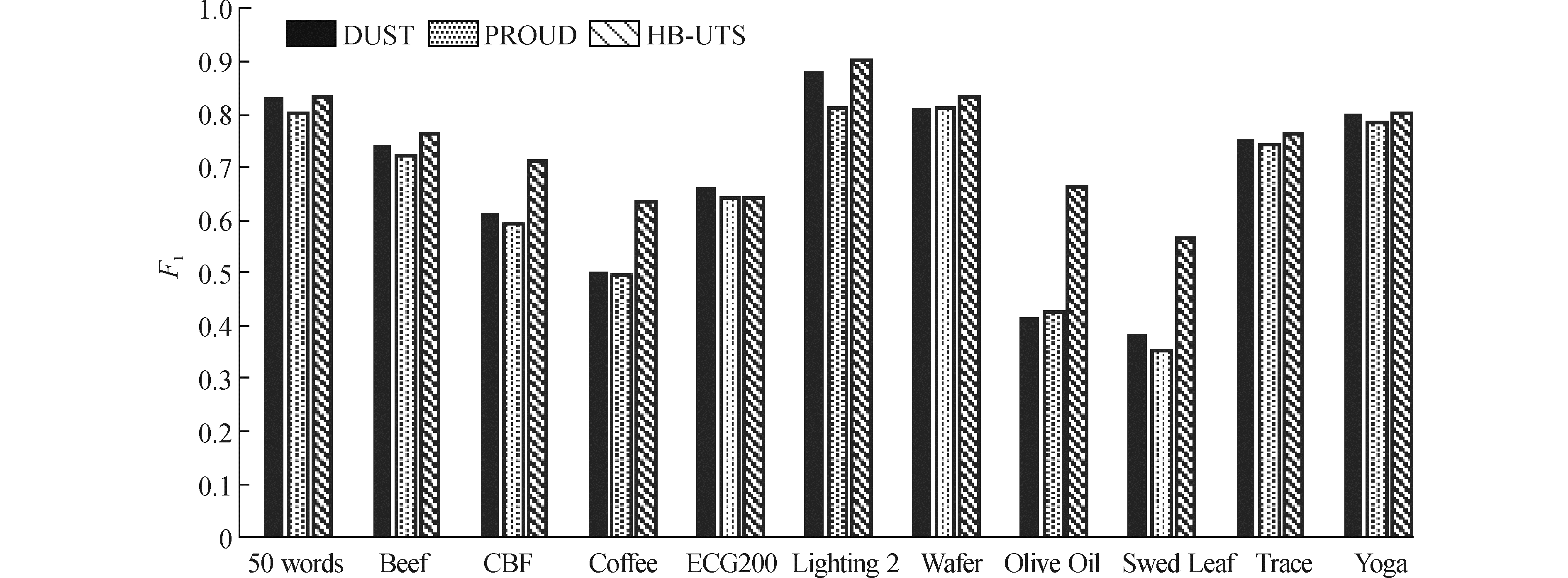
为了能在更复杂的情况下验证本方法的有效性,本文最后在数据流数据集上进行了HB-UTS、DUST以及PROUD算法的实施,比较其间的效果差异。本文选择了高斯分布以及各50%的高斯分布与均匀分布的混合分布两种策略和方差为0.2的条件下对样本进行随机化。本文选择F-Measure作为评价指标,F-Measure是信息检索领域的常用评价指标,P代表准确率,R代表召回率,在一般情况下。当样本的随机性为符合高斯分布的样本时,如图 4中样本的分布模式相同,使得HB-UTS算法能够较好地识别不确定数据流中各元素间的关系,索引结构能够准确保存序列模式,所以在同分布或不确定数据流序列的分布模式有规律的情况下,HB-UTS能够较为准确地获得查询结果。当随性为高斯分布与均匀分布各50%的随机混合时,如图 5,样本的分布随机选取,样本间的关系随机性较强,使得方法较难提取不确定数据流的序列模式,这就导致索引的准确性较低,查询结果误差较大。
|
Download:
|
| 图 4 高斯分布随机化后的F1值对比 Fig. 4 F1 comparison of Gaussian distribution randomization | |

|
Download:
|
| 图 5 高斯分布与均匀分布随机化后的F1值对比 Fig. 5 F1 comparison of mixture of Gaussian and uniform distribution randomization | |
1) 本方法可对属性级以及存在级的不确定数据流建模,有效保存其中的不确定性信息;
2) 基于频繁模式挖掘以及模糊语义的方法,可识别数据流的序列模式,并通过Markov索引进行快速匹配;
3) 通过随机化仿真实验,可知HB-UTS对不同规模的不确定数据流都具有稳定和较小的模型复杂性,在处理大规模数据时也可以确保算法的时效性;
4) 当样本的不确定性体现为密度分布模式相同或者不确定对象间的密度分布模式具有规律时,HB-UTS相对于其他的相似性查询方法具有较好的查询准确性,而当这种模式为完全随机时,查询效果则较差。
| [1] |
RE C, DALVI N, SUCIU D. Efficient top-k query evaluation on probabilistic data[C]//Proceedings of the 23rd International Conference on Data Engineering. Istanbul, Turkey, 2007: 886-895.
(  0) 0)
|
| [2] |
JEFFERY S R, GAROFALAKIS M, FRANKLIN M J. Adaptive cleaning for RFID data streams[C]//Proceedings of the 32nd International Conference on Very Large Data Bases. Seoul, Korea, 2006: 163-174. http://dl.acm.org/citation.cfm?id=1164143
(  0) 0)
|
| [3] |
TRAN T, SUTTON C, COCCI R, et al. Probabilistic inference over RFID streams in mobile environments[C]//Proceedings of the 25th IEEE International Conference on Data Engineering. Shanghai, China, 2009: 1096-1107. http://dl.acm.org/citation.cfm?id=1546683.1547385
(  0) 0)
|
| [4] |
CHEN Lei, ÖZSU M T, ORIA V. Robust and fast similarity search for moving object trajectories[C]//Proceedings of 2005 ACM SIGMOD International Conference on Management of Data. Baltimore, Maryland, 2005: 491-502. http://dl.acm.org/citation.cfm?id=1066213
(  0) 0)
|
| [5] |
LJOSA V, SINGH A K. APLA: indexing arbitrary probability distributions[C]//Proceedings of the 23rd IEEE International Conference on Data Engineering. Istanbul, Turkey, 2007: 946-955. http://doi.ieeecomputersociety.org/10.1109/ICDE.2007.367940
(  0) 0)
|
| [6] |
SARMA A D, BENJELLOUN O, Halevy A, et al. Working models for uncertain data[C]//Proceedings of the 22nd International Conference on Data Engineering. Atlanta, GA, USA, 2006. http://dl.acm.org/citation.cfm?id=1129867
(  0) 0)
|
| [7] |
WIDOM J. Trio: a system for integrated management of data, accuracy, and lineage[C]//Proceedings of the Biennial Conference on Innovative Data Systems Research., 2005: 262-276. http://www.researchgate.net/publication/220988230_Trio_A_System_for_Integrated_Management_of_Data_Accuracy_and_Lineage
(  0) 0)
|
| [8] |
FUXMAN A, FAZLI E, MILLER R. ConQuer: efficient management of inconsistent databases[C]//Proceedings of 2005 ACM SIGMOD International Conference on Management of Data. Baltimore, Maryland, 2005: 155-166. http://dl.acm.org/citation.cfm?id=1066176
(  0) 0)
|
| [9] |
DALVI N, SUCIU D. Efficient query evaluation on probabilistic databases[J]. The VLDB journal, 2007, 16(4): 523-544. DOI:10.1007/s00778-006-0004-3 (  0) 0)
|
| [10] |
SOLIMAN M A, ILYAS I F, CHANG K C C. URank: formulation and efficient evaluation of top-k queries in uncertain databases[C]//Proceedings of 2007 ACM SIGMOD International Conference on Management of Data. Beijing, China, 2007: 1082-1084. http://dl.acm.org/citation.cfm?id=1247613
(  0) 0)
|
| [11] |
赵越, 王意洁, 王媛, 等. 一种高效的不确定数据流并行Skyline查询处理方法[J]. 计算机研究与发展, 2013, 50(S1): 132-139. ZHAO Yue, WANG Yijie, WANG Yuan, et al. An efficient method of parallel skyline query processing over uncertain data stream[J]. Journal of computer research and development, 2013, 50(S1): 132-139. (  0) 0)
|
| [12] |
ZHOU Xu, LI Kenli, ZHOU Yantao, et al. Adaptive processing for distributed skyline queries over uncertain data[J]. IEEE transactions on knowledge and data engineering, 2016, 28(2): 371-384. DOI:10.1109/TKDE.2015.2475764 (  0) 0)
|
| [13] |
CICERI E, FRATERNALI P, MARTINENGHI D, et al. Crowdsourcing for top-K query processing over uncertain data[J]. IEEE transactions on knowledge and data engineering, 2016, 28(1): 41-53. DOI:10.1109/TKDE.2015.2462357 (  0) 0)
|
| [14] |
RAMÍREZ-GALLEGO S, KRAWCZYK B, GARCÍA S, et al. A survey on data preprocessing for data stream mining:current status and future directions[J]. Neurocomputing, 2017, 239: 39-57. DOI:10.1016/j.neucom.2017.01.078 (  0) 0)
|
| [15] |
张晨, 金澈清, 周傲英. 一种不确定数据流聚类算法[J]. 2010, 21(9): 2173-2182. ZHANG Chen, JIN Cheqing, ZHOU Aoying. Clustering algorithm over uncertain data streams[J]. Journal of software, 2010, 21(9): 2173-2182. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=rjxb201009008&dbname=CJFD&dbcode=CJFQ (  0) 0)
|
| [16] |
DALLACHIESA M, NUSHI B, MIRYLENKA K, et al. Uncertain time-series similarity:return to the basics[J]. Proceedings of the VLDB endowment, 2012, 5(11): 1662-1673. DOI:10.14778/2350229 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


