2. 哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001
2. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China
传统飞行器只在其设计点附近具有最优的飞行性能,而变体飞行器在执行不同的使命以及某一使命的各个任务段都能保持最优的飞行性能,故具有更高的环境适应、应变、攻击和生存能力[1]。变体飞行器技术已成为当今航空领域研究的热点[2-3],而可变形蒙皮技术无疑是其中最为关键的技术之一,同时也是技术难点[4-6]。
早期研究大多采用“鱼鳞叠片”分片式硬蒙皮,这种蒙皮虽然满足了机翼承载和变形需求,但是却无法满足机翼表面光滑、连续和整体气密性等要求。另外一种常用的变形蒙皮是弹性极佳的硅橡胶材料,虽然其可以满足大形变量的要求,但很难承受高的气动载荷。美国新一代航空公司在MAS计划的支持下,在2006年和2007年先后试飞了两架采用硅橡胶蒙皮的“滑动蒙皮”可变形无人验证机,但其最大试飞速度只有54 m/s[7]。为此,YIA等采用施加预应力的方法来提高硅橡胶蒙皮的承载能力,但是过大的预应力会给硅橡胶蒙皮带来疲劳和蠕变等新问题[8]。
为了较好地解决蒙皮变形与承载之间的矛盾,近几年来相继出现了一些基于变形蜂窝和柔性基体的复合式变形蒙皮结构。这种蒙皮结构可以充分地发挥蜂窝低面内刚度和高面外刚度的优势,辅助柔性基体的采用以保证蒙皮的光滑性和气密性。Olympio是最早提出将蜂窝结构用于变形蒙皮的[9]。此后,一些文献先后设计了多种具有特殊要求(如零泊松比、单向拉伸变形等)的蜂窝结构[10-15]。为了获得更低的面内弹性模量,邱涛等提出了一种四边形蜂窝结构[16]。以上研究表明变形蜂窝与柔性基体的复合是较好的可变形蒙皮解决方案。这个方案首要面对的问题是蜂窝结构的变形实现。然而,国内外对于蜂窝的变形设计还缺乏必要的理论指导。为此,本文重点研究如何通过结构设计来实现蜂窝的可变形实现问题,给出了蜂窝形变量与设计参数之间的解析关系。
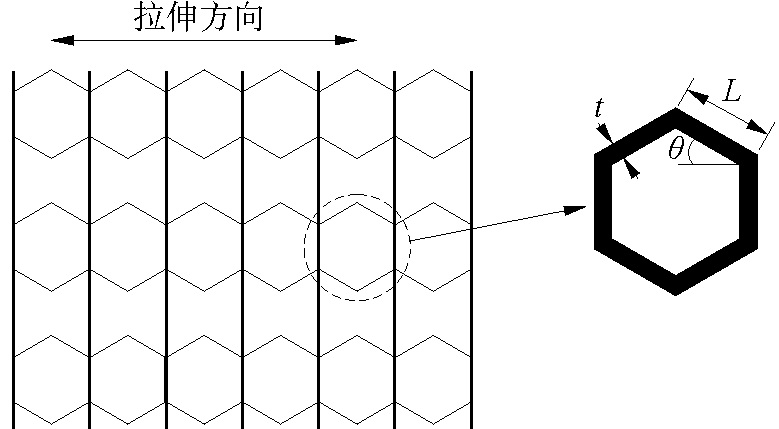
1 变形蜂窝力学建模与分析 1.1 变形蜂窝结构传统固定翼飞行器的蒙皮大多采用铝合金等金属材料,但是这类蒙皮受强度的限制几乎不能产生面内的拉伸变形,也就无法实现机翼结构的变形。如果把蒙皮结构设计成如图 1所示的结构形式,那么就可以利用蜂窝壁斜梁结构的面内弯曲变形来实现蒙皮结构的拉伸变形。在这个变形结构设计中,变形蜂窝作为蒙皮的主要承力结构和变形结构,采用硅橡胶等柔性基体材料覆盖或填充蜂窝空隙以维持气密光滑的气动外形。
|
图 1 可变形蜂窝的结构示意图 Fig.1 Sketch of morphing honeycomb |
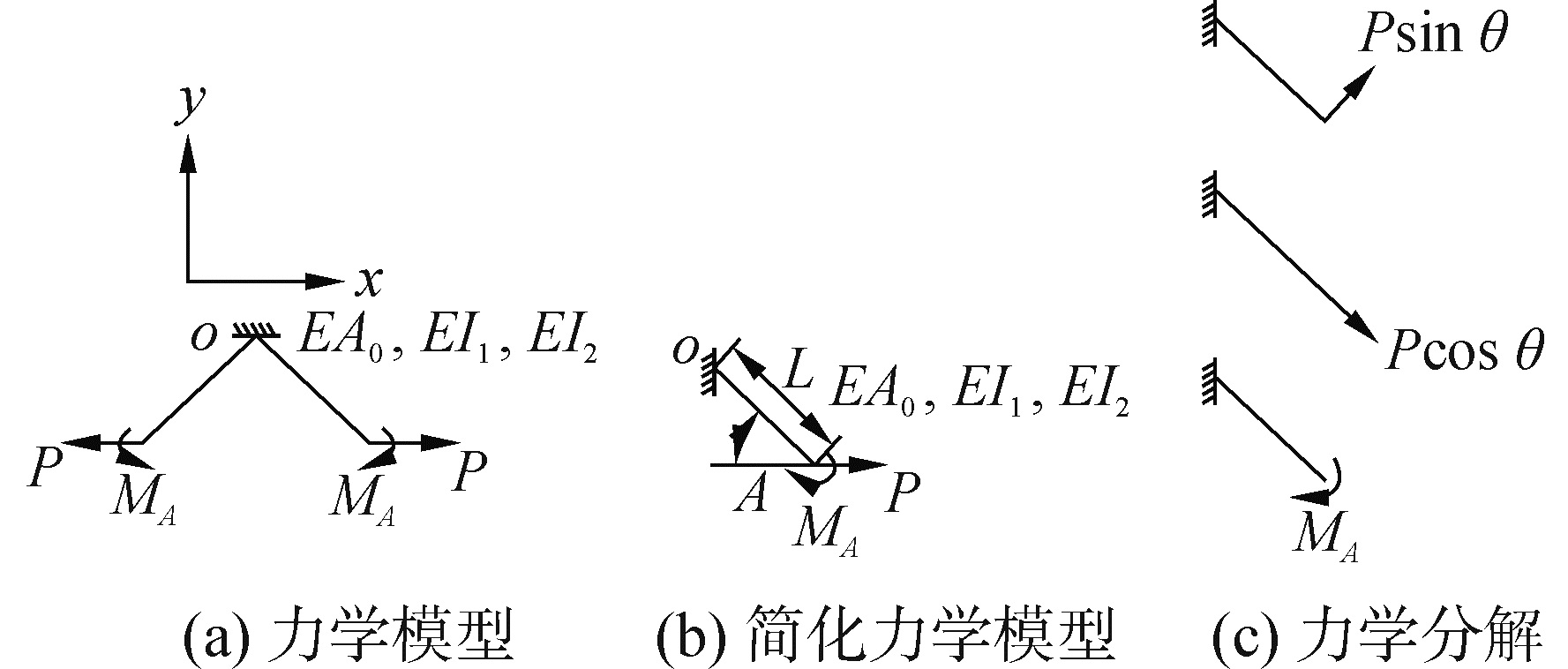
蜂窝结构的力学分析可以采用材料力学中的直梁理论[17-19]。可变形蜂窝结构的简化力学模型如图 2(a)所示。蜂窝壁的长度为L,与水平线之间的夹角为θ,称为蜂窝角。蜂窝壁的截面为矩形,高度为H、宽度为t。根据几何和边界条件的对称性,可以进一步简化成图 2(b)所示的力学模型。蜂窝壁OA的拉伸刚度、面内弯曲刚度和面外弯曲刚度分别为EA0、EI1和EI2,位移边界条件为:1) 端点A的面内转角为0;2) 端点O为固支边界条件。
|
图 2 变形蜂窝结构的力学模型 Fig.2 Model of morphing honeycomb |
如图 2(b)所示,蜂窝壁在水平拉力P的作用下将产生拉伸和弯曲变形,同时A点的面内转角也要发生变化,但根据边界条件1) 可知A点的面内转角应为0,在A点必然存在一个力矩MA使该点的总转角为0。因此,可将蜂窝壁在水平力P作用下的静力学问题分解成如图 2(c)所示的三个基本的弯曲和拉伸问题。
蜂窝壁在集中力Psin θ的作用下,端点A的转角和挠度分别为
| $ {\theta _1} = \frac{{P{L^2}\sin \theta }}{{2{\rm{E}}{{\rm{I}}_1}}} $ | (1) |
| $ {w_1} = \frac{{P{L^3}\sin \theta }}{{3{\rm{E}}{{\rm{I}}_1}}} $ | (2) |
蜂窝壁在集中力Pcos θ的作用下,端点A的拉伸位移为
| $ {\Delta _2} = \frac{{PL\cos \theta }}{{{\rm{E}}{{\rm{A}}_0}}} $ | (3) |
蜂窝壁在弯矩MA的作用下,端点A的转角和挠度分别为
| $ {\theta _3} = \frac{{{M_{\rm{A}}}}}{{{\rm{E}}{{\rm{I}}_1}}}L $ | (4) |
| $ {w_3} = \frac{{{M_{\rm{A}}}L}}{{2{\rm{E}}{{\rm{I}}_1}}} $ | (5) |
由边界条件1),可得
| $ {M_{\rm{A}}} = \frac{1}{2}PL\sin \theta $ | (6) |
由几何关系可得端点A的x向(拉力P的作用方向)位移为
| $ {\Delta _x} = \frac{{P{L^3}{{\sin }^2}\theta }}{{12{\rm{E}}{{\rm{I}}_1}}} + \frac{{PL{{\cos }^2}\theta }}{{{\rm{E}}{{\rm{A}}_0}}} $ | (7) |
| $ {\Delta _y} = \left( {\frac{{P{L^3}}}{{12{\rm{E}}{{\rm{I}}_1}}} - \frac{{PL}}{{{\rm{E}}{{\rm{A}}_0}}}} \right)\sin \theta \cos \theta $ | (8) |
蜂窝壁的等效轴向应变定义为
| $ \varepsilon _x^e = \frac{{{\Delta _x}}}{{L_x^e}} $ | (9) |
式中Lxe为蜂窝壁x向的投影长度。
对于可变形蜂窝结构而言,首先要满足形变量的设计要求,即εxe≥εd,其中εd为可变形蒙皮的设计形变量,将式(9) 代入整理得
| $ {\varepsilon _d} \le P\left( {\frac{{{L^2}{{\sin }^2}\theta }}{{12{\rm{E}}{{\rm{I}}_1}\cos \theta }} + \frac{{\cos \theta }}{{{\rm{E}}{{\rm{A}}_0}}}} \right) $ | (10) |
同时,可变形蜂窝结构必须要满足材料的强度要求,更重要的是结构的变形应具有可恢复性,要求材料变形应该在弹性区间内,即:
| $ {\varepsilon _{\max }} \le m/n $ | (11) |
式中:
根据直梁拉伸和弯曲应变计算公式,可得蜂窝壁在水平拉力P作用下的最大应变为
| $ {\varepsilon _{\max }} = \frac{{Lt\sin \theta }}{{4{\rm{E}}{{\rm{I}}_1}}} + \frac{{P\cos \theta }}{{{\rm{E}}{{\rm{A}}_0}}} $ | (12) |
将式(12) 代入式(11) 中,可得
| $ \frac{m}{n} \ge P\left( {\frac{{Lt\sin \theta }}{{4{\rm{E}}{{\rm{I}}_1}}} + \frac{{\cos \theta }}{{{\rm{E}}{{\rm{A}}_0}}}} \right) $ | (13) |
最后,联立式(10)、(13),消去P,整理得到关于tan θ的二次不等式,为
| $ a{\tan ^2}\theta + b\tan \theta + c \ge 0 $ | (14) |
式中:
当(b2-4ac)≥0时,即
| $ \tan \theta \ge \frac{{ - b + \sqrt {{b^2} - 4ac} }}{{2a}}\;或\;\tan \theta \le \frac{{ - b - \sqrt {{b^2} - 4ac} }}{{2a}} $ | (15) |
当m<nεd时,二次不等式系数c<0,则蜂窝角θ的取值范围为
| $ {90^ \circ } \ge \theta \ge \arctan \left( {\frac{{3n{\varepsilon _d} + \sqrt {9{n^2}\varepsilon _d^2 - 4m\left( {m - n{\varepsilon _d}} \right)} }}{{2m\beta }}} \right) $ | (16) |
式中β=L/t为蜂窝壁的长宽比。
当
| $ \begin{array}{l} {90^ \circ } \ge \theta \ge \arctan \left( {\frac{{3n{\varepsilon _d} + \sqrt {9{n^2}\varepsilon _d^2 - 4m\left( {m - n{\varepsilon _d}} \right)} }}{{2m\beta }}} \right)\;或\\ \;\;\;\;\;\;\;\;\;0 \le \theta \le \arctan \left( {\frac{{3n{\varepsilon _d} - \sqrt {9{n^2}\varepsilon _d^2 - 4m\left( {m - n{\varepsilon _d}} \right)} }}{{2m\beta }}} \right) \end{array} $ | (17) |
当(b2-4ac)<0时,不等式(14) 自然成立。将a、b和c的具体表达式代入,整理可得
| $ {m^2} - n{\varepsilon _d}m - \frac{9}{4}{n^2}\varepsilon _d^2 > 0 $ | (18) |
根据二次不等式定理,可知:
| $ m > \frac{{1 + \sqrt {10} }}{2}n{\varepsilon _d} $ | (19) |
蜂窝壁等效轴向应变与母体材料最大应变的比值定义为应变放大因子,用符号n来表示。这里主要讨论x向的形变问题。由式(14) 和(20) 可得,x向的应变放大因子为
| $ n = \frac{{\varepsilon _x^e}}{{{\varepsilon _{\max }}}} = \frac{{1 + {{\left( {\beta \tan \theta } \right)}^2}}}{{3\beta \tan \theta }} $ | (20) |
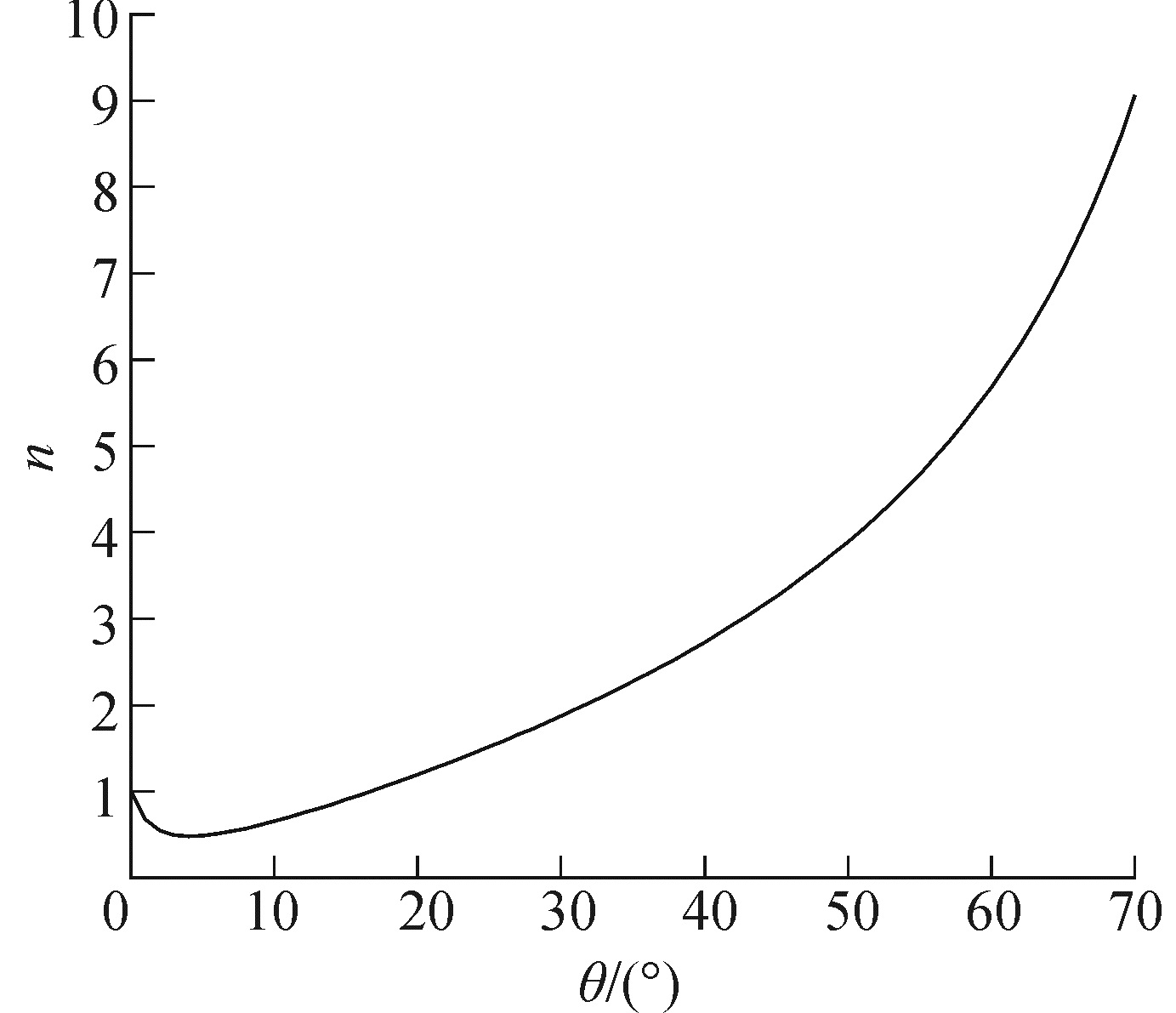
由式(20) 可以看出,应变放大因子只和蜂窝壁的长宽比和蜂窝角有关。图 3为应变放大因子随蜂窝角的变化曲线(β=10)。从图中可以看出,当蜂窝角大于16.5°时,蜂窝结构的应变放大因子将大于1,且随着蜂窝角的增加,应变放大因子是逐渐增大的。也就是说,只要蜂窝角大于一定值,母体材料的小应变就可以通过蜂窝壁的斜梁结构得以放大。这就是蜂窝结构可以实现面内大变形的机理所在。
|
图 3 应变放大因子随着蜂窝角的变化 Fig.3 Strain amplification factor vs. honeycomb angle |
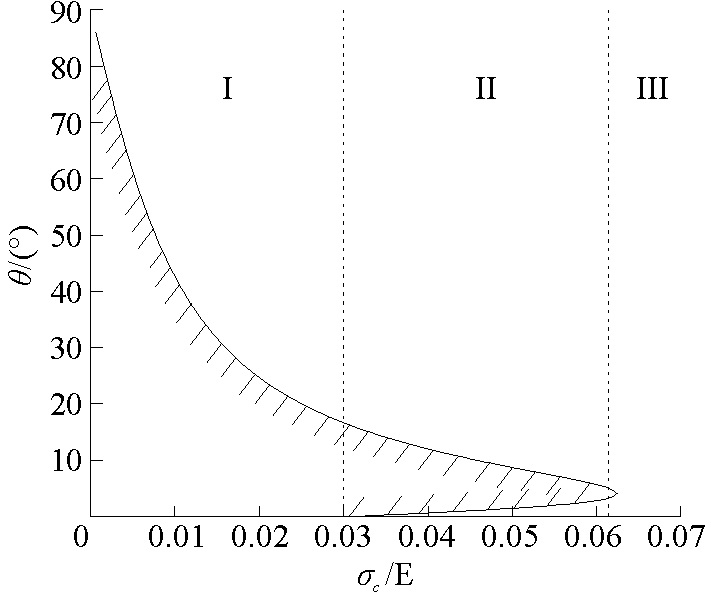
算例所用变形蜂窝的长度、宽度和高度分别为10、1和2 mm,变形蜂窝的设计形变量为3%。图 4为蜂窝壁的蜂窝角随着材料弹性极限与弹性模量比值的变化曲线。根据材料弹性极限与弹性模量比值的大小把图 4分成了Ⅰ、Ⅱ和Ⅲ区三个区域。
|
图 4 蜂窝角与材料弹性极限(3%形变量)关系 Fig.4 Ratio of elastic limit and elastic modulus vs. honeycomb angle |
可以看出,随着材料弹性极限与弹性模量比值的增大,蜂窝角的设计空间越来越大。当材料弹性极限与弹性模量的比值大于形变量的设计值,蜂窝角的选择空间落在Ⅱ和Ⅲ区内。在这两个设计区,蜂窝角可以取0°,即材料本身可以不通过蜂窝结构就可以实现所要求的设计形变量。
一般情况下,设计者总是希望通过蜂窝结构设计来实现母体材料小应变的放大,也就是说,材料弹性极限与弹性模量的比值小于或远小于变形结构的设计形变量,即m<εd。此时的蜂窝角存在最小值:
| $ {\theta _{\min }} = \arctan \left( {\frac{{3n{\varepsilon _d} + \sqrt {9{n^2}\varepsilon _d^2 - 4m\left( {m - n{\varepsilon _d}} \right)} }}{{2m\beta }}} \right) $ | (21) |
由式(21) 可以看出,当几何参数和设计形变量确定后,最小蜂窝角只和材料弹性极限与弹性模量的比值有关。表 1给出了四种常用材料的弹性极限、弹性模量和由式(21) 确定的最小蜂窝角(安全系数取为1.2)。在这四种材料中,铝(6160-T4) 的弹性极限与弹性模量比值最小,相应的最小蜂窝角最大,达到了80.1°;ABS塑料的弹性极限与弹性模量比值最大,相应的最小蜂窝角最小,为20.1°。
| 表 1 材料参数 Tab.1 Material parameters |
蜂窝壁在有限元建模时为了避免应力集中需要在弯角处进行圆弧过渡处理,这里圆弧半径取为1 mm。在Ansys有限元软件中进行结构建模和应力分析,单元采用Shell93,单元最小尺寸为0.1 mm。图 5(a)为蜂窝壁的有限元模型。假定蜂窝壁的材料为尼龙66,蜂窝角为25.2°。图 5(b)为蜂窝壁的应力云纹图。可以看出,最大应力发生在角点处,最大应力为54.7 MPa。

|
图 5 蜂窝壁的有限元模型及应力云纹图 Fig.5 FEM and stress distribution of honeycomb wall |
表 2为不同材料设计的蜂窝结构实现3%和15%两种设计形变量所需要最小蜂窝角的梁理论和有限元的结果比较。在设计形变量为15%的变形蜂窝设计中不考虑铝材料,因为铝材料的弹性极限与弹性模量的比值过低。从表中可以看出,梁理论预测的最小蜂窝角与有限元结果的绝对误差均在1°~5.4°内,相对误差均小于10%;尤其是,当蜂窝角为中等角度(30°~60°)时,二者结果误差非常小。
| 表 2 最小蜂窝角的比较(3%和15%形变量) Tab.2 Comparison of minimum angle (global strain of 3% and 15%) |
当蜂窝材料确定后,若想设计不同形变量的蜂窝结构,需要确定最小蜂窝角。假定所用材料为ABS塑料,长宽比为10,设计形变量为3%~15%。图 6为蜂窝角随设计形变量的变化曲线。可以看出,随着设计形变量的增加,最小蜂窝角也随之增加。当最小蜂窝角为20.1°、31.7°、50.9°和61.4°时,蜂窝结构可以分别实现3%、5%、10%和15%的最大设计形变量。图 7为ABS塑料实现上述四种不同设计形变量的蜂窝轮廓图和变形示意图,虚线为未变形蜂窝的轮廓图。

|
图 6 蜂窝角随着形变量的变化 Fig.6 Honeycomb angle vs. global strain |

|
图 7 同样材料实现不同形变量的蜂窝轮廓图 Fig.7 Profile of honeycomb for different global strain with same material |
当长宽比和蜂窝角给定时,设计形变量和弹性极限与弹性模量的比值之间要满足如下关系
| $ \frac{m}{n} \ge \frac{{{\varepsilon _d} + 3\beta {\varepsilon _d}\tan \theta }}{{1 + {\beta ^2}{{\tan }^2}\theta }} $ | (22) |
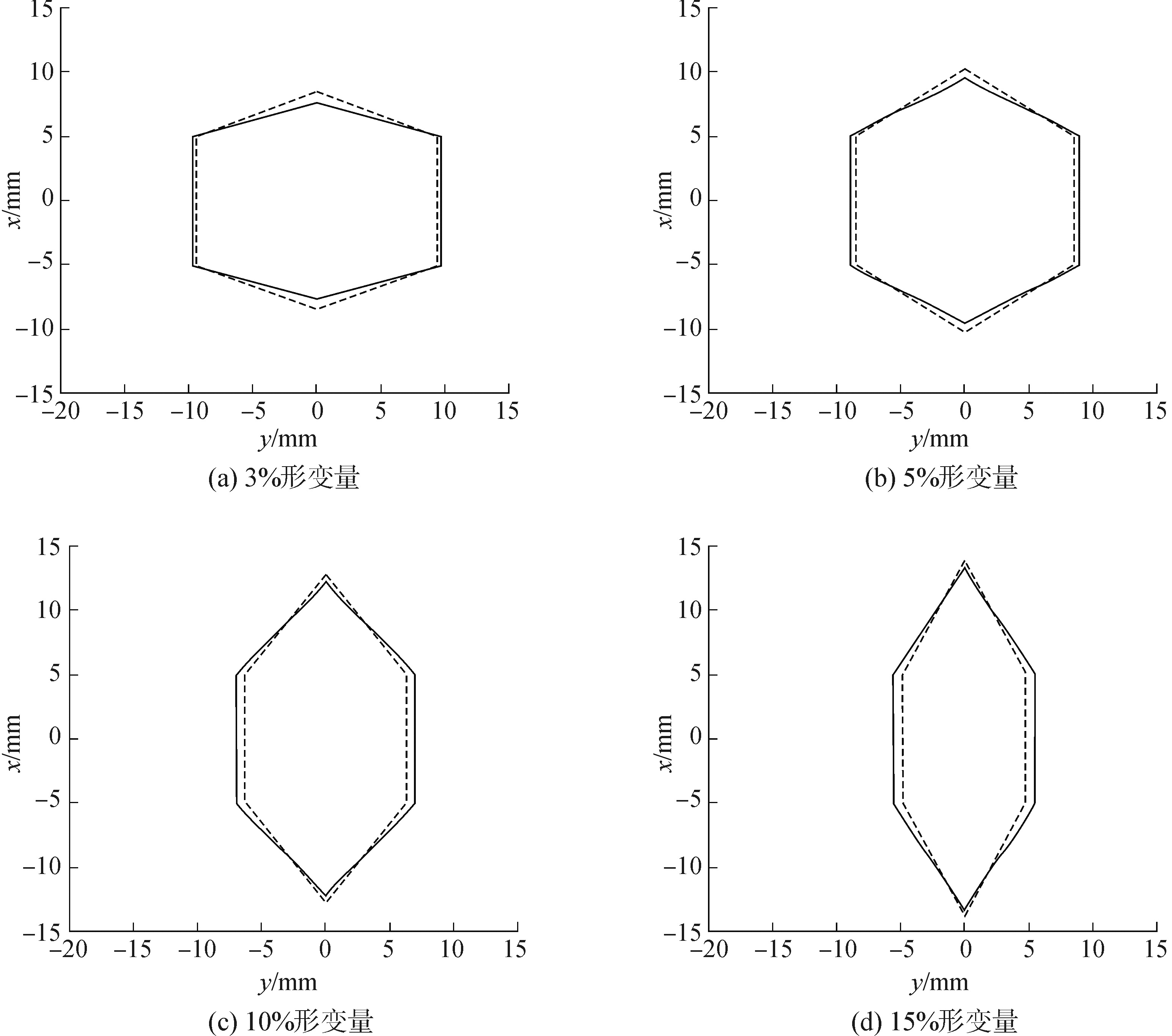
当蜂窝形状确定后,通过材料的选取可以实现蜂窝结构的不同形变量。当最大形变量为3%、5%、10%和15%时,材料弹性极限与弹性模量比值的最小值分别为0.019、0.032、0.064和0.096。图 8为同样蜂窝形状实现不同形变量的变形示意图,虚线为未变形蜂窝的轮廓图。
|
图 8 不同形变量的变形蜂窝示意图 Fig.8 Profile of honeycomb for different global strain with same angle |
当材料弹性极限与弹性模量比值和蜂窝角给定时,蜂窝的形变量和长宽比之间要满足如下关系:
| $ \beta \ge \frac{{3n{\varepsilon _d} + \sqrt {9{n^2}\varepsilon _d^2 - 4m\left( {m - n{\varepsilon _d}} \right)} }}{{2m\tan \theta }} $ | (23) |
图 9为形变量随长宽比的变化曲线(设计参数为m=0.029 9和θ=30°)。可以看出,当材料和蜂窝角给定时,长宽比随设计形变量的增大而线性增大。当设计形变量为3%时,蜂窝壁的长宽比必须大于6.4,当设计形变量为15%时,蜂窝壁的长宽比不能小于31.7。

|
图 9 形变量随长宽比的变化 Fig.9 Ratio of length and width vs. global strain |
1) 蜂窝角的取值范围取决于材料弹性极限与弹性模量之间的比值。
2) 当材料弹性极限与弹性模量的比值小于设计形变量,变形蜂窝的蜂窝角存在最小值。
3) 通过选择蜂窝壁的截面尺寸、蜂窝角和材料参数来设计不同结构方案的蜂窝结构,如“相同材料实现不同形变量”、“相同蜂窝形状实现不同形变量”和“相同材料相同蜂窝角实现不同形变量”。
| [1] |
崔尔杰, 白鹏, 杨基明. 智能变形飞行器的发展道路[J]. 航空制造技术, 2007, 8: 38-41. CUI Erjie, BAI Peng, YANG Jiming. Development of smart morphing aircraft[J]. Aeronautical manufacturing technology, 2007, 8: 38-41. DOI:10.3969/j.issn.1671-833X.2007.01.003 (  0) 0)
|
| [2] |
BARBARINO S, BILGEN O, AJAJ R, et al. A review of morphing aircraft[J]. Journal of intelligent material systems and structures, 2011, 22: 823-878. DOI:10.1177/1045389X11414084 ( 0) 0)
|
| [3] |
JIN H, KYUNG S, IN L. Shape adaptive airfoil actuated by a shape memory alloy and its aerodynamic characteristics[J]. Mechanics of advanced materials and structures, 2009, 16(3): 260-274. DOI:10.1080/15376490902746996 ( 0) 0)
|
| [4] |
THILL C, ETCHES J, BOND I, et al. Morphing skins[J]. The aeronautical journal, 2008, 112(1129): 117-139. DOI:10.1017/S0001924000002062 ( 0) 0)
|
| [5] |
GANDHI F, ANUSONTI P. Skin design studies for variable camber morphing airfoils[J]. Smart material and structure, 2008, 17: 1-8. ( 0) 0)
|
| [6] |
YIN Weilong. Stiffness requirement of flexible skin for variable trailing-edge camber wing[J]. Science China technological sciences, 2010, 53(4): 1077-1081. DOI:10.1007/s11431-009-0408-6 ( 0) 0)
|
| [7] |
JOHN S, ROLF C. Development and flight testing of a morphing aircraft, the NextGen MFX-1[C]//Proc of 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, USA:Hawaii, 2007.
( 0) 0)
|
| [8] |
YIN Weilong, LIU Jingcang, LENG Jinsong. Mechanical characteristics of shape memory polymer for morphing wing skin under airflow[J]. Frontiers of mechanical engineering in China, 2009, 4(4): 447-449. DOI:10.1007/s11465-009-0062-5 ( 0) 0)
|
| [9] |
OLYMPIO K, GANDHI F. Design of flexible skins for morphing aircraft structures using honeycomb cores[C]//47th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2006.
( 0) 0)
|
| [10] |
OLYMPIO K, GANDHI F. Zero-ν cellular honeycomb flexible skins for one-dimensional wing morphing[C]//Proc of 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, USA:Hawaii, 2007:50-65.
( 0) 0)
|
| [11] |
OLYMPIO K, GANDHI F. Skin designs using multi-objective topology optimization[C]//Proc of 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, USA:Schaumburg, 2008:1-12.
( 0) 0)
|
| [12] |
EDWARD A, BENJAMIN K, CURT S, et al. Design and fabrication of a passive 1-d morphing aircraft skin[C]//Proc of 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, USA:Schaumburg, 2008:65-76.
( 0) 0)
|
| [13] |
OLYMPIO K, GANDHI F. Modeling and numerical analyses of skin design concepts[C]//Proc of 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, USA:California, 2009:1-20.
( 0) 0)
|
| [14] |
VIPUL M, MARY F, GEORGE A. Stress relief in contact-aided compliant cellular mechanisms[J]. Journal of mechanical design, 2009, 131: 1-11. ( 0) 0)
|
| [15] |
VOCKE R, KOTHERA C, WOODS B, et al. Development and testing of a span-extending morphing wing[J]. Journal of intelligent material systems and structures, 2011, 22: 879-890. DOI:10.1177/1045389X11411121 ( 0) 0)
|
| [16] |
张平, 周丽, 邱涛. 一种新的柔性蜂窝结构及其在变体飞机中的应用[J]. 航空学报, 2011, 32(1): 156-163. ZHANG Ping, ZHOU Li, QIU Tao. A new flexible honeycomb structure and its application in structure design of morphing aircraft[J]. Acta aeronautica et astronautica sinica, 2011, 32(1): 156-163. (  0) 0)
|
| [17] |
GIBSON L, ASHBY M. Cellular solids structure and properties[M]. United Kingdom: Cambridge University Press, 1997: 102-103.
( 0) 0)
|
| [18] |
富明慧, 尹久仁. 蜂窝夹层的等效弹性参数[J]. 力学学报, 1999, 31(1): 113-118. FU Minghui, YIN Jiuren. Equivalent elastic parameters of the honeycomb core[J]. Chinese journal of theoretical and applied mechanics, 1999, 31(1): 113-118. (  0) 0)
|
| [19] |
卢子兴, 赵亚斌. 一种有负泊松比效应的二维多胞材料力学模型[J]. 北京航空航天大学学报, 2006, 32(5): 594-597. LU Zixing, ZHAO Yabin. Mechanical model oftwo-dimensional cellular materials with negative poisson's ratio[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(5): 594-597. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


