2. 滁州学院 地理信息与旅游学院, 安徽 滁州 239000;
3. 哈尔滨工程大学 航天与建筑工程学院, 黑龙江 哈尔滨 150001
2. College of Geographical Information and Tourism, Chuzhou University, Chuzhou 239000, China;
3. College of Astronautics and Architectural Engineering, Harbin Engineering University, Harbin 150001, China
对于工程中大多数结构体系,结构系统破坏的主要形式是结构在疲劳载荷作用下的失效破坏。在现实生活中,有很多结构常年受自然界的各种疲劳载荷的作用,在使用寿命期间内的主要失效形式是疲劳失效,因此,研究结构系统的疲劳可靠性分析意义重大。在国外,Wirsching等基于S-N曲线疲劳损伤分析方法对元件的疲劳可靠性进行了分析[1]。随后,Stahl等对结构元件的疲劳可靠性研究作了更进一步的分析讨论[2-4]。在国内,还有许多文献在结构系统的疲劳可靠性分析领域做了相关研究[5-10]。
张永苍研究了在对称循环载荷下的结构系统的疲劳可靠性分析的基本过程。董聪等研究了结构系统疲劳寿命的可靠性分析的基本理论与计算方法,提出了分枝-约界法。综上,结构系统的疲劳可靠性分析比结构元件的可靠性分析发展的缓慢,这是由于结构系统疲劳可靠性分析要比结构元件的疲劳可靠性分析复杂的多。由于实际工程中的绝大多数的结构是静不定结构,结构系统的失效形式非常复杂,如何高效地搜索主要失效模式,同时考虑各个失效模式之间的相关性仍是结构系统的疲劳可靠性分析的难点问题。大多数的疲劳可靠性分析主要针对桁架结构,对于实体结构的疲劳可靠性分析较为少见。因此,本文基于有限体积法对实体结构的疲劳可靠性进行了研究。
1 结构元件的疲劳可靠性研究 1.1 S-N曲线法S-N曲线是表达载荷应力S与疲劳寿命N之间关系的曲线,在疲劳设计分析中,一般采用确定斜率双对数线性模型,S-N曲线的表达式为
| $ \lg N = \lg A - m\lg S $ | (1) |
或者
| $ N{S^m} = A $ | (2) |
式中:S为选定的应力范围水平,N为在确定的应力作用下的疲劳寿命的某一统计特征值,m和A表示材料的常数。
在实际的工程应用中,结构的疲劳损伤累加到一定程度时,结构发生疲劳破坏,即循环载荷作用的时间越长,结构的疲劳累积损伤值在不断地增大。因此将累积损伤D(n)作为基本参数,则其安全余量方程为
| $ {M_D} = D\left( n \right) - {D_{\rm{c}}} \le 0 $ | (3) |
式中:D(n)为累积损伤,Dc为累积损伤临界值,这里认为Dc为一常数,且Dc=1。则元件的可靠度可写成
| $ P = P\left\{ {D\left( n \right) - {D_{\rm{c}}} \le 0} \right\} $ | (4) |
疲劳损伤D(n)的定义有很多种,一般工程上常采用Miner累积损伤理论[11]。通过理论分析和实验验证的结果表明累积损伤D(n)是个统计量。假设在常幅疲劳载荷作用下结构材料相应的疲劳寿命为N,则
| $ f\left( n \right) = \left\{ \begin{array}{l} \frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}} {\sigma _{\rm{N}}}n}}\exp \left\{ { - \frac{{{{\left( {\ln n - {\mu _{\rm{N}}}} \right)}^2}}}{{2\sigma _{\rm{N}}^2}}} \right\},&n > 0\\ 0,&n \le 0 \end{array} \right. $ | (5) |
累积损伤D(n)也可以用对数正态分布来描述,且在相同应力条件下,随着疲劳载荷循环数的增加,疲劳累积损伤的期望和方差等统计特性也是线性累加的。在常幅载荷作用下,构件的累积损伤是线性变化的。即当t=0时,构件还没有损伤,累积损伤的期望和方差为零,若一次循环载荷产生的损伤的期望和方差为dE和dD,则在t=n时刻元件累积损伤的期望和方差为dEn和dDn,dE和dD与载荷水平有关。对数正态分布的期望和方差可以表示为
| $ E = {{\rm{e}}^{\left( {\mu + \frac{1}{2}{\sigma ^2}} \right)}} $ | (6) |
| $ Var = {{\rm{e}}^{\left( {2\mu + {\sigma ^2}} \right)}}\left( {{{\rm{e}}^{{\sigma ^2}}} - 1} \right) $ | (7) |
由以上两式可求出
| $ \mu = - \frac{1}{2}\ln \left( {1 + \frac{{{d_{\rm{D}}}}}{{d_{\rm{E}}^2n}}} \right) + \ln \left( {{d_{\rm{E}}}n} \right) $ | (8) |
| $ \sigma = \sqrt {\ln \left( {1 + \frac{{{d_{\rm{D}}}}}{{d_{\rm{E}}^2n}}} \right)} $ | (9) |
则结构元件在常幅疲劳载荷作用下的疲劳可靠性指标的表达式为
| $ \beta \left( n \right) = \frac{{{\mu _{\rm{D}}}}}{{{\varepsilon _{\rm{D}}}}}\frac{{ - \frac{1}{2}\ln \left( {1 + \frac{{{d_{\rm{D}}}}}{{d_{\rm{E}}^2n}}} \right) + \ln \left( {{d_{\rm{E}}}n} \right)}}{{\sqrt {\ln \left( {1 + \frac{{{d_{\rm{D}}}}}{{d_{\rm{E}}^2n}}} \right)} }} $ | (10) |
累积损伤的分布可由疲劳寿命的分布分析得到,即
| $ {d_{\rm{E}}} = \frac{{{D_{\rm{c}}}}}{{{N_{\rm{f}}}}} + \frac{{{{\rm{e}}^{\frac{{{\sigma ^2}{\rm{N}}}}{2}}}}}{{{N_{\rm{f}}}}} $ | (11) |
| $ {d_{\rm{D}}} = \frac{{{{\rm{e}}^{\sigma _{\rm{N}}^2}}\left( {{{\rm{e}}^{\sigma _{\rm{N}}^2}} - 1} \right)}}{{{N_{\rm{f}}}}} $ | (12) |
式中:σN为疲劳寿命的方差,Nf为极限疲劳寿命。
2 结构系统的疲劳可靠性研究 2.1 结构系统的失效机理假设采用有限体积法将实体结构划分了N个实体单元,该结构系统受到常幅疲劳载荷的作用,经历了时间n(即载荷作用的循环数为n)后,采用有限体积法对结构系统进行内力分析,可求出每一个结构元件ki(i=1, 2, …, n)的内力分别为S1、S2、…、Sn,通过S-N曲线的表达式(2) 可以估算出在当前应力水平下的结构元件的疲劳寿命Nki,则可以计算出每一个结构元件ki的累积损伤为
| $ {P_{{\rm{f}}{k_i}}} = P\left\{ {D_{{k_i}}^{\left( 0 \right)}\left( n \right) - {D_{\rm{c}}} \le 0} \right\} = 1 - \mathit{\Phi }\left( {\beta _{{k_i}}^{\left( 0 \right)}\left( n \right)} \right) $ | (13) |
式中:Φ为标准正态分布函数,βki(0)(n)为结构系统处于完整时的结构每个元件的疲劳可靠性指标。由式(13) 可知
| $ {\beta _{{k_i}}}\left( n \right) = \frac{{{\mu _{\rm{D}}}}}{{{\sigma _{\rm{D}}}}}\frac{{ - \frac{1}{2}\ln \left( {1 + \frac{{{d_{\rm{D}}}}}{{d_{\rm{E}}^2n}}} \right) + \ln \left( {{d_{\rm{E}}}n} \right)}}{{\sqrt {\ln \left( {1 + \frac{{{d_{\rm{D}}}}}{{d_{\rm{E}}^2n}}} \right)} }} $ | (14) |
式中:dE、dD分别为累积损伤的期望和方差,可以通过式(11)、(12) 求出。
若假定各结构元件的疲劳失效概率均为同一值Pc,则由式(13)、(14) 可以反求出n,即当各结构元件的疲劳失效概率达到某一个相同值时,可以求出每个结构元件所需要的载荷循环数nki。结构元件的nki值越小,则说明该元件可能最先失效。因此,取nki值最小的结构元件作为第一个失效元,并选取nki值在一定范围内的元件作为第一级临界失效元。假设元件的最小nki值为nmin,则
| $ C \le {n_{\min }}/n \le 1 $ | (15) |
式中C的取值可根据具体分析情况而定。
当确定第一个失效元疲劳失效后,根据疲劳失效的特点,将该失效元从结构系统中去掉,重新对结构系统进行内力分析,可以计算出其他未失效元件的累积损伤和失效概率,同样也可以求出未失效元件的nki值。取未失效元件中nki值的最小的元件作为下一个失效元,并选取nki值在一定范围内的结构元件作为第二级临界失效元。这样重复计算,直到有m个元件失效后,在结构系统中形成一个临界破坏截面,该临界破坏截面的承载能力不断下降,此时如果计算未失效的元件中最小的nki值小于某一设定值nc时,nc的取值可根据后续失效元件的失效时间而定。此时可以认为其余未失效元件即将在很短的时间内失效,导致该临界破坏截面的承载能力即将丧失,而整个结构系统的承载能力大幅度降低,不能满足原有的承载能力,使得结构系统失效。以上过程为本文研究实体结构系统的疲劳可靠性分析的结构系统的失效机理。
2.2 结构系统主要失效模式的搜索 2.2.1 第一级临界失效元的确定对每一个结构元件所需的载荷循环数按从小到大的顺序进行排序n1k=1≤n2k=1≤n3k=1≤…≤nnk=1,取n值最小的结构元件作为第一个失效元,并选取n值在一定范围内的元件作为第一级临界失效元,即
| $ 1 \le \frac{{n_i^{k = 1}}}{{n_1^{k = 1}}} \le C $ | (16) |
式中C的取值可根据具体情况分析而定。由于此时结构处于完整的初始阶段,通过S-N曲线的表达式(2) 可知,元件的内力越大,其疲劳寿命就越小,元件累积损伤的越快,它的破坏概率就越大。因此,可以直接选取一定范围的内力较大的元件作为第一级的临界失效元,这样可以缩减许多工作量。
2.2.2 第k级临界失效元的确定假设在疲劳载荷的作用下,有k1、k2、…、kk-1共k-1个结构元件失效,将这k-1个结构元件在结构系统中去掉,内力重新分配,可以求出未失效的元件ki(i=k, k+1, …, N)的疲劳累积损伤值,即
| $ D_{{k_i}}^k = \sum\limits_{i = 1}^k {\frac{{{n_j}}}{{N_{{k_i}}^j}}} \;\;\;\;\;\;\left( {j = k,k + 1, \cdots ,N} \right) $ | (17) |
式中:nj(j=1, 2, …, k-1) 为第j级载荷作用的时间,Nkij为第j级应力水平下的疲劳寿命。
假设又经历了时间nk,可以由式(13)、(14) 计算出未失效元件ki的疲劳可靠性指标和疲劳失效概率。若假定各元件的疲劳失效概率均为同一值Pc,则由式(13)、(14) 可以反求出nk,可以取未失效元件中nk值最小的元件作为第k级的失效元,并选取nki值在一定范围内的结构元件作为第k级临界失效元。这样按上述方法重复搜索,直到满足整个结构系统失效的条件,最终形成系统的一个主要失效模式。
2.3 结构系统的失效概率考虑到疲劳破坏的特殊性,结构的疲劳破坏是一个时间历程,认为主要失效模式在同一时间同时发生破坏的可能性很小,即各主要失效模式破坏的共概率很小,近似为零。吕海波等提出了一种简化的疲劳可靠性分析方法[12]。
假设结构系统含有m个主要失效模式,每一个失效模式的失效概率分别为a1、a2、…、am,ai是当其余失效模式不发生时,第i个失效模式发生的概率。若用事件E1、E2、…、Em分别表示各个主要失效模式发生导致结构系统失效,P1、P2、…、Pm分别为相应的失效概率,则
| $ \begin{array}{*{20}{c}} {{a_i} = P\left\{ {{E_i}\left| {{{\bar E}_1} \cap \cdots \cap {{\bar E}_m}} \right.} \right\} = }\\ {\frac{{P\left\{ {{E_i}\left| {{{\bar E}_1} \cap \cdots {{\bar E}_i} \cap \cdots \cap {{\bar E}_m}} \right.} \right\}}}{{P\left\{ {{{\bar E}_1} \cap \cdots {{\bar E}_i} \cap \cdots \cap {{\bar E}_m}} \right\}}} \approx \frac{{{P_i}}}{{1 - \sum\limits_m {{P_j}} }}} \end{array} $ | (18) |
有以下方程组:
| $ \left[ {\begin{array}{*{20}{c}} 1&{{a_1}}& \cdots &{{a_1}}\\ {{a_2}}&1& \cdots &{{a_2}}\\ \vdots & \vdots &{}& \vdots \\ {{a_m}}&{{a_m}}& \cdots &1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{P_1}}\\ {{P_2}}\\ \vdots \\ {{P_m}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{a_1}}\\ {{a_2}}\\ \vdots \\ {{a_m}} \end{array}} \right] $ | (19) |
求解上面的方程组可得到P1、P2、…、Pm,整个系统的失效概率为
| $ {P_{\rm{f}}} = {P_{\rm{1}}} + {P_{\rm{2}}} + \cdots + {P_m} $ | (20) |
如图 1所示的实体结构模型,结构的一端是固定端,另一端是自由端,结构上作用着均匀分布的疲劳载荷F(t),载荷的形式表示为
| $ F\left( t \right) = - 1.0 \times {10^2}\sin \left( {5.0 \times {{10}^3}{\rm{ \mathit{ π} }}t} \right) $ | (21) |
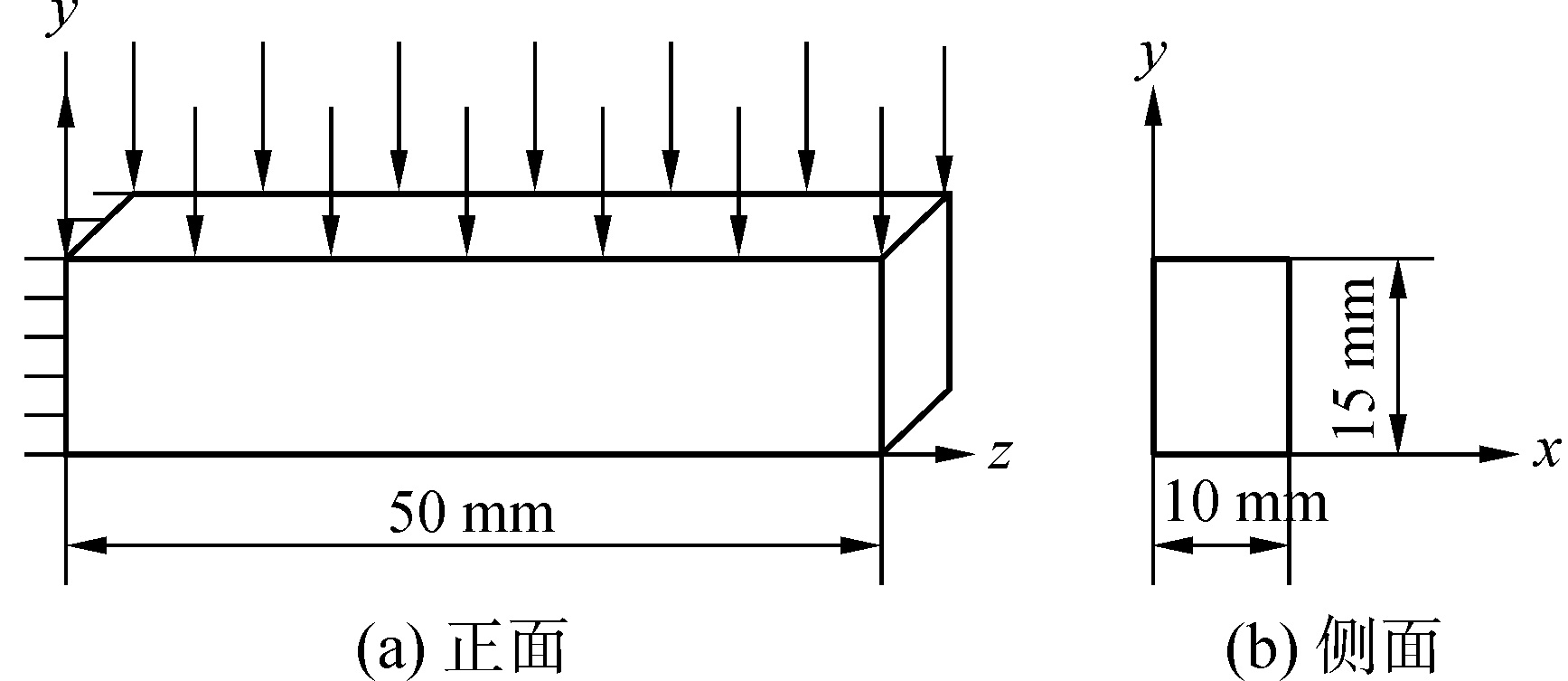
|
图 1 实体结构模型 Fig.1 Calculation model of entity structure |
结构的材料参数:密度为7 800 kg/m3、弹性模量为210 GPa、泊松比为0.3,根据文献[7]选取S-N曲线法中的参数为:m=3.152,A=3.26×1012。这里将结构的疲劳寿命N看作随机变量,且服从对数正态分布,疲劳寿命的均值通过S-N曲线法进行估算,变异系数取为0.54。将该实体结构采用有限体积法进行网格划分,共划分了418实体单元,151个节点。对该实体结构进行结构系统的疲劳可靠性分析。
采用有限体积法对结构系统进行内力分析,求出每个实体单元的最大应力σmax。并选取得到的σmax较大的实体单元作为第一级失效元件及临界失效元件。由于单元个数较多,只列出部分与分析有关的单元的最大应力值,如表 1所示。
| 表 1 单元的应力值 Tab.1 Stresses of elements |
这里选取实体单元359为第一级失效元,228、132、229、119为第一级临界失效元。
以单元号229为第一失效元的分支为例,分析失效模式形成的过程。单元229失效后,将单元229从结构系统中去掉,内力重新分配,由前述方法可以求出未失效元件的疲劳可靠性分析参数,由于单元数较多,只列出与分析有关的单元,计算当疲劳失效概率为50%时,单元所需要的载荷循环次数ni的值,见表 2。
| 表 2 第一级疲劳可靠性参数 Tab.2 Parameters of fatigue reliability for first stage |
从表 2中可看出,选取单元228作为第二级失效元。取C=1.02,第二级没有选取临界失效元。将单元228从结构系统中去掉,同理可求出未失效元件的疲劳可靠性分析参数见表 3。
| 表 3 第二级疲劳可靠性参数 Tab.3 Parameters of fatigue reliability for second stage |
由表 3可知,选取单元220作为第三级失效元。取C=1.02,第三级没有选取临界失效元。同理可求未失效元件的疲劳可靠性分析参数见表 4。
| 表 4 第三级疲劳可靠性参数 Tab.4 Parameters of fatigue reliability for third stage |
从表 4的计算结果可看出,n值最小的单元为244,因此,选取单元224作为第四级失效元。取C=1.02,第四级没有临界失效元。同理寻找下一级失效元,直到第十级失效单元132失效后,将未失效元的疲劳可靠性参数列于表 5中。
| 表 5 第十级疲劳可靠性参数 Tab.5 Parameters of fatigue reliability for tenth stage |
从表 5的计算结果可看出,n值最小的单元为119,因此,选取单元119作为第十一级失效元。取C=1.02,选取单元120作为第十一级临界失效元。从该计算分支的失效模式的失效路径可以看出,只有该级包含临界失效元,其他各级都不含有临界失效元。同样将单元119从结构系统中去掉,重新分配,按上述方法继续搜索下一级失效元,直到计算到第十四级失效元314失效后,计算未失效元的疲劳可靠性参数,计算结果列于表 6中。
| 表 6 第十四级疲劳可靠性参数 Tab.6 Parameters of fatigue reliability for fourteeth stage |
由表 6可知,选取单元311作为第十五级失效元。取C=1.02,第十五级没有临界失效元。同理可求未失效元件的疲劳可靠性分析参数见表 7。
| 表 7 第十五级疲劳可靠性参数 Tab.7 Parameters of fatigue reliability for fifteenth stage |
从表 7的计算结果可看出,单元为122的n值最小,最小值为488。取nc=1 000,则有n < nc,表明其余未失效元件即将在很短的时间内失效,整个结构系统的承载能力大幅度降低,不能满足原有的承载能力,导致结构系统失效。此时,满足结构系统失效条件,形成了一个失效模式,该失效路径如表 8中的失效模式号5所示。
| 表 8 失效模式 Tab.8 Failure modes |
一个失效模式形成后,检查该失效模式的最后失效级上是否还有临界失效元,因为该失效模式的最后失效级是第十五失效级,在第十五失效级上没有临界失效元,因此,恢复第十五失效级上的失效元。返回到第十四失效级上,继续查看是否存在临界失效元,按此方法进行搜索。由于该失效模式在第十一失效级上存在临界失效元,所以恢复第十一失效级上的失效元119后,返回到第十失效级上,重新选取临界失效元120作为第十一失效级上的失效元,将单元120从结构系统中去掉,内力重新分配,按上述方法继续搜索下一级失效元,直到满足结构系统失效的条件,又形成了一个新的失效模式,该失效模式的失效路径如表中的失效模式6所示。
由于该分支的所有失效级上已经没有临界失效元,所以该分支的失效模式搜索完毕,然后进行下一新分支的失效模式的搜索。例如以单元119为第一级失效元的新分支,按照上述方法进行新分支的失效模式的搜索。各主要失效模式的失效路径如表 8所示。
计算各主要失效模式在各个时刻下的失效概率,计算结果见表 9。根据表中的计算结果绘制了失效模式2的可靠度下降曲线,如图 2所示。
| 表 9 各个失效模式在不同时刻的失效概率 Tab.9 Failure probability of failure modes at different time |

|
图 2 可靠度下降曲线 Fig.2 Decline curve of reliability |
同理,其他失效模式也可以绘制出如图 2所示的可靠度下降曲线。从图中可以看出,该计算结果是令人满意的,即随着疲劳载荷循环次数的增加,结构系统的可靠度在不断减小。
各个主要失效模式的失效概率求出后,通过综合考虑主要失效模式的失效概率来计算实体结构系统的失效概率。首先采用简单界值法对结构系统的可靠性进行估算。估算结果如表 10所示。
| 表 10 疲劳可靠度估算值 Tab.10 Estimated value of fatigue reliability |
采用针对结构系统疲劳可靠性计算的简化算法计算了结构系统的疲劳可靠度和失效概率,结果列于表 11。
| 表 11 结构系统疲劳可靠性的简化算法计算结果 Tab.11 Results of fatigue reliability of structural system on the simplified method |
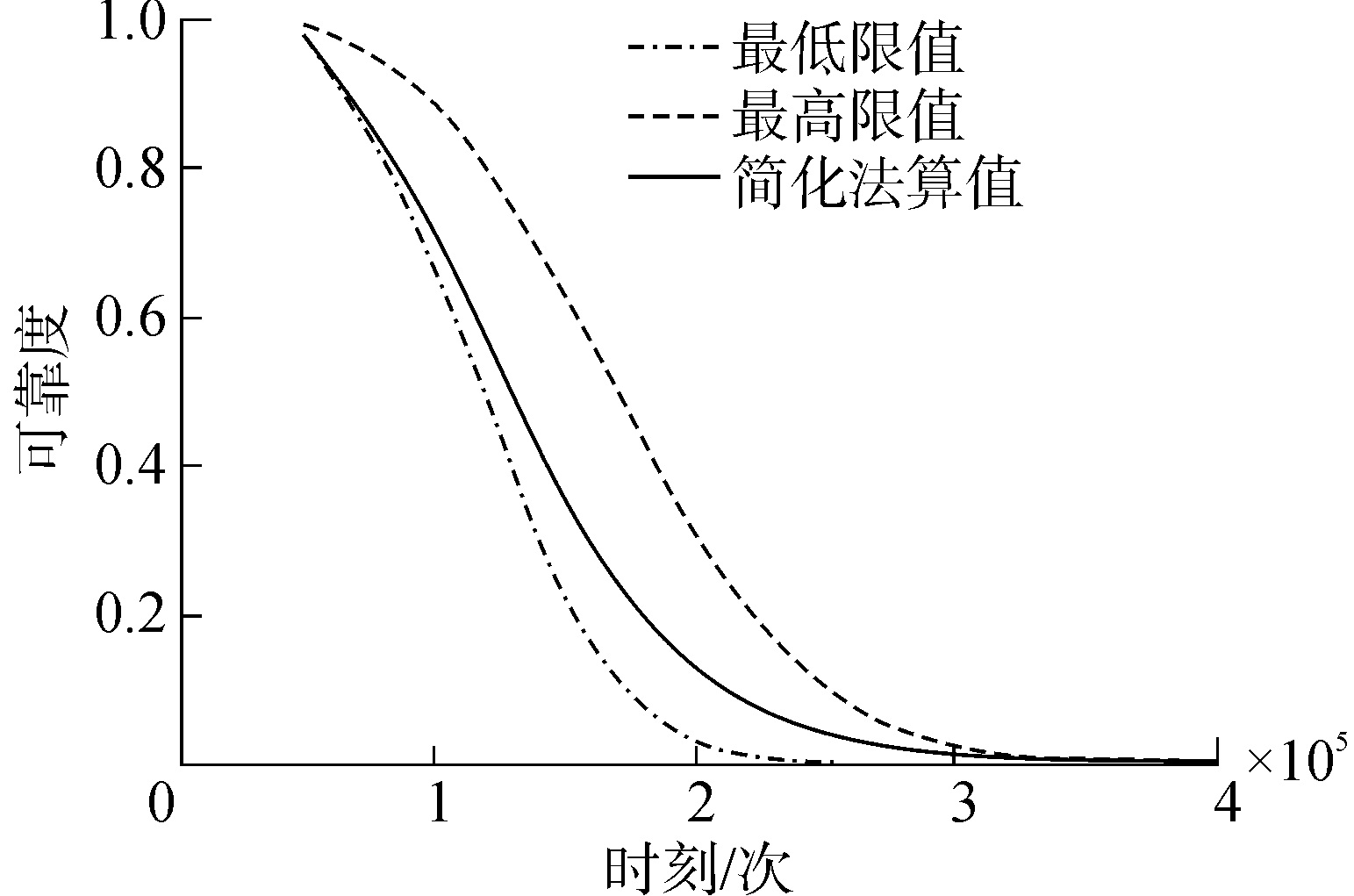
同时将表 10中的计算结果与表 11中的计算结果进行分析并绘制了结构系统的可靠度下降曲线,如图 3所示。
|
图 3 结构系统疲劳可靠度下降曲线 Fig.3 Decline curves of fatigue reliability of structural system |
从图 4的计算结果可以看出采用简化算法计算的结构系统的疲劳可靠度在估算的范围内,且结构系统的疲劳可靠度的计算结果的趋势是正确的,即随着疲劳载荷循环次数的增加,结构系统的可靠度在不断减小,结构系统的失效概率在不断增大,该计算结果是符合实际的。
4 结论1) 采用有限体积法分析了实体结构系统的疲劳可靠性。结构系统的疲劳可靠度的计算结果的趋势是正确的,即随着疲劳载荷循环次数的增加,结构系统的可靠度在不断减小。
2) 结构系统疲劳可靠性分析大多数以桁架结构为例采用杆单元作为结构元件研究,而文中以实体结构的实体单元作为结构元件研究,给出了实体结构系统疲劳失效的判别准则及搜索结构系统主要失效模式的基本过程,为实体结构系统的疲劳可靠性分析提供了理论参考。
由于采用简化的疲劳可靠性计算方法计算的结构系统的失效概率,因而没有充分考虑各失效模式之间的相关性,这点可作为后续工作进行深入研究。
| [1] |
MARTINDALE S G, WIRSCHING P H. Reliability-based progressive fatigue collapse[J]. Journal of structural engineering, 1983, 109(8): 1792-1811. DOI:10.1061/(ASCE)0733-9445(1983)109:8(1792) ( 0) 0)
|
| [2] |
STAHL B, GEYER J F. Fatigue reliability of parallel member systems[J]. Journal of structural engineering, 1984, 110(10): 2307-2323. DOI:10.1061/(ASCE)0733-9445(1984)110:10(2307) ( 0) 0)
|
| [3] |
KARSAN D I, KUMAR A. Fatigue failure paths for offshore platform inspection[J]. Journal of structural engineering, 1990, 116(6): 1679-1695. DOI:10.1061/(ASCE)0733-9445(1990)116:6(1679) ( 0) 0)
|
| [4] |
SAAD L, AISSANI A, CHATEAUNEUF A, et al. Reliability-based optimization of direct and indirect LCC of RC bridge elements under coupled fatigue-corrosion deterioration processes[J]. Engineering failure analysis, 2016, 59: 570-587. DOI:10.1016/j.engfailanal.2015.11.006 ( 0) 0)
|
| [5] |
DI C F, FANELLI P, VIVIO F. Fatigue reliability evaluation of riveted lap joints using a new rivet element and DFR[J]. International journal of fatigue, 2017, 101(2): 192-208. ( 0) 0)
|
| [6] |
XU Yazhou. Fatigue reliability evaluation using probability density evolution method[J]. Probabilistic engineering mechanics, 2015, 42: 1-6. DOI:10.1016/j.probengmech.2015.09.005 ( 0) 0)
|
| [7] |
YU Feng, GAO Chao, HE Yuting, et al. Investigation on tension-tension fatigue performances and reliability fatigue life of T700/MTM46 composite laminates[J]. Composite structures, 2016, 136: 64-74. DOI:10.1016/j.compstruct.2015.09.057 ( 0) 0)
|
| [8] |
GAO Haifeng, FEI Chengwei, BAI Guangchen, et al. Reliability-based low-cycle fatigue damage analysis for turbine blade with thermo-structural interaction[J]. Aerospace science and technology, 2016, 49: 289-300. DOI:10.1016/j.ast.2015.12.017 ( 0) 0)
|
| [9] |
KHASHABA U A, ALJINAIDI A A, HAMED M A. Fatigue and reliability analysis of nano-modified scarf adhesive joints in carbon fiber composites[J]. Composites part b-engineering, 2017, 120: 103-117. DOI:10.1016/j.compositesb.2017.04.001 ( 0) 0)
|
| [10] |
ROVINELLI A, GUILHEM Y, PROUDHON H. Assessing reliability of fatigue indicator parameters for small crack growth via a probabilistic framework[J]. Modelling and simulation in materials science and engineering, 2017, 25(4): 158-170. ( 0) 0)
|
| [11] |
MINER M A. Cumulative damage in fatigue[J]. Journal of applied mechanics, 1945, 12(3): 159-164. ( 0) 0)
|
| [12] |
吕海波. 结构疲劳可靠性分析方法[D]. 南京: 南京航空航天大学, 2000: 28-42. LV Haibo. Study on the method of structural fatigue reliability analysis[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2000:28-42. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


