雾化使连续液体破碎成为大量离散液滴,显著增大了气液两相的接触表面积。在动力装置燃烧室中,雾化效果直接关系到燃烧过程的稳定性和燃烧效率,良好的雾化会使传质传热过程大为加强。因此雾化机理的研究对于整个喷雾和燃烧过程是十分重要的。但由于雾化问题的复杂性,对雾化过程的数值模拟还有许多难点尚未解决。
根据射流稳定性理论分析,影响射流雾化的是初始扰动以及后期扰动的增加。经过长期大量研究知道雾化的初始扰动来源:射流液柱表面气液两相之间的相对运动、喷孔内流动状态等因素[1]。大量研究表明湍流扰动对液滴破碎过程的影响不容忽视,但人们对湍流的初始扰动认识不够。因此,开展湍流扰动对液滴初次破碎和二次破碎的影响研究很有必要。
本文将建立的耦合了喷嘴内部湍流影响的破碎模型写入GTEA(general transport equation analysis)程序中。首先进行单液滴破碎计算,分析射流内部湍流扰动与不稳定波之间的关系,对比分析了二者在液滴破碎过程中的作用。然后通过与实验数据对比,验证本文提出破碎模型的准确性,同时讨论了射流内部湍流扰动对液滴初次及二次破碎过程的影响。
1 液滴破碎模型目前经典的液滴破碎模型包括:TAB模型[2]将液滴的振动和变形与弹簧质量系统相类比,建立液滴变形方程,通过变形量判断液滴破碎;WAVE模型[3]和KH-RT模型[3-4]认为液滴表面不稳定波的增长导致液滴从射流表面剥落下来;Huh-Gosman模型[5]认为喷嘴内部湍流对喷雾破碎至关重要。为衡量初始扰动对液滴破碎的影响,本文提出的破碎模型采用KH-RT模型和部分Huh-Gosman模型的基本理论。
1.1 KH-RT模型 1.1.1 初次破碎(KH模型)临近喷嘴区域,用Kelvin-Helmholtz(K-H)机理模拟射流的初始雾化过程。KH模型[3]认为液滴破碎是由于射流表面不稳定波的增长引起。液滴破碎时间和新液滴半径与不稳定波的频率和波长有关,具体关系为
| $ {\tau _{{\rm{KH}}}} = \frac{{3.788{B_1}{r_0}}}{{{\mathit{\Omega }_{{\rm{wave}}}}{\mathit{\Lambda }_{{\rm{wave}}}}}} $ | (1) |
| $ {r_{{\rm{KH}}}} = {B_0}{\mathit{\Lambda }_{{\rm{wave}}}} $ | (2) |
式中:B0和B1为模型常数,Λwave为KH不稳定波的波长,Ωwave为KH不稳定波的频率。
液滴的半径变化率为
| $ \frac{{{\rm{d}}r}}{{{\rm{d}}t}} = - \frac{{r - {r_{{\rm{wave}}}}}}{\tau } $ | (3) |
远离喷嘴的下游区域,如果液滴的加速方向与密度梯度方向不一致,就会在液滴表面生产RT扰动,从而引起液滴破碎[4]。在RT模型中,破碎时间和破碎后液滴的半径为
| $ {\tau _{{\rm{RT}}}} = \frac{{{C_\tau }}}{{{\mathit{\Omega }_{{\rm{RT}}}}}} $ | (4) |
| $ {r_{{\rm{RT}}}} = \frac{{{\mathit{\Lambda }_{{\rm{RT}}}}}}{2} $ | (5) |
式中:Cτ为模型常数,ΛRT为RT不稳定波的波长,ΩRT为RT不稳定波的频率。
KH-RT模型认为在雾化长度以内为初次破碎区域,采用KH模型计算液滴破碎,超出雾化长度用KH机理和RT机理的竞争来描述液滴的二次雾化过程。
1.2 Huh-Gosman模型Huh认为射流破碎的原因在于喷孔内形成的湍流应力[5]。首先在喷嘴内形成的湍流在离开喷嘴时对射流表面施加初始扰动,随后扰动将快速增长,直到这些扰动足够大,从射流表面分离出来而形成液滴。通过动量守恒推导喷嘴出口处的平均湍流动能ka和湍流耗散率εa为
| $ {k_a} = \frac{{{U^2}D}}{{8L}}\left[ {\frac{1}{{c_d^2}} - {k_c} - \left( {1 - {s^2}} \right)} \right] $ | (6) |
| $ {\varepsilon _a} = \frac{{{k_\varepsilon }{U^3}}}{{2L}}\left[ {\frac{1}{{c_d^2}} - {k_c} - \left( {1 - {s^2}} \right)} \right] $ | (7) |
式中:cd为喷嘴流量系数,U为射流速度,D为液滴直径,L为喷嘴长度,kc为喷嘴形状系数,s为喷嘴面积收缩比。
相应的初始湍流长度尺度Lt0和时间尺度τt0为
| $ L_t^0 = {c_\mu }\frac{{k_a^{3/2}}}{{{\varepsilon _a}}} $ | (8) |
| $ \tau _t^0 = {c_\mu }\frac{{{k_a}}}{{{\varepsilon _a}}} $ | (9) |
式中cμ为湍流k-ε方程系数。
Lt0和τt0设为射流的初始扰动值,湍流长度尺度Lt和时间尺度τt随时间变化的关系如下
| $ {L_t} = L_t^0{\left( {1 + \frac{{0.082~8t}}{{\tau _t^0}}} \right)^{0.457}} $ | (10) |
| $ {\tau _t} = \tau _t^0 + 0.082~8t $ | (11) |
式中t为计算时间。
2 本文破碎模型本文认为湍流扰动和气液相互作用引起的表面不稳定波都是扰动,只是扰动的能量、频率和尺度不同。各种扰动对射流失稳是相互影响的,是一种耦合关系。喷嘴内部的湍流运动在射流内部产生初始扰动,当射流脱离喷嘴时,喷嘴内部形成的初始扰动与射流受到的空气动力扰动一起在射流表面形成不稳定波,最后导致液滴破碎[6-7]。湍流扰动增大不稳定波的振幅和频率,反过来表面不稳定波增大湍流扰动的动能。因此,为了考虑喷嘴内部湍流流动对液滴破碎过程的影响,在式(3)的右端加入了湍流项。
液滴的半径变化率为
| $ \frac{{{\rm{d}}r}}{{{\rm{d}}t}} = - \left[ {\frac{{r - {r_{{\rm{wave}}}}}}{\tau } + {C_a}\frac{{{L_t}}}{{{\tau _t}}}} \right] $ | (12) |
式中:Ca为模型常数,Lt为湍流长度尺度[5],τt为湍流时间尺度[5]。
本文引入权重系数来表示湍流扰动和表面波扰动对液滴破碎的影响程度。二者对于液滴破碎的权重系数之和为1:
| $ {C_t} + {C_w} = 1 $ | (13) |
式中:Ct为湍流权重系数,Cw为表面波权重系数。
式(13)中的权重系数表示为
| $ {C_i} = \frac{{{E_{ki}}}}{{{E_{kt}} + {E_{kw}}}} $ | (14) |
式中:Eki=(It/τt)2为湍流动能,Ekw=(Λ2Ω/r)2为表面波动能。
破碎后新形成的液滴半径rp为
| $ {r_p} = \frac{{{r_w}{r_t}}}{{\left( {1 - {C_t}} \right){r_t} + {C_t}{r_w}}} $ | (15) |
式中:rw为KH模型计算的新液滴半径,湍流作用下形成的液滴半径rt用概率密度函数(PDF)求解:
| $ {r_t} = \frac{1}{2}\frac{{\int_{{d_{\min }}}^{{d_{\max }}} {\frac{{x{{\left( {{k_e}x} \right)}^{ - 2}}}}{{{{\left[ {1 + {{\left( {{k_e}x} \right)}^{ - 2}}} \right]}^{11/6}}}}{\rm{d}}x} }}{{\int_{{d_{\min }}}^{{d_{\max }}} {\frac{{{{\left( {{k_e}x} \right)}^{ - 2}}}}{{{{\left[ {1 + {{\left( {{k_e}x} \right)}^{ - 2}}} \right]}^{11/6}}}}{\rm{d}}x} }} $ | (16) |
式中:dmax为液滴最大直径,dmin为液滴最小直径,ke=0.75/Lt。
在距离喷嘴较远的下游区域,喷嘴内部湍流对液滴破碎的影响变弱,液滴与空气的相互作用逐渐加强。因此,本文采用RT模型来描述液滴的二次破碎。
3 模拟计算及分析本文研究基于GTEA程序[8-9]。气相方程以流体力学控制方程为基础,采用有限体积法离散偏微分方程,用SIMPLE算法求解流场,线性方程组求解采用共轭梯度法和多重网格法。液相与气相的相互作用采用单元内颗粒源法,颗粒的追踪采用FFPT算法[10]。
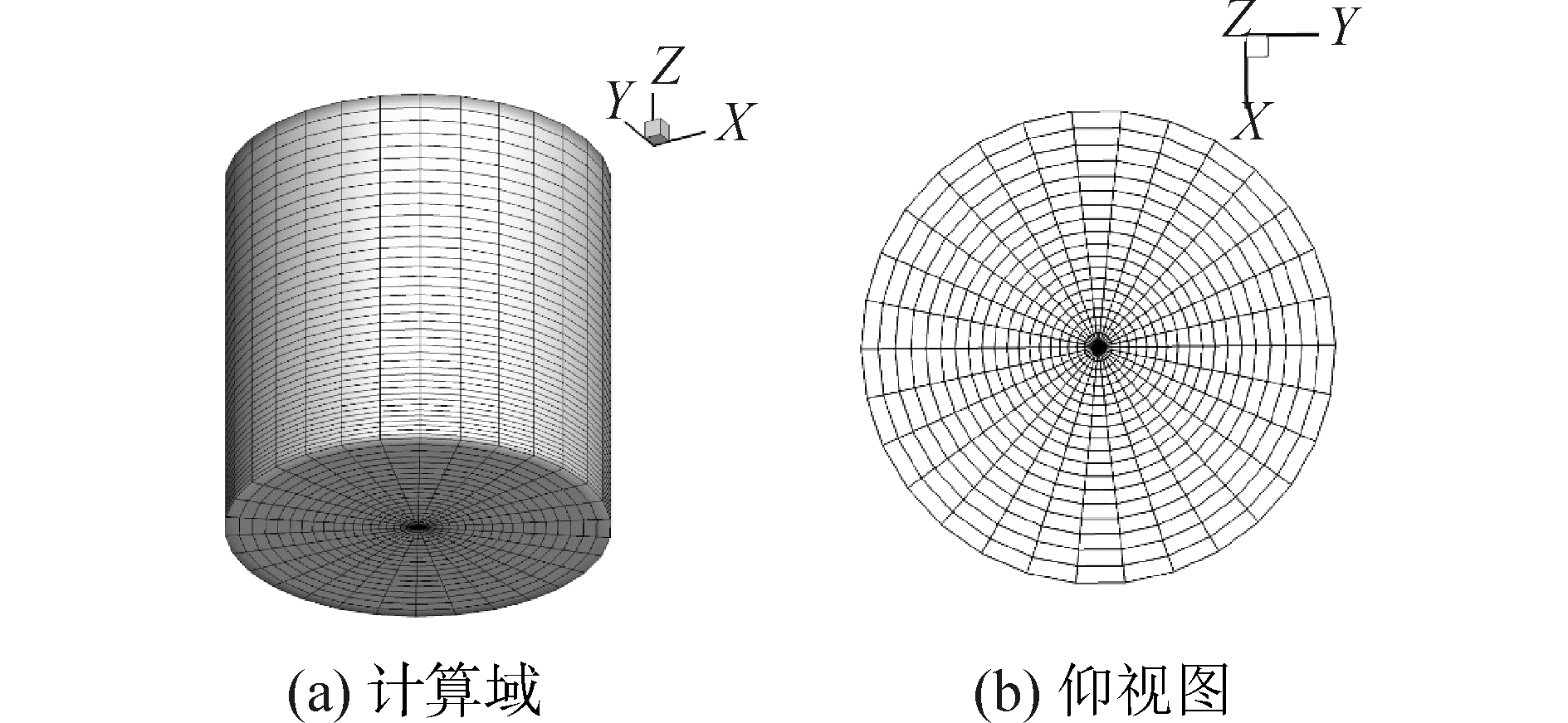
本文的计算区域为直径100 mm,高100 mm的圆柱,喷嘴位置高于边界中心1 mm。计算网格进行了无关性验证,所选网格对贯穿距的计算没有太大影响,如图 1所示。采用标准k-ε湍流方程,时间步长取为0.1~1,液滴碰撞采用网格依赖性较小的Nordin[11]模型。KH-RT模型的参数[12]取值如表 1。
|
Download:
|
| 图 1 计算网格 Fig. 1 The computational mesh | |
| 表 1 破碎模型常数[12] Tab.1 Constants for breakup models |
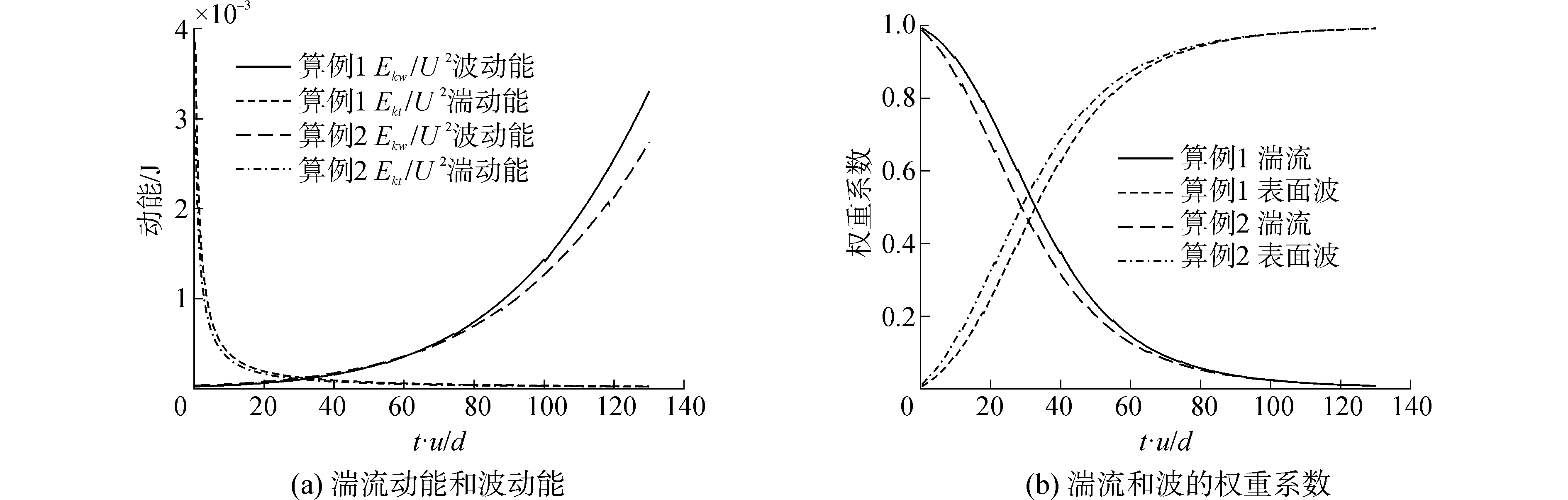
本文首先通过单液滴破碎来探讨湍流扰动对初次破碎的影响, 计算参数设定如表 2。本文的破碎模型中,射流表面不稳定波和湍流扰动在液滴破碎过程中都起到作用,生成液滴的大小与二者的长度和时间尺度有关(式(12)和式(15))。为消除液滴速度和喷嘴直径对计算结果分析的影响,本文引入无量纲参数t·u/d,其中t为计算时间,u为液滴运动速度,d为喷嘴直径,如图 2横坐标所示。图 2(a)可以看出,喷嘴内部的湍流流动使得初始湍流扰动的能量较高,并占主导地位,随着液滴破碎不断进行,其数值迅速减小,相反不稳定波动能的数值随运动距离增加而逐渐增大。算例1和算例2的对比可以看出,喷嘴内的射流流速对液滴破碎过程中的不稳定波动能有较大影响,进而影响后期破碎的发生。图 2(b)为破碎过程中湍流扰动和不稳定波对破碎过程影响的权重系数变化的情况对比。图中的趋势可以理解为高湍流强度在液滴破碎初始阶段起决定作用,随着液滴向下游移动,湍流动能逐渐被耗散,液滴破碎逐渐受表面不稳定波控制。算例1和算例2的对比看出,湍流强度越大,其在破碎过程中的影响越大,时间越长。
|
Download:
|
| 图 2 决定液滴大小的参数 Fig. 2 Parameters used to determine drop size | |
本节中KH-RT模型与本文提出的破碎模型都与实验数据进行对比,验证本文破碎模型的有效性。四个实验情况如表 3,计算中的喷油速率曲线根据文献的数据线性插值得出。喷雾贯穿距、液滴大小及液滴速度作为对比的对象。
| 表 3 实验情况 Tab.3 Experimental conditions |
不同入射压力下两个破碎模型计算的喷雾贯穿距对比如图 3所示。图 3(a)为喷嘴附近区域(低入射压力-21 MPa)喷雾贯穿距与实验对比图。从图中可以看出即使喷射压力较小,喷嘴内部湍流对贯穿距的影响还是通过两个模型的计算差值可以看出。图 3(b)为高入射压力(120 MPa)时两个模型贯穿距的比较。KH-RT模型与实验的误差为3%~11%,而本文模型则为2%~5%。当液滴破碎过程中考虑湍流的影响时,液滴破碎速率明显加快,液滴半径普遍小于KH-RT模型的计算值,在运动过程中受到气体作用较为明显,相同时间内运动距离小于KH-RT模型计算值。比较算例3和算例4计算值也可以得出入射压力越大,液滴破碎受湍流运动影响越明显。

|
Download:
|
| 图 3 计算和实验得到的贯穿距对比(算例3、4) Fig. 3 Comparisons of predicted and measured spray penetration(case 3 and case 4) | |
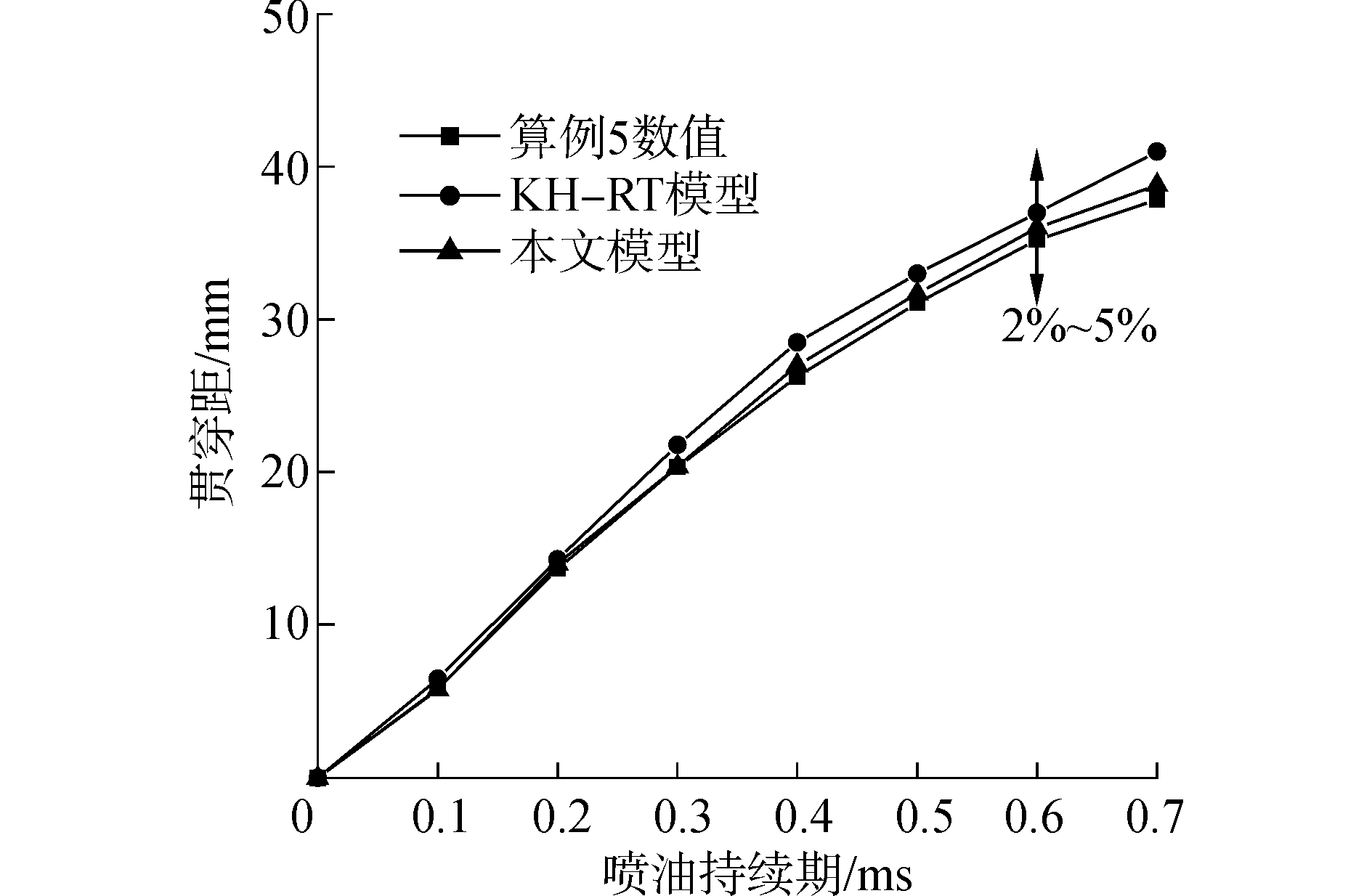
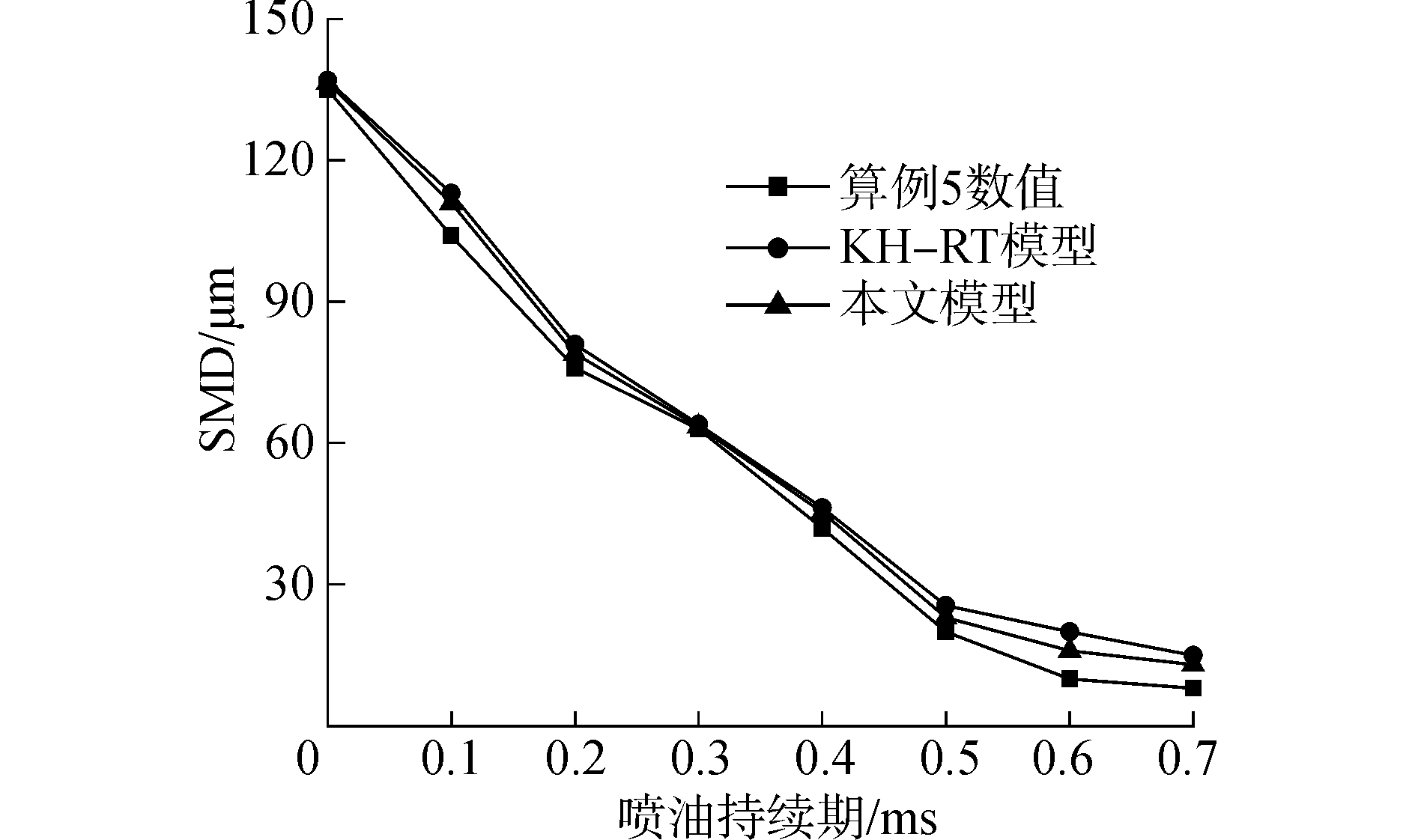
图 4和图 5为计算得到的贯穿距和索特尔平均直径(SMD)与实验数据的对比示意图。从图中可以看到KH-RT模型计算的贯穿距高于实验的数值,而本文的模型计算结果与实验值基本相符。是否考虑湍流作用会导致两个模型的计算结果相差2%~5%。在采用相同的二次破碎模型下,初次破碎过程中湍流扰动对计算结果有较大影响,二者SMD相差4%左右。这主要源于液滴初次破碎过程中,湍流扰动导致破碎后液滴的直径普遍较小。
|
Download:
|
| 图 4 计算和实验得到的贯穿距对比(算例5) Fig. 4 Comparisons of predicted and measured spray penetration(case 5) | |
|
Download:
|
| 图 5 不同破碎模型计算的SMD对比 Fig. 5 Comparisons of the sauter mean diameter (SMD) of different breakup models | |
图 6为相同条件下KH-RT模型和本文模型计算的喷雾场结构与实验值的对比。尽管KH-RT模型与本文模型的结果与实验基本相符,但喷雾形态上二者还是有些微小的差别,KH-RT模型略微有些失真。

|
Download:
|
| 图 6 计算和实验得到的喷雾变化对比 Fig. 6 Comparisons of predicted and measured spray evolution | |
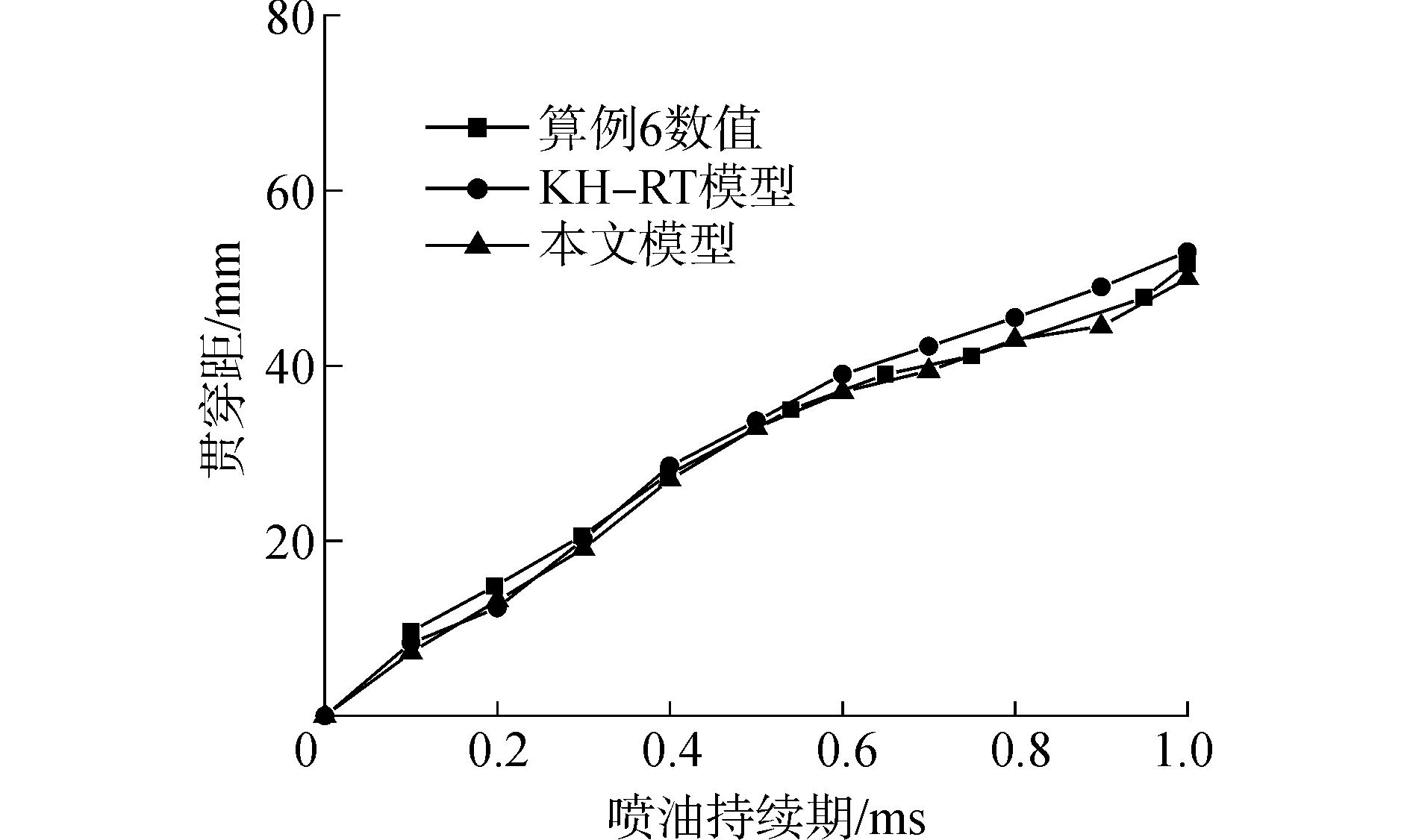
图 7为两个破碎模型计算的贯穿距与实验数据的对比,可以看出二者基本相差不大,整体数值都与实验数据相符。图 8为轴向45 mm和50 mm位置处,液滴在径向不同位置处的速度分布情况。喷雾核心区的液滴速度受外围气体的影响较小,速度相对较大,外围液滴受到周围气体作用有较大的速度变化和运动阻力,速度迅速较小。两个模型的计算结果沿径向都呈现下降趋势,这与实验观测的趋势相符。KH-RT模型的计算结果存在较大偏差,整体数值均高于实验和本文模型的结果。轴向距离45 mm和50 mm都超出雾化长度,破碎机理都为RT不稳定波理论,因此对速度的影响只能来源于初次破碎。湍流扰动因素导致破碎液滴的直径小于KH模型的计算数值,速度变化率较大,因此本文模型计算结果与实验值更贴近。
|
Download:
|
| 图 7 计算和实验得到的贯穿距对比(算例6) Fig. 7 Comparisons of predicted and measured spray penetration(case 6) | |

|
Download:
|
| 图 8 计算和实验得到的液滴速度对比 Fig. 8 Comparisons of predicted and measured droplet velocity | |
本文依据文献[15]的实验数据对喷射压力(40~180 MPa)和喷嘴直径(0.14~0.24 mm)进行了多组组合计算。为避免喷油量对计算结果的影响,根据不同的工况适当调整燃油喷射时间,保证每个工况喷油量相同。通过最小二乘法计算,可以得到初始液滴平均湍动能(K0)与喷射压力(P)和喷嘴直径(D)的关系:
| $ \begin{array}{*{20}{c}} {{K_0} = 687.85 + 8.17P - 8711.54D - 33.32PD - }\\ {0.000~756{P^2} + 24~845{D^2}} \end{array} $ | (17) |
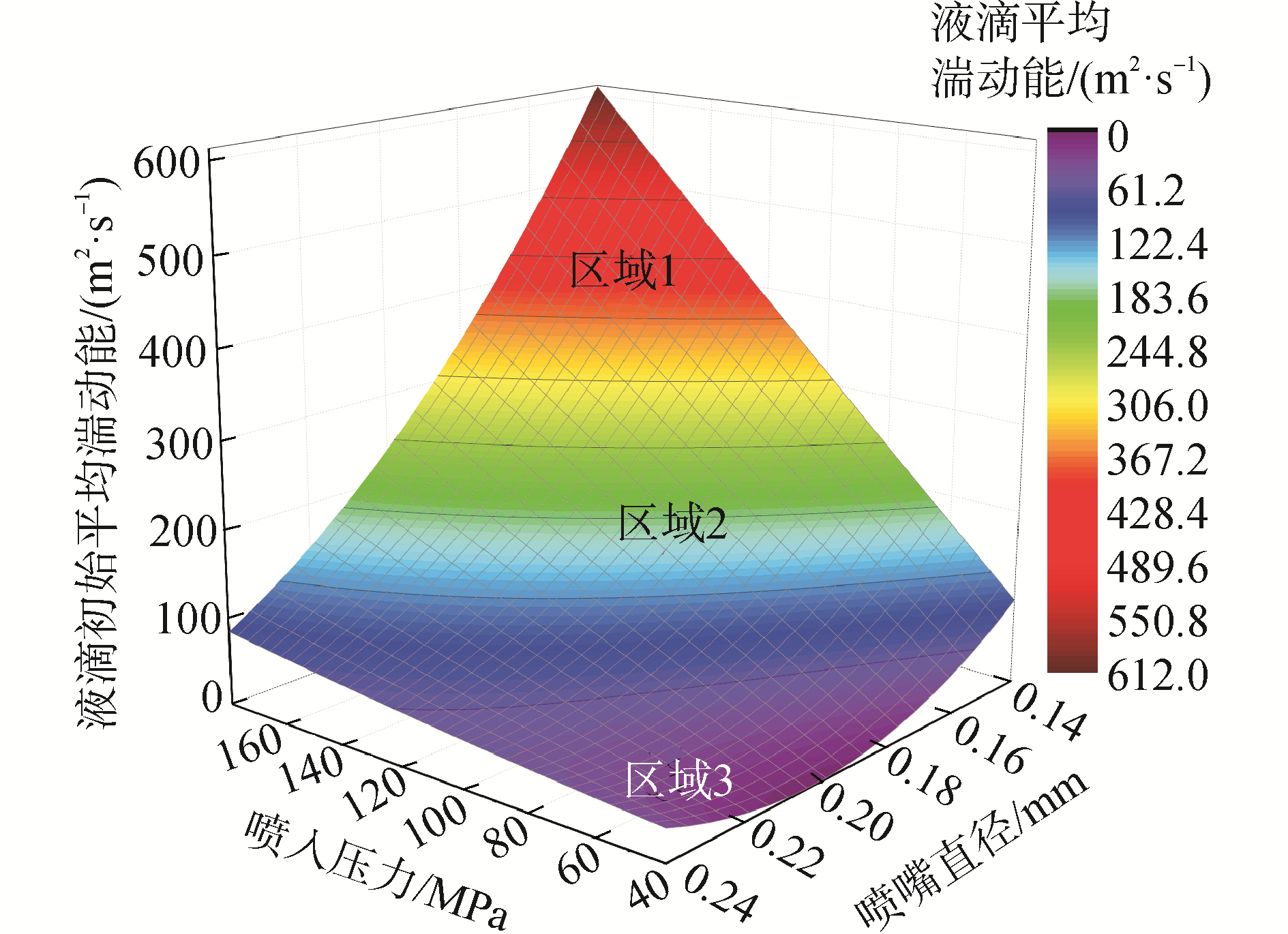
液滴初始平均湍动能、喷射压力和喷嘴直径之间的关系如图 9所示。根据计算结果,大致分为3个区域:区域1喷射压力和喷嘴直径对初始平均湍流影响最大,无论哪一个参数改变都会引起较大的初始平均湍动能;区域2可以看出即使喷射压力降低,但适当调整喷嘴直径也可以达到相同效果。同样,喷嘴采用小口径时,喷射压力提高也可以满足要求;区域3喷射压力与喷嘴直径对初始平均湍动能的影响较小。总体上看喷射压力和喷嘴直径对初始平均湍动能的影响大致相同。
|
Download:
|
| 图 9 液滴初始平均湍动能、喷射压力和喷嘴直径的关系 Fig. 9 The relationship between the initial average turbulent kinetic energy, injection pressure and nozzle diameter | |
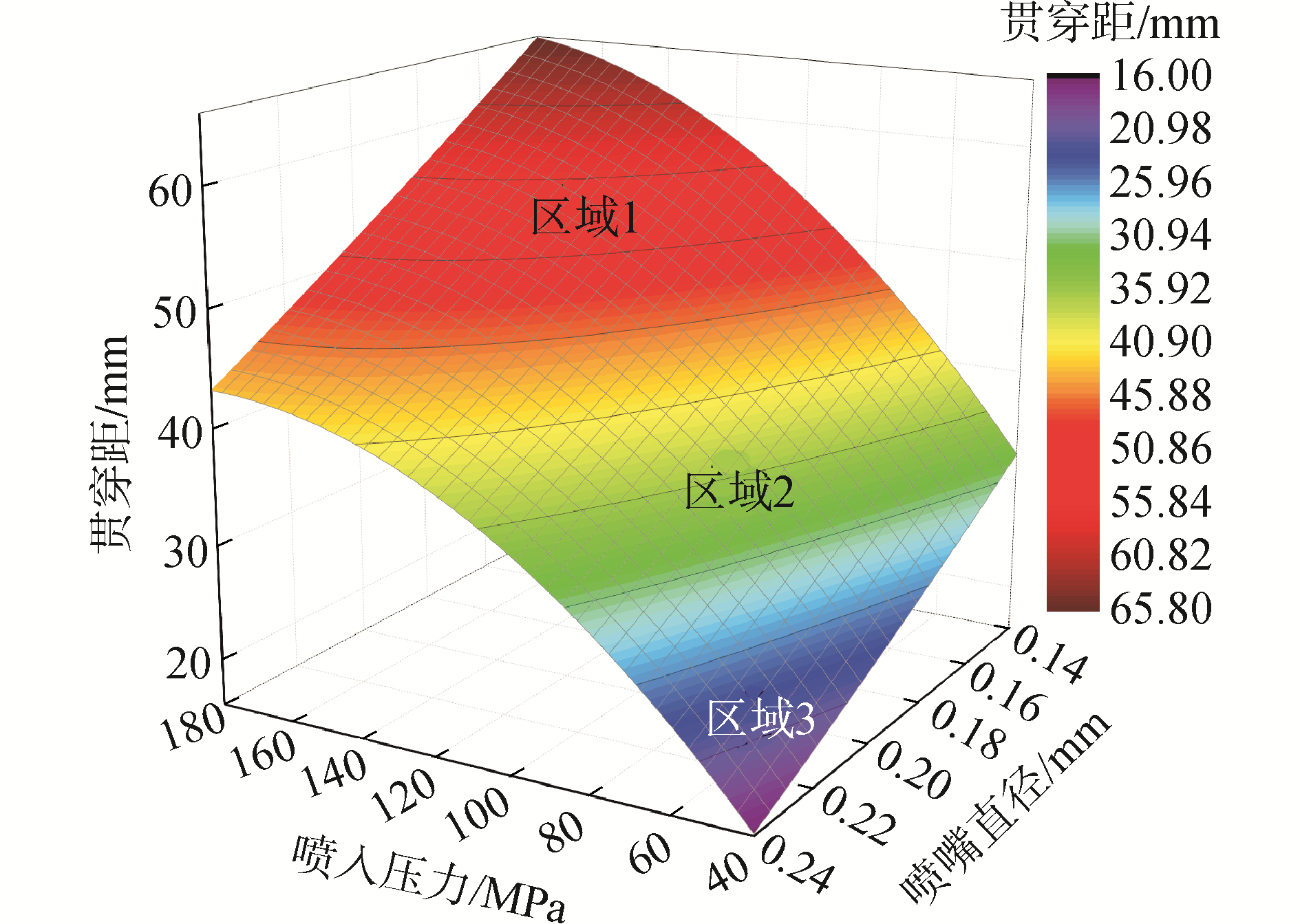
图 10显示了贯穿距、喷射压力和喷嘴直径三者之间的关系。贯穿距整体的变化趋势与图 9中液滴初始平均湍动能的变化趋势一样,喷嘴直径越小,喷射压力越大,贯穿距越大,反之亦然。采用相同喷嘴时,喷射压力区间120~180 MPa内,提高喷射压力对贯穿距的影响不大;采用相同喷射压力时,喷嘴直径的减小还是可以提高贯穿距。虽然喷嘴直径会对贯穿距产生一定影响,但根据贯穿距的变化率还是可以看出喷射压力对其影响更大。
|
Download:
|
| 图 10 贯穿距、喷射压力和喷嘴直径的关系 Fig. 10 The relationship between the spray penetrations, injection pressure and nozzle diameter | |
喷射压力和喷嘴直径对索特尔平均直径(SMD)的影响如图 11所示。SMD的变化规律也与图 10中液滴初始平均湍动能的变化规律相同。采用相同喷嘴时,喷射压力在120~180 MPa内,SMD的变化都是不很明显。虽然提高喷射压力可以达到减小液滴直径的目的,但喷嘴直径的变化带来的效果更佳明显

|
Download:
|
| 图 11 索特尔平均直径、喷射压力和喷嘴直径的关系 Fig. 11 The relationship between the sauter mean diameter injection pressure and nozzle diameter | |
1) 通过对比分析破碎过程中不稳定波和湍流扰动能的影响可知,射流中的湍流扰动对液滴破碎的影响不可忽略。随液滴运动时间增加湍流扰动对液滴破碎的影响逐渐减小,不稳定波的比重逐渐增大。远离雾化长度,湍流扰动对破碎的影响很微弱。
2) 通过两个模型计算对比发现,喷嘴内湍流运动会导致贯穿距相差很大,SMD相差4%左右。由此可以看出液滴破碎过程中对湍流扰动的研究很有必要。
3) 二次破碎过程虽然发生在距离喷嘴较远处,但初始湍流值的大小,还是能影响到二次破碎液滴的大小和运动速度。
4) 喷射压力与喷嘴直径对初始液滴平均湍动能的影响相同。喷射压力对贯穿距的影响更加明显。喷嘴直径的选择会直接影响最终整个喷雾场内液滴的大小。
| [1] |
史春涛, 任立红, 于善颖, 等. 喷雾破碎模型在内燃机CFD中的应用[J]. 拖拉机与农用运输车, 2006, 33(3): 1-3, 8. SHI Chuntao, REN Lihong, YU Shanying, et al. Application of spray breakup model in the CFD of IC engine[J]. Tractor & farm transporter, 2006, 33(3): 1-3, 8. (  0) 0)
|
| [2] |
O'ROURKE P J, AMSDEN A A. The TAB method for numerical calculation of spray droplet breakup[R]. SAE Paper 872089, Toronto, Canada: SAE, 1987. http://www.researchgate.net/publication/236466362_The_TAB_method_for_numerical_calculation_of_spray_droplet_breakup
(  0) 0)
|
| [3] |
REITZ R D, DIWAKAR R. Structure of high-pressure fuel sprays[R]. SAE Paper 870598, Warrendale, PA: SAE, 1987. http://www.researchgate.net/publication/236552488_Structure_of_high-pressure_fuel_sprays
(  0) 0)
|
| [4] |
PATTERSON M A, REITZ R D. Modeling the effects of fuel spray characteristics on diesel engine combustion and emission[R]. SAE Paper 980131, Madison: SAE, 1998. https://www.researchgate.net/publication/285879865_Modeling_the_effects_of_fuel_spray_characteristics_on_diesel_engine_combustion_and_emissions
(  0) 0)
|
| [5] |
HUH K Y, LEE E, KOO J. Diesel spray atomization model considering nozzle exit turbulence conditions[J]. Atomization and sprays, 1998, 8(4): 453-469. DOI:10.1615/AtomizSpr.v8.i4 (  0) 0)
|
| [6] |
SOM S. Development and validation of spray models for investigating diesel engine combustion and emissions[D]. Chicago: University of Illinois, 2009. http://www.researchgate.net/publication/234180735_Development_and_validation_of_spray_models_for_investigating_diesel_engine_combustion_and_emissions
(  0) 0)
|
| [7] |
ISHIMOTO J, HOSHINA H, TSUCHIYAMA T, et al. Integrated simulation of the atomization process of a liquid jet through a cylindrical nozzle[J]. Interdisciplinary information sciences, 2007, 13(1): 7-16. DOI:10.4036/iis.2007.7 (  0) 0)
|
| [8] |
雷国东. 非结构网格FVM在复杂几何结构的湍流反应流计算中的应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. LEI Guodong. The application and research of the unstructured grid FVM in the turbulent reaction flows simulation with complex geometries[D]. Harbin: Harbin Engineering University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10217-2009058604.htm (  0) 0)
|
| [9] |
明平剑. 基于非结构化网格气液两相流数值方法及并行计算研究与软件开发[D]. 哈尔滨: 哈尔滨工程大学, 2008. MING Pingjian. Development of numerical modeling for gas-liquid two-phase flows based on unstructured grids and parallel computing[D]. Harbin: Harbin Engineering University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1438345 (  0) 0)
|
| [10] |
刘永丰, 明平剑, 张文平, 等. 一种固定网格上拉格朗日点追踪的快速算法[J]. 计算物理, 2010, 27(4): 527-532. LIU Yongfeng, MING Pingjian, ZHANG Wenping, et al. An efficient Lagrange point tracking algorithm for fixed grids[J]. Chinese journal of computational physics, 2010, 27(4): 527-532. (  0) 0)
|
| [11] |
NORDIN P A N. Complex chemistry modeling of diesel spray combustion[D]. Göteborg: Chalmers Tekniska Högskola, 2001. https://www.researchgate.net/publication/34767324_Complex_chemistry_modeling_of_diesel_spray_combustion
(  0) 0)
|
| [12] |
JIA Ming, PENG Zhijun, XIE Maozhao. Evaluation of breakup models and application to the mixture preparation process for diesel HCCI engines[R]. SAE Paper 2008-01-0023, Dalian: SAE, 2008. https://www.researchgate.net/publication/293817176_Evaluation_of_Breakup_Models_and_Application_to_the_Mixture_Preparation_Process_for_Diesel_HCCI_Engines
(  0) 0)
|
| [13] |
HIROYASU H, KADOTA T. Fuel droplet size distribution in diesel combustion chamber[R]. SAE Paper 740715, SAE, 1974. http://www.researchgate.net/publication/315123259_Fuel_Drop-Size_Distribution_in_Diesel_Combustion_Chamber
(  0) 0)
|
| [14] |
RAMIREZ A I, SOM S, AGGARWAL S K, et al. Quantitative measurement of diesel fuel spray characteristics in the near-nozzle region of a heavy duty multi-hole injector[C]//21st ILASS Americas. 2008.
(  0) 0)
|
| [15] |
KANG J, BAE C, LEE K O. Initial development of non-evaporating diesel sprays in common-rail injection systems[J]. International journal of engine research, 2003, 4(4): 283-298. DOI:10.1243/146808703322743895 (  0) 0)
|
| [16] |
MARGOT X, PAYRI R, GIL A, et al. Combined CFD-phenomenological approach to the analysis of diesel sprays under non-evaporative conditions[J]. SAE Paper 2008-01-0962, Spain: SAE, 2008. https://www.researchgate.net/publication/286188215_Combined_CFD-Phenomenological_Approach_to_the_Analysis_of_Diesel_Sprays_under_Non-Evaporative_Conditions
(  0) 0)
|
| [17] |
WAIDMANN W, BOEMER A, BRAUN M. Adjustment and verification of model parameters for diesel injection CFD simulation[J]. SAE Paper 2006-01-0241, SAE, 2006. https://www.researchgate.net/publication/289929675_Adjustment_and_Verification_of_Model_Parameters_for_Diesel_Injection_CFD_Simulation?_sg=NgSQlLlz-sMEemwozQkGlHIHUL2_BIkexsfelARi2O2iUvthVZVdT7JhdSCVGlo5ZMiHPmrZhxg-OnixycWe7w
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


