2. 中广核研究院有限公司, 深圳 广东 518000
2. China Nuclear Power Research Institute Co., Ltd., CGN, Shenzhen 518000, China
对压水堆堆芯开展计算流体动力学(CFD)计算,可获得详细的流动与传热数据,指导组件的设计与优化。传统研究通常只针对流体域进行CFD分析,并通过热流边界模拟燃料释热[1-3]。然而流体域与固体域(芯块、包壳)传热过程互为彼此提供传热边界,针对单域采用简单固定的边界条件不能正确预测流体与燃料的温度分布,无法提供最高温度准确的量值与位置。将流体域与固体域内的传输方程进行耦合求解,通过能量方程平衡流体和固体界面上热流的方法,称为流固共轭传热[4-5]。开展堆内流固共轭传热的CFD计算能够避免单域边界条件的失真。流固共轭传热是高保真预测温度与热流分布的方法[6]。但因固体域网格量的加入,数值计算量会明显增加。
此外,典型压水堆内存在超过两万个燃料栅元,各栅元包含燃料芯块、气隙、包壳和冷却剂,这些结构的横向尺寸处于微米级到毫米级范围。例如,大亚湾核电厂典型燃料栅元中芯块直径为8.19 mm、气隙厚85 μm、包壳厚0.57 mm[7]。流固共轭传热的CFD计算需对这些结构均进行建模仿真,这些结构中气隙尺寸虽然极小,却不能简化忽略。由于包壳与芯块间狭窄的缝隙壁面对惰性气体(氦气)会产生较大的黏性力,限制气体的流动以及对流换热过程,所以气隙的换热方式主要是导热。又由于气体导热能力极小,气隙热阻会产生较大的温差,影响栅元内的传热与温度分布,所以精细化CFD计算必须要考虑气隙的模拟。为描述气隙微米级厚度中的物理过程,CFD计算需在各栅元内均建立气隙几何域,在该薄层上划分多层网格,并开展物理建模与仿真,会显著增加仿真计算的难度与资源的占用。
为提升PWR堆芯精细化热工水力计算分析的精度与效率,本文开展了堆芯区域流固共轭传热高效CFD计算方案研究,为工程化PWR堆芯性能CFD预测提供技术基础。
1 气隙CFD计算优化方案反应堆热工水力分析的焦点是燃料区与冷却剂的温度分布。为减轻堆芯CFD计算建模的难度与计算负担,尝试不对微米级气隙建模,而采用等效思想将气隙等效为包壳的一部分,研究能够正确反映气隙对传热过程影响的方案,以有效提高建模效率,减少计算资源需求,降低计算时间。
1.1 气隙等效方案气隙等效方案首先要保证几何结构的等效,即建模中包壳的厚度等于实际包壳和气隙厚度之和。此外,为保证物理过程仿真计算前后的一致性,还需开展一系列的模型等效设计。
1.1.1 等效区的质量守恒原则为保证等效区内部的质量守恒性:
| $ \rho '{\rm{ \mathsf{ π} }}\frac{{\left( {d_{{\rm{co}}}^2 - d_{\rm{f}}^2} \right)}}{4} = {\rho _{\rm{g}}}{\rm{ \mathsf{ π} }}\frac{{\left( {d_{{\rm{ci}}}^2 - d_{\rm{f}}^2} \right)}}{4} + {\rho _{\rm{c}}}{\rm{ \mathsf{ π} }}\frac{{\left( {d_{{\rm{co}}}^2 - d_{{\rm{ci}}}^2} \right)}}{4} $ | (1) |
由式(1)推得等效区密度:
| $ \rho ' = \frac{{{\rho _{\rm{g}}}\left( {d_{{\rm{ci}}}^2 - d_{\rm{f}}^2} \right) + {\rho _{\rm{c}}}\left( {d_{{\rm{co}}}^2 - d_{{\rm{ci}}}^2} \right)}}{{\left( {d_{{\rm{co}}}^2 - d_{\rm{f}}^2} \right)}} $ | (2) |
式中:dco、dci、df分别为包壳外径、内径与芯块直径,m;ρc、ρg、ρ′分别为包壳、气隙、等效区密度,kg/m3。
1.1.2 等效区的能量守恒原则为保证等效区内部的能量守恒性:
| $ \begin{array}{*{20}{c}} {\rho 'c'\frac{{{\rm{ \mathsf{ π} }}\left( {d_{{\rm{co}}}^2 - d_{\rm{f}}^2} \right)}}{4} = {\rho _{\rm{c}}}{c_{\rm{c}}}\frac{{{\rm{ \mathsf{ π} }}\left( {d_{{\rm{co}}}^2 - d_{{\rm{ci}}}^2} \right)}}{4} + }\\ {{\rho _{\rm{g}}}{c_{\rm{g}}}\frac{{{\rm{ \mathsf{ π} }}\left( {d_{{\rm{ci}}}^2 - d_{\rm{f}}^2} \right)}}{4}} \end{array} $ | (3) |
由式(3)推得等效区的比热:
| $ c' = \frac{{{\rho _{\rm{c}}}{c_{\rm{c}}}\left( {d_{{\rm{co}}}^2 - d_{{\rm{ci}}}^2} \right) + {\rho _{\rm{g}}}{c_{\rm{g}}}\left( {d_{{\rm{ci}}}^2 - d_{\rm{f}}^2} \right)}}{{\rho '\left( {d_{{\rm{co}}}^2 - d_{\rm{f}}^2} \right)}} $ | (4) |
式中:cc、cg、c′分别为包壳、气隙、等效区热容,J/(kg·K)。
1.1.3 等效区的热扩散能力一致原则为保证传热特性等效前后的一致性,等效区的传热能力与蓄热能力应维持不变。传热能力与热阻有关,蓄热能力与ρVcp有关,而ρVcp因能量守恒原则已进行等效,所以只需保证等效区等效前后的热阻一致:
| $ \frac{1}{{2{\rm{ \mathsf{ π} }}\lambda '}}\ln \frac{{{d_{{\rm{co}}}}}}{{{d_{\rm{f}}}}} = \frac{1}{{2{\rm{ \mathsf{ π} }}{\lambda _{\rm{g}}}}}\ln \frac{{{d_{{\rm{ci}}}}}}{{{d_{\rm{f}}}}} + \frac{1}{{2{\rm{ \mathsf{ π} }}{\lambda _{\rm{c}}}}}\ln \frac{{{d_{{\rm{co}}}}}}{{{d_{{\rm{ci}}}}}} $ | (5) |
由式(5)可推得等效区的导热系数:
| $ \lambda ' = \left( {\ln \frac{{{d_{{\rm{co}}}}}}{{{d_{\rm{f}}}}}} \right)/\left( {\frac{1}{{{\lambda _{\rm{g}}}}}\ln \frac{{{d_{{\rm{ci}}}}}}{{{d_{\rm{f}}}}} + \frac{1}{{{\lambda _{\rm{c}}}}}\ln \frac{{{d_{{\rm{co}}}}}}{{{d_{{\rm{ci}}}}}}} \right) $ | (6) |
式中:λc、λg、λ′分别为包壳、气隙、等效区导热系数,W/(m·K)。
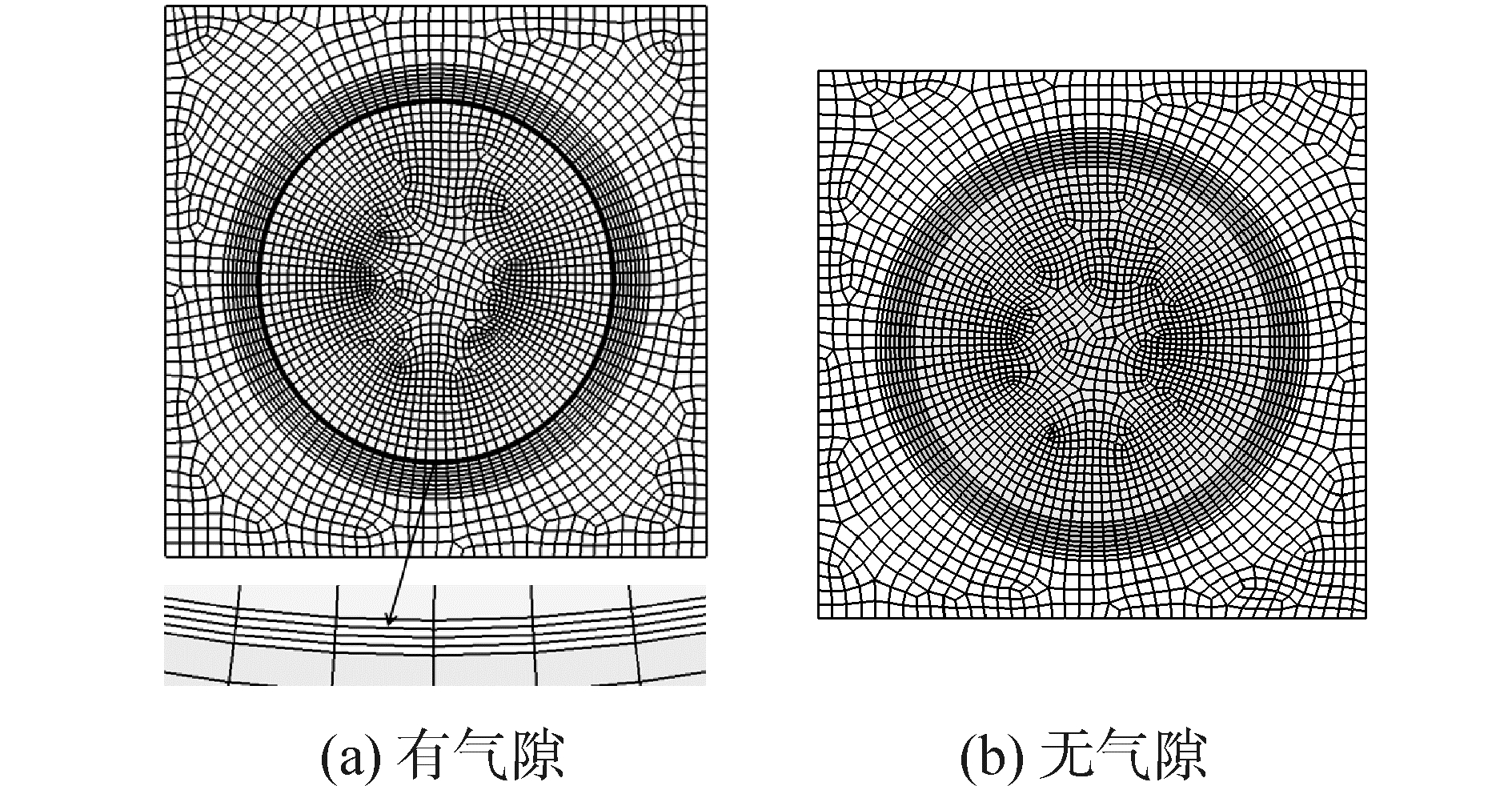
1.2 流固耦合仿真计算方案 1.2.1 研究对象由于堆内数万栅元结构与物理过程的一致性,选取典型单栅元进行仿真计算分析。研究对象为大亚湾核电厂的燃料栅元,其横向参数如图 1所示[7],轴向仿真长度为560 mm。针对该对象建立的网格方案如图 2所示,图 2(a)进行了气隙的几何建立与网格划分,图 2(b)进行气隙等效,省略了气隙层的几何与网格建立。

|
Download:
|
| 图 1 单燃料栅元结构示意图 Fig. 1 Structure of single fuel cell | |
|
Download:
|
| 图 2 有、无气隙的单栅元网格方案 Fig. 2 Mesh schemes with gas and no gas | |
冷却剂密度、比热、导热系数、黏性系数的变化通过IAPWS-IF97公式确定。
芯块密度取为95% UO2理论密度(10 431 kg/m3),导热系数:
| $ {\lambda _{{\rm{uo2}}}} = \frac{{3824}}{{402.55 + t}} + 4.788 \times {10^{ - 11}}{\left( {t + 273.15} \right)^3} $ | (7) |
比热计算[8]:
| $ {c_{{\rm{uo2}}}} = \left\{ \begin{array}{l} 304.38 + 2.51 \times {10^{ - 2}}t - 6 \times {10^6}/\\ \;\;\;\;{\left( {t + 273.15} \right)^2},\\ \;\;\;\;25{}^ \circ {\rm{C}} \le t \le 1226{}^ \circ {\rm{C}}\\ - 712.25 + 2.789t - 2.71 \times {10^{ - 3}}{t^2} + \\ \;\;\;\;\;1.12 \times {10^{ - 6}}{t^3} - 1.59 \times {10^{ - 10}}{t^4},\\ \;\;\;\;\;1~226{}^ \circ {\rm{C}} < t \le 2~800{}^ \circ {\rm{C}} \end{array} \right. $ | (8) |
式中:t为温度,℃;λuo2为芯块导热系数,W/(m·K);cuo2为芯块比热,J/(kg·K)。
气隙中气体为氦气,其密度根据理想气体状态方程P=ρRT计算,其中R=2 077 J/(kg·K)[9];氦气的定压比热随温度与压力的变化非常小,许多计算程序均假设其为恒值[9],按文献[10]取值为5 200 J/kg·K;导热系数计算[10]:
| $ {\lambda _{\rm{g}}} = 2.639 \times {10^{ - 3}}{\left( {t + 273.15} \right)^{0.7085}} $ | (9) |
包壳为锆4合金,其密度取为6 570 kg/m3[11],热导率的计算:
| $ \begin{array}{*{20}{c}} {{\lambda _{\rm{c}}} = 7.73 \times {{10}^{ - 2}} + 3.15 \times {{10}^{ - 4}}t - }\\ {2.87 \times {{10}^{ - 7}}{t^2} + 1.552 \times {{10}^{ - 10}}{t^3}} \end{array} $ | (10) |
比热计算式[12]:
| $ {c_{\rm{c}}} = \left\{ \begin{array}{l} 286.5 + 0.1t,0 < t < 750{}^ \circ {\rm{C}}\\ 360,\;\;t > 750{}^ \circ {\rm{C}} \end{array} \right. $ | (11) |
此外,反应堆运行中,随燃耗的加深、辐照的作用、裂变产物的产生与积累、结构的变化,燃料芯块、气隙、包壳的物理状态与物性状态会受到影响。这些影响可通过对各成分的密度、比热、导热系数计算公式增加修正系数来反映,其中修正系数需通过理论研究或实验测量来获得。
1.2.3 程序实现通过ANSYS15.0 Fluent的UDF宏按式(2)、(4)、(6)~(11)编写芯块、气隙、包壳及等效区的物性程序,将程序编译后链接到Fluent的物性计算模块,在每次迭代中获得每个网格对应的温度等参量,并经物性程序计算而实时更新材料物性。
1.2.4 仿真计算边界及数值方案设置仿真计算中入口速度为2 m/s,出口相对压力0,燃料芯块的体积释热率为3.4×108 W/m3。采用RNG k-ε模型模拟湍流运动,近壁处理采用标准壁面函数,设置第一层网格高度,保证30<y+<60;对压力、动量、湍流动能与耗散率进行二阶离散;各项的收敛残差保证在1×10-6以下。
2 优化方案性能分析图 3为分别采用热流边界的纯流体域仿真与流固共轭传热仿真的热流周向分布情况,该分布位于研究对象入口下游500 mm处的包壳外表面。根据燃料芯块的体积释热率可知燃料包壳表面的平均热流密度为0.6 MW/m2,纯流体域仿真在燃料棒周向使用的均匀热流密度即为该值。而流固共轭传热仿真中,周向冷却剂流道大小不同(方形栅元中四个角区域的流道大于上、下、左、右四个边流道的面积),流速不同,进行流固传热耦合求解时,对流换热状况在周向会存在差异,进而产生热流的周向非均匀分布。根据图 3可知不考虑固体区传热,仅通过给定燃料元件表面的热流密度将会导致横向传热边界的失真。

|
Download:
|
| 图 3 表面热流密度的周向分布 Fig. 3 Heat flux along circumferential length | |
此外,根据表 1可知,采用热流边界不能反映燃料区的温度状态;忽略气隙的仿真会造成结果失真;气隙等效方案在燃料区与冷却剂区能够获得与无简化流固共轭传热仿真计算相同精度级别的结果,精度的最大误差为0.1%。
| 表 1 仿真精度分析 Tab.1 Analysis on the accuracy of simulation K |
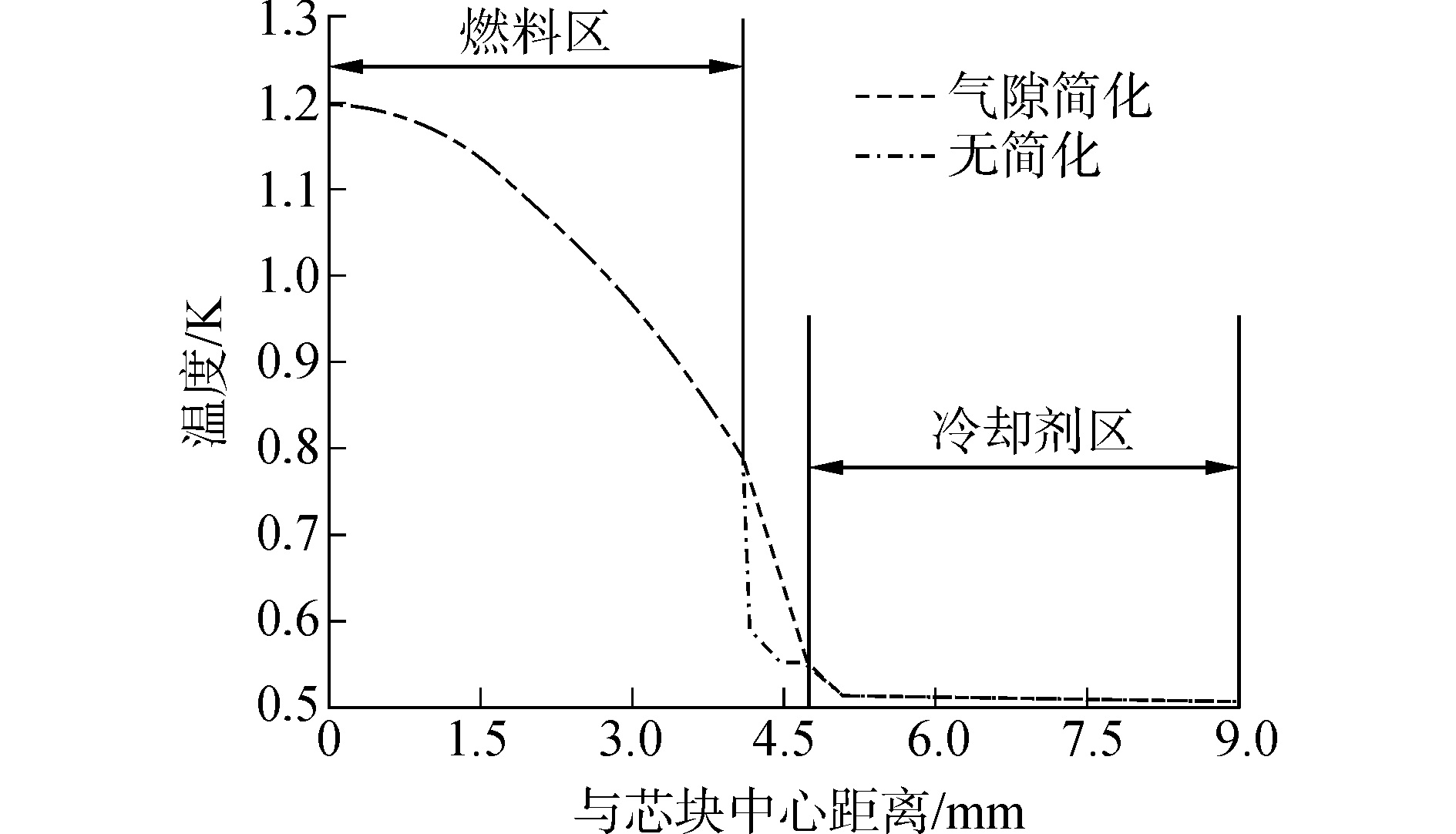
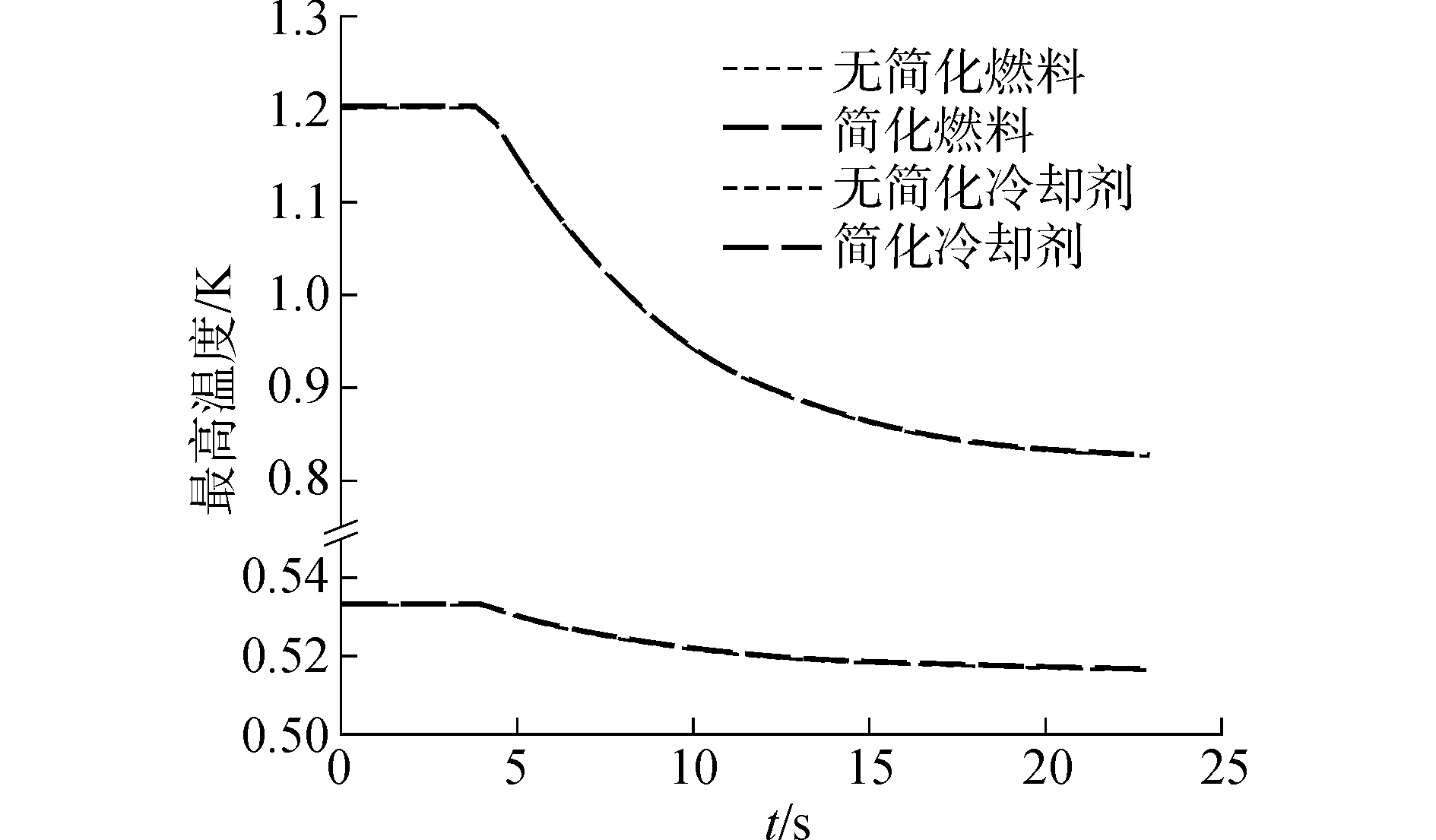
图 4为稳态工况下入口下游500 mm横截面上线性路径上的温度分布,该线性路径为燃料中心与栅元第一象限方形顶点间的连线;图 5为功率密度阶跃减半后瞬态工况下的燃料区与冷却剂区最高温度变化过程。通过这些算例可以发现,稳态与瞬态工况下,气隙等效方案均能合理地反映燃料与冷却剂的温度状态。
|
Download:
|
| 图 4 稳态工况温度分布分析 Fig. 4 Temperature at steady condition | |
|
Download:
|
| 图 5 瞬态工况下温度分析 Fig. 5 Maximum temperature at transient condition | |
表 2为包壳与气隙区采用不同方案的计算效率与资源占用情况。可知气隙等效方案因网格量需求更少能够节省更多硬件存储资源;而气隙层至少需要两层的网格划分,与采用这种网格方案的仿真对比,气隙等效方案仍具有效率优势,对存储资源的最小优化量为24.7%,效率的最小优化量为14.3%。
| 表 2 仿真效率分析 Tab.2 Analysis on the simulation efficiency |
当仿真对象的栅元数增加,尤其是针对典型组件(栅元数大于200)或者全堆芯仿真(栅元数大于2万),气隙等效方案在计算资源与效率上的优势将显著扩大。
3 结论1) 研究实现了流固共轭传热的CFD计算,并研究了流固共轭传热计算方案与纯流体域计算方案的差异,证明前者的优势在于准确预测PWR燃料栅元周向的非均匀传热特性。
2) 通过研究几何、质能守恒、传热过程的等效原则,设计气隙等效方案,编写变物性计算程序,实现了气隙等效方案在流固共轭传热CFD计算中的成功应用。解决了PWR堆芯CFD分析中微米级厚气隙的几何建立、网格划分、数值计算所引起的效率问题。
3) 经稳态与瞬态工况下冷却剂与燃料区的热工性能分析,证明了流固共轭等效计算方案与非等效方案精度相同,但能够至少节省近1/4的硬件存储资源,至少提高14.3%计算效率。
本研究可为PWR堆芯精细化CFD分析的工程化应用提供一定的技术基础。
| [1] |
YAN B H, YU L. URANS simulation of the turbulent flow in a tight lattice:effect of the pitch to diameter ratio[J]. Progress in nuclear energy, 2011, 53(4): 428-437. DOI:10.1016/j.pnucene.2011.02.009 (  0) 0)
|
| [2] |
TSENG Y S, FERNG Y M, LIN C H. Investigating flow and heat transfer characteristics in a fuel bundle with split-vane pair grids by CFD methodology[J]. Annals of nuclear energy, 2014, 64: 93-99. DOI:10.1016/j.anucene.2013.09.037 (  0) 0)
|
| [3] |
ZHU Xiaojing, MOROOKA S, OKA Y. Numerical investigation of grid spacer effect on heat transfer of supercritical water flows in a tight rod bundle[J]. International journal of thermal sciences, 2014, 76: 245-257. DOI:10.1016/j.ijthermalsci.2013.10.003 (  0) 0)
|
| [4] |
毕树茂, 刘昌文. 矩形通道的流固耦合传热模拟[J]. 核动力工程, 2012, 33(2): 78-82, 103. BI Shumao, LIU Changwen. Simulation of fluid-solid conjugate heat transfer in rectangular channels[J]. Nuclear power engineering, 2012, 33(2): 78-82, 103. (  0) 0)
|
| [5] |
徐建军, 陈炳德, 王小军. 矩形窄缝通道流固共轭传热数值分析[J]. 原子能科学技术, 2009, 43(3): 224-229. XU Jianjun, CHEN Bingde, WANG Xiaojun. Numerical analysis of conjugate heat transfer for liquid-solid in narrow rectangular channel[J]. Atomic energy science and technology, 2009, 43(3): 224-229. (  0) 0)
|
| [6] |
DUCHAINE F, JAURÉ S, POITOU D, et al. Analysis of high performance conjugate heat transfer with the OpenPALM coupler[J]. Computational science & discovery, 2015, 8(1): 015003. (  0) 0)
|
| [7] |
朱继洲, 单建强, 张斌. 压水堆核电厂的运行[M]. 2版. 北京: 原子能出版社, 2008: 17. ZHU Jizhou, SHAN Jianqiang, ZHANG Bin. The operation of PWR nuclear plant[M]. 2nd ed. Beijing: Atomic Energy Press, 2008: 17. (  0) 0)
|
| [8] |
郝老迷. 核反应堆热工水力学[M]. 北京: 原子能出版社, 2010: 4. HAO Laomi. Nuclear reactor thermal hydraulics[M]. Beijing: Atomic Energy Press, 2010: 4. (  0) 0)
|
| [9] |
任啟森, 杨小勇, 黄志勇, 等. 氦气热物性质计算方法比较分析[C]//中国工程热物理学会第十一届年会论文集工程热力学与能源利用(下册). 北京, 2006: 721-728. REN Qisen, YANG Xiaoyong, HUANG Zhiyong, et al. Comparison and analysis on the properties of the thermal properties of helium[C]//The Eleventh Annual Meeting of Chinese Society of Engineering Thermophysics. Beijing, 2006: 721-728. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=6021064 (  0) 0)
|
| [10] |
俞冀阳, 王松涛, 张向宇, 等. 燃料棒内氦气压力无损检测的数值模拟[J]. 核科学与工程, 2007, 27(3): 193-197. YU Jiyang, WANG Songtao, ZHANG Xiangyu, et al. Numerical simulation on scatheless measurement of helium pressure in fuel rod[J]. Chinese journal of nuclear science and engineering, 2007, 27(3): 193-197. (  0) 0)
|
| [11] |
张学学, 李桂馥, 史琳. 热工基础[M]. 2版. 北京: 高等教育出版社, 2006: 390. ZHANG Xuexue, LI Guifu, SHI Lin. Fundamental thermo-technology[M]. 2nd ed. Beijing: Higher Education Press, 2006: 390. (  0) 0)
|
| [12] |
俞冀阳, 贾宝山. 反应堆热工水力学[M]. 北京: 清华大学出版社, 2003: 33. YU Jiyang, JIA Baoshan. Thermal hydraulic of reactor[M]. Beijing: Tsinghua University Press, 2003: 33. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


