泵喷水推进器是由桨叶(叶轮)、导叶和导管等部件组合而成的高性能推进装置,叶轮是泵喷水推进器做功部件,很大程度上决定了推进器水动力性能;导叶为一组与来流成一定角度的固定叶片,其轴向位置可位于叶轮前或后,相应地能够使叶轮入流产生预旋,或者是能够回收叶轮出流的旋转能量,从而提高装置的推进效率;导管通常是流动性能较好的机翼型结构,其包围着叶轮和导叶,并分割出叶轮的内外流场,可以回收一定的叶轮叶稍径向环流和屏蔽泵喷内水动力辐射噪声。减速型导管可以通过减速增压提高叶轮的抗空化性能。因此,泵喷水推进器叶轮、导叶和导管三者合理配合,使得其具有低噪声、抗空化和高效率的优点[1],另外,泵喷水推进器还可以通过增加叶轮叶片数(降低叶片单位面积的推力负载)和侧斜(降低不均匀来流中的不稳定负载),来进一步推迟空化和降低辐射噪声[2]。
泵喷水推进器在国外高性能鱼雷和潜艇推进中已存在广泛应用,美国MK48/MK50鱼雷、英国Spearfish鱼雷、瑞典TP2000鱼雷、欧洲MU90鱼雷、美国Seawolf/Virginia级潜艇、英国Astute/Vanguard/Trafalgar级潜艇以及俄罗斯Borei级潜艇均采用泵喷水推进方式。但是,出于技术保密原因,国外极少有公开泵喷总体选型和设计文献发表,已发表的文献基本上都集中在试验研究和仿真计算方法上。美国在1986-1988年的国防报告(AD报告[3-5])中介绍了泵喷水推进器准三元设计方法的研究,但该方法很难满足在恶劣的进流条件下,泵喷高效、抗空化、低噪声的设计要求,采用更接近推进器内部流动规律的三元设计方法是泵喷设计的必然趋势。近几年,多家单位[6-10]陆续开展了泵喷水推进器的设计和试验研究,并取得了一定的进展。
本文主要针对泵喷水推进器的总体选型与设计方法开展相应的探索研究,并结合具有公开数据MK48鱼雷完成泵喷推进器选型和设计方法有效性的演示验证。
1 泵喷水推进总体选型方法 1.1 泵喷推进基本理论已知条件有:雷体阻力特性曲线R=F(V),主机额定功率PD和额定转速n。根据理想推进器理论可以求得推进器的推力T、扬程H和效率ηj为[11]
| $ T = \rho Q\left( {{V_j} - {V_s}} \right) $ | (1) |
| $ H = \frac{1}{{2g}}\left( {V_j^2 - V_s^2} \right) $ | (2) |
| $ {\eta _j} = \frac{{{P_T}}}{{{P_E}}} = \frac{{\rho Q\left( {{V_j} - {V_s}} \right){V_s}}}{{\frac{1}{2}\rho Q\left( {V_j^2 - V_s^2} \right)}} = \frac{{2{V_s}}}{{{V_j} + {V_s}}} $ | (3) |
式中:Vs表示泵未被扰动的进口速度,Vj表示泵出口的速度,Q表示泵的流量,PT表示泵的有效推力功率,PE推进器有效功率。
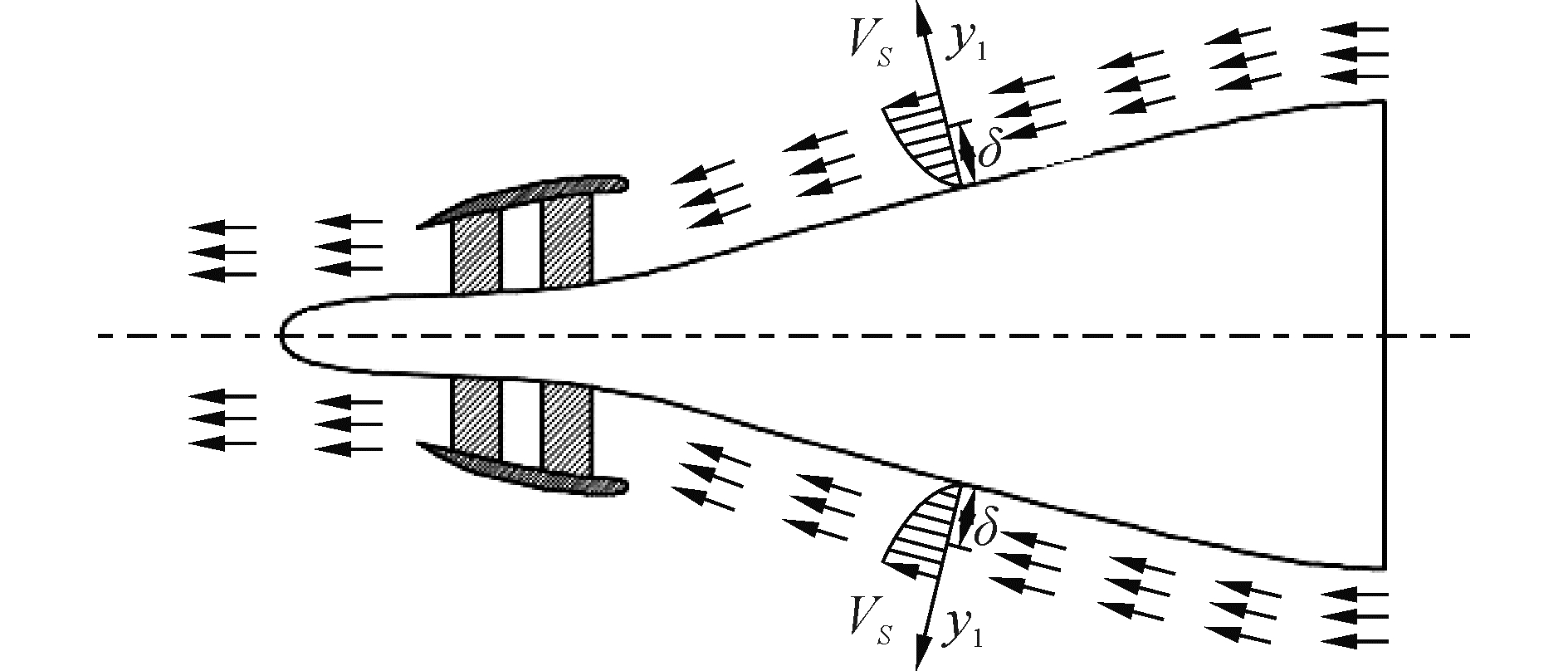
实际的水下航行体泵喷水推进器工作于航行体的伴流场中,安装于航行体尾部的泵喷进流会吸入部分边界层水流(如图 1)。由于边界层内水流速度低于边界层外的流速,使推进器进流速度小于航速Vs。设边界层对推进器进流的动量影响系数为α,动能影响系数为β[12],A1为进流面积,则进流面的流量、动量和动能分别如下
| $ Q = \iint_{{A_i}} {{V_z}{\text{d}}{A_i}} $ | (4) |
| $ \alpha \rho Q{V_s} = \rho \iint_{{A_i}} {V_z^2{\text{d}}{A_i}} $ | (5) |
| $ \beta \frac{1}{2}\rho QV_z^2 = \frac{1}{2}\rho \iint_{{A_i}} {V_z^3{\text{d}}{A_i}} $ | (6) |
|
Download:
|
| 图 1 泵喷推进器进流速度分布 Fig. 1 Velocity distribution of pumpjet inlet | |
由式(4)~(6)可以得到:
| $ \alpha = \frac{1}{{{V_s}}}\frac{{\iint_{{A_i}} {V_z^2{\text{d}}{A_i}}}}{{{V_s}\iint_{{A_i}} {{V_z}{\text{d}}{A_i}}}},\beta = \frac{1}{{V_s^2}}\frac{{\iint_{{A_i}} {V_z^3{\text{d}}{A_i}}}}{{V_s^2\iint_{{A_i}} {{V_z}{\text{d}}{A_i}}}} $ |
式中:Vz为进流截面处不同径向位置速度,Ai为进流面积。考虑航行体边界层影响后,泵喷水推进器推力T、扬程H和效率ηj变化为
| $ T = \rho Q\left( {{V_j} - \alpha {V_s}} \right) $ | (7) |
| $ H = \frac{{V_j^2}}{{2g}} - \beta \frac{{V_s^2}}{{2g}} $ | (8) |
| $ {P_E} = \frac{1}{2}\rho Q\left[ {V_j^2 - \beta V_s^2} \right] $ | (9) |
其中,喷速比μ=Vj/Vs,因此,泵喷的喷射效率为
| $ {\eta _j} = \frac{{\rho Q\left( {{V_j} - \alpha {V_s}} \right){V_s}}}{{\frac{1}{2}\rho Q\left( {V_j^2 - \beta V_s^2} \right)}} = \frac{{2\left( {\mu - \alpha } \right)}}{{{\mu ^2} - \beta }} $ | (10) |
1) 按照效率最优原则确定最佳喷速比。
对式(10)求导,求出效率最高时的最佳喷速比μopt为
| $ {\mu _{{\rm{opt}}}} = \alpha + \sqrt {{\alpha ^2} - \beta } $ | (11) |
2) 由主机额定功率计算推进航速Vmax。
根据能量传递,泵喷的输出功率为
| $ {P_T} = {P_D}{\eta _m}{\eta _p}{\eta _j} $ | (12) |
式中:ηm为轴系传动系统机械效率,ηp为泵效率。
由于受泵喷水推进器与航行体相互作用的影响,安装泵喷水推进器后航行体阻力不同于裸航行体阻力,工程上常将这一变化以推力减额的方式来描述,则考虑推力减额后泵喷水推进器推力作用下航行体动力学方程为
| $ \frac{{{P_T}}}{{{V_{\max }}}}\left( {1 - t} \right) - R = {m_b}a $ | (13) |
式中:t为推力减额,该值随航速而变化;R为裸航行体阻力,其是航速的函数;mb为航行体及附连水质量;a为船体运动加速度。船体航速稳定后,阻力与推力相平衡,此时可将式(13)简化求取航速Vmax:
| $ {V_{\max }} = \frac{{{P_T}\left( {1 - t} \right)}}{R} = \frac{{{P_D}{\eta _m}{\eta _p}{\eta _j}\left( {1 - t} \right)}}{R} $ | (14) |
进而,可以得到喷水推进泵轴向推力为
| $ T = \frac{{{P_T}}}{{{V_{\max }}}} = \frac{{{P_D}{\eta _m}{\eta _p}{\eta _j}}}{{{V_{\max }}}} $ | (15) |
3) 泵喷推进器的扬程H和流量Q。
由喷速比定义可知,Vj=μVs,代入式(8)求得泵扬程为
| $ H = \left[ {{\mu ^2} - \beta } \right]\frac{{V_s^2}}{{2g}} $ | (16) |
则泵喷的体积流量为
| $ Q = \frac{{{P_E}}}{{\rho gH}} = \frac{{{P_D}{\eta _m}{\eta _p}}}{{\rho gH}} $ | (17) |
喷口直径为
| $ {D_j} = \sqrt {\frac{{4Q}}{{{\rm{ \mathsf{ π} }}{V_j}}}} $ | (18) |
4) 确定泵喷的比转速Ns和汽蚀比转速C。
将转速n、流量Q和扬程H三个参数统一起来可以得到一个无量纲量即比转速Ns,其是根据流体力学的相似理论运用得到的一个技术参数,可以反映水泵的基本特性,例如,比转速Ns>500的泵通常为轴流泵,Ns<300的泵通常为离心泵,泵喷推进器在结构和性能特点上应属于高比转速轴流泵。比转速为
| $ {N_s} = \frac{{3.65n{Q^{1/2}}}}{{{H^{3/4}}}} $ | (19) |
通常用汽蚀比转速为标准来粗略地划分泵喷水推进器的工作范围,以便工程人员参考。但是,汽蚀比转速限制值是一个相对值,对于不同喷水推进器,由于其设计水平的差异,该值会有所不同。John Allison[13]指出对于一般的喷水推进泵,持续工作限制线对应的汽蚀比转速约为10 000(美国单位制),空化限制线为11 000,推力崩溃限制线为12 000。而KaMeWa公司的喷水推进器的持续工作限制线对应的汽蚀比转速约为12 000,空化限制线约为13 400。国内有关喷水推进器空化限制线的划分可以参考文献[14],文中指出喷泵持续工作限制线对应的汽蚀比转速约为1 300(国内单位制),空化限制线为1 400,推力崩溃限制线为1 600。
1.3 MK48鱼雷泵喷选型该鱼雷长5.85 m,直径533 mm,最高航速55 kn,采用500马力动力。根据已公开的MK48雷体截面数据,使用CAD软件UG完成MK48鱼雷雷体建模,如图 2所示。

|
Download:
|
| 图 2 MK48雷体几何模型 Fig. 2 Geometry of MK48 torpedo | |
裸雷体阻力的数值计算和理论预估精度已达到工程许可精度,本文采用数值计算手段与实际工程经常使用的经验公式相结合的方法完成雷体阻力的计算。图 3显示了整个MK48裸雷体阻力数值计算域,其中L为鱼雷长度,数值计算主要完成不同航速下雷体阻力计算,所以采用一致的速度进口和压力出口边界条件。采用六面体结构化网格对整个计算域进行网格划分,雷体表面网格及周围加密网格分布如图 4所示。

|
Download:
|
| 图 3 MK48雷体计算域及数值计算边界条件 Fig. 3 Computational domain and boundary conditions of the MK48 torpedo | |

|
Download:
|
| 图 4 MK48雷体计算模型网格分布 Fig. 4 Mesh distribution of MK48 torpedo CFD model | |
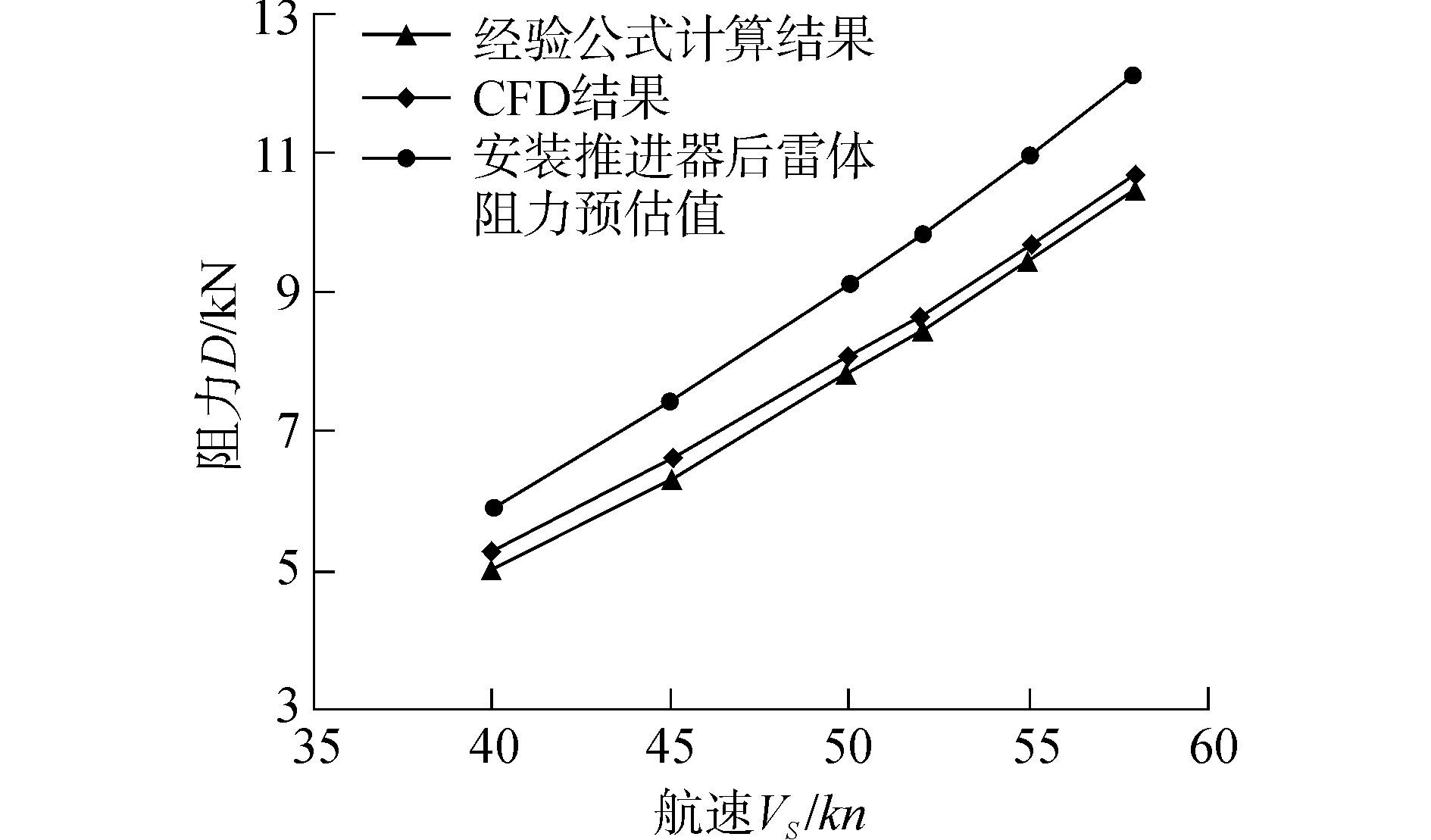
基于雷诺时均方法和SST湍流模型,对40~58 kn航速下MK48雷体周围粘性流场进行计算求解,计算得到如图 5中CFD计算结果。采用了实际工程经常使用的经验公式对该雷体阻力进行了预估[15],计算结果如图 5中的经验公式计算结果,可以看出,CFD计算结果和经验公式预估值一致,在50 kn设计航速下误差为3.4%,在整个计算航速下数值误差在4.6%以内。另外,实际MK48鱼雷安装推进器后将存在鳍舵等附体,以及由于推进器在雷艉工作引起雷体的附加阻力,本文近似采用15%裸雷体阻力作为附体及附加阻力,因此考虑安装推进器后MK48雷体阻力预估值如图 5所示。
|
Download:
|
| 图 5 MK48雷体阻力计算结果 Fig. 5 Numerical simulation of MK48 torpedo drag | |
在开展MK48鱼雷泵喷总体参数选型前还需要做一些假定和估算:1)泵效率ηp:按照结构形式和性能特点,泵喷水推进器采用的是轴流泵,按照作者设计经验ηp取为0.90;2)轴系传动系统机械效率ηm,按照工程经验取为0.99。总体选型需要确定的泵喷主要参数有:流量Q,扬程H,泵进口直径Di,喷口直径Dj。根据前面计算得到的MK48鱼雷全附体雷体阻力特性曲线、已知的主机功率500马力、设计航速50 kn等输入条件,按照前面介绍的泵喷选型步骤对MK48鱼雷所需要的泵喷水推进器主要参数进行选取,得到最高航速和主机允许功率下泵喷推进器转速2 200 r/min,流量1.4 m3/s,扬程23.5 m,进口直径0.345 m,喷口直径为0.22 m。
2 泵喷水推进器的设计与分析 2.1 泵喷水推进器的设计泵喷水推进器由导管、叶轮和导叶构成的组合式推进器,叶轮是整个推进器的水动力做功部件,其要拥有较高的水动力效率才能保证整个系统的高效。并且泵喷推进器为了产生尽可能大的推力,要求喷口出流速度均匀、沿轴向,这也对导叶的设计提出了更高的整流要求。另外,泵喷水推进器的抗空化能力也是水动力设计的要点,实际的泵喷水推进器工作在航行体的不均匀流场中,来流的不均匀并且存在涡旋,使得泵喷水推进器很容易工作在空化的状况下。因此,在恶劣的进流条件下,传统设计方法很难满足泵喷水推进器高效、抗空化的设计要求,采用考虑泵喷叶片轴向、周向和径向三个方向流动规律的三元设计方法,是完成高性能泵喷水推进器的必然选择。本文采用三元设计方法完成叶轮和导叶叶片的反问题设计,并与泵喷水推进器正问题的CFD计算相互迭代,来考虑粘性作用的影响以及进行相应的优化设计。
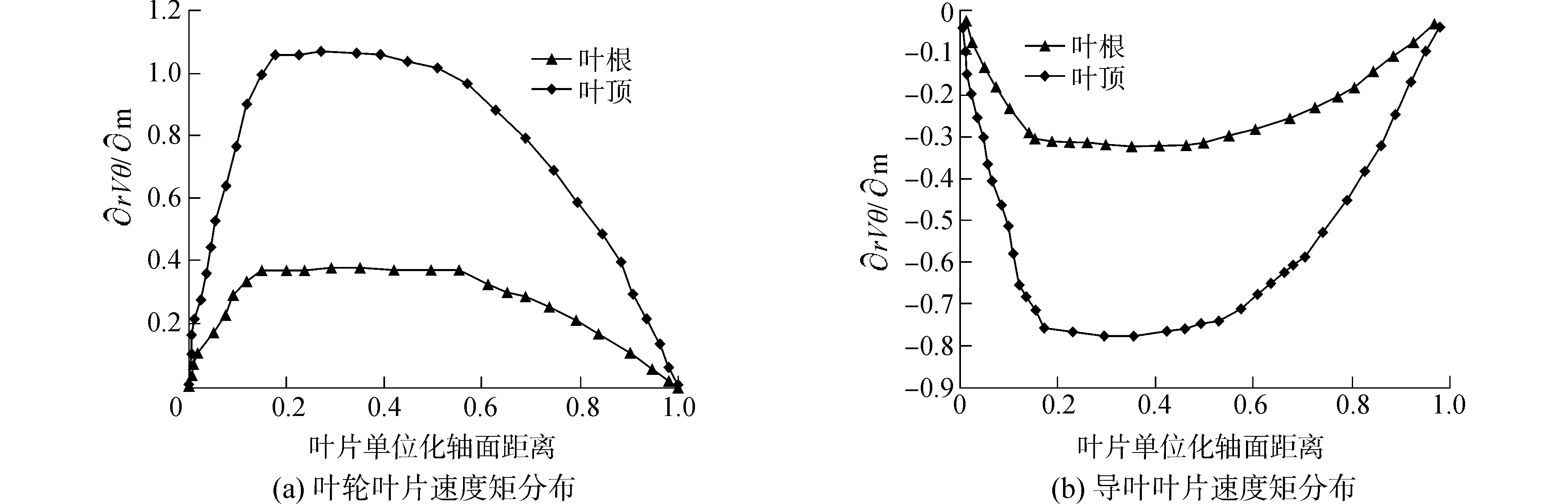
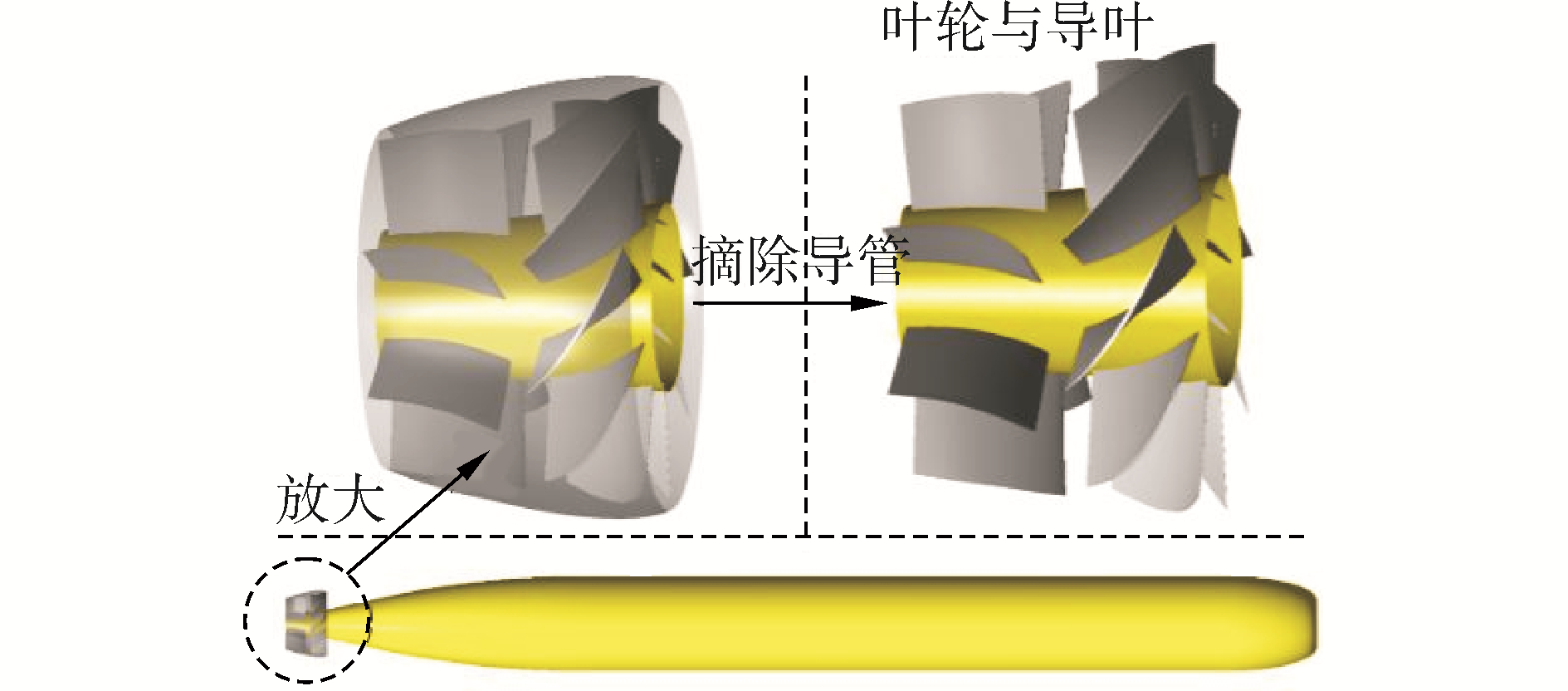
关于泵喷水推进器叶片的三元设计方法在文献[16]中已进行了详细阐述,本文不再赘述。根据已知扬程确定叶轮叶片进出口速度矩数值,在给定叶轮叶片不同截面速度矩沿轴面流线的分布规律的条件下,采用泵三元设计方法完成叶轮叶片外型设计。并且,为保证流动的流畅性,导叶的设计须与叶轮相匹配,以及为产生尽可能大的轴向力,导叶出口环量理论上应接近为零。采用了文献[17]推荐的叶轮和导叶叶片速度矩分布规律,如图 6所示。给定叶片在叶根、叶顶截面的速度矩分布后,通过线性插值的方法求得整个叶片轴面的环量分布,进而可以采用泵喷水推进器三元设计方法绘制叶片中心面形状,设计得到泵喷最终的几何如图 7所示。
|
Download:
|
| 图 6 叶轮和导叶叶片速度矩分布 Fig. 6 Blade loading distribution of the rotor and stator | |
|
Download:
|
| 图 7 MK48鱼雷泵喷设计结果 Fig. 7 Design result of the MK48 torpedo pumpjet | |
随着计算流体力学的不断完善以及计算机技术的提高,数值试验逐步成为泵喷水推进器研究中与模型试验并驾齐驱、相互补充的重要方法。本文借助CFD方法完成新设计泵喷水推进器的性能计算和分析,数值计算域和边界条件设置与雷体阻力数值计算模型相同(如图 2所示),基于雷诺时均方法和SST湍流模型完成泵喷推进器粘性流场的数值计算,采用全结构化六面体网格对流场计算域进行网格划分(如图 8所示),泵喷全通道网格节点数约320万,整个计算域网格节点数为905万,采用滑移网格处理叶轮和导叶动静交界面。

|
Download:
|
| 图 8 MK48鱼雷泵喷计算模型网格分布 Fig. 8 Mesh distribution of pumpjet+torpedo | |
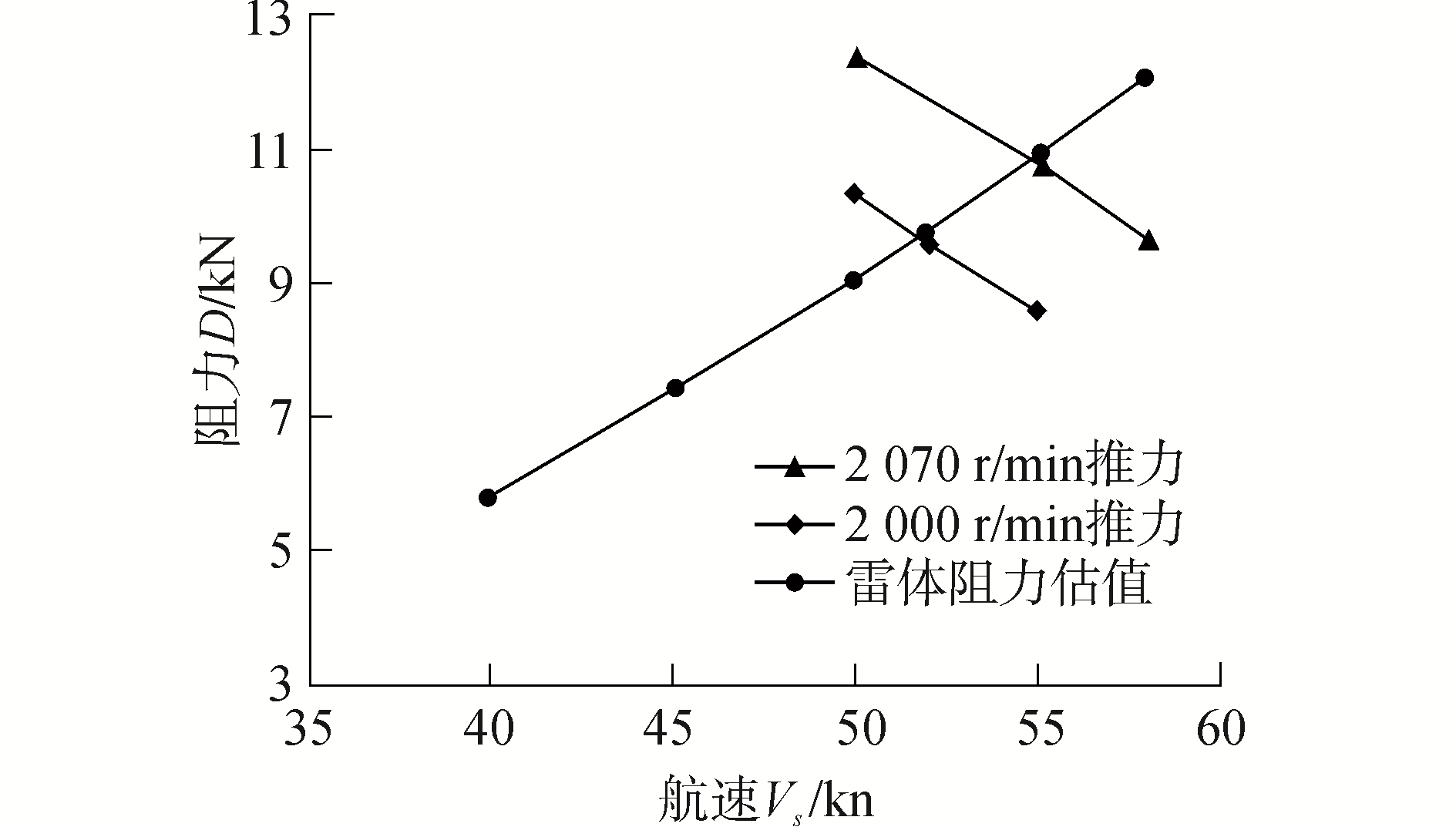
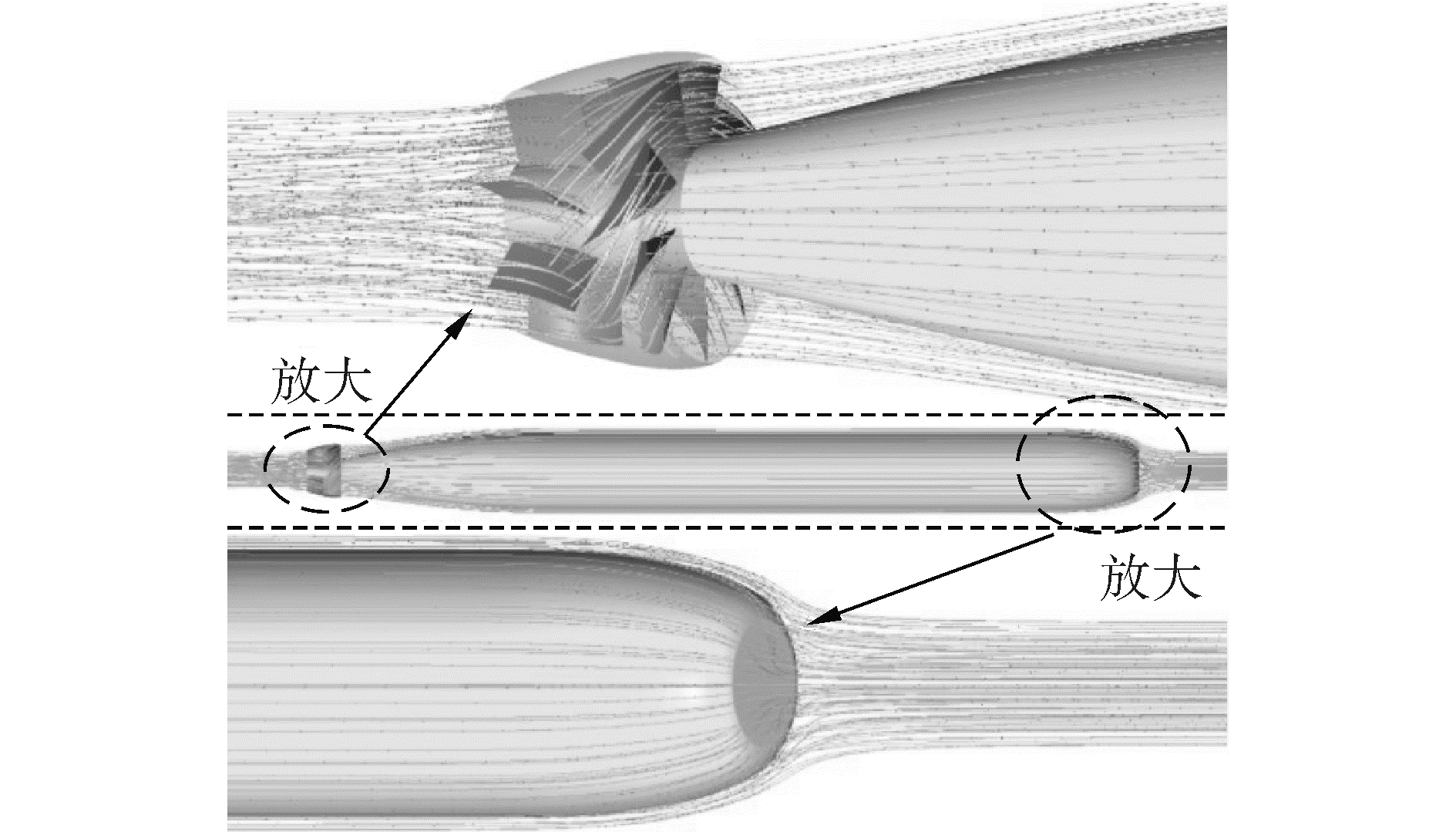
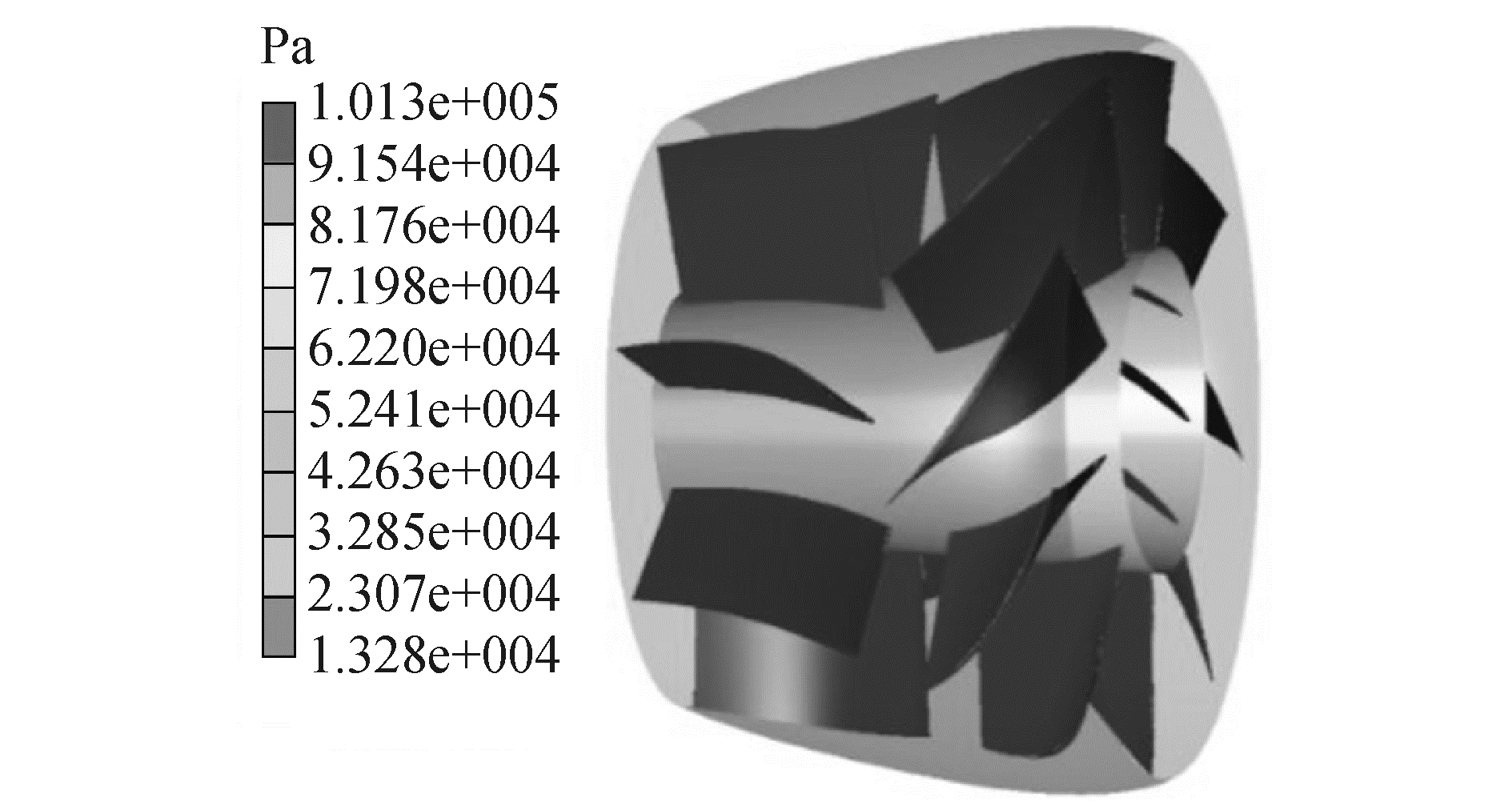
对转速为2 000和2 070 r/min时泵喷的推进航速进行了数值预报,将不同航速下计算得到的泵喷所能提供的净推力曲线和全附体雷体阻力曲线叠加,通过两曲线的交点来预报鱼雷航速,计算结果如图 9所示。在转速2 000 r/min工况下,鱼雷泵喷推进航速为52 kn,此时泵喷效率达到了90.3%,当转速提升到2 070 r/min时,主机功率367.2 kW,基本达到最大功率,此时推进航速达到了55 kn最大航速的设计要求。图 10显示了航速55 kn时泵喷内部流线图,图 11显示了此时叶片表面压力分布,可以看出泵喷内部流动通畅,喷口出流平整,叶片表面无低于空化压力区域(叶片表面压力均高于9 154 Pa,在汽化压力3 169 Pa之上)。
|
Download:
|
| 图 9 泵喷水推进器快速性预报 Fig. 9 Torpedo speed evaluation | |
|
Download:
|
| 图 10 雷尾泵喷内部流线分布 Fig. 10 Streamline in the pumpjet after torpedo | |
|
Download:
|
| 图 11 泵喷叶片表面压力分布 Fig. 11 Pressure distribution on the pumjet blades | |
1) 水下航行体泵喷推进器选型和设计方法结合MK48鱼雷泵喷的泵效率超过了90%,在相同的轴功率条件下估算其推进航速与国外水平相当,间接验证了方法的合理性。
2) 该方法可为水下航行体推进所用泵喷推进器的总体参数选型和水动力设计提供一定参考。
该方法主要针对泵喷效率和空化性能进行优化设计,噪声控制仅通过桨叶无空化设计方式来间接体现,下一步可以全面和深入的开展泵喷推进器低噪声设计技术研究。
| [1] |
靳栓宝. 鱼雷推进用喷水推进器的设计与性能分析[D]. 武汉: 海军工程大学, 2009. JIN Shuanbao. Design and performance analysis of waterjet of torpedo[D]. Wuhan: Naval University of Engineering, 2009. (  0) 0)
|
| [2] |
靳栓宝. 高性能喷水推进器和泵喷推进器的设计与性能分析[D]. 武汉: 海军工程大学, 2013. JIN Shuanbao. Design and analysis of high performance waterjet and pumje[D]. Wuhan: Naval University of Engineering, 2013. (  0) 0)
|
| [3] |
JIN Shuanbao. Design and analysis of high performance waterjet and pumpjet[D]. Wuhan: Naval University of Engineering, 2013.
(  0) 0)
|
| [4] |
FURUYA O, CHIANG W L. A new pumpjet design theory. TC-3037[R]. California, USA: Armed Services Technical Information Agency, 1986.
(  0) 0)
|
| [5] |
FURUYA O, CHIANG W L. A new pumpjet design theory[R]. California, USA: Armed Services Technical Information Agency, 1987. http://www.researchgate.net/publication/235036504_A_New_Pumpjet_Design_Theory
(  0) 0)
|
| [6] |
FURUYA O, CHIANG W L. A new pumpjet design theory[R]. Bethesda, MD: Armed Services Technical Information Agency, USA, 1988.
(  0) 0)
|
| [7] |
刘敏, 张宁, 李新汶, 等. 泵喷推进器导管对噪声传播特性的影响[J]. 舰船科学技术, 2011, 33(8): 20-23. LIU Min, ZHANG Ning, LI Xinwen, et al. Studies of the effects of pump-jet propeller duct on noise propagation characteristic[J]. Shipscience and techndogy, 2011, 33(8): 20-23. (  0) 0)
|
| [8] |
LIU Min, ZHANG Ning, LI Xinwen, et al. Studies of the effects of pump-jet propeller duct on noise propagation characteristic[J]. Ship science and technology, 2011, 33(8): 20-23. (  0) 0)
|
| [9] |
沈泓萃, 杨仁友, 姚惠之. 组合式推进器干扰特性敞水试验评估分析新方法研究[J]. 船舶力学, 2007, 11(2): 159-170. SHEN Hongcui, YANG Renyou, YAO Huizhi. A new experiment and assessment method for the open water performance and component interaction of integrated propulsor[J]. Journal of ship mechanics, 2007, 11(2): 159-170. (  0) 0)
|
| [10] |
饶志强. 泵喷推进器水动力性能数值模拟[D]. 上海: 上海交通大学, 2012. RAO Zhiqiang. Numerical simulation of hydrodynamical performance of pump jet propulsor[D]. Shanghai: Shanghai Jiao Tong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10248-1012017813.htm (  0) 0)
|
| [11] |
刘业宝. 水下航行器泵喷推进器设计方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. LIU Yebao. Study on design method of pump jet thruster for underwater vehicles[D]. Harbin: Harbin Engineering University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014134096.htm (  0) 0)
|
| [12] |
SHEN Yang, HU Pengfei, JIN Shuanbao, et al. Design of novel shaftless pump-jet propulsor for multi-purpose long-range and high-speed autonomous underwater vehicle[J]. IEEE transactions on magnetics, 2016, 52(7): 7403304. (  0) 0)
|
| [13] |
盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2004.
(  0) 0)
|
| [14] |
BULTEN N W H. Numerical analysis of a waterjet propulsion system[D]. Eindhoven: Technische Universiteit Eindhoven, 2006. https://www.researchgate.net/publication/242770605_Numerical_Analysis_of_a_Waterjet_Propulsion_System
(  0) 0)
|
| [15] |
ALLISON J. Marine waterjet propulsion[R]. New York, US: SNAME, 1993: 275-235.
(  0) 0)
|
| [16] |
王永生, 刘承江, 苏永生, 等. 舰船新型推进系统[M]. 北京: 国防工业出版社, 2014. WANG Yongsheng, LIU Chengjiang, SU Yongsheng, et al. Ship new propulsion system[M]. Beijing: National Defense Industry Press, 2014. (  0) 0)
|
| [17] |
黄景泉, 张宇文. 鱼雷流体力学[M]. 西安: 西北工业大学出版社, 1989. HUANG Jingquan, ZHANG Yuwen. Hydrodynamics of Torpedo[M]. Xi'an: Northwestern Polytechnical University Press, 1989. (  0) 0)
|
| [18] |
靳栓宝, 王永生, 丁江明, 等. 混流式喷水推进泵三元设计及数值试验[J]. 哈尔滨工程大学学报, 2012, 33(10): 1223-1227. JIN Shuanbao, WANG Yongsheng, DING Jiangming, et al. Three-dimensional design and numerical experiment of mixed-flow waterjet with CFD[J]. Journal of Harbin Engineering University, 2012, 33(10): 1223-1227. (  0) 0)
|
| [19] |
ZANGENEH M, GOTO A, HARADA H. On the design criteria for suppression of secondary flows in centrifugal and mixed flow impellers[J]. Journal of turbomachinery, 1998, 120(4): 723-735. DOI:10.1115/1.2841783 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


