水下目标探测是海洋开发、海防安全建设的重要技术。在浅海条件下,多径干扰严重影响目标探测的性能。使用自适应方法能有效抑制多径干扰。常用的自适应滤波算法有最小均方算法(least mean squares, LMS)及其改进算法、归一化最小均方算法(normalized least mean square, NLMS)和递归最小二乘算法(recursive least squares, RLS)等,其中LMS算法由于方法简单,实用性强,被广泛应用。传统的自适应滤波算法没有考虑多径干扰的稀疏特征, 普遍存在收敛性问题。
实际中的系统本身或其变换域大多具有稀疏性。浅海水声信道通常是典型的稀疏信道,利用信道多径干扰的稀疏性有利于降低自适应干扰抑制算法的计算量,促使了在自适应中引入信道的稀疏特性和对传统自适应算法的改进。金坚等[1]将与稀疏性有重要关联的l1范数引入LMS算法,对所有零系数和非零系数施加大小相同的零吸引力。GU等[2]将l0范数引入LMS算法,对零系数和非零系数施加不同权重的吸引力。研究表明使用l0范数是解决稀疏系统的最好方案。同时,一些改进的稀疏l0-LMS算法被相继提出[3-4]。但由于l1范数和l0范数的约束项本身并无调整因子,因此当信道稀疏程度下降时,该类算法的收敛性能也呈现较大的下降。
TAHERI等[5]将lp范数引入LMS算法(0 < p < 1),p取值越小越接近l0范数。FENG等[6]在文献[5]基础上,提出一种p值可变的lp-LMS算法,该算法依据根的相对偏差更新参数p,能更好的适应信道的稀疏程度,改善对信道稀疏程度的敏感性。但是lp-LMS算法复杂度较大,每次权系数更新过程均需要较大的计算消耗,给实际应用带来相当大的限制。WU等[7]提出采用简化的稀疏似p范数LMS算法,减小算法复杂度的同时,仍然保持较好的性能,但该算法仍然存在收敛速度较慢、失调误差较大的不足。本文在稀疏似p范数LMS算法中, 使用改进Sigmoid函数变化步长,同时采用与误差有关的函数值对零吸引项做出调整,得到一种变步长稀疏似p范数LMS算法,加快了自适应迭代的收敛速度,减小了稳态误差。
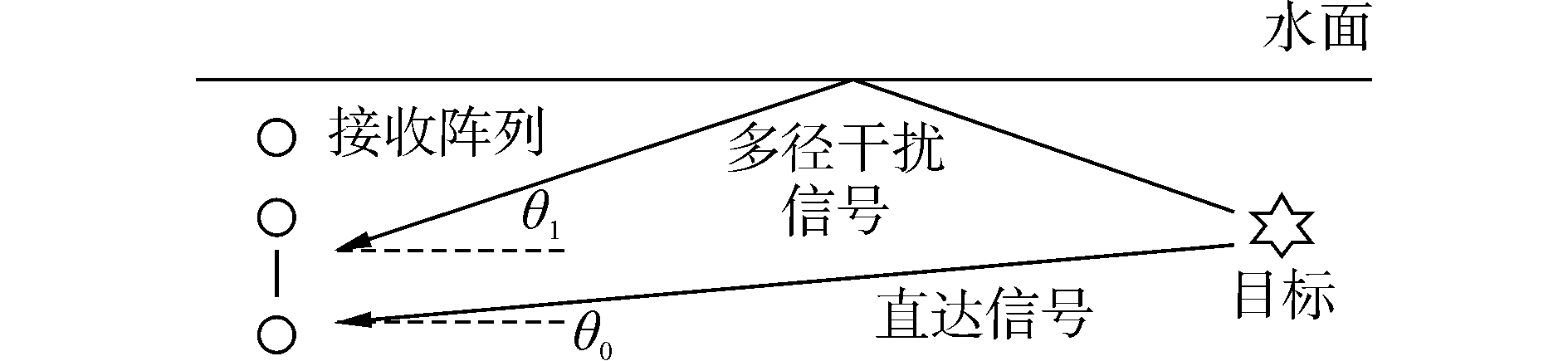
1 离散多径干扰的阵列信号处理模型声信号在实际的浅海环境传播时,由于水声信道为非均匀介质空间,除会受到一般的扩散和吸收损失外,还将受到多径干扰的影响。多径干扰通常是离散分布的,以一路多径干扰为例,其示意图如图 1所示。多径信号产生的回波,使信号产生振幅上的衰减和相位上的起伏。同时,在对水下目标进行探测过程中,通常情况下目标是运动着的而非静止状态,声呐和目标间的相对运动会使接收到的信号波形发生频率的偏移。设声源发射信号为u(t),则由于多径影响使得接收到的信号为
|
Download:
|
| 图 1 信号入射示意图 Fig. 1 Signal incidence diagram | |
| $ \hat u\left( t \right) = \sum\limits_{i = 1}^l {{\alpha _i}u\left[ {\left( {1 + \delta } \right)\left( {t - {\tau _i}} \right)} \right]{{\rm{e}}^{{\rm{j2 \mathsf{ π} }}{f_0}\left[ {\left( {1 + \delta } \right)\left( {t - {\tau _i}} \right)} \right]}}} $ | (1) |
式中:αi、τi分别表示多径信号幅度的衰减和时间上的延迟,f0为发射信号频率,I为多径信号的数目,通常情况下取I=2。其中,δ=2vcosθ/c,c表示声波传播速度,θ表示信号的入射角度,v表示声呐和目标间的相对运动速度,当目标与声呐相向运动时为正,速度越大,接收信号间的相关性越小。
以窄带信号为例,此时由声呐和目标间相对运动产生的包络偏差可以忽略不计,这种情况下,式(1)可简化为
| $ \hat u\left( t \right) = \sum\limits_{i = 1}^l {{\alpha _i}u\left( {t - {\tau _i}} \right){{\rm{e}}^{{\rm{j2 \mathsf{ π} }}{\xi _i}\left( {t - {\tau _i}} \right)}}} $ | (2) |
其中
| $ {\xi _i} = {f_0}{\delta _i} $ | (3) |
为频率偏移。则接收到的总信号为
| $ x\left( t \right) = u'\left( t \right) + \hat u\left( t \right) + z\left( t \right) $ | (4) |
式中:u′(t)为直达波信号,z(t)是均值为0,方差为σ2的加性高斯白噪声信号。
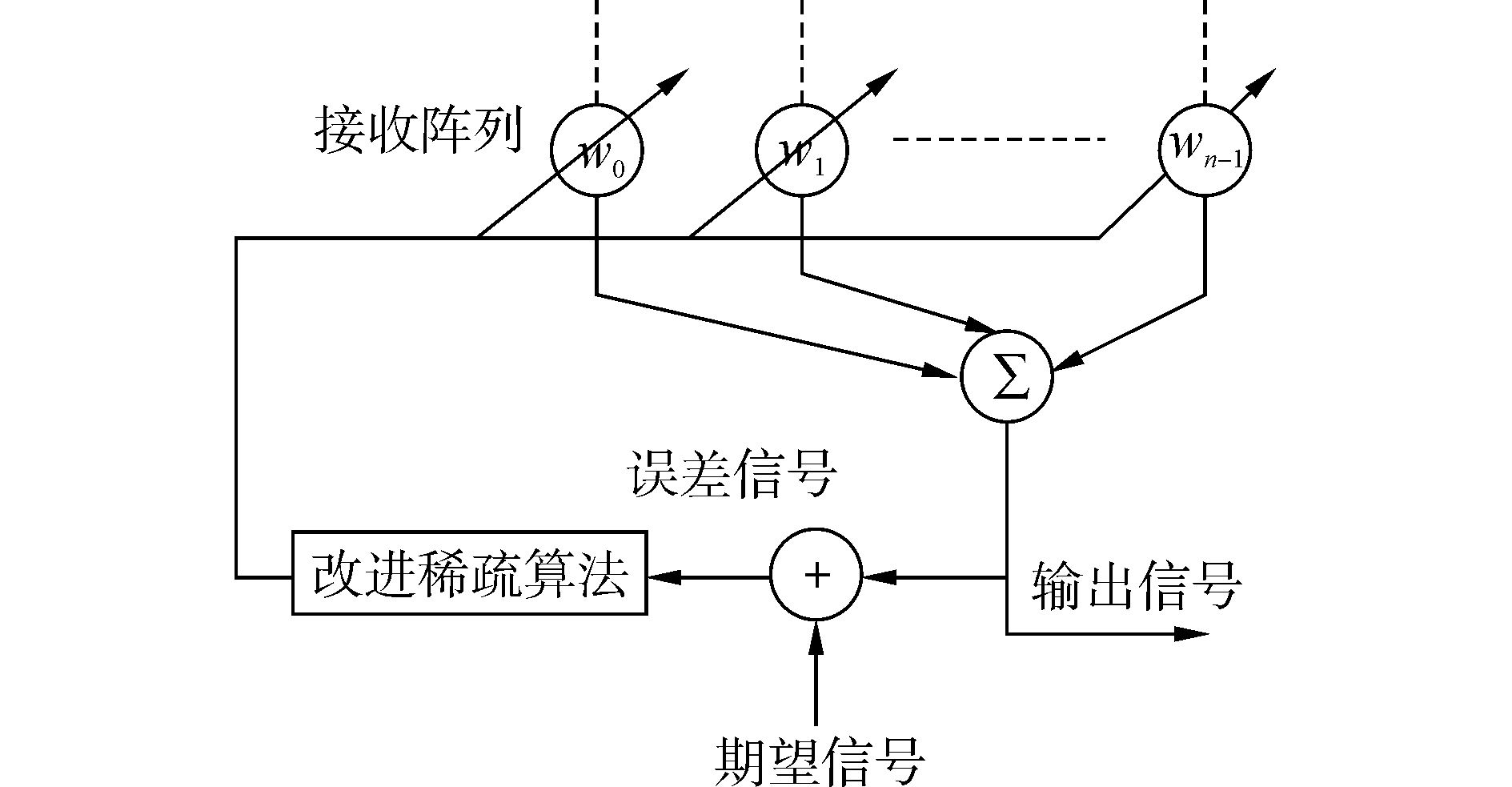
本文使用阵列模型的自适应干扰抑制结构,该结构由N个阵元组成的均匀线列阵,阵元间距为半波长,并对阵列模型做出如下假设:接收阵元位于信号源的远场,近似认为阵元接收到的信号为平面波;传输介质是无损的、线性的、非扩散的、均匀的且各向同性的;接收阵元本身无指向性;接收阵元的阵元间距远大于阵元几何尺寸,且各阵元间的相互影响忽略不计。信号处理模型如图 2所示。
|
Download:
|
| 图 2 阵列信号处理模型 Fig. 2 Array signal processing model | |
对LMS算法,有:
| $ e\left( n \right) = d\left( n \right) - {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right) \cdot \mathit{\boldsymbol{x}}\left( n \right) $ | (5) |
式中:d(n)表示期望信号,x(n)为输入信号向量,W(n)为滤波器的权矢量。该算法的代价函数ξ(n)为
| $ \xi \left( n \right) = {\left| {e\left( n \right)} \right|^2} $ | (6) |
由该代价函数可得滤波器权系数的迭代公式为:
| $ \mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + \mu e\left( n \right) \cdot \mathit{\boldsymbol{x}}\left( n \right) $ | (7) |
式中:μ为迭代步长,是用于控制自适应速度与稳定性的常数,且满足条件:
| $ 0 < \mu < 1/{\lambda _{\max }} $ | (8) |
式中λmax是输入信号自相关矩阵的最大特征值。
式(7)可以表示为
| $ \mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + f\left[ {e\left( n \right)} \right] $ | (9) |
式中f(x)表示自适应误差更新项。可以看出,LMS算法没有利用系统的稀疏特性,稀疏的自适应算法通常可以表示为
| $ \mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + f\left[ {e\left( n \right)} \right] + g\left[ {\mathit{\boldsymbol{W}}\left( n \right)} \right] $ | (10) |
式中g(x)表示零吸引项。
稀疏l1范数LMS算法将l1范数引入到标准LMS的代价函数中,实现了对系统稀疏特性的利用,其代价函数为
| $ \xi \left( n \right) = {\left| {e\left( n \right)} \right|^2} + \gamma {\left\| {\mathit{\boldsymbol{W}}\left( n \right)} \right\|_1} $ | (11) |
式中γ>0为平衡因子,用于调节稀疏性对代价函数的影响。对式(11)使用梯度估计,可得l1-LMS算法的权系数迭代公式为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + \mu e\left( n \right)\mathit{\boldsymbol{X}}\left( n \right) - }\\ {\kappa {\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{W}}\left( n \right)} \right)} \end{array} $ | (12) |
式中:κ=μγ>0,当κ=0时,上式退化成标准的LMS算法。与标准的LMS算法相比,式(12)增加了一个零吸引项,在每次迭代时“吸引”加权系数向零矢量靠近。但是该算法对所有的加权系数施加大小相同的零吸引力,对于稀疏程度较低的系统,算法性能有较大下降。
稀疏l0范数LMS算法将l0范数引入到标准LMS的代价函数中,其代价函数为
| $ \xi \left( n \right) = {\left| {e\left( n \right)} \right|^2} + \gamma {\left\| {\mathit{\boldsymbol{W}}\left( n \right)} \right\|_0} $ | (13) |
由于l0范数不可导,参考文献[2],得出算法的权系数迭代公式为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + \mu e\left( n \right)\mathit{\boldsymbol{X}}\left( n \right) - }\\ {\kappa {f_\beta }\left( {\mathit{\boldsymbol{W}}\left( n \right)} \right)} \end{array} $ | (14) |
其中,函数fβ(x)定义如下
| $ {f_\beta }\left( x \right) = \left\{ \begin{array}{l} {\beta ^2}x + \beta ,\;\;\;\; - 1/\beta \le x < 0\\ {\beta ^2}x - \beta ,\;\;\;\;0 < x \le 1/\beta \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (15) |
由式(14)可以看出,该算法对零系数和非零系数施加不同权重的吸引力,性能较l1-LMS算法更优。但是上述两种算法的约束项本身并无调整因子,因此当信道稀疏程度下降时,该类算法的收敛性能也呈现较大的下降。
稀疏lp范数LMS算法将lp范数引入到标准LMS的代价函数中,其代价函数为
| $ \xi \left( n \right) = {\left| {e\left( n \right)} \right|^2} + \gamma {\left\| {\mathit{\boldsymbol{W}}\left( n \right)} \right\|_{\rm{p}}} $ | (16) |
式中参数p满足0 < p < 1。使用梯度估计得,其权系数迭代公式为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + \mu e\left( n \right)\mathit{\boldsymbol{X}}\left( n \right) - }\\ {\frac{{\kappa \left\| {\mathit{\boldsymbol{W}}\left( n \right)} \right\|_p^{1 - p}{\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{W}}\left( n \right)} \right)}}{{\left( {{\varepsilon _p} + {{\left| {\mathit{\boldsymbol{W}}\left( n \right)} \right|}^{1 - p}}} \right)}}} \end{array} $ | (17) |
式中:参数εp是一个常量,以防止上式分母部分为零。通过对参数p选取不同的自适应调整方法[6, 8-10],以适应不同稀疏程度的信道。但是,该算法复杂度较大,每次权系数更新过程均需要较大的计算消耗,给实际应用带来相当大的限制。
3 变步长稀疏似p范数LMS算法文献[7]提出稀疏似p范数约束的最小均方算法,该算法的代价函数为
| $ \xi \left( n \right) = {\left| {e\left( n \right)} \right|^2} + \gamma {\left\| {\mathit{\boldsymbol{W}}\left( n \right)} \right\|_{{\rm{p}} - {\rm{like}}}} $ | (18) |
其中,似p范数‖W(n)‖p-like定义为
| $ {\left\| {\mathit{\boldsymbol{W}}\left( n \right)} \right\|_{{\rm{p}} - {\rm{like}}}} = \sum\limits_{i = 1}^n {{{\left| {\mathit{\boldsymbol{x}}\left( i \right)} \right|}^p}} ,0 \le p \le 1 $ | (19) |
式中:‖W(n)‖p-like并不是真正意义的范数,与范数lp不同,所以称为似p范数。由该代价函数求得权系数迭代公式为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + \mu e\left( n \right)\mathit{\boldsymbol{X}}\left( n \right) - }\\ {\kappa = \frac{{p{\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{W}}\left( n \right)} \right)}}{{{\varepsilon _p} + {{\left| {\mathit{\boldsymbol{W}}\left( n \right)} \right|}^{1 - p}}}}} \end{array} $ | (20) |
比较式(17)和式(20)可以看出,lp-like-LMS算法较大程度的减小了算法的复杂度。而参数p根据实际信道的特性进行自适应调整:
| $ {p_{n + T}} = {p_n} - \delta {\mathop{\rm sgn}} \left( {\frac{1}{T}\sum\limits_n^{n + T} {\left| {\mathit{\boldsymbol{W}}\left( n \right)} \right| - 1} } \right) $ | (21) |
式中:T为参数更新周期,δ为参数更新的步长因子。
尽管lp-like-LMS算法具有较小的算法复杂度,良好的性能,但是仍然存在两方面的问题:1)该算法的零吸引项缺少对误差函数的利用。通常情况下,我们希望算法的自适应调整过程在达到稳定状态时,减小稀疏项的约束,减小稳态误差,较大的稀疏约束易导致加权系数较大的波动幅度;2)该算法采用固定步长,未对收敛性能进行改善,通过对LMS算法的分析可知,自适应算法的收敛速度和步长有关,使用变步长方法可以提高LMS算法的收敛速度[11-12]。本文将从这两方面对lp-like-LMS算法做出改进。
利用误差函数对零吸引项进行调整,通常有三种选择,|e(n)|、e2(n)和e(n)e(n-1),误差项过高的阶数会导致计算量的大幅增加。由于|e(n)|项在误差较小时,变化陡峭,故本文考虑另两种选择。
由式(5)得
| $ {\rm{d}}\left( n \right) = e\left( n \right) + {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right) \cdot \mathit{\boldsymbol{x}}\left( n \right) $ | (22) |
同时,期望信号还可以表示为
| $ {\rm{d}}\left( n \right) = {{\mathit{\boldsymbol{\bar W}}}^{\rm{T}}}\left( n \right) \cdot \mathit{\boldsymbol{u}}\left( n \right) $ | (23) |
其中,W(n)是最佳权系数矢量,并记权系数偏差ΔW(n)为
| $ \Delta \mathit{\boldsymbol{W}}\left( n \right) = \mathit{\boldsymbol{\bar W}}\left( n \right) - \mathit{\boldsymbol{W}}\left( n \right) $ | (24) |
结合式(4)、(22)和(23)可得
| $ {\rm{e}}\left( n \right) = \Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{u}}\left( n \right) - {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{\hat u}}\left( n \right) - {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{z}}\left( n \right) $ | (25) |
则分别计算e2(n)、e(n)e(n-1),并对两者取期望,同时考虑到z(n)是均值为零的高斯白噪声,u(n)、
| $ \begin{array}{l} {\rm{E}}\left[ {{e^2}\left( n \right)} \right] = {\rm{E}}\left[ {\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{u}}\left( n \right)\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{u}}\left( n \right)} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{E}}\left[ {\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right) \times \mathit{\boldsymbol{u}}\left( n \right)\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{\hat u}}\left( n \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{E}}\left[ {\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{\hat u}}\left( n \right) \times \Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{\hat u}}\left( n \right)} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{E}}\left[ {\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{\hat u}}\left( n \right)\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right) \times \mathit{\boldsymbol{u}}\left( n \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{E}}\left[ {\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{z}}\left( n \right)\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{z}}\left( n \right)} \right] \end{array} $ | (26) |
| $ \begin{array}{*{20}{c}} {{\rm{E}}\left[ {e\left( n \right)e\left( {n - 1} \right)} \right] = {\rm{E}}\left[ {\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{u}}\left( n \right)\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( {n - 1} \right) \times } \right.}\\ {\left. {\mathit{\boldsymbol{u}}\left( {n - 1} \right)} \right] - {\rm{E}}\left[ {\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{u}}\left( n \right) \times } \right.}\\ {\left. {\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( {n - 1} \right)\mathit{\boldsymbol{\hat u}}\left( {n - 1} \right)} \right] + {\rm{E}}\left[ {\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right) \times } \right.}\\ {\left. {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over u} }}\left( n \right)\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( {n - 1} \right)\mathit{\boldsymbol{\hat u}}\left( {n - 1} \right)} \right] - }\\ {{\rm{E}}\left[ {\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{\hat u}}\left( n \right)\Delta {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( {n - 1} \right)\mathit{\boldsymbol{u}}\left( {n - 1} \right)} \right]} \end{array} $ | (27) |
从式(26)、(27)可以看出,e2(n)和e(n)e(n-1)的期望值相比,除受输入信号影响外,e2(n)不仅与多径干扰的大小有关,而且与噪声的大小有关,而e(n)e(n-1)仅与多径干扰的大小相关,不受噪声的影响,其抗干扰能力较优于前者,故本文采用e(n)e(n-1)项对零吸引项进行调整。
变步长算法能够有效加快算法的收敛速度。为优化算法性能,需要满足如下特征:在收敛起始时采用较大步长;在算法收敛后,调整步长使其变小,减小稳态失调;计算量尽可能小;具有较好的抗干扰能力。本文参考文献[13]中的基于改进Sigmoid函数的变步长方法,该步长函数为
| $ \mu \left( n \right) = b\left[ {1 - \exp \left( { - a{{\left| {e\left( n \right)} \right|}^2}} \right)} \right] $ | (28) |
该方法基本满足上述特征,同时在稳态阶段变化较为平缓,有利于减小稳态误差。结合上述分析,本文对该变步长方法进一步做出改进,即
| $ \mu \left( n \right) = b\left[ {1 - \exp \left( { - a\left| {e\left( n \right)e\left( {n - 1} \right)} \right|} \right)} \right] $ | (29) |
使用e(n)e(n-1)项替代e2(n)项,进一步提高其抗干扰特性。
综上所述,本文提出一种改进稀疏似p范数LMS算法,使用e(n)e(n-1)项调整零吸引项,进一步改进的Sigmod函数调整步长,算法流程:
初始化参数δ、T、p0、α、β、κ、εp
For n=2, 3, …… do
| $ e\left( n \right) = d\left( n \right) - {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)x\left( n \right) $ |
| $ {p_{n + T}} = {p_n} - \delta {\mathop{\rm sgn}} \left( {\frac{1}{T}\sum\limits_n^{n + T} {\left| {\mathit{\boldsymbol{W}}\left( n \right)} \right| - 1} } \right) $ |
| $ \mu \left( n \right) = b\left[ {\exp \left( { - a\left| {e\left( n \right)e\left( {n - 1} \right)} \right|} \right)} \right] $ |
| $ \begin{array}{l} \mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + \mu \left( n \right)e\left( n \right)X\left( n \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\kappa \frac{{{p_{n + T}} \cdot {\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{W}}\left( n \right)} \right)}}{{{\varepsilon _p} + {{\left| {\mathit{\boldsymbol{W}}\left( n \right)} \right|}^{1 - {p_{n + T}}}}}}\left| {e\left( n \right)e\left( {n - 1} \right)} \right| \end{array} $ |
End
上述初始化参数的选取准则,可参考文献[7, 13],在此不做赘述。
4 算法仿真和性能分析为了验证提出的变步长稀疏似p范数LMS算法性能,分别与标准LMS算法、稀疏似p范数LMS算法相比较。本文进行了如下仿真实验,其中计算机仿真条件为:接收阵列为均匀线列阵,阵元数目为16个,阵元间距取半波长;发射中心频率为20 kHz的单频脉冲信号;目标移动速度取2 m/s;设定期望来波方向为0°。参照上述多径信号模型,取两路多径干扰,分别从-15°和20°方向入射,时延分别为15和20 ms,同时叠加高斯白噪声;对每次仿真实验,独立重复100次取平均,算法选取参数如表 1所示。分别从干扰抑制前后的时域波形,干扰抑制前后的波束图、不同输入信干比与输出信干噪比关系以及收敛速度来验证其性能与效率。
| 表 1 算法参数 Tab.1 Algorithm parameters |
在输入信干噪比为3 dB条件下,比较原始发射信号波形,阵列中一路接收到的信号波形和经改进似p范数算法处理后的输出波形,得到结果如图 3所示。从图中结果可以看出,接收信号与发射信号相比,受干扰影响严重,产生较大的失真。接收到的信号经改进似p范数算法处理后,得到的输出波形与原始发射波形相接近,较好的抑制了干扰,恢复出原始信号,改善输出结果。

|
Download:
|
| 图 3 干扰抑制前后波形对比 Fig. 3 Waveform contrast before and after interference suppression | |
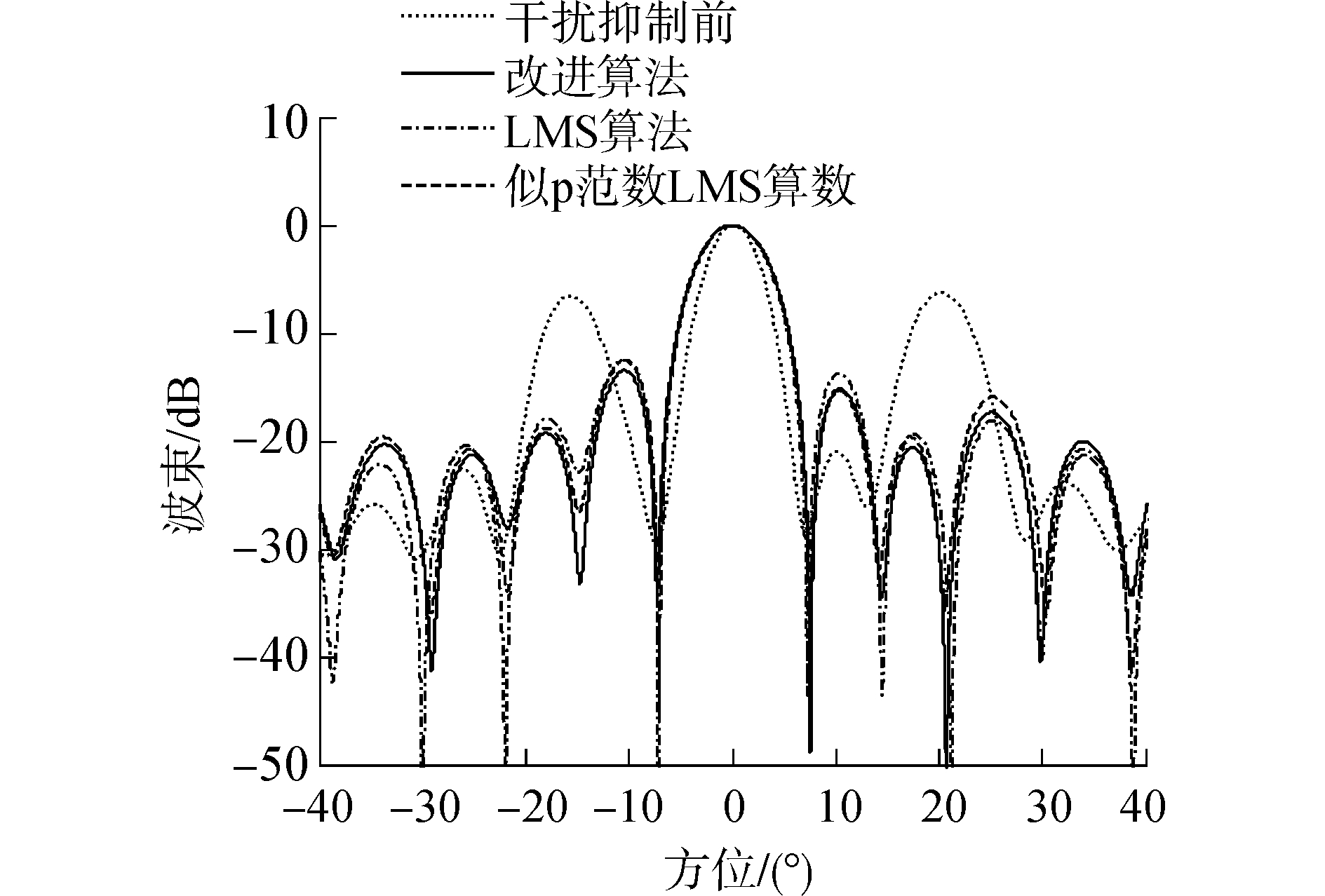
在输入信干噪比为3 dB条件下,分别比较干扰抑制前、经LMS算法处理、稀疏似p范数LMS算法处理和经改进算法处理后的波束,所得结果如图 4所示。从图中可以看出,接收信号受-15°和20°方向干扰的影响,经不同算法处理后,均能在干扰方向形成凹陷,有效降低干扰旁瓣,抑制干扰对有用信号的影响。
|
Download:
|
| 图 4 波束图比较 Fig. 4 Beam pattern comparison | |
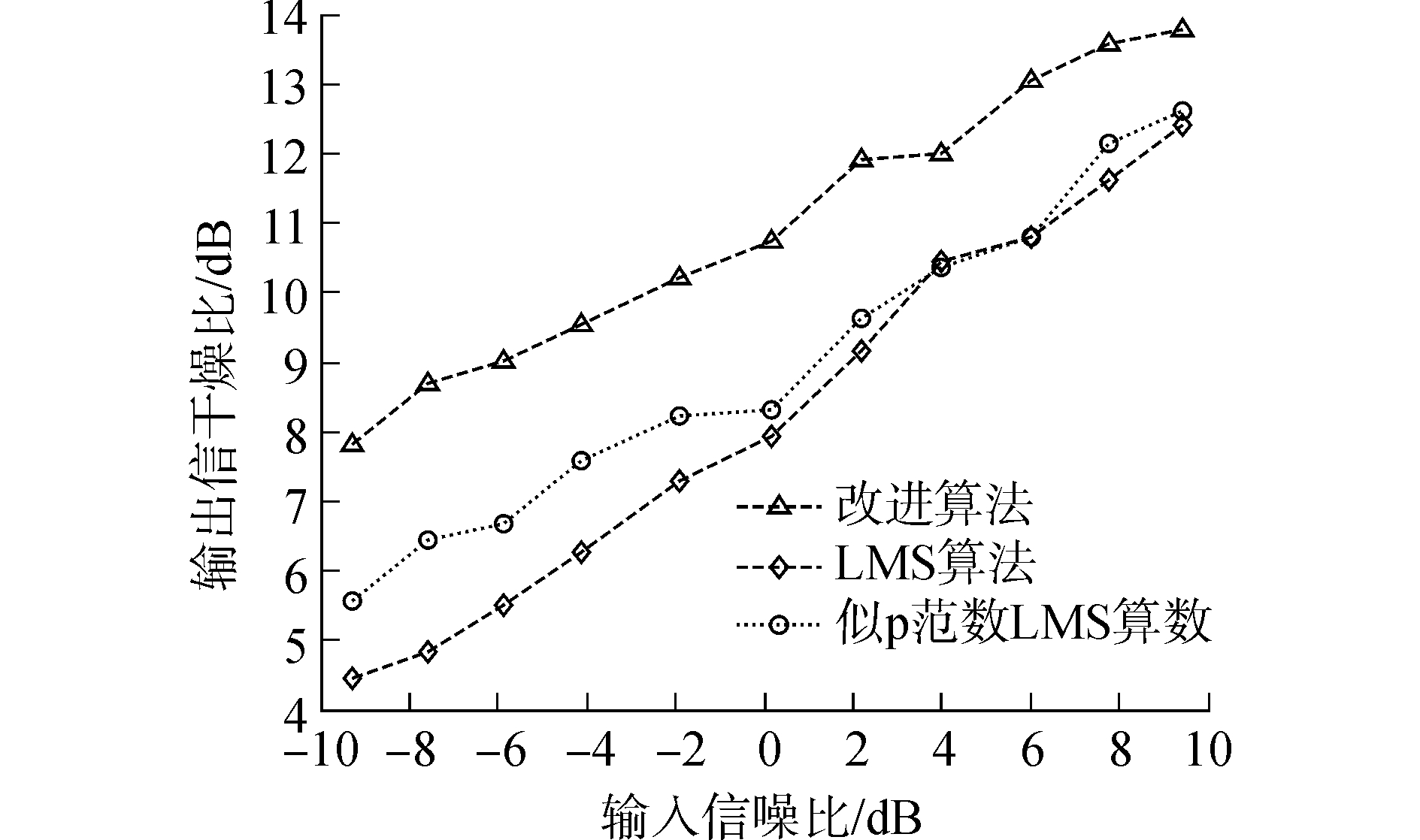
当输入信噪比为5 dB,分别比较经典LMS算法、稀疏似p范数LMS算法和改进算法在不同输入信干比条件下的输出信干噪比,所得结果如图 5所示。从图中可以看出,输入信噪比保持不变,随着输入信干比的增加,经三种算法处理后,信干噪比性能明显得到了较大的改善。相同信干比条件下,三种算法性能比较:改进算法性能最佳,似p范数LMS算法次之,经典LMS算法较差。且干扰信号越强,信道的稀疏程度越高,改进后算法的优势越明显。
|
Download:
|
| 图 5 不同输入信干比下输出信干噪比比较 Fig. 5 The output SINR comparison under different input SIR | |
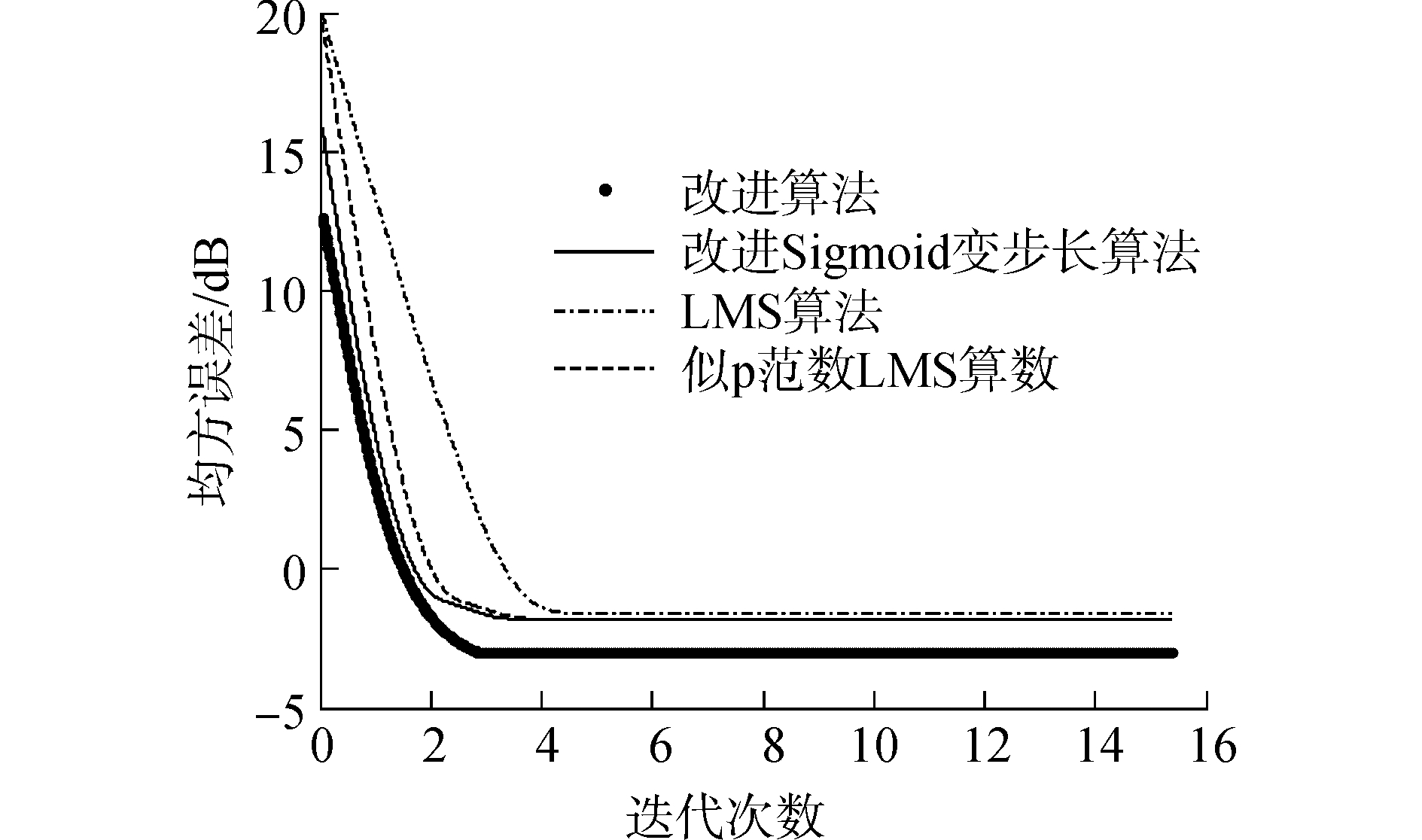
其他条件不变, 在输入信干噪比为3 dB条件下, 比较经典LMS算法、稀疏似p范数LMS算法、改进Sigmoid变步长算法和改进后算法的收敛曲线, 对结果进行平滑处理, 所得结果如图 6所示.从图 6可以看出, 经典LMS算法经400次左右的迭代达到收敛状态; 似p范数LMS算法由于零吸引项的存在, 收敛速度优于LMS算法, 经350次左右迭代达到收敛状态; 改进Sigmoid变步长算法由于采用了改变步长的方式, 同样具有较快的收敛速度, 三种算法到达稳定状态后的误差近似; 改进后算法, 经250次左右迭代达到收敛状态, 且到达稳定状态后的误差最小.
|
Download:
|
| 图 6 收敛曲线比较 Fig. 6 Convergence curves comparison | |
综合上述实验结果,证明改进后的算法在具有良好干扰抑制性能的同时,具有较快的收敛速度,较小的稳态误差。
5 结论1) 在文献[7]算法的基础上, 本文提出的变步长稀疏似p范数LMS算法使用改进Sigmoid函数变化步长,同时采用与误差有关的函数值对零吸引项做出调整,加快了自适应迭代的收敛速度,减小了稳态误差。
2) 经改进的似p范数LMS算法有效抑制了干扰,恢复出原始信号,信干比较经典LMS算法、稀疏似p范数LMS算法有明显改进。
3) 改进后的算法在保持良好干扰抑制性能的同时,迭代次数少,收敛速度快,且到达稳定状态后的误差最小。
| [1] |
金坚, 谷源涛, 梅顺良. 用于稀疏系统辨识的零吸引最小均方算法[J]. 清华大学学报(自然科学版), 2010, 50(9): 1656-1659. JIN Jian, GU Yuantao, MEI Shunliang. Adaptive algorithm for sparse system identification:Zero-attracting LMS[J]. Journal of Tsinghua university (science and technology), 2010, 50(9): 1656-1659. (  0) 0)
|
| [2] |
GU Yuantao, JIN Jian, MEI Shunliang. l0 norm constraint LMS algorithm for sparse system identification[J]. IEEE signal processing letters, 2009, 16(9): 774-777. DOI:10.1109/LSP.2009.2024736 (  0) 0)
|
| [3] |
曲庆, 金坚, 谷源涛. 用于稀疏系统辨识的改进l0-LMS算法[J]. 电子与信息学报, 2011, 33(3): 604-609. QU Qing, JIN Jian, GU Yuantao. An improved l0-LMS algorithm for sparse system identification[J]. Journal of electronics & information technology, 2011, 33(3): 604-609. (  0) 0)
|
| [4] |
管四海, 李智. 改进的l0范数LMS算法与分析[J]. 北京邮电大学学报, 2015, 38(4): 79-83. GUAN Sihai, LI Zhi. A modified l0_LMS algorithm and its performance analysis[J]. Journal of Beijing University of posts and Telecommunications, 2015, 38(4): 79-83. (  0) 0)
|
| [5] |
TAHERI O, VOROBYOV S A. Sparse channel estimation with LP-norm and reweighted L1-norm penalized least mean squares[C]//Proceedings of 2011 IEEE International Conference on Acoustics, Speech and Signal Processing. Prague, Czech Republic, 2011: 2864-2867. http://ieeexplore.ieee.org/document/5947082/
(  0) 0)
|
| [6] |
FENG Yong, CHEN Fei, WU Jiasong. Variable p norm constrained LMS algorithm based on gradient of root relative deviation. pdf[J]. arXiv: 1603. 09022, 2016.
(  0) 0)
|
| [7] |
WU F Y, ZHOU Y H, TONG F, et al. Simplified p-norm-like constraint LMS algorithm for efficient estimation of underwater acoustic channels[J]. Journal of marine science and application, 2013, 12(2): 228-234. DOI:10.1007/s11804-013-1189-7 (  0) 0)
|
| [8] |
伍飞云, 周跃海, 童峰. 引入梯度导引似p范数约束的稀疏信道估计算法[J]. 通信学报, 2014, 35(7): 172-177. WU Feiyun, ZHOU Yuehai, TONG Feng. Estimation algorithm for sparse channels with gradient guided p-norm like constraints[J]. Journal on communications, 2014, 35(7): 172-177. (  0) 0)
|
| [9] |
FENG Yong, CHEN Fei, ZENG Rui, et al. Error gradient-based variable-LP norm constraint LMS algorithm for sparse system identification[J]. arXiv: 1509. 07951, 2015.
(  0) 0)
|
| [10] |
WU F Y, TONG F. Gradient optimization p-norm-like constraint LMS algorithm for sparse system estimation[J]. Signal processing, 2013, 93(4): 967-971. DOI:10.1016/j.sigpro.2012.10.008 (  0) 0)
|
| [11] |
罗小东, 贾振红, 王强. 一种新的变步长LMS自适应滤波算法[J]. 电子学报, 2006, 34(6): 1123-1126. LUO Xiaodong, JIA Zhenhong, WANG Qiang. A new variable step size LMS adaptive filtering algorithm[J]. Acta electronica sinica, 2006, 34(6): 1123-1126. (  0) 0)
|
| [12] |
田福庆, 罗荣, 李克玉, 等. 基于改进的双曲正切函数变步长LMS算法[J]. 系统工程与电子技术, 2012, 34(9): 1758-1763. TIAN Fuqing, LUO Rong, LI Keyu, et al. New variable step-size LMS algorithm based on modified hyperbolic tangent function[J]. Systems engineering and electronics, 2012, 34(9): 1758-1763. (  0) 0)
|
| [13] |
姜冰磊, 冯西安. 一种权系数部分更新的变步长自适应多径干扰对消算法[J]. 振动与冲击, 2016, 35(13): 85-89. JIANG Binglei, FENG Xi'an. A variable step and adaptive multipath interference cancellation algorithm based on partial-update of weight coefficients[J]. Journal of vibration and shock, 2016, 35(13): 85-89. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


