2. 中交天津航道局有限公司 天津市疏浚技术企业重点实验室, 天津 300457
2. Tianjin Key Laboratory & Construction Vessel Design Institute for Dredging Engineering Enterprises, CCCC Tianjin Port & Waterway Prospection & Design Research Institute Co., Ltd., Tianjin 300457, China
绞吸式挖泥船是一类广泛应用于航道疏浚、港湾建设、水域环保、围海造地及人工造岛等领域的工程船舶。绞刀是绞吸式挖泥船的核心部件,在施工过程中高速旋转,直接与水下切削介质发生剧烈的相互作用并承受巨大的切削载荷。准确预测绞刀在工作过程中的受力和功率,对于优化绞刀结构设计、降低功耗、减少磨损、提高施工效率等具有重要意义。
由于绞刀空间结构特殊,岩石力学性质复杂,并且绞刀在挖岩过程中与岩体存在着复杂的接触作用,使得预测绞刀的切削力变得十分困难。长期以来,对绞刀切削力的预测只能靠粗略估算[1]。以往的研究主要集中在绞刀单齿切削泥沙、粘土的二维切削理论方面[2-3],或将绞刀简化为圆柱形,进而应用二维切削理论计算整个绞刀切削力[4]。近年来也出现了借鉴采煤机截齿切削煤岩的机理来预测绞刀受力的理论模型[5]。
随着数值模拟技术的不断成熟,有限元方法已经成为解决岩土切削问题的有力工具。应用有限元方法,不仅可以获得刀具在岩土切削过程中的切削力[6-7],进而根据模拟结果进行刀具优化设计[8]和新型刀具研发[9],还可以获得岩土的应力分布,变形情况,破坏位置和破碎程度,从而全面了解整个切削过程[10]。然而,针对绞刀的有限元模拟,还停留在静力分析层面[11-12],没有考虑切削过程,因而难以反映实际施工过程中工况条件对绞刀切削载荷的影响。
本文采用通用有限元软件ABAQUS,建立了绞刀连续切削岩体的三维有限元模型,完整模拟了绞刀挖岩过程,并结合模型实验,验证了数值模拟方法的有效性。讨论了绞刀切削力和功率随绞刀横移速度与绞刀转速的变化规律。
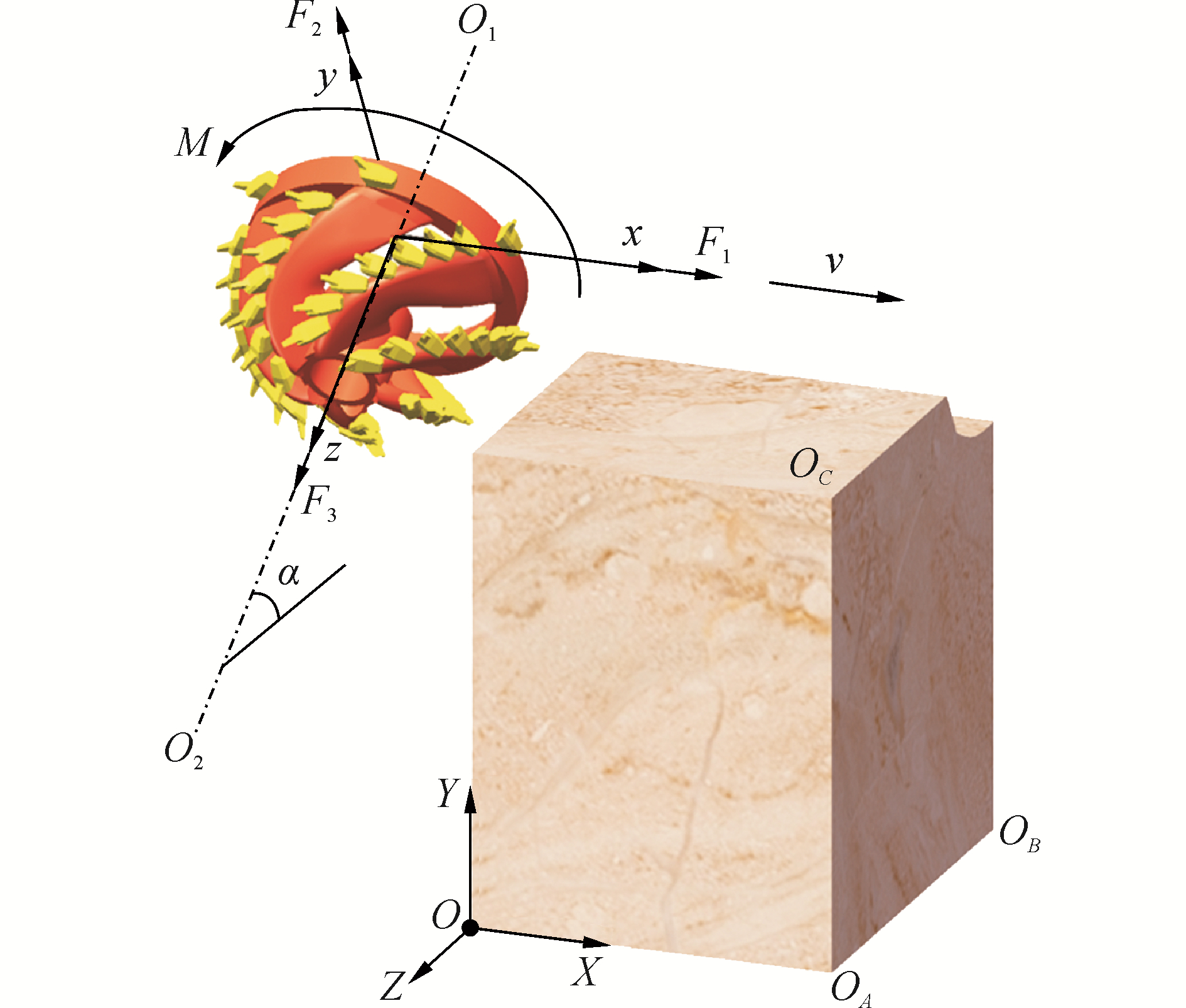
1 绞刀挖岩的数值仿真模型切削模型如图 1所示,采用三维建模软件CATIA建立绞刀的几何模型,共6个刀臂,48个刀齿,每个刀臂上装有8个刀齿,绞刀大圈外径为3 000 mm。在绞刀的横移切削方向布置岩体,岩体模型的几何参数如表 1所示。
|
Download:
|
| 图 1 绞刀与岩体模型 Fig. 1 Model of cutterhead and rock | |
| 表 1 岩体几何参数 Tab.1 Rock geometric parameter |
建立全局坐标系O-XYZ,绞刀轴线O1O2平行于OYZ面,并且与OXZ平面成α角,模拟时α角取30°。建立固定在绞刀上的随动坐标系R-xyz,选取大环底面中心点R为随动坐标系的原点,将绞刀所受合力沿随动坐标系x轴、y轴和z轴方向进行分解,依次为水平切削力F1,径向切削力F2,轴向切削力F3,绞刀主轴扭矩M,正方向按右手定则确定。v为绞刀横移速度,方向为x轴正向,绞刀的旋转方向为绕轴线O1O2逆时针方向,为反刀切削,该转向可以避免挖岩过程中动载荷过大造成刀架弹起。
由于本文旨在研究挖岩过程中绞刀整体的受力情况,因此将绞刀视为刚体,其边界条件施加于固定在绞刀上的随动坐标系的原点R上,即施加x方向横移速度v与绕z轴的转速ω,其他方向的速度与转速均为零。土体的边界条件在全局坐标系O-XYZ中给定,为底面固定,其余各面自由。
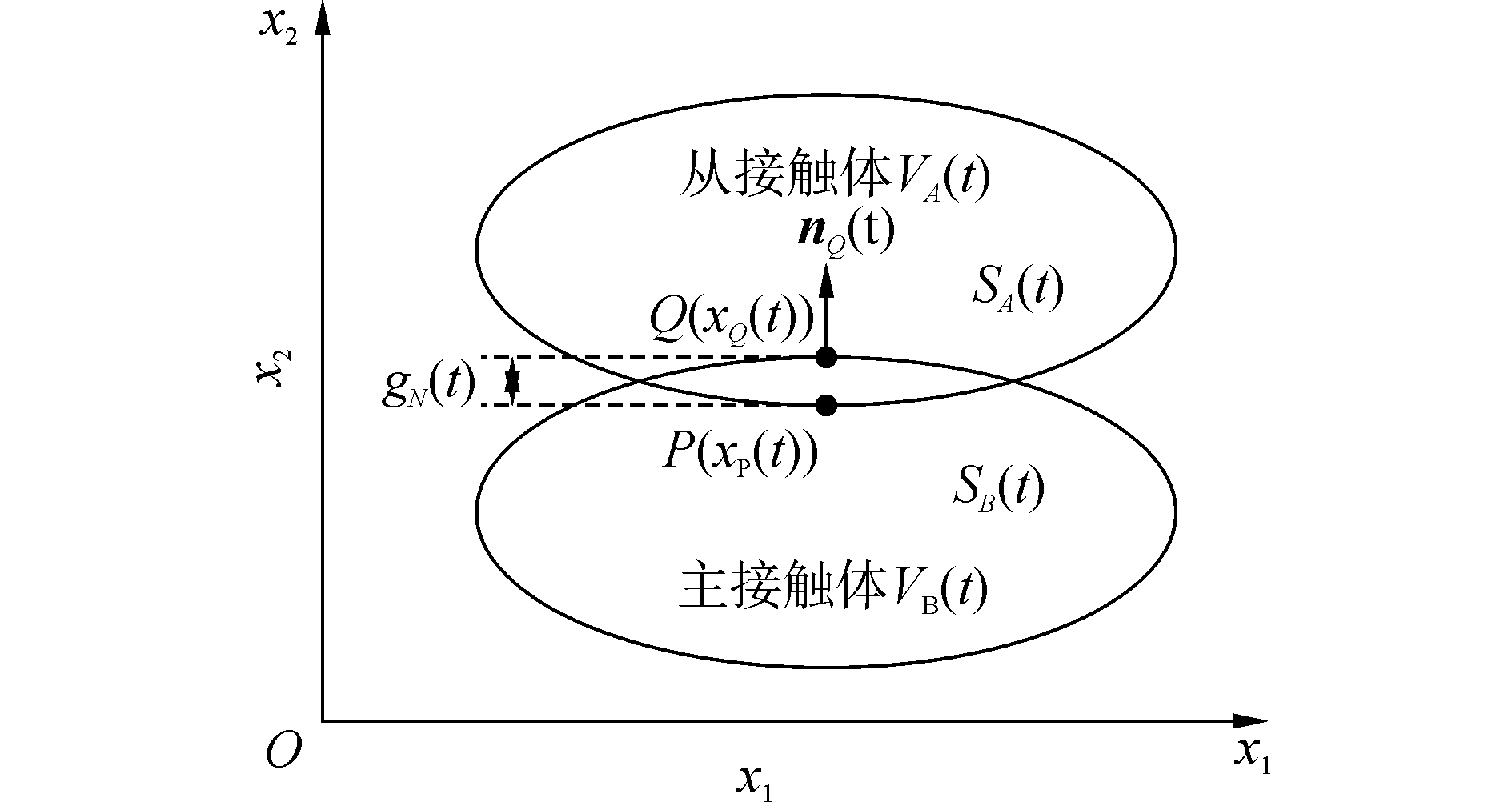
2 绞刀与岩体的接触作用模拟 2.1 接触判定条件接触判定条件是有限元方法中判定物体是否进入接触以及已经进入接触而不分离的条件。设t时刻从接触体VA(t)与主接触体VB(t)位形如图 2所示,xP(t)为从接触体表面SA(t)上任意一个指定点P的坐标,xQ(t)为主接触体表面SB(t)上距离P点最近的点Q的坐标,设nQ(t)为主接触体表面SB(t)的外法线方向向量,那么两个接触面间的法向间隙可表示为
| $ {g_N}\left( t \right) = [{x_Q}\left( t \right)-{x_P}\left( t \right)]{\mathit{\boldsymbol{n}}_Q}\left( t \right) $ | (1) |
|
Download:
|
| 图 2 接触状态示意图 Fig. 2 Sketch of contact state | |
接触过程中gN(t) < 0表示P点与SB(t)相互分离,gN(t)=0表示P点与SB(t)刚好接触,gN(t)>0表示主接触体表面已经侵入到从接触体内部。
2.2 罚刚度方法在确定绞刀与岩体的接触状态后,还需要计算每个接触单元界面上的切向、法向作用力,才能获得绞刀整体的切削力。罚刚度接触方法广泛应用于求解切削问题,如机械加工中金属切削过程的有限元模拟。该方法通过在接触界面之间引入附加刚度的方式来提高对复杂接触问题的求解能力。基于罚刚度方法的法向接触压力σn可表示为
| $ {\sigma _n} = \left\{ \begin{array}{l} {k_n}{g_N}, \;\;\;\;\;\;\;{g_N} \ge 0\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;{g_N} < 0 \end{array} \right. $ | (2) |
式中:kn为接触面法向罚刚度,gN为有限的接触穿透量。在求解过程中,罚刚度过大,将导致求解时间大幅增加;罚刚度过小,将造成穿透量过大,与实际不符。在本文模拟过程中,罚刚度kn取材料弹性刚度的十分之一。
通过罚刚度方法定义接触面法向压力模型之后,即可以相应地定义罚刚度形式的接触面切向摩擦模型。具体如下
| $ \tau = \left\{ \begin{array}{l} {k_s}{g_s}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;g \le {g_s}\\ {\rm{min}}({\tau _{{\rm{crit}}}}, \mu {\sigma _N}), \;\;\;\;\;g > {g_s} \end{array} \right. $ | (3) |
式中:τ为接触面切向摩擦力,g为接触面切向滑移距离,μ为接触面摩擦系数,ks为接触面切向罚刚度,gs相对滑移极限,τcrit为材料表面屈服的切向力极限。
3 岩体的本构模型 3.1 岩体本构模型Drucker-Prager模型可以考虑中间主应力和静水压力对材料屈服面的影响,并克服了Mohr-Coulomb模型因屈服面角隅处塑性流动方向不唯一而收敛困难的缺陷。本文采用的本构模型是扩展的Drucker-Prager模型[13],即
| $ \left\{ \begin{array}{l} F = t- p\tan \beta- d = 0\\ t = \frac{q}{2}{\rm{ }}\left[{1 + \frac{1}{K}-\left( {1-\frac{1}{K}} \right)\left( {\frac{r}{q}} \right)3} \right]\\ p = -\frac{1}{3}({\sigma _1} + {\sigma _2} + {\sigma _3}) \end{array} \right. $ | (4) |
式中:q为Mises等效应力,K为三轴拉伸屈服应力与三轴压缩屈服应力的比值,r为偏应力第三不变量,p为平均压应力,β为屈服面在p~t应力空间上的倾角,与岩体摩擦角有关,σ1、σ2和σ3分别为三个方向的主应力,d为屈服面在p~t应力空间上t轴的截距。
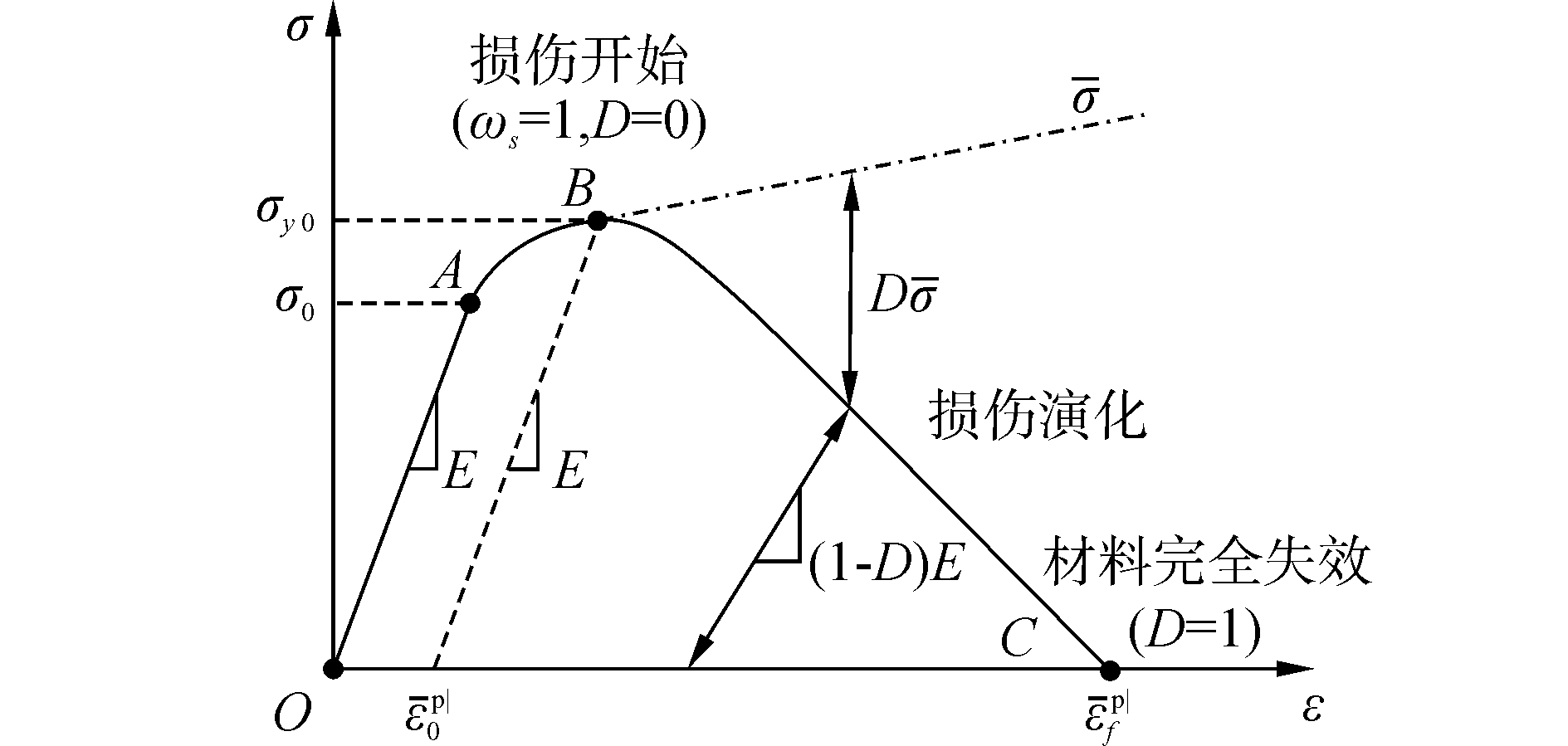
3.2 损伤演化模型损伤演化模型描述了损伤开始之后材料刚度的衰减规律,当单元刚度最终衰减至零时,将完全丧失承载能力。如图 3所示,一个完整的损伤失效过程应包括以下三个方面:1)损伤开始的标准,B点;2)损伤演化规律,BC段;3)损伤结束的标准,C点。本文采用剪切损伤模型来定义岩石材料的损伤失效。
|
Download:
|
| 图 3 损伤失效模型应力-应变响应曲线 Fig. 3 Stress-strain curve with progressive damage degradation | |
材料达到其强度极限时的等效塑性应变为εf,塑性变形随等效塑性应变递增的状态变量为ωS,
| $ {\omega _S} = \smallint \frac{{{\rm{d}}{{\bar \varepsilon }_p}}}{{{{\bar \varepsilon }_f}({\theta _s}, {{\dot {\bar \varepsilon} }_p})}} = 1 $ | (5) |
| $ {\theta _s} = (q + {k_s}p)/{\tau _{{\rm{max}}}} $ | (6) |
当ωS增加到1时,即达到损伤开始的标准B点,材料开始进入损伤阶段。
材料损伤开始之后的损伤演化规律由损伤演化方程定义,引入损伤因子D,
| $ \mathit{\boldsymbol{\sigma }} = \left( {1-D} \right)\mathit{\boldsymbol{\bar \sigma }} $ | (7) |
式中:σ为材料损伤开始后任意时刻的真实应力张量,σ为对应该时刻的不考虑损伤情况下的应力张量。由式(7)可见当损伤因子D=1时材料将完全丧失承载能力,失效单元将被从模型中删除。损伤因子D根据单元积分点的有效塑性位移up定义,即
| $ \dot d = {\rm{ }}\frac{{L{{\dot {\bar \varepsilon} }_p}}}{{{{\bar u}_f}}} = \frac{{{{\dot {\bar u}}_p}}}{{{{\bar u}_f}}} $ | (8) |
式中:L为单元特征长度,uf为损伤结束时的有效塑性位移。当D=1时,即达到图 3中C点,材料将完全失去承载能力。
4 实验验证及仿真结果分析 4.1 模型实验验证为检验前述数值模拟方法对绞刀挖岩问题的适用性,首先对中交天津航道局天津市疏浚技术重点实验室的切削实验进行模拟。实验中所用模型绞刀尺寸为实际疏浚绞刀大小的1/4。实验中采用人工配置的混凝土块代替实际疏浚中的砂岩材料,这是由于混凝土与砂岩均为脆性材料,力学性能与破坏机理相似。实验中,共制备具有不同抗压强度的三种混凝土块,材料参数如表 2所示。实验过程的工况参数如表 3所示。
| 表 2 有限元分析中所需材料参数 Tab.2 Material property parameters required in the FEA |
| 表 3 实验工况参数 Tab.3 Working parameters of the experiments |
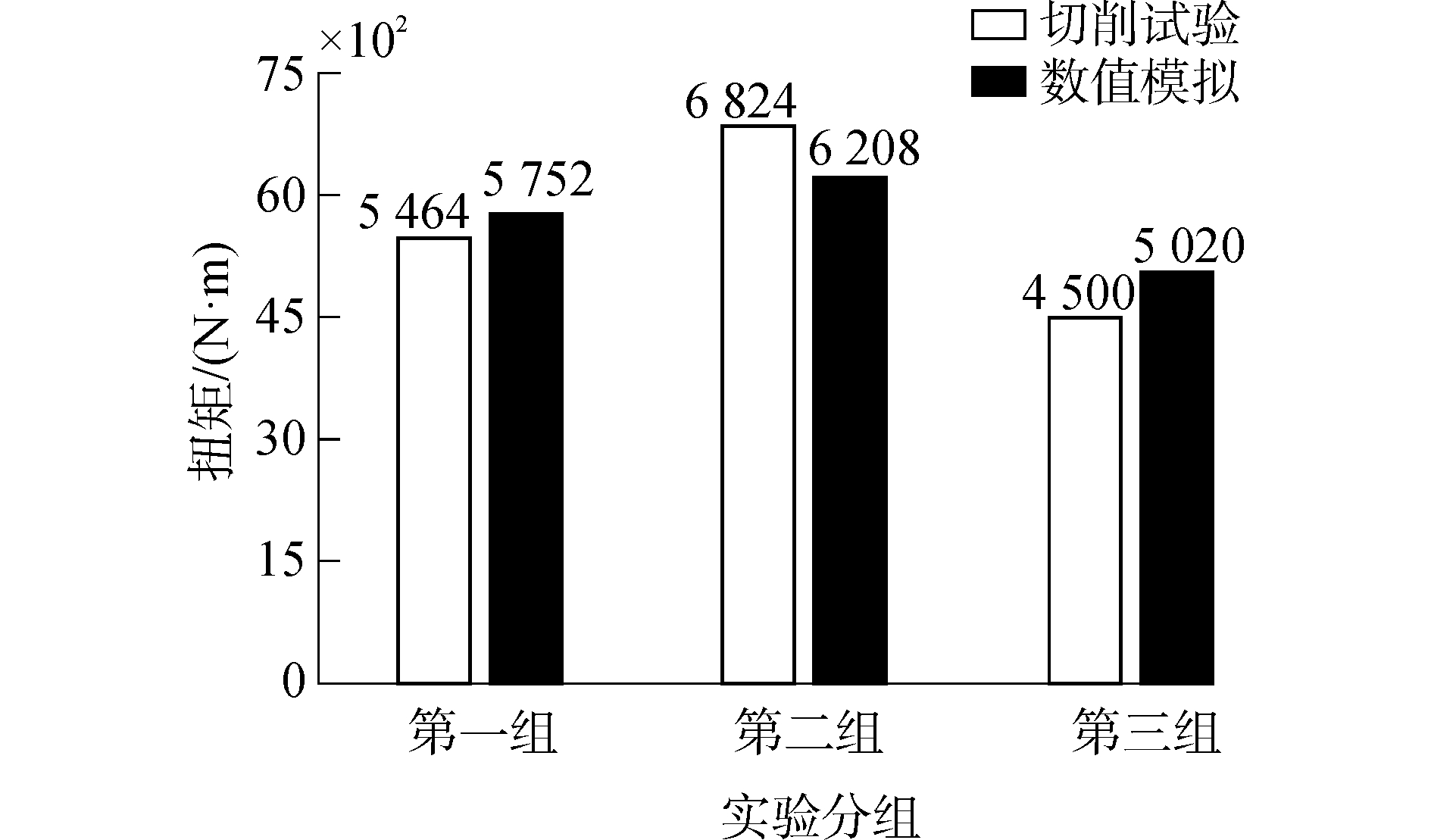
按照实验中材料参数与工况参数对三组切削实验分别建立有限元模型并进行数值模拟,将数值模拟得到的绞刀扭矩的平均值与实验测量结果进行对照,如图 4所示。三组数值模拟结果的相对误差分别为5.27%、9.03%和11.5%,与试验测量结果较为相符,从而验证了数值模拟方法的可行性。
|
Download:
|
| 图 4 数值模拟与实验结果对比 Fig. 4 Results of simulation and experiment | |
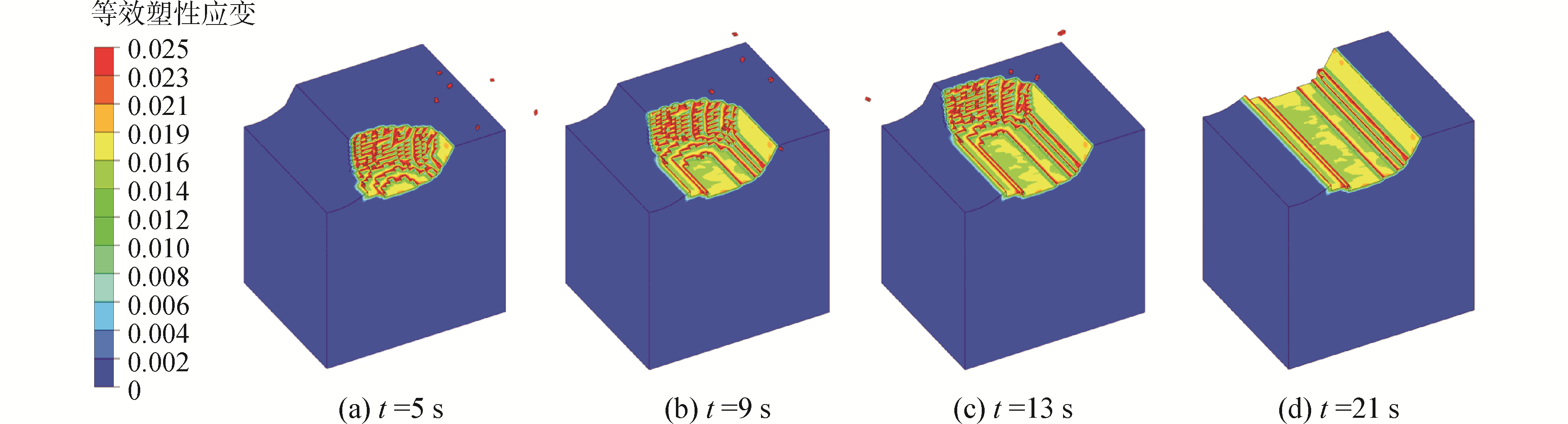
应用前述方法,对实际绞刀挖岩过程进行数值模拟。在实际绞刀挖岩的模拟过程中,保持绞刀轴线与水平面夹角为30°、步长为1.9 m、挖深为0.75 m不变。当绞刀转速为30 r/min,横移速度为15 m/min时,切削过程中不同时刻的岩体形貌如图 5所示。从图中可以看出,随着绞刀横移切削,切屑在惯性作用下不断飞出,破碎区域也随之行进。模拟结果成功反映了切屑的形成和分离过程,切屑呈破碎块状,与实际相符。
|
Download:
|
| 图 5 不同时刻的岩石破碎形态 Fig. 5 Rock breaking profile at different time | |
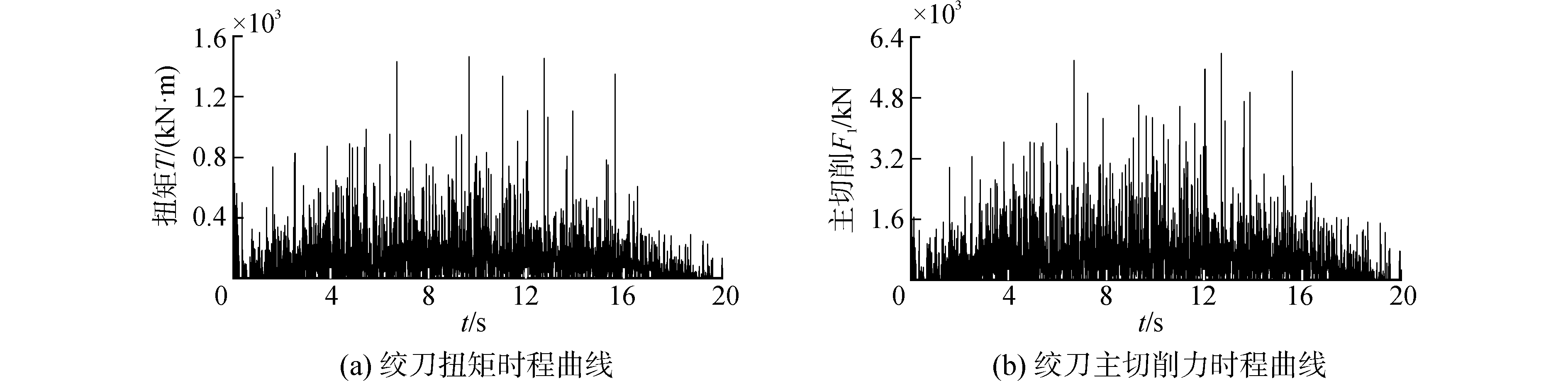
数值模拟得到的绞刀扭矩和主切削力曲线如图 6所示。挖岩过程中岩体破碎造成切削载荷曲线存在显著震荡,并且存在许多零点[14]。数据处理的方法为取稳定切削阶段的数据,去掉载荷最高峰值百分之一以下的数据后取平均值。
|
Download:
|
| 图 6 扭矩与主切削力的时程曲线 Fig. 6 Time history curves of torque and main cutting force | |
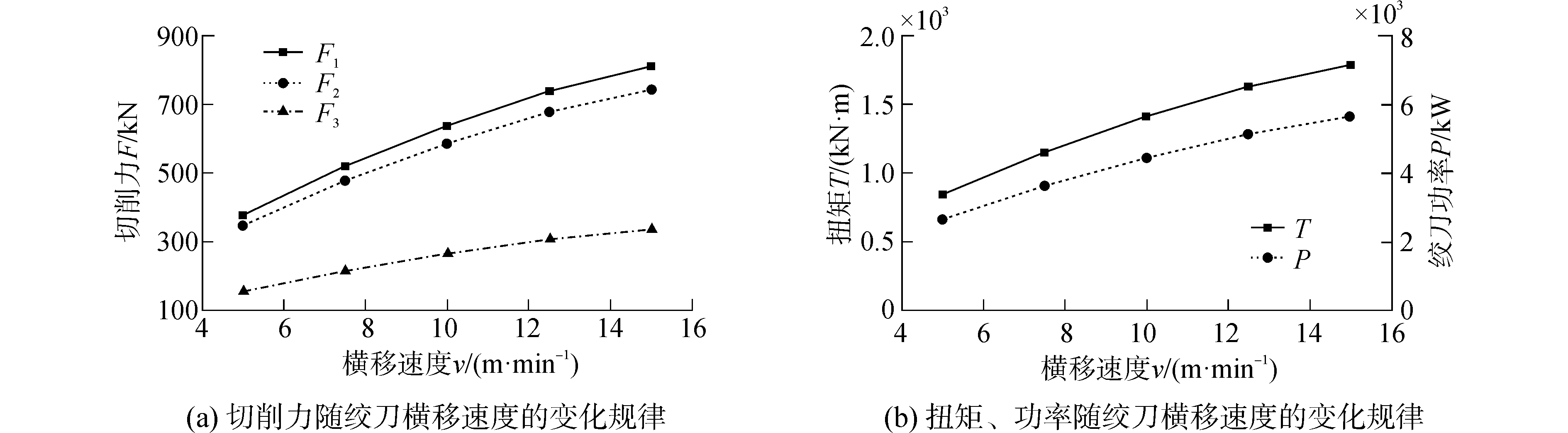
当绞刀转速为30 r/min时,分别取横移速度为5、7.5、10、12.5和15 m/min进行模拟。由图 7可知,三个方向的切削力均随横移速度增大而增大,且F1、F2增幅较大。F1为横移切削方向的切削力,横移速度越大,刀齿切削厚度越大,所以F1随横移速度增大而增大。F2为绞刀径向切削力,F2过大将造成刀架弹起,因此在实际疏浚施工中需要对绞刀施加足够的压载,以保证切削过程正常进行。
|
Download:
|
| 图 7 横移速度对切削力和功率的影响 Fig. 7 Effect of velocity on cutting forces and power | |
功率随横移速度增大而增大是因为横移速度越大则单位时间内挖岩量越大,所需的破岩能量越大。还可以看出,当横移速度从15 m/min下降到5 m/min时,扭矩与功率均大幅下降。正因如此,实际疏浚作业中才可以将横移速度作为调节参数,当绞刀受力和功率突然增大时,控制系统将适当降低横移速度以防止过载。
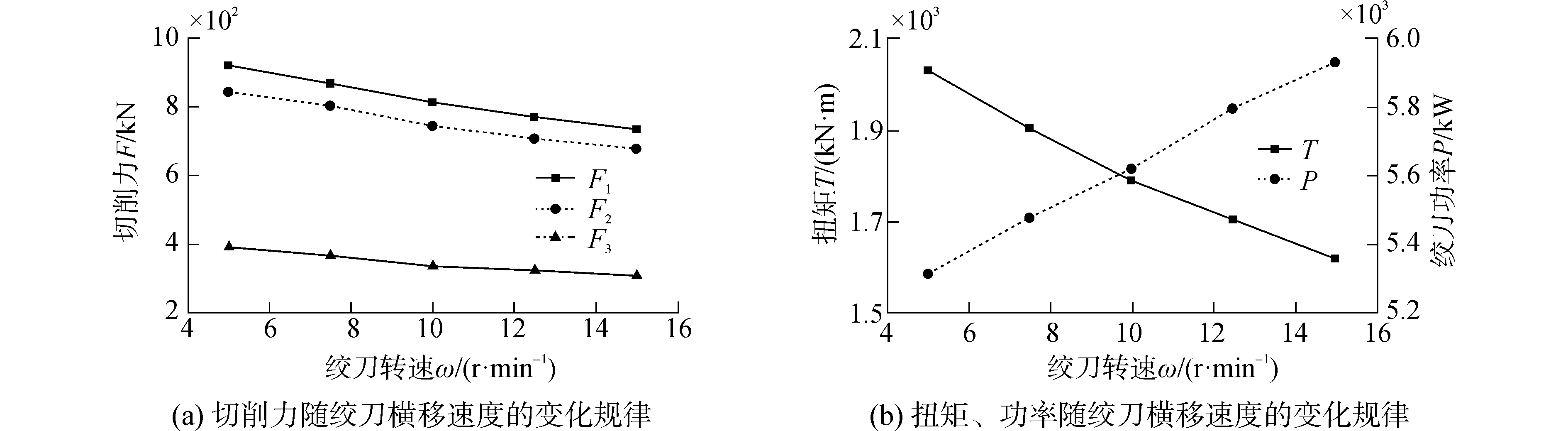
4.2.3 绞刀转速对绞刀切削力和功率的影响当横移速度为15 m/min时,分别取绞刀转速为25、27.5、30、32.5和35 r/min进行模拟。从图 8中可以看出,三个方向的切削力随绞刀转速增加均有所下降,这是因为在相同横移速度的条件下,绞刀转速增加,刀齿切削厚度变小所致。
|
Download:
|
| 图 8 绞刀转速对切削力与功率的影响 Fig. 8 Effect of rotation rate on cutting forces and power | |
绞刀功率随转速增加而呈现增加趋势,这是由于当绞刀横移速度恒定时,单位时间内挖岩总量恒定,此时绞刀转速越大,则对相同总量的岩石切削次数越多,结果是切屑更碎,因而需要消耗较多的能量,导致功率增加。岩石破碎程度对疏浚作业具有实际意义,例如要把水下破碎岩石经过泥浆泵吸出,如果破碎的岩石块体过大,将造成吸排困难。
4.2.4 切削比能岩石切削比能即切削破碎单位体积岩石所需的能量,比能直接反应了岩石切削过程中切削效率的高低,是岩石切削中的一个重要指标。切削比能可按下式计算:
| $ \eta = [T(2{\rm{ \mathsf{ π} }}n/60) + {F_1}v]/\left( {Sv} \right) $ | (9) |
式中:η为切削比能,T为绞刀扭矩,n为绞刀转速,v为绞刀横移速度,F1为绞刀横移拉力,S为被切削部分岩体的横断面面积。
应用最小二乘法对图 7和图 8中得到的数据进行二次拟合,将其代入式(9)并分别对v、n求导。当横移速度在5~15 m/min的范围内变化时η对v的导数值恒小于零,即切削比能随横移速度增大而单调递减。当绞刀转速在25~35 r/min的范围内变化时,η对n的导数值恒大于零,即切削比能随绞刀转速增大而单调递增。即适当提高横移速度与降低绞刀转速有利于降低岩石的切削比能,进而提高挖岩效率。
需要注意的是,实际施工中过度提高绞刀横移速度往往造成功率激增,甚至引起过载破坏,而绞刀转速过低将造成破碎岩石块体过大,导致吸排困难。因此,在施工中应综合考虑施工条件,对绞刀转速与横移速度进行合理调节,从而降低切削比能,提高挖岩效率。
5 结论1) 采用罚刚度形式的接触约束算法获得了任意时刻绞刀与岩体的接触状态和接触作用力。应用扩展的Drucker-Prager塑性模型以及包含单元删除功能的损伤演化模型模拟了岩体变形及破碎,从而实现了挖泥船绞刀挖岩过程的直接数值模拟。
2) 验证了有限元方法对挖泥船绞刀挖岩问题的适用性。不仅在几何形貌上再现了绞刀挖岩过程,而且获得的切削载荷与实验结果符合较好。
3) 获得了绞刀切削载荷与功率随绞刀转速与横移速度的变化规律。绞刀转速恒定时,切削载荷和功率随绞刀横移速度增大而显著增大。绞刀横移速度恒定时,功率随转速增大而增大,但切削载荷却有所下降。
4) 得到了绞刀挖岩效过程中切削比能随绞刀转速与横移速度的变化规律。研究表明:适当降低绞刀转速和提高横移速度有利于降低岩石切削比能,进而提高挖岩效率。
| [1] |
VLASBLOM W. Relation between cutting, sidewinch and axial forces for cutter suction dredgers[C]//Proceedings of the 15th World Dredging Congress. Las Vegas, Nevada, USA, 1998: 275-291.
(  0) 0)
|
| [2] |
MIEDEMA S A. New developments of cutting theories with respect to dredging, the cutting of clay and rock[J]. WEDA XXIX & Texas A&M, 2009, 40: 14-17. (  0) 0)
|
| [3] |
凌良勇. 绞吸式挖泥船绞刀切削受力及其影响因素分析[J]. 船海工程, 2014, 43(4): 156-159. LING Liangyong. Analysis on cutting forces and influence factors of the suction dredger's cutter[J]. Ship & ocean engineering, 2014, 43(4): 156-159. (  0) 0)
|
| [4] |
潘英杰, 杨启, 汤晶. 基于二维切削理论的绞吸式挖泥船绞刀头载荷分析[J]. 船海工程, 2009, 38(2): 35-39. PAN Yingjie, YANG Qi, TANG Jing. Cutting force calculation of the cutter suction dredger based on 2-D soil-cutting theory[J]. Ship & ocean engineering, 2009, 38(2): 35-39. (  0) 0)
|
| [5] |
陈晓华, 杨启. 大型绞吸挖泥船挖岩绞刀切削力计算分析[J]. 武汉理工大学学报(交通科学与工程版), 2013, 37(1): 106-110. CHEN Xiaohua, YANG Qi. Calculation of cutting forces for cutter head on large cutter suction dredger[J]. Journal of Wuhan university of technology (transportation science & engineering), 2013, 37(1): 106-110. (  0) 0)
|
| [6] |
ABO-ELNOR M, HAMILTON R, BOYLE J T. Simulation of soil-blade interaction for sandy soil using advanced 3D finite element analysis[J]. Soil and tillage research, 2004, 75(1): 61-73. DOI:10.1016/S0167-1987(03)00156-9 (  0) 0)
|
| [7] |
BENTAHER H, IBRAHMI A, HAMZA E, et al. Finite element simulation of moldboard-soil interaction[J]. Soil and tillage research, 2013, 134: 11-16. DOI:10.1016/j.still.2013.07.002 (  0) 0)
|
| [8] |
IBRAHMI A, BENTAHER H, MAALEJ A. Effect of the design moldboard on the tillage forces[C]//Proceedings of the 20135th International Conference on Modeling, Simulation and Applied Optimization. Hammamet, Tunisia, 2013: 1-6.
(  0) 0)
|
| [9] |
LI Mo, CHEN Donghui, ZHANG Shujun, et al. Biomimeitc design of a stubble-cutting disc using finite element analysis[J]. Journal of bionic engineering, 2013, 10(1): 118-127. DOI:10.1016/S1672-6529(13)60206-1 (  0) 0)
|
| [10] |
徐中华, 王建华. 有限元法分析土壤切削问题的研究进展[J]. 农业机械学报, 2005, 36(1): 134-137. XU Zhonghua, WANG Jianhua. Advances in finite element analysis of soil cutting[J]. Transactions of the Chinese society for agricultural machinery, 2005, 36(1): 134-137. (  0) 0)
|
| [11] |
杨桢毅, 朱汉华, 范世东, 等. 基于ANSYS的绞吸式挖泥船齿式绞刀结构强度分析[J]. 武汉理工大学学报, 2012, 33(11): 131-134. YANG Zhenyi, ZHU Hanhua, FAN Shidong, et al. Analyze the structural strength of cutter suction dredger based on ANSYS[J]. Journal of Wuhan University of Technology, 2012, 33(11): 131-134. (  0) 0)
|
| [12] |
刘姣, 李洪彬, 钱丽娜, 等. 基于SolidWorks与ANSYS的挖泥船绞刀有限元分析[J]. 机械设计与研究, 2010, 26(3): 64-66. LIU Jiao, LI Hongbin, QIAN Li'na, et al. Finite element analysis of a dredger cutterhead based on SolidWorks and ANSYS[J]. Machine design and research, 2010, 26(3): 64-66. (  0) 0)
|
| [13] |
HIBBITT K S. ABAQUS analysis user's manual help online[M]. USA: SIMULIA, 2005.
(  0) 0)
|
| [14] |
JAIME M C, ZHOU Yanneng, LIN J S, et al. Finite element modeling of rock cutting and its fragmentation process[J]. International journal of rock mechanics and mining sciences, 2015, 80: 137-146. DOI:10.1016/j.ijrmms.2015.09.004 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


