2. 哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
随着海洋开发进程的加快,无人无缆自主式水下机器人(autonomous underwater vehicle,AUV)作业技术逐渐引起人们的关注[1]。AUV载体与携带机械手构成一种新型的自主式水下机器人-机械手系统(autonomous underwater vehicle-manipulator system, AUVMS),是目前AUV研究的重要内容之一[2]。AUVMS在水下作业过程中,随着机械手展开,将引起系统重心、浮心位置发生变化,导致AUVMS产生纵倾或横倾,直接影响其作业姿态和作业能力;因此研究机械手展开引起的AUVMS姿态的稳定控制技术具有重要的研究意义和实用价值[3]。
目前国内外水下装备的姿态控制主要有两种形式[4-7]。即推进器控制姿态和重浮心变化控制姿态。本文AUVMS中,机械手展开作业时,重心变化将引起纵横倾姿态变化。由于AUVMS需推进器动力定位,如再用推进器进行纵横倾姿态控制,难以使系统定位和姿态控制两个目标同时达到最优;并且推进器一直工作能耗较大,因此本文不采用推进器姿态调节方式。文献[7]采用移动浮心法,通过执行机构驱动浮力材料运动,进而改变AUV浮心位置以调节姿态;但由于浮力材料密度较小、体积较大,本文AUVMS空间受限,因此不适用于本文水下机器人。从本质上看,文献[8-9]均为基于重心调节以控制AUV姿态,但文献[8]中水密度较小、姿态调节效率低、占用空间大,不适于本文AUVMS姿态调节。
AUV内部剩余空间较小,同时考虑到AUVMS能源有限[10],本文研究适用于微小型AUVMS的纵横倾姿态调节系统及其控制技术,研制原理样机,进行水池实验验证。
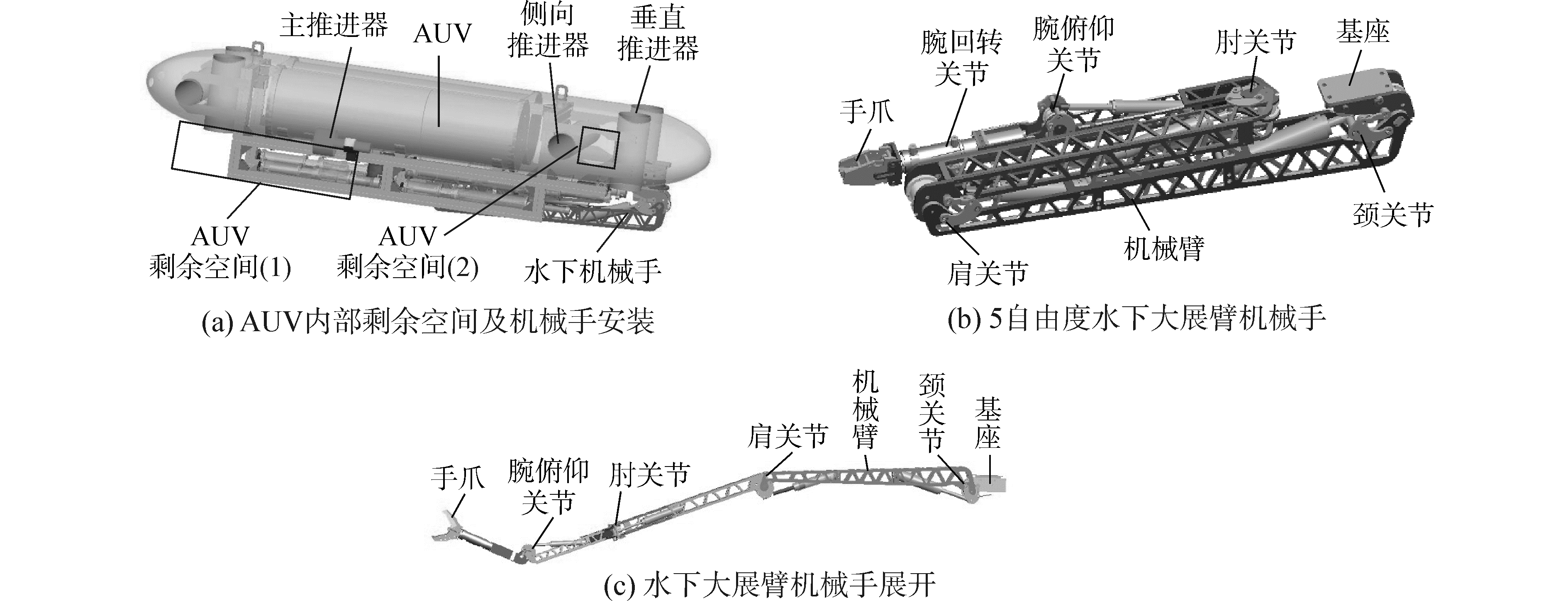
1 AUVMS姿态调节系统 1.1 AUVMS原理样机结构本文AUVMS样机如图 1(a)所示,属于微小作业型AUV,外形为椭圆流线型,长宽高为2.0 m×0.6 m×0.6 m,总重约205.0 kg;配置8个推进器,包括2个水平推进器、2个侧向推进器及4个垂直推进器,以及深度、速度、姿态角度传感器等。剩余空间(1)、(2)可用于安装纵横倾姿态调节系统。为不影响航行性能,机械手不工作时折叠收纳于AUV内部(如图 1(b)),机械手展开长度为2.3 m(如图 1(c))。
|
Download:
|
| 图 1 AUVMS原理样机图 Fig. 1 Assembly diagram of AUVMS principle prototype | |
根据AUVMS整体结构分析,机械手初始状态折叠收纳于AUV内部,导致AUV内部剩余空间较小;并且机械手臂展较长,估算其展开过程中产生的纵倾、横倾倾覆力矩分别约为10、0.8 N·m。经过分析,由于移动浮心法和液体抽排法占用空间较大、调节力矩较小,不适合本文内部空间小、调节力矩大的AUV系统。
分析移动重心法的占用空间和倾覆力矩调节能力。纵、横倾姿态调节力矩为10、0.8 N·m,纵横倾压载块质量约为15.0 kg;采用密度较大的铅块作为压载块时,姿态调节系统所占用空间Φ约为200 mm×800 mm(直径×长度),系统总重(压载块+密封舱体)约25 kg;对比图 1(a)的AUVMS,可满足AUV剩余空间(1)的安装要求。因此移动重心法可作为本文姿态调节方案。
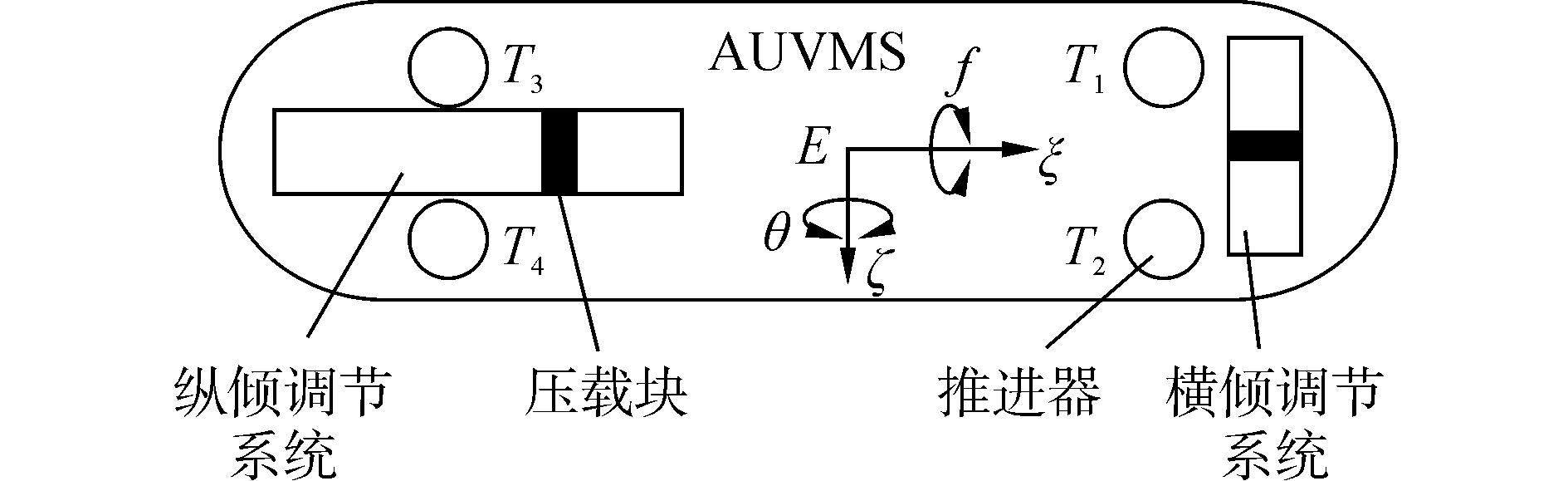
论证纵横倾姿态调节系统具体方案。根据功能要求和AUV内部可用空间情况,基于AUV水平轴线方向移动压载块以实现纵倾姿态调节。而横倾姿态调节具备旋转偏心压载块方式和横向平移压载块方式两种方式。进一步分析,旋转偏心压载块方式虽然能充分利用AUV内部空间,但此方式会影响AUV稳心高,进而影响AUV纵倾姿态;而横向平移压载块方式在空间利用方面相比旋转偏心压载块方式要差,但该方式不影响AUV稳心高。根据图 1(a)的AUVMS样机内部剩余空间分析,横倾姿态调节系统体积较小,可安装于图 1(a)中剩余空间(2)位置,因此本文采用横向平移压载块方式调节横倾姿态。本文纵倾姿态调节沿AUVMS水平轴线ξ方向布置,横倾姿态调节系统平行于AUVMS的ζ方向,如图 2所示。
|
Download:
|
| 图 2 AUVMS姿态调节系统分布示意图 Fig. 2 Distribution diagram of AUVMS attitude control system | |
针对AUVMS内部空间受限、姿态调节系统需要调节力矩较大的问题,在姿态调节系统结构设计方面,本文设计了“锥齿轮副+丝杠螺母副”结合的传动方式。该传动方式中,采用“锥齿轮副”进行转向,以减少电机占用空间;采用“丝杠螺母副”扩大输出力矩,以减小电机功率,提高姿态调节系统力矩调节能力。同时,利用梯形丝杠螺母副的反向自锁功能,实现电机停止时AUVMS的姿态保持,避免通过电机控制实现姿态保持,以减少能耗。
姿态调节系统设计过程中,考虑到姿态调节系统自身安全性问题,设计了“软件限位”和“硬件限位”两级保护。软件限位是指:在系统中,通过磁栅尺传感器监测压载块运动;当压载块单侧移动距离超过最大行程时,软件限位使得电机停止。硬件限位为:系统压载块两侧的移动极限位置设计有限位开关,当压载块位置超限时,电机自动停止。本文“软件限位”和“硬件限位”两者满足其中一个条件,姿态调节系统限位停止。
通过对电机驱动压载块进行20次(软、硬限位各10次)运动超限测试,软、硬件限位方法限位成功率为100%,验证了本文软件限位和硬件限位方法的有效性。
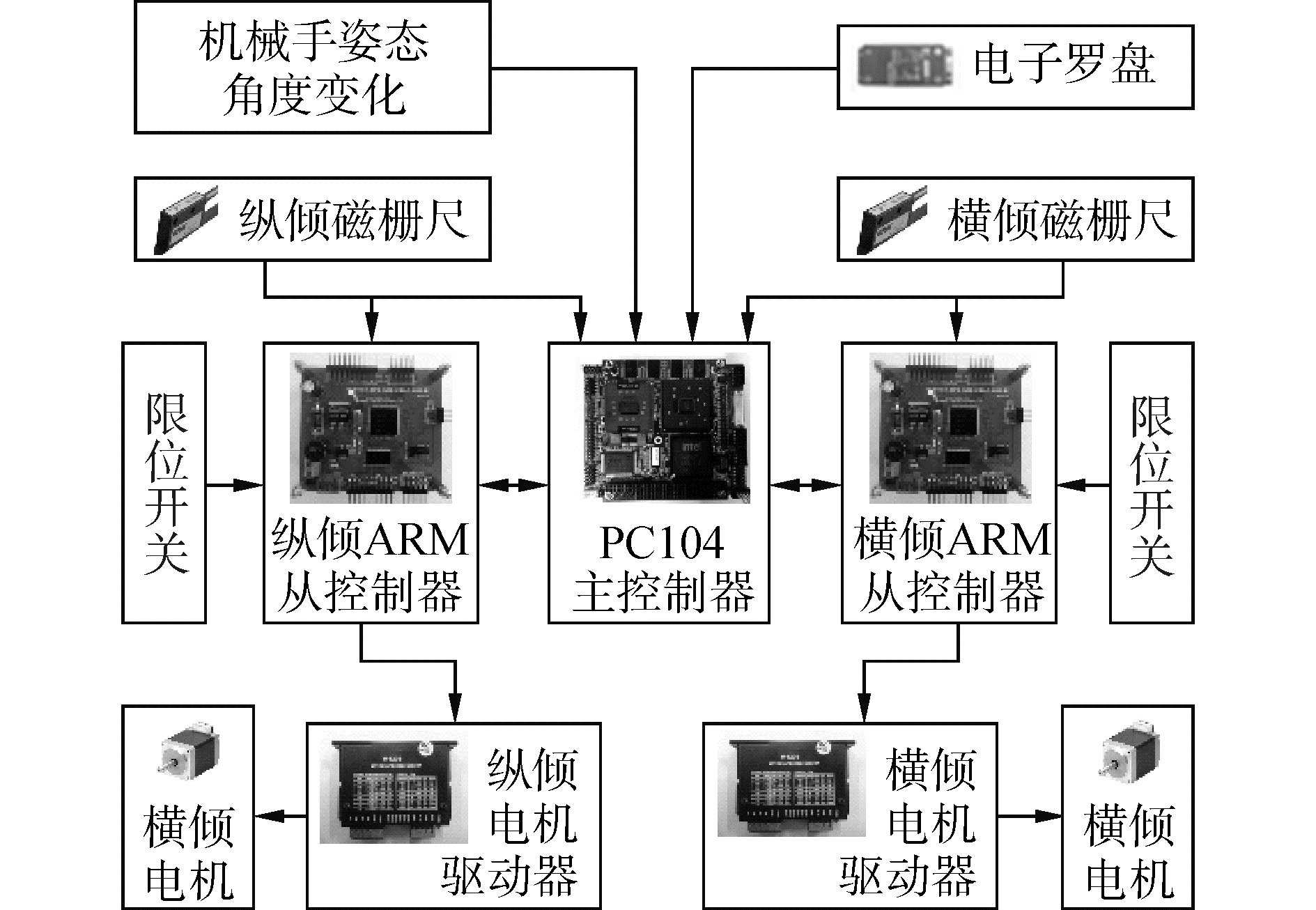
1.4 姿态调节控制系统设计为满足信号实时采集和控制信号实时收发,姿态调节系统控制器需具备高速信息处理能力和丰富I/O端口;同时还应具备电机负载驱动能力。为满足上述要求,本文设计的硬件总体框图如图 3所示。
|
Download:
|
| 图 3 姿态调节控制系统总体框图 Fig. 3 Overall block diagram of attitude control system | |
为充分利用控制器的数据处理能力,以及避免信号采集对数据运算的干扰,姿态调节系统分为主从两级控制。主控制器“PC104”用于数据处理,其高速处理能力(速度达300 MHz)、丰富I/O端口、串并口通信能力,可满足本文系统控制通信要求。从控制器为自研“ARM”控制板,集成运算放大、光耦隔离、信号采集等功能,分别实现电机驱动、电磁隔离和信息采集。
2 AUVMS姿态控制技术 2.1 AUVMS姿态方程由于机械手排水量约占AUVMS总排水量的2.9%,可近似认为机械手作业过程中其浮心位置基本不变,导致AUVMS姿态变化的主要原因为机械手展开引起的重心变化,因此本文研究基于重心调节的姿态控制方法。在研究姿态控制方法之前,本文首先分析AUVMS作业过程的系统重心变化,得出机械手重心公式,并以此为基础,推导基于重心变化的AUVMS姿态动力学方程。
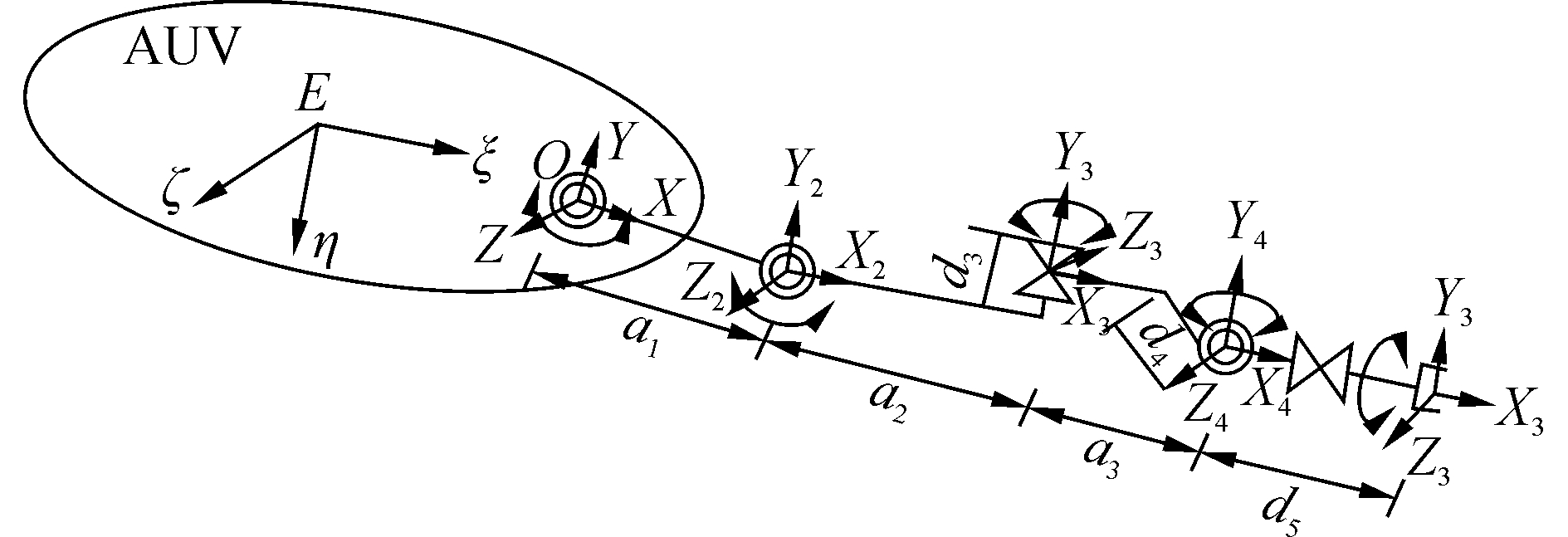
本文机械手和AUV艇体坐标系,如图 4所示。
|
Download:
|
| 图 4 AUVMS坐标系 Fig. 4 The coordinate system of the AUVMS | |
图 4所示,AUV坐标系E-ξηζ的原点E为AUVMS初始重心位置(x0, y0, z0),原点O为机械手肩关节中心点;O与E的位置关系可通过AUVMS三维模型得出。在机械手坐标系O-XYZ下,基于机械手关节参数,得到颈、肩、肘、腕关节重心位置如下
| $ \begin{array}{l} \left\{ \begin{array}{l} x{'_1} = {a_1}{c_1}\\ y{'_1} =-{a_1}{s_1}\\ z{'_1} = 0, \end{array} \right.\;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} x{'_2} = {a_1}{c_1} + {a_2}{C_{12}}\\ y{'_2} =-{a_1}{s_1}-{a_2}{S_{12}}, \\ z{'_2} = 0 \end{array} \right.\\ \left\{ \begin{array}{l} x{'_3} = {a_1}{c_1} + {a_2}{C_{12}} + {a_3}{c_3}{C_{12}} - {d_3}{S_{12}}\\ y{'_3} = - {a_1}{s_1} - {a_2}{S_{12}} - {a_3}{S_{12}}{c_3} - {d_3}{C_{12}}\\ z{'_3} = - {a_3}{s_3} \end{array} \right.\\ \left\{ \begin{array}{l} x{'_4} = {a_1}{c_1} + {a_2}{C_{12}} + {\rm{ }}{a_3}{C_{12}}{c_3} - {d_3}{S_{12}} - \\ \;\;\;\;\;\;{\rm{ }}{d_4}{C_{12}}{s_3} + {d_5}\left( {{S_{12}}{c_4} - {C_{12}}{c_3}{s_4}} \right)\\ y{'_4} = - {a_1}{s_1} - {a_2}{S_{12}} - {a_3}{S_{12}}{c_3} + \\ \;\;\;\;\;\;\;\;\;\;\;{d_4}{S_{12}}{s_3} + {\rm{ }}{d_5}\left( {{C_{12}}{c_4} + {S_{12}}{c_3}{s_4}} \right)\\ z{'_4} = - {a_3}{s_3} - {d_4}{c_3} + {d_5}{s_3}{s_4} \end{array} \right. \end{array} $ | (1) |
式中:a1、a2、a3、d3、d4、d5为图 4(a)中机械手各关节臂展长度。
基于重心坐标公式[7],结合式(1)可得机械手整体重心坐标为
| $ \left\{ \begin{array}{l} x' = ({m_{a1}}x{'_1} + {m_{a2}}x{'_2} + {\rm{ }}{m_{a3}}x{'_3} + {m_{a4}}x{'_4})/{m_4}\\ y' = ({m_{a1}}y{'_1} + {m_{a2}}y{'_2} + {\rm{ }}{m_{a3}}y{'_3} + {m_{a4}}y{'_4})/{m_4}\\ z' = ({m_{a1}}z{'_1} + {m_{a2}}z{'_2} + {\rm{ }}{m_{a3}}z{'_3} + {m_{a4}}z{'_4})/{m_4} \end{array} \right. $ | (2) |
式中:ma1、ma2、ma3、ma4为颈、肩、肘、腕关节的机械臂质量,m4为机械手整体重量。
基于式(2),得到任意t、t+1时刻机械手位姿变化导致的机械手整体重心变化量为
| $ \left\{ \begin{array}{l} \Delta x' = x{'_{t + 1}}-x{'_t}\\ \Delta y' = y{'_{t + 1}}-y{'_t}\\ \Delta z' = z{'_{t + 1}}-z{'_t} \end{array} \right. $ | (3) |
坐标系E-ξηζ下,t时刻AUVMS重心位置为(xt, yt, zt),t+1时刻重心位置(xt+1, yt+1, zt+1)为
| $ \left\{ \begin{array}{l} {x_{t + 1}} = \sum\limits_{i = 1}^4 {{m_i}{x_i}} /\sum\limits_{i = 1}^4 {{m_i}} = {x_t} + {m_4}\Delta x'/\sum\limits_{i = 1}^4 {{m_i}} \\ {y_{t + 1}} = \sum\limits_{i = 1}^4 {{m_i}{\mathit{y}_i}} /\sum\limits_{i = 1}^4 {{m_i}} = {y_t} + {m_4}\Delta y'{\rm{/}}\sum\limits_{i = 1}^4 {{m_i}} \\ {z_{t + 1}} = \sum\limits_{i = 1}^4 {{m_i}{z_i}} /\sum\limits_{i = 1}^4 {{m_i}} = {z_t} + {m_4}\Delta z'/\sum\limits_{i = 1}^4 {{m_i}} \end{array} \right. $ | (4) |
式中:俯仰和横滚姿态调节系统压载块重量为m1、m2,AUV重量为m3。式(4)为机械手运动位姿变化而引起的AUVMS重心位置变化公式。
由于AUVMS姿态变化的动力学方程与重心变化量相关,因此基于重心变化公式(式4)以及文献[11]中推导的AUV纵倾、横倾运动的动力学方程,得出基于AUVMS重心变化的纵横倾姿态方程。并根据本文AUVMS样机参数、水动力系数和重心变化数值代入纵横倾姿态方程,可得
纵倾姿态方程:
| $ \begin{array}{l} 56.13\dot p = 3{\rm{ }}213.2p\left| p \right|-(204.5x-203.9{x_{\rm{c}}}){\rm{ }}\cdot\\ {\rm{cos}}\theta {\rm{cos}}\varphi-(7.46z - 7.44{z_{\rm{c}}}){\rm{sin}}\theta \end{array} $ | (5) |
横倾姿态方程:
| $ \begin{array}{l} 6.36\dot q = 1{\rm{ }}532.9{\rm{ }}q\left| q \right|-(204.5y-203.9{y_{\rm{c}}})\cdot\\ {\rm{cos}}\theta {\rm{cos}}\varphi-(7.46z - 7.44{z_{\rm{c}}}){\rm{cos}}\theta {\rm{sin}}\varphi \end{array} $ | (6) |
式中:p、q分别为纵倾、横倾角速度,(xc, yc, zc)为浮心位置坐标,(x, y, z)为式(4)的重心坐标量。
根据AUVMS纵横倾姿态动力学方程,可得重心重心坐标量(x, y, z)与姿态角速度(p、q)、纵横倾角(θ、
本文基于AUVMS纵横倾姿态动力学方程,进行姿态控制方法仿真研究,分析姿态角度变化,检验控制方法是否满足课题指标要求。纵横倾姿态调节指标要求为:1) 姿态调节过程中,纵倾、横倾的最大姿态偏差不超过±5°,姿态稳态误差小于±0.5°;2) 纵横倾姿态调节时间不超过150 s,AUVMS完成水下剪缆作业时间不超过600 s。
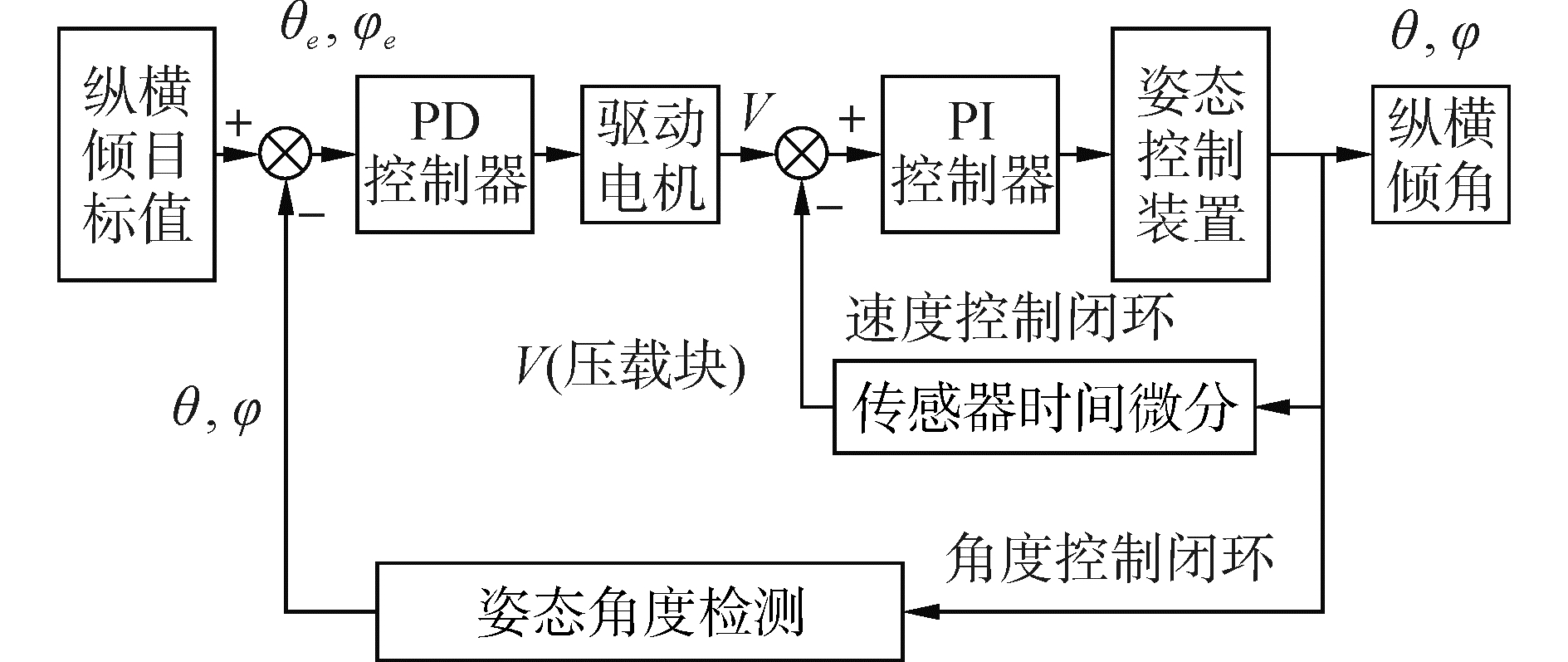
2.2.1 双闭环PID控制仿真结果分析本文首先分析常用的双闭环PID控制是否满足纵横倾姿态控制要求;以课题指标的姿态偏差、调节时间作为控制性能评价指标,进行仿真实验研究。AUVMS姿态双闭环控制框图如图 5所示。
|
Download:
|
| 图 5 双闭环PID控制原理图 Fig. 5 The control schematic of double-closed-loop PID | |
基于2.1节纵横倾姿态动力学方程进行仿真实验,实验过程与参数如下:模拟AUV在水池环境中悬停作业,即AUV自身绝对位置不固定。机械手从AUVMS内部展开(其颈、肩、肘、腕关节展开角度均分0°~170°,此机械手的展开角度对AUVMS纵横倾影响最大)过程中,检验姿态调节系统的姿态控制性能。
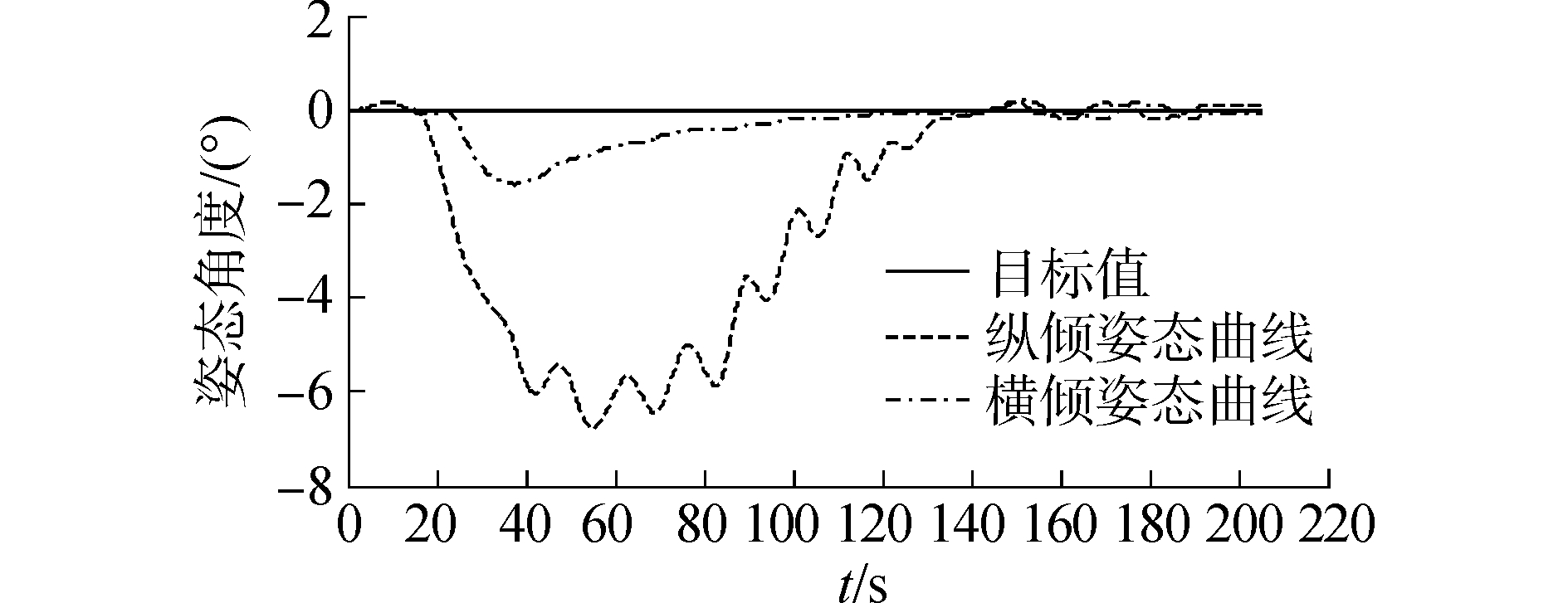
纵横倾姿态控制仿真结果如图 6所示。纵倾和横倾姿态稳态误差在±0.5°范围内部,满足课题指标要求。图 6中,横倾姿态偏差(-1.8°)满足课题指标要求;但纵倾姿态偏差为-6.8°(大于±5°),不满足指标要求。从姿态调节时间分析,纵、横倾调节时间分别为160.6、164.2 s,均不满足课题指标(<150 s)要求。
|
Download:
|
| 图 6 纵横倾姿态角度曲线 Fig. 6 Attitude angle curve of pitch and roll | |
姿态调节过程中,为满足稳态误差指标要求,双闭环PID控制的角度外环(PD控制)Kp取值较小,Kd取值较大;此参数取值虽然可以减少稳定误差,但会导致姿态调节时间过长,纵横倾姿态偏差较大。进一步分析,双闭环PID控制中,控制参数恒定;而水中的AUVMS具有时变的非线性特性,因此恒定控制参数难以满足姿态控制精度要求。
2.2.2 AUVMS姿态控制方法改进针对参数难以满足课题指标要求问题,考虑纵横倾姿态调节系统的时变非线性特性,基于模糊控制适用于二阶非线性系统的优点[12-13],本文对上述方法进行改进,改进的出发点为:在姿态角度闭环中加入模糊推理,使得整个姿态控制过程中,Kp、Kd等控制参数是变化的。
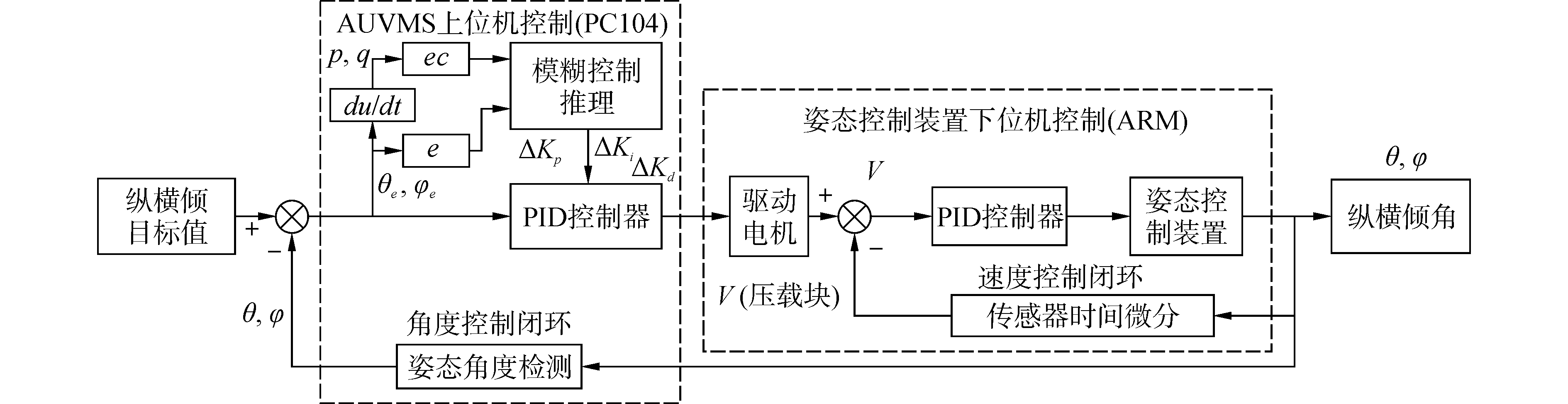
本文改进后的模糊双闭环PID控制框图如图 7所示。图 7方法与图 5控制方法区别在于,图 7中加入模糊控制,基于实时姿态偏差(θe、
|
Download:
|
| 图 7 AUVMS姿态控制原理图 Fig. 7 The attitude control schematic of AUVMS | |
在图 7中,纵、横倾姿态角度偏差量θe、
|
Download:
|
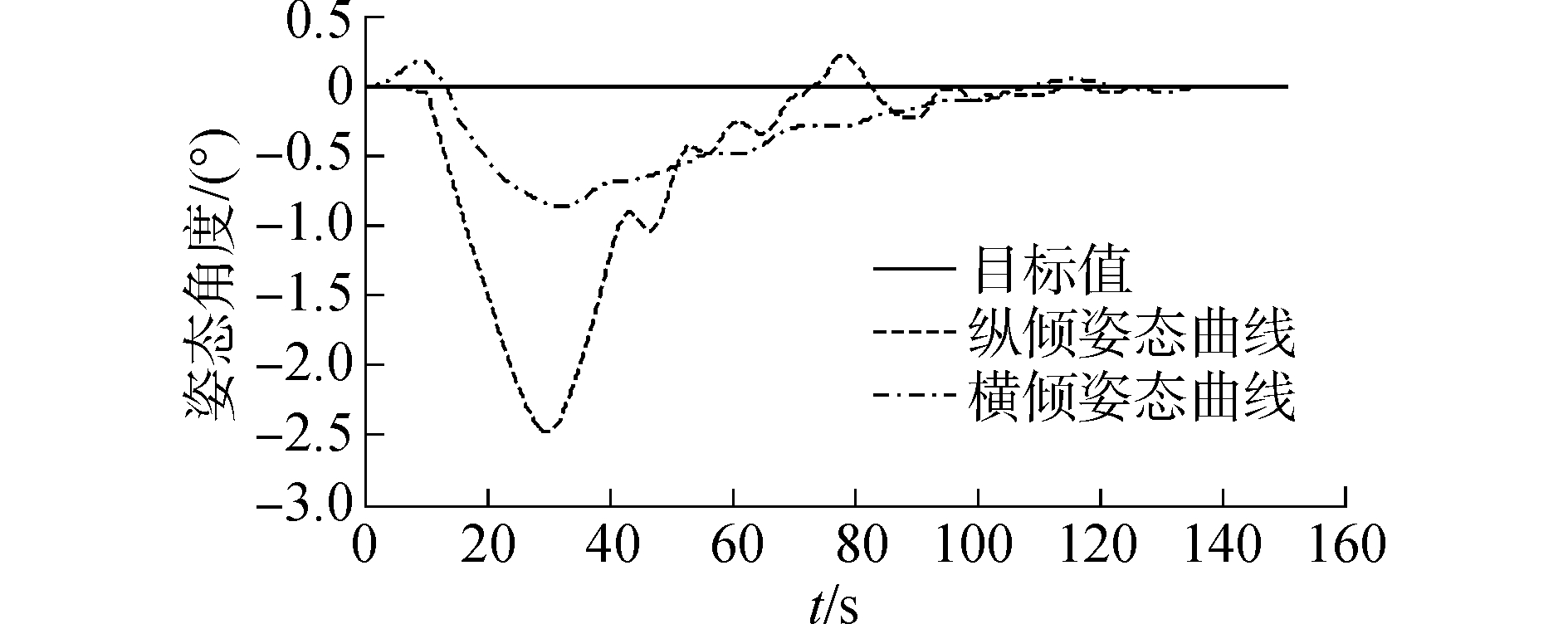
| 图 8 模糊双闭环PID控制下的姿态角度曲线 Fig. 8 The attitude angle curves under the fuzzy double-closed-loop PID control | |
图 8的仿真实验结果可以得出:
1) 纵横倾姿态稳态误差在±0.5°以内,满足课题指标要求。
2) 本文改进方法的纵倾最大姿态偏差和调节时间为-2.5°、109.8 s,横倾为-0.9°、114.5 s,均满足小于±5°和150 s的课题要求。而双闭环PID方法的纵倾姿态偏差和调节时间为-6.8°、160.6 s,横倾为-1.6°、164.2 s,不满足课题要求。
3) 与双闭环PID方法相比较,在姿态偏差方面,本文改进方法纵横倾姿态偏差分别降低63.2%、43.7%;调节时间方面,本文改进方法纵横倾姿态调节时间分别降低31.6%、30.3%。仿真验证了本文改进方法的有效性。
3 姿态调节实验研究 3.1 AUVMS姿态控制实验为验证研制的姿态调节系统性能,在水池环境下,水下机械手展开和作业状态,进行AUVMS纵横倾姿态调节实验;并且实验检验改进后的模糊双闭环PID方法的有效性;验证姿态调节指标是否满足课题要求。AUVMS原理样机如图 9所示。

|
Download:
|
| 图 9 AUVMS样机试验平台 Fig. 9 The AUVMS experimental platform | |
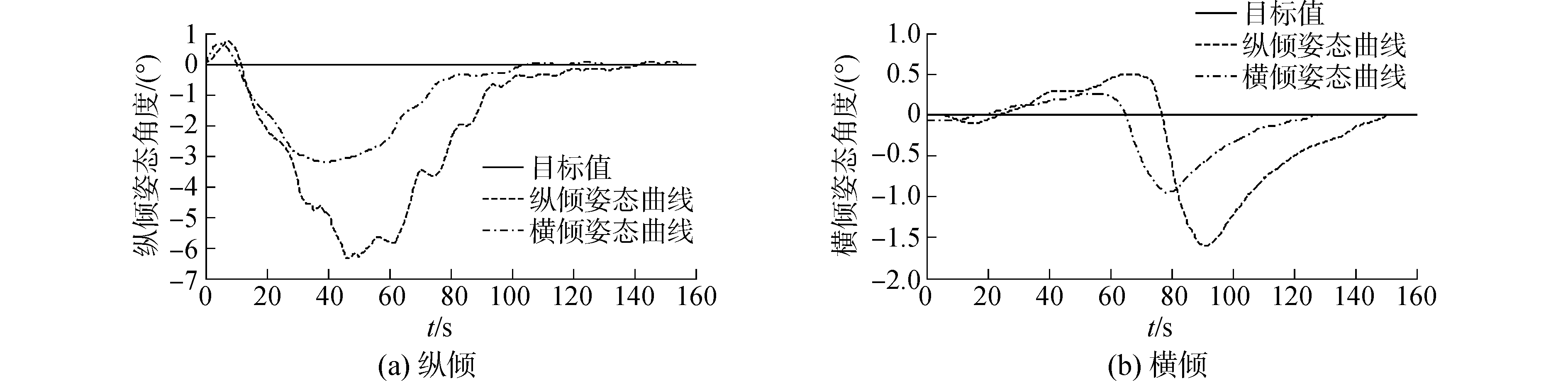
实验过程及主要参数如下:姿态控制时,机械手颈、肩、肘、腕各关节运动角度范围均为0°~170°(与仿真实验一致),纵倾(θ)、横倾(
|
Download:
|
| 图 10 水池环境下AUVMS姿态角度曲线 Fig. 10 Attitude angle curves of AUVMS in pool environment | |
图 10的实验结果可以得出:
1) 本文改进方法姿态稳态误差分别为-0.3°和0.2°,其数值在±0.5°以内,满足课题指标要求。
2) 本文改进方法的纵横倾最大姿态偏差和调节时间分别为-3.2°、119.0 s和-0.9°、103.6 s,均满足小于±5°和150 s课题要求。而双闭环PID方法的纵横倾姿态偏差和调节时间为-6.4°、155.6 s和-1.6°、150.2 s,不满足课题要求。
3) 与双闭环PID方法相比较,在姿态偏差方面,本文改进方法纵横倾姿态偏差分别降低49.6%、44.4%;调节时间方面,本文改进方法纵横倾姿态调节时间分别降低23.5%、31.0%;并且本文改进方法与双闭环PID比较,纵倾姿态振荡明显减少。
4) 与图 8的仿真结果相比,双闭环PID方法与本文改进方法的水池实验数据(姿态调节时间、姿态偏差)均与仿真数据大致相同。因此,水池实验数据仿真结果的可信度较高。
3.2 AUVMS水下剪缆实验为验证水下剪缆时间指标是否满足小于600 s的课题要求,进行AUVMS水下剪缆作业实验。
水下剪缆实验过程为:AUVMS原理样机距离目标物2.5 m时,机械手从AUVMS内部收纳状态开始展开;接下来基于视觉信息进行剪缆作业,直到机械手剪断线缆,目标物上浮,作业过程结束。
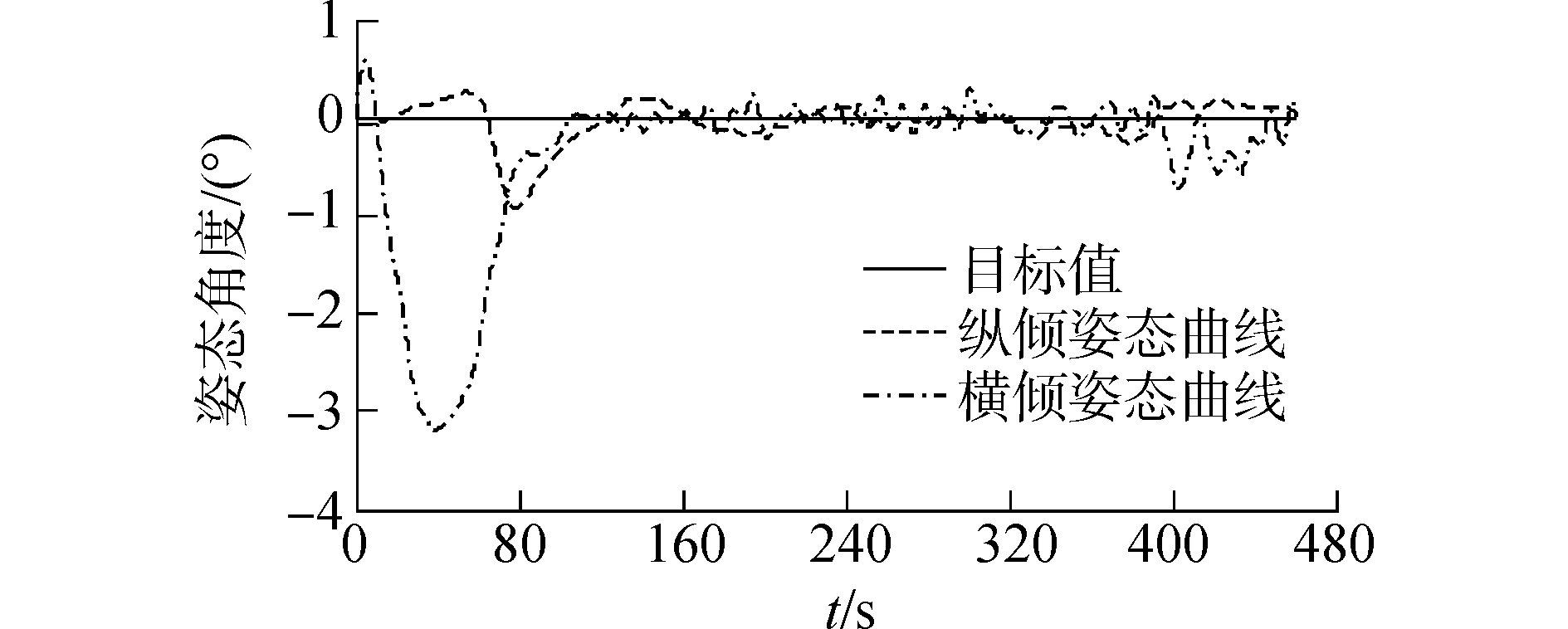
水下剪缆作业中纵横倾姿态变化如图 11所示。
|
Download:
|
| 图 11 剪缆作业的姿态角度曲线 Fig. 11 Attitude angle curves of cable cutting operation | |
分析图 11,在本文改进方法控制下,水下剪缆最大姿态偏差和调节时间分别为-3.5°、142 s,满足2.2节课题姿态偏差和调节时间要求;最大姿态偏差角度(-3.5°)较小,能保证目标物处于AUVMS水下视觉视场内部。并且剪缆作业过程时间为460 s,满足课题剪缆时间(小于600 s)指标要求。
上述水下作业实验结果表明:本文研制的姿态调节系统运行有效、工作可靠,实用效果良好,改进的控制方法可以满足课题对水下作业的要求。
3.3 AUVMS能耗实验由于AUV水下作业携带能源有限,能源的有效利用是AUV研究中需要考虑的问题之一。因此,在机械手水下展开作业过程中,通过水池实验分析研究姿态调节系统能耗;并与传统推进器姿态方案进行对比,验证姿态调节系统的低能耗特性。
能耗实验过程及参数:在水池环境中,AUVMS样机水中悬停状态下,机械手各关节角度分别展开到170°过程中,检测本文姿态调节系统和推进器方案的系统能耗。
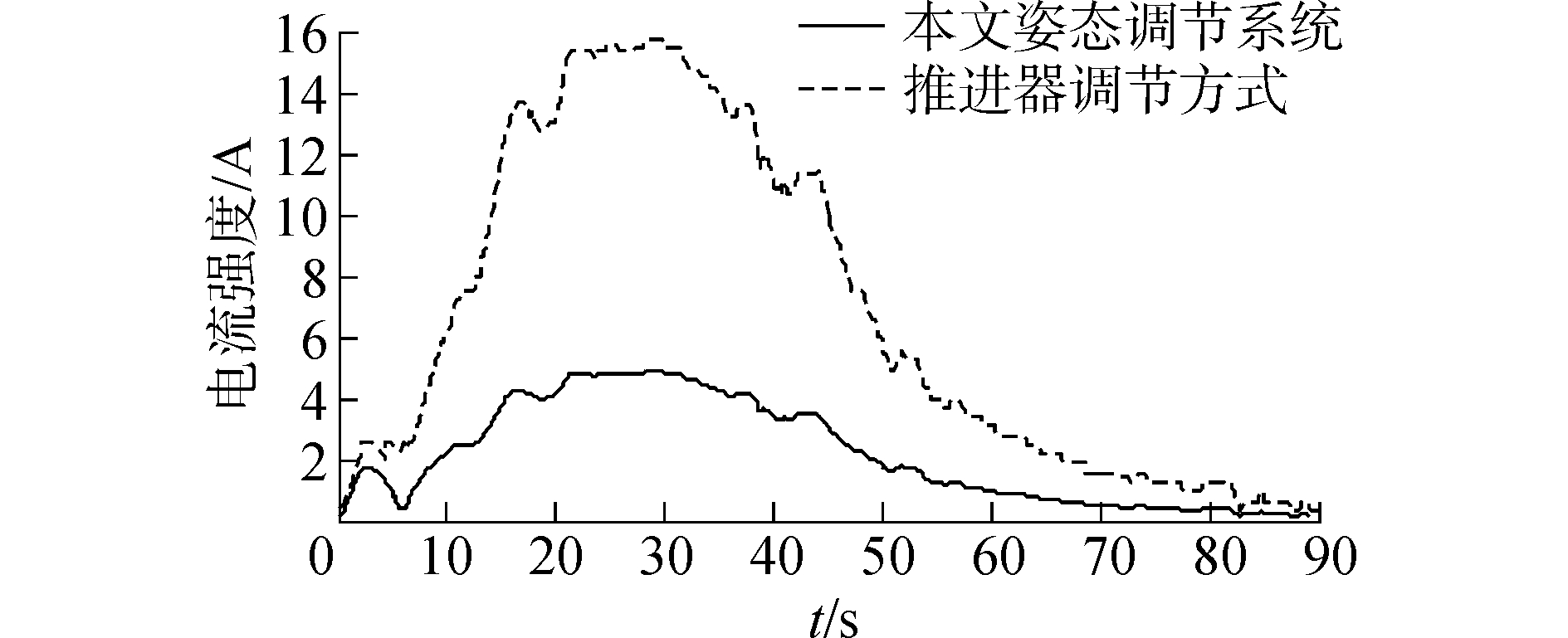
两种方案的系统输出电流数据如图 12所示。
|
Download:
|
| 图 12 AUV能源系统电流变化 Fig. 12 Current variation of AUV energy system | |
图 12系统电流变化,通过式(7)可转换为姿态调节过程的系统能耗[14]:
| $ Q = {\smallint _t}I\left( t \right){\rm{d}}t $ | (7) |
式中:t为姿态调整时间(0~90 s),I(t)为实验过程中电流变化曲线。通过式(7)计算,姿态调节过程的系统能耗如表 1所示。
| 表 1 不同姿态控制方案下的AUVMS能耗 Tab.1 The energy consumption of AUVMS under different attitude control schemes |
分析表 1,姿态调节过程中,本文姿态调节系统能耗为1.03×104 J,与推进器方案相比,本文姿态调节系统的能耗下降64.7 %;本文姿态调节系统的最大电流为5.05 A,相较于推进器方案的最大电流15.8 A,本文方法最大电流降低了68 %。实验数据得出,本文姿态方案能有效的降低AUVMS系统能耗,有利于增加AUV一次下潜的作业时间。
4 结论1) 与双闭环PID方法相比,本文方法纵横倾姿态偏差降低49.6%、44.4%,姿态调节时间降低23.5%、31.0%;验证本文方法的有效性。
2) 通过AUVMS水池剪缆作业和能耗实验验证:系统纵横倾最大姿态偏差为-3.5°、稳态误差小于±0.5°,满足课题要求;姿态调节最长时间为142 s,满足课题调节时间(150 s)要求。并且相较于推进器方案,本文姿态调节系统能耗降低64.7%,验证本文系统的低能耗特性。
| [1] |
徐玉如, 李彭超. 水下机器人发展趋势[J]. 自然杂志, 2011, 33(3): 125-132. XU Yuru, LI Pengchao. Developing tendency of unmanned underwater vehicles[J]. Chinese journal of nature, 2011, 33(3): 125-132. (  0) 0)
|
| [2] |
MARANI G, CHOI S K, YUH J. Underwater autonomous manipulation for intervention missions AUVs[J]. Ocean engineering, 2009, 36(1): 15-23. DOI:10.1016/j.oceaneng.2008.08.007 (  0) 0)
|
| [3] |
CONTI R, MELI E, RIDOLFI A, et al. An innovative decentralized strategy for I-AUVs cooperative manipulation tasks[J]. Robotics and autonomous systems, 2015, 72: 261-276. DOI:10.1016/j.robot.2015.06.006 (  0) 0)
|
| [4] |
SIMETTI E, CASALINO G, TORELLI S, et al. Floating underwater manipulation:developed control methodology and experimental validation within the trident project[J]. Journal of field robotics, 2014, 31(3): 364-385. DOI:10.1002/rob.2014.31.issue-3 (  0) 0)
|
| [5] |
苏玉民, 万磊, 李晔, 等. 舵桨联合操纵微小型水下机器人的开发[J]. 机器人, 2007, 29(2): 151-154. SU Yumin, WAN Lei, LI Ye, et al. Development of a small autonomous underwater vehicle controlled by thrusters and fins[J]. Robot, 2007, 29(2): 151-154. (  0) 0)
|
| [6] |
LI Qingmei, XIE Shaorong, LUO Jun, et al. Pitch reduction system design and control for an underwater vehicle[C]//Proceedings of 2014 IEEE International Conference on Mechatronics and Automation. Tianjin, China, 2014: 168-173.
(  0) 0)
|
| [7] |
SAKAGAMI N, SHIBATA M, KAWAMURA S, et al. An attitude control system for underwater vehicle-manipulator systems[C]//Proceedings of 2010 IEEE International Conference on Robotics and Automation. Anchorage, AK, USA, 2010: 1761-1767.
(  0) 0)
|
| [8] |
DETWEILER C, SOSNOWSKI S, VASILESCU I, et al. Saving energy with buoyancy and balance control for underwater robots with dynamic payloads[C]//Proceedings of the 11th International Symposium on Experimental Robotics. Berlin, Heidelberg, 2009: 429-438.
(  0) 0)
|
| [9] |
苏浩. 微小型水下机器人模块化技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2011: 30-38. SU Hao. Research on the modularization technology for mini underwater vehicle[D]. Harbin: Harbin Engineering University, 2011: 30-38. (  0) 0)
|
| [10] |
徐建安, 任立国, 杨立平, 等. 水下机器人广义预测控制算法及能耗问题研究[J]. 控制理论与应用, 2009, 26(10): 1148-1150. XU Jian'an, REN Liguo, YANG Liping, et al. Generalized predictive control and energy consumption analysis of autonomous underwater vehicle[J]. Control theory & applications, 2009, 26(10): 1148-1150. (  0) 0)
|
| [11] |
孙元泉, 马运义, 邓志纯. 潜艇和深潜器的现代操纵理论与应用[M]. 北京: 国防工业出版社, 2001: 145-156. SUN Yuanquan, MA Yunyi, DENG Zhichun. Modern maneuver theory and application of submarine and deep-diving submersible vehicle[M]. Beijing: National Defend Industry Press, 2001: 145-156. (  0) 0)
|
| [12] |
赵文德, 李建朋, 张铭钧, 等. 基于浮力调节的AUV升沉运动控制技术[J]. 南京航空航天大学学报, 2010, 42(4): 411-417. ZHAO Wende, LI Jianpeng, ZHANG Mingjun, et al. AUV heave motion control technology based on buoyancy adjusting[J]. Journal of Nanjing university of aeronautics & astronautics, 2010, 42(4): 411-417. (  0) 0)
|
| [13] |
王晓鸣, 张宏伟, 王树新. 基于模糊控制的水下自航行器着陆策略分析[J]. 机械工程学报, 2009, 45(3): 84-88. WANG Xiaoming, ZHANG Hongwei, WANG Shuxin. Analysis on the landing strategy of autonomous underwater vehicle based on fuzzy control[J]. Journal of mechanical engineering, 2009, 45(3): 84-88. (  0) 0)
|
| [14] |
张铭钧, 韩金华, 李洪志. 基于神经网络的水下机器人航向角跟踪控制[J]. 哈尔滨工程大学学报, 1999, 20(6): 1-8. ZHANG Mingjun, HAN Jinhua, LI Hongzhi. The heading angle trail control of AUV based on neural network[J]. Journal of Harbin engineering university, 1999, 20(6): 1-8. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


