2. 哈尔滨工程大学 机电工程学院, 黑龙江 哈尔滨 150001
2. Harbin Engineering University, Harbin 150001, China
控油装置是水下应急控油转接系统的核心装备,其工作稳定性将直接影响救援系统的整体性能[1-2]。控油装置研发中,海流和海底土质等主要因素发生变化时,即使是相同结构尺寸控油装置的设计重量及稳定性也是不同的。控油装置插入海土中,主要依靠海土的嵌固作用维持其姿态,不规则的海流对控油装置的冲击,将会使装备产生失稳的危险。
目前对插入式基础结构的分析多采用经典土力学理论,并在其成果基础上做修正,但考虑到土体效应,需对土压力做小幅折减[3-4]。控油装置箱是临时性“桩体结构”,除受到海底土载荷以外,还受到海流、泄漏压强等动载荷的作用,而针对这方面的研究非常少。本文采用真实模拟控油装置海底泥插入过程以及受到的海流力,以验证对其承载机理、失稳形式、位移等特性研究的正确性。
1 稳定性力学建模 1.1 土体极限平衡理论土的抗剪强度是指土体抵抗剪切破坏的极限能力。不同组成成份土壤的抗剪强度也不相同,海底土属于粘性土,库仑根据粘性土剪切试验,提出粘性土抗剪强度的表达式为
| $ {\tau _{\rm{f}}} = c + \sigma {\rm{tan}}\;\varphi $ | (1) |
式中:τf为土的抗剪强度,c为土的粘聚力,σ为作用在剪切面上的法向应力,
当土体中某点M任一平面上的剪应力等于土的抗剪强度时,由极限平衡条件和材料力学应力状态分析可以得到,该土单元任意截面m-n上的法向应力σ和剪应力τ可以用莫尔应力圆来表示[5]。该点土单元两个相互垂直的面上分别作用有最大的主应力σ1和最小主应力σ3。
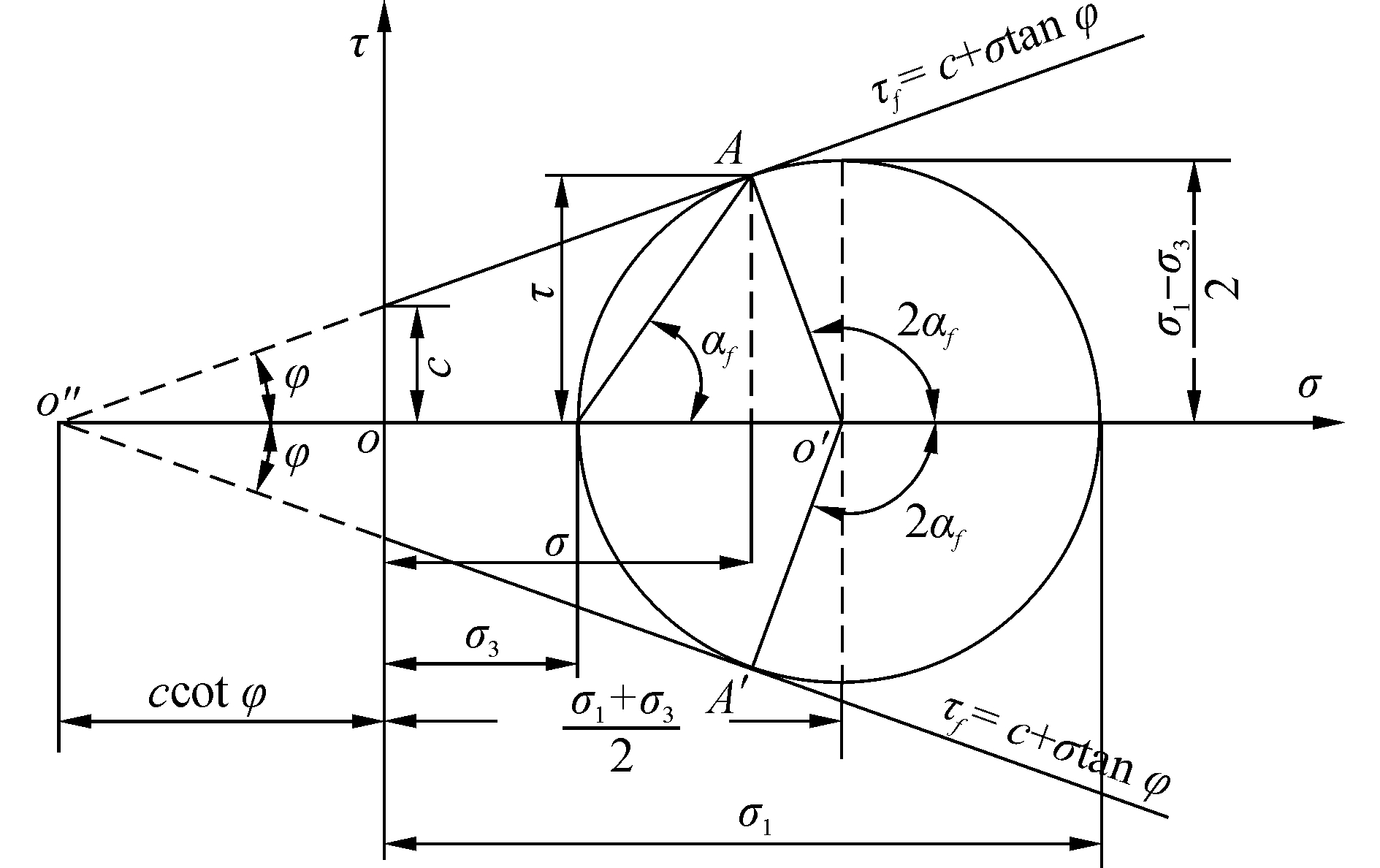
莫尔应力圆与抗剪强度包线之间的关系如图 1所示,分析可知,在粘性海土中,当M点处于极限平衡状态时,可以得到
| $ \left\{ \begin{array}{l} {\sigma _1} = {\sigma _3}{\rm{ta}}{{\rm{n}}^2}\left( {45^\circ + \frac{\varphi }{2}} \right) + 2c{\rm{tan}}\left( {45^\circ + \frac{\varphi }{2}} \right)\\ {\sigma _3} = {\sigma _1}{\rm{ta}}{{\rm{n}}^2}\left( {45^\circ-\frac{\varphi }{2}} \right)-2c{\rm{tan}}\left( {45^\circ-\frac{\varphi }{2}} \right) \end{array} \right. $ | (2) |
|
Download:
|
| 图 1 极限平衡状态时的莫尔圆与抗剪强度包线 Fig. 1 Mohr circle and shear strength envelope of limit equilibrium state | |
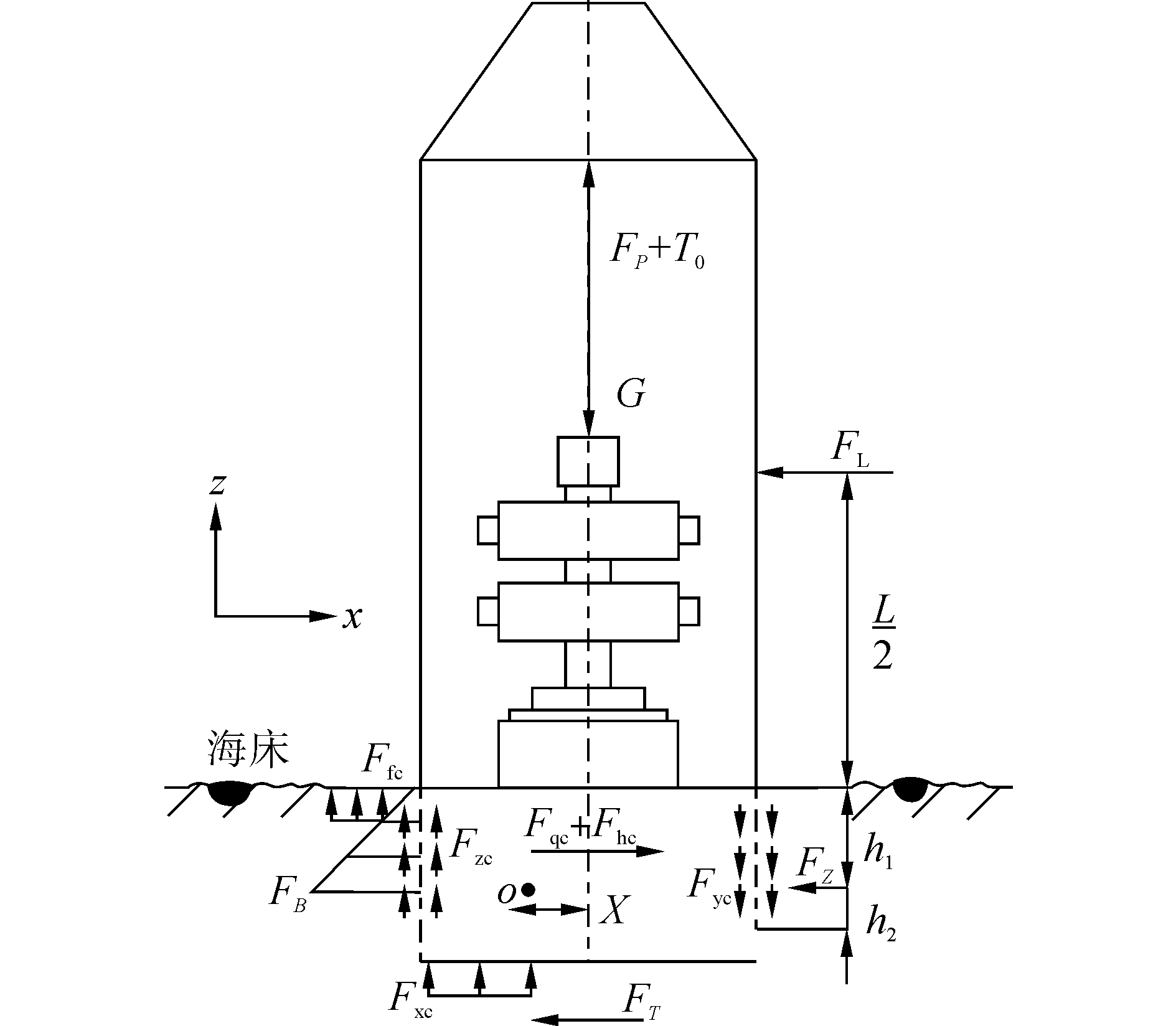
水下500 m深油气设施发生泄漏时,在遥控无人潜水器(remote operated vehicle, ROV)协助下,被下放至漏油点处的控油装置依靠自身重力克服粘性海土阻力下沉,直至防沉挡板与海床充分接触时停止下沉,此时,控油装置工作的稳定性由海土基的嵌固作用维持。根据极限平衡条件,转动支点的位置是建立控油装置稳定性分析模型的关键。控油装置简化为沉入式方体结构,分析模型如图 2所示。
|
Download:
|
| 图 2 控油装置力学模型 Fig. 2 Mechanics model of containment device | |
控油装置防沉挡板与下沉钢板底部距离,即为入泥深度h,在控油装置侧面受到海流力FL的作用,考虑内部油气泄漏载荷的侧向力作用,计算时为海流力乘以一个放大系数k1,控油装置将会绕着海床下某点发生转动。此时,水平方向上除海流力FL,还包括控油装置土体左右侧的水平抗力FB和FZ以及底部切力FT,由于控油装置是方体,还受到前后侧壁摩阻力τ3和τ4,竖直方向有控油装置顶端输油软管初始拉力T0,内部压力FP,控油装置竖向自重G,海床对防沉挡板的土反力应力σ1,海土对下沉钢板两侧作用力应力τ1和τ2,钢板底部土反力σ2。
在外部载荷的作用下,控油装置绕O点发生向左的转动,在极限状态设计方法中,可假设控油装置下沉钢板左右侧水平土抗力FB和FZ,土基底反力应力σ1和σ2,左侧钢板内、外向上的作用力应力τ1,前后侧壁的摩阻力τ3和τ4视为达到了极限值,如果右侧下沉钢板内、外侧向下的竖向作用力τ2也达到极限值的话可能会造成竖向力不平衡的情况,因此乘以折减系数λ,按照土力学桩侧工程计算习惯λ一般取0.5~0.8。
由x、z方向力平衡条件,以及O点的力矩平衡条件可得
| $ \left\{ \begin{array}{l} \sum H = {F_{\rm{B}}} + 2{F_{{\rm{qc}}}} + 2{F_{{\rm{he}}}} - {F_{\rm{T}}} - {F_{\rm{Z}}} - {\rm{ }}{k_1}{F_{\rm{L}}} = 0\\ \sum V = {T_0} + {F_{\rm{P}}} + {F_{{\rm{fc}}}} + {F_{\mathit{xc}}} + {\rm{ }}2{F_{{{\rm{ \mathsf{ τ} }}_{\rm{1}}}}} - 2\lambda {F_{{{\rm{ \mathsf{ τ} }}_{\rm{2}}}}} - G = 0\\ \sum M = {M_{\rm{L}}} - {F_{\rm{B}}}{l_{\rm{B}}} - {G_0}x - {M_{\rm{T}}} - {M_{\rm{ \mathsf{ τ} }}} - {M_5} - {M_6} = 0 \end{array} \right. $ | (3) |
式中:ML为水平海流力的力矩,lB为被动土力作用点距O点距离,G0为竖向力G、T0、FP的合力,Mτ为左右两侧下沉钢板竖向作用力应力τ1、τ2产生的力矩以及前后两侧下沉钢板侧壁摩阻力τ3、τ4产生的力矩,M5、M6为海土的反力应力σ1、σ2对转动点的力矩,MT为钢板底部切力T产生的力矩。
由水平力、垂直力和力矩平衡条件建立的平衡方程(3)可求得h1、h2和x,从而确定满足稳定性要求的入泥深度h=h1+h2。
1.3 倾覆失稳条件分析控油装置在自身重力作用下克服海床基面极限承载力和侧壁摩阻力下沉,当阻力大于控油装置自重或者到达防沉挡板以后,控油装置停止下沉,即
| $ {F_{\rm{f}}} + {F_\sigma } < G $ | (4) |
控油装置开始转接后,其受力包括:控油装置自重、海底海流力、内部泄漏载荷以及海底土的作用力,而当水平方向上的载荷超过控油装所能承受的极限扭矩,控油装置将发生倾覆失稳,因此,要保证安全的入泥深度至关重要。
由式(3)、(4)得到入泥深度满足如下要求:
| $ {h_1} + {h_2} < h < {h_{\max }} $ | (5) |
式中:h1+h2为满足其不发生倾覆失稳的最小入泥深度,hmax为满足侧摩阻力条件时极限入泥深度。
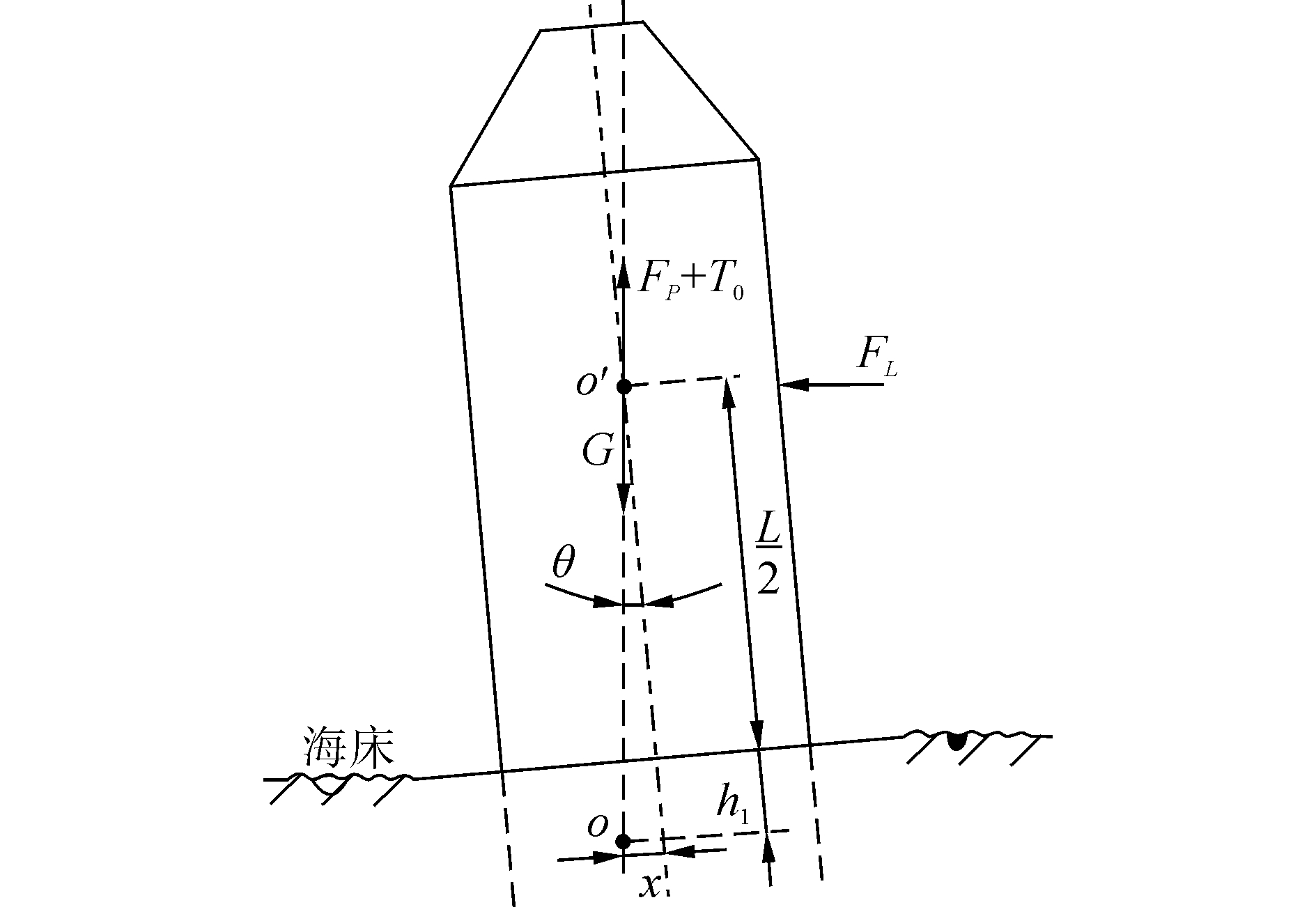
2 稳定性分析 2.1 抗倾覆稳定性分析控油装置在海流力和内部泄漏载荷的作用下,可能发生侧向倾覆的危险,在抗倾稳定性分析中,稳定性与转动点的位置以及转角密切相关,转动点的位置和转角可以由三个参量定量描述:x、h1、θ。其中x为转动点O距离控油装置中轴线的距离,在中轴线处为0,在倾覆一侧方向正,反之为负;h1为转动点O距离海底面的距离;θ为控油装置绕O点的旋转角度,如图 3所示。
|
Download:
|
| 图 3 抗倾覆稳定性示意图 Fig. 3 Schematic diagram of anti-inclining stability | |
控油装置在侧向倾覆力的作用下向左侧倾斜,起初其重心O′在转动点O的右侧,自重等竖向力起到的是阻止倾覆的有利力矩(G-FP-T0)x,当跨过转动点O以后自重等竖向力将会成为有害力矩加速其倾覆,因此,控制转动角度将是维持其稳定性的关键,入泥深度h是核心参数。所以,在满足式(3)力矩条件以后,采用日本规范的海洋工程结构物允许变位标准进行分析[6],即重心水平位移与未入土深度之比作为极限控制值,判别标准如下
| $ K = \frac{{\left( {L/2 + h} \right)\theta }}{L} \le 0.15 $ | (6) |
由文献[7-8]中海流及土力学载荷公式,vm=2.05 m/s时,得到h为3.19代入后可得:K=(7.5+3.19)×0.095/15=0.068 < 0.15,满足条件,符合安全要求,此时安全系数为SK=2.2,安全倾角θ=5.5°。
2.2 海床承载力分析控油装置钢板结构在外力作用下,地基受到偏心倾斜荷载。对于偏心倾斜荷载作用下的地基承载力计算,由于采用极限承载力公式计算方法有大量工程经验,因而得到了广泛引用。
控油装置底部宽度为2 m的防沉挡板与海底粘土之间的反作用力能很好维持地基稳定性。采用公式(7)计算其在粘土中地基极限承载力:
| $ {Q_{\rm{u}}} = {A_1}\alpha {C_{\rm{u}}} + {A_2}9{C_{\rm{u}}} $ | (7) |
式中:A1、A2为与海床基面接触的面积,A1=7h,Cu为粘土抗剪强度,α为粘着系数,当Cu < 24.5 kPa时,α取值为1.0;如果Cu处在24.5~73.0 kPa,α的大小随着Cu成直线下降趋势,Cu>73.0 kPa时,α值取0.5,一般经验得到粘性土侧摩阻力f不大于粘土的不排水抗剪强度[9]。
将h=2.5代入式(7)中,计算得到Qu=(19.8+126+140)×10=2 858 kN, 大于控油装置的自重G=2 058 kN,安全系数SQ=1.4,此时控油装置满足海床承载力要求。
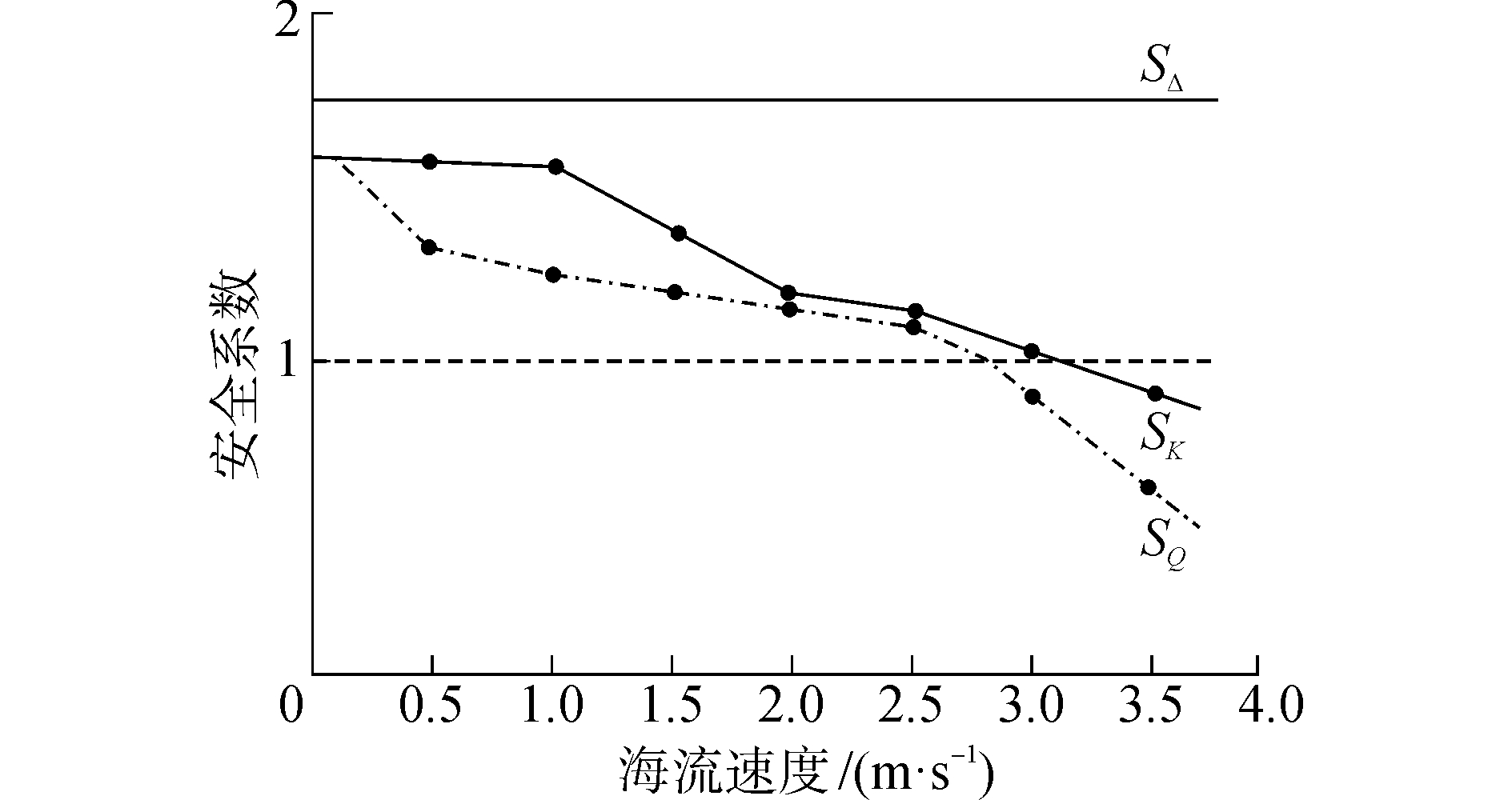
2.3 整体稳定性分析结合维持控油装置稳定性的平衡方程,对其进行抗倾稳定分析、海床承载力分析,观察到影响其稳定性的主要因素:海流速度vmax、海土的土性指标即抗剪强度Cu以及作业时间t。取海土土性指标Cu=10 kPa时,根据式(3)计算不同的海流速度vmax,得到其与控油装置各项稳定性分析安全系数的关系曲线,如图 4所示。
|
Download:
|
| 图 4 安全系数和海流速度的关系 Fig. 4 Relation between safety factor and current speed | |
由图 4看出,起初海流力对SK影响较小,随着海流速度的增加,其抗倾和海床承载稳定性安全系数SK和SQ随之下降明显,当海流速度达到2.85 m/s时,海床承载力稳定性被破坏,其工作的海床面出现被压溃塌陷危险;当速度达到3.20 m/s时,抗倾覆稳定性也遭到破坏,此时稳定性失效。
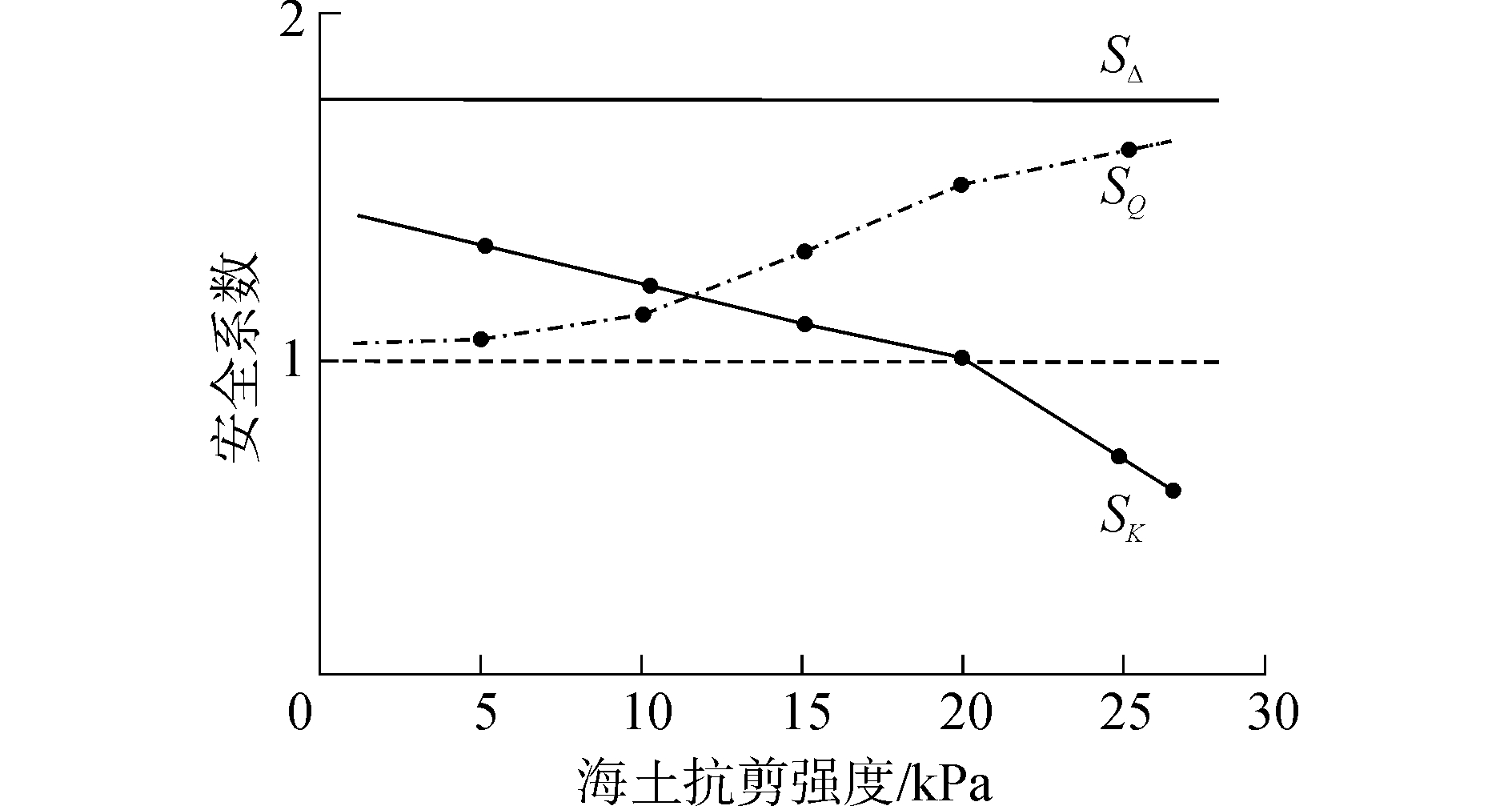
根据一般可作业海况,取控油装置受到的海流速度vmax=2.05 m/s,根据式(3)计算不同的海土抗剪强度Cu与控油装置各项稳定性分析的安全系数的关系曲线,如图 5所示。
|
Download:
|
| 图 5 安全系数与海土抗剪强度的关系 Fig. 5 Relation between safety factor and shear strength | |
由图 5可见,当Cu>20 kPa时,海床承载力安全系数趋于稳定。但抗倾覆稳定性安全系数不断下降,由式(4)、(5)可知,基底反力Fσ作用的减弱以及自重G的增加,引起x减小和阻抗倾力矩Mσ减小,因此当自重G达到一定值时,控油装置将发生倾覆危险,无法工作。
综上所述,控油装置工作稳定性与自重和入泥深度有最直接关系,但不能盲目的通过增加自重来维持工作的稳定性,那样会使各项安全系数失效。对控油装置进行了初步尺寸设定后,对其所受到的外力海流载荷、海土载荷等进行计算,并通过抗倾覆稳定性分析、海床承载力分析以及整体稳定性分析,确定了控油罩装置的自重G、入泥深度、下沉钢板厚度B、下沉钢板宽度D。
3 控油罩性能试验研究为了验证控油装置理论与工程实践的关系,对其整体建立缩比模型,并进行试验研究,为工程样机的水下应用提供指导。
3.1 缩比试验样机研制控油装置缩比模型的试验要根据相似定理进行设计,以保证本试验模型不仅与原型的几何相似,更重要的是物理现象的相似,即与控油装置稳定性相关的受力情况、边界条件等保持相似[10-11]。缩比模型材料选取与原型机相同的材料Q235 A,考虑到模型的加工制造成本、周期、运输以及试验场地等因素,选取模型与原型的几何尺寸比为1:10,由相似理论可得到各个物理量相似比,确定控油装置相似模型试验中的物理条件、初始条件和边界条件。本文设计的控油装置主要由顶部为锥体结构、中部钢结构支撑框架,底部下沉钢板三部分组成。控油装置三维设计图及缩比模型样机如图 6所示。

|
Download:
|
| 图 6 控油装置三维图及试验样机 Fig. 6 3D Figure and prototype of containment device | |
试验前2个月培养试验用海底粘土,并进行常规土工试验,使其基本符合本试验海土要求。
3.2 抗倾覆稳定性试验控油装置侧向力由拉力电机施加,其上布置有拉力传感器,箱体上布置有角度仪和电子卡尺。通过操作手柄点控拉力电机,每次施加拉力200 N,记录下对应时刻传感器的数值,并记录下该时刻角度仪和电子卡尺的示数。
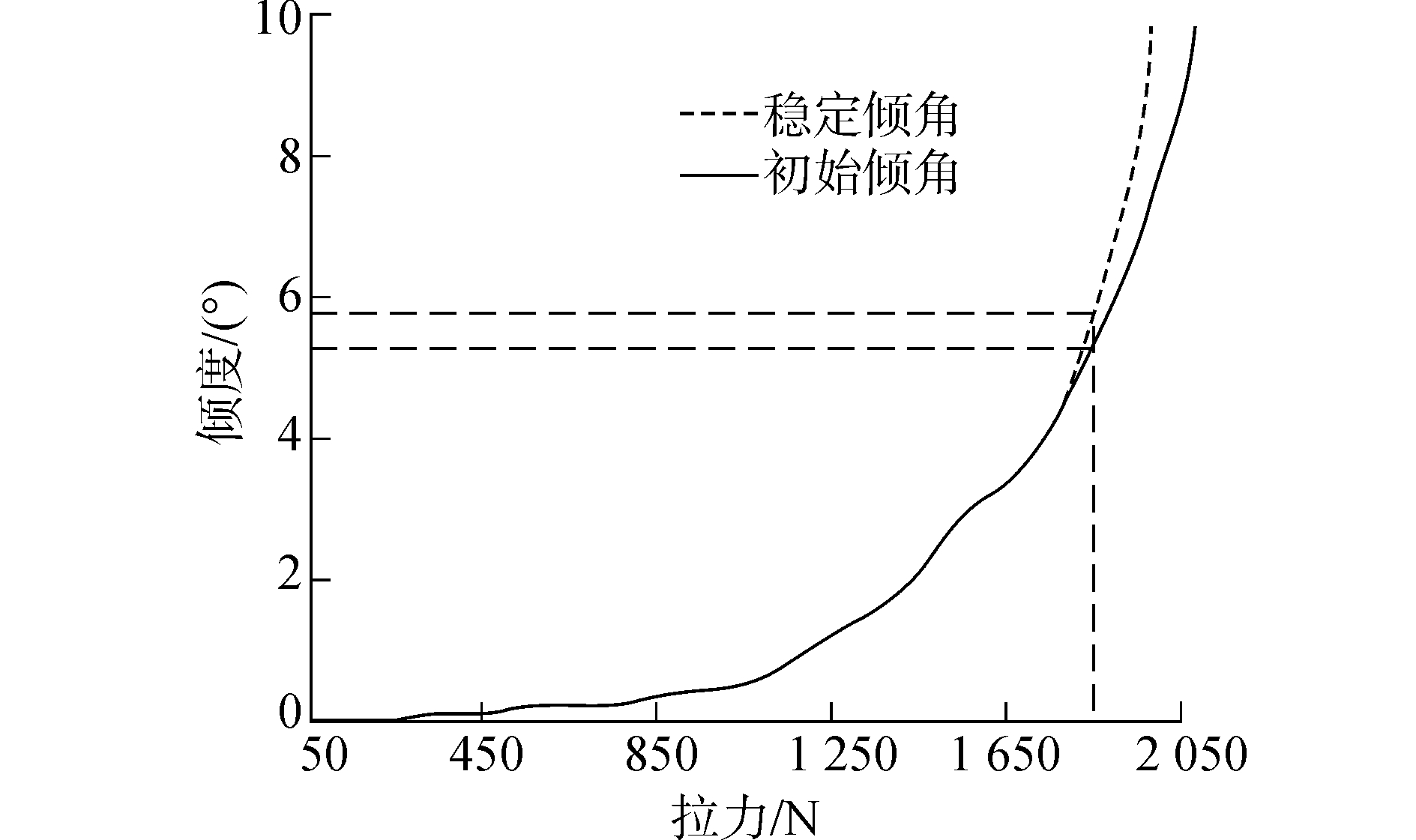
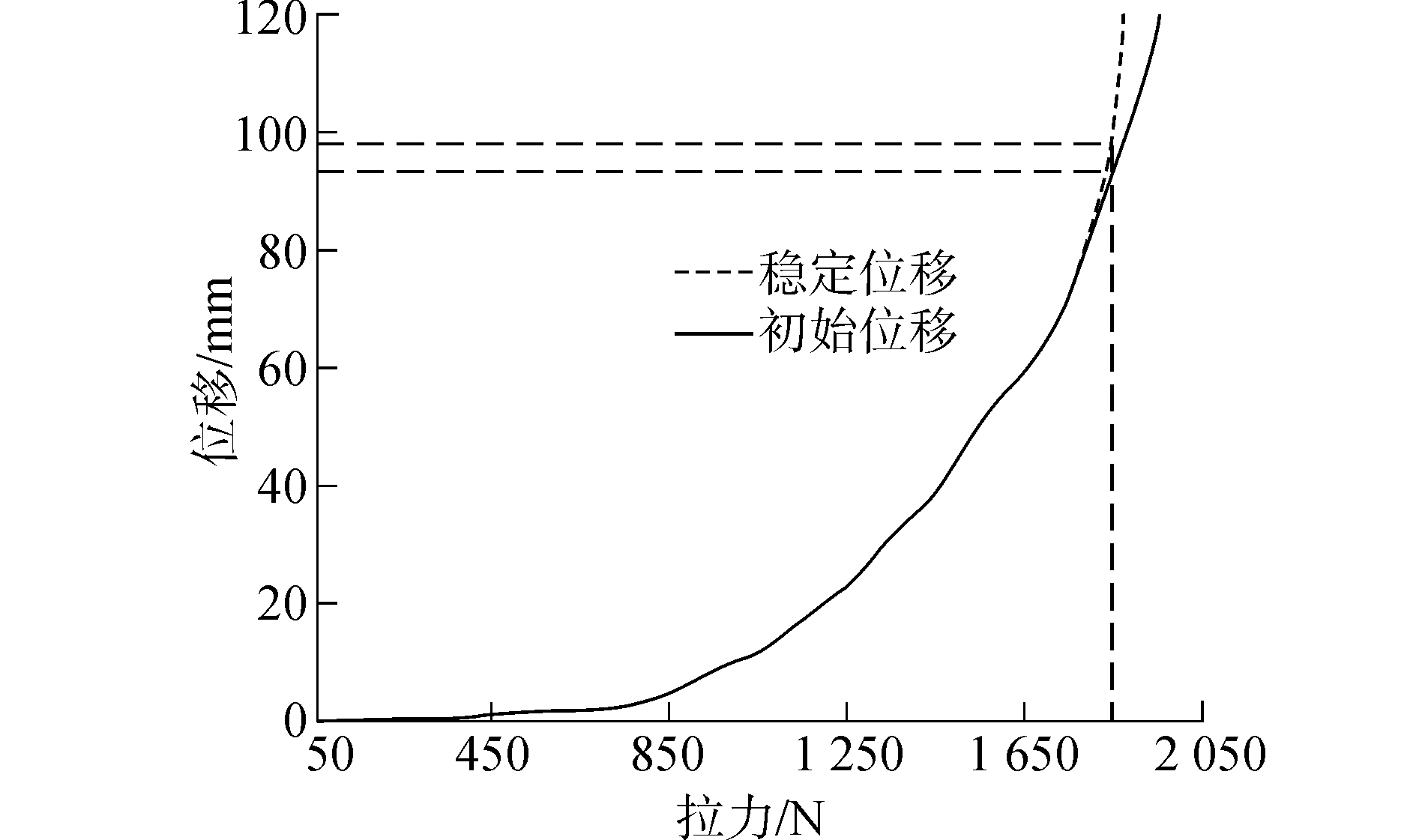
根据试验数据绘制拉力、倾角和位移间曲线图,如图 7、8所示。由图看出,施加的拉力小于1 250 N时,此时模拟的海流力对控油装置的倾覆稳定性影响很小,随着海流力的增加,倾角也在迅速变大,当拉力达到1 850 N时,倾角θ=5.2°,停止施加拉力稳定后倾角变为θ=5.8°,倾角变化趋势与位移一致。
|
Download:
|
| 图 7 倾角与拉力的关系 Fig. 7 Relation between angle and tension | |
|
Download:
|
| 图 8 位移与拉力的关系 Fig. 8 Relation between Displacement and Tension | |
分析知当拉力大于1 850 N时,设备重心已经跨过转动支点O的竖直位置,自重产生的力矩已经转化为倾覆力矩,继续施加拉力,初始倾角和稳定倾角数值将成直线增大,控油装置完全失稳。对比图 4控油装置抗倾覆安全系数曲线发现,控油装置安全系数与试验中获取的倾角变化趋势相同。
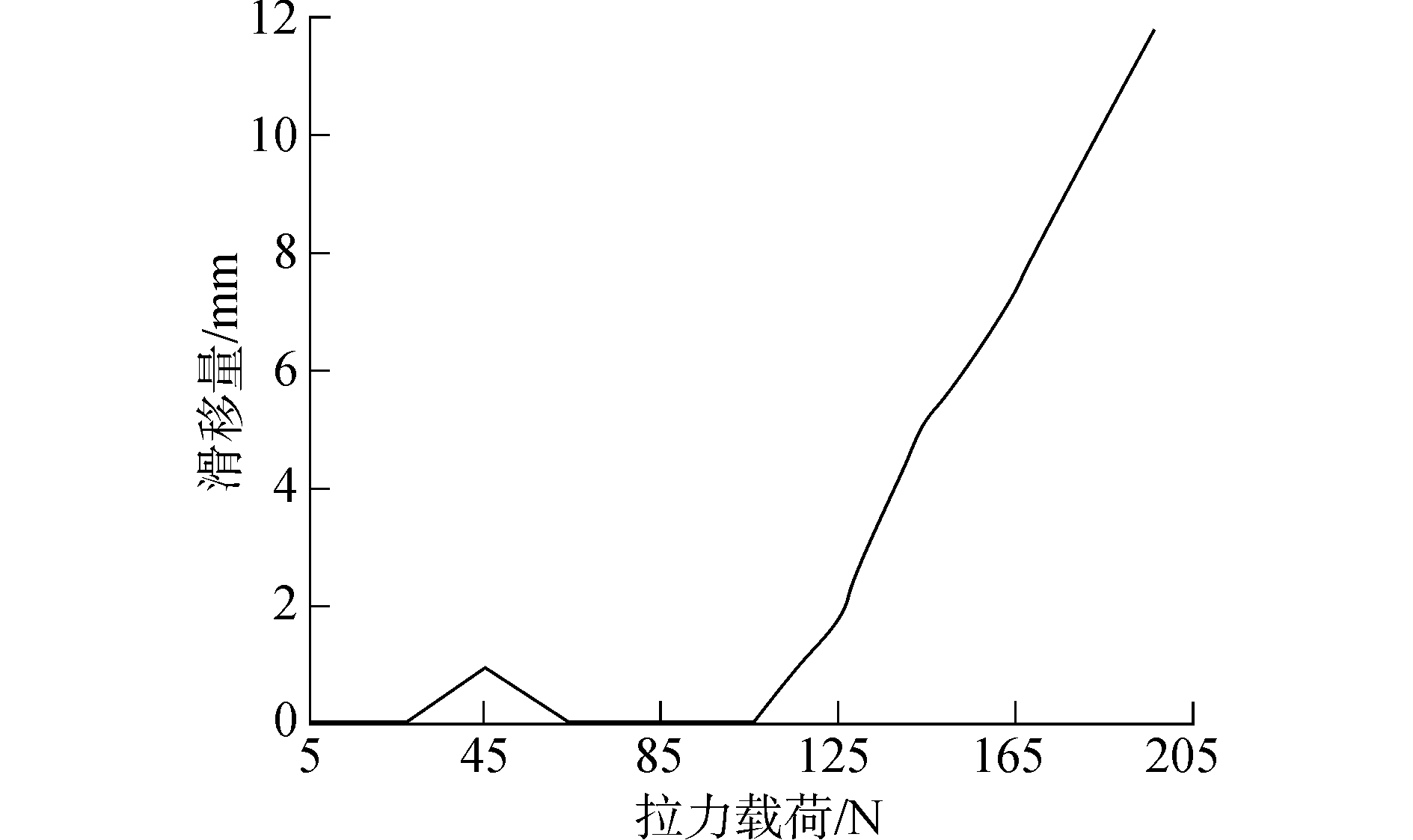
试验得到极限倾角θ≤5.2°,此时得到重心的极限位移为96.2 mm,由模型与原型相似比及式(4)~(6)得到,当极限倾角θ=5.2°时,重心极限位移应为95.1 mm,试验数据与计算数据之间存在差异。结合试验现象和土力学计算公式发现,在侧向载荷作用下底部钢板有轻微的水平滑移现象,使得重心实际位移大于理论值,绘制滑移量P-S曲线,如图 9所示。
|
Download:
|
| 图 9 控油装置滑移量P-S曲线 Fig. 9 Slippage P-S curve of containment device | |
当海流速度达到一定的值时,在进行控油装置稳定性分析时要考虑底部钢板的水平滑移量,计算得到发生滑移时海流速度v=1.8 m/s,由试验结果知,保证控油装置水平滑移量在基础宽度的1%以内,将不会影响控油装置稳定性。
计算得到极限倾角θ=5.4°,理论计算和试验引起误差的原因有两个方面:首先,试验中随着侧向拉力的增加,下沉钢板背侧土体受压,造成土性指标Cu变化,而计算时按Cu等于定值计算;其次,由于水平滑移量的影响,使倾覆转动点有小幅位置变化。综上所述,试验中极限倾角和重心极限位移略小于理论计算值,根据设计参数加工的样机,可抗海流速度为vmax=2.15 m/s,与理论计算值vm=2.05 m/s接近,表明装备设计参数符合要求。
3.3 入泥密封试验当控油装置下沉钢板入泥深度达到一定值以后,钢板与粘土之间形成密封,实际转接过程中,如果下沉钢板和泥土不能形成有效的密封,将会造成原油泄漏、转接效率下降、海底监测环境降低、下沉钢板附近海床土体破坏等问题,进一步影响转接工作的稳定性。利用气压泵给控油装置内部打压,完成密封性能检验,记录下不同深度的密封压力值。
控油装置密封试验中,测量了控油装置在泥池中不同入泥深度情况下的多组数据,整理试验数据和美国石油学会(American petroleum institute,API)标准的计算值[12],见表 1,绘制理论密封压力与实际密封压力与入泥深度的关系曲线,如图 11所示。由图可见,API理论密封压力与实际密封压力随深度变化规律一致。
| 表 1 不同入泥深度的密封压力 Tab.1 Seal pressure with different driving depths |
随着入泥深度的增加,密封压力在逐渐增大,由表 1可以看出,理论密封压力和试验密封压力存在一定的差异,试验值略小于API的规范值,入泥深度450 mm时差值最大为3 kPa,仅为计算值的6.25%,在误差波动范围内。
试验中,出于安全角度,采取保守的加压策略,所以实际压力值会偏小。由于泥池面积有限,相邻试验位置土体发生轻微破坏,导致不可避免的试验误差的出现。控油装置设计的入泥钢板尺寸为3 m×7 m,理论上与海底粘土密封压力能达到3.8 MPa,满足技术要求。实际工程中,控油装置装有分流阀,通过ROV监控,实时保持罩体内外压力平衡,使整个控油转接装置保持安全性与稳定性。
4 结论1) 控油装置发生倾覆的主要原因是海流冲击和原油泄漏压力,增加本身入泥深度和自重能够增加其稳定性,但是,控油装置自重及入泥深度不是无限制增加,要做整体稳定性分析,综合考虑参数间影响关系,将安全系数和极限倾角作为设计的判别标准。由于箱体的迎流面较大,工程中可以通过加入迎流面小、质量大的配重来增加控油装置稳定性。
2) 控油装置密封性能随着入泥深度和抗剪强度增加,所能实现的密封压力越高。
数值计算和试验中针对控油装置在倾覆力的作用下的整体稳定性进行研究,考虑到安全问题,高压转接时,倾覆力作用下控油装置的稳定性还有待进一步研究。
| [1] |
王丽春. 水下油气设施泄漏救援技术研究与控油装置设计[D]. 哈尔滨: 哈尔滨工程大学, 2014: 15-16. WANG Lichun. Research on the technology of subsea oil and gas facilities leakage rescue and Containment device design[D]. Harbin: Harbin Engineering University, 2014: 15-16. (  0) 0)
|
| [2] |
魏会东, 姜瑛, 琚选择, 等. 深水海管终端设备管线应力计算研究[J]. 石油机械, 2015, 43(3): 64-67. WEI Huidong, JIANG Ying, JU Xuanze, et al. Calculation of pipe stress for terminal facilities of deep-sea pipelines[J]. China petroleum machinery, 2015, 43(3): 64-67. (  0) 0)
|
| [3] |
ZHANG Huaqing, SUN Xiping, WANG Yuanzhan, et al. Dynamic characteristics and simplified numerical methods of an all-vertical-piled wharf in offshore deep water[J]. China ocean engineering, 2015, 29(5): 705-718. DOI:10.1007/s13344-015-0050-y (  0) 0)
|
| [4] |
苏堪华, 管志川, 龙芝辉. 海底浅部地层性质对深水钻井井口稳定性的影响[J]. 石油钻采工艺, 2012, 34(3): 7-10, 23. SU Kanhua, GUAN Zhichuan, LONG Zhihui. Impact of the seabed soil properties on the stability of subsea wellhead for deepwater drillingv[J]. Oil drilling & production technology, 2012, 34(3): 7-10, 23. (  0) 0)
|
| [5] |
赵明华. 土力学与基础工程[M]. 武汉: 武汉理工大学出版社, 2003: 140-145. ZHAO Minghua. Soil mechanics and foundations[M]. Wuhan: Wuhan University of Technology Press, 2003: 140-145. (  0) 0)
|
| [6] |
HESAR M. Geotechnical design of the Barracuda and Caratinga suction anchors[C]//Offshore Technology Conference. Houston, Texas, 2003: 1-9.
(  0) 0)
|
| [7] |
邹佳星, 任慧龙, 李陈峰. 极端海况下FPSO系泊系统安全性评估与分析[J]. 哈尔滨工程大学学报, 2015, 36(1): 104-108. ZOU Jiaxing, REN Huilong, LI Chenfeng. The safety assessment and analysis of FPSO mooring system under extreme sea conditions[J]. Journal of Harbin Engineering University, 2015, 36(1): 104-108. (  0) 0)
|
| [8] |
王元战, 郭富林, 刘旭菲, 等. 格型钢板桩结构抗倾覆稳定性与地基承载力的计算方法[J]. 港工技术, 2013, 50(2): 32-35, 42. WANG Yuanzhan, GUO Fulin, LIU Xufei, et al. Calculation method for stability against overturning and ground bearing capacity of celled steel sheet piles[J]. Port engineering technology, 2013, 50(2): 32-35, 42. (  0) 0)
|
| [9] |
American petroleum institute (API). API RP 2A-WSD, Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design[S]. Washington: American Petroleum Institute Production Department, 1996.
(  0) 0)
|
| [10] |
王国栋, 赵宏林, 段梦兰, 等. JZ20-2MUQ型导管架平台相似模型设计研究[J]. 石油矿场机械, 2011, 40(11): 1-5. WAND Guodong, ZHAO Honglin, DUAN Menglan, et al. Research on design for similar model of jz20-2muq jacket platform[J]. Oil field equipment, 2011, 40(11): 1-5. DOI:10.3969/j.issn.1001-3482.2011.11.001 (  0) 0)
|
| [11] |
HARRIS H G, SABNIS G M. Structural modeling and experimental techniques[M]. Engle-wood Cliffs: Prentice-Hall, 1999: 30-35.
(  0) 0)
|
| [12] |
American petroleum institute (API). API RP 2SK, Recommended practice for design and analysis of station-keeping systems for floating structures[S]. 3rd ed. American Petroleum Institute, 2005.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


