作为各类舰艇和民用船舶的核心导航系统,捷联式惯导系统的精度和可靠性直接影响了其装备载体的各项性能指标[1]。由于其核心器件(陀螺仪和加速度计)与载体固连,极易受到外部冲击、振动及舰艇大幅度摇摆等复杂工况的干扰,惯导系统除面临高精度要求外,其可靠性也一直面临严峻挑战。
冗余技术是用于提高惯导系统可靠性最常采用的现代容错技术[2]。其中,器件级冗余技术通过单纯增加器件数量即可大幅提升系统可靠性,因此在提高可靠性和控制成本等方面,较系统级冗余技术具有较大优势[3]。
在设计冗余式捷联惯导系统方案时,一方面需要兼顾可靠性、成本和体积等约束条件,选取最优的冗余配置方案[4],如六陀螺冗余配置的惯导系统至多允许三个陀螺发生故障,且具有体积和成本等优势, 因此是一种提升捷联惯导系统可靠性和精度的重要冗余配置方案;另一方面需要设计对应的故障检测和隔离方案,在系统单个或多个器件发生故障时,能实现故障器件的隔离。
基于解析模型的故障检测与隔离方法,能深入系统本质的动态性质和实时诊断,目前应用成熟的方法有广义似然比故障检测法,最优奇偶向量法以及奇异值分解法等。Daly等[5]提出的广义似然比故障检测法检测灵敏度高,适用于单故障的检测与隔离,但该方法将故障检测与隔离分开进行,导致故障隔离率低于故障检测率;杨伯军等[6]提出的最优奇偶向量检测法故障检测与隔离同时进行,提高了故障的正确隔离率,更适用于单故障检测;Duk-Sun Shim等[7-8]提出的奇异值分解法虽然成功的检测并隔离了冗余式捷联惯导系统的双故障,但其计算量大,故障检测延时大,且无法准确隔离三个陀螺同时发生故障的情况。以上的故障检测方法都可应用于发生单故障的冗余式捷联惯导系统,但当系统发生两个或三个故障时,这些故障检测方法将失效。
基于此,本文设计了一种广义似然比法和线性估计思想相结合的故障检测与隔离方案,利用广义似然比方法(generalized likelihood test,GLT)检测灵敏度高、计算量小、广泛应用于工程研究的特点,对系统进行快速有效的故障检测;利用线性估计思想对陀螺输出值进行预测。
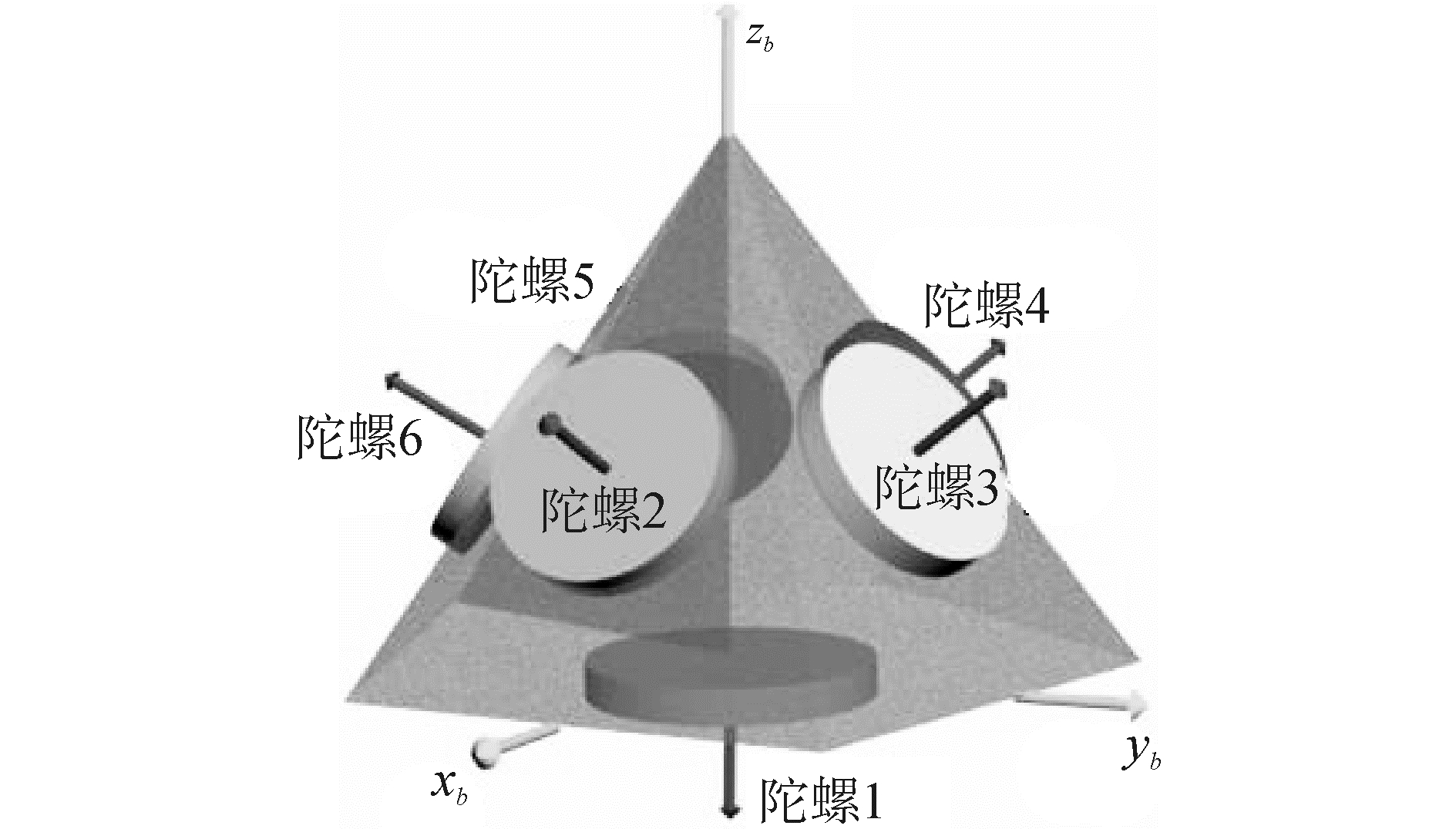
1 六陀螺锥体垂向对称配置模型六陀螺椎体垂向对称配置结构如图 1所示,2号、3号、4号以及5号陀螺分布在椎体侧面,分别与平面xoy的角度α为63.43°。1号陀螺在z轴上,1号、2号、3号、4号以及5号陀螺之间的角度β为72°。
|
Download:
|
| 图 1 六陀螺椎体垂向配置结构示意图 Fig. 1 Six-gyro vertical symmetrical configuration structural representation | |
按照图 1所示的配置方式,可获得六陀螺冗余系统量测方程为[9]
| $ \mathit{\boldsymbol{Z}} = \mathit{\boldsymbol{HX}} + \mathit{\boldsymbol{f}} + \mathit{\boldsymbol{\varepsilon }} $ | (1) |
式中:Z∈Rm为m个传感器陀螺测量值,X∈R3是需要计算的状态变量(直接用于捷联惯导系统解算载体角运动信息),f为故障向量,ε为传感器量测噪声,H为传感器配置矩阵:
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} 0&0&1\\ {0.894}&0&{0.447}\\ {0.276}&{0.850}&{0.447}\\ { - 0.723}&{0.525}&{0.447}\\ { - 0.723}&{ - 0.525}&{0.447}\\ {0.276}&{ - 0.850}&{0.447} \end{array}} \right] $ | (2) |
相较于其他冗余配置结构,六陀螺圆锥垂向配置结构优越性体现如下:1) 与四陀螺、五陀螺、七陀螺等冗余配置方案相比,六陀螺冗余系统兼顾可靠性和成本最优特性; 2)与其他六陀螺冗余配置方案相比,六陀螺圆锥垂向配置结构同时满足可靠性最大化和导航精度最优准则[10],即:
| $ {\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H = }}\frac{n}{3}{\mathit{\boldsymbol{I}}_3} $ | (3) |
通过对冗余系统测量方程引入奇偶矩阵,构造了奇偶方程,用于实现系统故障检测和隔离。即对传感器测量值Z引入线性变换,用于实现系统故障检测和隔离:
| $ \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{VZ}} = \mathit{\boldsymbol{VHX}} + \mathit{\boldsymbol{Vf}} + \mathit{\boldsymbol{V\varepsilon }} $ | (4) |
式中:V是(m-3)×m维奇偶矩阵,且满足VH=0,VVT=Im-3。
由此,式(4)变为
| $ \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{Vf}} + \mathit{\boldsymbol{V\varepsilon }} $ | (5) |
此时,P是一个仅与故障向量或噪声有关的函数。当传感器正常工作时,P仅由量测噪声决定,而由于奇偶向量P是关于ε的线性函数,因此P服从m-3维正态分布。
定义GLT的故障检测函数为
| $ {F_{{\rm{GLT}}}} = \frac{1}{{{\sigma ^2}}}\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right) $ | (6) |
式中:故障检测函数FGLT服从(m-3)维卡方分布,即F~χ2(m-3)。该函数可用于判断系统是否发生故障。当系统无故障时,奇偶向量P仅与量测噪声有关,此时由P构成的故障检测函数值FGLT未超过故障检测门限值TD;当系统发生故障时,奇偶向量P不仅与量测噪声有关,还与故障信息有关,此时由P构成的故障检测函数值FGLT必然超过故障检测门限值。因此,广义似然比故障检测方法可以判断出系统发生故障。
对于广义似然比隔离方法,在3维空间,隔离单故障至少需要4个陀螺,隔离双故障至少需要2×2+3=7个陀螺,而隔离三故障至少需要2×3+3=9个陀螺[11]。因此对于单自由度六陀螺惯性导航系统,可以检测并隔离单故障,对于多故障则只能检测却不能正确隔离。文献[12]的仿真证明了GLT方法在六陀螺冗余惯导系统的应用中只能隔离单故障不能隔离多故障的结论,但未给出证明。本文给出理论证明如下:
由VH=0和VVT=Im-3可得
| $ {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V = }}{\mathit{\boldsymbol{I}}_m} - \mathit{\boldsymbol{H}}{\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}} $ | (7) |
式(7)两边同时乘以故障向量f,可得
| $ \mathit{\boldsymbol{f}} = {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{Vf}} + \mathit{\boldsymbol{H}}{\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{f}} $ | (8) |
式中:H(HTH)-1HTf为故障向量f在H的列向量张成的空间上的投影;VTV为幂等矩阵,由其幂等矩阵性质,易证VTVf为f在H左零空间上的投影,用
| $ {{\mathit{\boldsymbol{\hat f}}}_{{\rm{null}}}} = {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{Vf}} $ | (9) |
当系统发生双故障时可得
| $ {{\mathit{\boldsymbol{\hat f}}}_{ij}} = {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}}\left( {{f_i}{\mathit{\boldsymbol{e}}_i} + {f_j}{\mathit{\boldsymbol{e}}_j}} \right) $ | (10) |
式中:fi和fj为陀螺故障幅值;ei和ej为m×1维故障向量,故障陀螺所对应行为1,其余行为0。
不同的双故障系统故障在H左零空间上的投影的差值为
| $ \Delta {{\mathit{\boldsymbol{\hat f}}}_{{\rm{null}}}} = {{\mathit{\boldsymbol{\hat f}}}_{ij}} - {{\mathit{\boldsymbol{\hat f}}}_{lk}} = {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}}\left( {{f_i}{\mathit{\boldsymbol{e}}_i} + {f_j}{\mathit{\boldsymbol{e}}_j} - {f_l}{\mathit{\boldsymbol{e}}_l} - {f_k}{\mathit{\boldsymbol{e}}_k}} \right) $ | (11) |
由V和VTV的性质可知rank(VTV)=m-3,即VTV有m-3个列线性无关。当m=6,必存在fifjfl和fk某种组合,使式(11)为零。因此,在六陀螺冗余惯导系统中采用广义似然比方法无法识别双故障,并得到推论:对于六陀螺冗余惯导系统,采用广义似然比方法无法识别多故障。
3 基于线性估计思想的故障隔离方法GLT方法的优势在于能判断陀螺仪是否出现故障,当陀螺仪工作正常时,由于载体角运动的连续性,在足够小的时间段内,陀螺仪测量输出值呈连续性;当且仅当陀螺仪出现故障时,陀螺仪测量输出值将呈现不连续性。即当t时刻发生故障时,可根据前面时刻的陀螺仪测量真值,估计出t时刻陀螺仪测量估计值。通过求取t时刻陀螺仪测量估计值与t时刻陀螺仪真值残差,判断出故障陀螺。
设定冗余系统测量式(1)的传感器测量输出为Z=[W1 W2 W3 W4 W5 W6]T,Wi(i=1, 2, …, 6)为单个陀螺测量输出值。
由t-2时刻与t-1时刻陀螺仪测量输出值Wk(t-1)和Wk(t-2)得到陀螺仪变化趋势:
| $ \Delta {W_k} = {W_{k\left( {t - 1} \right)}} - {W_{k\left( {t - 2} \right)}} $ | (12) |
由此获得t时刻陀螺仪量测估计值为
| $ {{\hat W}_{k\left( t \right)}} = {W_{k\left( {t - 1} \right)}} + \Delta {W_k} $ | (13) |
根据式(10),可计算t时刻的陀螺仪量测值与估计值的差值为
| $ \delta {W_k}\left( t \right) = {W_{k\left( t \right)}} - {{\hat W}_{k\left( t \right)}} $ | (14) |
δWk(t)为第k号陀螺输出残差值。理论上,陀螺发生故障时,δWk(t)中最大的元素即为故障陀螺。但在实际系统中,陀螺仪测量值必然包含测量噪声。测量噪声将干扰测量残差δWk(t)中元素的比较,导致无法准确隔离故障陀螺。
为降低测量噪声的影响,提高残差δWk(t)识别度,本文引入多时刻残差矩阵。即通过线性估计方法,分别得到t-1时刻、t+1时刻陀螺测量输出值与测量估值的差值为
| $ \delta {W_k}\left( {t - 1} \right) = {W_{k\left( {t - 1} \right)}} - {{\hat W}_{k\left( {t - 1} \right)}} $ | (15) |
| $ \delta {W_k}\left( {t + 1} \right) = {W_{k\left( {t + 1} \right)}} - {{\hat W}_{k\left( {t + 1} \right)}} $ | (16) |
计算三个时刻残差矩阵之和:
| $ \mathit{\boldsymbol{\bar Q}} = \left[ \begin{array}{l} \left[ {\delta {w_1}\left( {t - 1} \right) + \delta {w_1}\left( t \right) + \delta {w_1}\left( {t + 1} \right)} \right]/3\\ \left[ {\delta {w_2}\left( {t - 1} \right) + \delta {w_2}\left( t \right) + \delta {w_2}\left( {t + 1} \right)} \right]/3\\ \left[ {\delta {w_3}\left( {t - 1} \right) + \delta {w_3}\left( t \right) + \delta {w_3}\left( {t + 1} \right)} \right]/3\\ \left[ {\delta {w_4}\left( {t - 1} \right) + \delta {w_4}\left( t \right) + \delta {w_4}\left( {t + 1} \right)} \right]/3\\ \left[ {\delta {w_5}\left( {t - 1} \right) + \delta {w_5}\left( t \right) + \delta {w_5}\left( {t + 1} \right)} \right]/3\\ \left[ {\delta {w_6}\left( {t - 1} \right) + \delta {w_6}\left( t \right) + \delta {w_6}\left( {t + 1} \right)} \right]/3 \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{{\bar Q}_1}}\\ {{{\bar Q}_2}}\\ {{{\bar Q}_3}}\\ {{{\bar Q}_4}}\\ {{{\bar Q}_5}}\\ {{{\bar Q}_6}} \end{array}} \right] $ | (17) |
记
| $ \begin{array}{*{20}{c}} {\delta \mathit{\boldsymbol{Z}}\left( t \right) = }\\ {{{\left[ {\begin{array}{*{20}{c}} {\delta {w_1}\left( t \right)}&{\delta {w_2}\left( t \right)}&{\delta {w_3}\left( t \right)}&{\delta {w_4}\left( t \right)}&{\delta {w_5}\left( t \right)}&{\delta {w_6}\left( t \right)} \end{array}} \right]}^{\rm{T}}}} \end{array} $ |
计算陀螺残差矩阵,得
| $ \mathit{\boldsymbol{P}} = \delta \mathit{\boldsymbol{Z}}\left( t \right) - \mathit{\boldsymbol{\bar Q}} = \left[ {\begin{array}{*{20}{c}} {\delta {w_1}\left( t \right) - {{\bar Q}_1}}\\ {\delta {w_2}\left( t \right) - {{\bar Q}_2}}\\ {\delta {w_3}\left( t \right) - {{\bar Q}_3}}\\ {\delta {w_4}\left( t \right) - {{\bar Q}_4}}\\ {\delta {w_5}\left( t \right) - {{\bar Q}_5}}\\ {\delta {w_6}\left( t \right) - {{\bar Q}_6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{d_1}}\\ {{d_2}}\\ {{d_3}}\\ {{d_4}}\\ {{d_5}}\\ {{d_6}} \end{array}} \right] $ | (18) |
| $ \left| d \right| = \max \left| {{d_x}} \right|\left( {x = 1,2,3,4,5,6} \right) $ | (19) |
测量残差的最大值即为发生故障的陀螺。
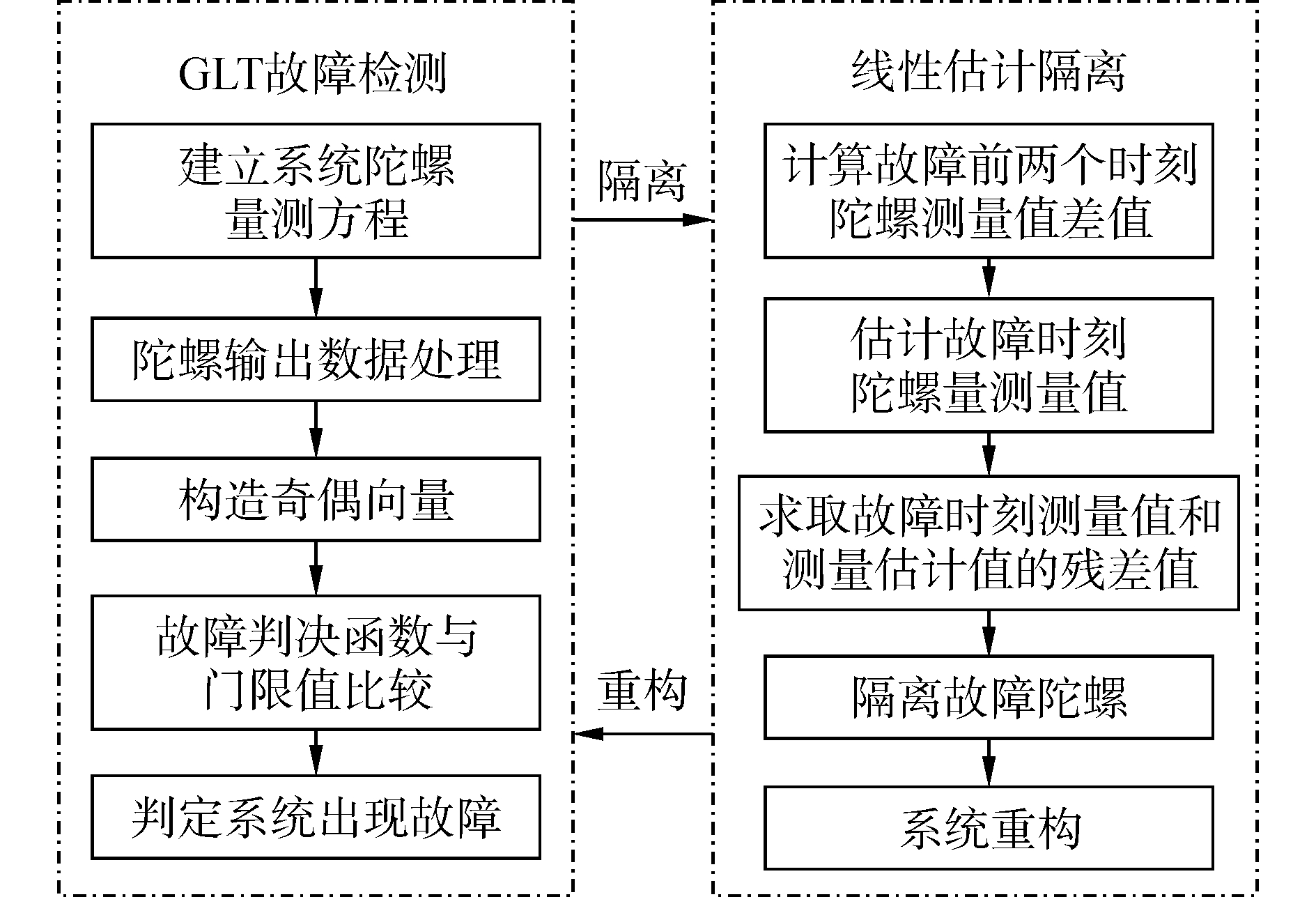
4 故障检测与隔离方法实现图 2为广义似然比故障检测与线性估计隔离方案流程图。采用广义似然比故障检测方法判断该冗余系统是否发生故障,若系统发生故障,判断故障发生的时刻,并采用线性估计的故障隔离方法判断该冗余系统中的哪些陀螺发生故障。
|
Download:
|
| 图 2 广义似然比故障检测与线性估计故障隔离方案流程图 Fig. 2 GLT detection and isolation based on linear estimation program flow chart | |
在隔离故障陀螺后,需进行系统重构并更新陀螺测量输出,使其不含有故障信息。
假设t时刻通过广义似然比故障检测方法判断系统发生故障并采用线性估计方法隔离出故障陀螺k,构建故障信息矩阵C,进行系统重构。
根据故障信息矩阵C得到系统重构公式为
| $ \mathit{\boldsymbol{\hat X}} = {\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{CH}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{CZ}} $ | (20) |
式中:
t时刻出现故障,根据最小二乘法冗余惯导系统重构后的状态量为
| $ \mathit{\boldsymbol{\hat X}}\left( t \right) = {\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{CH}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{CZ}}\left( t \right) $ | (21) |
t时刻被隔离的第k号陀螺的测量输出估计值为
| $ {{\mathit{\boldsymbol{W'}}}_{k\left( t \right)}} = {\mathit{\boldsymbol{H}}_k}{{\mathit{\boldsymbol{\hat X}}}_{\left( t \right)}} $ | (22) |
式中Hk为H的第k行。
5 仿真及试验验证 5.1 双故障检测及隔离方法仿真故障检测及隔离仿真条件如下:
1) 陀螺仪噪声标准差ση=0.5(°)/h;
2) 假设虚警率α=0.001,则故障门限值为:TD=χ0.9992(6-3)=16.27;
3) 仿真时长共计5 s,采样时间间隔为0.005 s。
双故障仿真条件为3号陀螺和4号陀螺在第3 s后发生故障,即在3号陀螺和4号陀螺输出中分别加入一个噪声信噪比为20ση的阶跃信号。
4) 三轴角运动设为X:50sin(8πt)(°)/s;Y:50cos(πt)(°)/s;Z:50t(°)/s。
根据上述仿真条件,可得六陀螺系统导航系统故障检测曲线以及各个陀螺故障隔离函数曲线如图 3~5所示。
|
Download:
|
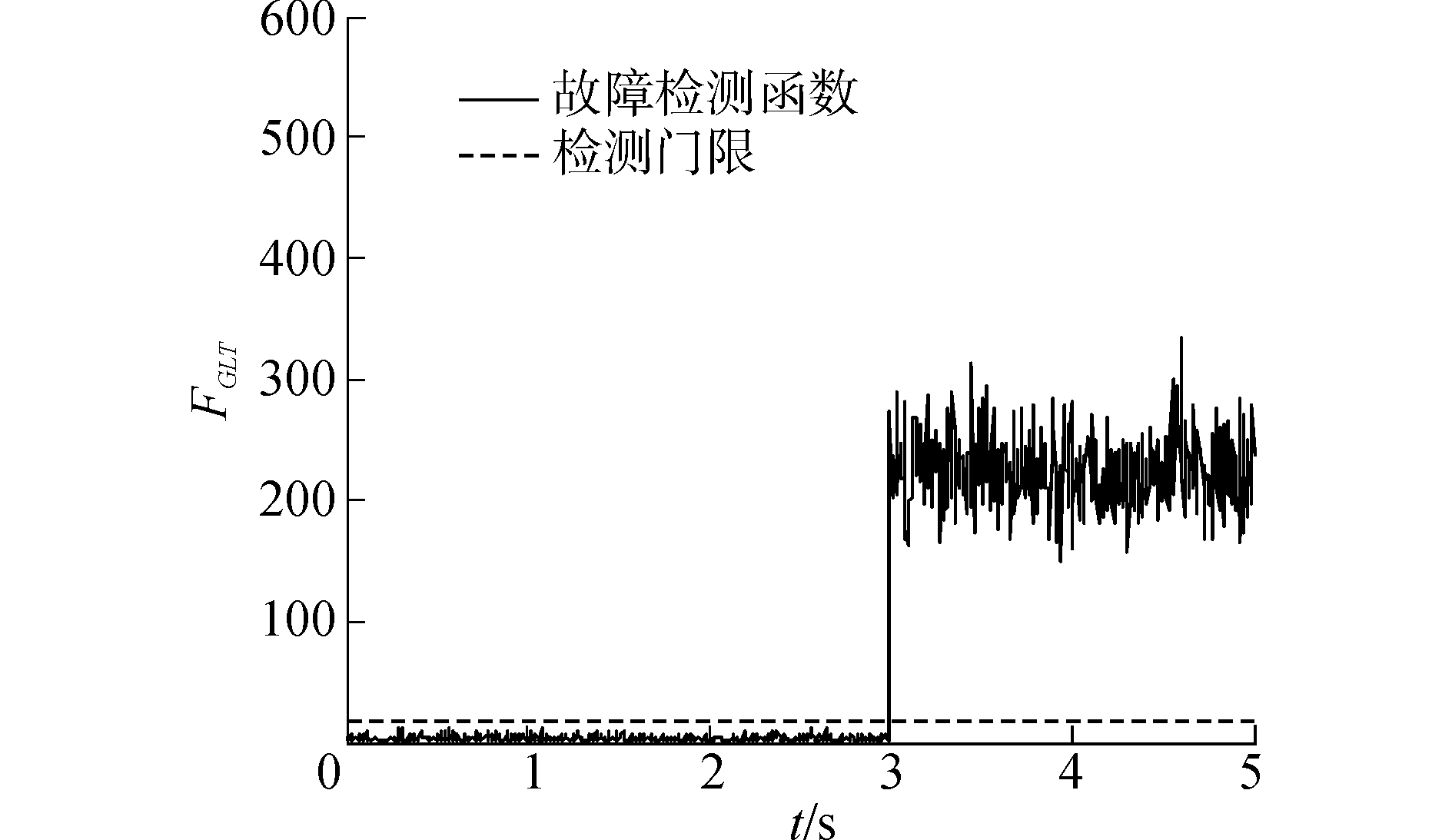
| 图 3 双故障下GLT故障检测函数曲线 Fig. 3 GLT detection function curves with double faults | |
|
Download:
|
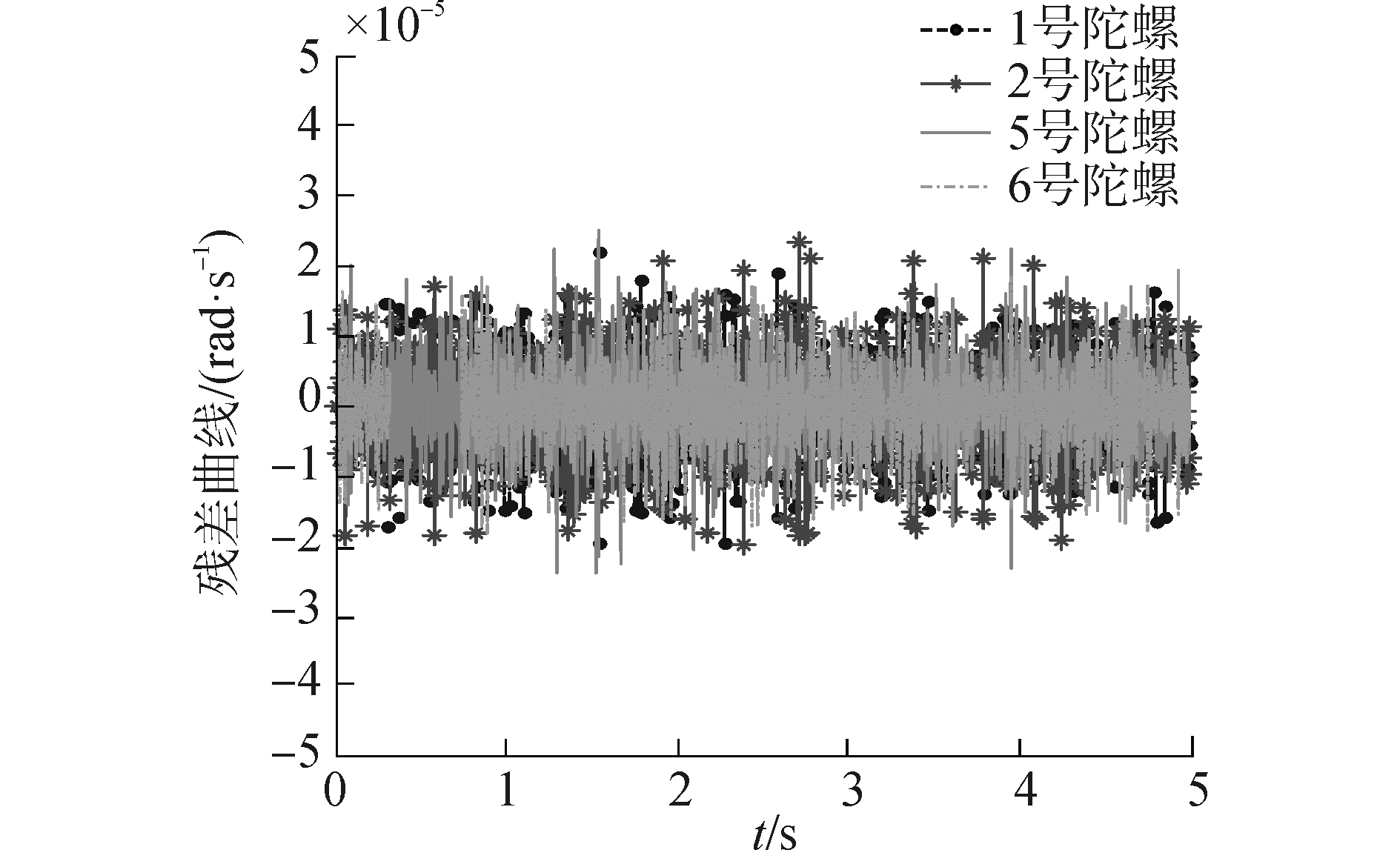
| 图 4 双故障下陀螺线性估计残差曲线 Fig. 4 Linear estimation residual curve with double faults | |

|
Download:
|
| 图 5 双故障下3号、4号陀螺线性估计残差曲线 Fig. 5 The 3th and 4th gyro linear estimation residual curves with double faults | |
由图 3可知,当系统双故障时,GLT故障检测故障函数值在第3 s超出了故障门限值,因此,GLT故障检测方法可以准确判断出第3 s开始六陀螺冗余惯导系统发生故障;由图 4、5可知,3号陀螺和4号陀螺在3 s时线性估计残差值明显高于其他陀螺,说明3号和4号陀螺发生故障。因此,六陀螺惯性导航系统发生双故障时,基于线性估计的故障隔离方法能正确隔离出故障陀螺。
5.2 三故障检测及隔离方法仿真三陀螺故障条件为:3号、4号和5号陀螺在第3 s后发生故障,即在3号陀螺、4号陀螺以及5号陀螺输出中分别加入一个噪声信噪比为20ση的阶跃信号。其他仿真条件同上。
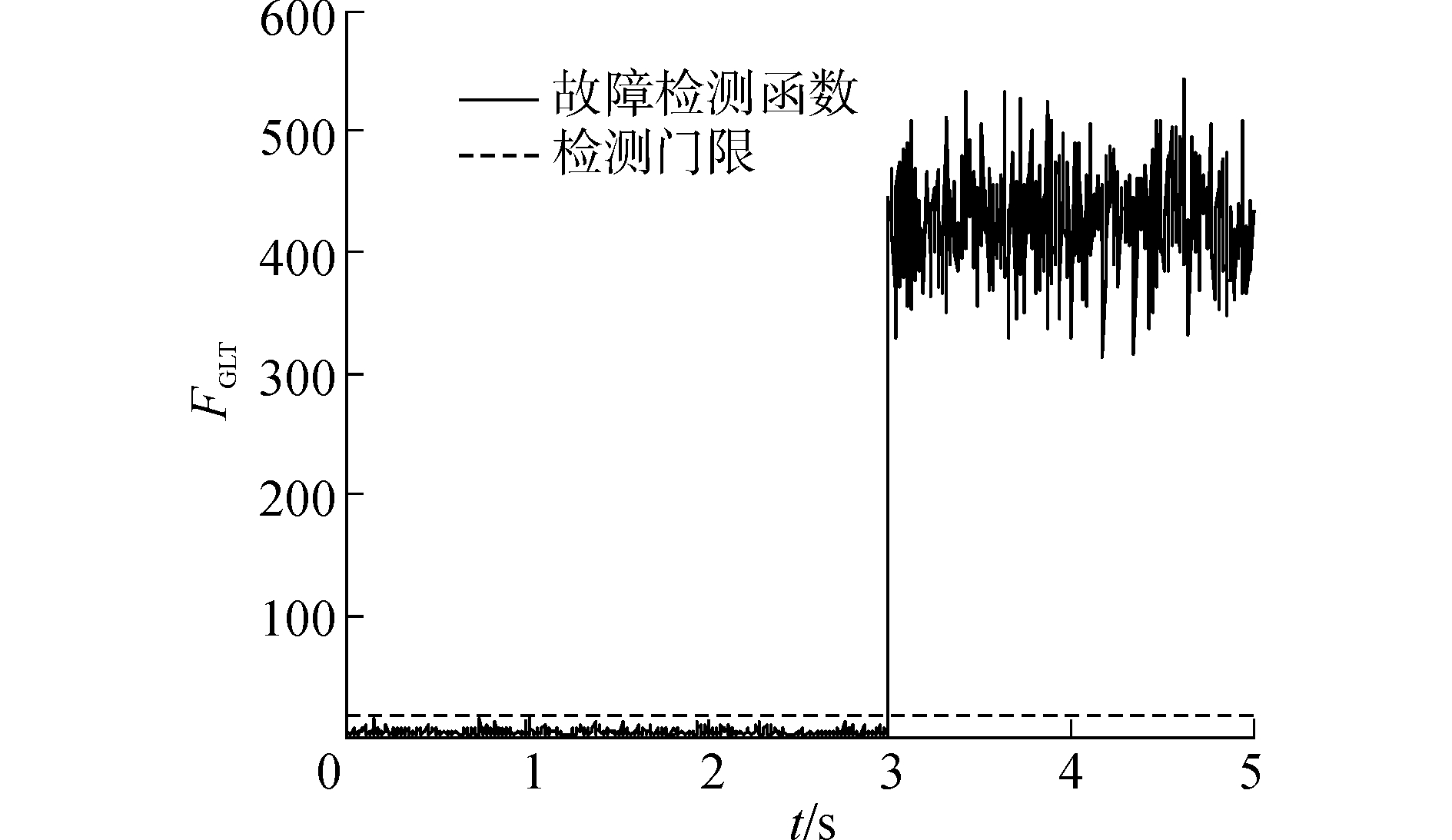
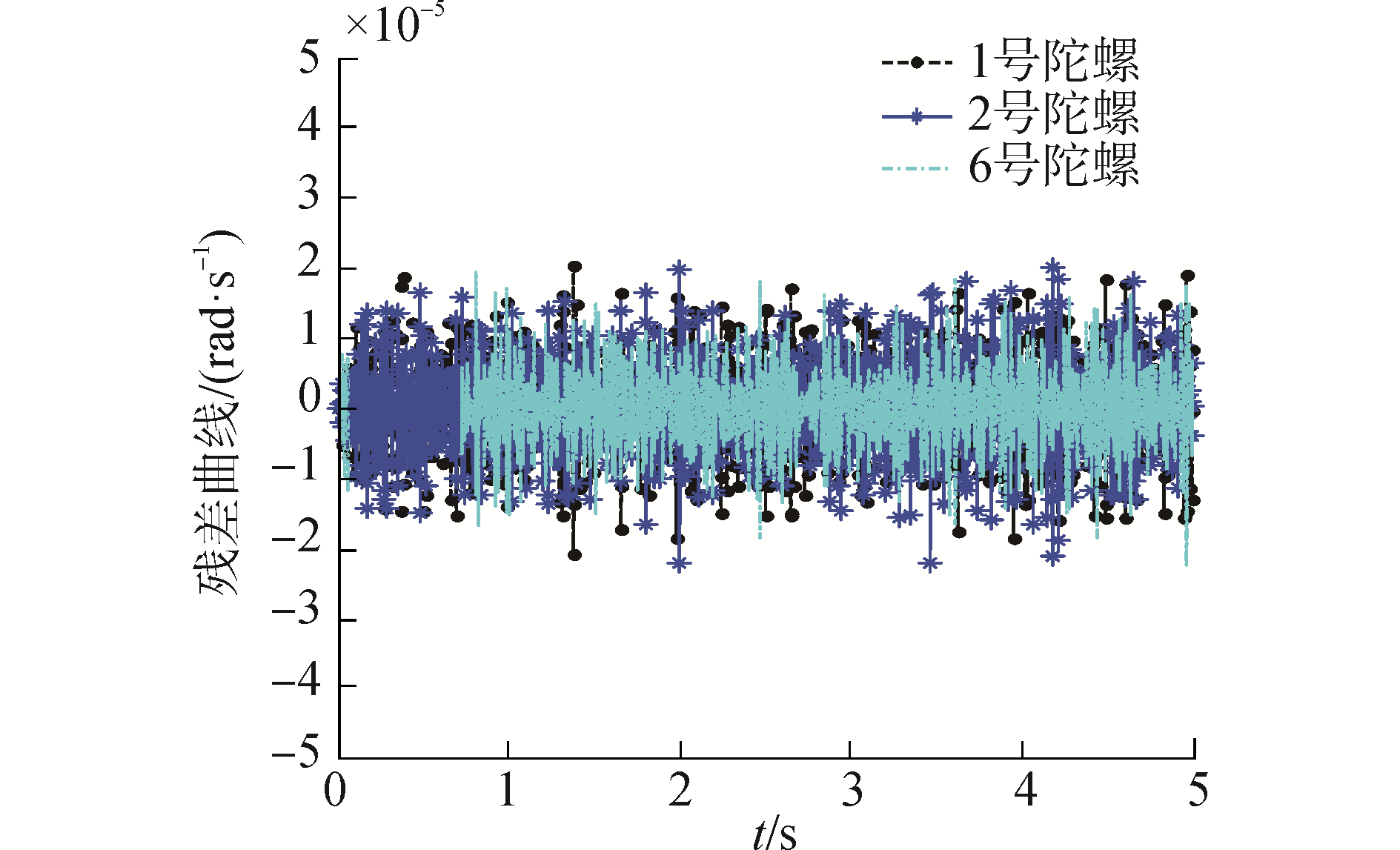
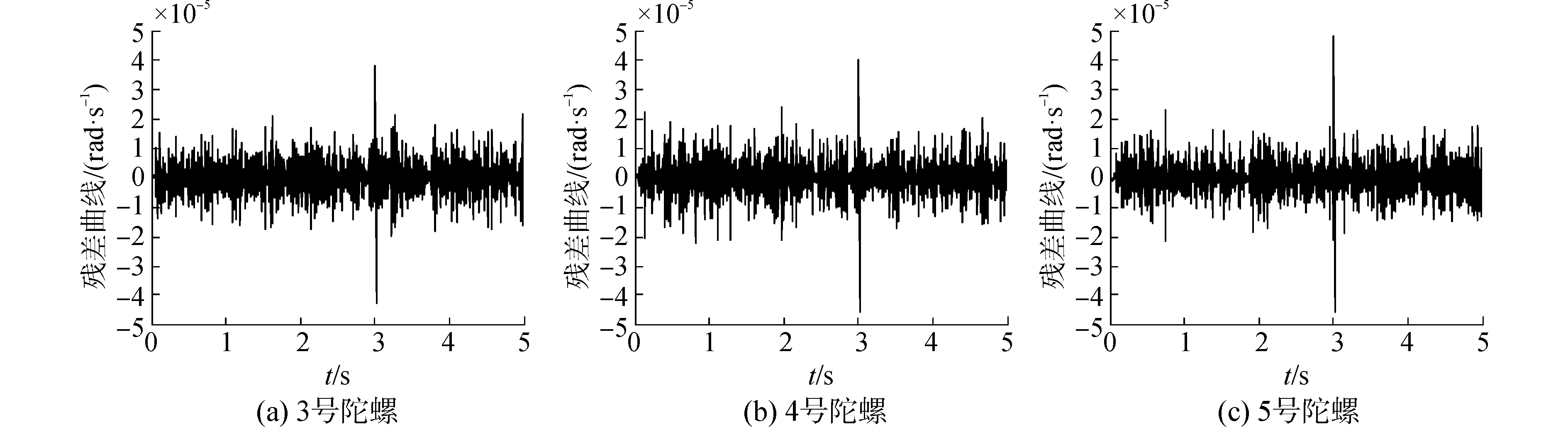
根据上述仿真条件,可得六陀螺系统导航系统如图 6~8所示。由图可知,六陀螺惯性导航系统发生三故障时,基于线性估计的故障隔离方法能正确隔离出故障陀螺。
|
Download:
|
| 图 6 三故障下GLT故障检测函数曲线 Fig. 6 GLT detection function curves with three faults | |
|
Download:
|
| 图 7 三故障下陀螺线性估计残差曲线 Fig. 7 Gyro linear estimation residual curve with three faults | |
|
Download:
|
| 图 8 三故障下3号、4号、5号陀螺线性估计残差曲线 Fig. 8 The 3th, 4th and 5th gyros linear estimation residual curves with three faults | |
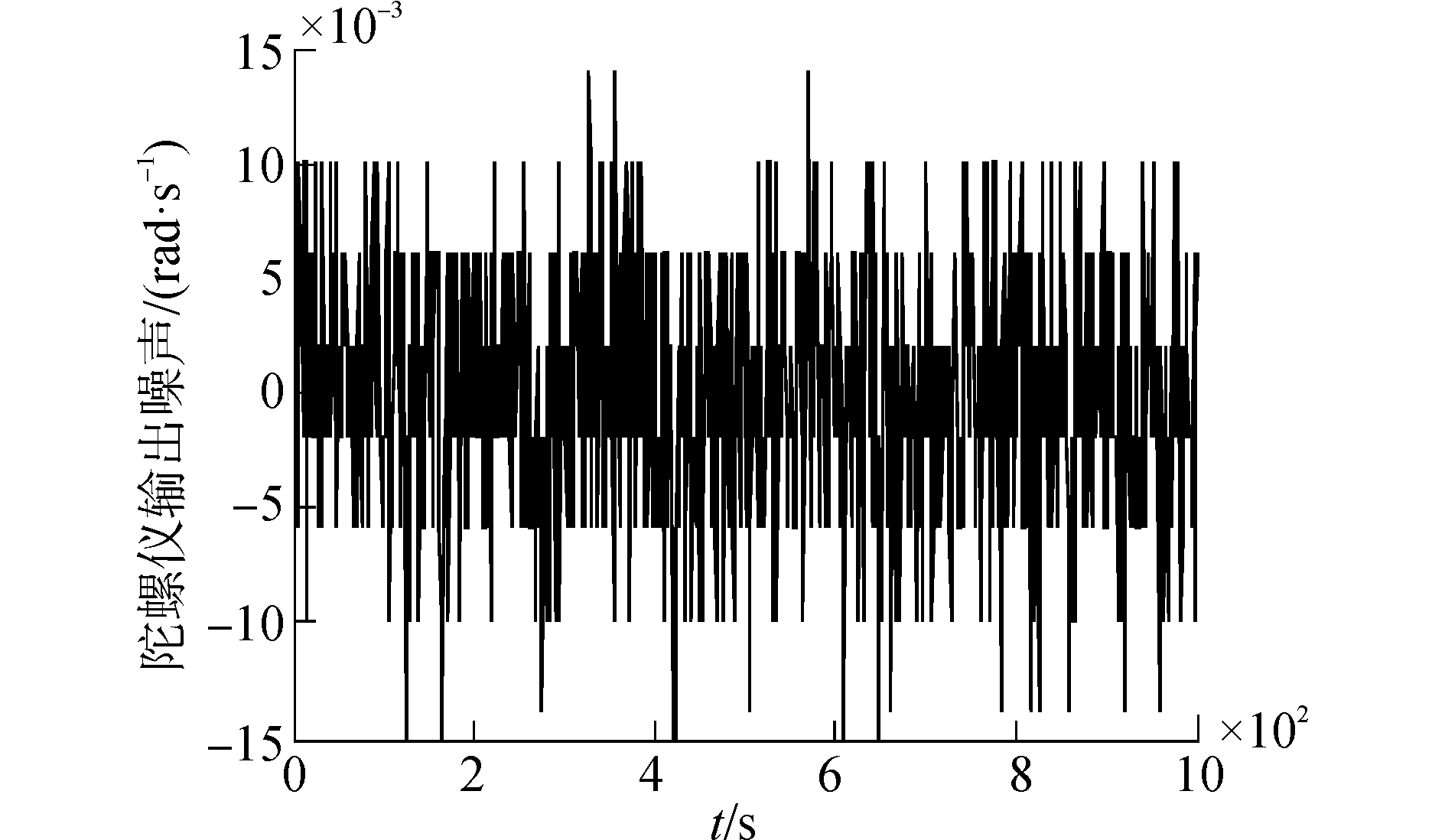
本实验所需冗余式捷联惯导系统由芯片L3GD20和LSM303DLHC构成,其中L3GD20是数字输出陀螺仪,LSM303DLHC是数字输出加速度计,由图 1所示配置方式安装。为验证六陀螺垂向配置结构惯导系统双故障以及三故障情况下故障隔离算法的有效性,采用该实验系统提供的频率为200 Hz角速率数据,并得到系统陀螺仪噪声,如图 9所示。
|
Download:
|
| 图 9 陀螺仪输出噪声 Fig. 9 Noise of analog gyro | |
1) 双故障验证
在实验所测数据基础上加入双故障条件,可得六陀螺系统导航系统故障检测曲线以及各个陀螺故障隔离函数曲线如图 10~12所示。

|
Download:
|
| 图 10 真实情况双故障下GLT故障检测函数曲线 Fig. 10 GLT detection function curves with double faults in real situation | |
|
Download:
|
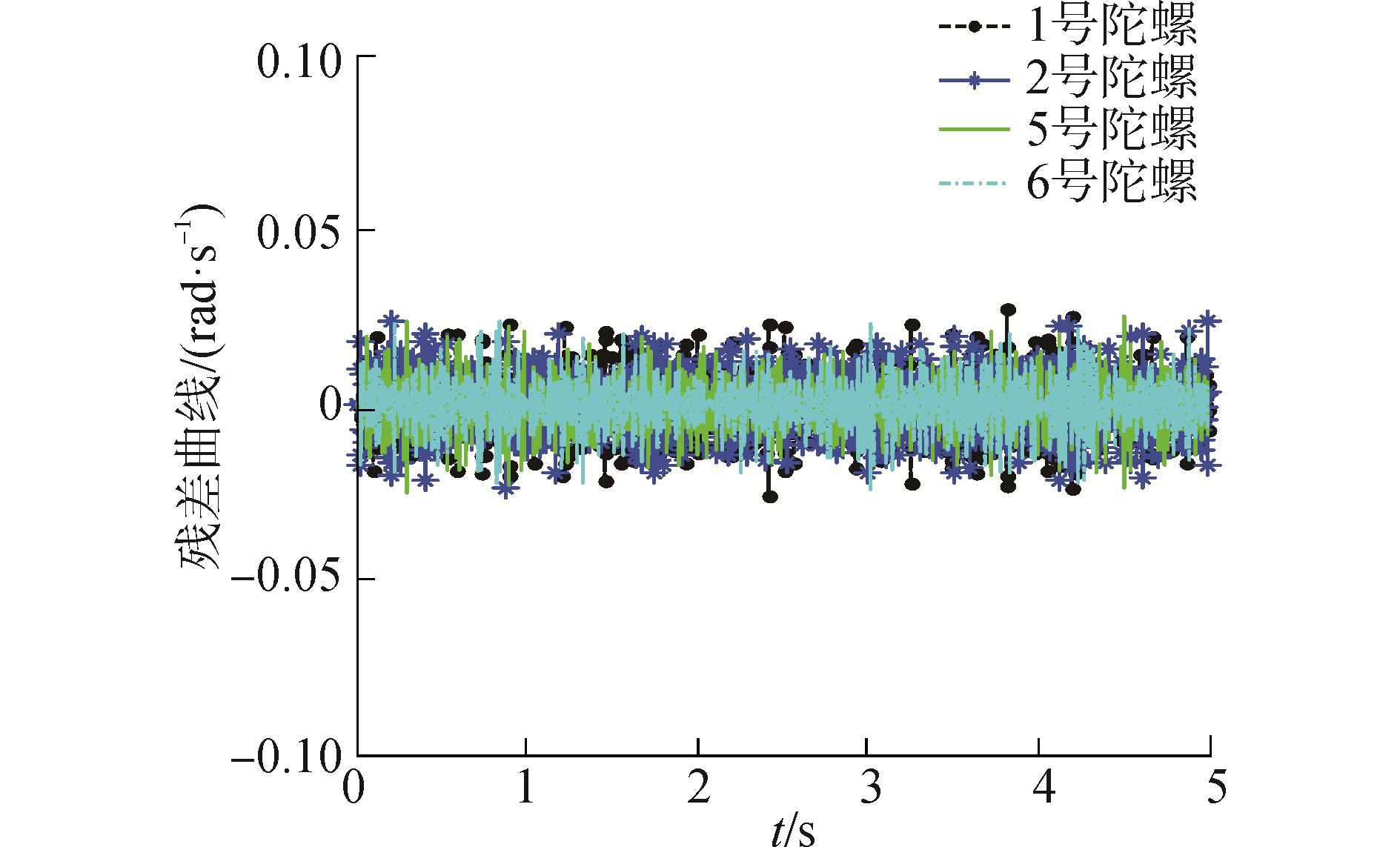
| 图 11 真实情况双故障下陀螺线性估计残差曲线 Fig. 11 Gyro linear estimation residual curve with double faults in real situation | |
|
Download:
|
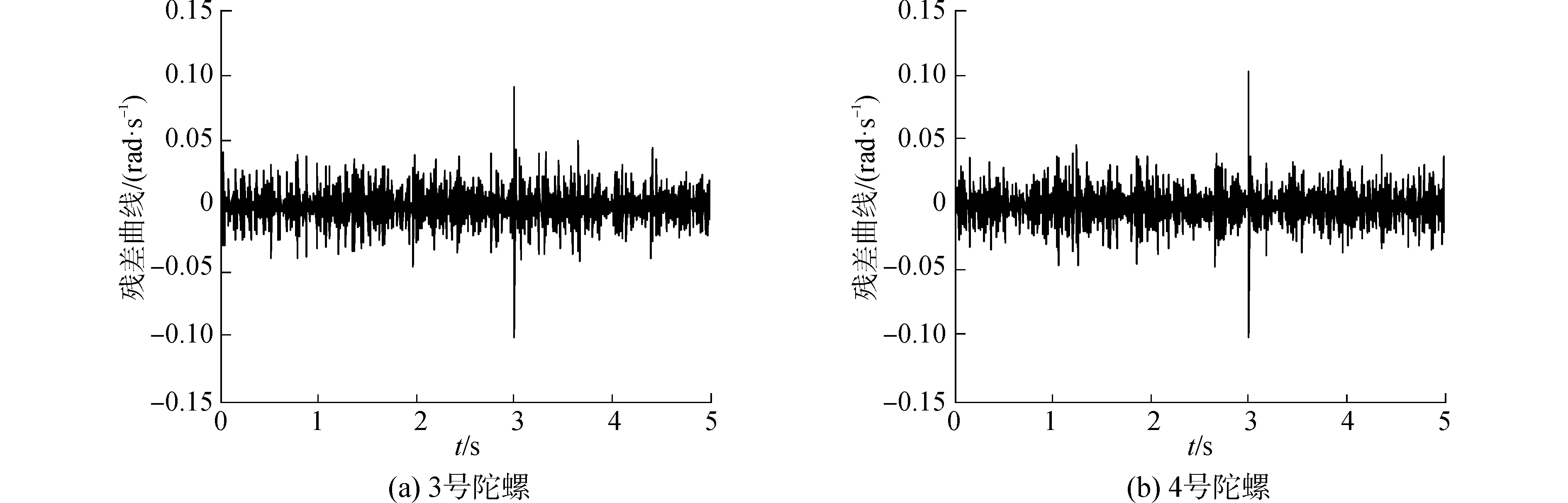
| 图 12 真实情况双故障下3号、4号陀螺线性估计残差曲线 Fig. 12 The 3th, 4th gyro linear estimation residual curves with double faults in real situation | |
由图 10~12可知,当系统双故障时,GLT故障检测方法可以准确判断出第3 s开始六陀螺冗余惯导系统发生故障且3号陀螺和4号陀螺在3 s时线性估计残差值明显高于其他陀螺,说明3号和4号陀螺发生故障。因此,六陀螺惯性导航系统发生双故障时,基于线性估计的故障隔离方法能正确隔离出故障陀螺。通过实测数据仿真得到了与模拟条件仿真相同的效果和结论。
2) 三故障验证
根据上述仿真条件,并加入三故障条件,可得六陀螺系统导航系统故障检测曲线以及各个陀螺故障隔离函数曲线如图 13~15所示。
|
Download:
|
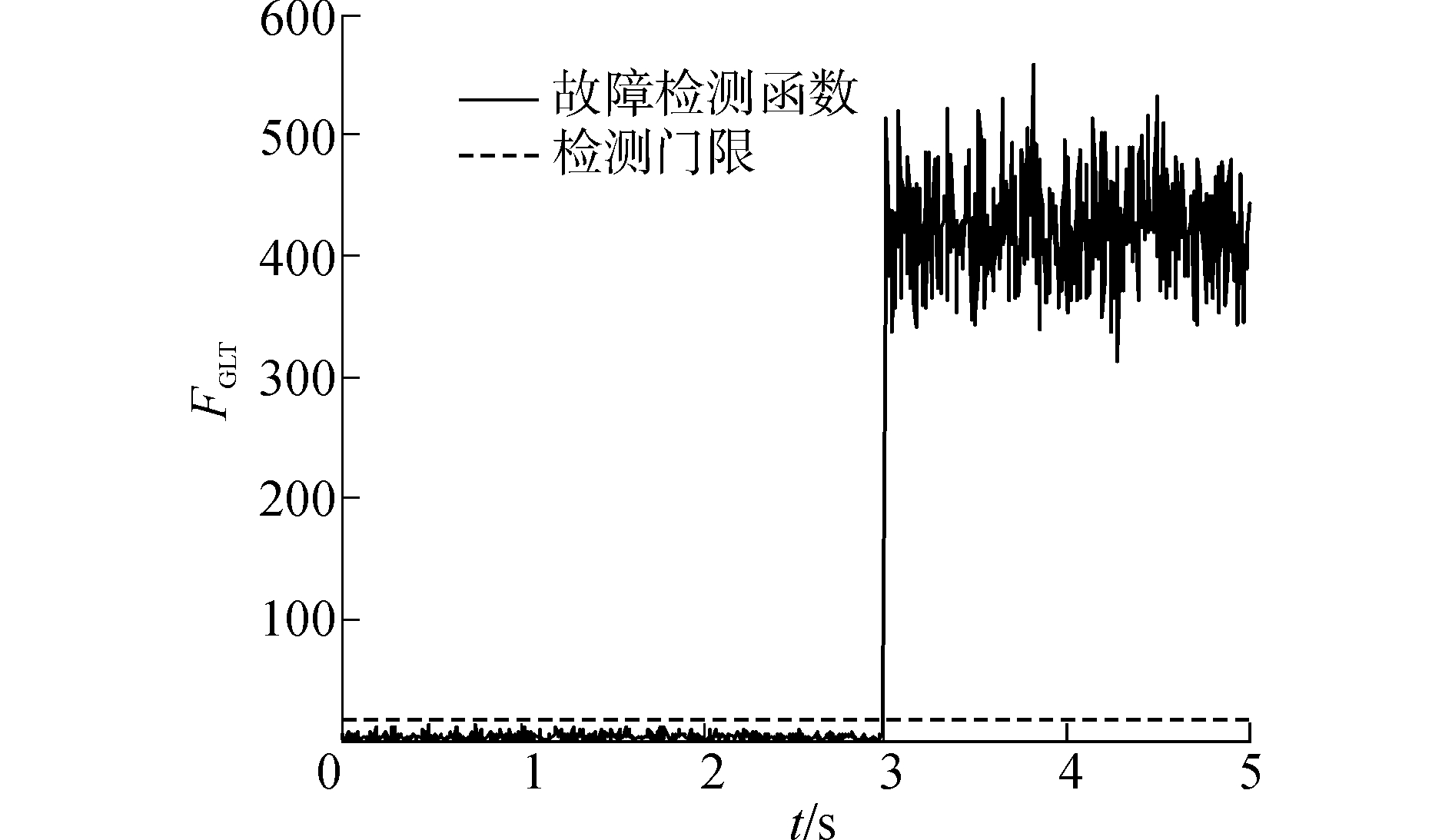
| 图 13 真实情况三故障下GLT故障检测函数曲线 Fig. 13 GLT detection linearfunction curves with three faults in real situation | |
|
Download:
|
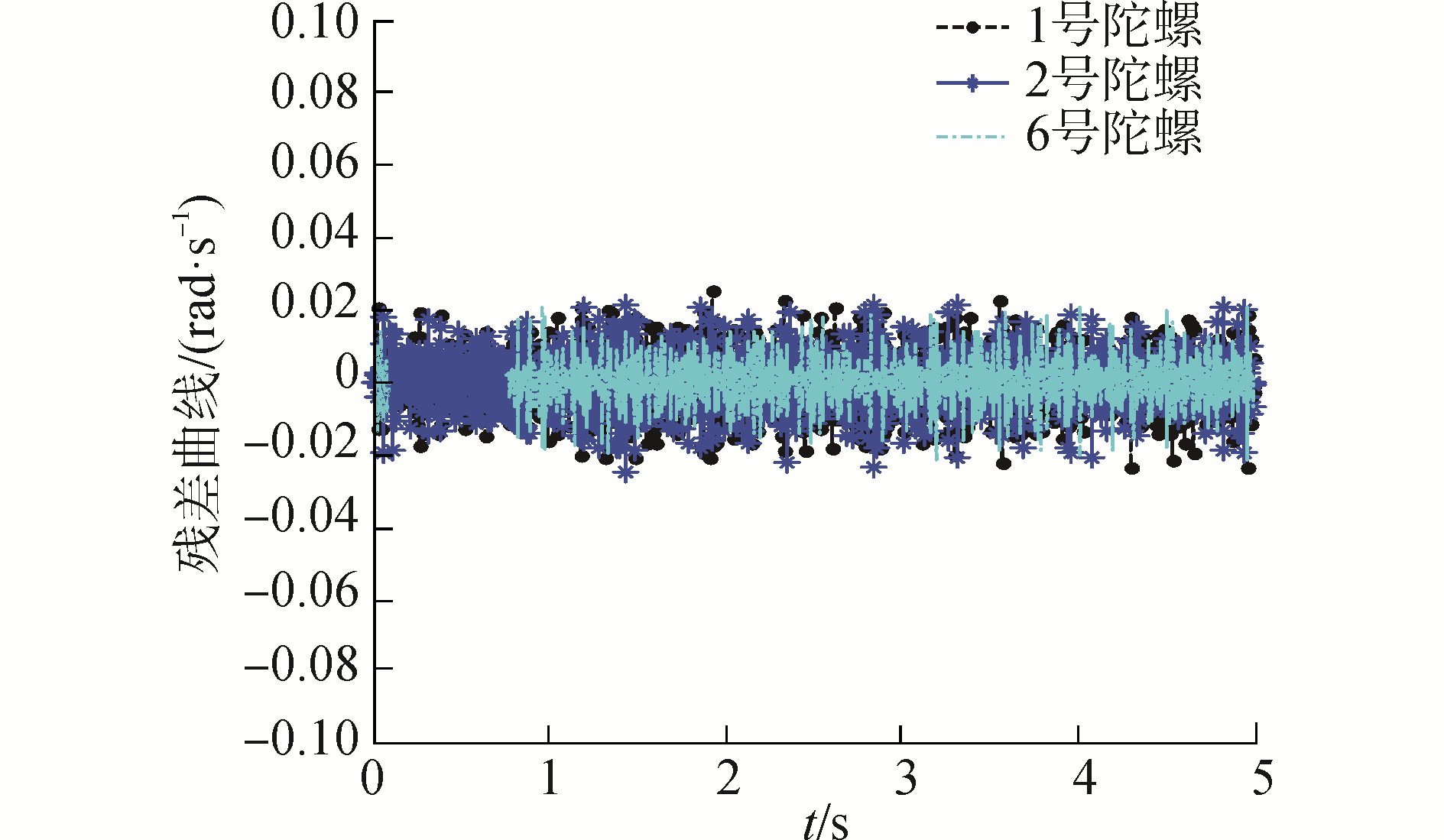
| 图 14 真实情况三故障下陀螺线性估计残差曲线 Fig. 14 Gyro estimation residual curve with three faults in real situation | |
|
Download:
|
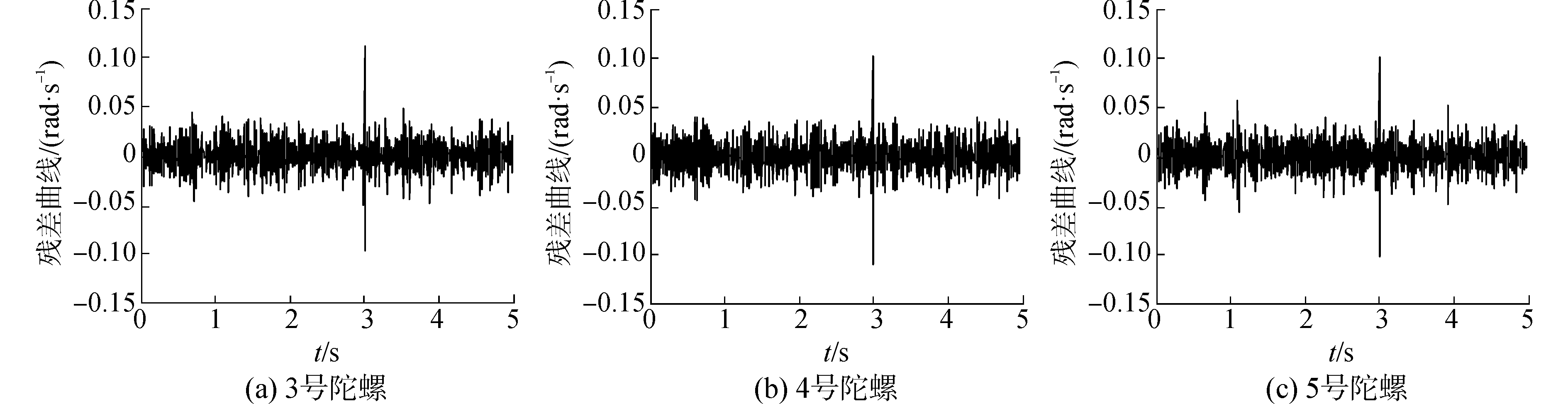
| 图 15 真实情况三故障下3号、4号、5号陀螺线性估计残差曲线 Fig. 15 The 3th, 4th and 5th gyro linear estimation residual curves with three faults in real situation | |
同理,由图 13~15可知,当系统三故障时,GLT故障检测故障函数值在第3 s超出了故障门限值且3号陀螺、4号陀螺和5号陀螺在3 s时线性估计残差值明显高于其他陀螺,说明3号、4号和5号陀螺发生故障。因此,六陀螺惯性导航系统发生三故障时,基于线性估计的故障隔离方法能正确隔离出故障陀螺。通过实测数据仿真得到了与模拟条件仿真相同的效果和结论,说明该故障检测与隔离方案可以检测并隔离冗余式惯导系统多故障。
5 结论1) 提出的方案在六陀螺冗余惯导系统发生多故障时,可实时监测且准确隔离故障陀螺。通过对两种故障情况的仿真,验证了广义似然比故障检测与隔离方法在六陀螺捷联惯导系统中能够对单故障进行检测与隔离结论的正确性,并说明了基于线性估计的故障隔离方法在故障隔离时的优势。
2) 该方法能够广泛应用于多陀螺冗余惯导系统的故障检测与隔离,对于提高冗余式捷联惯导系统的可靠性具有重要的实际意义。
| [1] |
秦永元. 惯性导航[M]. 2版. 北京: 科学出版社, 2015: 1-10. QING Yongyuan. Inertial navigation[M]. 2nd ed. Beijing: Science Press, 2015: 1-10. (  0) 0)
|
| [2] |
颜东, 陈家斌, 刘星桥. 冗余技术提高惯性导航系统可靠性的应用[J]. 中国惯性技术学报, 2003, 11(3): 68-72. YAN Hua, CHEN Jiabin, LIU Xingqiao. Application of redundancy technology in inertial navigation systems[J]. Journal of Chinese inertial technology, 2003, 11(3): 68-72. (  0) 0)
|
| [3] |
富立, 王新玲, 岳亚洲. 基于可靠性分析的最优冗余配置数量确定方法[J]. 北京航空航天大学学报, 2010, 36(9): 1010-1033. FU Li, WANG Xinling, YUE Yazhou. Method for investigation of the optimal redundant gyros number based on reliability analysis[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(9): 1010-1033. (  0) 0)
|
| [4] |
CHENG Jianhua, DONG Jinlu, LANDRY JR R, et al. A novel optimal configuration form redundant MEMS inertial sensors based on the orthogonal rotation method[J]. Sensors, 2014, 14(8): 13661-13678. (  0) 0)
|
| [5] |
DALY K C, GAI E, HARRISON J V. Generalized likelihood test for FDI in redundant sensor configurations[J]. Guidance and control, 1979, 2(1): 9-17. DOI:10.2514/3.55825 (  0) 0)
|
| [6] |
杨柏军, 潘鸿飞, 才晓锋. 惯性冗余系统奇偶向量法故障检测与识别技术研究[J]. 战术导弹技术, 2009(4): 68-72. YANG Baijun, PAN Hongfei, CAI Xiaofeng. Study of fault detection and recognition technique in inertial redundancy system based on parity vector[J]. Tactical missile technology, 2009(4): 68-72. (  0) 0)
|
| [7] |
SHIM D S, YANG C K. Geometric FDI based on SVD for redundant inertial sensor systems[C]//Proceedings of the 5th Asian Control Conference. Melbourne, Victoria, Australia, 2004, 2: 1094-1100.
(  0) 0)
|
| [8] |
任子君, 符文星, 张通, 等. 冗余捷联惯组故障诊断的奇异值分解新方法[J]. 仪器仪表学报, 2016, 37(2): 412-419. REN Zijun, FU Wenxing, ZHANG Tong, et al. New SVD method in FDI of redundant IMU[J]. Chinese journal of scientific instrument, 2016, 37(2): 412-419. (  0) 0)
|
| [9] |
JAFARI M. Optimal redundant sensor configuration for accuracy increasing in space inertial navigation system[J]. Aerospace science and technology, 2015, 47: 467-472. DOI:10.1016/j.ast.2015.09.017 (  0) 0)
|
| [10] |
JAFARI M, ROSHANIAN J. Optimal redundant sensor configuration for accuracy and reliability increasing in space inertial navigation systems[J]. The journal of navigation, 2013, 66(2): 199-208. DOI:10.1017/S0373463312000434 (  0) 0)
|
| [11] |
高豫强, 祝君冬, 赵剡. 捷联式惯导系统陀螺仪冗余配置研究[J]. 战术导弹技术, 2008(2): 62-66. GAO Yuqiang, ZHU Jundong, ZHAO Yan. Study on redundancy configuration of strap-down inertial gyros[J]. Tactical missile technology, 2008(2): 62-66. (  0) 0)
|
| [12] |
董金鲁. 船用捷联式惯性导航系统冗余配置方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2015: 41-44. DONG Jinlu. The research of redundant configuration of shipborne strapdown inertial navigation system[D]. Harbin: Harbin Engineering University, 2015: 41-44. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


