2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西 南昌 330013;
3. 长江水利委员会长江口水文水资源勘测局, 上海 200136
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, Nanchang 330013, China;
3. Yangtze Estuary Hydrology and Water Resources Survey Bureau, Shanghai 200136, China
实时、准确地获取流量信息, 有助于水文工作者和管理人员更好地了解河段的水动力过程, 为防洪减灾、水资源规划和管理提供可靠的科学依据[1]。实时流量通常可采用水位-流量比率曲线进行估计[2-4]。该方法虽然计算简便, 但对于受潮汐涨落影响的感潮河段, 其水力条件复杂, 水位不是流量的单一函数, 二者并无稳定的对应关系[5-6], 因此水位-流量比率曲线并不适用[7]。
近年来, 随着声学多普勒流速剖面仪(ADCP)等现代声学仪器的出现, 不少学者提出了一种流量实时估计的新方法—指标流速法(IVM)。该方法的基本原理是:首先将断面中固定ADCP流速剖面的某一水深单元流速或垂线平均流速作为指标流速u, 然后建立u与断面平均流速U之间的函数关系, 即u-U关系模型; 对于断面面积A, 则建立水位G与A之间的函数关系, 即G-A关系模型; 断面流量则可由U与A的乘积获得。Chen等[8]使用单垂线指标流速法在台湾淡水河进行实验, 结果表明该方法对感潮河段的流量实时估计不仅计算简单, 而且具有较高的可靠性。Nihei等[9]提出了一种基于水平式ADCP单个剖面流速进行动态内插和外推的流量估计方法。Hoitink等[10]采用半确定半随机的方法将水平式ADCP的某一位置指标流速转换为实时流量。Sassis等[11]采用边界层模型对壁面效应进行修正, 然后将水平式ADCP特定的流速剖面数据转换成断面流量值。沈鸿金[12]利用水平式ADCP的指标流速与断面平均流速的率定关系, 在珠江天河水文站建立了潮流量自动监测系统, 并验证了系统的可行性和正确性。由于指标流速法能够实时、快速的获得断面流量, 因此在感潮河段得到了广泛应用。
然而, 基于单个垂线剖面或水深单元的指标流速法在在长江口河段的应用中存在以下不足:1)已有研究均聚焦于宽度小于1 000 m的断面[13], 这些断面流速横向差异并不明显。长江口某些水域断面宽度可达6 000 m, 其横断面方向流速差异显著[14], 基于单一指标流速u很难构建反映整个断面平均流速U的模型; 2)长江口流量季节性变化显著[15], 借助单一时段的流速流量建立的u-U模型并不一定适用于其他季节; 3)受科氏力和河道弯曲影响[16-18], 长江口某些水域的水面并非平面, 而是一个坡面, 基于单一水位值估计断面面积并不准确。
为此, 本文以长江口徐六泾断面为研究对象, 根据断面形态布设了2条固定式ADCP垂线, 并分析上游的径流、潮流周期及垂线位置对断面平均流速估计的影响, 对单垂线指标流速法进行改进, 建立满足位置、季节、流量和水位复杂变化下的合理、准确的u-U模型和G-A模型, 实现大型感潮河段实时流量的精确估计, 扩展指标流速法的应用范围。
1 单垂线指标流速法 1.1 u-U关系模型构建天然河道的垂线流速分布可表示为[19]
| $ \frac{{{u}_{z}}}{{{u}_{*}}}=c{{\left( \frac{z}{{{z}_{0}}} \right)}^{b}} $ | (1) |
式中:uz为水深z对应的流速;
| $ {{u}_{z}}=a{{z}^{b}} $ | (2) |
根据ADCP实测流速剖面的各水深层流速值, 可采用最小二乘方法对式(2)进行拟合以得到a值, 这样垂线平均流速u可表示为
| $ u=\frac{\int_{0}^{H}{a{{z}^{b}}\text{d}z}}{H} $ | (3) |
式中:H为垂线水深。垂线平均流速u通常作为指标流速, 用于构建断面平均流速U的函数模型。u-U关系模型通常表示为线性形式[13]:
| $ U={{a}_{0}}+{{a}_{1}}u $ | (4) |
式中:a0和a1为待定系数, 可利用实测的断面平均流速U和垂线平均流速u, 根据最小二乘解算得到。
1.2 G-A关系模型构建感潮河段水位变化快, 因此有必要建立水位(G)-面积(A)估计模型以快速确定断面面积。G-A关系模型一般可表达为多项式形式[13]:
| $ A={{c}_{0}}+{{c}_{1}}G+{{c}_{2}}{{G}^{2}} $ | (5) |
式中:c0、c1和c2为待定系数。水位G可通过验潮站实时获得, 断面面积A则可以通过梯形计算的方法获得。获得了断面面积及水位, 对于式(5)中的参数可同样根据最小二乘原理解算得到。
2 双垂线流量估计方法双垂线流量估计方法是单垂线指标流速法的拓展, 主要体现在两个方面:1)根据断面形态布设2条固定垂线, 利用这2个垂线平均流速u的组合来构建u-U关系模型; 2)对于存在水面横比降的河道, 采用水力模型或双验潮站进行水位改正。
2.1 u-U关系模型的构建对于长江口这种大型感潮河段, 其横断面方向流速差异较大, 特别是在转流或二次流情况下, 中泓与两岸之间的流速差异显著。因此, 可考虑在断面中泓和浅滩位置分别布设固定垂线, 利用二者的垂线平均流速u的组合模型来估计断面平均流速U。一阶双垂线u-U关系模型可表示为
| $ U={{k}_{1}}{{u}_{1}}+{{k}_{2}}{{u}_{2}}+\alpha $ | (6) |
式中:α为常数项, ki为指标流速ui对应的系数或权值。理论上来讲, 垂线的代表性越强, 其系数k值越大。对于单垂线法, 垂线布设位置一般位于断面中泓, 该位置的流速相对来说代表性较强, 式(6)中的系数k应接近于1。对于双垂线法, 由于中泓流量比重大, 所以中泓处的k值较大, 浅滩处的k值则可能较小。另外, 由于长江流域降水的季节性差异较大, 有必要在不同季节分别建立u-U模型, 以获取更精确的断面平均流速。
2.2 水位改正对于弯曲河道, 水流由直线段进入曲线段后, 在离心力作用下将作曲线运动, 从而形成水面横比降。若仍采用单站水位值来计算各控制点的水深, 势必同实际值产生系统偏差, 进而影响断面面积的估计。因此, 有必要对水位观测值进行精确改正, 水位改正可采用水力模型和双验潮站两种方法。
2.2.1 水力模型改正在离心力作用下, 弯道横比降产生的水位差ΔZ可表示为[18]
| $ \Delta Z=B{{{\bar{U}}}^{2}}/\left( gR \right) $ | (7) |
式中:B为水面宽度, U为断面平均流速, R为弯道曲率半径。采用水力模型进行水位改正的关键是获取准确的U和R。
2.2.2 双验潮站改正如图 1所示, 受弯道横比降影响, 水面为斜面, 凹岸的验潮仪S1高程为HS1, 距第一个控制点f0的横向距离为dS1, 验潮仪获得的实测水深值为DS1, 那么水面处的水位GS1=HS1+DS1; 设凸岸的验潮仪S3高程为HS3, 距f0的横向距离为dS3, 验潮仪获得的实测水深值为HS3, 则水面处的水位GS3=HS3+DS3。这样, 其余各控制点处的水位改正值ΔGi可由式(8)改正得到。
| $ \Delta {{G}_{i}}=\frac{{{G}_{{{S}_{3}}}}-{{G}_{{{S}_{1}}}}}{{{d}_{{{S}_{3}}}}-{{d}_{{{S}_{1}}}}}({{d}_{i}}-{{d}_{{{S}_{1}}}}) $ | (8) |

|
Download:
|
| 图 1 弯曲河道断面面积计算示意图 Fig. 1 Sectional area estimation in the bend channel | |
这样, 获得了改正后的水位及已知的河底高程, 断面面积仍可由梯形面积法得到。
2.3 流量计算获得了断面平均流速U及断面面积A, 断面流量就可以由二者乘积Q=UA直接获得。流量估计精度一般可利用估计流量Qf和实测流量Qd之间的均方根误差RMSE及相对标准偏差RSD=RMSE·
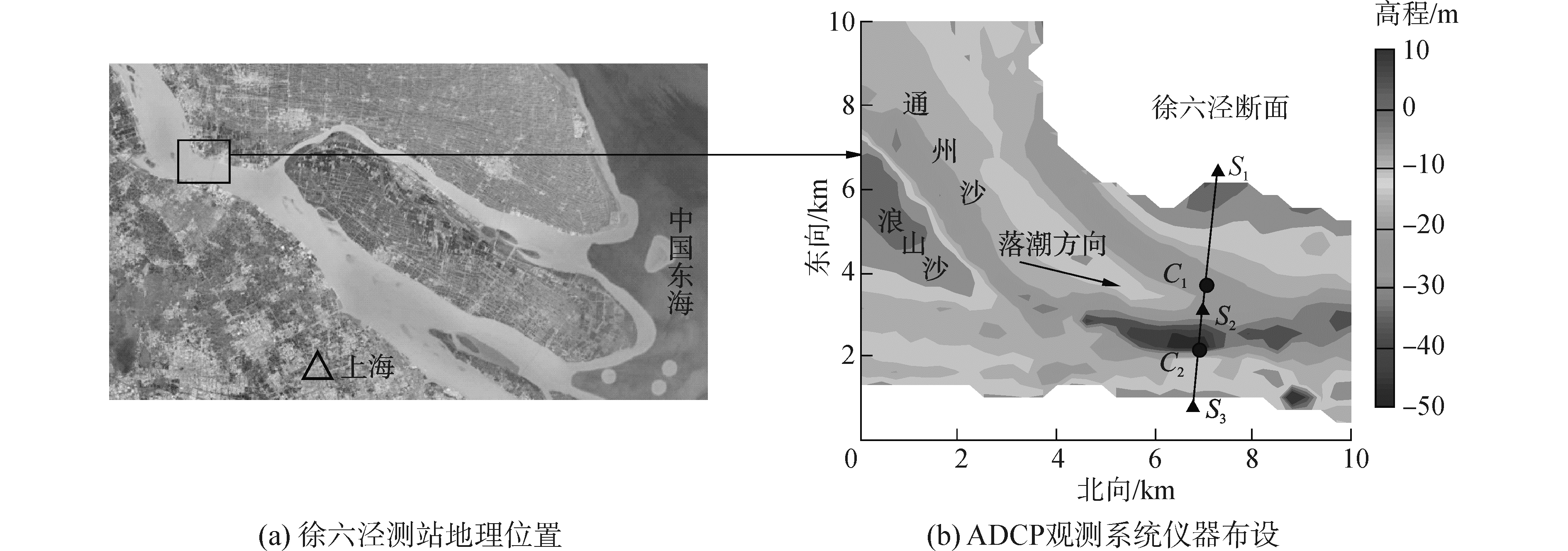
长江口水量丰沛, 输沙量大, 据大通站水文测验资料可知, 长江年均流量为28 700 m3/s, 年均输沙量为4.330×108 t[2]。徐六泾站距长江口门约110 km(图 2), 它既是南北支的分流点, 又是整个长江口多级分汊的起点。作为长江进入河口区的重要边界点, 徐六泾水文泥沙特征的研究不仅对河口科学研究本身, 而且对探讨长江三峡大坝、南水北调和长江口深水航道等重大工程对河口地区的影响都显得非常及时和重要。
|
Download:
|
| 图 2 徐六泾测站地理位置及ADCP观测系统仪器布设 Fig. 2 Location of Xuliujing section in Yangtze Estuary and the set up of ADCP system | |
相对于已有研究中的感潮河段, 徐六泾断面具有以下特点:1)徐六泾断面宽5.67 km, 远大于已有研究的实验断面(< 1 km)[13, 20], 且断面流速横向差异明显; 2)徐六泾断面处于弯道的中间位置(图 2), 受离心力及科氏力的综合影响, 断面水位将产生横比降, 即出现河道凹岸水位高, 凸岸水位低的情况; 3)徐六泾河段流量变化受径流影响较大(图 3):春季为枯水期, 上游来水较少, 断面日平均流量小于2.0×104 m3/s; 夏季为洪水期, 日平均流量为4.0×104 m3/s, 为春季的两倍, 并在七月份达到峰值5.3×104 m3/s; 到了秋季, 由于降水减少, 流量则缓慢回落。上述特点决定了借助单垂线单时段流速数据很难实现断面流量的准确计算, 而需结合这些特点开展不同季节的u-U、G-A关系模型构建, 实现实时流量的准确估计。

|
Download:
|
| 图 3 徐六泾断面2011年日平均流量及水位变化图 Fig. 3 Time series of the net discharges and water level at Xuliujing section in 2011 | |
实验将2台RDI公司生产的300 kHz的4探头ADCP分别布设在徐六泾断面浅水及中泓区域, 用C1和C2表示, 以检验垂线布设位置对u-U关系模型构建的影响(图 2、图 4)。ADCP水深单元设置为1.0 m, 采样间隔为30 min。同时, 在徐六泾断面进行走航式ADCP测量, 获得的流量数据作为已知流量Qd, 用于u-U模型的校准。为了检验u-U模型的季节变化, 实验采集了2011年春、夏、秋3个时段的数据, 并分别构建u-U关系模型。实验期间的水位、面积和流量统计参数如表 1所示。

|
Download:
|
| 图 4 徐六泾2011年不同季节的断面形态及垂线位置 Fig. 4 Shapes of Xuliujing section and the location of verticals in different seasons of 2011 | |
| 表 1 实验期间的参数统计(2011年) Tab.1 Parameters statistics of the experiment data in 2011 |
此外, 为验证弯道横比降对两岸水位的影响, 在2012年9月1~2日进行了徐六泾断面水位观测实验。在断面的左岸、中间及右岸位置(图 2)分别布设S1、S2及S3三个GPS验潮站, 水位测量精度均优于±0.05 m。
4 实验结果及分析 4.1 u-U关系模型 4.1.1 模型阶数对拟合结果的影响在构建u-U关系模型时, 已有学者选择1阶线性模型[13], 或采用2阶或3阶模型[20]。因此, 有必要探讨徐六泾断面的u-U关系模型的最佳阶数。由于C2垂线水深最大, 且夏季的径流潮流相互作用最强, 水文条件最为复杂, 因此选取C2垂线夏季的流速数据进行建模, 实验结果如图 5所示。

|
Download:
|
| 图 5 采用C2垂线数据构建的各阶u-U关系模型 Fig. 5 The u-U models established by the data of C2 vertical | |
从图 5所示结果可以看出:1)总体来说, 拟合结果随模型阶数增大逐步变好; 2)常用的1阶或2阶模型并未接近于最佳拟合效果, 需要采用更高阶数模型; 3)当模型阶数达到3阶时, 拟合结果接近于最佳值:随模型阶数增加, 拟合效果基本不变。因此, 后续实验将采用3阶多项式进行u-U关系建模。
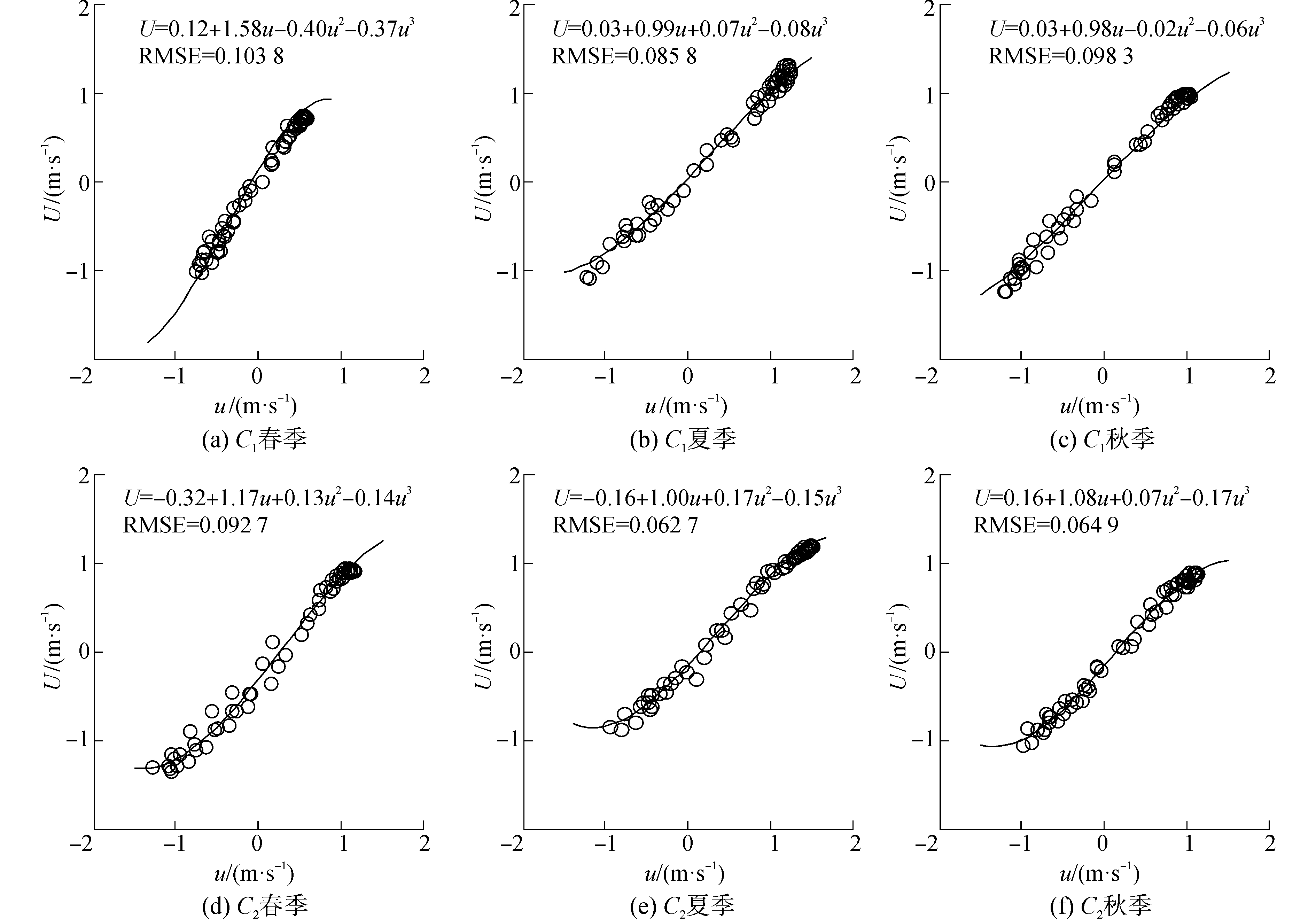
4.1.2 季节变化和垂线位置对u-U关系模型的影响分别利用C1和C2测站不同季节的的垂线平均流速, 采用单垂线法构建不同季节的u-U关系模型, 结果如图 6所示。
|
Download:
|
| 图 6 C1和C2垂线不同季节的u-U模型率定曲线 Fig. 6 u-U models of vertical C1 and C2 in different seasons | |
由图 6可知:
1) 不同季节的数据拟合得到的u-U关系模型不同:春季u-U关系模型中, 1阶项u的系数较大, 主要是由于春季为枯水期, 浅水区流速流量较小, 而中泓流速流量较大, 因此, 中泓的相关性则变得比较强(u项系数k>1);到了夏季, 雨量显著增大, 整个断面平均流速与垂线平均流速基本持平, u与U的关系弱化, 模型退化为线性模型(k≤1);秋季流量缓慢回退, u-U模型与夏季模型基本一致。
2) 对于同一季节, 2条垂线的u-U模型均不相同, 但两个垂线模型系数在夏季比较接近。分析认为, 夏季流量大, C2垂线位于深水区, 流速较大; C1位置水深稍浅但流速仍较大, 代表性也较强。因此, 二者的垂线平均流速均可较好地反映整个断面的平均流速。
3) 单垂线u-U模型精度不高。C1的单垂线模型均方根误差RMSE为0.08~0.10 m/s, 均值大于0.09 m/s; C2模型的精度相对较好, 其RMSE值为0.06~0.09 m/s, 均值约为0.07 m/s。对于大型感潮河段来说, 较小的断面平均流速误差也将引起巨大的流量估计误差。因此, 有必要对单垂线法进行改进, 实现断面流速的精确估计。
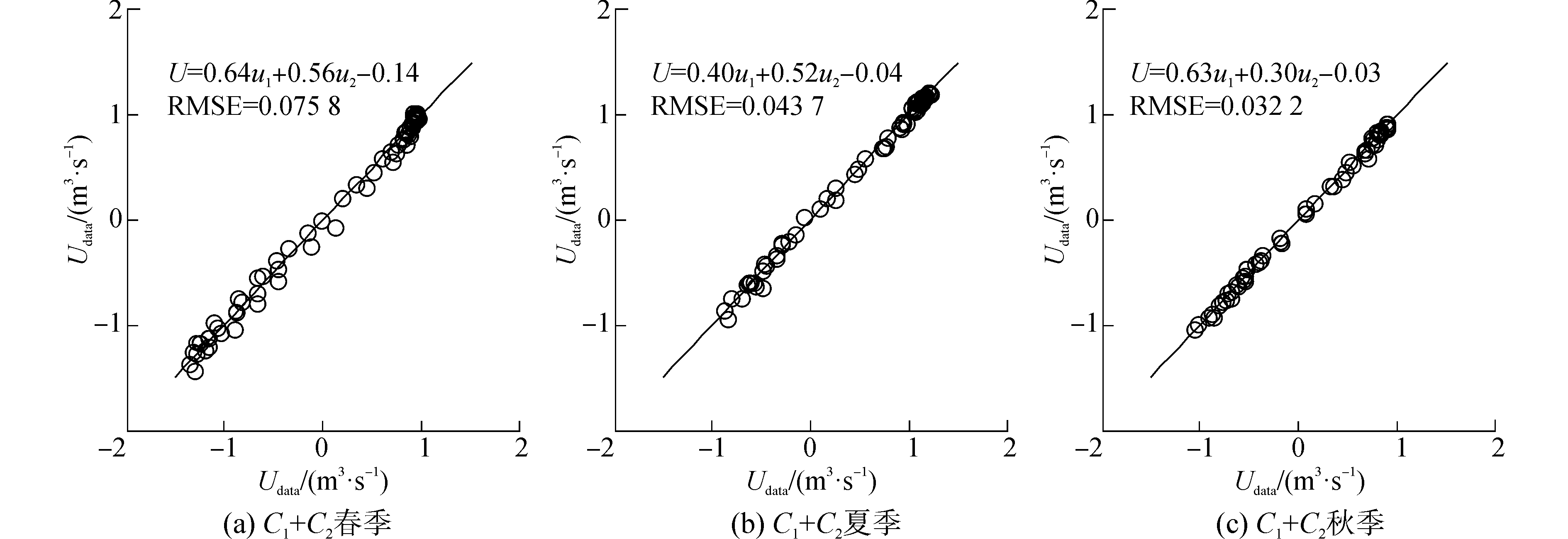
4.1.3 双垂线u-U关系模型的构建实验利用C1和C2各季节同时刻的垂线平均流速, 根据式(6), 求解未知参数, 得到双垂线u-U模型以及对应的拟合曲线, 如图 7所示。相对于单垂线法, 双垂线组合法获得的断面平均流速拟合结果要好:双垂线模型的RMSE值为0.03~0.07 m/s, 均值约为0.05 m/s, 均优于C1和C2单垂线模型精度。
|
Download:
|
| 图 7 C1, C2双垂线组合模型率定曲线 Fig. 7 u-U models established by C1, C2 double verticals | |
由双垂线法构建的各季节u-U关系模型可以看出, 系数值k1和k2之和基本接近于1, 且二者差值较小。该现象说明在长江口徐六泾水域, 中泓和浅水区的垂线流速代表性均较强, 对于断面平均流速的估计所占权重基本一致, 且缺一不可。
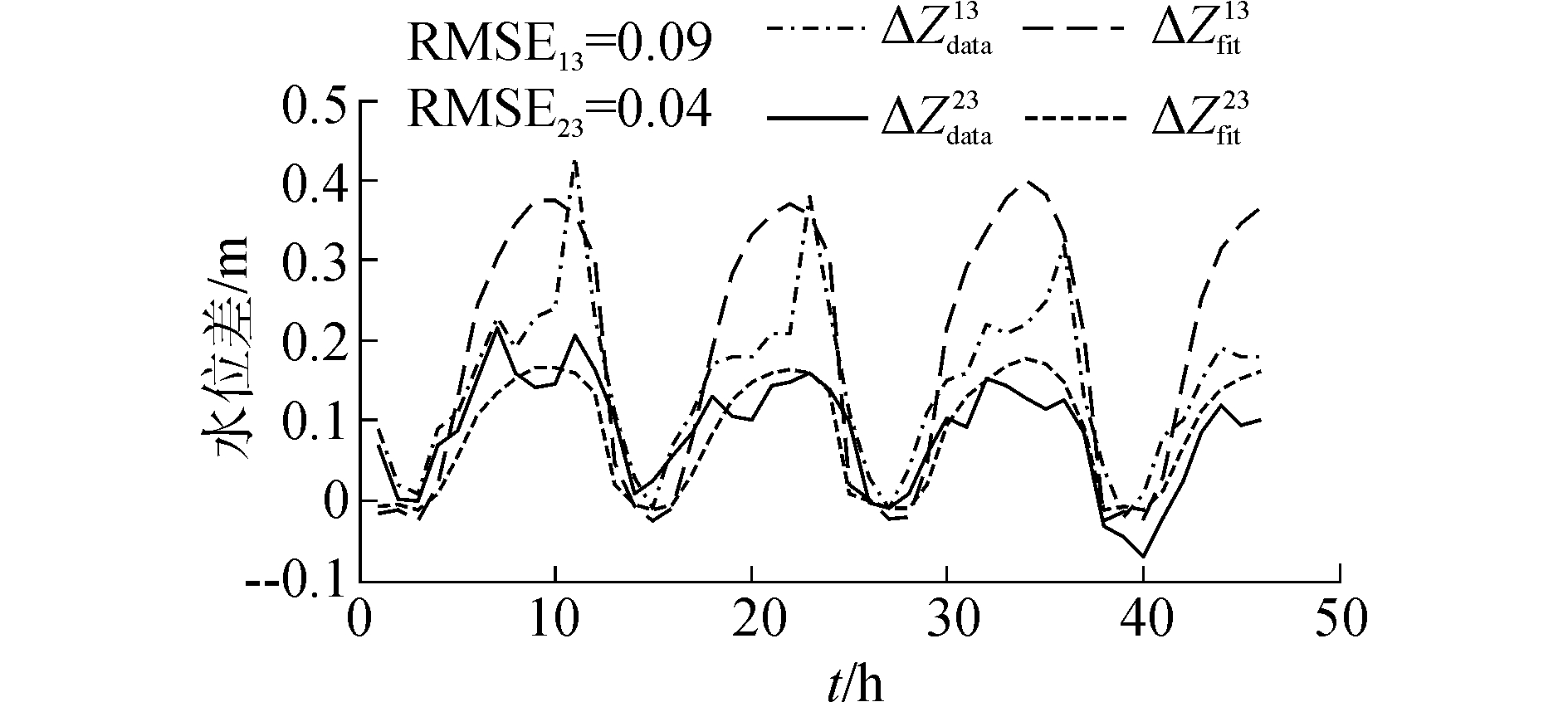
4.2 G-A关系模型 4.2.1 弯道河段横比降对断面面积估计的影响为验证水力模型的水位改正效果, 实验计算了徐六泾断面两端S1与S3之间水位差的实测结果和水力模型估计结果(ΔZdata13, ΔZfit13), 以及中泓S2与南岸S3之间水位差的实测和估计结果(ΔZdata23, ΔZdata23), 如图 8、9所示。
|
Download:
|
| 图 8 徐六泾断面水位差实测值和估计值 Fig. 8 Difference between measured and estimated water level in Xuliujing section | |
|
Download:
|
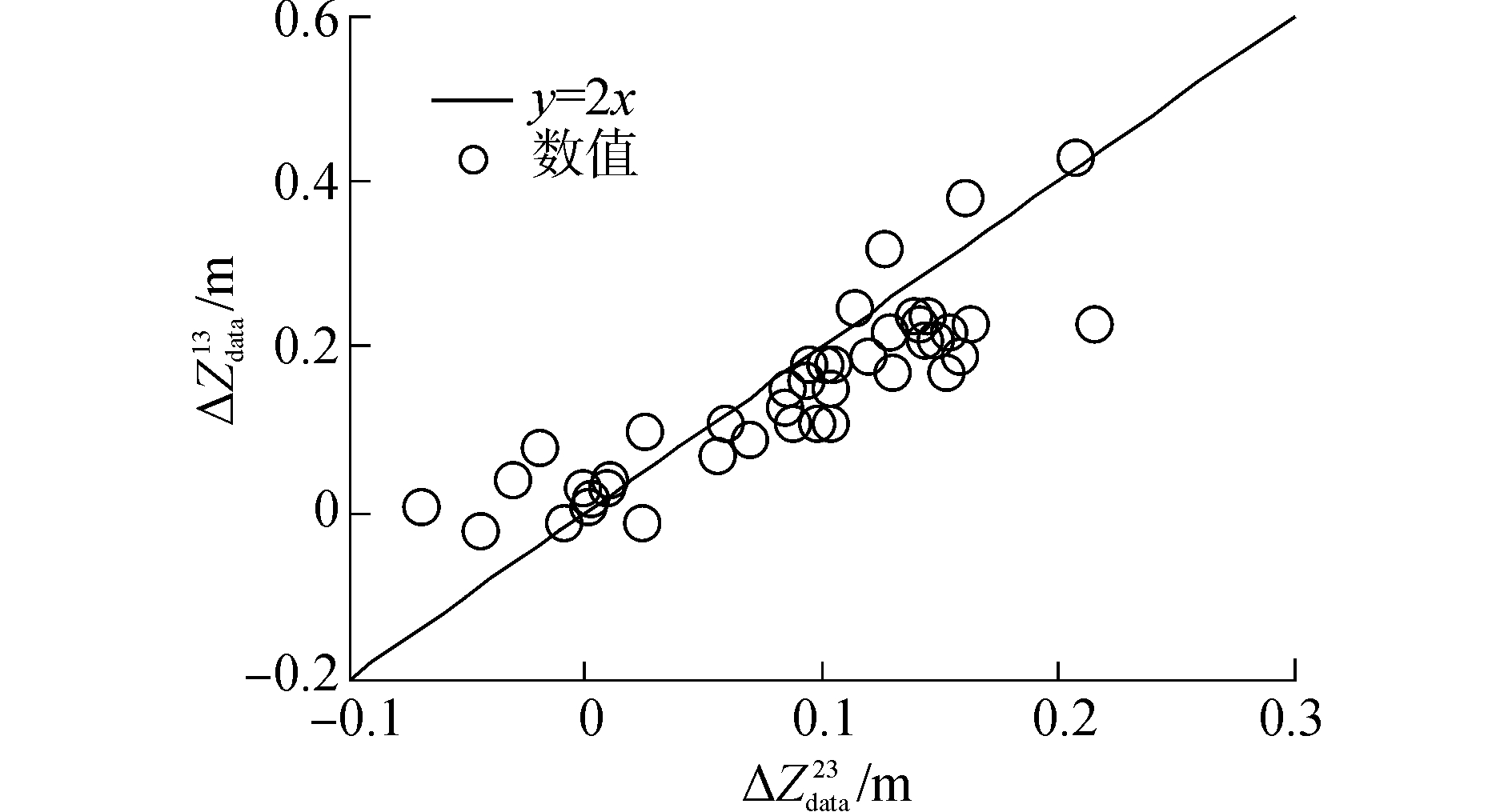
| 图 9 ΔZdata13和ΔZdata23的关系 Fig. 9 Relationship between ΔZdata13 and ΔZdata23 | |
1) 在徐六泾断面, 横比降存在于潮周期的各个阶段, 且其周期同半日潮周期一致, 约为12 h; 在憩流或停流阶段, 断面流速基本为0, 其水位差也接近为0。
2) 横比降对断面两端水位差的最大影响达到0.4 m, 对于宽度约为6 km的徐六泾断面来说, 其对断面面积估计的影响最大可达1 200 m2/s, 约占总断面面积的1.3%~1.7%。因此, 在弯道河段对水位观测值进行改正是有必要的。
3) 断面两端水位差估计值ΔZfit13与实测值ΔZdata13的最大差异达到了0.16 m, 均方根误差RMSE13为0.09 m; 而岸边和中泓实测水位差ΔZdata23与估计值ΔZfit13的最大差异为0.06 m, 均方根误差RMSE23为0.04 m, 该现象表明水力改正模型并不能很好的反映水位差的横向变化。
4) 从图 9所示的ΔZdata23和ΔZdata13的线性拟合关系可以看出, ΔZdata23在各观测时刻的值约为ΔZdata13的一半, 二者采样数据基本落在y=2x曲线附近, 表明徐六泾断面的水面基本呈斜坡形状。
根据以上实验结果可以看出, 单个验潮站的水位改正模型并不能很好的反映两岸水位差变化, 因此可考虑采用图 2所示的双测站进行水位改正。
4.2.2 G-A模型阶数对拟合结果的影响对水位进行改正后, 即可以根据水位值G和梯形面积计算法计算得到的断面面积A构建G-A关系模型。同u-U横型构建类似, 首先有必要探讨徐六泾断面的G-A关系模型的最佳阶数。如图 10所示, 对于徐六泾断面, 1阶G-A关系模型的拟合结果已经很好, K值大于0.999, 更高阶次的拟合效果基本不变。因此, 实验采用1阶线性模型进行G-A关系建模。

|
Download:
|
| 图 10 构建的1~3阶G-A模型 Fig. 10 Different-order G-A models | |
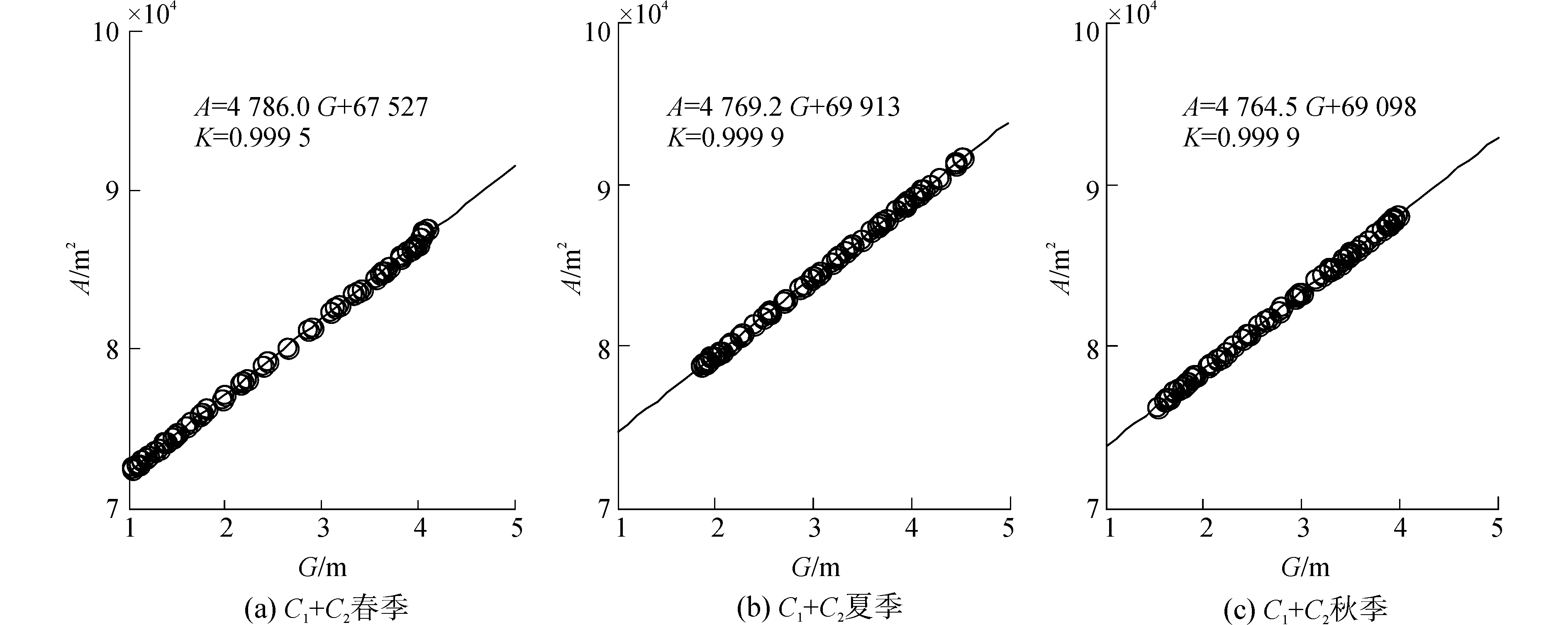
图 11为不同季节的1阶G-A关系模型。对于不同季节, G的系数c1基本一致, 分别为4 786.0、4 769.2和4 764.5;常数项c2的差别较大, 春季和夏季的差值达到了2 400 m2, 约占总断面面积的2.6%~3.3 %。对比图 4所示的断面形态可知, 由于春季的冲刷较大, 相同水位情况下断面面积明显要小。因此, 对于徐六泾断面, 每个季度需至少实施一次断面地形测量, 以保证断面面积的估计精度。
|
Download:
|
| 图 11 不同季节的G-A关系模型 Fig. 11 G-A models and their curves in different seasons | |
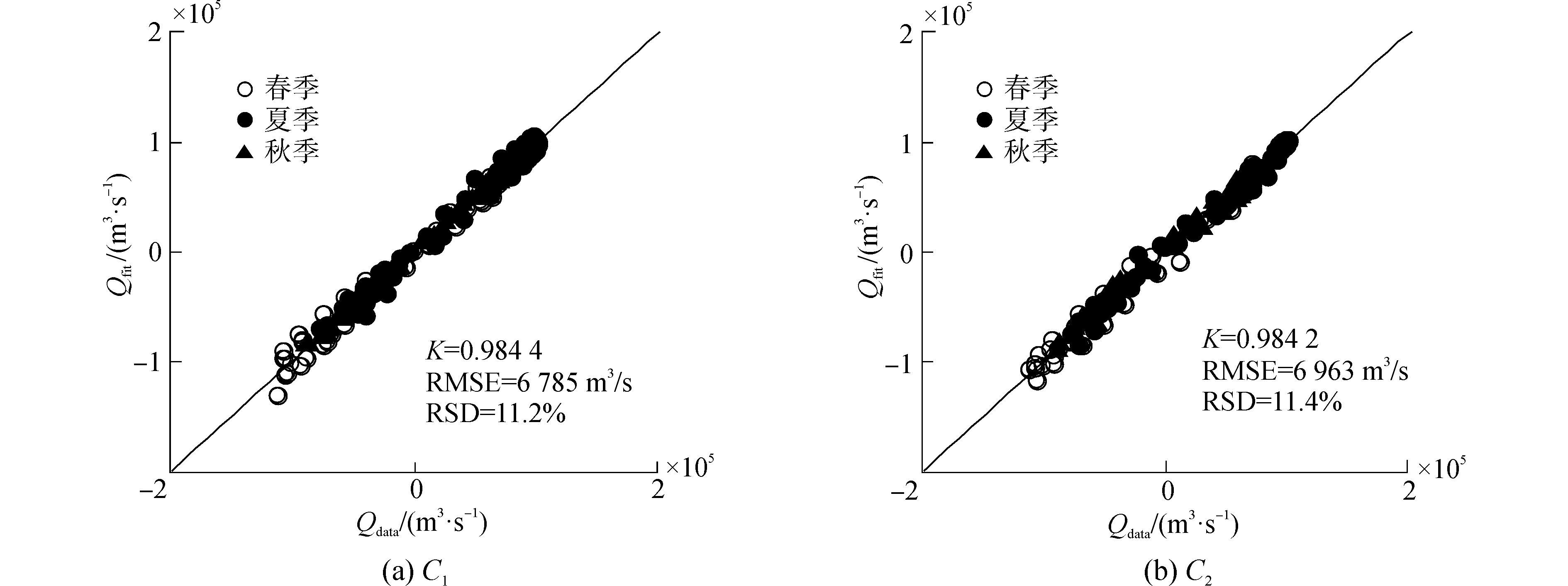
综上所述, 分别利用单垂线和双垂线u-U关系模型计算出各季节的断面平均流速U, 然后利用双验潮站数据对弯道横比降造成的水位差进行改正, 建立各季节的G-A关系模型以获得断面面积A, 最后将U、A二者相乘即得到断面流量。图 12为利用图 6所示的单垂线u-U模型计算的断面流量Qfit和实测流量Qdata的比较结果, 图 13则是利用图 7所示的双垂线u-U模型计算得到的流量与实测流量比较结果。
|
Download:
|
| 图 12 利用单垂线法进行流量估计的结果 Fig. 12 Discharge calculated by the single-vertical method | |

|
Download:
|
| 图 13 C1和C2双垂线法流量估计结果 Fig. 13 Discharges calculated by the double-vertical method | |
1) 总体来说, 单垂线法的流量估计精度不高, 相关系数K值均小于0.99, 均方根误差RMSE大于6 700 m3/s, 且相对标准偏差RSD大于11%。
2) C1、C2双垂线组合法的断面估计流量Qfit和实测流量Qdata吻合较好:Qfit和Qdata的相关系数K值大于0.99;相对标准偏差RSD值则为7.3%, 相比单垂线法提高了约4%;均方根误差RMSE为4 411 m3/s, 相对单垂线法提高了近2 300 m3/s。因此, 对于年均流量为2.8×104 m3/s的长江口来说, 4%的流量估计精度的提高非常可观。
3) 徐六泾断面的u-U关系模型和G-A关系模型在不同季节需要分别建模, 在有条件的情况下, 可以每一个月或半个月建立一次模型, 以提高流量估计精度。
5 结论1) 双垂线法的断面平均流速估计精度仅比单垂线法提高约0.03 m/s, 断面流量相对精度仅提高了4%, 但断面流量的绝对精度提高了近2 300 m3/s。因此, 对于大型感潮河段来说, 较小的断面平均流速估计精度的提高显得必要且有意义。
2) 受降水的季节性变化及河道冲淤影响, 大型感潮河段的u-U关系模型和G-A关系模型有必要在不同季节分别建模。在有条件的情况下, 可以每一个月或半个月建立一次u-U关系模型和G-A关系模型, 以提高流量估计精度。
| [1] |
KAWANISI K, WATANABE S, KANEKO A, et al. River acoustic tomography for continuous measurement of water discharge[C]//Proceedings of the 3rd International Conference and Exhibition on Underwater Acoustic Measurements: Technologies and Results. Nafplion, Greece: Hellas Foundation for Research and Technology, 2009: 613-620.
(  0) 0)
|
| [2] |
MORSE B, RICHARD M, HAMAÏ K, et al. Gauging rivers during all seasons using the Q2D velocity index method[J]. Journal of hydraulic engineering, 2010, 136(4): 195-203. DOI:10.1061/(ASCE)HY.1943-7900.0000143 (  0) 0)
|
| [3] |
SIMPSON M R, OLTMANN R N. Discharge-measurement system using an acoustic Doppler current profiler with applications to large rivers and estuaries[M]. Leiston: USGS, 1993.
(  0) 0)
|
| [4] |
顾西辉, 张强, 陈晓宏, 等. 基于贝叶斯方法的水位流量关系—以东江干流为例[J]. 武汉大学学报(理学版), 2014, 60(4): 356-362. GU Xihui, ZHANG Qiang, CHEN Xiaohong, et al. Stage-discharge relationship based on Bayesian methods-a case study of East River[J]. Journal of Wuhan University (natural science edition), 2014, 60(4): 356-362. (  0) 0)
|
| [5] |
MAYS L W. Water resources handbook[M]. New York: McGraw-Hill, 1996.
(  0) 0)
|
| [6] |
EL-JABI N, ASCE M, WAKIM G, et al. Stage-discharge relationship in tidal rivers[J]. Journal of waterway, port, coastal, and ocean engineering, 1992, 118(2): 166-174. DOI:10.1061/(ASCE)0733-950X(1992)118:2(166) (  0) 0)
|
| [7] |
CHOO T H, YOON H C, LEE S J. An estimation of discharge using mean velocity derived through chiu's velocity equation[J]. Environmental earth sciences, 2013, 69(1): 247-256. DOI:10.1007/s12665-012-1952-0 (  0) 0)
|
| [8] |
CHEN Yenchang, YANG T M, HSU N S, et al. Real-time discharge measurement in tidal streams by an index velocity[J]. Environmental monitoring and assessment, 2012, 184(10): 6423-6436. DOI:10.1007/s10661-011-2430-y (  0) 0)
|
| [9] |
NIHEI Y, KIMIZU A. A new monitoring system for river discharge with horizontal acoustic Doppler current profiler measurements and river flow simulation[J]. Water resources research, 2008, 44(4). DOI:10.1029/2008WR006970 (  0) 0)
|
| [10] |
HOITINK A J F, BUSCHMAN F A, VERMEULEN B. Continuous measurements of discharge from a horizontal acoustic Doppler current profiler in a tidal river[J]. Water resources research, 2009, 45(11). DOI:10.1029/2009WR007791 (  0) 0)
|
| [11] |
SASSI M G, HOITINK A J F, VERMEULEN B, et al. Discharge estimation from H-ADCP measurements in a tidal river subject to sidewall effects and a mobile bed[J]. Water resources research, 2011, 47(6). DOI:10.1029/2010WR009972 (  0) 0)
|
| [12] |
沈鸿金. 感潮河流流量监测系统研究[D]. 南京: 河海大学, 2005. SHEN Hongjin. Research on tidal discharge measurement system[D]. Nanjing: Hohai University, 2005. (  0) 0)
|
| [13] |
CHEN Yenchang, CHIU C L. An efficient method of discharge measurement in tidal streams[J]. Journal of hydrology, 2002, 265(1/2/3/4): 212-224. (  0) 0)
|
| [14] |
窦润青. 长江口北槽落潮分流比变化原因的分析研究[D]. 上海: 华东师范大学, 2013. DOU Runqing. Hydro-morph-dynamic mechanism of ebb flow diversion ratio's variation in north passage of the Yangtze River Estuary[D]. Shanghai: East China Normal University, 2013. (  0) 0)
|
| [15] |
游性恬, 朱禾. 两大江河流量的半世纪变化与南水北调[J]. 地球科学进展, 2002, 17(6): 811-817. YOU Xingtian, ZHU He. The discharge varaiation in the two main rivers of China during the recent half century and the relationship with the south-to-north water transfer project[J]. Advance in earth science, 2002, 17(6): 811-817. (  0) 0)
|
| [16] |
景晓菊, 赵志舟. 过渡段横断面形态对弯道横向比降的影响研究[J]. 重庆交通大学学报(自然科学版), 2013, 32(4): 681-686. JING Xiaoju, ZHAO Zhizhou. Experimental study on the effect of cross-sectional shape of transition section on the transverse slope in successive bends[J]. Journal of Chongqing jiaotong university (natrue science_, 2013, 32(4): 681-686. (  0) 0)
|
| [17] |
孙英, 金如义. 横比降在长江口河演中的作用[J]. 东海海洋, 1985, 3(4): 1-11. SUN Ying, JIN Ruyi. Role of transverse slope in river-bed evolution in the Changjiang Estuary[J]. Donghai marine science, 1985, 3(4): 1-11. (  0) 0)
|
| [18] |
许光祥, 童思陈, 钟亮. 弯道水面横比降沿程分布特性研究[J]. 水力发电学报, 2009, 28(4): 114-118. XU Guangxiang, TONG Sichen, ZHONG Liang. Study on the longitudinal distribution of water surface transverse slope in curved conduits[J]. Journal of hydroelectric engineering, 2009, 28(4): 114-118. (  0) 0)
|
| [19] |
CHEN C L. Unified theory on power laws for flow resistance[J]. Journal of hydraulic engineering, 1991, 117(3): 371-389. DOI:10.1061/(ASCE)0733-9429(1991)117:3(371) (  0) 0)
|
| [20] |
RUHL C A, SIMPSON M R. Computation of discharge using the index-velocity method in tidally affected areas[M]. Leiston: USGS, 2005.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


