我国是频繁遭受台风灾害侵袭的国家之一, 仅2016年我国就受到近30次台风影响, 约有70万危险地区的人口进行了疏散。为了减少台风带来的人员伤亡和财产损失, 政府需要完善台风应急管理体系, 建立可行有效的应急疏散预案。台风疏散的政策制定者和被疏散个体决策者需要考虑台风带来的风险和不确定性, 同时管理并控制疏散行为来提高疏散的效率。在台风疏散的过程中, 交通拥堵问题成为影响疏散效率的首要问题[1], 因此, 需要充分理解被疏散者的决策行为并预测台风疏散的交通需求, 从而制定有效的台风应急预案以减少拥堵, 提高疏散效率。
疏散需求模型通常用来预测疏散人口数量以及被疏散者的撤离时间[2]。在台风疏散领域, 由于台风灾害的可预知性, 通常会提前发布疏散预警信息, 由公众自行选择撤离的时间和方式[3]。为了估计疏散的需求, 被疏散者的撤离行动需要按时间进行分布[4]。现有的疏散需求分布曲线的估计是建立在经验数据、意向调查研究、规划者的判断和预警信息传播的仿真基础上的[5]。很多研究表明, 其分布服从S曲线[6]。疏散行为预测的模型多从集计模型出发, 运用Logistic回归[7]、神经网络[8]和有序的Logit模型[9], 通过对模型的估计和利用搜集疏散行为选择数据来验证模型, 预测疏散交通需求, 这些模型忽视了个体之间的独立性以及相互的影响。另外, 在疏散行为研究领域, 很多研究都表明个体根据他们如何感知风险来做出疏散决策[10], 如Hasan等[11]将个体的风险感知作为个体异质性的参数, 用以理解家庭层级的疏散时间决策。国内关于台风灾害下的疏散行为决策的研究相对较少, 安实等[12]将模糊逻辑和离散选择模型相结合针对台风灾害分析了影响人员疏散决策行为的因素并构建了混合疏散预测模型。崔娜[13]对无车群的应急疏散决策行为进行了探讨, 构建了基于有限理性理论的风险容忍阈值模型。关于台风疏散行为决策的研究对个体之间相互作用的关注较少, 个体决策和集计层面的出行分布模式的相互影响作用在现有研究中并没有得到体现。目前, 解决这种分布—控制问题的比较新的方法是以Han Qi等的研究为代表, 将博弈论和离散选择理论相结合运用随机最优反应均衡理论研究了个体日常出行的时间决策机理, 并提出此方法的适用范围[14]。
随机最优反应均衡理论(quantal response equilibrium, QRE)由Mckelvey和Palfrey最早提出, 基于有限理性理论对纳什均衡理论的进一步发展, 假定参与者根据博弈中各个策略的预期效用进行选择, 但由于认知能力的限制, 不能正确的评估预期效用, 而是受到随机误差的干扰, 达到所谓的“最优反应”[15]。目前, QRE理论在国内应用较少, 安毅等将随机最优反应均衡与认知层级理论相结合, 构建了参与者依据Logit反应函数来决定策略选择概率的模型[16]。牛志勇的研究分析了参与人的不同偏好对参与人的最优反应的影响[17]。
基于Han Qi等[18]的研究, 本文提出了台风疏散时间决策模型, 明确了个体交互作用及其与疏散需求分布的交互作用在台风疏散过程中的体现以及具体应用, 并根据随机最优反应均衡理论修正了完全理性假设, 运用数值仿真对模型的性质进行验证。本研究的主旨是帮助政策制定者和执行者提高预测台风疏散交通需求的能力并且选择合适的策略来提高疏散效率, 为未来的疏散准备提供理论依据。
1 问题描述及博弈分析本文分析被疏散者在疏散过程中的撤离时间选择行为, 将私家车群体作为研究对象考虑在区域内大规模疏散的过程中, 其他参与人的行为对环境(道路交通)的影响, 从效用最大化角度出发, 确定自己的撤离时间。因此, 本研究在非集计层面, 构建一个n位参与人的非合作博弈模型。设被疏散地区私家车群体的集合N={1, 2, …, n}, 每辆私家车i∈N作为一个决策主体, 有J个撤离时间的纯策略, 即Si={si1, si2, …, siJ}, 概率分布pi={pi1, pi2, …, piJ}为主体i的一个混合策略, pij=p(sij)是i选择sij的概率。s=(s1, s2, …, sn)∈S是每个个体对应一个由n个策略构成的策略组合。s-i=(s1, s2, …, si-1, si+1, …, sn)是除了个体i以外其他个体的策略组合。则有
| $ \sum\limits_{{{s}_{ij}}\in {{S}_{i}}}{{{p}_{i}}({{s}_{ij}})}=1 $ | (1) |
对于每个被疏散主体i∈N, 有支付函数Ui, 代表在其他参与者可能选择的策略情况下驱动该主体选择某特定策略的效用, 则有Ui(sij, p-i)表示当主体i选择纯策略sij而其他参与者选择他们的策略时的效用, 被疏散主体i的支付函数为
| $ {{U}_{i}}({{p}_{i}})=\sum\limits_{j=1}^{J}{{{p}_{ij}}\cdot {{U}_{i}}({{s}_{ij}}, {{p}_{-i}})} $ | (2) |
根据研究问题特点提出以下假设:
假设1:每个被疏散主体的决策是关于台风疏散撤离起始时间的选择, 将疏散的时间划分为时间间隔相同的多个时段作为撤离时间的策略, 则被疏散主体的参与撤离行动起始时间的选择决策是离散选择问题。
假设2:被疏散主体基于撤离时间策略的期望效用来决定何时采取撤离的行动。撤离时间策略的期望效用一方面受到被疏散主体的偏好影响, 另一方面还与主体对于这类集聚行动模式所导致的环境状态(交通拥堵)的判断有关。因此, 被疏散主体的疏散时间策略的期望效用由撤离行动时间策略的吸引力和所有其他主体参与行动的均衡分布的函数两部分表示。
假设3:假设不同主体的效用的系统项部分即撤离行动时间策略的吸引力是由主体对于停留(不撤离)的风险主观估计(风险感知)和撤离的成本的不同所导致的。由于其他主体不能轻易观测到某主体的疏散时间策略选择行为, 构成了被疏散主体的私人信息部分, 因此所有被疏散主体参与撤离行动的均衡分布是不完全信息博弈的结果。
假设4:当某被疏散主体作出特定的时间选择时, 会考虑其他参与者的行为, 当某主体估计某时段撤离人口数量到达一定水平时, 会导致此参与者选择此时段行动的效用降低。
2.2 模型构建基于以上假设, 将被疏散主体i选择j撤离时间策略的效用放到离散选择的框架下, 得到效用函数由三部分组成:1)撤离时间策略选项效用的系统项, 即一个撤离时间策略效用的可观测部分; 2)交互作用部分Ud, 即其他参与者选择的撤离时间对该个体的效用的影响; 3)一个特殊的误差项ε, 它是个体选择该策略偏好的异质性的体现, 其分布是所有个体的普遍知识量, 但确切值是个体的私人信息, 表示为
| $ {{U}_{ij}}={{U}_{j}}^{g}+{{U}_{j}}^{d}+{{\varepsilon }_{ij}} $ | (3) |
式中:Ujg是离散选择模型中影响出行时间策略收益的传统的系统项, 随着时间和空间变化而变的采取撤离行动时间的效用, 即撤离时间策略的吸引力, 反映了该撤离时间策略若选择停留的风险感知水平(时间压力)和该撤离时间策略下的撤离成本消耗, 表示为
| $ {{U}_{j}}^{g}=\beta {{x}_{j}}={{\beta }_{1}}{{x}_{j}}^{\text{risk}}+{{\beta }_{2}}{{x}_{j}}^{\text{cost}} $ | (4) |
式中:Ujd代表其他被疏散主体选择该策略对于该主体的交互作用, 将其表示为其他个体行为的函数, 由选择同样时间策略的个体的期望数量和这些个体的影响力变量表示:
| $ {{U}_{j}}^{d}=h({{f}_{j}}\left( n \right), n) $ | (5) |
这里fj(n)函数表示被疏散个体数量的影响力, 表示个体内部相互作用于效用的部分, 其具体表达形式取决于研究问题的情境。举例说明, 如果一个个体选择撤离的时间策略和大多数个体的选择相同, 则在某时间和空间内就会集聚个体, 在区域疏散过程中, 交通阻塞会导致排队成本的提高和逃生机会的下降, 因而会对个体选择该策略的效用产生负面的影响。然而, 由于疏散的人数增加会提高人们对于台风风险的感知水平, 则会对个体选择该策略的效用产生积极的影响。
式(3)中εij是主体选择此撤离时间效用的不可观测的部分, 包括被疏散主体本身偏好的不确定性, 他人选择的不确定性, 以及计算误差。此干扰项取决于主体的私人信息, 即类型, 是一个随机变量, 其分布为所有主体的普遍认知。由于私人信息的分布是相同的, 所以每一组主体对于第三方的私人信息的猜测都是相同的。为了计算方便, 假设主体类型为独立同分布(IID), 先验概率服从于贝尔极值分布, 那么累积密度分布为
| $ F({{\varepsilon }_{ij}})=\text{exp}[-\text{exp}(-{{\varepsilon }_{ij}}/\mu )] $ | (6) |
式中:μ代表了分布的规模参数。反映了个体关于其他人猜测的不确定性, 或理性程度, 是传统意义中主体的私人信息部分。
3 有限理性的均衡策略求解及分析根据问题的描述, 主体i的干扰项向量, εi=(εi1, εi2, …, εiJ)服从密度函数为fi(εi), 且E(εi)=0的联合分布。因此, 当被疏散主体i选择j策略的效用高于所有其他可能策略的效用时, j策略会被选择, 即满足:
| $ \begin{array}{l} \;\;\;\;\;\;\;{U_{ij}}({s_{ij}},{p_{ - ij}}) \ge {U_{ij\prime }}({s_{ij\prime }},{p_{ - ij\prime }}) = \\ {\rm{E}}[{{\bar U}_j}({p_{ - ij}}) + {\varepsilon _{ij}}] \ge {\rm{E}}[{{\bar U}_{j\prime }}({p_{ - ij\prime }}) + {\varepsilon _{ij\prime }}]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall i,\forall j \ne j\prime \end{array} $ | (7) |
式(4)并未给出具体的求解方法, 但可以得到期望效用取决于时间策略选择的密度分布。Mckelvey等[17]为式(4)形式的博弈提供了一个统计上的均衡, 即随机最优反应均衡, 主体基于相对的期望效用选择策略, 并假设其他主体也会同样基于此作出选择。由于个体误差项的对称性, 即同一类分布, 每个被疏散主体关于其他主体的最优策略的估计均相同。具体而言, 被疏散主体k对于主体i选择j策略的先验概率的估计, 与被疏散主体i对于主体k选择j策略的先验概率估计是一致的。因此, 每个个体对时间策略选择的交互作用影响力是相同的, 且由于其期望效用的结构相同, 个体基于效用最大化而采取的策略选择行为概率也相等, 进一步推导出均衡条件下, 所有个体选择策略j的概率都是一致的:p-ij*=p-kj*=pj*, 并且每个策略对应的都是相同的非随机的效用:U-ij*=U-kj*=Uj*, 则一个被疏散主体对于所有策略的估计都由策略集J本身的效用来决定。因此, 没有任何单独个体的行为偏好会影响系统均衡。由于最优反应模型是由随机部分(误差项)的分布所决定的, 由于被疏散者类型服从指数分布, 则最优反应曲线则服从Logit分布, 又称LogitQRE。根据最优反应均衡理论可以得到, 被疏散主体i选择策略j的概率是期望效用的比例指数函数:
| $ {{p}_{j}}^{*}=\frac{\text{exp}(\text{E}[{{{\bar{U}}}_{j}}]/\mu )}{\sum\limits_{j\prime =1}^{J}{\text{exp}(\text{E}[{{{\bar{U}}}_{j\prime }}]/\mu )}} $ | (8) |
式中:μ代表误差参数, 当μ→0时, 表明不存在误差, p*将沿着某唯一的路径收敛于纳什均衡, 最高期望支付的决策将以概率1被选择; 当μ→∞时, 说明参与者的计算误差很大, 所有策略的选择概率均相等, 表明参与者几乎无法判断各策略的优劣。误差参数值越高代表策略选择的概率对期望效用越不敏感, 相反则越敏感。
4 模型仿真与分析 4.1 示例说明为验证本模型提出的基于个体间相互作用的策略选择模型, 根据仿真需要设定具体的场景以及决策内容。设某地区发布了台风疏散预警, 台风将在未来10 h内抵达此地区, 则有10个时段(每1 h为一个起始时段选择), 记为起始时间1, 2, …, 10, 并且设定每个出行的平均时间为1 h。根据式(4), 研究分别考虑了时间策略的风险感知β1X1和成本β2X2两方面, 其中撤离出发时间策略的风险感知是选择某撤离时间的时间压力, 而损失是选择某时间出发的撤离过程带来的成本。另外, 对于交互部分Ujd, 本示例设定了一个线性函数表示边际负效用h(n), 表明当选择相同的撤离起始时间的个体增加会对该时间策略的效用带来一定的负面影响。因此, 根据式(3), 某起始时间策略j的期望效用函数E[Uj]可以表示为
| $ \text{E}[{{{\bar{U}}}_{j}}]={{\beta }_{^{1}}}{{X}_{j}}^{1}+{{\beta }_{2}}{{X}_{j}}^{2}+h(\left( N-1 \right){{p}_{j}}^{*}+1) $ | (9) |
式中:pj*表示其他个体可能选择在时间j参与活动的均衡概率, (N-1)pj*表示个体i∈N判断其他个体选择在时间j参与活动的数量。当个体i也同样选择在时间策略j时, 则在时间j出行的个体的预期数量需要增加一个个体, 增长为(N-1)pj*+1。若个体选择在前几个时段撤离, 虽然道路中的撤离车辆相对较少, 但由于台风来临的不确定性, 可能会导致台风风险较低, 不如停留家中的效用更高; 在中间时段出发, 相对较为稳妥, 但会面临严重的交通拥堵问题, 大大的增加了撤离过程的成本; 而在最后几个时段出发, 虽然道路不会十分拥堵, 可以减少疏散成本, 但会增加疏散所带来的风险。由此可见, 均衡条件下的疏散参与模式是由起始时间策略的吸引力和个体间交互作用博弈结果的体现。
4.2 仿真过程为探究被疏散群体疏散时间选择模型中各参数变化对均衡策略下疏散需求的影响, 验证模型的有效性, 本文用Matlab软件进行算例的数值仿真分析。设有1 000个被疏散主体参与选择在台风来临前疏散的出发时间的策略, 为模型设定每个撤离时间的偏好矢量和需要的参量, 采用以下步骤:
1) 生成1 000个随机变量的集合, 共有10个维度的偏好矢量, 密度分布服从均值为0方差为1的正态分布, 每个集合定义一个主体的类型, 即代表一个被疏散车辆;
2) 定义每个个体的效用值时在其随机量基础上加平均效用偏好值;
3) 利用以上步骤得到的数值和式(5)计算每个主体选择特定起始时间的概率;
4) 将1 000个仿真主体的每个起始时间的概率求和, 总结出10段撤离时间选择的分布。
4.3 结果和分析仿真得到被疏散个体最优撤离时间选择策略的分布代表了在特定时间开始参加疏散的概率, 而并非确切的时间选择。仿真以一个简单的场景为示例分析了不同的情境, 分别探讨个体撤离时间的风险感知和成本消耗, 个体间交互作用以及对于其他个体行为估计对于疏散参与的总体均衡分布的影响。
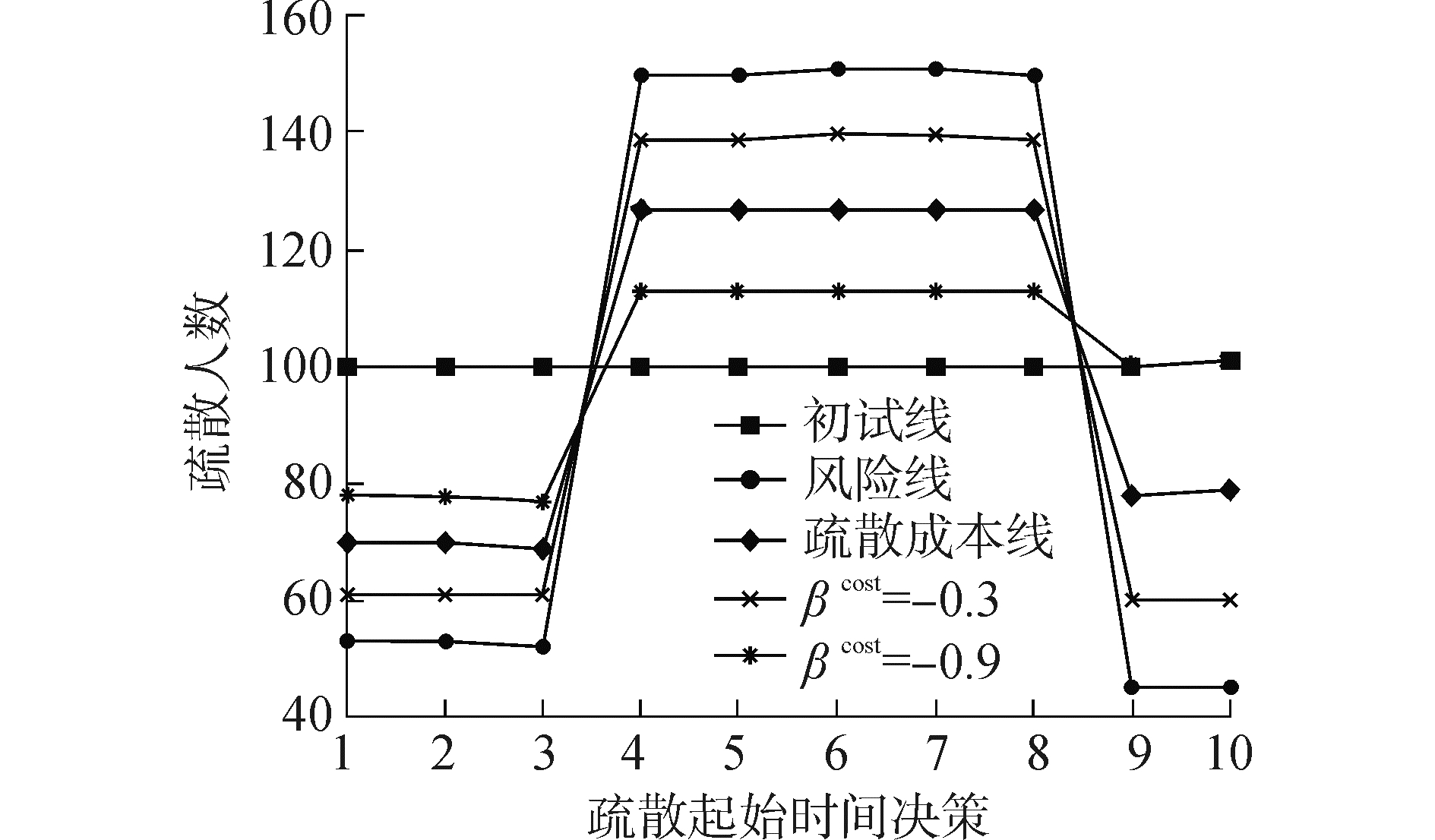
4.3.1 备选策略效用的敏感性分析为探讨其他备选策略效用对个体疏散时间决策的影响, 通过参数的变化来观察对系统演化结果的影响。令β1=1, β2=-0.6, h=0, μ=6.6, Xrisk=Xcost={10, 10, 10, 10, 10, 10, 10, 10, 10, 10}。其中, μ的取值参考Goeree等对QRE的研究结果所得[19]。得到10个时段总水平的基本分布的初始向量为{100, 101, 99, 99, 100, 100, 101, 100, 99, 100}, 每次改变一个参数值, 可得到不同因素对均衡分布的累积影响, 如图 1所示。
|
Download:
|
| 图 1 备选策略效用变化对疏散人口时间分布的影响 Fig. 1 Choice alternative impact on the time distribution of evacuation number | |
1) 将被疏散群体的对疏散时间策略的平均风险感知值进行调整, 从对不同时间有相同感知的模式Xrisk={10, 10, 10, 10, 10, 10, 10, 10, 10, 10}, 调整为不同时间策略有不同的风险感知值的模式Xrisk′={3, 3, 3, 10, 10, 10, 10, 10, 2, 2}, 反映了对于台风来临的风险感知, 起初处于信息接收阶段, 对于风险的感知能力较低; 而中间时段台风来临的环境线索愈加明显, 对于撤离的意愿愈加强烈; 在最后两阶段由于时间的压力, 以及撤离行动过程不可预知的风险, 会导致撤离意愿下降。对比图 1中的风险线和初始线发现, 其他条件不变, 被疏散个体在集计层面的撤离行动的分布依据不同时段的平均风险感知水平变化模式成比例的变化, 在4~8几个时段的风险感知的程度最高, 虽然与初始设置值相同, 但在这几个时段疏散的人数会明显高于初始设置和其他时段, 而其他时段的风险感知程度偏低, 疏散人数则低于初始设置水平。说明当不考虑成本消耗的时间差别和被疏散个体之间的相互作用时, 被疏散群体的撤离时间决策的总体分布取决于对各个时段风险水平的感知程度, 且成比例变化。
2) 将与时间相关的成本消耗从相同值Xcost={10, 10, 10, 10, 10, 10, 10, 10, 10, 10}变为Xcost′={5, 5, 5, 10, 10, 10, 10, 10, 2, 2}时, 表现出在不同时段被疏散人群愿意为选择某时段撤离而付出的成本花费, 起初由于风险的不确定性并不愿意花费过多成本出行; 而中间阶段当确定台风来临的可能性增加, 且完成撤离准备工作后, 此时愿意付出更多的成本选择撤离; 在最后阶段随着已经撤离的人数增多, 剩余被疏散者的疏散意愿较低, 且出行风险较高, 导致愿意付出成本减少。结果如图 1所示, 疏散成本线为成本消耗变化后得到的疏散人口数量, 当其他条件不变, 可以适当的调节疏散过程的成本消耗, 以此影响疏散总人数的时间分布。这说明, 当被疏散人群的风险感知依据时间有差别, 且忽略其相互作用时, 疏散成本的变化会对选择不同时间疏散的人数有一定的影响力, 可以起到调节作用。
3) 将成本消耗的权重改变时, 固定其他参数值, 将原权重的系数-0.6分别取值-0.3(βcost=-0.3)和-0.9(βcost=-0.3), 得到结果如图 1所示。观察发现, 随着成本消耗的权重系数的改变, 疏散的总人口数量的时间分布也会改变。说明当被疏散群体对于成本消耗的敏感性越高, 调节疏散成本对疏散人口时间分布的影响越大, 符合实际生活中的认知。
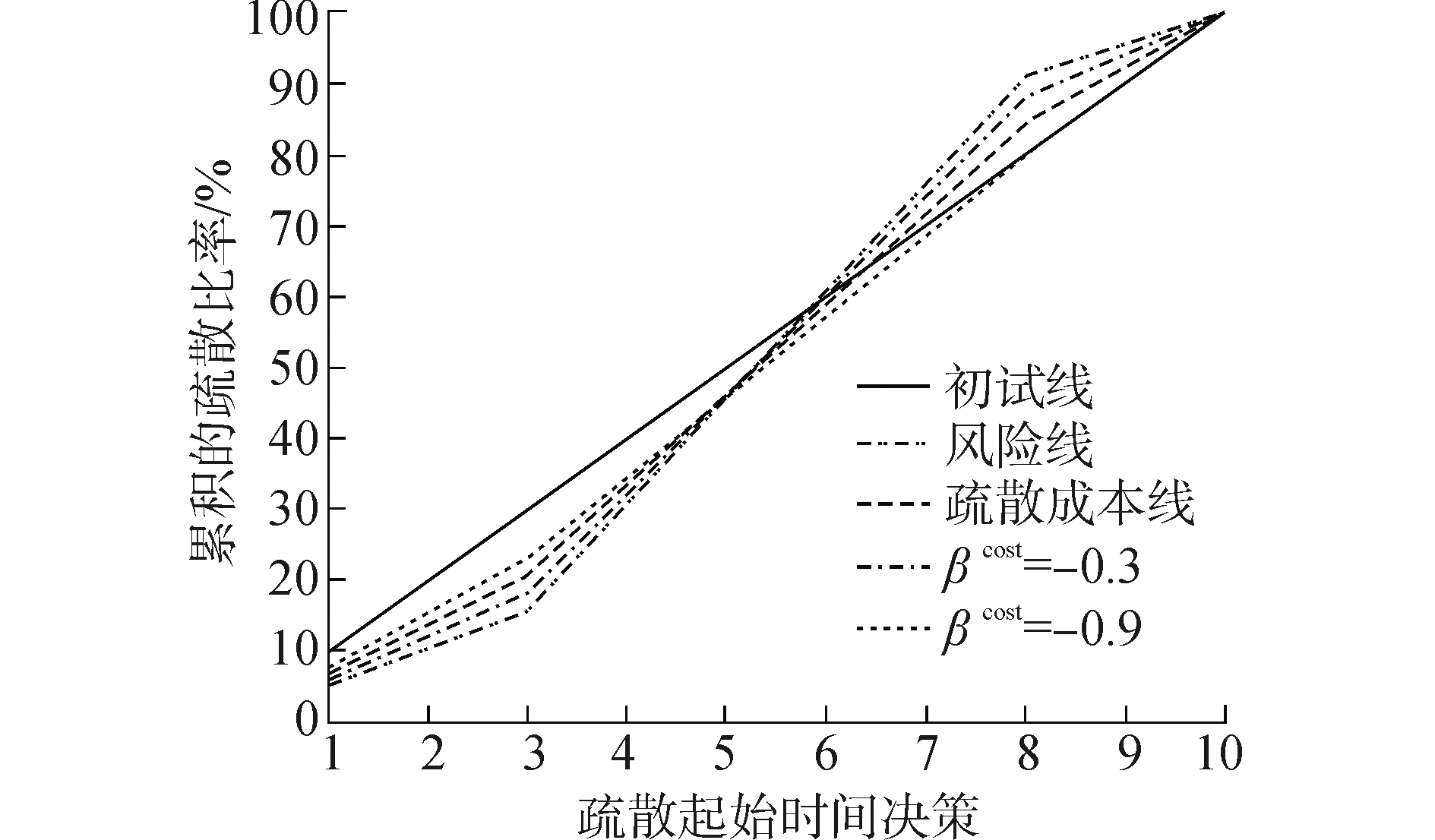
另外, 图 2表示调节参数变化后, 累积疏散比率的曲线图, 由于初始设置只为对比需要, 所以呈均匀分布, 但改变参数设置更符合实际情况后, 可以发现总体呈S型分布, 在初始和末尾阶段, 疏散的人群比例增长较为缓慢, 中间时段(3~8时段)增长迅速。这与目前现有大规模区域疏散的研究结论一致, 在一定程度上说明了模型的有效性。
|
Download:
|
| 图 2 不同效用作用下的累积疏散比率 Fig. 2 Accumulated evacuation rate under different utilities | |
为考察交互作用对于被疏散人群时间决策的影响, 令其他参数设置不变, 即β1=1, β2=-0.6, μ=6.6, Xrisk={3, 3, 3, 10, 10, 10, 10, 10, 2, 2}, Xcost={5, 5, 5, 10, 10, 10, 10, 10, 2, 2}和Xcost′={10, 10, 10, 10, 10, 10, 10, 10, 10, 10}, 将个体间交互作用效用函数的权重h分别取为0、-0.02和-0.1, 得到的结果如图 3所示, 其中实线表示成本消耗有变化的情况, 虚线表示各个时间策略成本消耗相同。观察发现, 如果被疏散个体考虑交互作用的影响, 即考虑交通拥堵所造成撤离行动的效用值减少, 则被疏散的群体会有策略的采取行动。为了避免交通拥堵以获取更大的效用, 被疏散群体会偏离原来的时间策略选择。而拥堵现象对被疏散群体的影响越大, 交互作用越明显, 则他们会越偏离原有时间策略选择。并且, 这种影响力是叠加到对成本消耗敏感性基础上的, 即若选择某时间策略的个体数量较少时, 此时间策略的成本消耗越少, 被疏散个体越倾向于选择此时段进行撤离行动。

|
Download:
|
| 图 3 交互作用对疏散人口时间分布的影响 Fig. 3 Interaction impact on the time distribution of evacuation number | |
为考察被疏散个体对于其他个体选择估计的理性程度对于时间决策的影响, 令其他参数不变, 而h=-0.02, Xrisk={3, 3, 3, 10, 10, 10, 10, 10, 2, 2}, Xcost={5, 5, 5, 10, 10, 10, 10, 10, 2, 2}。被疏散人群对于其他人选择的估计的理性程度是由参数μ体现的, 当μ取值为1时达到最优策略选择的概率为1的纳什均衡情况; 而在有限理性下, 根据Mckelvey等的研究, 将μ值设为6.6表示每个被疏散个体都依据LogitQRE反应函数选择各策略的概率。观察图 4发现, 纳什均衡条件下预测的疏散均衡分布最接近于被疏散者对于时间策略的风险感知水平, 但在实际中不可能达到完全理性的以高概率选择最优策略; 而随机最优反应均衡的情况更符合实际生活中的常理, 当被疏散者对于其他人的时间决策有一定认知后, 可以得到策略选择的优势, 而随机最优反应的分布也更平衡。这说明被疏散人群在收到了关于其他人可能采取的时间策略的信息后, 或是从已有的疏散经验中得到此类信息, 则他们的疏散行为会被类似政府等信息提供者所积极的影响。

|
Download:
|
| 图 4 估计的不确定性对疏散人口时间分布的影响 Fig. 4 Uncertainty of conjecture on the time distribution of evacuation number | |
1) 被疏散者在有限理性下基于期望效用来决定何时采取撤离的行动, 构成了基于疏散需求的分布曲线, 因此本模型可为预测疏散需求提供支持;
2) 由被疏散者内生决定的交互作用也与外生变量同样影响疏散时间策略的选择, 即其他个体的疏散时间决策会影响被疏散个体的疏散时间选择;
3) 被疏散者个体对于其他个体选择的推断能力对疏散个体时间选择的分布也有显著的影响, 因此当为被疏散个体提供足够的信息时, 可以提高其推断能力, 进而达到信息提供者的目标。
研究结果可以帮助台风疏散的政策制定者更好的理解被疏散群体的决策行为, 是提高台风风险沟通水平的基础。未来的研究可以进一步探讨如何通过提供信息引导被疏散者在特定时间内撤离, 并将模型具体化的应用到疏散需求的预测中。
| [1] |
BROWN C, WHITE W, VAN SLYKE C, et al. Development of a strategic hurricane evacuation-dynamic traffic assignment model for the Houston, Texas, region[J]. Transportation research record:journal of the transportation research board, 2009, 2137: 46-53. DOI:10.3141/2137-06 (  0) 0)
|
| [2] |
HUANG S K, WU Haoche, LINDELL M K, et al. Perceptions, behavioral expectations, and implementation timing for response actions in a hurricane emergency[J]. Natural hazards, 2017, 88(1): 533-558. DOI:10.1007/s11069-017-2877-4 (  0) 0)
|
| [3] |
LINDELL M K, LU J C, PRATER C S. Household decision making and evacuation in response to Hurricane Lili[J]. Natural hazards review, 2005, 6(4): 171-179. DOI:10.1061/(ASCE)1527-6988(2005)6:4(171) (  0) 0)
|
| [4] |
MURRAY-TUITE P, WOLSHON B. Evacuation transportation modeling:an overview of research, development, and practice[J]. Transportation research part C:emerging technologies, 2013, 27: 25-45. DOI:10.1016/j.trc.2012.11.005 (  0) 0)
|
| [5] |
SOUTHWORTH F. Regional evacuation modeling: a state of the art reviewing[R]. Oak Ridge National Laboratory, 1991.
(  0) 0)
|
| [6] |
SWAMY R, KANG J E, BATTA R, et al. Hurricane evacuation planning using public transportation[J]. Socio-economic planning sciences, 2017, 59: 43-55. DOI:10.1016/j.seps.2016.10.009 (  0) 0)
|
| [7] |
WHITEHEAD J C, EDWARDS B, VAN WILLIGEN M, et al. Heading for higher ground:factors affecting real and hypothetical hurricane evacuation behavior[J]. Global environmental change part B:environmental hazards, 2000, 2(4): 133-142. DOI:10.1016/S1464-2867(01)00013-4 (  0) 0)
|
| [8] |
WILMOT C G, MEI Bing. Comparison of alternative trip generation models for hurricane evacuation[J]. Natural hazards review, 2004, 5(4): 170-178. DOI:10.1061/(ASCE)1527-6988(2004)5:4(170) (  0) 0)
|
| [9] |
FU Haoqiang, WILMOT C G. A sequential logit dynamic travel demand model for hurricane evacuation[J]. Transportation research record:journal of the transportation research board, 2004, 1882: 19-26. DOI:10.3141/1882-03 (  0) 0)
|
| [10] |
BROWN S, PARTON H, DRIVER C, et al. Evacuation during hurricane sandy:data from a rapid community assessment[J]. PLoS currents, 2016. (  0) 0)
|
| [11] |
HASAN S, MESA-ARANGO R, UKKUSURI S. A random-parameter hazard-based model to understand household evacuation timing behavior[J]. Transportation research part C:emerging technologies, 2013, 27: 108-116. DOI:10.1016/j.trc.2011.06.005 (  0) 0)
|
| [12] |
安实, 崔建勋, 王健. 基于模糊逻辑与离散选择模型的混合疏散人口估计模型[J]. 交通运输工程学报, 2009, 9(5): 78-82, 105. AN Shi, CUI Jianxun, WANG Jian. Hybrid evacuation population estimation model based on fuzzy logic and discrete choice model[J]. Journal of traffic and transportation engineering, 2009, 9(5): 78-82, 105. (  0) 0)
|
| [13] |
崔娜. 台风灾害下无车群体疏散需求预测与集散设施选址研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. CUI Na. Research on carless evacuation demand forecasting and pickup facility location design under typhoon disasters[D]. Harbin: Harbin Institute of Technology, 2012. (  0) 0)
|
| [14] |
HAN Q, DELLAERT B G C, VAN RAAIJ W F, et al. Modeling strategic behavior in anticipation of congestion[J]. Transportmetrica, 2007, 3(2): 119-138. DOI:10.1080/18128600708685669 (  0) 0)
|
| [15] |
MCKELVEY R D, PALFREY T R. Quantal response equilibria for normal form games[J]. Games and economic behavior, 1995, 10(1): 6-38. DOI:10.1006/game.1995.1023 (  0) 0)
|
| [16] |
安毅, 杨忠直, 刘晓峰. 基于随机最优反应均衡的认知层级模型[J]. 系统管理学报, 2008, 17(6): 610-614. AN Yi, YANG Zhongzhi, LIU Xiaofeng. A cognitive hierarchy model based on quantal response equilibrium[J]. Journal of systems & management, 2008, 17(6): 610-614. (  0) 0)
|
| [17] |
牛志勇, 黄沛, 高维和. 基于最优反应均衡的渠道数量折扣模型及实验分析[J]. 管理科学, 2010, 23(2): 45-51. NIU Zhiyong, HUANG Pei, GAO Weihe. The research on quantity discount model of channel based on quantal response equilibrium and experiment[J]. Journal of management science, 2010, 23(2): 45-51. (  0) 0)
|
| [18] |
HAN Q, DELLAERT B, VAN RAAIJ F, et al. Modeling impact of emerging uncertain time-dependent aggregate activity-travel patterns on individual activity participation and timing decisions[J]. Transportation research record:journal of the transportation research board, 2004, 1894: 28-36. DOI:10.3141/1894-04 (  0) 0)
|
| [19] |
GOEREE J K, HOLT C A. A model of noisy introspection[J]. Games and economic behavior, 2004, 46(2): 365-382. DOI:10.1016/S0899-8256(03)00145-3 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


