2. 天地一体化信息技术国家重点实验室, 北京 100086
2. Beijing Institute of Satellite Information Engineering, Beijing 100086, China
随着GPS、GLONASS、Galileo、BDS四大全球导航卫星系统(global navigation satellite system, GNSS)、各种区域导航卫星系统以及星基增强系统的飞速发展, 预计到2030年导航卫星的数目将超过160颗, 导航信号将超过400个[1], 这无疑会进一步加剧L频段(1 164~1 610 MHz)GNSS信号的频谱拥挤。提高信号的频谱效率以降低互干扰[2]和开发新的频段是解决上述问题的主要手段。国际电联(international telecommunication union, ITU)已将C频段(5 010~5 030 MHz)分配给导航下行服务业务, 客观上使L与C频段联合导航成为可能, 可以预测多波段联合导航将成为下一代高精度导航定位系统的关键技术之一[3]。
当前多频导航仍局限于L频段多频, 随着C频段对导航业务的开放, 多频可以采用大间隔的多频段, 它更有利于消除频变误差, 有利于快速求解模糊度, 有利于抗干扰, 有利于与通信系统的融合和互补[4]。信号体制设计决定了导航系统的性能上界, 而调制方案是导航信号体制设计中的关键环节, 其通过影响导航信号的自相关函数和功率谱, 进而影响导航信号的各项性能[5]。在L/C双频段联合导航模式下, 设计一种能满足不同频段兼容性约束条件的通用调制方案具有重要现实意义, 可有效降低多频终端的复杂度, 加快多波段联合导航的实用化进程。
C频段导航信号的设计必须首先满足与射电天文(radio astronomy, RA)和微波着陆(microwave landing system, MLS)系统的兼容性约束要求。文献[6]的研究结果表明:基于二进制相移键控(binary phase shift keying, BPSK)和二进制偏移载波(binary offset carrier, BOC)的导航信号在占用C频段20 MHz的全部可利用带宽时, 如果没有带外抑制较强的输出滤波器限制, 均不能满足C频段信号设计的兼容性约束要求。这就需要C频段的调制具有更高的旁瓣衰落特性, 以减小带外频谱泄漏, 相位连续的调制方式成为C频段调制方案的首选[7]。在L频段, 大多数GNSS信号采用BOC调制, 文献[8-9]提出一类可代替BOC的连续相位调制子集信号, 该类CPM信号在定位精度、多径消除、抗干扰、兼容性等方面具有和BOC调制相比拟的性能。
实际上, CPM并不是一个单一参数的调制方式, 而是一类参数可配置的调制总称, 其信号储备丰富, 通过对调制参数进行设计与优化可满足多频段的兼容性约束条件, 具备多波段和多频点的部署能力, 因此, 本文提出将CPM调制作为L/C双频段联合导航的通用调制方案。针对BDS B3信号的频点分布, 设计一种L和C频段的双频组合模型, 即C频段信号主瓣中心频率为L频段信号主瓣中心频率的4倍, 可有利于快速求解整周模糊度, 显著提高精密单点定位的鲁棒性和精度。同时基于L/C频段载波中心频率的设置以及兼容性的约束条件, 分别提出了适用于双频段的CPM信号, 即BM1REC(2)和BM2RC(4)。
1 CPM信号模型 1.1 时域模型CPM调制信号的时域表达式为
| $ s\left( t \right) = \sqrt {\frac{{2E}}{T}} {\rm{cos}}(2{\rm{ \mathsf{ π} }}{f_0}t + \varphi \left( {t, \mathit{\boldsymbol{\alpha }}} \right) + {\phi _0}) $ | (1) |
式中:E为符号能量, T为符号周期, φ0是初始相位, f0为调制信号的载波频率, φ(t, α)是载有信息序列α的相位函数, 可表示为
| $ \begin{array}{l} \varphi \left( {t, \mathit{\boldsymbol{\alpha }}} \right) = 2{\rm{ \mathsf{ π} }}h\sum\limits_{i = 0}^n {{\alpha _i}\int_{-\infty }^{t-iT} {g\left( \tau \right){\rm{d}}\tau, } } \\ nT \le t \le \left( {n + 1} \right)T \end{array} $ | (2) |
式中:αi∈[±1, ±3, …, ±(M-1)]为M进制的信息; h为调制指数; g(t)表示时间间隔为LT的频率响应函数, 其中矩形脉冲(LREC)和升余弦脉冲(LRC)是最常见的脉冲函数。从式(1)~(2)可知, 通过改变M、h、g(t)以及L的参数, 理论上就能够得到不同类型的CPM信号。为表述方便, 本文采用简称LREC以表示关联长度为L且g(t)为矩形脉冲函数的CPM信号, 比如进制数M=2, 关联长度L=1, T=1/(N×1.023 MHz)和g(t)为升余弦脉冲函数的CPM信号可简写为BM1RC(N)。
1.2 功率谱密度当所有输入信息码元出现概率相等时, CPM信号的平均自相关函数可表示为[10]
| $ \begin{array}{l} \mathit\Re \;\left( \tau \right) = \frac{1}{T}\int_0^T {\mathop {\mathit{\Pi }}\limits_{k = 1 - L}^{\left\lfloor {\tau /T} \right\rfloor } } \frac{1}{M} \cdot\\ \frac{{{\rm{sin}}\{ 2{\rm{\pi }}hM\left[ {q\left( {t + \tau - kT} \right) - q\left( {t - KT} \right)} \right]\} }}{{{\rm{sin}}\{ 2{\rm{\pi }}h\left[ {q\left( {t + \tau - kT} \right) - q\left( {t - KT} \right)} \right]\} }}{\rm{d}}t \end{array} $ | (3) |
式中:q(t)为相位响应函数, T为符号周期, L为关联长度, M为进制数, τ为相关时间。根据维纳-辛钦定理, 对式(3)进行傅里叶变换, 则CPM信号相应的功率谱密度函数可表示为
| $ \begin{array}{l} P\left( f \right) = 2\left\{ {\int_0^{LT} {\Re \left( \tau \right)} {\rm{cos}}2({\rm{ \mathsf{ π} }}f\tau ){\rm{d}}\tau + } \right.\\ \frac{{1-\psi ({\rm{j}}h){\rm{cos}}(2{\rm{ \mathsf{ π} }}fT)}}{{1 + {\psi ^2}({\rm{j}}h)-2\psi ({\rm{j}}h){\rm{cos}}(2{\rm{ \mathsf{ π} }}fT)}}\cdot\\ \int_{LT}^{\left( {L + 1} \right)T} {\Re \left( \tau \right){\rm{cos}}(2{\rm{ \mathsf{ π} }}f\tau ){\rm{d}}\tau-} \\ \frac{{\psi ({\rm{j}}h){\rm{sin}}(2{\rm{ \mathsf{ π} }}fT)}}{{1 + {\psi ^2}({\rm{j}}h) - 2\psi ({\rm{j}}h){\rm{cos}}(2{\rm{ \mathsf{ π} }}fT)}}\cdot\\ \left. {\int_{LT}^{\left( {L + 1} \right)T} {\Re \left( \tau \right)} {\rm{sin}}(2{\rm{ \mathsf{ π} }}f\tau ){\rm{d}}\tau } \right\} \end{array} $ | (4) |
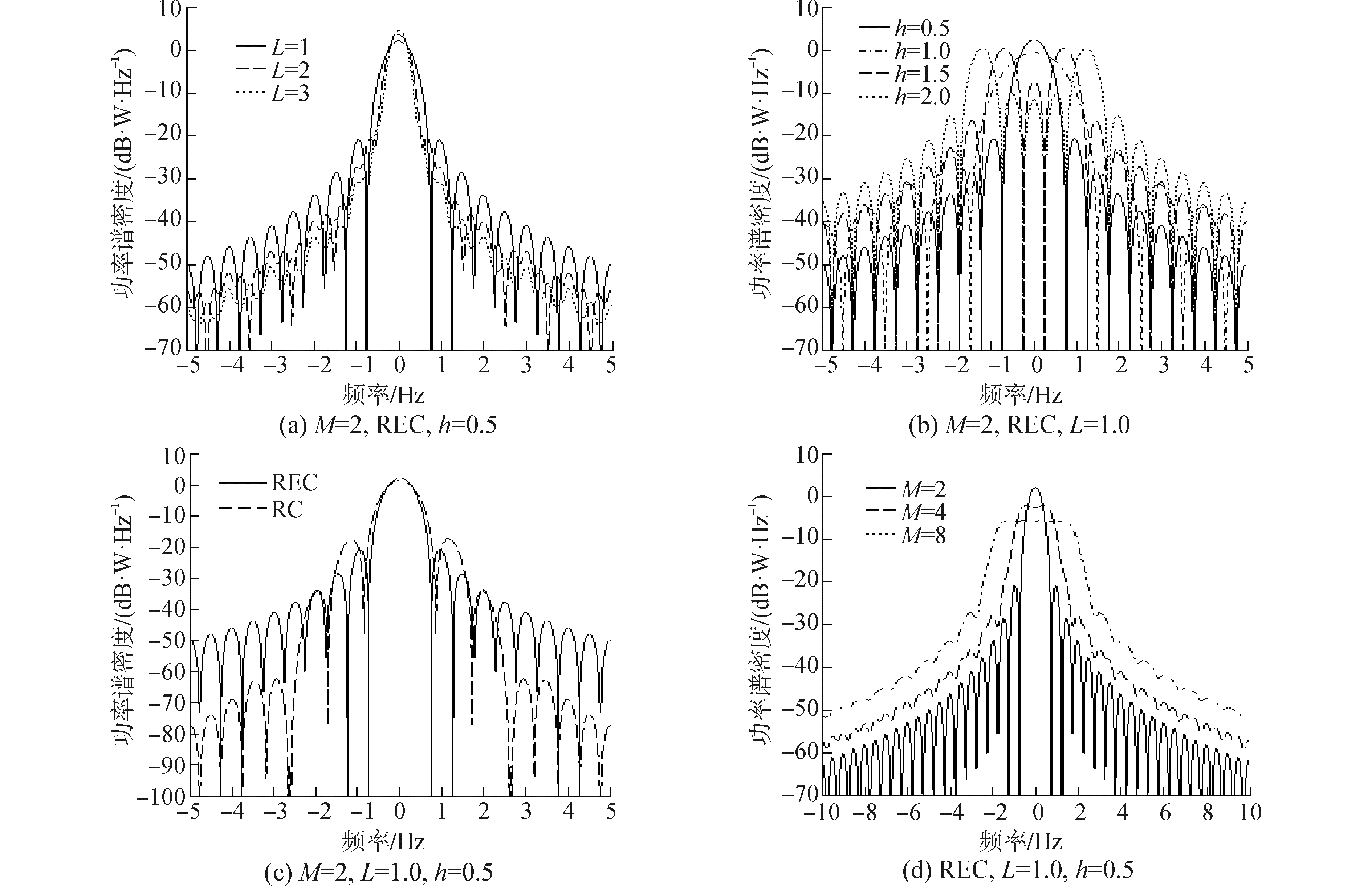
式中:ψ(jh)=(sin(Mπh))/(Msin(πh))。不难发现, 参数M、h、g(t)以及L的选取与CPM信号的功率谱特性有着密切的联系。图 1为CPM信号在不同参数条件下的功率谱密度, 由图 1可知, 较长的关联长度L和平滑的频率响应函数g(t)能有效提高功率谱旁瓣的衰减速度, 使能量更加集中。同时增大M和h可提高CPM信号功率谱的主瓣宽度, 而且在h>1的情况下, 功率谱主瓣呈现出频谱分裂现象, 能够使更多的能量集中在主瓣高频部分。由于调制波形的功率谱对信号的码跟踪性能、抗多径以及兼容性等方面都有着重要的影响[11], 那么选取适当参数, 优化其频谱分布, 便可以满足不同波段中的兼容性约束条件, 使CPM作为各波段通用的信号波形进行多波段联合导航成为可能。
|
Download:
|
| 图 1 CPM信号在不同参数条件下的功率谱密度 Fig. 1 Power spectral density of CPM signals with various parameters | |
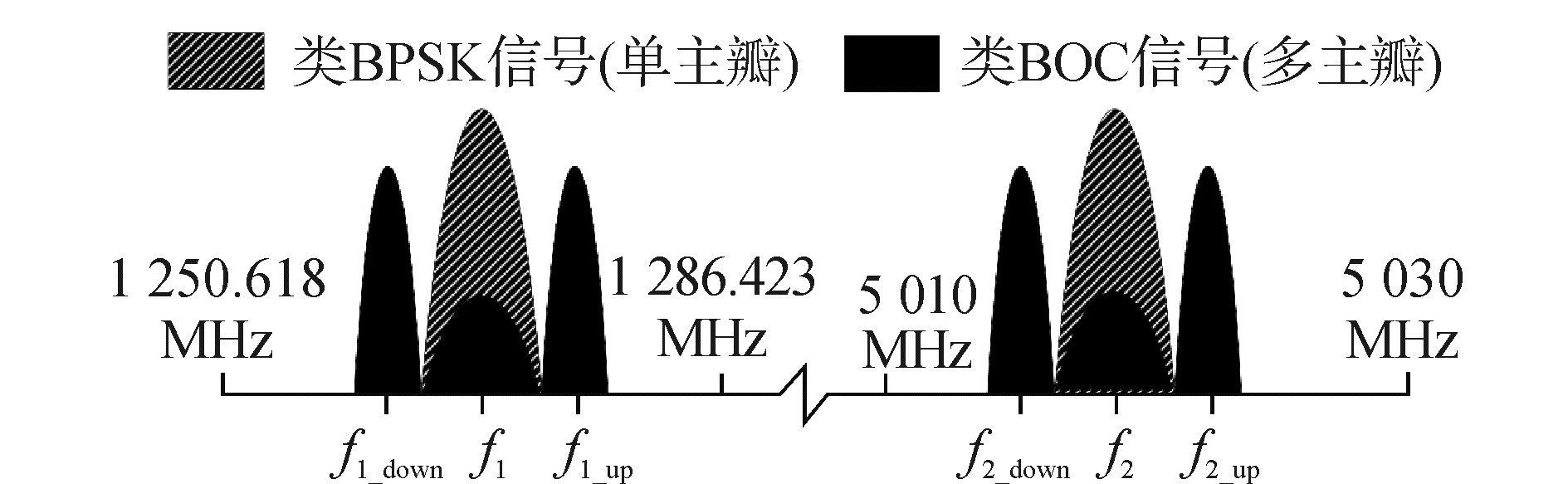
对于多频信号的处理, 载波相位观测量的线性组合能够消除并减小高精度定位中出现的电离层误差和噪声的影响, 且有助于整周模糊度的解算, 提高定位精度[12]。文献[13]指出:一个导航系统能够播发两个不同频率的载波信号, 其中一个载波频率是另一个载波频率的整数倍, 那么整周模糊度的解算更加容易且定位精度高。考虑到C波段载波频率的1/4刚好位于我国BDS B3频段(1 250.618~1 286.423 MHz)内, 如果未来的BDS能够播发L和C波段组合信号, 且满足C波段信号载波频率为L波段信号的4倍, 则利用多频信号处理技术可使得终端快速获得高精度定位。
结合图 2, 本文给出了L和C波段信号频点组合方案, L和C波段的载波频率要满足:
| $ {f_2} = 4{f_1} $ | (5) |
|
Download:
|
| 图 2 L和C波段信号的频点分布方案 Fig. 2 Frequency distribution schemes of combined signals for L and C bands | |
对于具有多个主瓣的类BOC信号, 接收机可以使用BPSK-like技术对其进行单一主瓣的跟踪[14], 那么L和C波段信号存在多种频点组合方案, 即
| $ \begin{array}{l} {f_{2\_{\rm{up}}}} = 4{f_1}, {f_{2\_{\rm{up}}}} = 4{f_{1\_{\rm{up}}}}, {f_{2\_{\rm{up}}}} = 4{f_{{\rm{1\_down}}}}\\ {f_{2\_{\rm{down}}}} = 4{f_1}, {f_{{\rm{2\_down}}}} = 4{f_{1\_{\rm{up}}}}, {f_{2\_{\rm{down}}}} = 4{f_{1\_{\rm{down}}}}\\ {f_2} = 4{f_1}, {f_2} = 4{f_{1\_{\rm{up}}}}, {f_2} = 4{f_{1\_{\rm{down}}}} \end{array} $ | (6) |
信号频点一般选取1.023 MHz的倍数, 考虑到BDS在B3频段的使用情况以及信号间的兼容性问题, 本文将1 256.755 5 MHz作为L波段信号的参考频点。那么, C波段的参考频点设为L波段的4倍即5 027.022 MHz, 其刚好位于C波段导航服务频段内。
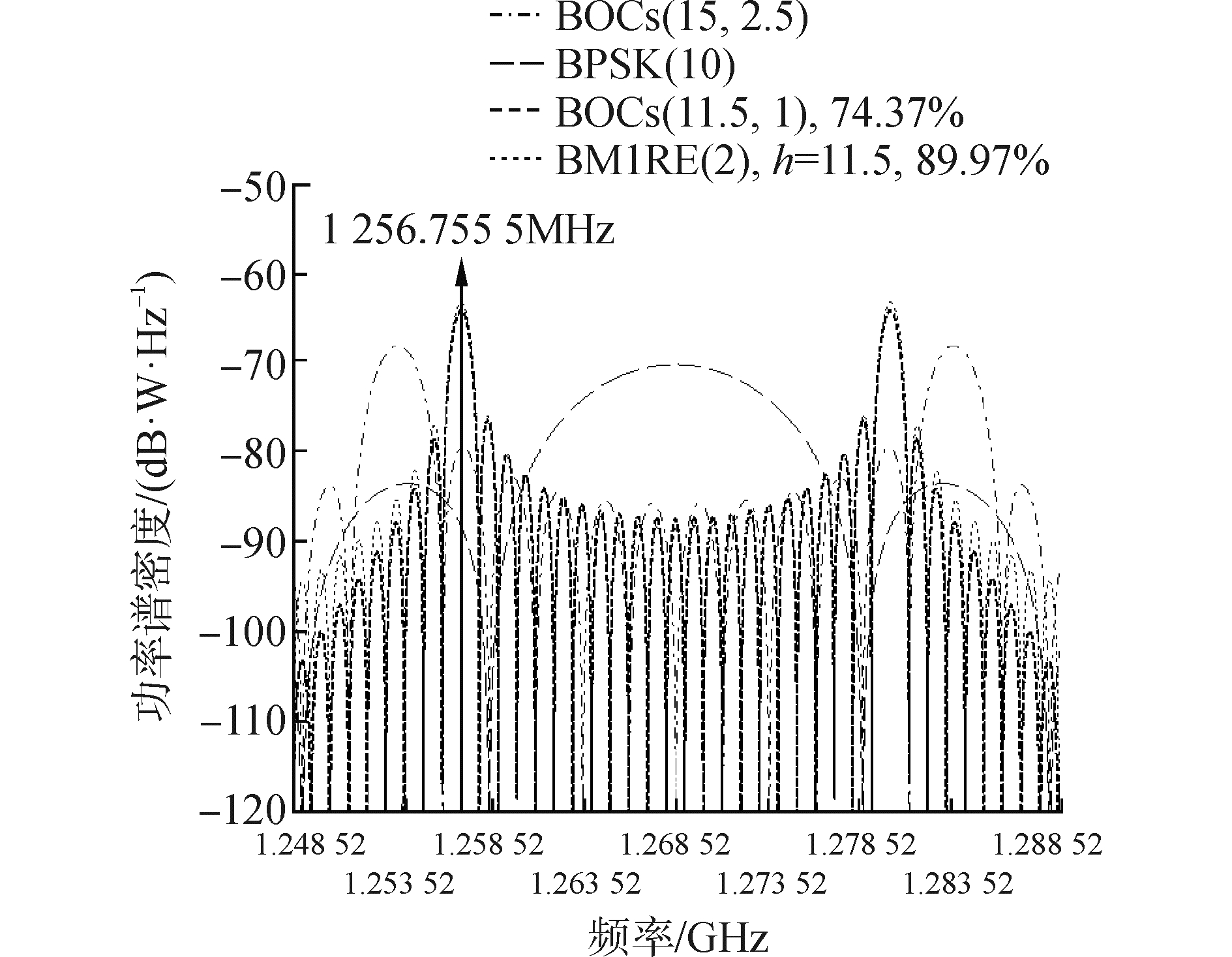
2.2 L波段信号设计我国BDS在B3频段播发BPSK(10)和BOCs(15, 2.5)信号, 其载波频率均为1 268.52 MHz, 如图 3所示, 其中BPSK(m)和BOC(n, m)表示扩频码速率为m×1.023 MHz和子载波频率为n×1.023 MHz的BPSK和BOC信号。为了使新的导航信号具有良好的频谱分离, 实现与现有信号共存, 本文将1 256.755 5 MHz作为组合信号在L波段的参考频率。此外, 就单频信号处理而言, 相比于类BPSK信号, 类BOC信号能够表现出更好的测距性能, 同时为了最小化与同频段信号的干扰, 本文设计一个高频谱效能的CPM信号即BM1REC(2), 调制指数为11.5, 载波频率为1 268.52 MHz。为公平比较, 具有相同频点分布的BOCs(11.5, 1)作为参考信号也将进行讨论与分析。
|
Download:
|
| 图 3 L波段信号的功率谱密度 Fig. 3 Power spectral density of navigation signals in L band | |
由图 3可知, BOCs(11.5, 1)和BM1REC(2)信号具有相似的频谱包络且两个主瓣与BDS B3信号表现出良好的频谱分离, 且其左侧主瓣的中心频率准确的位于1 256.755 5 MHz, 这为L和C波段双频信号的组合, 提高定位精度创造了条件。此外, BM1REC(2)具有较高的频谱效能, 其89.97%的信号功率集中在主瓣宽度内, 优于传统的BOCs(11.5, 1)信号约15.6%。导航信号的性能主要体现在码跟踪精度和抗多径方面, 在白噪声下非相干环路的码跟踪误差为[15]
| $ \begin{array}{*{20}{l}} {{\sigma _{{\rm{NELP}},{\rm{s}}}} = c\sqrt {\frac{{{B_L}(1 - 0.5{B_L}{T_i})\int_{{B_\gamma }/2}^{{B_\gamma }/2} {{G_s}\left( f \right){\rm{d}}f} }}{{4{\rm{ }}{{\rm{\pi }}^2}\frac{{{G_s}}}{{{N_0}}}\left( {\int_{ - {B_\gamma }/2}^{ - {B_\gamma }/2} {f{G_s}\left( f \right)} {\rm{sin}}({\rm{ \pi }}f\Delta ){\rm{d}}f} \right)}}} \times }\\ {\sqrt {\left( {1 + \frac{{\int_{{B_\gamma }/2}^{{B_\gamma }/2} {{G_s}\left( f \right){\rm{co}}{{\rm{s}}^2}({\rm{ \pi }}f\Delta ){\rm{d}}f} }}{{{T_i}\frac{{{G_s}}}{{{N_0}}}{{\left( {\int_{ - {B_\gamma }/2}^{ - {B_\gamma }/2} {f{G_s}\left( f \right)} {\rm{cos}}({\rm{\pi }}f\Delta ){\rm{d}}f} \right)}^2}}}} \right)} } \end{array} $ | (7) |
式中:BL为环路带宽, Cs/N0为载噪比, Δ为相关器间隔, c为光速, Ti为相关积分时间, Gs(f)为信号功率谱。很显然其权值越小, 信号的码跟踪精度越高。
同时为了研究信号的抗多径能力, 平均多径误差包络是一种有效的分析方法, 仅考虑一条反射路径信号时, 其表达式为[16]
| $ {\varepsilon _{\tau, av}} = \frac{1}{{\Delta {\tau _{av}}}}\int_0^{\Delta {\tau _{av}}} {\frac{{|{\varepsilon _\tau }(\Delta {\tau _1}){|_0}| + |{\varepsilon _\tau }(\Delta {\tau _1}){|_\pi }|}}{2}} {\rm{d}}\Delta {\tau _1} $ | (8) |
| $ \begin{array}{l} {\varepsilon _\tau }( \mathit\Delta {\tau _1}) = \\ \frac{{ \pm {{\bar a}_1}\int_{- B/2}^{B/2} {P\left( f \right){\rm{sin}}({\rm{ \mathsf{ π} }}fd){\rm{sin}}(2{\rm{ \mathsf{ π} }}f\Delta {\tau _1}){\rm{d}}f} }}{{2{\rm{ \mathsf{ π} }}\int_{- B/2}^{B/2} {fP\left( f \right){\rm{sin}}({\rm{ \mathsf{ π} }}fd)[1 \pm \overline {{a_1}} {\rm{cos}}(2{\rm{ \mathsf{ π} }}f\Delta {\tau _1})]{\rm{d}}f} }} \end{array} $ | (9) |
式中:a1为反射信号和直达信号幅度之比, d为相关间隔, Δτ1为多径时延, ετ(Δτ1)|0和ετ(Δτ1)|π分别为多径信号与直达信号的载波相位差为0与π时的多径误差。由图 4(a)可知, 在接收机带宽为24.552 MHz, 环路带宽为1 Hz, 相关积分时间为2 ms, 相关间隔为0.1个码片时, BM1REC(2)较BOCs(11.5, 1)信号表现出更优的码跟踪精度。图 4(b)给出了在接收机带宽为24.552 MHz, 相关间隔为0.1个码片, 多径与直达信号幅度比为-6 dB的条件下, L波段信号的抗多径性能。相比于BOCs(11.5, 1)信号, BM1REC(2)在不同多径时延下都表现出较低的多径误差, 且在多径时延高于100 m时具有多于0.1 m的优势。

|
Download:
|
| 图 4 L波段信号的码跟踪精度和平均多径误差包络 Fig. 4 Code tracking errors and running average multipath errors of L band signals | |
兼容性是信号设计中首要考虑的问题。国际上统一采用等效载噪比衰减Δ(Cs/N0)eff来分析GNSS兼容性[17]。Δ(Cs/N0)eff与信号体制, 导航星座和接收功率有关, 本文构建BDS星座计算B3频段中最大系统内干扰等效载噪比衰减Δ(Cs/N0)effmax, 其表达式为
| $ \Delta {({C_s}/{N_0})_{_{{\rm{eff}}}}}^{{\rm{max}}} = \frac{{{C_s}/{N_0}}}{{{C_s}/({N_0} + {I_{{\rm{Intra}}}}^{{\rm{max}}})}} = 1 + \frac{{{I_{{\rm{Intra}}}}^{{\rm{max}}}}}{{{N_0}}} $ | (10) |
| $ {I_{{\rm{Intra}}}}^{{\rm{max}}} = {\rm{max}}\left( {\sum\limits_{i = 1}^{M\left( t \right)} {\sum\limits_{j = 1}^{{K_i}} {{P_i}A\frac{{\int_{-B/2}^{B/2} {{G_s}\left( f \right){G_{i, j}}\left( f \right){\rm{d}}f} }}{{\int_{-B/2}^{B/2} {{G_s}\left( f \right){\rm{d}}f} }}} } } \right) $ | (11) |
式中:热噪声功率谱密度N0取值为-204 (dB·W)/Hz, IIntramax为最大系统内干扰等效噪声功率谱密度, M(t)为t时刻可见卫星数, Pi为对第i颗卫星的最大接收功率, A为接收端天线增益, Ki为第i颗卫星发射的信号类型数, Gs(f)为有用信号的功率谱密度, Gi, j(f)为第i颗卫星发射的第j个干扰信号功率谱密度, 星座参数如表 1所示。
| 表 1 北斗星座参数和仿真参数 Tab.1 BDS space constellations and simulation parameters |
表 2计算了BOCs(11.5, 1)和BM1REC(2)信号对BDS系统B3波段信号所造成的Δ(Cs/N0)effmax, 其中接收功率为跟踪精度达到0.05 m时对应的载波功率。由表可知, BM1REC(2)对BOCs(15, 2.5)和BPSK(10)造成的Δ(Cs/N0)effmax分别为0.051 1 dB和0.425 2 dB, 低于BOCs(11.5, 1)信号约0.001 8 dB和0.000 7 dB。因此, BM1REC(2)具有与BDS B3信号更好的兼容性。
| 表 2 L波段候选信号对BDS B3波段信号造成的Δ(Cs/N0)effmax Tab.2 The Δ(Cs/N0)effmax of BDS signals in B3 band induced by potential signals of L band |
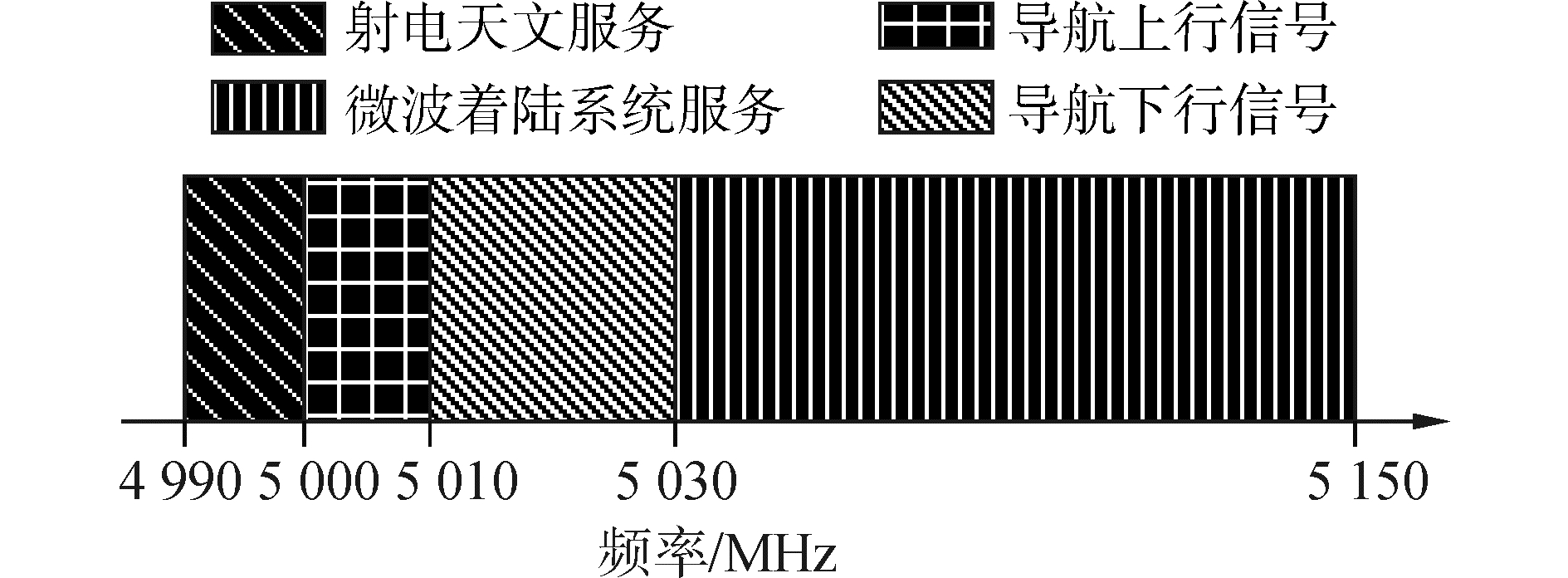
为了解决L波段信号拥挤的问题, 国际电联将C波段资源分配给导航频段。虽然C频段导航资源目前并没有被占用和触及, 但Galileo计划在C波段播发最小频移键控(minimum shift keying, MSK)调制的导航服务信号[18]。为了抢占C波段频率资源, 增加卫星导航服务的多样性, 使BDS卫星有能力播发L和C波段组合信号以提升定位能力, 因此C波段信号的设计已成为我国BDS的紧迫任务。C波段频率资源分布如图 5所示。
|
Download:
|
| 图 5 C波段频率资源分布 Fig. 5 Frequency allocations in C band | |
国际电联规定未来C波段信号不能影响射电天文服务RA和微波着陆系统服务MLS的正常工作, 满足C波段下行导航信号在10颗干扰卫星下的RA波段功率通量密度(power flux density, PFD)小于-196.5 (dB·W)/m2且在MLS波段其每150 kHz的PFD小于-124.5 (dB·W)/m2[19]。很显然, RA波段的约束性尤为苛刻, 如果没有带外抑制较强的输出滤波器, C波段信号很难限制其带外发射功率(out-of-band emission, OOBE)满足上述要求[18-19]。仅从信号设计的角度, 带外发射是主要考虑的因素, 带外发射功率较低的信号, 有助于减小对邻间服务的噪声级别, 同时也降低了非理想滤波器所带来的信号失真和滤波器设计的复杂度以满足RA波段严格的约束性条件。为此, C波段信号的功率谱主瓣能量集中度要高, 旁瓣衰减要快, 以减小带外频谱泄露。但信号高频成分的削弱, 会使信号的性能有所下降。为了兼顾C波段信号的带外约束性和导航性能, 同时考虑L和C波段组合信号的频点分布, 本文设计将BM2RC(4)作为C波段BDS信号, 其调制指数为3.5, 载波频率为5 019.861 MHz, 其主瓣准确的位于5 027.022 MHz。为公平比较, BOCs(7, 2), BPSK(7)和MSK(7)作为C波段参考信号也将进行讨论与分析, 如图 6所示, 其中MSK(m)表示扩频码速率为m×1.023 MHz的MSK信号。

|
Download:
|
| 图 6 C波段信号的功率谱密度 Fig. 6 Power spectral density of C band signals | |
由图 6可知, 与主瓣宽度相同的参考信号相比, BM2RC在主瓣具有更高的能量集中度, 且旁瓣呈现出较强的频谱滚降, 其次是MSK。而BOC和BPSK信号则表现出更多高频分量在RA和MLS波段以及上行信号波段, 间接地提高了对不同服务频段的噪声级别。
图 7呈现了在接收机带宽为20 MHz, 相关间隔为0.1个码片, 环路带宽为1 Hz, 相关积分时间为2 ms, 多径与直达信号幅度比为-6 dB的条件下, C波段信号的跟踪精度与抗多径性能。其中, BM2RC(4)表现出与BOC相当的码跟踪误差, 且明显优于BPSK和MSK。当载噪比为35 dB·Hz时, 其跟踪误差分别低于MSK和BPSK约0.12 m和0.2 m。同时在抗多径能力上, BM2RC的峰值平均多径误差分别低于MSK和BPSK信号多达0.4 m和0.6 m, 且特别适合于多径延时小于60 m的多径环境下。而且BM2RC的抗多径能力整体也略优于BOC信号。这是因为在C波段20 MHz有限带宽内, BM2RC具有更高的能量集中度, 且具有频谱分裂特性使得更多功率集中在C波段带宽边缘附近。
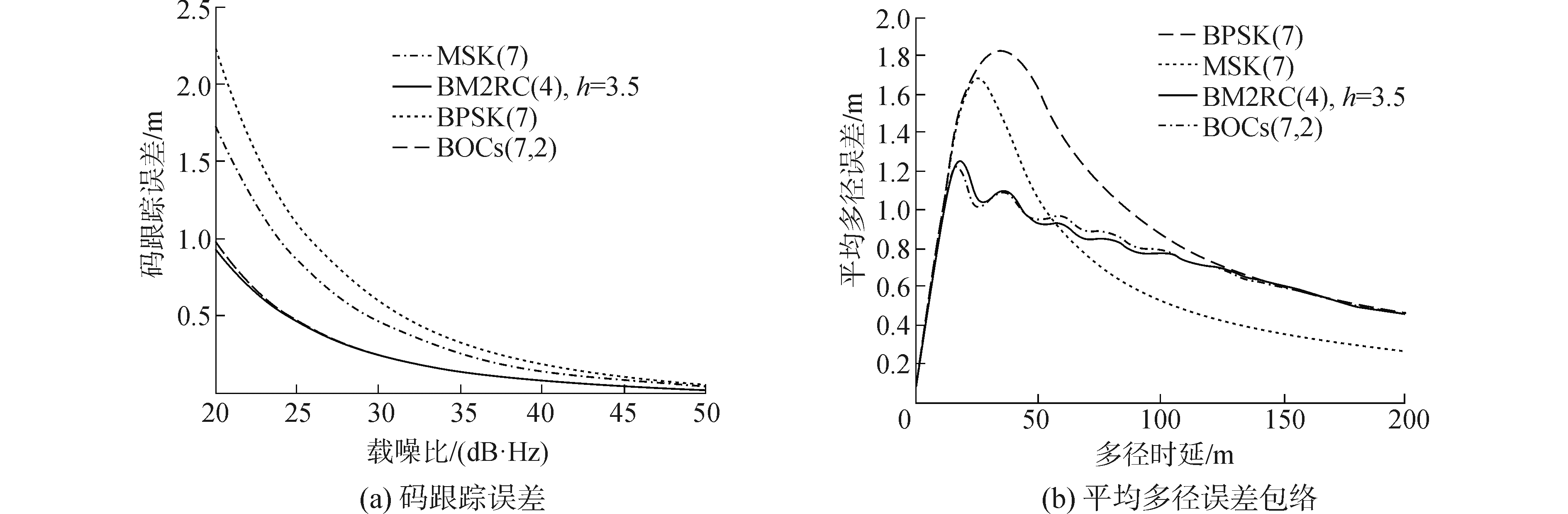
|
Download:
|
| 图 7 C波段信号的码跟踪误差和平均多径误差包络 Fig. 7 Code tracking errors and running average multipath errors of C band signals | |
表 3计算了上述理想信号在不同服务频段下的OOBE和PFD, 其中PFD的表达式为
| $ \text{PFD}=\frac{{{10}^{0.1\times (\text{EIRP}-{{L}_{\text{atm}}})}}}{4\text{ }\!\!\pi\!\!\text{ }{{d}^{2}}}\underset{\begin{smallmatrix} f=\Delta f\_\text{RA} \\ f=\Delta f\_\text{MLS} \end{smallmatrix}}{\mathop{\int }}\,G\left( f \right)\text{d}f $ | (12) |
| 表 3 C波段信号在不同服务带宽下的带外发射功率和功率通量密度 Tab.3 The PFD and OOBE of C band signals in various service bands |
式中:服务频段间的大气损耗Latm为0.5 dB; MEO卫星到地球表面的距离d为21 528 km; Δf_RA为RA服务频段; Δf_MLS为MLS服务频段内任意150 kHz频率范围; G(f)为C波段下行信号功率谱密度; EIRP为等效全向辐射功率, 根据链路预算公式可表示为
| $ \begin{array}{l} {\rm{EIRP}} = [{\left( {{C_s}/{N_0}} \right)_{{\rm{eff}}}} + {L_{Im}} + {N_0}-A + \\ \;\;\;\;\;\;\;\;\;\;\;{L_{{\rm{free}}}} + {\rm{ }}{L_{{\rm{polar}}}} + {I_{{\rm{tro}}}}{]_{{\rm{dB}}}} \end{array} $ | (13) |
式中:各导航信号的(Cs/N0)eff为跟踪精度达到0.1 m时对应的载噪比, 接收机处理损耗LIm为6 dB, 热噪声功率谱密度N0取值为-204 (dB·W)/Hz, 接收端天线增益A为3 dB, C波段空间损耗Lfree为195.4 dB, 极化损耗Ipolar为3 dB, C波段对流层衰减Itro为5.9 dB。如表 3所示, 在RA和MLS服务带宽内, BM2RC具有最少的OOBE且分别低于Galileo候选信号MSK约36.23 dB和2.14 dB。同时BM2RC在C波段上行信号带宽内也呈现出最小的OOBE, 分别低于MSK和BPSK以及BOC信号约1.85 dB、4.63 dB和12.05 dB。此外, 所有C波段信号在MLS波段的PFD均低于-124.5 (dB·W)/m2, 满足MLS对信号的约束条件。然而就RA波段严格的约束条件, 很显然, 如果发射端没有较强的输出滤波限制, C波段信号的PFD几乎很难去满足RA波段所要求的限制级别。从信号设计角度, 由于BM2RC较高的带外抑制特性, 未来C波段信号能够与RA和MLS服务实现更好的频率分离, 同时也降低了非理想滤波器所带来的信号失真和滤波器设计的复杂度以满足RA严格的约束条件。此外, 相比于其他候选信号, BM2RC也最小化了对C波段上行信号接收的干扰。
综上所述, 与现有调制方案相比, BM2RC信号具有较高的频带利用率, 降低了星上滤波处理的复杂度以满足RA波段严格的约束性条件, 而且减小了邻间服务波段的干扰级别。同时, 在码跟踪精度与抗多径方面, BM2RC也呈现出较好或相当的性能。因此, BM2RC能够很好的兼顾C波段信号的带外约束性和导航性能的要求。
3 结论1) 在L频段, BM1REC(2)较BOCs(11.5, 1)具有更好的码跟踪精度和抗多径能力, 同时表现出与B3信号更好的兼容性。2)在C频段, BM2RC(4)很好的兼顾C波段信号的带外约束性和导航性能的要求, 不仅呈现出与C波段候选信号相当或更好的性能, 而且具有更低的OOBE, 很大程度上降低了星上滤波处理的复杂度以满足RA波段严格的约束性条件。
由于目前导航系统普遍采用恒包络复用技术以降低星载有效载荷, 因此如何实现多路CPM信号恒包络复用仍是一个亟待解决的问题, 已成为今后值得深入研究的方向。
| [1] |
LUO Ruidan, XU Ying, YUAN Hong. Performance evaluation of the new compound-carrier-modulated signal for future navigation signals[J]. Sensors, 2016, 16(2): 142. DOI:10.3390/s16020142 (  0) 0)
|
| [2] |
LIU Xiaoli, LIANG Muqing, MORTON Y, et al. Performance evaluation of MSK and OFDM modulations for future GNSS signals[J]. GPS solutions, 2014, 18(2): 163-175. DOI:10.1007/s10291-014-0368-6 (  0) 0)
|
| [3] |
XUE Rui, SUN Yanbo, ZHAO Danfeng. CPM signals for satellite navigation in the S and C bands[J]. Sensors, 2015, 15(6): 13184-13200. DOI:10.3390/s150613184 (  0) 0)
|
| [4] |
施浒立, 景贵飞, 崔君霞. 后GPS和GPS后时代的卫星导航系统[M]. 北京: 科学出版社, 2012: 10-16.
(  0) 0)
|
| [5] |
MARGARIA D, MOTELLA B, ANGHILERI M, et al. Signal structure-based authentication for civil GNSSs:recent solutions and perspectives[J]. IEEE signal processing magazine, 2017, 34(5): 27-37. DOI:10.1109/MSP.2017.2715898 (  0) 0)
|
| [6] |
朱亮, 陆明泉, 冯振明. 北斗系统C频段导航信号的波形设计[J]. 电子技术应用, 2012, 38(8): 89-92. ZHU Liang, LU Mingquan, FENG Zhenming. Waveform design for Beidou C band navigation signal[J]. Application of electronic technique, 2012, 38(8): 89-92. (  0) 0)
|
| [7] |
XUE Rui, CAO Qingming, WEI Qiang. A flexible modulation scheme design for C-band GNSS signals[J]. Mathematical problems in engineering, 2015, 2015: 165097. (  0) 0)
|
| [8] |
SU Chengeng, GUO Shuren, ZHOU Hongwei. A substitute for BOC modulation based on SS-CPM[J]. Advances in space research, 2013, 51(6): 942-950. DOI:10.1016/j.asr.2012.06.012 (  0) 0)
|
| [9] |
EMMANUELE A, ZANIER F, BOCCOLINI G, et al. Spread-spectrum continuous-phase-modulated signals for satellite navigation[J]. IEEE transactions on aerospace and electronic systems, 2012, 48(4): 3234-3249. DOI:10.1109/TAES.2012.6324699 (  0) 0)
|
| [10] |
ANDERSON J B, AULIN T, SUNDBERG C E. Digital phase modulation[M]. New York: Plenum Press, 1986: 149-153.
(  0) 0)
|
| [11] |
ZHANG Jiayi, YAO Zheng, LU Mingquan. Generalized theory and decoupled evaluation criteria for unmatched despreading of modernized GNSS signals[J]. Sensors, 2016, 16(7): 1128. DOI:10.3390/s16071128 (  0) 0)
|
| [12] |
ZHANG Xiaohong, HE Xiyang. BDS triple-frequency carrier-phase linear combination models and their characteristics[J]. Science China earth sciences, 2015, 58(6): 896-905. DOI:10.1007/s11430-014-5027-9 (  0) 0)
|
| [13] |
ISSLER J L, PAONNI M, EISSFELLER B. Toward centimetric positioning thanks to L-and S-band GNSS and to meta-GNSS signals[C]//Proceedings of the 5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing. Noordwijk, Netherlands, 2010: 1-8.
(  0) 0)
|
| [14] |
LOHAN E S. Statistical analysis of BPSK-like techniques for the acquisition of Galileo signals[J]. Journal of aerospace computing, information, and communication, 2006, 3(5): 234-243. DOI:10.2514/1.17441 (  0) 0)
|
| [15] |
BETZ J W, KOLODZIEJSKI K R. Generalized theory of code tracking with an early-late discriminator part Ⅱ:Noncoherent processing and Numerical Results[J]. IEEE transactions on aerospace and electronic systems, 2009, 45(4): 1557-1564. DOI:10.1109/TAES.2009.5310317 (  0) 0)
|
| [16] |
HE Chengyan, GUO Ji, LU Xiaochun, et al. Multipath performance analysis of GNSS navigation signals[C]//Proceedings of IEEE Workshop on Electronics, Computer and Applications. Ottawa, ON, Canada, 2014: 379-382.
(  0) 0)
|
| [17] |
SUN Yanbo, XUE Rui, ZHAO Danfeng, et al. Radio frequency compatibility evaluation of S band navigation signals for future BeiDou[J]. Sensors, 2017, 17(5): 1039. DOI:10.3390/s17051039 (  0) 0)
|
| [18] |
AVILA-RODRIGUEZ J A, WALLNER S, WON J H, et al. Study on a Galileo signal and service plan for C-band[C]//Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation. Savannah, 2008: 2515-2529.
(  0) 0)
|
| [19] |
COLZI E, LOPEZ-RISUENO G, SAMSON J, et al. assessment of the feasibility of GNSS in c-Band[C]//Proceedings of the 26th International Communications Satellite Systems Conference. San Diego, 2008: 131-137.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


