无线传感器网络(wireless sensor network, WSN)是由部署在监测区域内大量体积小、成本低、具有无线通信、传感、数据处理的传感器节点通过自组织方式组成的一种网络。无线传感器节点通常由电池供电, 传感网络大多部署在人烟稀少或是人类无法到达的地区, 这使得更换节点电池变得非常困难。为解决这个关键问题, 需要降低节点的能量消耗, 获得更长的网络生命周期[1]。然而, 在环境监测预警系统等此类应用中, 对信息的采集实时性要求较高。因此, 针对此类无线传感网络应用进行网络协议设计时, 需要综合考虑能量和时延两种因素。
为了降低传感节点的能量消耗, 一种有效的节能方法是使节点尽可能多地进入睡眠模式。Crossbow公司的数据表明, 如果节点一直保持在活跃模式下只能存活100~120 h, 而在1%的占空比下工作, 其寿命可达一年以上[2]。因此, 低占空比WSN可以克服节点能量消耗问题, 满足长期监测应用的需求。然而, 由于每个节点的周期性睡眠, 会产生较长的延迟, 因为发送节点必须等到它的邻居节点醒来才能转发数据包, 这段等待时间被称为等待时延。等待时延在低占空比WSN的端到端时延中占了主导。而且如果永远选择最先苏醒的传感节点作为转发节点, 可能导致其与被选节点间的链路质量很差, 从而消耗更多的能量, 所以在进行低占空比无线传感器网络路由算法设计时需要综合考虑能量和时延两种因素。
低占空比下的实时数据传输问题已经引起许多学者的关注, 文献[3-6]提出了一些问题解决方案。文献[3]提出了一个时延感知的数据聚合调度方案。方案构建了一个连通支配集(connected dominating set, CDS)树, 在节点的调度上, 该方法不仅可确保无数据冲突, 还可以降低sink节点接收源节点数据的时延, 从而减少无线传感网络的延迟。文献[4]基于无线传感网络中端到端时延提出了一种综合分析框架, 框架采用随机队列模型, 可以根据不同的MAC协议设置参数, 从而预测端到端的时延分布情况。文献[5]提出了最小时延路由(minimum delay routing, MDR)协议, 它是一种针对事件驱动型无线传感网络的数据传输最低时延技术, MDR协议利用CTS消息机制来建立无线传感网络中节点间的路由机制, 并对汇聚节点收集各源节点的数据的时延进行了优化。文献[6]提出了一种节点休眠调度算法(link-quality and energy-aware based scheduling scheme, LES)这种算法采用增加节点苏醒时隙的方式来减少延时, 但由于时隙增加过多, 增加了节点的能量消耗, 降低了网络的寿命。
本文结合低占空比无线传感网络中实时业务的需求, 对数据收集时延的阈值进行分析, 提出了最低时延数据收集(minimum-delay data collection, MDDC)算法:基于原始的网络拓扑设计了一种基于节点映射的虚拟网络, 从而将数据收集时延最小化问题转化为虚拟网络的最大流问题。通过使用Ford-fulkerson最大流算法获得最低数据收集时延。
1 网络模型假设一个低占空比无线传感网络中有N个传感节点, 每个节点有两种状态:活跃状态和休眠状态。节点处于活跃状态时能够感知周围事物, 或者接收来自邻节点的数据包, 在休眠状态下节点会关闭除了唤醒定时器之外的所有其他功能模块来减少能量消耗。在TDMA MAC协议中, T被分成等时间长度的时隙τ, 在一个时隙τ内有足够的时间保证成功发送一个数据包。在低占空比工作模式下, 节点可以在任意时隙发送数据包, 但只有当在工作时隙时它才能接收数据包。网络中的所有节点的工作时隙是异步的, 即所有节点都能独立地决定自己的工作调度。
为使节点的工作调度更为清晰直观, 现将每个节点描述为一个二进制字符串, 1代表节点处于活跃状态, 0代表节点处于休眠状态。例如, 若节点Vi的工作调度表为0010, 即ωi=0010, 说明节点当前的工作周期T=4τ, 它在每个周期的第3个时隙处于活跃状态而在其他时隙处于休眠状态。相邻的两节点间发送一个数据包所需时间为τ, 如果节点不休眠, 则两节点间传输时延为τ。由于采用低占空比技术, 接收节点只能在其工作时隙才能接收数据, 产生了额外的等待时延。例如, 发送节点Vi的工作调度表为0010, 接收节点Vj的工作调度表为0100, 等待时延为3τ。
2 问题描述节点的低占空比技术是为了减少节点的活跃时间, 节约能量。假定除了汇聚节点VN外其他节点都为源节点, 每个源节点在一个周期内只有一个工作时隙, 源节点将感知的信息形成一个数据包, 经过单跳或多跳将数据包发送给汇聚节点。收集时延为从(N-1)个源节点发送数据包到汇聚节点完成这(N-1)个数据包的收集所需的时间。本文的目标是计算汇聚节点完成数据收集所需的最小时间, 以及收集时延最小的数据传输路径。用EED(Vi)表示源节点Vi在单跳或多跳情况下到汇聚节点的端到端的时延, 本文的目标旨在最小化T:
| $ T = {\rm{max}}\{ {\rm{EED}}({V_i})\} \;\;\;\;\;\;\;\;{\rm{ }}1 \le i \le N-1 $ | (1) |
对于给定的网络, 假设x(i, j, t)为布尔变量, 表示节点Vj是否在t时刻收到来自于Vi的数据包。tj表示节点Vj的工作时隙, Nj表示节点j的邻居节点。因此, 汇聚节点完成数据收集所需的最小时间问题可以描述为
| $ x(i, j, {t_j}) + x(m, j, {t_j}) \le 1{\rm{ }}\;\;\;(i \in {N_j}, m \in {N_j}) $ | (2) |
| $ x\left( {i, j, t} \right) = 0{\rm{ }}\;\;\;(t \in \left[{0, T} \right], t \ne {t_j}) $ | (3) |
| $ {\rm{min}}\left( T \right) $ | (4) |
式(2)确保了每个节点处于活跃状态时都只能接收一个来自邻居节点的数据包, 而且节点不能同时接收和发送数据包。图 1(a)中的两条链路不能同时被使用。式(3)表明节点在休眠状态时不能接收数据。式(4)表示最小化数据收集时延。

|
Download:
|
| 图 1 相邻链路间的三种约束 Fig. 1 Three constraints on neighbor links | |
根据链路间冲突类型, 链路的干扰分为两种:交叉链路和干扰链路。交叉链路是两条有相同目的节点的链路, 如图 1(b)所示, 由于节点中只有一个半双工无线发射器, 交叉链路不能在同一时隙传输数据包。图 1(c)中, 节点1在节点3的通信范围内, 当节点2和节点3分别同时向其下一跳节点1和节点4发送数据包时, 节点1将同时收到节点2和3发来的数据包, 干扰将发生, 虚线表示干扰。式(2)的约束条件保证了数据收集路径中不存在交叉链路。干扰链路通过TDMA协议使两跳之内的节点不存在相同的工作时隙来避免。
3 数据收集算法设计 3.1 数据收集时延的下限在一个周期内汇聚节点始终处于苏醒状态, 其他节点只有一个工作时隙。把网络拓扑分为多个子网, 每个子网都包含一个汇聚节点的邻居节点, 如图 2所示。这些子网的数据收集时延是互不影响的。由此可以得出, 数据收集时延的下限为所有子网的最小数据收集时延的最大值。

|
Download:
|
| 图 2 子网的划分 Fig. 2 Division of network | |
图 3(a)为其中一个子网。汇聚节点在邻居节点的工作时隙的下一个时隙去接收数据包。子网的数据收集时延的下限为S(Neighbor(sink))+1+(n-1)T, T是一个循环周期, n为不包含汇聚节点的节点数量, S(Neighbor(sink))表示汇聚节点的邻居节点的工作时隙。

|
Download:
|
| 图 3 时延下限调度示意图 Fig. 3 The schedule with the least delay | |
如图 3所示, 图 3(a)中括号中的二进制字符串表示每个节点的工作调度表。从图 3(b)可以看到汇聚节点S接收某个源节点数据包的具体时间, 以及源节点到达汇聚节点S的传输过程; 括号中的数字代表数据包的源节点。根据图 3(a)和(b)中的调度表, 汇聚节点S在第1个周期接收了源节点1的数据包, 在第2个周期接收了由源节点2发送过来的数据包, 在第3个周期接收了源节点3发送过来的数据包。至此, 在第10个时隙汇聚节点能收集所有的数据包。由于汇聚节点的邻居节点调度表为1 000, 则S(Neighbor(sink))为1, 源节点的个数为3个, 工作周期T为4个时隙, 即最小界限为10个时隙。故该子网数据收集时延的下限为S(Neighbor(sink))+(n-1)T+1。
如果汇聚节点有多个邻居节点, 则该网络可以分为多个子网。该网络的数据收集时延的下限为所有子网的数据收集时延下限的最大值, 即
| $ {\rm{max}}(S({\rm{Neighbor}}({\rm{sink}})) + \left( {n-1} \right)T) + 1 $ | (5) |
为了更清楚描述节点工作状态和数据传输过程, 基于原始的网络拓扑G, 本文设计了一种基于节点映射的虚拟网络G′。假设原始网络G=(V, E), 其中E为链路的集合, V为节点的集合, 虚拟网络G′=(V′, E′)。网络G中节点Vi有多个工作时隙, 每个工作时隙ti对应网络G′中的虚拟节点Vi, t, Vi, t∈V′。图 3(b)中, 节点1在时隙1, 5和9向节点S发送数据, 因此在网络G′中存在三个对应的虚拟节点V1, 1、V1, 5、V1, 9。根据节点的作用不同将原始子网络G中的节点分为三类。
叶节点:只用作源节点, 即只传输自己采集的数据, 不能转发数据。
中继节点:用作源节点和转发节点, 即不仅传输自己收集的数据, 也转发来自邻居节点的数据。为平衡各源节点的数据搜集时延, 中继节点优先转发来自邻居节点发的数据。
汇聚子节点:收集所有源节点的数据包。
如果在网络G中节点Vi和邻居节点Vj有一条链路, 节点Vi和Vj的工作时隙分别为m和n且n>m, 则网络G′中从Vi, m到Vj, n之间存在一条虚拟链路。因为叶节点只传输自身的数据, 且只有一个数据包, 在其他活跃时间内没有数据需要发送。
为了让汇聚节点快速地收集到传感节点采集的数据, 本文将完成数据收集所需的最小时延问题转化为最大流问题去获得一个优化的结果。为此引入两个虚拟顶点:源节点(S′)和汇聚节点(D′), 用来表示子网中全部数据流的源节点和目的节点。汇聚节点(D′)与网络G中汇聚子节点映射对应的所有虚拟节点进行连接。源节点(S′)与网络G中源节点映射对应的最先苏醒的虚拟节点进行连接, 因为源节点使用第一个工作时隙发送自身采集的数据。
以图 4为例详细描述如何根据原始网络拓扑和节点的工作调度表(如图 3(a)的网络为例)建立虚拟网络。首先, 根据子网G中每个节点的工作调度表确定虚拟网络G′中虚拟节点位置。然后根据前面的规则确定虚拟节点间的虚拟链路。

|
Download:
|
| 图 4 VNM网络模型的构建 Fig. 4 Construction of VNM network model | |
对于叶节点v2, 当邻居节点v1处于活跃状态时, v1接收来自v2的数据包。因此, 构建链路V2, 2→V1, 5和V2, 2→V1, 9。对于另一个叶节点v3, 它也可以在邻节点v1处于活跃状态时向v1传输一个数据包, 构建链路V3, 4→V1, 5和V3, 4→V1, 9。
对于中继节点v1, 它向汇聚节点S发送一个数据包。因此, 建立链路V1, 1→Vs, 2、V1, 1→Vs, 6、V1, 1→Vs, 10。同时, 作为一个中继节点, 当v1为活跃状态时可以接收来自其他节点的数据包, 并向汇聚节点S转发数据包, 由此建立链路V1, 5→Vs, 6, V1, 5→Vs, 10和V1, 9→Vs, 6。
对于汇聚子节点S, 建立其对应的虚拟节点到汇聚节点D′之间的链路, 即VS, 2→D′、VS, 6→D′和VS, 10→D′。最后, 建立从源节点S′到网络G中源节点对应的的第一个苏醒的虚拟节点的链路, 即S′→V1, 1、s′→V2, 2和s′→V3, 4。图 4为构建好的虚拟网络。
3.3 最大流问题对于给定虚拟网络G′, 优化的目的是使源节点S′到汇聚节点D′的传输流量最大化, 即在给定时间内汇聚子节点能收集到源节点数据包的最大数量。F(s, d)表示从源节点到目的节点的总流量, f(*, *)表示两个虚拟节点之间链路是否有流量通过。本文的目标是max{F(s, d)}。
数据收集时延为汇聚节点完成数据收集所需的总时间, 这取决于每个源节点的max(EED)(源节点到汇聚子节点的端到端最大时延)。因此, 汇聚子节点完成数据收集所需的最小时延问题可以描述为
| $ {\rm{min}}({\rm{max}}\{ {\rm{EED}}({V_i})\} ){\rm{ }}\;\;\;\;1 \le i < N $ | (6) |
| $ \begin{array}{l} \sum\limits_{u \in N\left( i \right)} {f\left( {{V_{u, {t_u}}}, {V_{i, {t_i}}}} \right)} = \sum\limits_{v \in N\left( i \right)} {f\left( {{V_{i, {t_i}}}, {V_{v, {t_v}}}} \right)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{t_u}, {t_i}, {t_v} \in \left[{0, T} \right] \end{array} $ | (7) |
| $ \begin{array}{l} f({V_i}, {t_i}, {V_{j, {t_j}}}) + f({V_j}, {t_j}, {V_{m, {t_m}}}) \le 1\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{t_i}, {t_j}, {t_m} \in \left[{0, T} \right] \end{array} $ | (8) |
| $ \sum\limits_{j \in N\left( i \right)} {f({V_{j, {t_j}}}, {V_i}, {t_i})} \le {C_{{V_i}}}, {t_i} = 1\;\;\;\;\;\;\;{\rm{ }}{t_j}, {t_i} \in \left[{0, T} \right] $ | (9) |
式(6)表示基于各源节点到汇聚子节点为最大时延的基础上使得收集各源节点的数据包的时延最小, 这个问题可等同于虚拟网络中的最大流问题。最大流问题需要符合式(7)和式(8)两个条件, 其中式(7)约束了每条链路上的流量都不小于0, 并且对于虚拟网络中任一顶点, 顶点流进量与流出量相等, 其中N(i)表示网络G中节点i的邻居节点的集合。式(8)规定了一个节点不能同时传送和接收数据包。式(9)表示当节点间的链路有流量时, f(vj, vi)为1, 否则为0。
在将数据收集时延问题转化为最大流问题之后, 本文基于Ford-fulkerson最大流算法提出了MDDC算法, 该算法可以获得较低的数据收集时延。
算法1 最低时延数据收集算法(MDDC)
输入:VNM虚拟网络模型G(V, E), 顶点个数n
输出:数据收集时延T
for each edge(u, v)∈E {
f[u, v]=0
f[v, u]=0
}
while i < n do {
使用BFS在残留网络G′中查找增广路径
if 剩余网络G′中存在一条S-D传输路径P then
Cf(p)=min{ Cf(u, v) | (u, v) is in path P}
for each edge(u, v) in path P
{ f[u, v]+=Cf(p)
f[v, u]=-f[u, v]
}
更新剩余网络G′
maxFlow+=Cf(p)
}
得到G的最大流量maxFlow和优化的数据流路径
数据收集时延T=maxFlow
4 仿真实验与分析将通过仿真实验来评估本文提出的数据收集时延最小算法(MDDC)的性能, 将其与路由协议FaST[16]通过各项性能指标比较进行对比分析。
4.1 仿真环境和评价标准将50个传感器节点随机置于100 m×100 m的正方形区域。汇聚节点位于区域正中心, 每个传感节点通过一跳或多跳传输方式向汇聚节点传输数据。除汇聚节点外, 所有节点在一个周期内只有一个工作时隙, 工作调度表已经提前设置。如果发生数据发送冲突, 采用重传机制。
评价标准如下:
1) 收集时延:网络中的源节点开始发送数据包到汇聚节点收集所有数据包所需要的时间。收集时延用汇聚节点收集所有数据包所需的总时隙数表示。
2) 能耗:汇聚节点收集所有源节点发送的数据包所需要的能量, 能量消耗的多少用传输次数来表示。
4.2 仿真结果在不同占空比对MDDC算法的传输时延和能耗进行仿真实验分析, 每种情况都重复实验100次, 并取平均值作为统计结果。
在低占空比无线传感网络中, 传输时延与节点的占空比有着很大的关系, 占空比越大传输时延越小。
图 5显示了MDDC和FaST两种算法的收集时延随着节点占空比变化的曲线。由仿真结果可知, 节点的占空比从0.05变化到0.25。随着占空比的增加, 两种算法的平均收集时延均显著地降低, 但MDDC算法的平均收集时延一直保持最低, 尤其是在占空比很低的情况下, 收集时延下降了20%。另外, MDDC算法下的收集时延与时延下限几乎相等。由此可见, MDDC算法可以获得最小数据收集时延。

|
Download:
|
| 图 5 占空比与时隙个数 Fig. 5 Slots vs.duty cycle | |
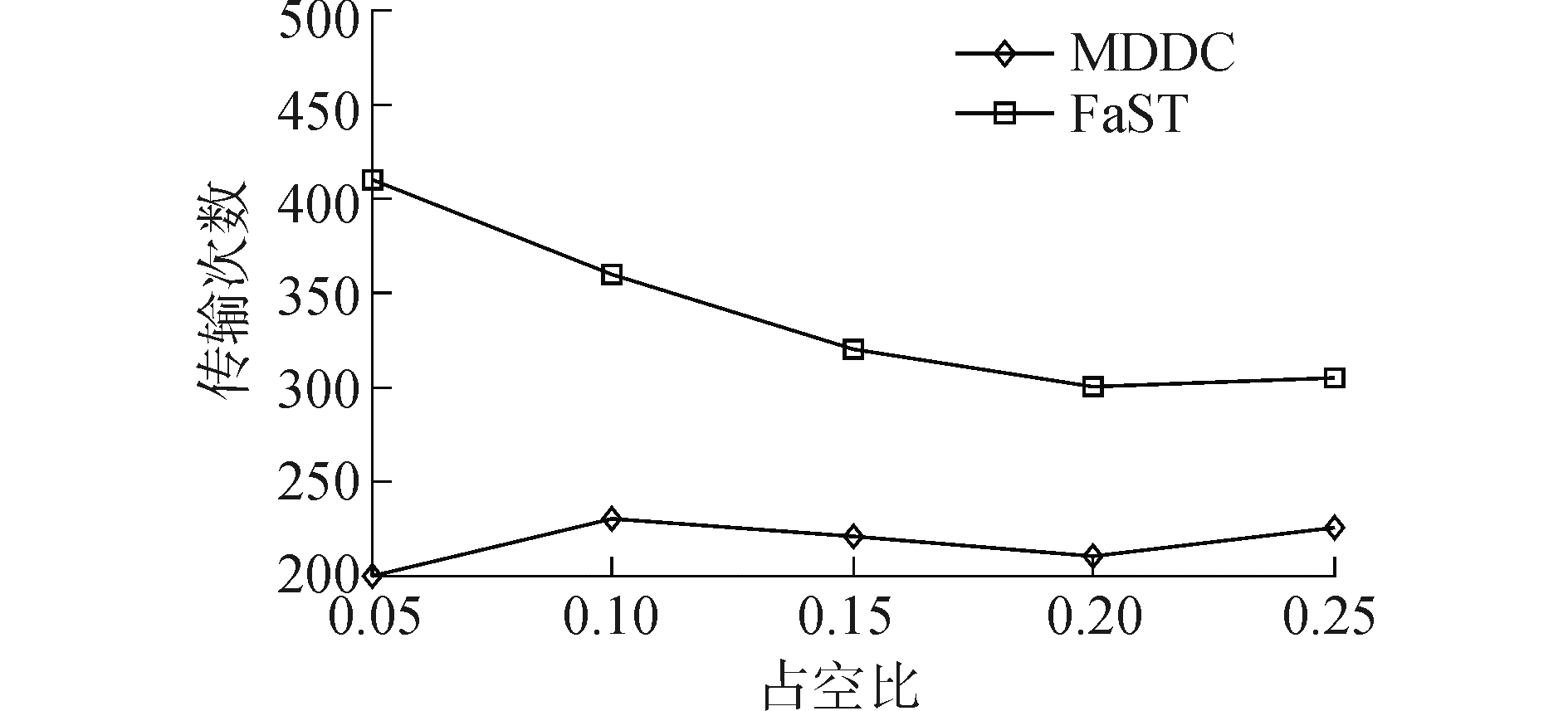
图 6显示了两种算法的能耗随着节点占空比变化的曲线。根据仿真结果可以看出, MDDC算法在降低数据收集时延的同时其能耗几乎没有多大变化, 相对于FaST算法, MDDC算法保持着明显优势, 其能耗始终保持比较低的水平, 大约为FaST算法的50%~70%。由于MDDC算法中节点的占空比与收集所有数据包所需要的传输次数关系不大, 说明低占空比无线传感网络中的时延主要来源于节点休眠的等待时延而不是数据重传。
|
Download:
|
| 图 6 占空比与传输次数 Fig. 6 Numbers of transmission vs.duty cycle | |
1) 数据收集时延接近时延的下限值, 在占空比较低时, 收集时延大约为FaST算法的80%。
2) 在降低数据收集时延的同时, 能耗始终保持比较低的水平, 大约为FaST算法的50%~70%。
| [1] |
毕玉婷, 陈昕. 低占空比无线传感器网络能量感知路由算法[J]. 北京信息科技大学学报, 2012, 27(6): 93-98. BI Yuting, CHEN Xin. Energy-aware routing algorithm for low duty cycle wireless sensor networks[J]. Journal of Beijing Information Science and Technology University, 2012, 27(6): 93-98. (  0) 0)
|
| [2] |
Mote Battery Life Calculator[EB/OL]. [2013-01-05]. http://www.xbow.com/Support/wAppNotes.aspx.
(  0) 0)
|
| [3] |
LEE T, KIM D S, CHOO H. A delay-aware scheduling for data aggregation in duty-cycled wireless sensor networks[C]//Proceedings of the 9th International Conference on Mobile Ad-hoc and Sensor Networks. Dalian, China, 2013: 254-268
(  0) 0)
|
| [4] |
WANG Yunbo, VURAN M C, GODDARD S. Cross-layer analysis of the end-to-end delay distribution in wireless sensor networks[J]. IEEE/ACM transactions on networking, 2012, 20(1): 305-318. DOI:10.1109/TNET.2011.2159845 (  0) 0)
|
| [5] |
刘韬, 李天瑞, 谭颖. 事件驱动型无线传感器网络最小时延路由协议[J]. 传感器与微系统, 2015, 34(3): 130-133. LIU Tao, LI Tianrui, TAN Ying. Minimum delay routing protocol for event-driven wireless sensor networks[J]. Transducer and microsystem technologies, 2015, 34(3): 130-133. (  0) 0)
|
| [6] |
陈良银, 王金磊, 张靖宇, 等. 低占空比WSN中一种节点休眠调度算法[J]. 软件学报, 2014, 25(3): 631-641. CHEN Liangyin, WANG Jinlei, ZHANG Jingyu, et al. Scheduling scheme algorithm in low-duty-cycle WSN[J]. Journal of software, 2014, 25(3): 631-641. (  0) 0)
|
| [7] |
李燕君, 孙扬. 低占空比传感网的端到端延迟控制方法[J]. 中南大学学报(自然科学版), 2013, 44(S1): 171-175. LI Yanjun, SUN Yang. End-to-end delay control for low-duty-cycled sensor networks[J]. Journal of Central South University (science and technology), 2013, 44(S1): 171-175. (  0) 0)
|
| [8] |
陈权, 高宏. 低占空比无线传感器网络中基于动态切换的实时路由协议[J]. 通信学报, 2015, 36(10): 224-234. CHEN Quan, GAO Hong. Dynamic switching based real-time routing in low-duty-cycle wireless sensor networks[J]. Journal on communications, 2015, 36(10): 224-234. DOI:10.11959/j.issn.1000-436x.2015213 (  0) 0)
|
| [9] |
段轶, 吴小兵, 陈贵海. 低占空比无线传感器网络中的动态数据传输协议[J]. 计算机研究与发展, 2011, 48(S2): 145-151. DUAN Yi, WU Xiaobing, CHEN Guihai. Dynamic data forwarding in low-duty-cycle sensor networks[J]. Journal of computer research and development, 2011, 48(S2): 145-151. (  0) 0)
|
| [10] |
LUO Shuyun, MAO Xufei, SUN Yongmei, et al. Delay minimum data collection in the low-duty-cycle wireless sensor networks[C]//Proceedings of 2012 IEEE Global communications Conference. Anaheim, CA, USA, 2012: 232-237.
(  0) 0)
|
| [11] |
FAN Zuzhi. Delay-driven routing for low-duty-cycle sensor networks[J]. International journal of distributed sensor networks, 2013, 9(9). DOI:10.1155/2013/198283 (  0) 0)
|
| [12] |
INCEL O D, KRISHNAMACHARI B. Enhancing the data collection rate of tree-based aggregation in wireless sensor networks[C]//Proceedings of the 5th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks. San Francisco, CA, USA, 2008: 569-577.
(  0) 0)
|
| [13] |
YAO Yanjun, CAO Qing, VASILAKOS A V. EDAL:an energy-efficient, delay-aware, and lifetime-balancing data collection protocol for heterogeneous wireless sensor networks[J]. IEEE/ACM transactions on networking, 2015, 23(3): 810-823. DOI:10.1109/TNET.2014.2306592 (  0) 0)
|
| [14] |
SHEN Zhong, JIANG Hai, YAN Zhongjiang. Fast data collection in linear duty-cycled wireless sensor networks[J]. IEEE transactions on vehicular technology, 2014, 63(4): 1951-1957. DOI:10.1109/TVT.2013.2288259 (  0) 0)
|
| [15] |
PAN M S, LIU PingLin. Quick event detection and reporting in low-duty-cycled wireless sensor networks[C]//Proceedings of the International Conference on Computing, Networking and Communications. Honolulu, HI, USA, 2014: 1071-1075.
(  0) 0)
|
| [16] |
KACIMI R, MAMMERI Z. Efficient delay-aware data collection in mostly-off wireless sensor networks[C]//Proceedings of 7th IFIP Wireless and Mobile Networking Conference. Vilamoura, Portugal, 2014: 1-6.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


