无人水面艇(unmanned surface vessel, USV)有体型小、机动性能强、智能程度高等特点,可以执行水质监测、海上救援和舰艇跟踪等不适合人员参与的任务,具有广泛市场应用前景。航向保持问题不仅关系到航行的经济性与安全性,更是研究自动避碰、航迹跟踪等问题的基础,所以其一直是船舶研究领域的热点[1-3]。与普通船舶不同,USV航速快且抗扰能力弱,所以在复杂多变的海洋环境以USV的航向保持策略需要有较快的收敛速度和较强的鲁棒性。
USV航行过程中,因航速、装载和外界干扰等因素的影响,其航向保持系统存在明显的非线性特性,再加上模型参数的不确定性和未建模动态的影响,导致航向保持领域存在两个关键性问题:运动过程中的非线性;航向保持过程中的模型不确定性。目前研究航保持的策略主要包括;反步(backstepping)、滑模控制、模糊控制、自抗扰控制(ADRC)等。Fan等[4]应用滑模控制(SMC)实现了船舶的航向和航迹控制,但SMC的高频抖振现象难以解决。为了解决抖振问题,文献[5]采用模糊滑模算法,仿真证明其性能明显优于常规的SMC控制。文献[6]为克服滑模面切换带来的抖振,提出一种新型的双曲正弦函数的指数趋近律,实现自适应调节,使切换平缓。文献[7]将ADRC与滑模方控制相结合设计航向保持控制策略,并通过坐标变化解决由风、流产生的漂角。根据万能逼近理论,模糊逻辑可逼近任意非线性函数,在文献[8-9]基础上分别采用backstepping与终端滑模和参数自适应相结合的方法设计航向控制器,但backstepping存在的“计算爆炸”问题没有得到解决。文献[10]针对船舶离散非线性系统的航向保持问题,采用单一神经网络逼近系统所有未知部分,有效的减轻了“计算爆炸”问题。由于大部分文献都是针对桨—舵推进的大型船舶研究航向保持问题,但其在一定程度上并不适用于吊舱推进的小型USV。
本文通过MMG(manoeurring mathematical model group)分离建模的思想建立吊舱推进USV三自由度模型,然后在受力分析和假设的基础上将MMG模型化简为响应型船舶运动模型。在得到响应模型后,基于多模态控制思想提出快速收敛航向保持策略,并通过径向基(RBF)神经网络[11-12]万能逼近解决了模型不确定性问题,然后通过扰动观测器、饱和函数和模糊软切换降低了系统的抖振。最终通过仿真验证本文提出航向保持策略的快速性和鲁棒性。
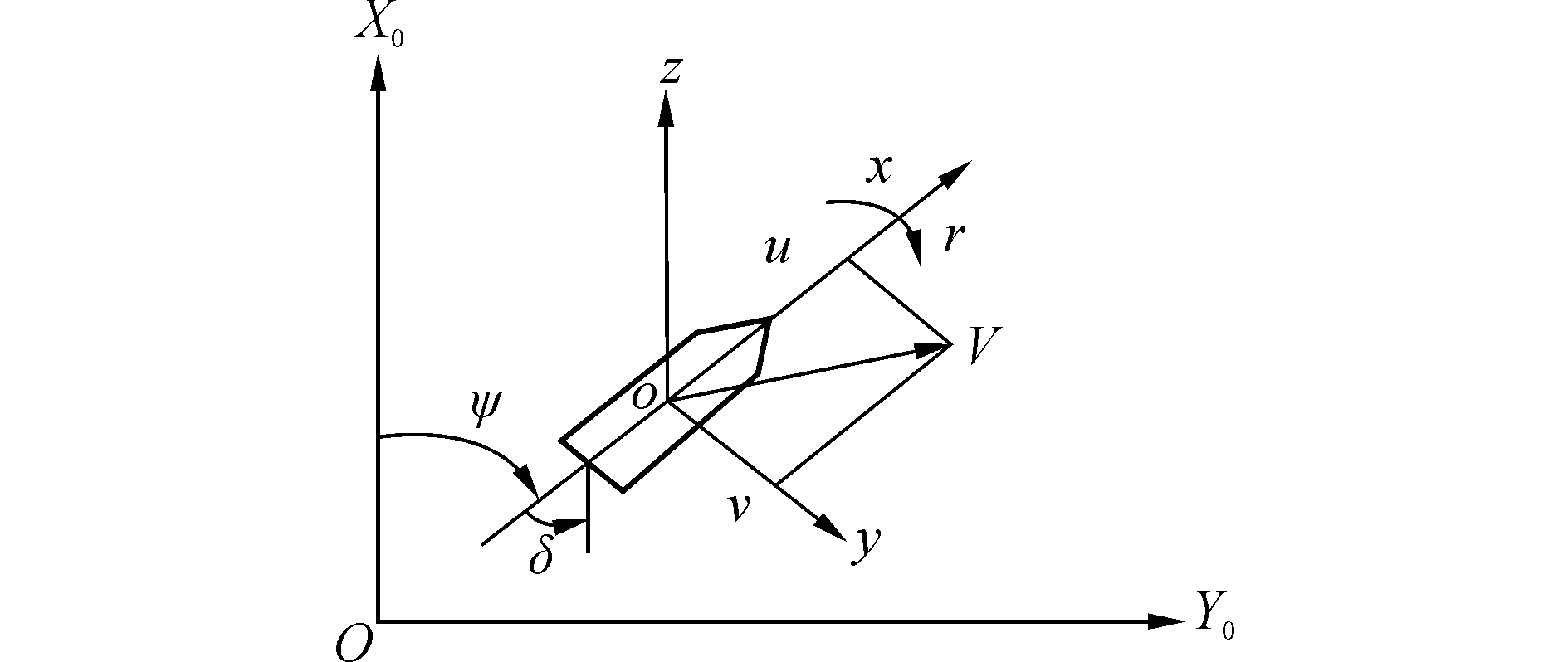
1 吊舱推进USV建模在实际航行过程中USV的运动状态是非常复杂的,一般情况包括前进速度u、横漂速度v、起伏速度w,艏摇角速度r、横摇角速度p及纵摇角速度q六个自由度的运动。根据现有经验,可以忽略起伏、纵摇及横摇运动,即认为船舶做平面运动,即w=p=q=0。USV的平面运动及其各个变量如图 1所示。
|
Download:
|
| 图 1 USV平面运动变量描述 Fig. 1 Planar motion variable description of USV | |
图 1中V表示USV运动速度,ψ表示航向角,由于吊舱不同于传统意义上的螺旋桨和舵,所以称δ为推进角。假设USV前后对称且附体坐标系的原点和重心重合,则三自由度的平面运动模型可以表示为[13]
| $ \left\{ \begin{array}{l} \left( {m + {m_x}} \right)\dot u - \left( {m + {m_y}} \right)vr = {X_{\rm{H}}} + {X_{\rm{P}}}\\ \left( {m + {m_y}} \right)\dot v + \left( {m + {m_x}} \right)ur = {Y_{\rm{H}}} + {Y_{\rm{P}}}\\ \left( {{I_{zz}} + {J_{zz}}} \right)\dot r = {N_{\rm{H}}} + {N_{\rm{P}}} \end{array} \right. $ | (1) |
式中:m为USV重量,mx为x轴方向的附加质量,my为y轴方向的附加质量,Izz为ox轴的惯性矩,Jzz为z轴方向上的附加惯性矩。X、Y、N分别为作用在船体上的流体动力和力矩,下标H为作用于裸船体的流体动力,下标P为关于推进器的力。
参考文献[13],作用于裸船体流体动力为
| $ \left\{ \begin{array}{l} {X_{\rm{H}}} = {X_0} + {X_{{\rm{Hu}}}}\Delta u\\ {Y_{\rm{H}}} = {Y_{{\rm{Hv}}}}v + {Y_{{\rm{Hr}}}}r\\ {N_{\rm{H}}} = {N_{{\rm{Hv}}}}v + {N_{{\rm{Hr}}}}r \end{array} \right. $ | (2) |
式中:X0为USV在初始状态时的直航阻力,XHu、YHv、YHr、NHv和NHr是相应的水动力系数。其它参数及其推导过程请参考文献[13]。为了简化分析,我们不考虑吊舱支架、艉鳍等起到舵作用的控制面的影响。根据文献[14],推进器(螺旋桨)推力TP为
| $ {T_P} = cV{\delta _n} + d\left| {{\delta _n}} \right|{\delta _n} $ | (3) |
式中:δn为螺旋桨转速,c和d为相应常数。当推进角为δ时,各个方向的推力大小分别为
| $ \left\{ \begin{array}{l} {X_{\rm{P}}} = \left( {cV{\delta _n} + d\left| {{\delta _n}} \right|{\delta _n}} \right)\cos \delta \\ {Y_{\rm{P}}} = \left( {cV{\delta _n} + d\left| {{\delta _n}} \right|{\delta _n}} \right)\sin \delta \\ {N_{\rm{P}}} = {x_{\delta s}}\left( {cV{\delta _n} + d\left| {{\delta _n}} \right|{\delta _n}} \right)\sin \delta \end{array} \right. $ | (4) |
式中:xδs为从旋转中心到推进器支点的纵向力臂长度。假设δ为小量,所以sin δ≈δ,cos δ≈1,则式(4)可以化简为
| $ \left\{ \begin{array}{l} {X_{\rm{P}}} = cV{\delta _n} + d\left| {{\delta _n}} \right|{\delta _n}\\ {Y_{\rm{P}}} = \left( {cV{\delta _n} + d\left| {{\delta _n}} \right|{\delta _n}} \right)\delta \\ {N_{\rm{P}}} = {x_{\delta s}}\left( {cV{\delta _n} + d\left| {{\delta _n}} \right|{\delta _n}} \right)\delta \end{array} \right. $ | (5) |
因为在初始状态下,USV所受阻力等于推进器推力,所以X0+XP=0,即
| $ \left\{ \begin{array}{l} {X_{\rm{H}}} + {X_{\rm{P}}} = {X_u}\Delta u\\ {Y_{\rm{H}}} + {Y_{\rm{P}}} = {Y_{{\rm{Hv}}}}v + {Y_{{\rm{Hr}}}}r + {X_{\rm{p}}}\delta \\ {N_{\rm{H}}} + {N_{\rm{P}}} = {N_{{\rm{Hv}}}}{\rm{v}} + {N_{{\rm{Hr}}}}r + {x_{\delta s}}{X_{\rm{p}}}\delta \end{array} \right. $ | (6) |
将式(6)代入式(1),再根据文献[13]的假设得
| $ \left\{ \begin{array}{l} \left( {m + {m_x}} \right)\Delta \dot u = {X_u}\Delta u\\ \left( {m + {m_y}} \right)\dot v = \left( {m + {m_x}} \right){u_0}r = {Y_{Hv}}v + {Y_{{\rm{Hr}}}}r + {X_p}\delta \\ \left( {{I_{zz}} + {J_{zz}}} \right)\dot r = {N_{Hv}}{\rm{v}} + {N_{Hr}}r + {x_{\delta s}}{X_p}\delta \end{array} \right. $ | (7) |
根据文献[13],可以将式(7)化简为
| $ T\dot r + r + \alpha {r^3} = K\delta $ | (8) |
式(8)是经典的Norrbin模型[15-16],由此可得,吊舱推进USV仍然符合Norrbin模型结构,并可以将此推论推广到一般矢量推进船舶。
2 航向保持控制策略 2.1 控制目标选取状态变量
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = f\left( x \right) + bu + d\left( x \right)\\ y = {x_1} \end{array} \right. $ | (9) |
式中:f(x)=-x2/2-αx23/T,b=K/T。由于受航行状态的变化和未建模动态的影响,所以f(x)是不确定的。d(x)为环境干扰且‖d(x)‖ < ld,ld>0。在应用过程中,输入量u的变化范围为|u|≤35°,变化速率
在控制输入u的作用下,航向ψ能够跟踪目标航向xd。
定义航向跟踪误差e1=x1-xd且
LSM控制器:
设s=c1e1+e2,c1>0,其控制律为
| $ u = - \frac{1}{b}\left[ {f\left( x \right) + {c_1}{e_2} + \left( {{l_d} + {\eta _1}} \right){\mathop{\rm sgn}} \left( s \right) - {{\ddot x}_d}} \right] $ | (10) |
式中η1>0为LSM控制器的设计参数。
NTSM控制器:
设
| $ u = - \frac{1}{b}\left[ {f\left( x \right) + {\lambda _1}\frac{{{q_1}}}{{{p_1}}}e_2^{2 - \frac{{{p_1}}}{{{q_1}}}} + \left( {{l_d} + {\eta _2}} \right){\mathop{\rm sgn}} \left( s \right) - {{\ddot x}_d}} \right] $ | (11) |
式中η2>0为NTSM控制器的设计参数。
针对模型的不确定性,可以通过提高控制律(10)和(11)的增益η1和η2来增强系统的鲁棒性,也可以提高系统的收敛速度,但会加剧系统抖振,不利于系统的稳定性。
当s=0时,LSM可以表示为
| $ {e_2} = - {c_1}{e_1} $ | (12) |
NTSM可以表示为
| $ {e_2} = {\left( { - {\lambda _1}{e_1}} \right)^{\frac{{{q_1}}}{{{p_1}}}}} $ | (13) |
对比式(12)和(13),由于0.5 < q1/p1 < 1,当系统靠近平衡点时,NTSM的收敛速度高于LSM的收敛速度;当系统状态远离平衡点时,NTSM的收敛速度低于LSM的收敛速度。针对这一特性,结合LSM与NTSM组成FNTSM控制律,解决了NTSM的全局快速收敛的问题。FNTSM的切换函数为
| $ s = \left\{ \begin{array}{l} {c_2}{e_1} + {e_2},\;\;\;\;\;\;\;\;\;\;\;\left| {{e_1}} \right| > \varepsilon \\ {e_1} + \frac{1}{{{\lambda _2}}}e_2^{\frac{{{p_2}}}{{{q_2}}}},\;\;\;\;\;\;\;\;\left| {{e_1}} \right| \le \varepsilon \end{array} \right. $ | (14) |
式中:c2>0,λ2>0,p2和q2为正奇数且1 < p2/q2 < 2。FNTSM的切换函数由LSM和NTSM的切换函数分段连接而成,由于LSM和NTSM各自独立,可以分别设计其控制律。根据式(10)、(11),则FNTSM的控制律为
| $ u = \left\{ \begin{array}{l} - \frac{1}{b}\left[ {f\left( x \right) + {c_2}{e_2} + \left( {{l_d} + {\eta _3}} \right){\mathop{\rm sgn}} \left( s \right) - {{\ddot x}_d}} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\left| {{e_1}} \right| > \varepsilon \\ - \frac{1}{b}\left[ {f\left( x \right) + {\lambda _2}\frac{{{q_2}}}{{{p_2}}}e_2^{2 - \frac{{{p_2}}}{{{q_2}}}} + \left( {{l_d} + {\eta _4}} \right){\mathop{\rm sgn}} \left( s \right) - {{\ddot x}_d}} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\left| {{e_1}} \right| \le \varepsilon \end{array} \right. $ | (15) |
在此控制律下,系统在FNTSM上的收敛时间是有限的[18]。
2.3 扰动观测器的设计扰动d(x)由风、流和二阶浪引起,相对USV动态这些干扰频率是很低的,所以
定理1 对于系统(9)在分段滑模控制律的作用下,将在有限时间内达到滑模面,并使得滑模面上的跟踪误差在有限时间内收敛到零。
由定理1可知,满足Lyapunov稳定性的一个重要条件是:系统(9)中d(x)满足‖d(x)‖ < ld,ld是滑模控制切换增益的组成部分,它直接决定抖振现象的严重程度。当d(x)增大时,ld会增大,从而增大控制系统的抖振,影响系统的稳定性,为了减弱扰动量对控制系统的影响,本文设计了扰动观测器来解决上述问题。在扰动观测器下控制律为
| $ u = \left\{ \begin{array}{l} - \frac{1}{b}\left[ {f\left( x \right) + {c_2}{e_2} + \hat d\left( x \right) + {\eta _3}{\mathop{\rm sgn}} \left( s \right) - {{\ddot x}_d}} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\left| {{e_1}} \right| > \varepsilon \\ - \frac{1}{b}\left[ {f\left( x \right) + {\lambda _2}\frac{{{q_2}}}{{{p_2}}}e_2^{2 - \frac{{{p_2}}}{{{q_2}}}} + \hat d\left( x \right) + {\eta _4}{\mathop{\rm sgn}} \left( s \right) - {{\ddot x}_d}} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\left| {{e_1}} \right| \le \varepsilon \end{array} \right. $ | (16) |
设计的扰动观测器为
| $ \left\{ \begin{array}{l} {{\dot {\hat x}}_2} = f\left( x \right) + \hat d\left( x \right) + bu + {k_{1i}}{{\tilde x}_2}\\ \dot {\hat d}\left( x \right) = {k_{2i}}{{\tilde x}_2} \end{array} \right. $ |
式中:k1i、k2i>0为设计常数,i=1, 2。当|e1|>ε时i=1;当|e1| < ε时i=2。
1) 当|e1|>ε时,对式(14)进行求导:
| $ \dot s = {c_2}{{\dot e}_1} + {{\dot e}_2} = {c_2}{e_2} + f\left( x \right) + bu + d\left( x \right) - {{\ddot x}_d} $ |
定义第一个Lyapunov函数:
| $ {V_1} = \frac{1}{2}{s^2} + \frac{1}{{2{k_{21}}}}\tilde d{\left( x \right)^2} + \frac{1}{2}\tilde x_2^2 $ | (17) |
对式(17)求导得
| $ \begin{array}{*{20}{c}} {{{\dot V}_1} = s\dot s + \frac{1}{{{k_{21}}}}\tilde d\left( x \right)\dot {\tilde d}\left( x \right) + {{\tilde x}_2}{{\dot {\tilde x}}_2} = }\\ {s\left[ {d\left( x \right) - \hat d\left( x \right) - {\eta _3}{\mathop{\rm sgn}} \left( s \right)} \right] + }\\ {\frac{1}{{{k_{21}}}}\tilde d\left( x \right)\left( {\dot d\left( x \right) - \dot {\hat d}\left( x \right)} \right) + {{\tilde x}_2}\left( {{{\dot x}_2} - {{\dot {\hat x}}_2}} \right) = }\\ {s\left[ {\tilde d\left( x \right) - {\eta _3}{\mathop{\rm sgn}} \left( s \right)} \right] - {k_{11}}\tilde x_2^2 \le }\\ { - \left( {{\eta _3} - \tilde d\left( x \right)} \right) - {k_{11}}\tilde x_2^2} \end{array} $ |
取
所以在Lyapunov意义下是渐进稳定的。
2) 当
| $ \begin{array}{*{20}{c}} {\dot s = s\left( {{e_2} + \frac{1}{{{\lambda _2}}}\frac{{{p_2}}}{{{q_2}}}e_2^{\frac{{{p_2}}}{{{q_2}}} - 1}{{\dot e}_2}} \right) = }\\ {{e_2} + \frac{1}{{{\lambda _2}}}\frac{{{p_2}}}{{{q_2}}}e_2^{\frac{{{p_2}}}{{{q_2}}} - 1}\left( {f\left( x \right) + bu + d\left( x \right) - {{\ddot x}_d}} \right)} \end{array} $ |
设
| $ \dot s = {e_2} + \phi \left( {{e_2}} \right)\left( {f\left( x \right) + bu + d\left( x \right) - {{\ddot x}_d}} \right) $ |
定义第二个Lyapunov函数:
| $ {V_2} = \frac{1}{2}{s^2} + \frac{1}{{2{k_{22}}}}\tilde d{\left( x \right)^2} + \frac{1}{2}\tilde x_2^2 $ | (18) |
对式(18)求导得
| $ \begin{array}{*{20}{c}} {{{\dot V}_2} = s\dot s + \frac{1}{{{k_{22}}}}\tilde d\left( x \right)\dot {\tilde d}\left( x \right) + {{\tilde x}_2}{{\dot {\tilde x}}_2} = }\\ {s\phi \left( {{e_2}} \right)\left[ {\tilde d\left( x \right) - {\eta _4}{\mathop{\rm sgn}} \left( s \right)} \right] - {k_{12}}\tilde x_2^2 \le }\\ { - \phi \left( {{e_2}} \right)\left( {{\eta _4} - \tilde d\left( x \right)} \right)\left| s \right| - {k_{12}}\tilde x_2^2} \end{array} $ |
取
所以在Lyapunov意义下是渐进稳定的。另外对比两次控制输入可知,采用扰动观测器后扰动项由d(x)变成了
因为f(x)未知,上述控制律便不适用。为了解决这个问题,本文采用RBF[19]逼近定理使
当|e1|>ε时,
| $ f\left( x \right) = {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right) + {\omega _1},\hat f\left( x \right) = {{\mathit{\boldsymbol{\hat W}}}^{\rm{T}}}\mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right)。$ |
当|e1|≤ε时,
| $ f\left( x \right) = {\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{x}} \right) + {\omega _2},\hat f\left( x \right) = {{\mathit{\boldsymbol{\hat \varphi }}}^{\rm{T}}}\mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{x}} \right)。$ |
ω1和ω2分别为理想神经网络逼近f(x)的误差,
| $ \tilde f\left( x \right) = f\left( x \right) - \hat f\left( x \right),\mathit{\boldsymbol{\tilde W}} = \mathit{\boldsymbol{W}} - \mathit{\boldsymbol{\hat W}},\mathit{\boldsymbol{\tilde \varphi }} = \mathit{\boldsymbol{\varphi }} - \mathit{\boldsymbol{\hat \varphi }}。$ |
分别取自适应率为
则控制律为
| $ u = \left\{ \begin{array}{l} - \frac{1}{b}\left[ {\hat f\left( x \right) + {c_2}{e_2} + \hat d\left( x \right) + {\eta _3}{\mathop{\rm sgn}} \left( s \right) - {{\ddot x}_d}} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\left| {{e_1}} \right| > \varepsilon \\ - \frac{1}{b}\left[ {\hat f\left( x \right) + {\lambda _2}\frac{{{q_2}}}{{{p_2}}}e_2^{2 - \frac{{{p_2}}}{{{q_2}}}} + \hat d\left( x \right) + {\eta _4}{\mathop{\rm sgn}} \left( s \right) - {{\ddot x}_d}} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\left| {{e_1}} \right| \le \varepsilon \end{array} \right. $ | (19) |
当|e1|>ε时,
| $ \begin{array}{*{20}{c}} {\dot s = {c_2}{{\dot e}_1} + {{\dot e}_2} = }\\ {{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right) + d\left( x \right) - \hat d\left( x \right) - {\eta _3}{\mathop{\rm sgn}} \left( s \right) + {\omega _1}} \end{array} $ |
定义第三个Lyapunov函数:
| $ {V_3} = \frac{1}{2}\left( {{s^2} + \frac{1}{{{\gamma _1}}}{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{\tilde W + }}\frac{1}{{{k_{21}}}}\tilde d{{\left( x \right)}^2} + \tilde x_2^2} \right) $ | (20) |
对式(20)进行求导得
| $ \begin{array}{*{20}{c}} {{{\dot V}_3} = s\dot s - \frac{1}{{{\gamma _1}}}{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{\dot {\hat W} + }}\frac{1}{{{k_{21}}}}\tilde d\left( x \right)\dot {\tilde d}\left( x \right) + {{\tilde x}_2}{{\dot {\tilde x}}_2} = }\\ {s\left( {{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right) + d\left( x \right) - \hat d\left( x \right) - {\eta _3}{\mathop{\rm sgn}} \left( s \right) + {\omega _1}} \right) - }\\ {\frac{1}{{{\gamma _1}}}{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{\dot {\hat W} + }}\frac{1}{{{k_{21}}}}\tilde d\left( x \right)\dot {\tilde d}\left( x \right) + {{\tilde x}_2}{{\dot {\tilde x}}_2} \le }\\ {s\left[ {\tilde d\left( x \right) - {\eta _3}{\mathop{\rm sgn}} \left( s \right) + {\omega _1}} \right] - \tilde d\left( x \right){{\tilde x}_2} + }\\ {{{\tilde x}_2}\left( {d\left( x \right) - \hat d\left( x \right) - {k_{11}}{{\tilde x}_2}} \right) \le }\\ { - \left( {{\eta _3} - \tilde d\left( x \right) - {\omega _1}} \right)\left| s \right| - {k_{11}}\tilde x_2^2} \end{array} $ |
取
所以在Lyapunov意义下是渐进稳定的。
当|e1|≤ε时,
| $ \begin{array}{*{20}{c}} {\dot s = {e_2} + \phi \left( {{e_2}} \right)\left( {f\left( x \right) + bu + d\left( x \right) - {{\ddot x}_d}} \right) = }\\ {\phi \left( {{e_2}} \right)\left( {{{\mathit{\boldsymbol{\tilde \varphi }}}^{\rm{T}}}\mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{x}} \right) - {\eta _4}{\mathop{\rm sgn}} \left( s \right) + d\left( x \right) - \hat d\left( x \right) + {\omega _2}} \right)} \end{array} $ |
定义第四个Lyapunov函数:
| $ {V_4} = \frac{1}{2}\left( {{s^2} + \frac{1}{{{\gamma _2}}}{{\mathit{\boldsymbol{\tilde \varphi }}}^{\rm{T}}}\mathit{\boldsymbol{\tilde \varphi + }}\frac{1}{{{k_{22}}}}\tilde d{{\left( x \right)}^2} + \tilde x_2^2} \right) $ | (21) |
对公式(21)进行求导得
| $ \begin{array}{*{20}{c}} {{{\dot V}_4} = s\dot s - \frac{1}{{{\gamma _2}}}{{\mathit{\boldsymbol{\tilde \varphi }}}^{\rm{T}}}\mathit{\boldsymbol{\dot {\hat \varphi} }} + \frac{1}{{{k_{22}}}}\tilde d\left( x \right)\dot {\tilde d}\left( x \right) + {{\tilde x}_2}{{\dot {\tilde x}}_2} = }\\ {s\phi \left( {{e_2}} \right){{\mathit{\boldsymbol{\tilde \varphi }}}^{\rm{T}}}\mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{x}} \right) - \frac{1}{{{\gamma _2}}}{{\mathit{\boldsymbol{\tilde \varphi }}}^{\rm{T}}}\mathit{\boldsymbol{\dot {\hat \varphi} }} + s\phi \left( {{e_2}} \right)\left( { - {\eta _4}{\mathop{\rm sgn}} \left( s \right) + } \right.}\\ {\left. {d\left( x \right) - \hat d\left( x \right) + {\omega _2}} \right) + \frac{1}{{{k_{22}}}}\tilde d\left( x \right)\dot {\tilde d}\left( x \right) + {{\tilde x}_2}{{\dot {\tilde x}}_2} \le }\\ {\phi \left( {{e_2}} \right)\left( {s{\omega _2} + s\tilde d\left( x \right) - {\eta _4}\left| s \right|} \right) - \tilde d\left( x \right){{\tilde x}_2} + }\\ {{{\tilde x}_2}\left( {d\left( x \right) - \hat d\left( x \right) - {k_{12}}{{\tilde x}_2}} \right) \le }\\ { - \phi \left( {{e_2}} \right)\left| s \right|\left( {{\eta _4} - \tilde d\left( x \right) - {\omega _2}} \right) - {k_{12}}\tilde x_2^2} \end{array} $ |
取
式中:σ>0,ϕ(e2)>0,k12>0,则
| $ {{\dot V}_4} \le - \phi \left( {{e_2}} \right)\sigma \left| s \right| - {k_{12}}\tilde x_2^2 \le 0 $ |
所以在Lyapunov意义下是渐进稳定的。
定义函数
| $ \Xi \left( t \right) = \phi \left( {{e_2}} \right)\sigma \left| s \right| + {k_{12}}\tilde x_2^2 = - {{\dot V}_5} $ | (22) |
将式(22)两边对时间求积分,可得
| $ \int_0^t {\Xi \left( \tau \right){\rm{d}}\tau } = {V_5}\left( {s\left( 0 \right),{{\tilde x}_2}\left( 0 \right)} \right) - {V_5}\left( {s\left( t \right),{{\tilde x}_2}\left( t \right)} \right) $ |
由于
| $ \int_0^t {\Xi \left( \tau \right){\rm{d}}\tau } < \infty $ |
显然,
由于开关函数的不连续性,在滑模面附近来回穿越形成抖振。抖振不仅影响控制的精度,还会激发高频未建模动态,所以必须对抖振加以限制。因为快速性主要体现在LSM阶段,而鲁棒性主要体现在NTSM的滑动模态,所以在|e1|>ε时,仍采用符号函数sgn(s),当|e1|≤ε采用饱和函数sat(s)代替符号函数。
| $ {\rm{sat}}\left( s \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;s > \Delta \\ \sigma s,\;\;\;\;\;\left| s \right| \le \Delta \\ - 1,\;\;\;\;\;s < - \Delta \end{array} \right. $ | (23) |
式中:
采用模糊加权方法来转化切换过程中系统参数变化带来的抖振,提高系统的暂态响应。其基本思想是:根据系统状态误差,运用模糊推理方法,得到切换过程中LSM控制器控制增益v,则NTSM控制器增益为1-v,并由此来加权两个模态的增益向量来设计切换控制器。
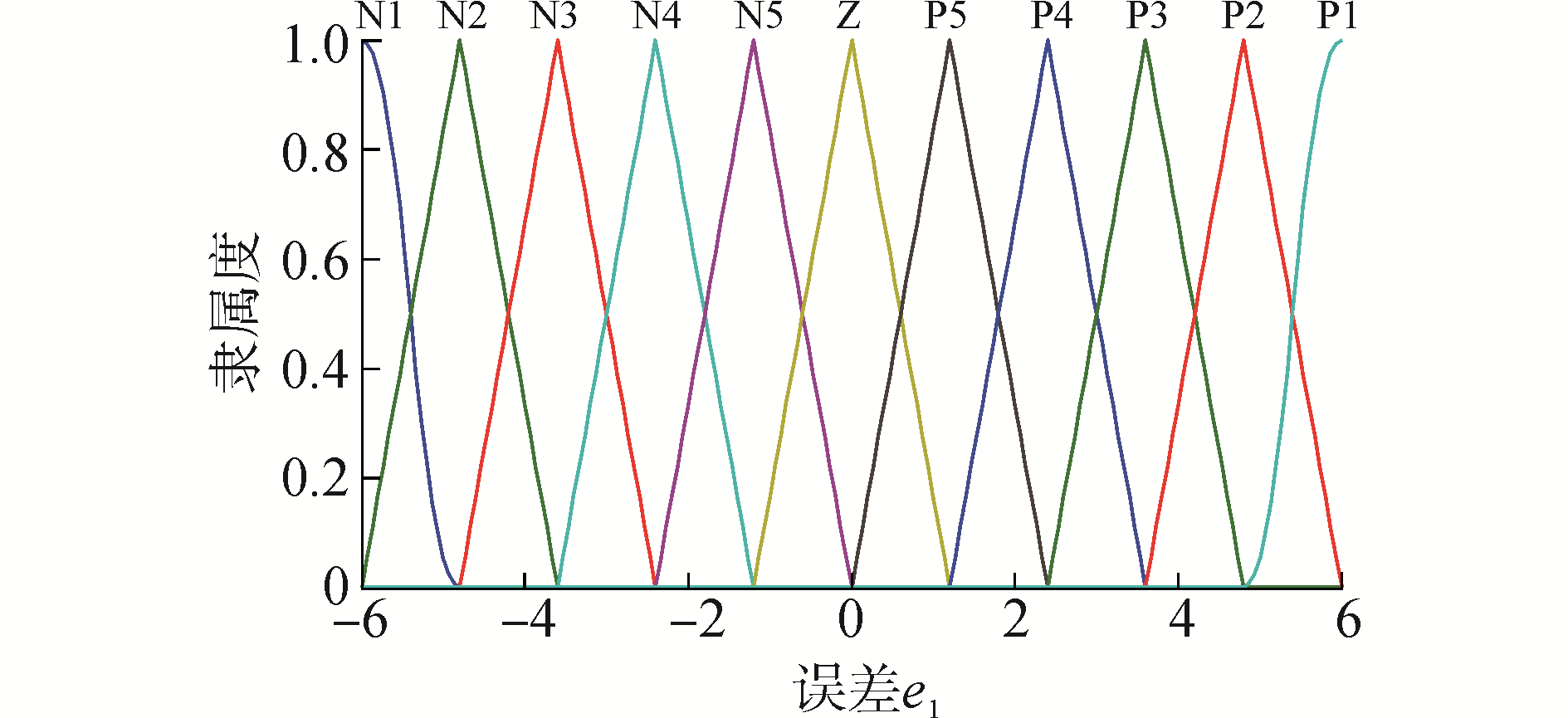
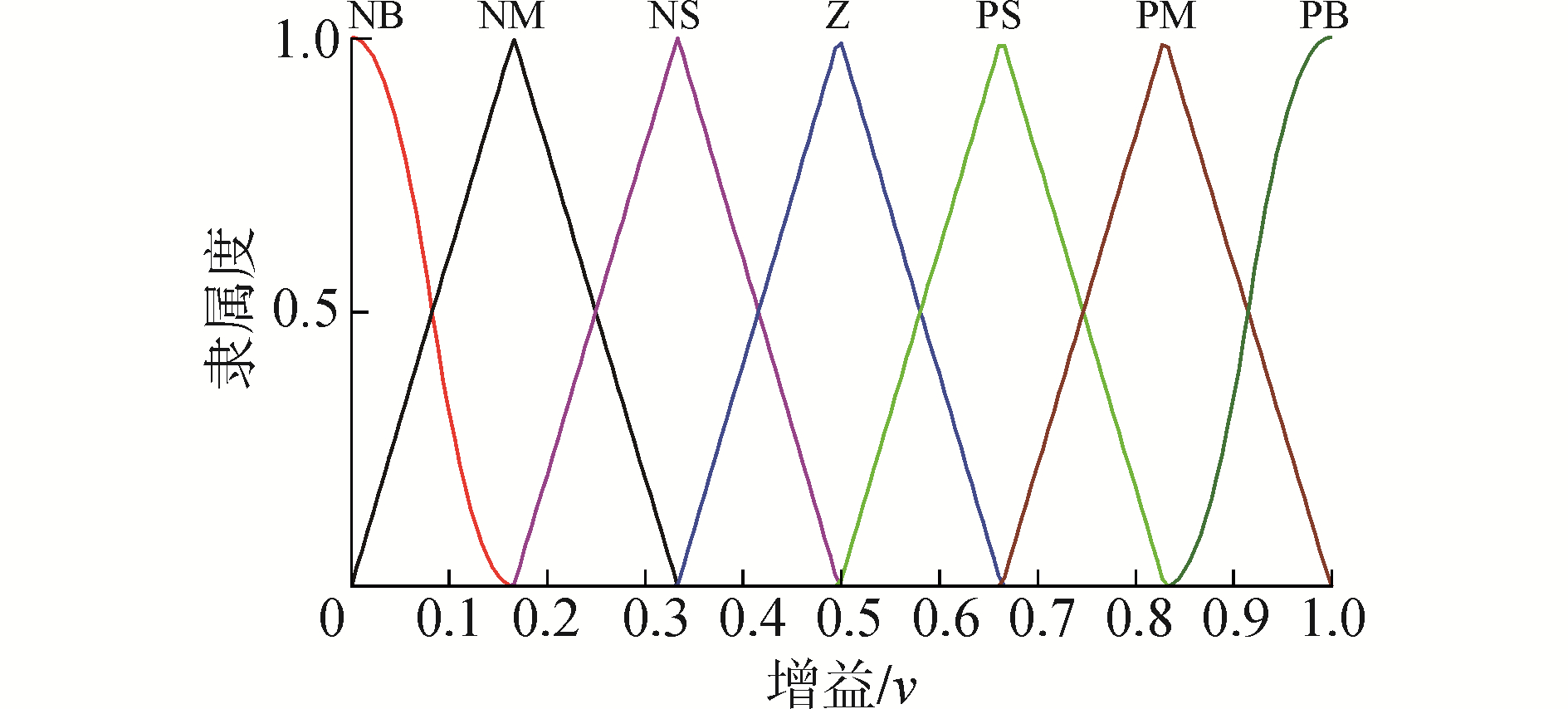
1) 模糊控制器为单输入单输出系统。输入为系统误差将e1,输出为LSM控制器控制增益v。首先将系统误差e1的论域归一化为[-6 6],输出v的论域为[0 1],其隶属函数分别如图 2和3所示。
|
Download:
|
| 图 2 误差e1的隶属度函数 Fig. 2 The membership function of e1 | |
|
Download:
|
| 图 3 输出v的隶属度函数 Fig. 3 The membership function of v | |
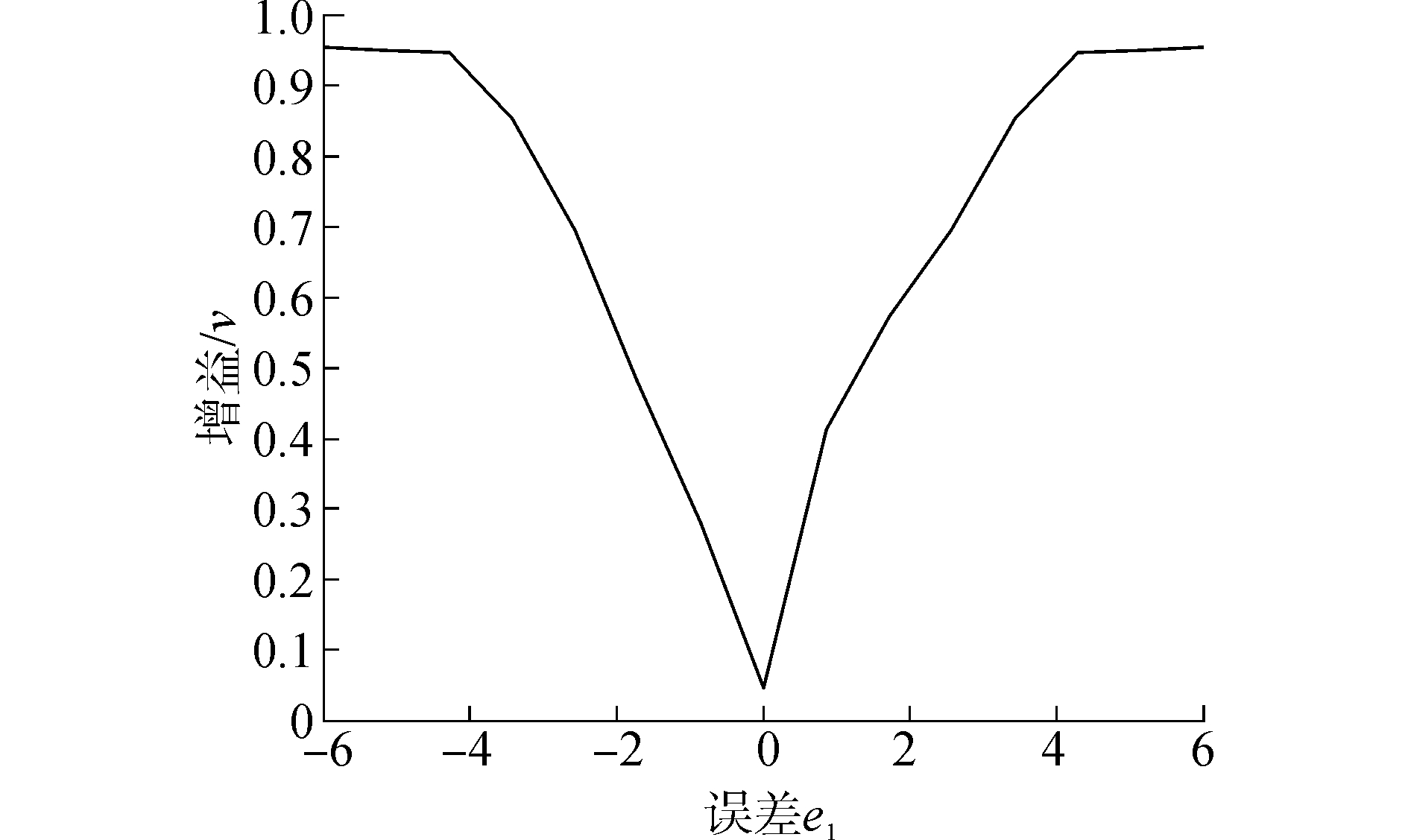
2) 控制规则为当系统误差|e1|减小时,控制增益v也减小,控制规则如图 4所示。
|
Download:
|
| 图 4 控制规则 Fig. 4 Control rules | |
3) 模糊推理采用Zadeh和Max-min法,反模糊化采用centroid面积重心法。
至此,最终的控制律为
| $ \begin{array}{*{20}{c}} {u = \left[ { - {b^{ - 1}}\left[ {\hat f\left( x \right) + {c_2}{e_2} + \hat d\left( x \right) + {\eta _3}{\mathop{\rm sgn}} \left( s \right) - } \right.} \right.}\\ {\left. {\left. {{{\ddot x}_d}} \right]} \right]v + \left[ { - {b^{ - 1}}\left[ {\hat f\left( x \right) + {\lambda _2}\frac{{{q_2}}}{{{p_2}}}e_2^{2 - \frac{{{p_2}}}{{{q_2}}}} + \hat d\left( x \right) + } \right.} \right.}\\ {\left. {\left. {{\eta _4}{\rm{sat}}\left( s \right) - {{\ddot x}_d}} \right]} \right]\left( {1 - v} \right)} \end{array} $ | (24) |
本文在不同的误差范围内,使用LSM或NTSM,分别针对不同的控制器证明了稳定性。考虑到在FNTSM下,系统为一切换系统,因此应该针对切换系统的特点,进行更为严格的稳定性证明。
切换系统稳定性分析建立在Lyapunov稳定性理论基础上,已有的研究结果主要有公共Lyapunov函数法、多Lyapunov函数法、驻留时间法等。多Lyapunov函数法的基本思想是通过为每个子系统构造相应的Lyapunov函数,并比较切换时刻的Lyapunov函数值的大小来研究切换系统的稳定性。根据多Lyapunov函数法思想,Johansson等[20]提出了分段连续Lyapunov函数法,即每个子系统可以找到一个Lyapunov函数,且该函数是递减的;在切换时刻上,参与切换的两个子系统的Lyapunov函数相等,则切换系统是渐进稳定的[21]。
首先,使用分段连续Lyapunov函数法证明系统的稳定性。
1) 在第2.4节,已经证明
2) 正如2.4节中对稳定性分析所示,
| $ {V_3} = \frac{1}{2}\left( {{s^2} + \frac{1}{{{\gamma _1}}}{{\tilde W}^T}\tilde W + \frac{1}{{{k_{21}}}}\tilde d{{\left( x \right)}^2} + \tilde x_2^2} \right) $ | (25) |
| $ {V_4} = \frac{1}{2}\left( {{s^2} + \frac{1}{{{\gamma _2}}}{{\tilde \varphi }^T}\tilde \varphi + \frac{1}{{{k_{22}}}}\tilde d{{\left( x \right)}^2} + \tilde x_2^2} \right) $ | (26) |
在相应参数选择合理的情况下,V3=V4。所以,根据分段连续Lyapunov函数法可以证明切换系统是渐进稳定性的。
其次,如果不同模态之间的切换采用硬切换,可能会引起系统状态的大幅度跳变,导致系统的不稳定。为解决这一问题,可以采用软切换策略。例如文献[22]设计惯性环节切换控制律完成高低转速控制器间的切换,虽然取得了良好控制效果,但引入了非线性因素。文献[23]针对民航客机不同模态间的切换,引入惯性延迟淡化器抑制切换瞬态,这种切换方法结构简单,适用于控制律变化不大的模态切换过程。本文在2.5节使用模糊来实现软切换,在一定程度上也保证了切换系统的稳定性。
3 航向保持模拟仿真为了验证本文所设计的快速终端滑模航向保持策略正确性,对大连海事大学“蓝信”号吊舱推进无人艇进行航向保持仿真研究。当USV以9 kn的速度行驶时,方程(9)中船舶运动模型主要参数为K=0.707,T=0.332,α=0.001。选取控制律(24)的控参数c2=0.45,η3=12,λ2=1.3,p2=11,q2=9,Δ=1,η4=3, k11=2,k21=10,k12=1,k22=15,γ1=3.5,γ2=4.5。为了对照比较,将FNTSM与典型的自适应控制算法进行对比,本文选用反步自适应控制策略,控制律如式(27)所示,具体推导过程参考文献[24]。
| $ u = \hat \vartheta \bar \omega $ | (27) |
其中,
| $ \begin{array}{*{20}{c}} {\dot {\hat \vartheta} = - \rho {\mathop{\rm sgn}} \left( b \right)\bar \omega {z_3},}\\ {\bar \omega = \left[ { - {z_2} - \left( {{l_3} + \frac{1}{{l_4^2}}} \right){z_3} - {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}{{\left[ {\begin{array}{*{20}{c}} {{x_2}}&{x_2^3} \end{array}} \right]}^{\rm{T}}} + \dot \eta } \right],}\\ {\mathit{\boldsymbol{\dot {\hat \theta} }} = \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( {{{\left[ {\begin{array}{*{20}{c}} {{x_2}}&{x_2^3} \end{array}} \right]}^{\rm{T}}}{z_3} - \kappa \left( {\hat \theta - {\theta _0}} \right)} \right),}\\ {{z_1} = \int {\left( {{x_1} - {x_d}} \right){\rm{d}}t} ,{z_2} = {x_1} - {x_d},{z_3} = {x_2} - \eta ,}\\ {\eta = - {l_1}{z_1} - {l_2}{z_2} + {{\dot x}_d}。} \end{array} $ |
参数l1=0.01,l2=0.6,l3=1,l4=1,Γ=
当外界扰动较弱取2.5sin(0.6t)时,FNTSM和反步自适应的仿真情况如图 5所示。

|
Download:
|
| 图 5 弱扰动下比较曲线 Fig. 5 The comparison curves under weak disturbance | |
从图 5可以看出,当扰动为弱扰时,与反步自适应航向保持控制策略相比,本文提出的FNTSM具有较快的收敛速度和较好的航向保持能力,航向无超调且静态误差为零,这说明扰动观测器起到了良好的效果;而反步自适应策略控制下的航向有较大的波动,其绝对误差的最大值为3。从推进角的变化曲线可以看出,两个推进角变化都在合理的范围内。虽然FNTSM的推进角存在一定的抖振现象,但滑模控制的本质就是利用抖振来增强系统的鲁棒性,这是难以避免的。
为了进一步验证FNTSM的鲁棒性,在所有控制参数不变的情况下,当外界扰动较强取5×2.5sin(0.6t)时,仿真情况如图 6所示。

|
Download:
|
| 图 6 强扰动下航向曲线 Fig. 6 The comparison curves under strong disturbance | |
从图 6可以看出,当扰动为强扰时,FNTSM依然可以保持航向的稳定,无超调且其稳态误差为零。而反步自适应策略控制下的航向误差进一步变大,绝对误差的最大值为6。进一步观察推进角的比较曲线可以看出,FNTSM和反步自适应的推进角的变化在合理的范围内。综上所述:无论在弱扰动还是强扰动的作用下,FNTSM依然保持了良好的控制效果,且控制效果明显优于反步自适应航向保持策略,进一步体现了本文提出控制策略的快速性和鲁棒性。
4 结论1) 在相同弱扰动下,FNTSM收敛速度快于反步自适应航向保持策略。
2) 在相同强扰动下,控制参数不变时,FNTSM的鲁棒性优于反步自适应航向保持策略。
3) 吊舱推进USV符合Norrbin结构可以推广到一般矢量推进船舶。
在下一步的研究中理论联系实际,将本文提出的控制策略应用于实船以验证FNTSM的有效性。
| [1] |
YAN R J, PANG S, SUN H B, et al. Development and missions of unmanned surface veh, 2010, 9(4):451-457.
(  0) 0)
|
| [2] |
MU D D, WANG G F, FANICLE. Design of adaptive neural tracking controller for pod propulsion unmanned vessel subject to unknown dynamics[J]. Journal of electrical engineering & technology, 2017, 12: 1921-1933. (  0) 0)
|
| [3] |
MU D, WANG G, FAN Y, et al. Adaptive LOS Path Following for a Podded Propulsion Unmanned surface vehicle with uncertainty of model and actuator saturation[J]. Applied sciences, 2017, 7(12): 1232-1252. DOI:10.3390/app7121232 (  0) 0)
|
| [4] |
FANG M C, LUO J H. On the track keeping and roll reduction of the ship in random waves using different sliding mode controllers[J]. Ocean engineering, 2007, 34(3/4): 479-488. (  0) 0)
|
| [5] |
高键, 陈高阳. 船舶航向模糊滑模控制及仿真[J]. 江苏科技大学学报(自然科学版), 2010, 24(4): 372-376. GAO Jian, CHEN Gaoyang. Fuzzy sliding mode control and simulation for ship's course steering[J]. Journal of Jiangsu university of science and technology (natural science edition), 2010, 24(4): 372-376. (  0) 0)
|
| [6] |
赵越, 王仁强, 缪克银. 基于新型滑膜控制的船舶航向自动舵设计[J]. 船舶工程, 2015, 37(9): 58-62. ZhAO Yue, WANG Renqiang, NIAO keyin. Design of ship's autopilot based on new type of synovial control[J]. Ship engineering, 2015, 37(9): 58-62. (  0) 0)
|
| [7] |
LI Ronghui, LI Tieshan, BU Renxiang, et al. Active disturbance rejection with sliding mode control based course and path following for underactuated ships[J]. Mathematical problems in engineering, 2013, 2013: 743716. (  0) 0)
|
| [8] |
YUAN Lei, WU Hansong. Terminal sliding mode fuzzy control based on multiple sliding surfaces for nonlinear ship autopilot systems[J]. Journal of marine science and application, 2010, 9(4): 425-430. DOI:10.1007/s11804-010-1029-y (  0) 0)
|
| [9] |
杜佳璐, 郭晨, 杨承恩. 船舶航向非线性系统的自适应跟踪控制器设计[J]. 应用科学学报, 2006, 24(1): 83-88. DU Jialu, GUO Chen, YANG Cheng'en. Adaptive nonlinear design of autopilot for ship course tracking[J]. Journal of applied sciences, 2006, 24(1): 83-88. (  0) 0)
|
| [10] |
田佰军, 刘正江, 郑云峰. 考虑暂态/稳态性能的船舶航向保持控制[J]. 哈尔滨工程大学学报, 2016, 37(5): 640-645. TIAN Baijun, LIU Zhengjiang, ZHENG Yunfeng. Robust course-keeping control for ships with the prescribed transient/steady performance[J]. Journal of Harbin Engineering University, 2016, 37(5): 640-645. (  0) 0)
|
| [11] |
ZHANG S, REN G. Design of robust fuzzy controller for ship course-tracking based on RBF network and backstepping approach[J]. Journal of marine science and application, 2006, 5(3): 5-10. DOI:10.1007/s11804-006-0017-8 (  0) 0)
|
| [12] |
ZHANG G, ZHANG X, ZHENG Y. Adaptive neural path-following control for underactuated ships in fields of marine practice[J]. Ocean engineering, 2015, 104: 558-567. DOI:10.1016/j.oceaneng.2015.05.013 (  0) 0)
|
| [13] |
贾欣乐, 杨盐生. 船舶运动数学模型——机理建模与辩识建模[M]. 大连: 大连海事大学出版社, 1999. JIA Xinle, YANG Yansheng. The mathematical model of ship motion mechanism modeling and identification modeling[M]. Dalian: Dalian Maritime University Press, 1999. (  0) 0)
|
| [14] |
SONNENBURG C R. Modeling, identification, and control of an unmanned surface vehicle[D]. Virginia:Virginia Polytechnic Institute and State University, 2013.
(  0) 0)
|
| [15] |
YUAN L, WU H. Simulation and design of fuzzy sliding-mode controller for ship heading-tracking[J]. Journal of marine science and application, 2011, 10(1): 76-81. DOI:10.1007/s11804-011-1044-7 (  0) 0)
|
| [16] |
YUAN L, WU H. Terminal sliding mode fuzzy control based on multiple sliding surfaces for nonlinear ship autopilot systems[J]. Journal of marine science and application, 2010, 9(4): 425-430. DOI:10.1007/s11804-010-1029-y (  0) 0)
|
| [17] |
YU Xinghuo, MAN Zhihong. Fast terminal sliding-mode control design for nonlinear dynamical systems[J]. IEEE transactions on circuits and systems Ⅰ:fundamental theory and applications, 2002, 49(2): 261-264. DOI:10.1109/81.983876 (  0) 0)
|
| [18] |
赵霞, 姜玉宪, 吴云洁, 等. 基于多模态滑模的快速非奇异终端滑模控制[J]. 北京航空航天大学学报, 2011, 37(1): 110-113. ZHAO Xia, JIANG Yuxian, WU Yunjie, et al. Fast nonsingular terminal sliding mode control based on multi-slide-mode[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(1): 110-113. (  0) 0)
|
| [19] |
GE S S, WANG C. Adaptive NN control of uncertain nonlinear pure-feedback systems[J]. Automatica, 2002, 38(4): 671-682. DOI:10.1016/S0005-1098(01)00254-0 (  0) 0)
|
| [20] |
JOHANSSON M, RANTZER A. Computation of piecewise quadratic lyapunov functions for hybrid systems[J]. IEEE transactions on automatic control, 1998, 43(4): 555-559. DOI:10.1109/9.664157 (  0) 0)
|
| [21] |
方志明. 切换系统稳定性分析与优化控制若干问题研究[D]. 南京: 南京理工大学, 2012. FANG Zhiming, Study on several problems of stability and optimal control of switched systems[D]. Nanjing:Nanjing University of Science and Technology, 2012. (  0) 0)
|
| [22] |
王佳雯. 变速变桨距风电系统建模与智能控制技术研究[D]. 南京: 南京航空航天大学, 2012. WANG Jiawen. Modeling and intelligent control technology research on variable-speed variable-pitch wind power system[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2012. (  0) 0)
|
| [23] |
李欣. 大型客机自动飞行控制律研究[D]. 南京: 南京航空航天大学, 2013. LI Xin, Research on automatic flight control law for the jumbo jet[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2013. (  0) 0)
|
| [24] |
林永屹, 杜佳璐, 牛杰. 基于Backstepping的船舶航向自适应鲁棒非线性控制器设计[J]. 船舶工程, 2007, 29(1): 24-27. LIN Yongyi, DU Jialu, NIU Jie. Design of backstepping based adaptive robust nonlinear controller of ship course[J]. Ship engineering, 2007, 29(1): 24-27. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


