2. 武汉理工大学 能源与动力工程学院, 湖北 武汉 430063
2. School of Energy and Power Engineering, Wuhan University of Technology, Wuhan 430063, China
船舶自主航行控制需要对船舶操纵运动建立一个参数准确的模型,而对模型参数进行辨识是控制理论中的一种有效建模方法。卡尔曼滤波(Kalman filter, KF)作为一种可以同时对噪声和状态进行预测估计的滤波方法[1],较早地被应用到船舶运动模型的参数辨识中。该算法本身基于线性系统假设,在对非线性系统进行估计时需要使用扩展卡尔曼滤波算法(extended Kalman filter, EKF)。早在1975年,就有国外学者将EKF应用于船舶水动力模型辨识,在整体型模型[2]和分离型模型[3-4]方面都有研究。但由于EKF的辨识精度对过程误差和量测误差的初始估计比较敏感[5],且算法对强非线性系统的辨识不稳定,容易发散。对此,有很多学者在此基础上进行改进,或通过对数据源进行滤波以提高EKF辨识准确性[6],或通过将EKF并行处理以达到高效辨识的目的[7],但这些算法没有从EKF算法结构上进行改进,在提高辨识效果的同时降低了算法的实时性。
为实现实时自校正滤波辨识,有学者将多新息辨识理论[8]与扩展卡尔曼滤波相结合形成多新息扩展卡尔曼滤波算法(multi-innovation extended Kalman filter, MI-EKF),该方法通过对旧信息的重复使用来改进原EKF辨识效果。目前对MI-EKF的研究主要集中在数据预测估计[9]和图像去噪[10]等方面,在模型参数辨识方面尚处于理论阶段。文献[11]针对MI-EKF中新息长度的选择进行了实验研究,表明MI-EKF算法在提高了预测估计精度的同时,也存在多个新息下辨识不稳定,参数估计不精确的问题[12]。
针对上述问题,本文尝试使用遗忘因子对MI-EKF加以改进,以实现多个新息下MI-EKF的精确辨识,并使用改进后的MI-EKF对模型中的参数进行辨识,并通过辨识所得模型进行操纵性预报,与经典EKF算法进行对比,并对改进后多新息卡尔曼滤波辨识的有效性进行验证。
1 用于参数辨识的MI-EKF方法首先,考虑如下的非线性模型的MI-EKF辨识模型:
| $ \mathit{\boldsymbol{X}}\left( {k + 1} \right) = \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{X}}\left( k \right),\mathit{\boldsymbol{u}}\left( {k + 1} \right)} \right) + \mathit{\boldsymbol{w}}\left( k \right) $ | (1) |
| $ \mathit{\boldsymbol{Z}}\left( {k + 1} \right) = \mathit{\boldsymbol{g}}\left( {X\left( {k + 1} \right)} \right) + \mathit{\boldsymbol{v}}\left( {k + 1} \right) $ | (2) |
式中:X为系统状态矩阵,包含待辨识参数,随机变量w(k)为过程噪声,随机变量v(k)为测量噪声,一般情况下都为零均值白噪声序列。
式(1)是系统自身的状态更新方程,式(2)是系统的测量方程。标准EKF使用系统状态量非线性函数f的Jacobian矩阵用来计算预测和估计时的协方差矩阵,流程如下[11]
| $ \mathit{\boldsymbol{\hat X}}\left( {\bar k} \right) = \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{\hat X}}\left( {k - 1} \right),\mathit{\boldsymbol{u}}\left( k \right)} \right) $ | (3) |
| $ \mathit{\boldsymbol{P}}\left( {\bar k} \right) = \mathit{\boldsymbol{AP}}\left( {k - 1} \right){\mathit{\boldsymbol{A}}^{\rm{T}}} + \mathit{\boldsymbol{Q}}\left( {k - 1} \right) $ | (4) |
| $ \mathit{\boldsymbol{K}}\left( k \right) = \mathit{\boldsymbol{P}}\left( {\bar k} \right){\mathit{\boldsymbol{H}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{HP}}\left( {\bar k} \right){\mathit{\boldsymbol{H}}^{\rm{T}}} + \mathit{\boldsymbol{R}}\left( k \right)} \right)^{ - 1}} $ | (5) |
| $ \mathit{\boldsymbol{\hat X}}\left( k \right) = \mathit{\boldsymbol{\hat X}}\left( {\bar k} \right) + \mathit{\boldsymbol{K}}\left( k \right)\left( {\mathit{\boldsymbol{Z}}\left( k \right) - \mathit{\boldsymbol{H\hat X}}\left( {\bar k} \right)} \right) $ | (6) |
| $ \mathit{\boldsymbol{P}}\left( k \right) = \left( {1 - \mathit{\boldsymbol{K}}\left( k \right)\mathit{\boldsymbol{H}}} \right)\mathit{\boldsymbol{P}}\left( {\bar k} \right) $ | (7) |
式中:
定义
为提高辨识的精度和收敛的速度,将式(6)中的单新息e(t)扩展如下
| $ \mathit{\boldsymbol{E}}\left( {p,k} \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Z}}\left( k \right) - \mathit{\boldsymbol{H\hat X}}\left( {\bar k} \right)}\\ {\mathit{\boldsymbol{Z}}\left( {k - 1} \right) - \mathit{\boldsymbol{H\hat X}}\left( {\bar k - 1} \right)}\\ \vdots \\ {\mathit{\boldsymbol{Z}}\left( {k - p + 1} \right) - \mathit{\boldsymbol{H\hat X}}\left( {\bar k - p + 1} \right)} \end{array}} \right] $ | (8) |
式中p为扩展的新息长度。鉴于矩阵维数的兼容性,对状态增益矩阵进行扩展:
| $ \mathit{\boldsymbol{K}}\left( {p,k} \right) = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}\left( k \right)}&{\mathit{\boldsymbol{K}}\left( {k - 1} \right)}& \cdots &{\mathit{\boldsymbol{K}}\left( {k - p + 1} \right)} \end{array}} \right]^{\rm{T}}} $ | (9) |
则状态矩阵更新方程变为
| $ \mathit{\boldsymbol{\hat X}}\left( k \right) = \mathit{\boldsymbol{\hat X}}\left( {\bar k} \right) + \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{E}}\left( {p,k} \right) $ | (10) |
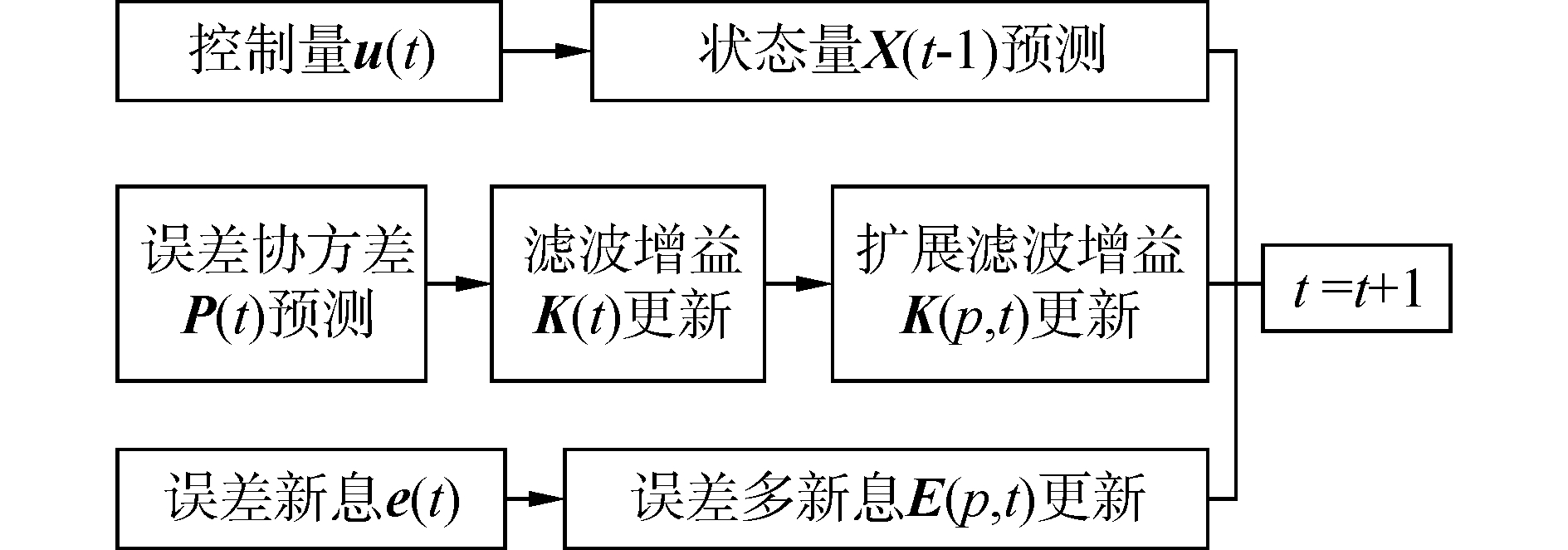
MI-EKF算法步骤如图 1所示,总结为:
|
Download:
|
| 图 1 MI-EKF算法步骤 Fig. 1 MI-EKF algorithm steps | |
1) 状态预测如式(3)所示;
2) 误差协方差预测如式(4)所示;
3) 滤波增益更新如式(5)所示;
4) 扩展滤波增益矩阵更新:
| $ \mathit{\boldsymbol{K}}\left( {p,k} \right) = \left[ {\begin{array}{*{20}{c}} {\bf{0}}&{\bf{0}}\\ \mathit{\boldsymbol{I}}&{\bf{0}} \end{array}} \right]\mathit{\boldsymbol{K}}\left( {p,k - 1} \right) + \left[ {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right]\mathit{\boldsymbol{K}}\left( k \right) $ | (11) |
5) 误差状态修正:
| $ \mathit{\boldsymbol{\hat X}}\left( k \right) = \mathit{\boldsymbol{\hat X}}\left( {\bar k} \right) + \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{E}}\left( {p,k} \right) $ | (12) |
6) 误差协方差修正,如式(7)所示。
可以看出,MI-EKF对于EKF的改进之处,在于误差状态修正中对于滤波增益矩阵历史数据的重复使用,而这种多新息扩展是基于滑动数据窗口的形式对扩展后的矩阵进行更新的,在算法未达到所设定的新息长度p之前,可使用传统EKF方法得到扩展矩阵K(p, k)中的初始值。
2 MI-EKF辨识方法的改进 2.1 基于遗忘因子的改进一般地,递推辨识存在辨识精度低或收敛速度慢的问题。理论上,得益于有效信息的重复使用,MI-EKF的参数辨识精度应随新息长度p的增大而提高。但算法只在时间维度上扩展了每次递推所使用的信息,并没有依据信息的新旧程度对数据进行区分,故同时存在陈旧数据对参数估计的累积干扰,不利于辨识收敛速度的提高,以至降低辨识精度。针对MI-EKF中新息数量p对算法精度的影响问题,文献[12]通过仿真实验验证了当p=2时的MI-EKF算法效果最佳,而当新息数量继续增加时,旧信息累积干扰增加,算法估计误差开始增大。
借鉴文献[13]对于卡尔曼衰减记忆滤波的分析,为防止MI-EKF中陈旧量测值的修正作用相对上升,引入遗忘因子[14]进行辨识改进,通过递推过程减弱历史数据的修正效果,减小产生的累积干扰,使算法具有对新量测输入变化的快速响应能力。
式(9)中增益矩阵K维度为p,考虑通过对增益矩阵K左乘遗忘因子矩阵α来减小旧信息的权重,增加新量测信息的权重,从而改进递推算法。
将MI-EKF中的增益矩阵变为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}\left( {p,k} \right) = \mathit{\boldsymbol{\alpha }} \cdot }\\ {{{\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}\left( k \right)}&{\mathit{\boldsymbol{K}}\left( {k - 1} \right)}& \cdots &{\mathit{\boldsymbol{K}}\left( {k - p + 1} \right)} \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (13) |
并定义矩阵α=diag(λ1 λ2 … λp),则有状态更新方程:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}\left( k \right) = \mathit{\boldsymbol{\hat X}}\left( {\bar k} \right) + \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{E}}\left( {p,k} \right) = }\\ {\mathit{\boldsymbol{\hat X}}\left( {\bar k} \right) + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\lambda }}_1}}&{}&{}&{}\\ {}&{{\mathit{\boldsymbol{\lambda }}_2}}&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{{\mathit{\boldsymbol{\lambda }}_p}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}\left( k \right)}\\ {\mathit{\boldsymbol{K}}\left( {k - 1} \right)}\\ \vdots \\ {\mathit{\boldsymbol{K}}\left( {k - p + 1} \right)} \end{array}} \right]\mathit{\boldsymbol{E}}\left( {p,k} \right) = }\\ {\mathit{\boldsymbol{\hat X}}\left( {\bar k} \right) + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\lambda }}_1}\mathit{\boldsymbol{K}}\left( k \right)}\\ {{\mathit{\boldsymbol{\lambda }}_2}\mathit{\boldsymbol{K}}\left( {k - 1} \right)}\\ \vdots \\ {{\mathit{\boldsymbol{\lambda }}_p}\mathit{\boldsymbol{K}}\left( {k - p + 1} \right)} \end{array}} \right]\mathit{\boldsymbol{E}}\left( {p,k} \right)} \end{array} $ | (14) |
为使当前信息的增益权重最大,可取:
| $ {\mathit{\boldsymbol{\lambda }}_1} \ge \left( {{\mathit{\boldsymbol{\lambda }}_2} + {\mathit{\boldsymbol{\lambda }}_3} + \cdots + {\mathit{\boldsymbol{\lambda }}_p}} \right) $ | (15) |
对旧信息增益进行加权处理后,使得算法在有效修正和抑制累积干扰之间达到相对平衡,为使多新息方法至少优于经典卡尔曼滤波,可取:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\lambda }}_1} = 1,\\ {\mathit{\boldsymbol{\lambda }}_2} = {\mathit{\boldsymbol{\lambda }}_3} = \cdots = {\mathit{\boldsymbol{\lambda }}_p} = \frac{a}{{p - 1}},0 \le a \le 1 \end{array} \right. $ | (16) |
式中:a为遗忘因子矩阵的设计参数,该参数为0≤a≤1时,式(15)成立。
将MI-EKF辨识步骤结合式(14)、(16),即形成改进后的MI-EKF算法。
2.2 改进后MI-EKF的收敛性分析对于MI-EKF方法的收敛性理论分析,文献[12]已给出了其辨识一般收敛性的理论推导过程,本文对于引用遗忘因子矩阵之后的改进MI-EKF方法,进一步分析辨识满足有界收敛性的条件。
定义参数估计误差为
定理1 假设系统量测噪声的均方差有界,方差为σ2,即
| $ {\rm{E}}\left( {{{\left\| {{\mathit{\boldsymbol{v}}_k}} \right\|}^2}} \right) = {\sigma ^2} $ | (17) |
且持续激励条件成立,即增益矩阵K(k)满足:
| $ \alpha \mathit{\boldsymbol{I}} \le \frac{1}{N}\sum\limits_{i = 1}^N {\mathit{\boldsymbol{K}}\left( {t - i + 1} \right){\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {t - i + 1} \right)} \le \beta \mathit{\boldsymbol{I}} $ | (18) |
那么
证明:由MI-EKF辨识步骤,有
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde X}}\left( k \right) = \mathit{\boldsymbol{\tilde X}}\left( {\bar k} \right) + \mathit{\boldsymbol{K}}\left( {p,k} \right)\left[ {\mathit{\boldsymbol{Z}}\left( {p,k} \right) - \mathit{\boldsymbol{H\hat X}}\left( {\bar k} \right)} \right] - }\\ {\mathit{\boldsymbol{X}}\left( k \right) = \mathit{\boldsymbol{\tilde X}}\left( {\bar k} \right) + \mathit{\boldsymbol{K}}\left( {p,k} \right)\left[ {\mathit{\boldsymbol{Z}}\left( {p,k} \right) - \mathit{\boldsymbol{H\hat X}}\left( {\bar k} \right)} \right] = }\\ {\mathit{\boldsymbol{\tilde X}}\left( {\bar k} \right) + \mathit{\boldsymbol{K}}\left( {p,k} \right)\left[ {\mathit{\boldsymbol{HX}}\left( k \right) + \mathit{\boldsymbol{v}}\left( {p,k} \right) - \mathit{\boldsymbol{H\hat X}}\left( {\bar k} \right)} \right] = }\\ {\left[ {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}}} \right]\mathit{\boldsymbol{\tilde X}}\left( {\bar k} \right) + \mathit{\boldsymbol{K}}\left( {p.k} \right)\mathit{\boldsymbol{v}}\left( {p.k} \right)} \end{array} $ | (19) |
对式(19)取范数,并引用不等式
| $ \begin{array}{*{20}{c}} {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( k \right)} \right\|}^2} = \left\| {\left[ {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}}} \right]\mathit{\boldsymbol{\tilde X}}\left( {\bar k} \right) + } \right.}\\ {{{\left. {\mathit{\boldsymbol{K}}\left( {p.k} \right)\mathit{\boldsymbol{v}}\left( {p.k} \right)} \right\|}^2} \le }\\ {\left( {1 + b} \right){{\left\| {\left[ {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}}} \right]\mathit{\boldsymbol{\tilde X}}\left( {\bar k} \right)} \right\|}^2} + }\\ {\left( {1 + \frac{1}{b}} \right){{\left\| {\mathit{\boldsymbol{K}}\left( {p.k} \right)\mathit{\boldsymbol{v}}\left( {p.k} \right)} \right\|}^2}} \end{array} $ | (20) |
对式(20)取期望,有
| $ \begin{array}{*{20}{c}} {{\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( k \right)} \right\|}^2}} \right) \le \left( {1 + b} \right){\rm{E}}\left( {\left\| {\left[ {\mathit{\boldsymbol{I}} - } \right.} \right.} \right.}\\ {\left. {{{\left. {\left. {\mathit{\boldsymbol{K}}\left( {p.k} \right)\mathit{\boldsymbol{H}}} \right]\mathit{\boldsymbol{\tilde X}}\left( {\bar k} \right)} \right\|}^2}} \right) + }\\ {\left( {1 + \frac{1}{b}} \right){\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{v}}\left( {p,k} \right)} \right\|}^2}} \right) \le }\\ {\left( {1 + b} \right){\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( k \right)} \right\|}^2}} \right){\rm{E}}\left( {{{\left\| {\left[ {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}}} \right]} \right\|}^2}} \right) + }\\ {\left( {1 + \frac{1}{b}} \right)p{\sigma ^2}{\rm{E}}{{\left\| {\mathit{\boldsymbol{K}}\left( {p,k} \right)} \right\|}^2}} \end{array} $ | (21) |
设矩阵K(p, k)的最大特征值为λmax,根据式(18)及式(16)可得
| $ \begin{array}{*{20}{c}} {{\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{K}}\left( {p,k} \right)} \right\|}^2}} \right) \le {\rm{E}}\left( {{\lambda _{\max }}\left( {\mathit{\boldsymbol{K}}\left( {p,k} \right) \cdot {\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {p,k} \right)} \right)} \right) \le }\\ {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \end{array} $ | (22) |
对于一般辨识过程,观测矩阵H=[I 0],有
| $ \begin{array}{*{20}{c}} {{\rm{E}}\left( {{{\left\| {\left[ {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}}} \right]} \right\|}^2}} \right) = }\\ {{\rm{E}}\left( {{\lambda _{\max }}{{\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}}} \right)} \right) = }\\ {{\rm{E}}\left( {{\lambda _{\max }}\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}} - {\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {p,k} \right) + } \right.} \right.}\\ {\left. {\left. {{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {p,k} \right)\mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}}} \right)} \right) \le }\\ {{\rm{E}}\left( {{\lambda _{\max }}\left( {\mathit{\boldsymbol{I}} - 2\sqrt {{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {p,k} \right)\mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}}} + } \right.} \right.}\\ {\left. {\left. {{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {p,k} \right)\mathit{\boldsymbol{K}}\left( {p,k} \right)\mathit{\boldsymbol{H}}} \right)} \right) \le }\\ {\left( {1 - 2\sqrt {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\alpha } + \left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \right)} \end{array} $ | (23) |
结合式(21)、式(22)和式(23)可得
| $ \begin{array}{*{20}{c}} {{\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( k \right)} \right\|}^2}} \right) \le \left( {1 + b} \right){\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( {\bar k} \right)} \right\|}^2}} \right) \cdot }\\ {\left( {1 - 2\sqrt {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\alpha } + \left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \right) + }\\ {\left( {1 + \frac{1}{b}} \right)p{\sigma ^2}\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \end{array} $ | (24) |
假设过程噪声wk均方差有界,方差分别为E(‖wk‖2)=γ2,状态转移矩阵A均方有界,E(‖A‖2)≤τ2,由估计误差定义可得
| $ \begin{array}{*{20}{c}} {{\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( k \right)} \right\|}^2}} \right) = {\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\hat X}}\left( {\bar k} \right) - \mathit{\boldsymbol{X}}\left( k \right)} \right\|}^2}} \right) \approx }\\ {{\rm{E}}\left( {{{\left\| {\left. {\mathit{\boldsymbol{A\hat X}}\left( {k - 1} \right) - \mathit{\boldsymbol{AX}}\left( {k - 1} \right) - \mathit{\boldsymbol{w}}\left( \mathit{\boldsymbol{k}} \right)} \right)} \right\|}^2}} \right) = }\\ {{\rm{E}}\left( {\left\| {\left. {\mathit{\boldsymbol{A\tilde X}}\left( {k - 1} \right) - \mathit{\boldsymbol{w}}\left( \mathit{\boldsymbol{k}} \right)} \right)} \right\|} \right) \le }\\ {{\tau ^2}{\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( {k - 1} \right)} \right\|}^2}} \right) + {\gamma ^2}} \end{array} $ | (25) |
将式(25)代入式(24)有
| $ \begin{array}{*{20}{c}} {{\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( k \right)} \right\|}^2}} \right) \le \left( {1 + b} \right) \cdot }\\ {\left( {{\tau ^2}{\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( {k - 1} \right)} \right\|}^2}} \right) + {\gamma ^2}} \right) \cdot }\\ {\left( {1 - 2\sqrt {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\alpha } + \left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \right) + }\\ {\left( {1 + \frac{1}{b}} \right)p{\sigma ^2}\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta \le }\\ {\left( {1 + \frac{1}{b}} \right){\tau ^2}\left( {1 - 2\sqrt {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\alpha } + } \right.}\\ {\left. {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \right){\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( {k - 1} \right)} \right\|}^2}} \right) + \left( {1 + b} \right) \cdot }\\ {{\gamma ^2}\left( {1 - 2\sqrt {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\alpha } + \left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \right) + }\\ {\left( {1 + \frac{1}{b}} \right)p{\sigma ^2}\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \end{array} $ | (26) |
取常量条件如下:
| $ \begin{array}{*{20}{c}} {0 < b < }\\ {\frac{1}{{\left( {1 - 2\sqrt {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\alpha } + \left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \right){\tau ^2}}} - 1}\\ {M = \left( {\left( {1 + b} \right){\tau ^2}\left( {1 - 2\sqrt {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\alpha } + } \right.} \right.}\\ {\left. {\left. {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \right)} \right) < 1}\\ {N = \left( {1 + b} \right){\gamma ^2}\left( {1 - 2\sqrt {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\alpha } + } \right.}\\ {\left. {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \right) + \left( {1 + \frac{1}{b}} \right)p{\sigma ^2}\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \end{array} $ | (27) |
则有
| $ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{k \to \infty } {\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( k \right)} \right\|}^2}} \right) \le \mathop {\lim }\limits_{k \to \infty } M \cdot {\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( {k - 1} \right)} \right\|}^2}} \right) + }\\ {N \le \mathop {\lim }\limits_{k \to \infty } {M^{k - 1}}{\rm{E}}\left( {{{\left\| {\mathit{\boldsymbol{\tilde X}}\left( 1 \right)} \right\|}^2}} \right) + \frac{{1 - {M^{k - 1}}}}{{1 - M}}N \le }\\ {\frac{N}{{1 - M}}} \end{array} $ | (28) |
式中M、N为常数。
因此,
此外,为满足式(27)不等式条件,a的取值需满足:
| $ \left( {1 - 2\sqrt {\left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\alpha } + \left( {1 + \frac{{{a^2}}}{{p - 1}}} \right)\beta } \right){\tau ^2} < 1 $ | (29) |
求解不等式得:
| $ a < \sqrt {\left( {\frac{1}{{{\tau ^2}}} + 2\sqrt {\frac{\alpha }{\beta }} - 2} \right)\left( {p - 1} \right)} $ | (30) |
即当上述不等式成立,遗忘因子存在上界时,改进后的MI-EKF方法的辨识结果可有界收敛。而由于N/(1-M)关于a为增函数,改进前的MI-EKF可视为遗忘因子为(p-1)≥a,故相比较标准MI-EKF,改进后的MI-EKF算法的辨识误差均方上界更小,辨识结果更精确。
3 基于改进MI-EKF的船舶响应模型参数辨识将改进后的MI-EKF方法应用于船舶非线性响应模型参数辨识,以解决船舶模型参数精确辨识问题。
3.1 船舶响应模型响应型模型是描述船舶艏向角相对于舵角变化的响应关系的模型。该模型参数较少,认为船舶在匀速航行时,有如下二阶微分方程[15]:
| $ \begin{array}{*{20}{c}} {{T_1}{T_2}\ddot r + \left( {{T_1} + {T_2}} \right)\dot r + r + \alpha {r^3} = }\\ {K\left( {{\delta _r} + \delta } \right) + K{T_3}\dot \delta } \end{array} $ | (31) |
式中:r为艏向角速度,δ为操舵角,K为增益系数,T1、T2、T3为时间常数,α为非线性系数,δr为初始直航所需压舵角,该模型为船舶操纵响应的非线性模型。
为方便辨识,将模型参数作如下简化:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \theta }} = {{\left[ {\begin{array}{*{20}{c}} {\frac{{{T_1} + {T_2}}}{{{T_1}{T_2}}}}&{\frac{1}{{{T_1}{T_2}}}}&{\frac{a}{{{T_1}{T_2}}}}&{\frac{{K{\delta _{\rm{r}}}}}{{{T_1}{T_2}}}}&{\frac{K}{{{T_1}{T_2}}}}&{\frac{{K{T_3}}}{{{T_1}{T_2}}}} \end{array}} \right]}^{\rm{T}}} = }\\ {{{\left[ {\begin{array}{*{20}{c}} {{\theta _1}}&{{\theta _2}}&{{\theta _3}}&{{\theta _4}}&{{\theta _5}}&{{\theta _6}} \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (32) |
则有参数对应关系:
| $ \begin{array}{*{20}{c}} {K = \frac{{{\theta _2}}}{{{\theta _4}}}{\delta _r}{\rm{ = }}\frac{{{\theta _3}}}{{{\theta _2}}}\alpha {\rm{ = }}\frac{{{\theta _5}}}{{{\theta _4}}}}\\ {{T_1} = \frac{{2{\theta _1} - \left( {{\theta _1} - \sqrt {\left( {\theta _1^2 - 4{\theta _4}} \right)} } \right)}}{{2{\theta _4}}}}\\ {{T_2} = \frac{{\left( {{\theta _1} - \sqrt {\left( {\theta _1^2 - 4{\theta _4}} \right)} } \right)}}{{2{\theta _4}}}{T_3} = \frac{{{\theta _6}}}{{{\theta _2}}}} \end{array} $ | (33) |
非线性控制系统常用状态空间模型来描述系统的状态变化,结合式(32)、(33)做如下变换:
| $ {\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}} \end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{c}} \psi &r&{\dot r}&\delta &{\dot \delta } \end{array}} \right]^{\rm{T}}} $ | (34) |
则有如式(35)所示的状态方程:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = {x_3}\\ {{\dot x}_3} = - {\theta _1}{x_3} - {\theta _2}{x_2} - {\theta _3}x_2^3 + {\theta _4} + {\theta _5}{x_4} + {\theta _6}{x_5}\\ {{\dot x}_4} = {x_5}\\ {{\dot x}_5} = 0 \end{array} \right. $ | (35) |
该方程可以用来作为参数辨识的参考方程,由于参数可辨识性问题[16],本文对响应模型辨识结果以
由改进后MI-EKF辨识结构可知,针对船舶非线性响应模型辨识,首先需要将待估计参数作为新的状态量与模型中的原状态量一起参与辨识,并构造增广状态矩阵,便可使用所提出的改进MI-EKF对离散线性模型进行辨识。
关于船舶响应模型构造增广矩阵的方法,文献[8]只使用原状态量x1与带估计参数合成增广矩阵,其辨识过程中的观测值只有ψ。鉴于目前实船实验中可使用高精度惯导设备获取精确的r和
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = {{\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}&{{x_3}}&{{\theta _1}}&{{\theta _2}}&{{\theta _3}}&{{\theta _4}}&{{\theta _5}}&{{\theta _6}} \end{array}} \right]}^{\rm{T}}} = }\\ {{{\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}}&{{x_6}}&{{x_7}}&{{x_8}}&{{x_9}} \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (36) |
定义fX为离散后的下一时刻状态关于前一时刻的状态量和控制量的非线性函数,则结合式(35)、(36)进行前向差分,可得到:
| $ {\mathit{\boldsymbol{f}}_X} = {\left[ {\begin{array}{*{20}{c}} {{f_1}}&{{f_2}}&{{f_3}}&{{f_4}}&{{f_5}}&{{f_6}}&{{f_7}}&{{f_8}}&{{f_9}} \end{array}} \right]^{\rm{T}}} $ |
其中
| $ \left\{ \begin{array}{l} {f_1} = {x_1}\left( k \right) + h{x_2}\left( k \right)\\ {f_2} = {x_2}\left( k \right) + h{x_3}\left( k \right)\\ {f_3} = {x_3}\left( k \right) + h\left( { - {x_4}\left( k \right){x_3}\left( k \right) - {x_5}\left( k \right){x_2}\left( k \right) - } \right.\\ \;\;\;\;\;\;\;{x_6}\left( k \right){x_2}\left( k \right)3 + {x_7}\left( k \right) + {x_8}\left( k \right)u\left( k \right) + \\ \;\;\;\;\;\;\;\left. {{x_9}\left( k \right)\dot u\left( k \right)} \right)\\ {f_4} = {x_4}\left( k \right),{f_5} = {x_5}\left( k \right),{f_6} = {x_6}\left( k \right)\\ {f_7} = {x_7}\left( k \right),{f_8} = {x_8}\left( k \right),{f_9} = {x_9}\left( k \right) \end{array} \right. $ | (37) |
式中:h为采样周期,u(k)=δ(k),则重定义状态矩阵后,式(35)即可简化为如式(1)所示的离散非线性模型。其中,观测矩阵只包含可观测量,可定义为
| $ \mathit{\boldsymbol{Z}}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{x_1}\left( k \right)}&{{x_2}\left( k \right)}&{{x_3}\left( k \right)} \end{array}} \right]^{\rm{T}}} $ | (38) |
进一步,将函数fX对k时刻状态量X(k)、控制量u(k)进行线性化以得到状态转移矩阵:
| $ \mathit{\boldsymbol{A}} = \frac{{\partial {\mathit{\boldsymbol{f}}_X}}}{{\partial \mathit{\boldsymbol{X}}}}\left| {_{X = \hat X}} \right. = \\ \left[ {\begin{array}{*{20}{c}} 1&h&{}&{}&{}&{}&{}&{}&{}\\ {}&1&h&{}&{}&{}&{}&{}&{}\\ {}&{ - h\left( {3{x_6}x_2^2 + {x_5}} \right)}&{1 - h{x_4}}&{ - h{x_3}}&{ - h{x_2}}&{ - hx_2^3}&{hu}&h&{h\dot u}\\ {}&{}&{}&1&{}&{}&{}&{}&{}\\ {}&{}&{}&{}&1&{}&{}&{}&{}\\ {}&{}&{}&{}&{}&1&{}&{}&{}\\ {}&{}&{}&{}&{}&{}&1&{}&{}\\ {}&{}&{}&{}&{}&{}&{}&1&{}\\ {}&{}&{}&{}&{}&{}&{}&{}&1 \end{array}} \right] $ | (39) |
同理有
| $ \mathit{\boldsymbol{H}} = \frac{{\partial \mathit{\boldsymbol{Z}}}}{{\partial \mathit{\boldsymbol{X}}}} = {\left[ {\begin{array}{*{20}{c}} 1&0&0&0& \cdots &0\\ 0&1&0&0& \cdots &0\\ 0&0&1&0& \cdots &0 \end{array}} \right]_{3 \times 9}} $ | (40) |
故由式(39)、(40)可得到递推辨识所需要的Jacobi矩阵,应用改进MI-EKF辨识算法,即可完成式(36)中各参数的辨识。
4 参数辨识实验验证针对船舶二阶非线性响应模型,使用改进前后的MI-EKF算法进行参数辨识,并选取不同的遗忘因子矩阵,以验证遗忘因子改进的有效性;使用EKF和改进MI-EKF方法进行参数辨识,并利用辨识结果进行船舶操纵预报对比分析,以验证多新息方法的有效性。
使用一艘模型船的试验平台进行辨识试验,如图 2所示,模型船船长为0.9 m,定常回转率为1.55,设计航速为0.5 m/s,其执行机构采用实船上常见的舵桨分离机构,且为单桨单舵模型船,其运动特性与文献[15]中所述船舶一致,可作为辨识参数采集的平台。

|
Download:
|
| 图 2 模型船试验平台 Fig. 2 The model ship | |
通过采用文献[17]中基于单目视觉的高精度定位方法,对船艏艉的标志灯进行检测,以获取室内环境下相对精确的船舶艏向角数据;通过绝对式角度传感器获取船舶实时舵角数据;通过岸基计算机远程控制模型船以执行Z形试验,为模型船的响应模型参数辨识提供数据基础。
值得注意的是,模型船与实际船舶在操舵响应时延上有所不同,使用绝对值舵角传感器获取实际舵角,保证模型船Z形实验预报的结果对实际船舶操纵性预报具有可参考性。
4.1 遗忘因子改进的有效性试验验证由2.2节中的理论分析可知,遗忘因子矩阵参数a取值过大,会使得辨识误差上界变大,甚至无法有界收敛;而从MI-EKF辨识结构可知,遗忘因子矩阵参数a取值过小,会抹去多新息方法产生的有效增益,同样会限制辨识精度。需要选取合适的遗忘因子进行辨识试验,以达到更精确的辨识效果。
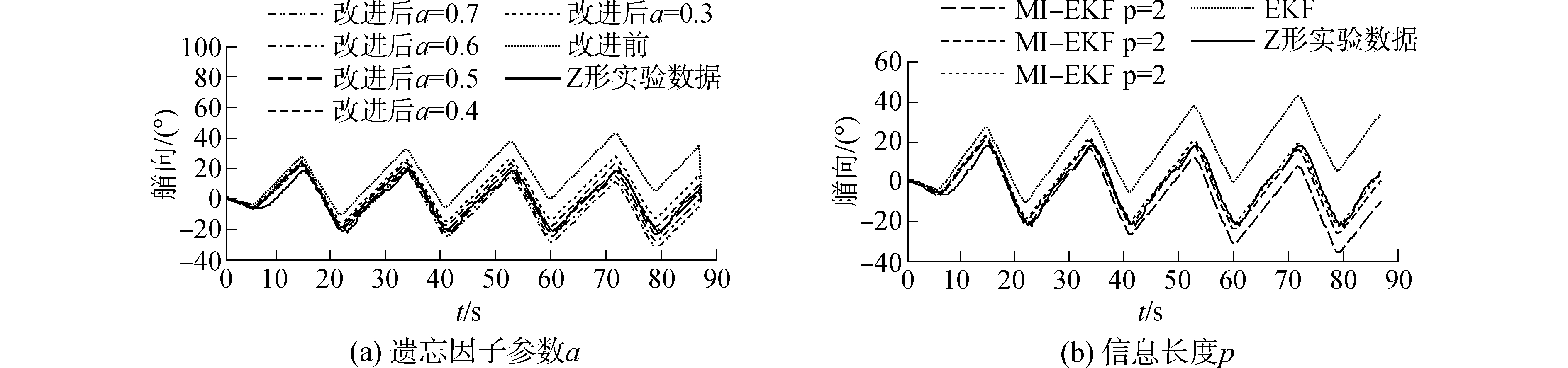
首先,以新息长度p=4为例,使用改进前后进MI-EKF方法进行辨识,并选取不同的a以验证改进效果,辨识结果的预报曲线如图 3(a)所示。
|
Download:
|
| 图 3 预报结果 Fig. 3 The forecast results | |
选取均方误差为拟合度评价函数,对新息长度p=4的情况下,计算得:改进前的MI-EKF算法辨识模型预报误差为3.576;改进后的MI-EKF中,遗忘因子a为0.3、0.4、0.5、0.6、0.7下的预报误差分别为0.915、0.325、0.159、0.283和0.649(°)2。
然后,针对不同的新息长度p,使用同样方法设定不同的遗忘因子矩阵参数a进行实验。由于新息长度的增加会带来计算量的增大,不利于辨识的实时性,故取p为2、3、4、5进行实验,得到最佳遗忘因子参数a分别为0.52、0.49、0.50、0.51。
由图 3和误差结果可以看出:1)改进后的MI-EKF在选取合适的遗忘因子参数时,辨识结果均比改进前精确;2)实验测得,不同的新息长度下,最佳的遗忘因子矩阵参数略有不同,但基本维持在0.5左右。在一定的新息长度下,遗忘因子矩阵参数a取值大于或小于最佳参数都将导致辨识误差上升。以上实验结果均符合对算法改进的理论分析。
4.2 多新息算法的有效性试验验证 4.2.1 试验结果在辨识过程中,过程噪声和量测噪声矩阵的初始值设定如下:
| $ \mathit{\boldsymbol{Q}} = {\rm{diag}}\left( {\begin{array}{*{20}{c}} 4&4&{43}&4&4&4&4&{160}&4 \end{array}} \right) \times {10^4} $ |
| $ R = 2 \times {10^{ - 2}} $ |
1) 参数辨识结果
为验证多个新息下改进的MI-EKF整体算法辨识结果的准确性和收敛速度,在遗忘因子矩阵参数a=0.5时,分别取不同信息长度p=2、3、4下的改进后MI-EKF辨识的结果与传统EKF算法进行对比,如表 1所示。
| 表 1 辨识结果 Tab.1 Parameter identification results |
2) 操纵性预报结果
由表 2中所辨识的参数结合状态方程(5)进行Z形试验预报,预报结果如图(b)所示:
| 表 2 不同参数的收敛步数 Tab.2 Convergence step number of different parameters |
对于算法辨识的结果,从辨识准确性和辨识收敛速度两方面分析:
1) 准确性
计算均方误差得:改进前的MI-EKF算法辨识模型预报误差为5.675,改进后的MI-EKF中,在新息长度p为2、3、4下的预报误差分别为1.199、0.213和0.159。
可以看出:改进后MI-EKF辨识结果的预报误差明显比经典EKF方法辨识的误差低,均方误差在2(°)2以下,满足辨识精度要求;随着信息长度p的增加,改进后MI-EKF辨识结果的预报误差逐渐降低,辨识精确度越来越高,可以实现多个新息长度(p>2)下的参数准确辨识。
2) 辨识结果收敛性
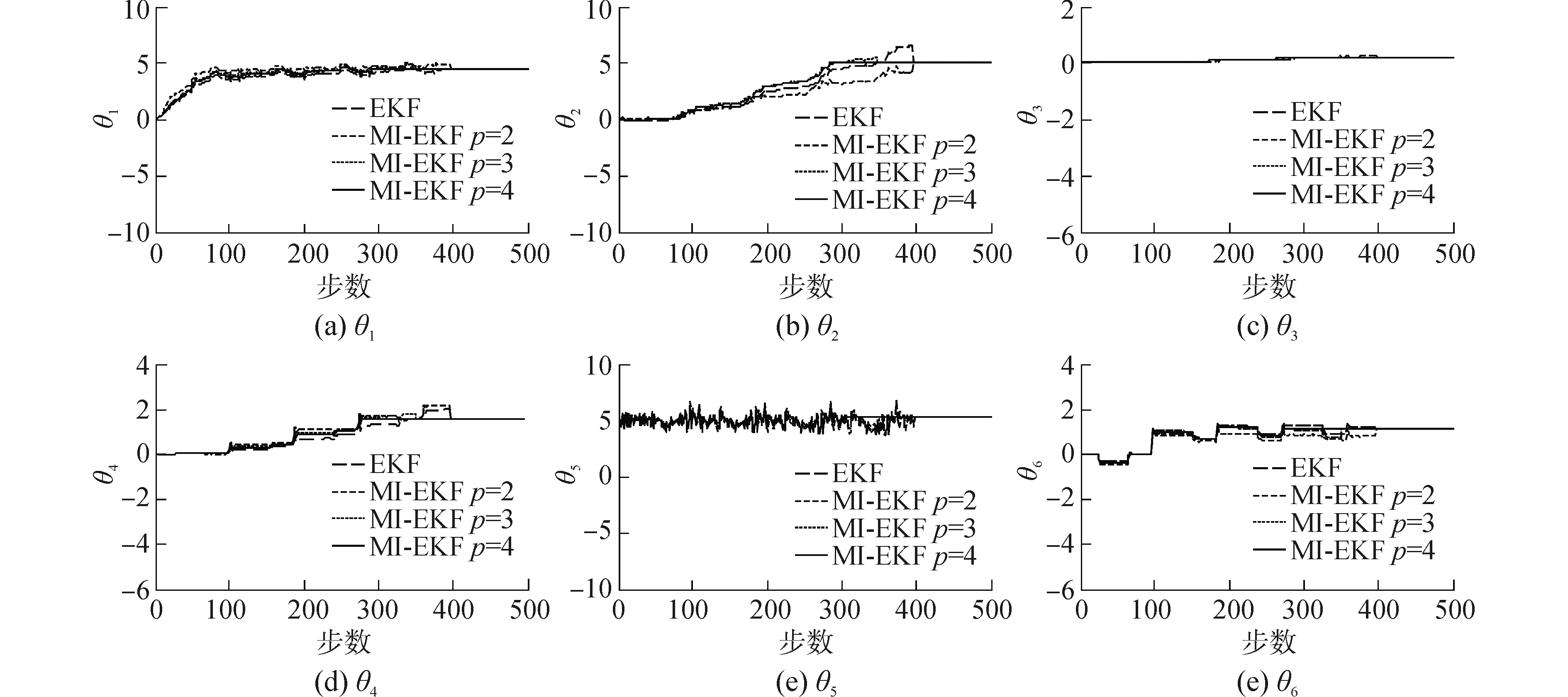
分别将EKF与p为2、3、4下改进的MI-EKF每次递推修正的各参数θ1、θ2、θ3、θ4、θ5、θ6的结果记录下来,并进行对比,结果如图 4所示。
|
Download:
|
| 图 4 参数辨识结果 Fig. 4 The parameter identification results | |
从图中曲线可以看出各参数收敛时需要经过的递推步数,具体如表 2所示。
其中,Nθ1、Nθ2、Nθ3、Nθ4、Nθ5、Nθ6分别表示θ1、θ2、θ3、θ4、θ5、θ6这六个参数收敛至稳定值所需的递推步数。
从表 2中数据可以看出:1)改进的MI-EKF方法辨识的各参数收敛的速度与EKF相当,在经过400步递推之后,参数辨识基本都可以收敛。2)随着改进的MI-EKF方法的信息长度p的增加,算法的收敛速度略有加快。
5 结论1) 辨识准确性方面,在选取了合适的遗忘因子矩阵参数之后,改进的MI-EKF进行辨识的精度比MI_EKF更高,均方误差可达到0.2(°)2以下,且由模型船实验数据得出的最佳遗忘因子参数在0.5左右;
2) 辨识收敛性方面,在一定的遗忘因子参数下,随着新息长度的增加,改进算法的收敛速度随之加快。且在不同的新息长度下,算法辨识的参数在400步递推之后都可以收敛。
本文没有对最佳遗忘因子矩阵参数进行更深入的计算研究,后续可以考虑根据多新息扩展卡尔曼滤波扩展的信息长度进行遗忘因子自适应调节。
| [1] |
KALMAN R E. A new approach to linear filtering and prediction problems[J]. Transaction of the ASME-J (basic engineering), 1960: 35-45. (  0) 0)
|
| [2] |
ABKOWITZ M A. Measurement of hydrodynamic characteristics from ship maneuvering trials by system identification[J]. SNAME transaction, 1980, 33(88): 283-318. (  0) 0)
|
| [3] |
FOSSEN T I, SAGATUN S I, SØRENSEN A J. Identification of dynamically positioned ships[J]. Control engineering practice, 1996, 4(3): 369-376. DOI:10.1016/0967-0661(96)00014-7 (  0) 0)
|
| [4] |
MA Feichun, TONG S H. Real time parameters identification of ship dynamic using the extended Kalman filter and the second order filter[C]//Proceedings of 2003 IEEE Conference on Control Applications. Istanbul, Turkey, Turkey, 2003, 2:1245-1250.
(  0) 0)
|
| [5] |
HASELTINE E L, RAWLINGS J B. Critical evaluation of extended Kalman filtering and moving-horizon estimation[J]. Industrial & engineering chemistry research, 2005, 44(8): 2451-2460. (  0) 0)
|
| [6] |
赵大明, 施朝健, 彭静. 应用扩展卡尔曼滤波算法的船舶运动模型参数辨识[J]. 上海海事大学学报, 2008, 29(3): 5-9. ZHAO Daming, SHI Caojian, PENG Jing. Parameter identification to motion model of ship by extended Kalman filter[J]. Journal of Shanghai Maritime University, 2008, 29(3): 5-9. (  0) 0)
|
| [7] |
丁彦侃, 俞孟蕻. 并行扩展卡尔曼滤波的船舶模型参数辨识研究[J]. 船舶工程, 2015, 37(1): 72-74, 99. DING Yankan, YU Menghong. Parallel EKF identification methods for mathmatics model of ship[J]. Ship engineering, 2015, 37(1): 72-74, 99. (  0) 0)
|
| [8] |
丁锋. 系统辨识(6):多新息辨识理论与方法[J]. 南京信息工程大学学报, 2012, 4(1): 1-28. DING Feng. System identification. Part F:Multi-innovation identification theory and methods[J]. Journal of Nanjing University of information science & technology, 2012, 4(1): 1-28. (  0) 0)
|
| [9] |
刘毛毛. 基于机器视觉的运动目标实时跟踪算法研究[D]. 太原: 中北大学, 2015. LIU Maomao. Research on real-time moving object tracking algorithm based on machine vision[D]. Taiyuan:North University of China, 2015. (  0) 0)
|
| [10] |
常江. 基于特征匹配的三维点云配准算法研究[D]. 太原: 中北大学, 2015. CHANG Jiang. Algorithm research of third point cloud registration based on feature matching[D]. Taiyuan:North University of China, 2015. (  0) 0)
|
| [11] |
FUJⅡ K. Extended Kalman filter[M]. Refernce manual, 2013(1):1-27.
(  0) 0)
|
| [12] |
吕国宏, 秦品乐, 苗启广, 等. 基于多新息理论的EKF算法研究[J]. 小型微型计算机系统, 2016, 37(3): 576-580. LYU Guohong, QING Pinle, MIAO Qiguang, et al. Research of extended kalman filter based on multi-innovation theory[J]. Journal of Chinese computer systems, 2016, 37(3): 576-580. (  0) 0)
|
| [13] |
徐景硕, 秦永元, 彭蓉. 自适应卡尔曼滤波器渐消因子选取方法研究[J]. 系统工程与电子技术, 2004, 26(11): 1552-1554. XU Jingsuo, QING Yongyuan, PENG Rong. New method for selecting adaptive Kalman filter fading factor[J]. Systems engineering and electronics, 2004, 26(11): 1552-1554. DOI:10.3321/j.issn:1001-506X.2004.11.006 (  0) 0)
|
| [14] |
张旭光, 张云, 王艳宁, 等. 基于遗忘因子与卡尔曼滤波的协方差跟踪[J]. 光学学报, 2010(8): 2317-2323. ZHANG Xuguang, ZHANG Yun, WANG Yanning, et al. Covariance tracking based on forgetting factor and kalman filter[J]. Acta optica sinica, 2010(8): 2317-2323. (  0) 0)
|
| [15] |
王春园. 模型船的数学模型辨识[D]. 大连: 大连海事大学, 2012. WANG Chunyuan. Identification of mathematic model of the model ship[D]. Dalian:Dalian Maritime University, 2012. (  0) 0)
|
| [16] |
罗伟林. 基于支持向量机方法的船舶操纵运动建模研究[D]. 上海: 上海交通大学, 2009. LUO Weilin. On the modeling of ship manoeuvring motion by using support vector machines[D]. Shanghai:Shanghai Jiao Tong University, 2009. (  0) 0)
|
| [17] |
柳晨光, 初秀民, 谢朔, 等. 基于单目视觉的水面船舶多目标定位方法[J]. 交通运输工程学报, 2015(5): 91-100. LIU Chenguang, CHU Xiumin, XIE Shuo, et al. Multi-target locating method of surface ship based on monocular vision[J]. Journal of traffic and transportation engineering, 2015(5): 91-100. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


