2. 集美大学 轮机工程学院, 福建 厦门 361021
2. School of Marine Engineering, Jimei University, Xiamen 361021, China
畸形波(又称凶波或大波)是指海上偶然出现的具有超大波高的波浪,其概念由Draper[1]首次提出,几十年来不断有畸形波造成船舶失事和海洋结构物破坏的报道。畸形波出现在除北冰洋以外的三大洋中的不同海域,北海[2-3]、南非东南海域[4]和日本海域[5]等都有观测到畸形波的记录。畸形波的形式与产生条件多样,其可发生在不同水深(深水、有限水深和浅水),可伴随显著海流或无明显海流,可能为孤立的大波或一组大波,但其共同特征为超高的波高(强非线性)、出现的偶然性及存在的短暂性。目前常从波高角度定义畸形波,常用为Kjeldsen[6]及Klinting等[2]的定义。Kjeldsen定义畸形波为波高超过有意波高2倍的波浪。Klinting等在Kjeldsen定义的基础上考虑了畸形波相邻波浪的影响。
畸形波结构物相互作用研究多在实验室或数值水池中开展[7-12]。由于研究建立在畸形波机理及模拟的基础上,故相关研究仍不成熟。其中数值方法多基于商业势流软件或CFD求解器[13-14],目标畸形波多基于线性叠加模型。前者可方便快捷地得到预报结果,然而往往无法准确考虑畸形波的强非线性及期间伴随的上浪砰击效应。后者可模拟上浪砰击及过程中的湍流效应,但是计算耗时,且多数研究不考虑结构的变形(即流固耦合)。无论采用势流方法亦或CFD方法,正确模拟强非线性畸形波都是前提也是难点。在畸形波上浪砰击过程中,巨大的砰击压力使局部结构在很短时间内改变运动状态,进而影响流场的状态和砰击压力。因此的瞬态砰击作用过程中有必要考虑流固耦合效应。
本文构建求解N-S方程的二维数值波浪水槽,基于速度入口和守恒消波法模拟某北海实测畸形波[3]。采用一种基于SIMPLE法的隐式算法求解畸形波对垂直弹性板的上浪砰击问题,并分析不同条件对结构响应的影响。
1 数值波浪水槽数值水槽利用交错网格离散求解域,采用有限差分法求解N-S方程,使用部分单元参数处理复杂流场边界,采用体积分数(volume of fluid, VOF)法重构自由液面。数值波浪水槽的控制方程为
连续性方程:
| $ \nabla \left( {\lambda \mathit{\boldsymbol{u}}} \right) = 0 $ | (1) |
动量方程:
| $ \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \nabla \mathit{\boldsymbol{uu}} = - \frac{1}{\rho }\nabla p + \mathit{\boldsymbol{f + }}\frac{\gamma }{\rho }{\nabla ^2}\mathit{\boldsymbol{u}} $ | (2) |
体积分数输运方程:
| $ \frac{{\partial \lambda F}}{{\partial t}} + \nabla \left( {\lambda \mathit{\boldsymbol{u}}F} \right) = 0 $ | (3) |
式中:u为流场速度,p为流场压力,ρ为流体密度,γ为动力粘性系数,λ为部分单元参数,f为体积力,F为体积分数,▽为散度(梯度)算子。利用SIMPLE算法求解速度压力耦合方程,使用VOF-Youngs法[15]重构自由液面,压力梯度项和速度耗散项采用中心差分法离散,通过一阶迎风差分与中心差分的混合格式离散扩散项,其中迎风差分的权重设为0.4。忽略表面张力,则自由液面条件为
| $ \frac{{\partial {\mathit{\boldsymbol{u}}_n}}}{{\partial \tau }} + \frac{{\partial {\mathit{\boldsymbol{u}}_\tau }}}{{\partial n}} = 0 $ | (4) |
| $ - p + 2\mu \frac{{\partial {\mathit{\boldsymbol{u}}_n}}}{{\partial n}} = - {p_0} $ | (5) |
式中:un和uτ分别为自由液面处速度矢量的法向和切向分量,p0为自由液面上方大气压力。水底采用无滑移条件。采用速度入口方式造波。造波边界的速度、压力和自由液面抬升根据相应模型给出的理论值设定。
消波方法的好坏直接影响数值水槽模拟波浪的质量。Mayer等[16]提出了松弛消波法,其优点为无需改变控制方程,可以吸收多种类型的波浪。松弛法的表达式为
| $ \left\{ \begin{array}{l} {u_1} = C{u_0}\\ {v_1} = C{v_0}\\ {\eta _1} = C{\eta _0} \end{array} \right. $ | (6) |
式中:下标0表示消波前的物理量,下标1为消波后的物理量,C为空间分布的消波权重且仅与水平位置有关。在消波区始端C取1,末端C取0。实际应用中C的函数形式多种多样,本文取
| $ C = 1 - \exp \left[ { - 5{{\left( {1 - {x^ * }} \right)}^n}} \right] $ | (7) |
式中:x*=(x-xa)/(xb-xa),xa和xb分别为消波区始端和末端的水平坐标位置。Hu等[17]提出了一种守恒消波法以适应变化的流场状态,提高消波效率,其中参数C表示如下
| $ \int_{{x_{\rm{a}}}}^{{x_{\rm{b}}}} {\left[ {CJ + \left( {C - 1} \right)\eta } \right]{\rm{d}}x} = 0 $ | (8) |
式中:
采用波列叠加模型模拟类似北海实测的确定性畸形波。波列叠加模型将畸形波视为随机波列和汇聚波浪按一定能量比例的叠加,其表达式为
| $ \begin{array}{*{20}{c}} {\eta = \sum\limits_{i = 1}^{{N_1}} {{a_{1i}}\cos \left( {{k_{1i}}x - {\omega _{1i}}t + {\theta _{1i}}} \right)} + }\\ {\sum\limits_{i = 1}^{{N_2}} {{a_{2i}}\cos \left[ {{k_{2i}}\left( {x - {x_c}} \right) - {\omega _{2i}}\left( {t - {t_c}} \right)} \right]} } \end{array} $ | (9) |
式中:第一个求和项为随机波列,第二个求和项为汇聚波列;下标1和2分别代表随机波列和汇聚波列,a1i和a2ii个组成波的波幅;ki、ωi和θii个组成波的波数、圆频率和随机相位;常数xc和tc分别为汇聚位置和汇聚时刻;N1和N2为相应波列的组成波数目。组成波波幅常通过海浪谱(如P-M谱)按比例分配得到,即
| $ \left\{ \begin{array}{l} {a_{1i}} = \sqrt {2{p_1}S\left( {{\omega _{1i}}} \right)\Delta {\omega _1}} \\ {a_{2i}} = \sqrt {2{p_2}S\left( {{\omega _{2i}}} \right)\Delta {\omega _2}} \end{array} \right. $ | (10) |
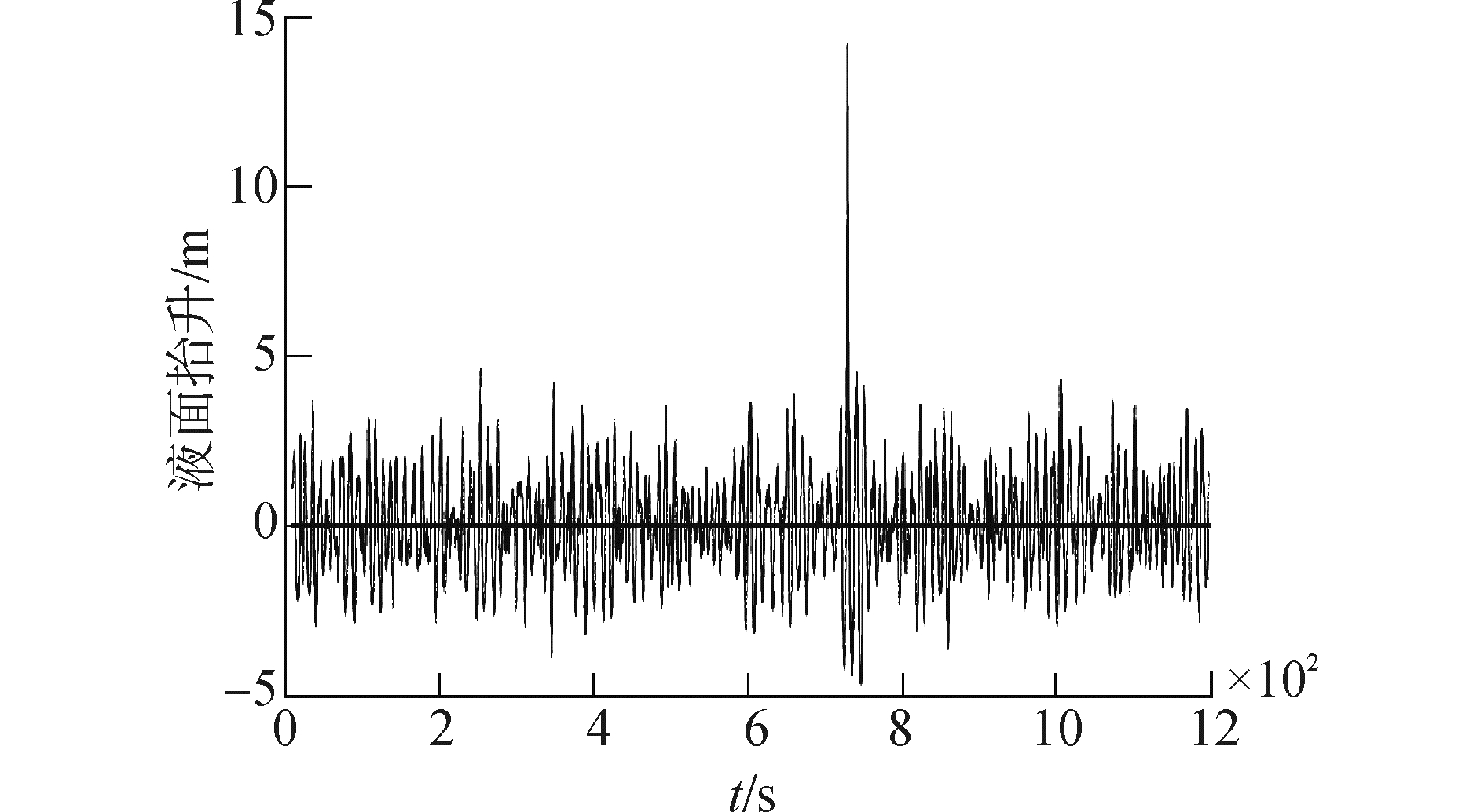
式中辽阔p1、p2影响了畸形波波高及模拟效率。本文的目标谱为P-M谱,表达式为S(ω)=Aexp(-B/ω4)/ω5,其中A和B为常数。目标谱的选取参考北海实测畸形波[3],观测位置水深130 m,有意波高为5.65 m,畸形波波高为18.04 m,波峰高度13.9 m。能量比例取为p1=0.9与p2=0.1。汇聚波列组成波数目为N1=250与N2=500。数值水槽长680 m,高150 m。畸形波最大波高出现位置距造波端120 m,出现时刻t=432 s。图 1为北海实测畸形波液面时历曲线,图 2为数值水槽模拟得到的液面时历,可见两者在畸形波出现时刻较接近。图 3对比了实测谱和数值模拟得到的波浪谱,两者吻合较好。表 1对比了数值模拟和观测数据得到的畸形波参数,两者吻合良好。表 1中,α=Hj/Hs、β1=Hj/Hj-1,β2=Hj/Hj+1、μ=ηj/Hj,其中Hj、Hj-1和Hj+1分别为畸形波,畸形波前方相邻波及畸形波后方相邻波的波高,ηj为畸形波波峰液面抬升。以上对比表明模拟生成的畸形波是正确合理的,可用于进一步研究上浪砰击。图 4给出了结构前端的畸形波轮廓,可见模拟得到的畸形波前端陡峭,后端平坦,最大波峰处出现波浪翻卷,具有强非线性。
|
Download:
|
| 图 1 北海实测畸形波液面时历曲线 Fig. 1 Time series plot for the freak wave recorded in North Sea | |

|
Download:
|
| 图 2 数值模拟畸形波液面时历曲线 Fig. 2 Time series plot for the simulated freak wave | |

|
Download:
|
| 图 3 数值模拟波浪谱与目标谱对比 Fig. 3 Comparison of the target wave spectrum with the simulated | |

|
Download:
|
| 图 4 畸形波液面轮廓图 Fig. 4 Screen shot of freak wave before structure | |
| 表 1 实测畸形波与模拟畸形波参数对比 Tab.1 Parameters of the recorded freak wave and the simulated wave |
通过向数值波浪水池求解器中添加结构求解模块和耦合处理算法实现流固耦合模拟。结构空间离散采用有限元法。由于在二维数值波浪水槽中平板可简化为板条梁模型,因此采用Euler梁单元进行结构离散。每个单元具有两个节点,每个节点具有2个自由度,即线位移ui和角位移θi。欧拉梁满足∂ui/∂y=θi(其中y轴垂直于梁截面),因此单元具有三阶精度。动力分析中采用集中质量矩阵和比例阻尼矩阵,结构控制方程为
| $ \mathit{\boldsymbol{M\ddot U}} + \mathit{\boldsymbol{C\dot U}} + \mathit{\boldsymbol{KU}} = \mathit{\boldsymbol{F}} $ | (11) |
式中:U为节点位移,
采用Houbolt格式求解方程(11)。Houbolt是一种无条件稳定格式,相应加速度和速度的离散格式如下
| $ {{\mathit{\boldsymbol{\ddot U}}}_{t + \Delta t}} = \frac{1}{{\Delta {t^2}}}\left( {2{\mathit{\boldsymbol{U}}_{t + \Delta t}} - 5{\mathit{\boldsymbol{U}}_t} + 4{\mathit{\boldsymbol{U}}_{t + \Delta t}} - {\mathit{\boldsymbol{U}}_{t - \Delta t}}} \right) $ | (12) |
| $ {{\mathit{\boldsymbol{\dot U}}}_{t + \Delta t}} = \frac{1}{{6\Delta t}}\left( {11{\mathit{\boldsymbol{U}}_{t + \Delta t}} - 18{\mathit{\boldsymbol{U}}_t} + 9{\mathit{\boldsymbol{U}}_{t - \Delta t}} - 2{\mathit{\boldsymbol{U}}_{t - 2\Delta t}}} \right) $ | (13) |
将式(12)、(13)代入式(11),得到离散的结构方程为
| $ \begin{array}{*{20}{c}} {\left( {2{a_1}\mathit{\boldsymbol{M}} + 11{a_2}\mathit{\boldsymbol{C}} + \mathit{\boldsymbol{K}}} \right){\mathit{\boldsymbol{U}}_{t + \Delta t}} = }\\ {{\mathit{\boldsymbol{F}}_{t + \Delta t}} + \left( {5{a_1}\mathit{\boldsymbol{M}} + 18{a_2}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{U}}_t} - }\\ {\left( {4{a_1}\mathit{\boldsymbol{M}} + 9{a_2}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{U}}_{t - \Delta t}} + \left( {{a_1}\mathit{\boldsymbol{M}} + 2{a_2}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{U}}_{t - 2\Delta t}}} \end{array} $ | (14) |
其中,a1=1/Δt2,a2=1/6Δt。已知Ft+Δt则求解方程(14)可得t+Δt该时刻节点位移,进而利用式(12)、(13)得到节点加速度和节点速度。同时,作为流场的边界条件,结构的运动也会改变流场的状态,即Ut+Δt和
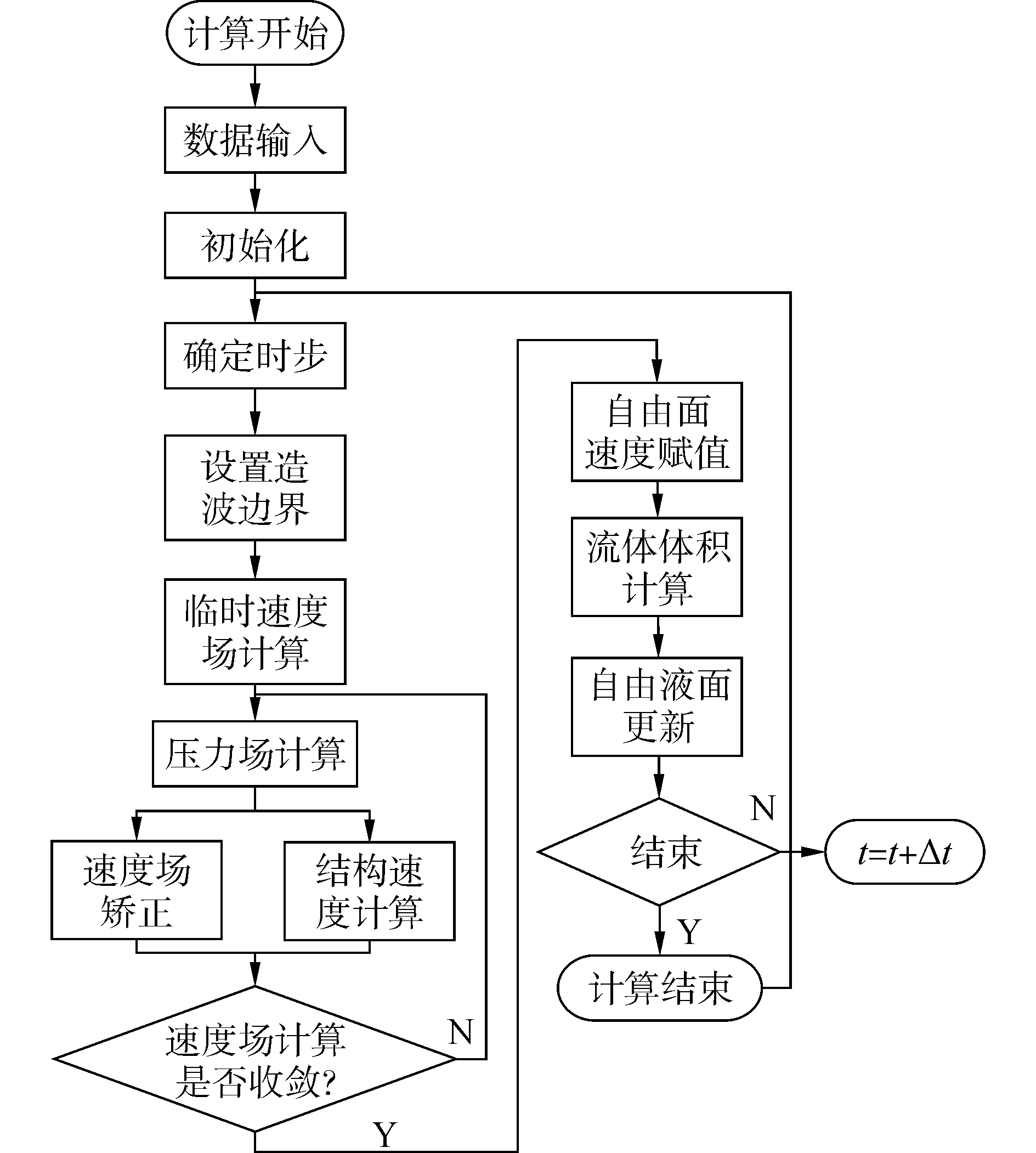
如图 5所示,“数据输入”模块读取计算必须的流体与结构信息,以及计算控制参数。其中流体运动粘性系数为0.000 001 145 m2/s,流体密度为1 000 kg/m3,重力加速度为9.8 m/s2,板长为22 m,弹性模量为2.1×1011 Pa,Poisson比为0.3,结构密度为7 860 kg/m3,横截面积为0.2 m2,横截面惯性矩为0.000 666 7 m4。“初始化”模块划分计算网格并设置网格属性。“确定时步”模块根据稳定性条件计算最大允许时步。“设置造波边界”模块基于式(9)设置造波端的边界条件实现造波。在“临时速度场计算”完成后进行n+1时步的压力场迭代(“压力场计算”模块)。根据更新后的压力场进行“速度场矫正”,同时将压力场转化为结构节点力进行“结构速度计算”。若流场速度与结构速度在耦合面处相等,则迭代收敛,否则继续调整压力场。“自由面速度赋值”模块根据收敛后的速度场设置自由液面边界条件,接着采用施主-受主网格技术进行“流体体积计算”。根据新时步的流体体积进行“自由液面更新”。重复上面过程直至计算结束。
|
Download:
|
| 图 5 流固耦合计算流程图 Fig. 5 Flow chart of the fluid-structure solver | |
模拟总网格数约50 000,并在水平与垂直板附近进行局部加密。模拟时步应足够小以捕捉到结构振动的不同模态和脉冲压力,这里取为0.000 5 s。垂直弹性板(简化为板条梁模型)等分为44个Euler单元,并从底至顶依次编号。模拟过程中,畸形波从甲板左侧涌入,向右传播并最终砰击垂直板。整个上浪砰击过程持续时间约10 s,不考虑相邻波浪的连续上浪砰击。
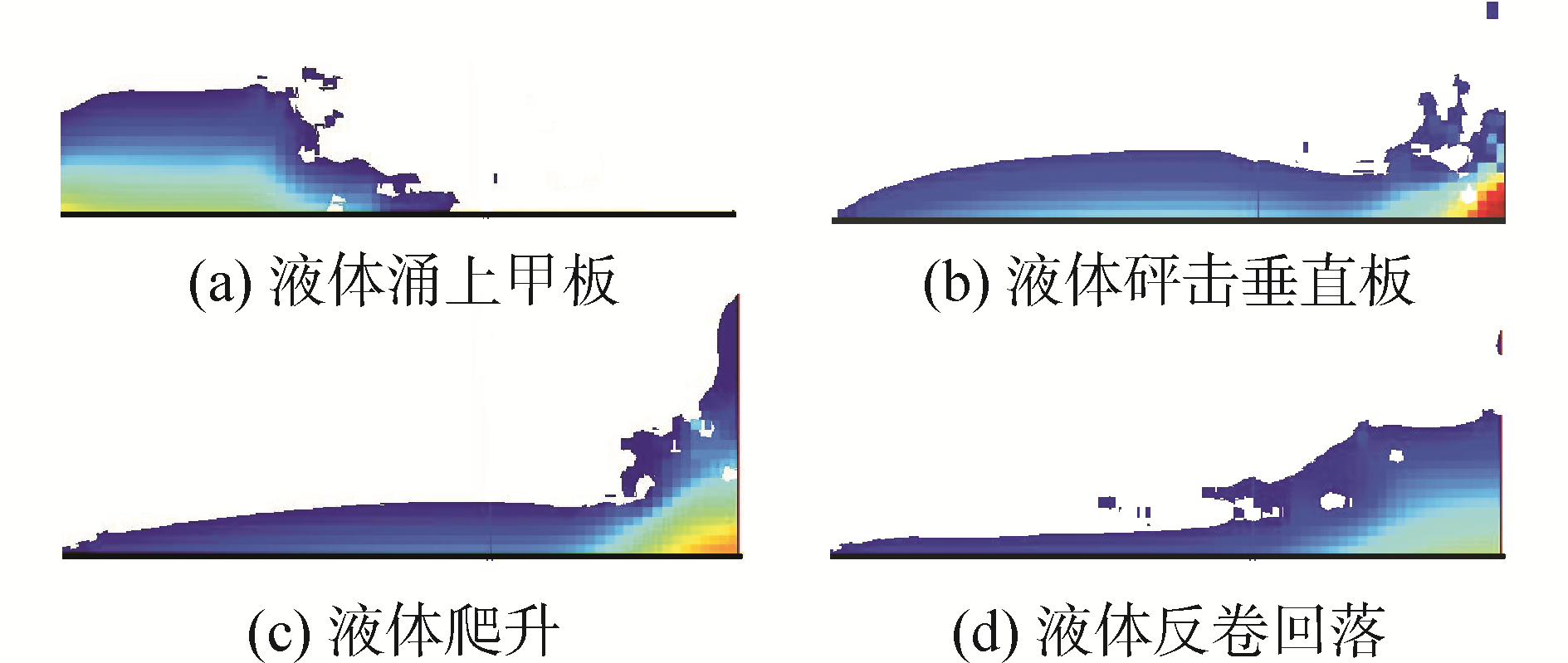
图 6为上浪砰击过程中不同阶段的液面形态。从图 6中可以看出,在到达垂直板之前,甲板上的波浪已经溃塌并伴随破碎现象,高速水体到达垂直板时对板底部造成较大的砰击载荷。由于板的阻碍作用,上浪水体开始沿垂直板爬升,此时,由于流体的反作用力,垂直板底端前部的水平甲板受到较大局部载荷。当爬升至最高点后,流体开始下落,并从甲板左端流入“大海”,此过程伴随着大量的波浪翻卷、破碎以及气泡现象。
|
Download:
|
| 图 6 畸形波上浪砰击液面轮廓 Fig. 6 Screen shots of the freak wave slamming | |
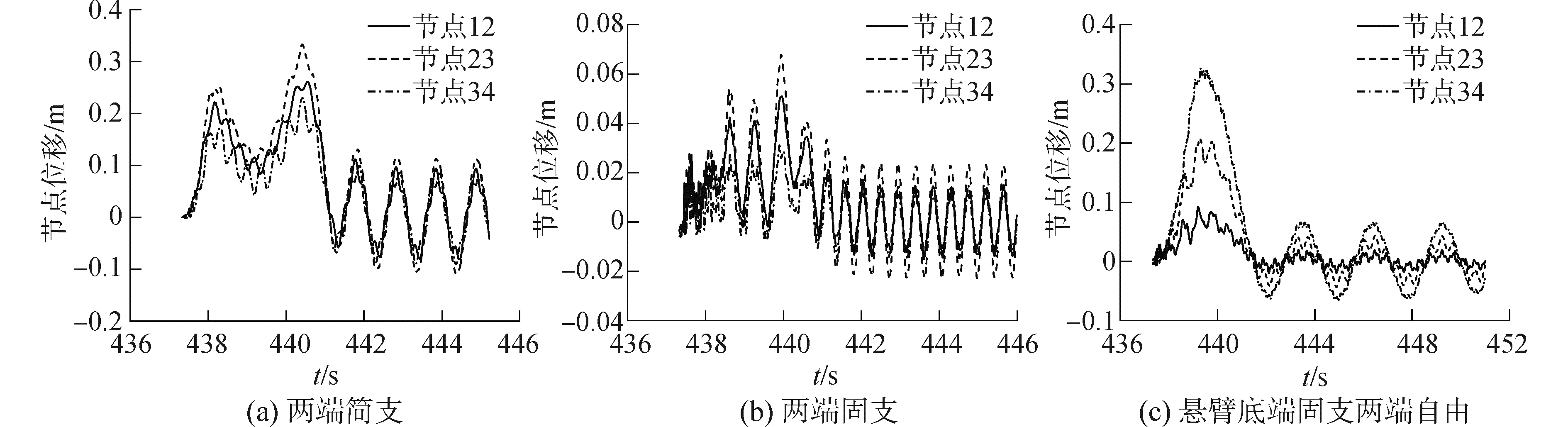
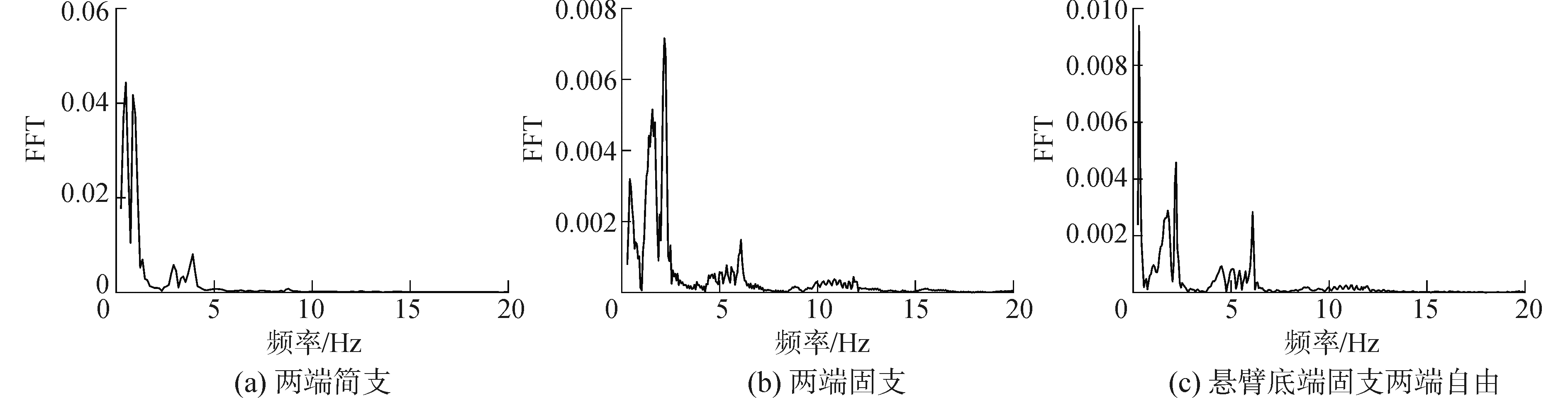
为研究不同边界条件下的垂直板动力响应,这里选择三种支撑形式:两端简支、两端固支和底端固支顶端自由。图 7为以上三种支撑形式的板节点位移,其中节点12、23和34分别距底部6、11.5和17 m,图中正向表示与上浪水体传播方向相同,波浪砰击开始于约302 s。可以看出,垂直板的节点位移曲线并不规则,且包括多阶模态的振动,这与上浪砰击现象的复杂性与瞬态冲击载荷有关。为研究激发的振动模态,图 8给出了三种支撑形式板节点位移的FFT曲线,注意这里选择节点4以便捕捉到振动的所有模态。
|
Download:
|
| 图 7 不同支撑形式板的节点位移 Fig. 7 Nodal displacement response of the beams with various supporters | |
|
Download:
|
| 图 8 不同支撑形式板的节点位移FFT变换 Fig. 8 FFT on the nodal displacement of beams with various supporters | |
表 2为不同支撑形式板的干频率以及通过FFT变换得到的湿频率。从表 2中可以看出砰击载荷激发了三阶模态。在图 8中可发现某频率附近出现双峰值,在表 3中体现为某干频率附近有2个湿频率与之对应。双峰值的产生是由于在上浪砰击的过程中结构呈现两种运动。以图 7(a)为例,在437~441 s时间范围内,由于流体与结构接触充分,附加质量效应明显,结构振动周期较长;而441 s后由于流体下落回流,流体与结构接触面积变小,附加质量效应减弱,结构振动频率相应增大,此时结构振动频率一般与干频率接近。对于不同支撑形式,其FFT变换峰值对应频率不同,但规律大体相似。
| 表 2 垂直板的干、湿频率 Tab.2 Wet and dry frequencies of beams |
| 表 3 不同位置处的最大有效砰击压力 Tab.3 Slamming pressure peaks at various positions |
表 3给出了三种支撑形式下不同高度位置处的最大砰击压力,并与刚性板进行对比。可以看出,考虑结构水弹性效应后,流场的砰击压力有所减小。在垂直板底部,简支边界对最大砰击压力的减小幅度较大,固支与悬臂边界对于砰击压力的减少效果小于简支边界,这是由于固支和悬臂边界在根部处的约束更强,更趋近于刚性边界。同时可以发现,固支和悬臂边界的垂直板底部砰击压力相同,这是由于两种支撑在底部接近,而顶端约束区别对于底部局部砰击压力的影响可以忽略。
5 结论1) 上浪砰击整体过程中垂直板振动频谱有双峰值现象发生。
2) 由于受到瞬态的砰击载荷,结构的动力响应中往往包含高阶模态。
3) 上浪后期水弹性附加质量效应影响较小,结构振动频率与干频率相当。
4) 受到水弹性效应的影响,与刚性结构相比,弹性结构表面的局部砰击压力有所降低,且结构的刚度越低,砰击压力的减小约明显。
| [1] |
DRAPER L. 'Freak' waves[J]. Marine observer, 1965, 35: 193-195. (  0) 0)
|
| [2] |
SAND S E, HANSEN N E, KLINTING P, et al. Freak wave kinematics[M]. Water Wave Kinematics. Dordrecht:Kluwer Academic, 1990:535-549.
(  0) 0)
|
| [3] |
STANSELL P. Distributions of freak wave heights measured in the North Sea[J]. Applied ocean research, 2004, 26(1/2): 35-48. (  0) 0)
|
| [4] |
LAVRENOV I. The wave energy concentration at the Agulhas current of South Africa[J]. Natural hazards, 1998, 17: 117-127. DOI:10.1023/A:1007978326982 (  0) 0)
|
| [5] |
MORI N, LIU P C, YASUDA T. Analysis of freak wave measurements in the Sea of Japan[J]. Ocean engineering, 2002, 29: 1399-1414. DOI:10.1016/S0029-8018(01)00073-7 (  0) 0)
|
| [6] |
KJELDSEN P S. Measurements of freak waves in Norway and related ship accidents[C]//Royal institution of naval architects international conference-Design and Operation for Abnormal Conditions Ⅲ. London, United Kingdom, 2005:31-38.
(  0) 0)
|
| [7] |
HU Zhe, XUE Hongxiang, TANG Wenyong, et al. A combined wave-dam-breaking model for rogue wave overtopping[J]. Ocean engineering, 2015, 104: 77-88. DOI:10.1016/j.oceaneng.2015.05.009 (  0) 0)
|
| [8] |
HU Zhe, TANG Wenyong, XUE Hongxiang, et al. Response of beams under the impact of freak waves[C]//Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering. San Francisco, USA, 2014:28.
(  0) 0)
|
| [9] |
DENG Yangfei, YANG Jianmin, TIAN Xinliang, et al. Experimental investigation on rogue waves and their impacts on a vertical cylinder using the Peregrine breather model[J]. Ships and offshore structures, 2016, 11(7): 757-765. DOI:10.1080/17445302.2015.1062654 (  0) 0)
|
| [10] |
邹丽, 王爱民, 宗智, 等. 岛礁地形畸形波演化过程的试验及小波谱分析[J]. 哈尔滨工程大学学报, 2017, 38(3): 344-350. ZOU Li, WANG Aimin, ZONG Zhi, et al. Experiment and wavelet analysis of the evolution process of freak waves around reefs[J]. Journal of Harbin Engineering University, 2017, 38(3): 344-350. (  0) 0)
|
| [11] |
刘首华, 牟林, 刘克修, 等. 畸形波研究的进展及存在问题[J]. 地球科学进展, 2013, 28(6): 665-673. LIU Shouhua, MU Lin, LIU Kexiu, et al. Research advance and problems in freak waves[J]. Advances in earth science, 2013, 28(6): 665-673. DOI:10.11867/j.issn.1001-8166.2013.06.0665 (  0) 0)
|
| [12] |
邓燕飞, 杨建民, 李欣, 等. 波浪水池中畸形波生成的研究综述[J]. 船舶力学, 2016, 20(8): 1059-1070. DENG Yanfei, YANG Jianmin, LI Xin, et al. A review on the freak wave generation in the wave tank[J]. Journal of ship mechanics, 2016, 20(8): 1059-1070. (  0) 0)
|
| [13] |
GAO Ningbo, YANG Jianmin, ZHAO Wenhua, et al. Numerical simulation of deterministic freak wave sequences and wave-structure interaction[J]. Ships and offshore structures, 2016, 11(8): 802-817. DOI:10.1080/17445302.2015.1073864 (  0) 0)
|
| [14] |
SOARES C G, FONSECA N, PASCOAL R, et al. Analysis of wave induced loads on a FPSO accounting for abnormal waves[J]. Journal of offshore mechanics and arctic engineering, 2006, 128(3): 241-247. DOI:10.1115/1.2166656 (  0) 0)
|
| [15] |
YOUNGS D L. Time-dependent multi-material flow with large fluid distortion[M]. New York: Academic Press, 1982: 273-285.
(  0) 0)
|
| [16] |
MAYER S, GARAPON A, SØRENSEN L S. A fractional step method for unsteady free-surface flow with applications to non-linear wave dynamics[J]. International journal for numerical methods in fluids, 1998, 28: 293-315. DOI:10.1002/(ISSN)1097-0363 (  0) 0)
|
| [17] |
HU Zhe, TANG Wenyong, XUE Hongxiang, et al. Numerical wave tank based on a conserved wave-absorbing method[J]. China ocean engineering, 2015, 30(1): 137-148. (  0) 0)
|
| [18] |
HU Zhe, TANG Wenyong, XUE Hongxiang, et al. A SIMPLE-based monolithic implicit method for strong-coupled fluid-structure interaction problems with free surfaces[J]. Computer methods in applied mechanics and engineering, 2016, 299: 90-115. DOI:10.1016/j.cma.2015.09.011 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


