2. 武汉理工大学 交通学院, 湖北 武汉 430063;
3. 北京树优信息技术有限公司, 北京 100006
2. School of Transportation, Wuhan University of Technology, Wuhan 430063, China;
3. SOYOTEC LIMITED, Beijing 100006, China
船型优化属于典型的高维、计算昂贵、“黑盒”, 需采用高性能优化算法才能在有限时间内搜索性能最优解。目前,该领域学者关注最多的是几种常规智能优化算法及其改进方法。在国外,Dejhalla等[1]采用遗传算法对S60兴波阻力进行优化。Tahara等[2]基于CFD方法采用多目标遗传算法对某油船快速性和操纵性进行优化。Campana等[3]提出一种粒子群优化算法,用于优化船舶垂荡运动的幅度。Huang等[4]将精英方案和摄动法相结合提出一种性能更优的人工蜂群算法,用于对某船型阻力性能进行优化。在国内,张宝吉[5]采用基本遗传算法和小生境遗传算法研究Wigley和S60船型的阻力性能。冯佰威[6]在自主开发的软件平台上将遗传算法与梯度方法进行组合,应用于船型水动力性能优化。李胜忠[7]将改进的粒子群全局优化算法应用在某船快速性、耐波性、操纵性三目标优化。唐正茂[8]将遗传算法应用于35 000吨油船的概念设计阶段。
随着基于仿真优化技术的提出,传统优化算法优化效率低的缺点较为突出。尤其对于高维问题,常规优化算法易出现“早熟”现象。若单次仿真分析所需时间长,会导致有限时间内很难直接进行仿真优化。因此,采用高效、适用船型优化的算法来缓解基于仿真优化计算费用高的缺陷是船型优化中应该重点研究的内容。近几年出现的一类基于概率模型的随机优化算法,如交叉熵法[9]、模型参考自适应搜索[10]等具有处理高维复杂优化问题的能力、控制参数少且具有理论收敛性。本文研究的方法是在文献[11]基础上改进而来,该方法还处于理论研究阶段,不适合应用在带约束的实际优化问题。本文从3方面对CE法进行改进:1)设计自适应的初始方差选取方法;2)在算法中嵌入“接受-拒绝”法;3)将最优迭代残差值满足指定精度作为一个停止准则。通过数值算例测试改进方法的可行性和高效性并将其应用于5100TEU集装箱船兴波阻力性能优化。
1 CE法的基本原理及改进CE法是由Rubinstein提出并将其应用于稀少事件概率估计。随后,Rubinstein又将该方法演变成优化算法用于求解不同类型的优化问题。CE法是一种典型的基于概率模型的算法,已成功应用于解决“旅行商问题”、“背包问题”等复杂优化问题。
CE法包括两个基本步骤:1)从抽样分布中随机抽取一组候选方案;2)根据候选方案更新抽样分布。假设设计空间服从概率分布gk的递推式为
| $ {g_{k + 1}}\left( \mathit{\boldsymbol{x}} \right) = \frac{{H\left( \mathit{\boldsymbol{x}} \right){g_k}\left( \mathit{\boldsymbol{x}} \right)}}{{\int_x {H\left( \mathit{\boldsymbol{x}} \right){g_k}\left( \mathit{\boldsymbol{x}} \right)\nu {\rm{d}}x} }} $ | (1) |
式中:H(x)是向量x的函数值,x=[x1, x2, …, xn], ν是勒贝格测度。
因为H(x)满足分布gk的期望值可以定义为:
| $ {E_{{g_k}}}\left[ {H\left( \mathit{\boldsymbol{x}} \right)} \right] = \int_\mathit{\boldsymbol{x}} {H\left( \mathit{\boldsymbol{x}} \right){g_k}\nu {\rm{d}}\mathit{\boldsymbol{x}}} $ | (2) |
对式(1)两边同时乘上H(x),再分别求积分可得
| $ \begin{array}{*{20}{c}} {{E_{{g_{k + 1}}}}\left[ {H\left( \mathit{\boldsymbol{x}} \right)} \right] = \frac{{\int_x {{H^2}\left( \mathit{\boldsymbol{x}} \right){g_k}\nu {\rm{d}}\mathit{\boldsymbol{x}}} }}{{\int_x {H\left( \mathit{\boldsymbol{x}} \right){g_k}\nu {\rm{d}}\mathit{\boldsymbol{x}}} }} = }\\ {\frac{{{E_{{g_k}}}\left[ {{{\left( {H\left( \mathit{\boldsymbol{x}} \right)} \right)}^2}} \right]}}{{{E_{{g_k}}}\left[ {H\left( \mathit{\boldsymbol{x}} \right)} \right]}} \ge {E_{{g_k}}}\left[ {H\left( \mathit{\boldsymbol{x}} \right)} \right]} \end{array} $ | (3) |
式(3)表明:迭代后抽取更优解的概率会更大,当迭代一定次数时,概率分布收敛到退化分布,得到的解逐渐逼近全局最优值。
由于概率分布gk很难直接用于抽样,实际应用中通常会选用抽样方便的参数分布fθ代替参考分布gk。图 1为采用CE法对一元函数H(x)进行优化的迭代过程示意图。图 1(a)是抽样分布的迭代示意图,图中抽样分布为高斯分布,横坐标为变量取值,纵坐标为概率密度函数值;图 1(b)是函数的性能空间结构图,横坐标为变量的取值,纵坐标为目标函数值。概率分布的更新顺序是1-2-3-4, 最终收敛到退化分布并找到最优方案x*。
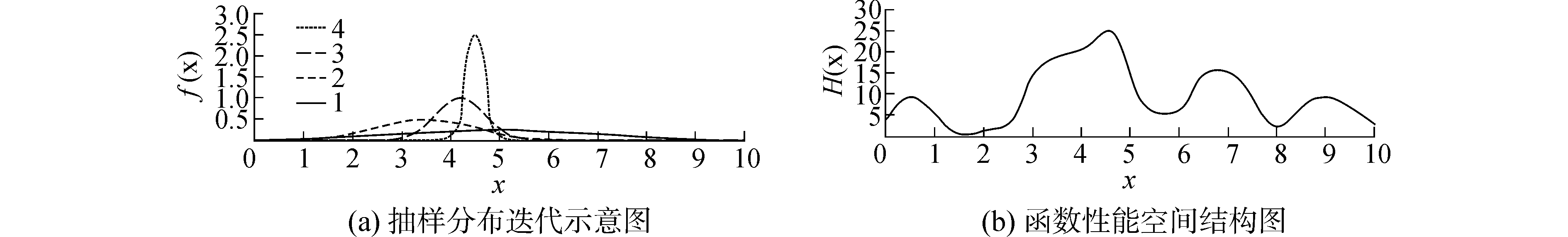
|
Download:
|
| 图 1 CE法的优化迭代示意图 Fig. 1 Optimization iteration diagram for CE method | |
对于求最大值的优化问题:
| $ {\mathit{\boldsymbol{x}}^ * } = \arg \left( {\max H\left( \mathit{\boldsymbol{x}} \right)} \right),\mathit{\boldsymbol{x}} \in \mathit{\boldsymbol{X}},\mathit{\boldsymbol{X}} \subseteq {{\bf{R}}^n}, $ | (4) |
式中:x*是最优解,H是目标函数,X是解空间。
采用改进的CE法对式(4)进行优化,优化的基本步骤及改进方法如下:
1) 确定初始概率密度函数fθ0(·),指定参数ρ∈(0, 1]及非递减函数S(·),给出期望和方差的初始取值,令迭代步数k=0。
为了将CE法应用于工程优化,本文设计了一种自适应的初始方差取值方法,即按公式
2) 从选取的概率密度函数中抽取Nk个样本点,并计算各个样本点对应的目标函数值,将目标函数值按从小到大排序,再计算目标函数值1-ρ的分位数γk。
本文将“接受-拒绝”法嵌入算法中用于处理除变量变化范围之外的约束优化问题,即
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{xN}^k = \left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}_i} \cup \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{{x_i} - 1}^k,\;\;\;h\left( {{\mathit{\boldsymbol{x}}_i}} \right) \in I\left( {{\mathit{\boldsymbol{x}}_i}} \right)\\ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{{x_i} - 1}^k,\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right.}\\ {i \le {N_k}} \end{array} $ | (5) |
式中:ΛkxN为第k次迭代时N个可行方案的集合,xi为第i个候选方案,Λkxi-1为第k次迭代前i-1个可行方案的集合,h(xi)是xi对应的约束函数值,I(xi)是xi的约束条件。
从而避免了违反约束的方案进入函数评估阶段,造成不必要的计算资源浪费。
3) 确定参考分布gk+1(x),并计算参考分布gk+1(x)与参数分布fθ之间的库尔贝克-莱布勒(Kullback-leibler,KL)散度。
KL散度的定义式为
| $ K\left( {g,f} \right) = {{\rm{E}}_g}\left[ {\ln \frac{{g\left( \mathit{\boldsymbol{x}} \right)}}{{f\left( \mathit{\boldsymbol{x}} \right)}}} \right] $ | (6) |
参考分布gk+1(x)可定义为
| $ \begin{array}{*{20}{c}} {{g_{k + 1}}\left( \mathit{\boldsymbol{x}} \right) = {\alpha _k}\frac{{S\left( {H\left( \mathit{\boldsymbol{x}} \right)} \right)I\left( {H\left( \mathit{\boldsymbol{x}} \right),{\gamma _k}} \right){f_{{\theta _k}}}\left( \mathit{\boldsymbol{x}} \right)}}{{{{\rm{E}}_{{\theta _k}}}\left[ {S\left( {H\left( \mathit{\boldsymbol{x}} \right)} \right)I\left( {H\left( \mathit{\boldsymbol{x}} \right),{\gamma _k}} \right)} \right]}} + }\\ {\left( {1 - {\alpha _k}} \right){f_{{\theta _k}}}\left( \mathit{\boldsymbol{x}} \right)} \end{array} $ | (7) |
式中:αk∈(0, 1]称为光滑参数,Eθk[·]为服从概率密度函数fθk的期望值,I(H(x), γk)为指示函数,用于筛选“精英”方案。
抽样分布采用多元正态分布,其表达式为
| $ \begin{array}{*{20}{c}} {f\left( {{x_1},{x_2}, \cdots ,{x_n}} \right) = {{\left( {2{\rm{ \mathsf{ π} }}} \right)}^{ - \frac{n}{2}}}{{\left| \mathit{\boldsymbol{C}} \right|}^{ - \frac{1}{2}}} \cdot }\\ {\exp \left\{ { - \frac{1}{2}{{\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\mu }}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{C}}^{ - 1}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\mu }}} \right)} \right\}} \end{array} $ | (8) |
式中:C为协方差矩阵,x=[x1 x2 … xn]T,μ=[μ1 μ2 … μn]T,μi=E(xi)。
期望和协方差矩阵的更新公式为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\mu }}_{k + 1}} = {\alpha _k}\frac{{{\Sigma _{x \in {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_k}}}S\left( {H\left( \mathit{\boldsymbol{x}} \right)} \right)I\left( {H\left( \mathit{\boldsymbol{x}} \right),{\gamma _k}} \right)\mathit{\boldsymbol{x}}}}{{{\Sigma _{x \in {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_k}}}S\left( {H\left( \mathit{\boldsymbol{x}} \right)} \right)I\left( {H\left( \mathit{\boldsymbol{x}} \right),{\gamma _k}} \right)}} + }\\ {\left( {1 - {\alpha _k}} \right){\mathit{\boldsymbol{\mu }}_k}}\\ {{\mathit{\boldsymbol{C}}_{k + 1}} = {\alpha _k} \cdot }\\ {\frac{{{\Sigma _{x \in {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_k}}}S\left( {H\left( \mathit{\boldsymbol{x}} \right)} \right)I\left( {H\left( \mathit{\boldsymbol{x}} \right),{\gamma _k}} \right)\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{\mu }}_{k + 1}}} \right){{\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{\mu }}_{k + 1}}} \right)}^{\rm{T}}}}}{{{\Sigma _{x \in {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_k}}}S\left( {H\left( \mathit{\boldsymbol{x}} \right)} \right)I\left( {H\left( \mathit{\boldsymbol{x}} \right),{\gamma _k}} \right)}} + }\\ {\left( {1 - {\alpha _k}} \right)\left( {{\mathit{\boldsymbol{C}}_k} + \left( {{\mathit{\boldsymbol{\mu }}_k} - {\mathit{\boldsymbol{\mu }}_{k + 1}}} \right){{\left( {{\mathit{\boldsymbol{\mu }}_k} - {\mathit{\boldsymbol{\mu }}_{k + 1}}} \right)}^{\rm{T}}}} \right)} \end{array} $ | (10) |
式中:Λk是每次迭代抽取样本的集合。算法收敛时,μk→μ*,协方差矩阵Ck的各元素接近于0。
4) 判断是否满足停止准则。若满足,则算法停止;若不满足,则令k=k+1,同时算法跳回到步骤2)。
优化算法的停止准则一般为最大迭代次数和最大迭代时间,取值太大,会造成计算资源的浪费;取值太小,优化迭代不收敛。为保证迭代收敛时函数评估数最小,本文根据改进的CE法每次迭代的最优值构成一个非递减函数的特点,将每次迭代后最优值的残差满足指定精度作为一个停止准则,即:
| $ {S_i} = \left\{ \begin{array}{l} 0,\;\;\;\;\;{\left[ {H_k^ * \left( \mathit{\boldsymbol{x}} \right) - H_{k - 1}^ * \left( \mathit{\boldsymbol{x}} \right) \le \varepsilon } \right]_n}\\ 1,\;\;\;\;\;其他 \end{array} \right. $ | (11) |
式中:Hk*(x)是第k次迭代的最优值,[·]n定义为·连续n次成立。
2 数值算例的测试本文分别采用改进的CE法、非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA2)和多岛遗传算法(multi-island genetic algorithm,MIGA)对4个高维数值函数进行优化。
4个数值测试函数分别代表不同类型的高维空间,式(12)~(15)为其具体表达式。改进的CE法参数设置为:αk=2/(k+100)0.501,ρ=0.1,Nk=max{100, k1.01},初始概率模型的期望值在变量范围内随机选取,各变量的方差都取为100。用于对比的遗传算法采用的是集成优化平台ISIGHT内嵌的NSGA2和MIGA。NSGA2中种群规模和遗传代数、MIGA中“岛”数、子种群规模和遗传代数设置见表 1,其余参数取为专家推荐值。
| 表 1 NSGA2和MIGA中参数的设置 Tab.1 Parameters in NSGA2 and MIGA |
1) Griewank函数(n=20, -10≤xi≤10, i=1, 2, …, n)
| $ {H_1}\left( \mathit{\boldsymbol{x}} \right) = \frac{1}{{4000}}\sum\limits_{i = 1}^n {x_i^2} + \prod\limits_{i = 1}^n {\cos \left( {\frac{{{x_i}}}{{\sqrt i }}} \right) - 1} $ | (12) |
2) Powell函数(n=20, -10≤xi≤10, i=1, 2, …, n)
| $ \begin{array}{*{20}{c}} {{H_2}\left( \mathit{\boldsymbol{x}} \right) = 1 + \sum\limits_{i = 1}^{\left( {n - 2} \right)/2} {\left[ {{{\left( {{x_{2i - 1}} + 10{x_{2i}}} \right)}^2} + } \right.} }\\ {5{{\left( {{x_{2i + 1}} - {x_{2i + 2}}} \right)}^2} + {{\left( {{x_{2i}} - 2{x_{2i + 1}}} \right)}^4} + }\\ {\left. {10{{\left( {{x_{2i - 1}} - {x_{2i + 2}}} \right)}^4}} \right]} \end{array} $ | (13) |
3) Levy函数(n=40, -10≤xi≤10, i=1, 2, …, n)
| $ \begin{array}{*{20}{c}} {{H_3}\left( \mathit{\boldsymbol{x}} \right) = 10{{\sin }^2}\left( {{\rm{ \mathsf{ π} }}{x_1}} \right) + }\\ {\sum\limits_{i = 1}^{n - 1} {100x_i^2\left( {1 + 10{{\sin }^2}\left( {{\rm{ \mathsf{ π} }}{x_{i + 1}}} \right)} \right)} + }\\ {100\left( {_n^x - 1} \right)2 + 1} \end{array} $ | (14) |
4) Pinter函数(n=20, -10≤xi≤10, i=1, 2, …, n)
| $ \begin{array}{*{20}{c}} {{H_4}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^n {ix_i^2} + \sum\limits_{i = 1}^n {20i{{\sin }^2}\left( {{x_{i - 1}}\sin {x_i} - } \right.} }\\ {\left. {{x_i} + \sin {x_{i + 1}}} \right) + \sum\limits_{i = 1}^n {i\lg \left( {1 + i\left( { - 2{x_i} + } \right.} \right.} }\\ {\left. {{{\left. {3{x_{i + 1}} - \cos {x_i} + 1} \right)}^2}} \right)} \end{array} $ | (15) |
由于随机机理的影响,对同一优化问题,优化算法重复搜索的结果存在一定差异。本文采用10次独立重复试验的平均值作为最优值(见表 2),图 2为优化测试函数的迭代收敛对比图。

|
Download:
|
| 图 2 优化迭代收敛对比图 Fig. 2 Contrast of convergence history | |
| 表 2 不同算法的测试结果 Tab.2 Test results of different algorithms |
由表 2可知:函数评估数相同时,改进的CE法较NSGA2和MIGA能得到更接近理论最优值的解。图 2表明:对4个数值函数,改进的CE法较NSGA2和MIGA的综合优化性能更好,MIGA的优化性能最差。测试Griewank函数时,当函数评估次数小于13 000, 改进的CE法性能较NSGA2差;当函数评估数超过13 000时,改进的CE法较NSGA2的性能更好并最终搜索到最优解,而NSGA2收敛到0.014 8附近并不再下降。测试Powell函数时,改进的CE法在整个优化过程中性能一直最好并最终收敛到全局最优解。测试Levy函数时,改进的CE法与NSGA2的性能接近。测试Pinter函数时,改进的CE法可以搜索到全局最优解,而NSGA2最终收敛到700附近,MIGA随着迭代的进行仍然有进一步下降的趋势,但所需函数评估数过大。
由于改进的CE法具有概率统计学作为理论支撑,相比通过模拟生物进化过程而演化出的遗传算法更具有数学上的指导性。从产生候选方案的机理分析,改进的CE法是从概率模型中抽样,不仅保证了抽样的全局性,而且通过保留的“精英方案”指引参数更新,从而为寻找更优方案提供搜索方向,相比通过选择、交叉、变异(MIGA中还包含迁移)产生新方案的遗传算法,改进的CE法能更直接的向高性能区域进行搜索。因此,改进的CE法表现出较传统遗传算法更优的性能。
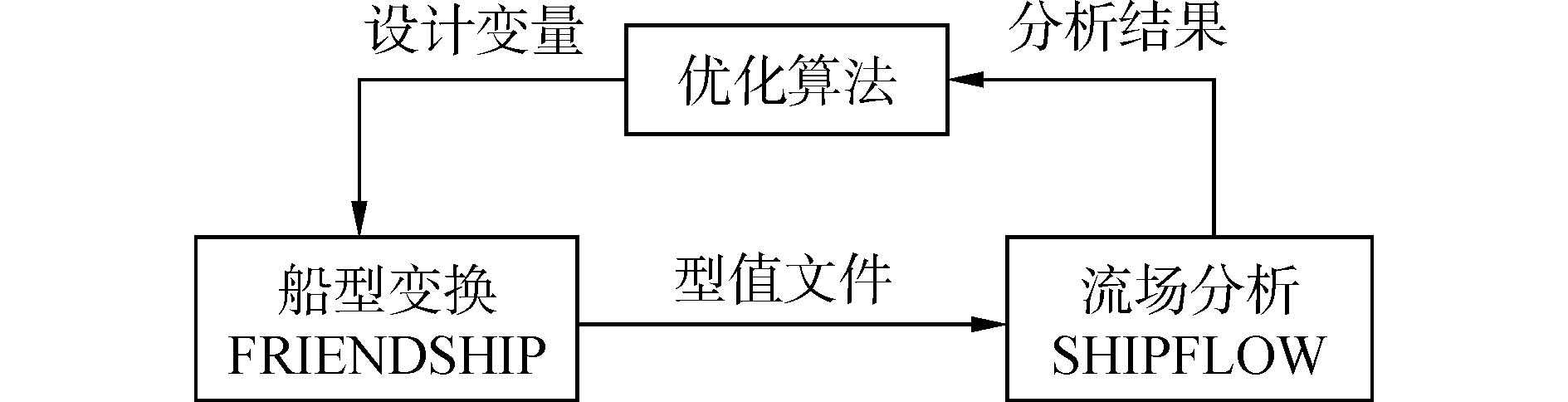
3 5100TEU集装箱船艏部线型优化为研究改进的CE法在基于仿真船型优化中的性能。本文将改进的CE法用于5100TEU集装箱船船型艏部参数对兴波阻力性能的优化。船型变换采用参数建模软件FRIENDSHIP,兴波阻力性能通过SHIPFLOW软件中的势流计算模块进行分析,优化算法包括改进的CE法、NSGA2和MIGA。仿真优化框架见图 3,每次迭代需判断是否满足算法停止准则,如果满足则算法停止;否则继续迭代。
|
Download:
|
| 图 3 仿真优化框架示意图 Fig. 3 Simulation optimization framework | |
船型参数化模型为快速生成光顺船型提供了技术支撑。FRIENDSHIP中曲面的生成方式有多种,需根据曲面的几何特征确定具体的曲面生成方式。参数化曲面生成的一般流程为:1)确定曲线所在位置的特征参数;2)通过宏文件描述曲面位置域上的横剖线;3)采用元曲面法生成光顺的船体曲面。5100TEU集装箱船主尺度参数为船长Lpp=284.16 m,水线长LWL=288.66 m,型宽Bwl=21.8 m, 型深D=13.5 m, 排水量Δ=82 885 t, 方形系数Cb=0.681。
优化设计变量有10个,变量的名称、物理含义、初始值以及变化范围见表 3。
| 表 3 10个优化设计变量 Tab.3 10 optimization design variables |
SHIPFLOW软件可用于进行船舶水动力性能分析,其中兴波阻力性能是基于势流理论采用高阶面元法计算得到。SHIPFLOW计算精度在可接受的范围内使得计算时间大大缩减,为在有限时间内完成基于仿真的船型优化提供支撑。
兴波阻力性能计算过程中,假设流体为理想流体,定常速度势为φ,满足非线性自由液面边界条件、物面边界条件和辐射条件。采用Rankine源法求解φ,根据伯努利方程计算流场压力分布,将得到的流体压力沿船体湿表面进行积分,从而得到船体受到的作用力,该作用力在运动方向的投影取负值即为船体所受兴波阻力,最后将兴波阻力无因次处理可得兴波阻力系数。
采用SHIPFLOW对5100TEU集装箱船兴波阻力性能进行计算,模型的缩尺比为50,流体的密度取为999.34 kg/m3,重力加速度为9.81 m/s2,计算工况为Fr=0.26。船体曲面采用面元网格,为保证流场计算的准确性,船模艏、艉部网格和自由液面网格适当加密。计算域为横向宽度取1.046 Lpp,纵向艏部向前取0.5 Lpp,艉部向后取1.137 Lpp,总的面元数为10 072个。
文献[12]表明SHIPFLOW的势流计算模块对集装箱船兴波阻力性能的预报满足船型优化对精度的要求。通过计算,母型船兴波阻力系数计算结果为:Cw=0.837 ×10-3。
3.3 优化数学模型及结果分析 3.3.1 优化数学模型的建立优化对象:5100TEU集装箱船艏部型线;
优化目标:Fr=0.26时,兴波阻力系数最小;
优化变量:如表 3所示;
约束条件如式(16)所示
| $ \left\{ \begin{array}{l} \frac{{\Delta - {\Delta _{{\rm{opt}}}}}}{\Delta } \le 1\% \\ \frac{{L - {L_{{\rm{opt}}}}}}{L} \le 1\% \\ \frac{{S - {S_{{\rm{opt}}}}}}{S} \le 1\% \end{array} \right.; $ | (16) |
式中:Δ、L、S分别为母型船的排水量、浮心纵向位置和湿表面积,下标opt为其最优值。
优化算法:
1) 改进的CE法:光滑参数αk=8/(k+100)0.501、每次迭代抽取的方案数Nk=120、迭代50次、初始概率模型的期望值在约束范围内随机选取,各变量的方差按公式
2) NSGA2:种群规模为120、遗传代数为50;
3) MIGA:子种群规模为30、“岛”数为4、遗传代数为50。
仿真优化流程如图 3所示,优化在多台品牌机上进行,处理器为i5-3470 CPU @ 3.20 GHz 3.60 GHz,单次兴波阻力性能计算需要2.5 min,精度ε= 10-6。
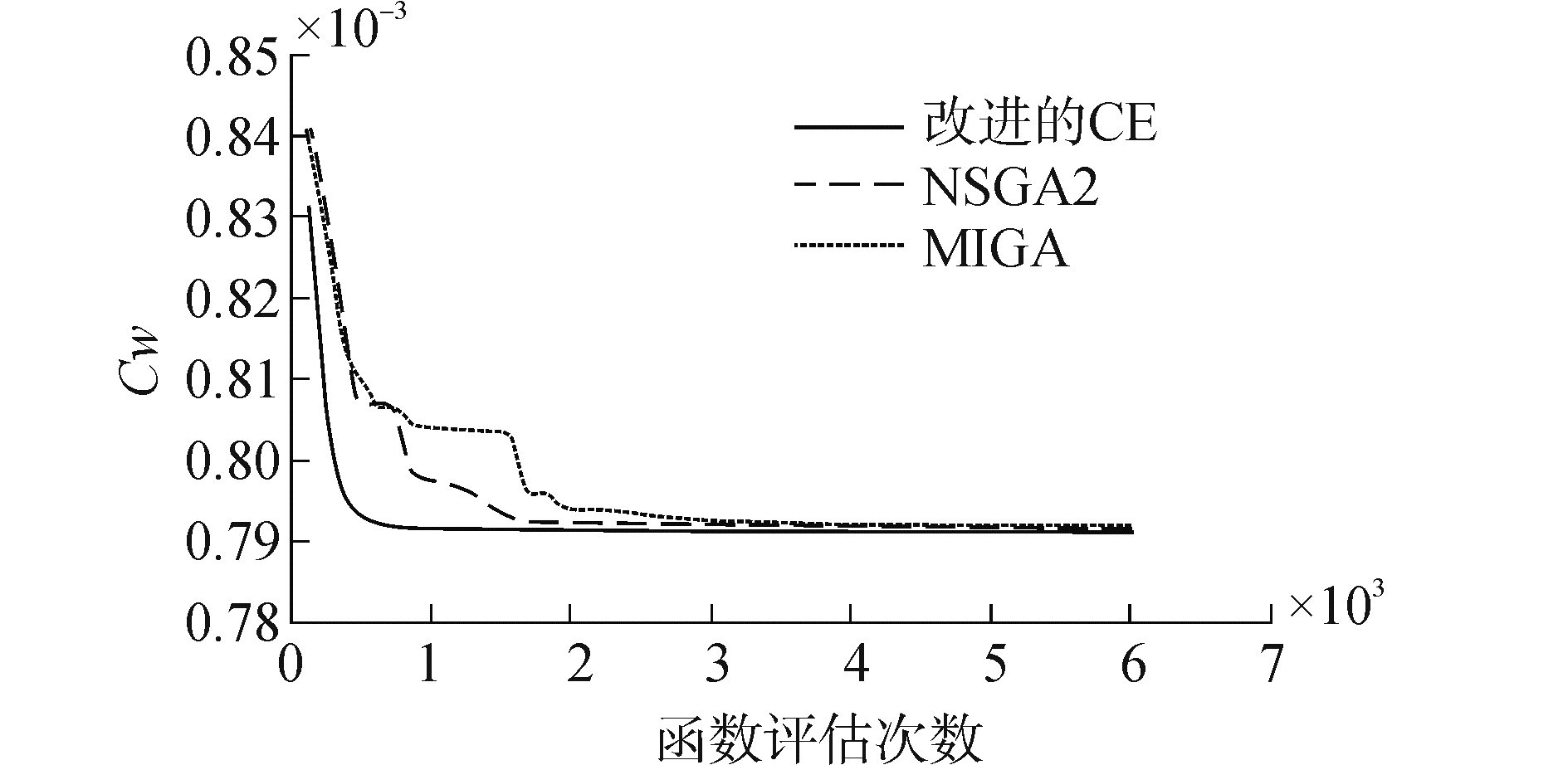
3.3.2 优化结果分析考虑随机优化算法中存在的随机性,重复10次优化,每次优化结果如表 4所示。取10次优化结果的均值作迭代收敛对比图,如图 4所示(横坐标为总的函数评估数,纵坐标为兴波阻力系数)。
|
Download:
|
| 图 4 优化迭代收敛对比图 Fig. 4 Contrast of convergence history | |
| 表 4 10次重复试验的结果 Tab.4 Results of 10 repeated trials |
根据表 5可知,改进的CE法鲁棒性最好,NSGA2的鲁棒性较MIGA略好。图 4表明:改进的CE法在迭代初期就向性能较优的方向移动并很快收敛到最优解,性能较优的是NSGA2,收敛速度最慢的是MIGA。3种优化算法最优解都收敛到Cw=0.791 ×10-3,优化后兴波阻力性能降低5.5%。在达到相同最优解的试验中,改进的CE法进行了2 160次函数评估,NSGA2进行了3 215次函数评估,MIGA进行了4 088次函数评估。优化结果表明:改进的CE法在5100TEU集装箱船兴波阻力性能优化中,优化效率较NSGA2和MIGA高。优化后,兴波阻力性能最优的方案如表 5所示。
| 表 5 兴波阻力性能最优的方案 Tab.5 Hull form parameters with optimum wave-making resistance |
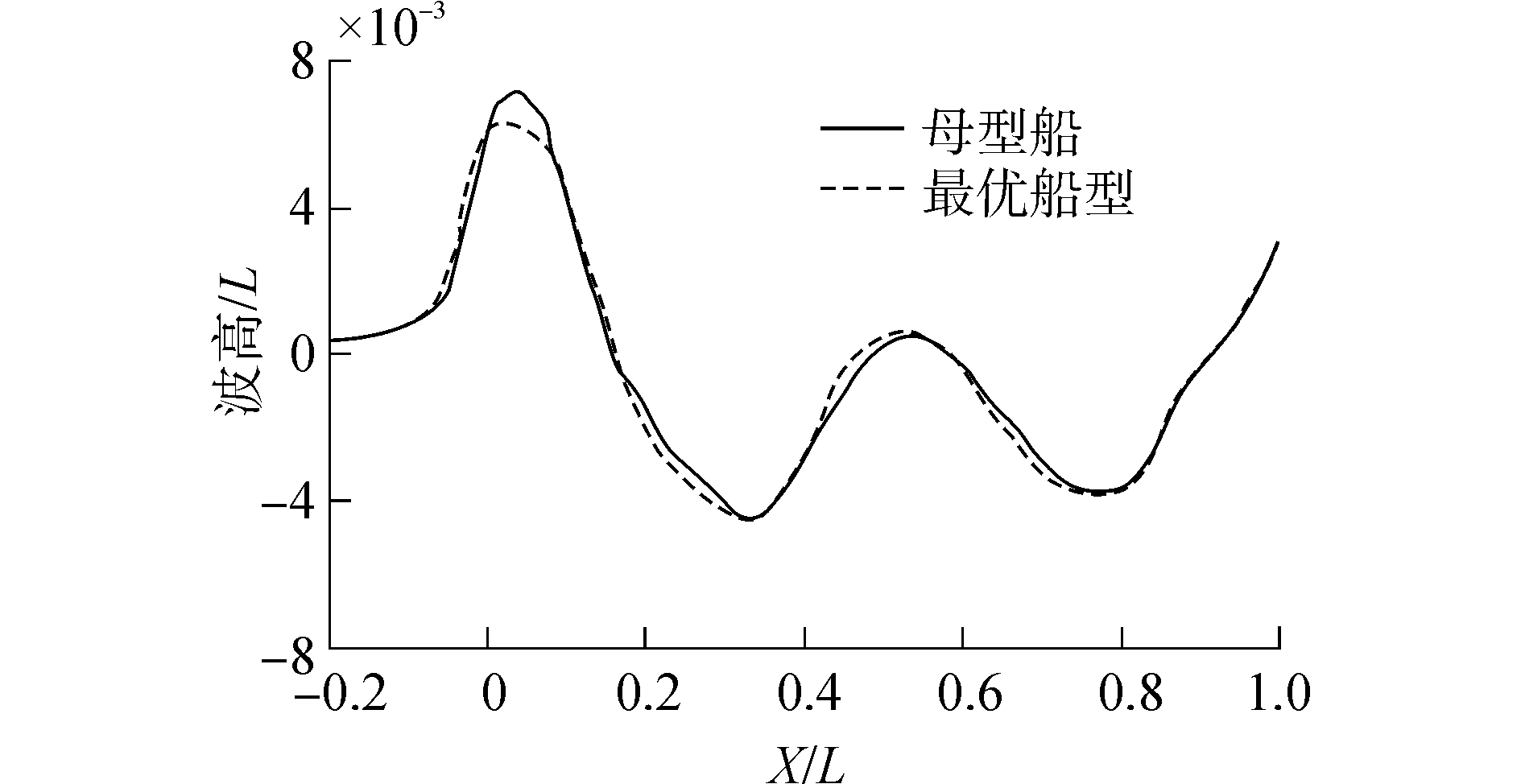
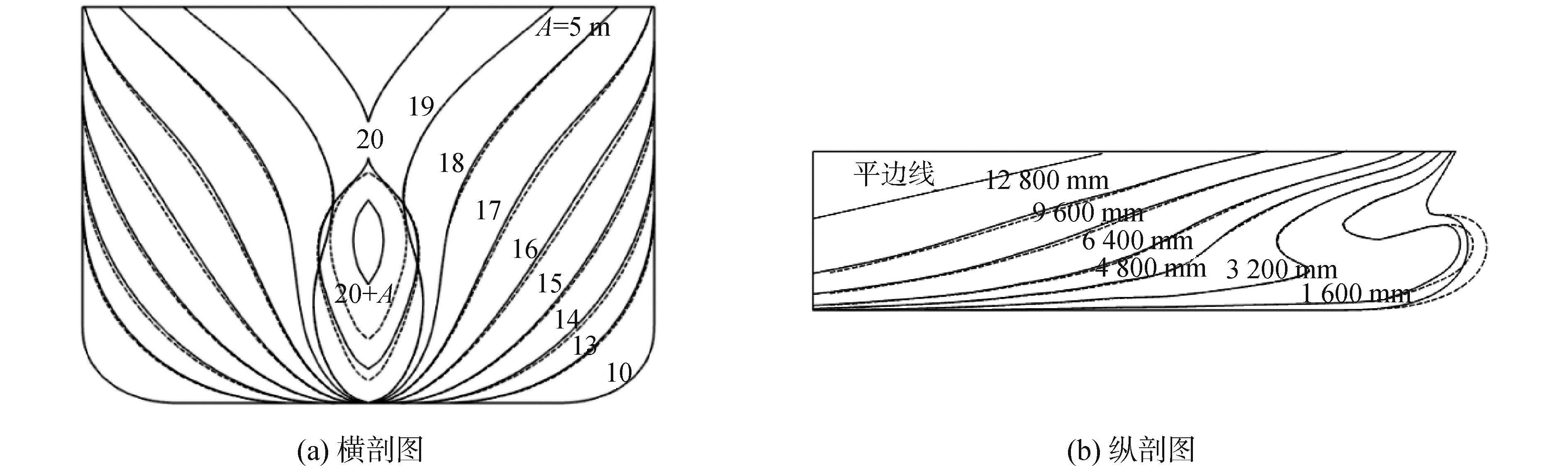
母型船与兴波阻力性能最优船型的船体表面波形对比如图 5所示,横剖线和纵剖线对比图分别如图 6所示, 图中A为20站位向船艏方向移动的距离,A为5 m。
|
Download:
|
| 图 5 船体表面波形对比图 Fig. 5 Contrast of hull surface waveform | |
|
Download:
|
| 图 6 剖线对比图 Fig. 6 Contrast of full form lines | |
根据图 5可知,优化后的5100TEU集装箱船船型艏部兴波下降明显。对母型船和兴波阻力最优船型进行总阻力性能分析,母型船的总阻力系数Ct=4.066 ×10-3,兴波阻力最优船型的总阻力系数Ct=4.009 × 10-3,即总阻力性能降低1.4%。图 6表明:优化后的船型球鼻艏型线改变较大,其中球鼻艏长度达到变量允许的最大值,球鼻艏高度略有下降。使得优化后的船型球鼻艏产生的波系和船体的波系形成更有利的干扰,对船艏兴波起到抑制作用,从而降低船艏兴波高度。
4 总结1) 改进的CE法可以自适应的根据变量变化范围确定初始方差的取值,且能处理带复杂约束的优化问题。
2) 通过数值函数的测试结果可知:改进的CE法较常规智能优化算法(NSGA2和MIGA)具有更好的优化性能。
3) 对5100TEU集装箱船兴波阻力性能优化问题,改进的CE法鲁棒性好且搜索到相同最优解时所需函数评估数最少。
| [1] |
DEJHALLA R, MRŠA Z, VUKOVIČ S. Application of genetic algorithm for ship hull form optimization[J]. International shipbuilding progress, 2001. (  0) 0)
|
| [2] |
TAHARA Y, TOHYAMA S, KATSUI T. CFD-based multi-objective optimization method for ship design[J]. International journal for numerical methods in fluids, 2006, 52(5): 499-527. DOI:10.1002/(ISSN)1097-0363 (  0) 0)
|
| [3] |
CAMPANA E F, LIUZZI G, LUCIDI S, et al. New global optimization methods for ship design problems[J]. Optimization and engineering, 2009, 10(4): 533-555. DOI:10.1007/s11081-009-9085-3 (  0) 0)
|
| [4] |
HUANG Fuxin, WANG Lijue, YANG Chi. A new improved artificial bee colony algorithm for ship hull form optimization[J]. Engineering optimization, 2016, 48(4): 672-686. DOI:10.1080/0305215X.2015.1031660 (  0) 0)
|
| [5] |
张宝吉. 船体线型优化设计方法及最小阻力船型研究[D]. 大连: 大连理工大学, 2009. ZHANG Baoji. Research on optimization design of hull lines and minimum resistance hull form[D]. Dalian:Dalian University of Technology, 2009. (  0) 0)
|
| [6] |
冯佰威. 基于多学科设计优化方法的船舶水动力性能综合优化研究[D]. 武汉: 武汉理工大学, 2011. FENG Baiwei. The comprehensive optimization research of the ship hydrodynamic performance based on MDO[D]. Wuhan:Wuhan University of Technology, 2011. (  0) 0)
|
| [7] |
李胜忠. 基于SBD技术的船舶水动力构型优化设计研究[D]. 北京: 中国舰船研究院, 2012. LI Shengzhong. Research on hull form design optimization based on SBD technique[D]. Beijing:China ship research and development academy, 2012. (  0) 0)
|
| [8] |
唐正茂. 智能优化算法适用性研究及其在船舶工程中的应用[D]. 武汉: 华中科技大学, 2013. TANG Zhengmao. Research on the fitness of intelligent optimization algorithms to some applications in ship engineering[D].Wuhan:Huazhong University of Science and Technology, 2013. (  0) 0)
|
| [9] |
RUBINSTEIN R Y, KROESE D P. The cross-entropy method:a unified approach to combinatorial optimization, Monte-Carlo simulation and machine learning[M]. New York: Springer, 2004.
(  0) 0)
|
| [10] |
HU Jiaqiao, FU M C, MARCUS S I. A model reference adaptive search method for global optimization[J]. Operations research, 2007, 55(3): 549-568. DOI:10.1287/opre.1060.0367 (  0) 0)
|
| [11] |
HU Jiaqiao, HU Ping. On the performance of the cross-entropy method[C]//Proceedings of 2009 Winter Simulation Conference. Austin, TX, USA, 2009:459-468.
(  0) 0)
|
| [12] |
徐力. 基于CFD的船体阻力性能优化[D]. 上海: 上海交通大学, 2012. XU Li. Optimization of ship hull resistance based on CFD Method[D]. Shanghai:Shanghai Jiao Tong University, 2012. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


