波形钢腹板组合箱梁桥在国内外得到了广泛的应用,据不完全统计,截止2015年,世界范围内此类桥梁已超过200座,国内已建成和在建的此类桥梁已超过30座[1-6]。波形钢腹板箱梁的抗扭及纵横向抗弯刚度相比混凝土箱梁有不同程度的降低,其桥面板横向内力与混凝土箱梁必然有所差异。国内学者近年来针对波形钢腹板箱梁的横向内力问题开展了系统的研究,东南大学方太云将适用于简支正交异性板横向分布计算的G-M法运用到波形钢腹板箱梁桥面板有效分布宽度的计算中。湖南大学李立峰以弹性薄板理论为基础,推导了波形钢腹板箱梁的横向内力计算公式,并通过试验及有限元分析进行了验证[7-14]。
从现有研究现状来看,对单箱单室波形钢腹板箱梁横向内力研究较多,而针对单箱多室的受力研究较少。单箱多室箱梁相对于单箱单室箱梁结构而言,在后者的基础上增设了中腹板;鉴于前者的横向跨距较大,波形钢腹板相对刚度较小,其横向受力比单箱单室箱梁的受力要复杂。鉴于上述背景,本文对单箱多室波形钢腹板箱梁的横向内力进行了研究,基于框架分析法基本原理,结合波形钢腹板单箱多室箱梁的结构特点和力学特性,采用能量法建立适用于该结构的横向内力计算模型。
1 波形钢腹板箱梁横向内力计算模型针对波形钢腹板单箱双室箱梁将采用能量法并结合其自身结构特点及力学性能来计算其横向内力。该方法基于框架分析法的基本原理,考虑了箱梁横向弯曲和畸变翘曲的影响[15]。文中以增设一个中腹板的波形钢腹板单箱双室箱梁为例来解析单箱多室箱梁的横向内力。
一般将荷载分解为对称荷载和反对称荷载,对称荷载作用下的内力分析采用一般结构力学方法可求得,不再详述;反对称荷载作用下的箱梁横向内力求解包括加支撑的结构分析和支撑释放后的结构分析。
1.1 反对称荷载作用下加支撑的结构分析 1.1.1 横向弯曲应变能1) 外荷载P作用下的内力和位移。
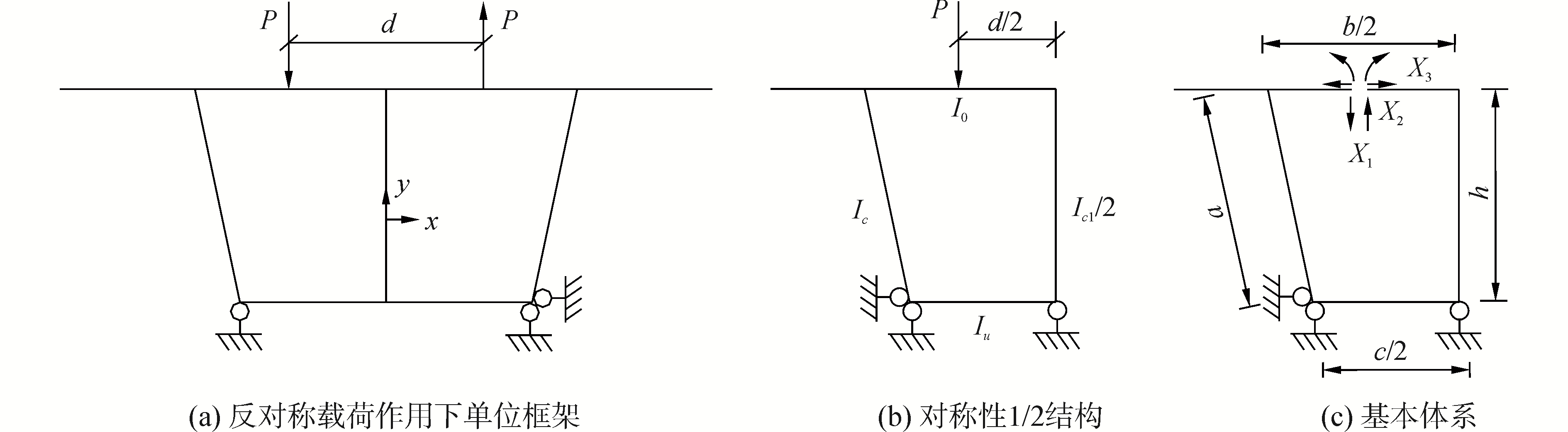
对于反对称荷载作用下沿跨径方向的单位框架,如图 1(a)所示。由于箱梁截面关于中腹板轴线位置对称即结构关于Y轴对称,荷载关于Y轴反对称,根据对称性可取1/2结构进行分析如图 1(b)所示。取图 1(c)所示的基本体系,采用力法方程进行分析。
|
Download:
|
| 图 1 框架图示 Fig. 1 Frame illustration | |
各角点弯矩M1、M2、M3、M4、M5分别为顶板与边腹板交界处的弯矩值、底板与边腹板交界处的弯矩值、底板与中腹板交界处的弯矩值、底板与中腹板交界处的弯矩值、单室顶板跨中位置的弯矩值、顶板与中腹板交界处的弯矩值。具体表达式为
| $ \begin{array}{*{20}{c}} {{M_1} = \frac{{\left( {b - d} \right)P}}{2} - \frac{b}{4}{X_1} - {X_2}}\\ {{M_2} = \frac{{\left( {c - d} \right)P}}{2} - \frac{b}{4}{X_1} - {X_2} - h{X_3}}\\ {{M_3} = \frac{b}{4}{X_1} - {X_2} - h{X_3}}\\ {{M_4} = {X_2},{M_5} = \frac{b}{4}{X_1} - {X_2}} \end{array} $ | (1) |
各角点弯矩M1、M2、M3、M4、M5的表达式中系数X1、X2、X3表达式为

|

|
| $ {X_3} = \frac{{P \cdot C}}{B} $ |
其中:
| $ A = \frac{{6b{c^2}{h^3}{n^2}}}{{{I_c} \cdot I_{\rm{u}}^2}} + \frac{{108bc{h^4}n}}{{I_{\rm{c}}^2 \cdot {I_{\rm{u}}}}} + \frac{{144b{h^5}}}{{I_{\rm{c}}^3}} + \frac{{3b{c^2}{h^3}{n^3}}}{{{I_0} \cdot I_{\rm{u}}^2}} + \\\frac{{6c{b^2}{h^3}{n^2} + 60cb{h^4}{n^2}}}{{{I_0} \cdot {I_c} \cdot {I_{\rm{u}}}}} + \frac{{9n{b^2}{h^4} + 99nb{h^5}}}{{{I_0} \cdot I_{\rm{c}}^2}} + \frac{{3{b^2}c{n^3}{h^3}}}{{I_0^2 \cdot {I_{\rm{u}}}}} + \frac{{6{b^2}{n^2}{h^4}}}{{I_0^2 \cdot {I_{\rm{c}}}}} $ |
| $ \begin{array}{*{20}{c}} {B = \frac{{24{c^2}{h^3}{n^2}}}{{{I_c} \cdot {I_{\rm{u}}}}} + \frac{{432c{h^4}n}}{{I_{\rm{c}}^2}} + \frac{{576{h^5} \cdot {I_{\rm{u}}}}}{{I_{\rm{c}}^3}} + \frac{{12{c^2}{h^3}{n^3}}}{{{I_0} \cdot {I_{\rm{u}}}}} + \frac{{240c{h^4}{n^2} + 24cb{h^3}{n^2}}}{{{I_0} \cdot {I_c}}} + }\\ {\frac{{\left( {396n{h^5} + 36nb{h^4}} \right) \cdot {I_{\rm{u}}}}}{{{I_0} \cdot I_{\rm{c}}^2}} + \frac{{12bc{n^3}{h^3}}}{{I_0^2}} + \frac{{24b{n^2}{h^4} \cdot {I_{\rm{u}}}}}{{I_0^2 \cdot {I_{\rm{c}}}}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {C = \frac{{3{c^3}{h^3}{n^3}}}{{I_{\rm{u}}^2}} - \frac{{59{c^2}{h^3}{n^2}}}{{{I_{\rm{c}}} \cdot {I_{\rm{u}}}}} - \frac{{48cn{h^4}}}{{I_{\rm{c}}^2}} + \frac{{96{h^5} \cdot {I_{\rm{u}}}}}{{I_{\rm{c}}^3}} + \frac{{\left( {3{c^2}{h^3}{n^3} - 3b{c^2}{h^2}{n^3}} \right)}}{{{I_0} \cdot {I_{\rm{u}}}}} + \frac{{\left( {61c{n^2}{h^4} - 2bc{n^2}{h^3}} \right)}}{{{I_0} \cdot {I_{\rm{c}}}}} + }\\ {\frac{{\left. {90n{h^5} + 6bn{h^4}} \right) \cdot {I_{\rm{u}}}}}{{{I_0} \cdot I_{\rm{c}}^2}} + \frac{{3bc{n^3}{h^3}}}{{I_0^2}} + \frac{{3b{n^2}{h^4} \cdot {I_{\rm{u}}}}}{{I_0^2 \cdot {I_{\rm{c}}}}}} \end{array} $ |
式中:n为钢材与混凝土的弹性模量之比, 即n=Eg/Eh;I0、Iu、Ic、Ic1分别为沿纵向单位长度的顶、底板及波形钢腹板边、中腹板横向抗弯惯矩:
| $ \begin{array}{*{20}{c}} {{I_0} = \frac{{t_0^3}}{{12\left( {1 - {\mu ^2}} \right)}},{I_u} = \frac{{t_u^3}}{{12\left( {1 - {\mu ^2}} \right)}}}\\ {{I_c} = {I_{c1}} = \frac{{2{L_c}{t_c}{{\left( {\frac{{{h_c}}}{2}} \right)}^2} + \frac{{{t_c}h_c^3}}{6}\sin \theta }}{q}} \end{array} $ | (2) |
式中:μ为材料的泊松比,t0、tu、tc分别为波形钢腹板箱梁顶、底板及腹板的厚度,q、hc、Lc为波形钢腹板的波长、波高及水平面板宽。
单箱双室箱梁在外荷载P作用下的横向弯矩值见图 2。

|
Download:
|
| 图 2 横向弯矩分布图(外载荷) Fig. 2 Transverse moment distribution(external load) | |
根据弯矩图 2便可以计算由于P作用而引起框架顶部与底部相对的侧移值为
| $ \begin{array}{*{20}{c}} {{\Delta _q} = \frac{{\left[ {\left( { - 2b + d + c} \right)P + \frac{b}{4}{X_1} + {X_2} - h{X_3}} \right]{h^2}}}{{3nE{I_c}}} + }\\ {\frac{{\left[ {\left( {c - d} \right)P - \frac{b}{4}{X_1} - 3{X_2} - 3h{X_3}} \right]hc}}{{3E{I_u}}}} \end{array} $ | (3) |
2) 剪力差T′i作用下的内力和位移。
框架的畸变剪力差见图 3。

|
Download:
|
| 图 3 框架与畸变荷载 Fig. 3 Frame and distortion load | |
由于边腹板的畸变剪力差T′h与底板的畸变剪力差T′x均由支座链杆代替,仅作用于框架顶部的T′s使框架产生横向变形的效果。剪力差产生的横向内力值:
| $ \left\{ \begin{array}{l} {{M'}_1} = \frac{b}{4}{X_{11}} + {X_{22}}\\ {{M'}_2} = \frac{{Ph}}{2} - \frac{b}{4}{X_{11}} - {X_{22}} - h{X_{33}}\\ {{M'}_3} = \frac{b}{4}{X_{11}} - {X_{22}} - h{X_{33}}\\ {{M'}_4} = {X_{22}},{{M'}_5} = \frac{b}{4}{X_{11}} - {X_{22}} \end{array} \right. $ | (4) |
其中参数X11、X22、X33的物理意义同于X1、X2、X3。
剪力差作用产生的最终横向弯矩图见图 4。

|
Download:
|
| 图 4 横向弯矩分布图(剪力差) Fig. 4 Transverse moment distribution(shear difference) | |
同样可以根据弯矩图计算由于剪力差T′s作用而引起框架顶部与底部相对的侧移值ΔT,将X11、X22、X33的表达式代入式(4)中即可得出
| $ \begin{array}{*{20}{c}} {{\Delta _T} = \frac{{\left[ {\frac{{{{T'}_s}h}}{2} - \frac{{3b}}{4}{X_{11}} - 3{X_{22}} - h{X_{33}}} \right]{h^2}}}{{3nE{I_c}}} + }\\ {\frac{{\left[ {{{T'}_s}h - \frac{{3b}}{4}{X_{11}} - {X_{22}} - h{X_{33}}} \right]hc}}{{3E{I_u}}}} \end{array} $ | (5) |
式中:

|
(7) |
| $ {X_{22}} = \frac{{{{T'}_s} \cdot F}}{B} $ |
| $ {X_{33}} = \frac{{{{T'}_s} \cdot G}}{B} $ |
其中,
| $ \begin{array}{*{20}{c}} {D = \left[ {\frac{{6\left( {c - d} \right){c^2}{h^3}{n^2}}}{{{I_{\rm{c}}} \cdot I_{\rm{u}}^2}} + \frac{{4\left( {15c + 12b - 27d} \right)c{h^4}n}}{{I_{\rm{c}}^2 \cdot {I_{\rm{u}}}}} + \frac{{24{h^5}\left( {3b + 3c - 5d} \right)}}{{I_{\rm{c}}^3}} + \frac{{3\left( {c - d} \right){c^2}{h^3}{n^3}}}{{{I_0} \cdot I_{\rm{u}}^2}} + } \right.}\\ {\frac{{6{{\left( {b - d} \right)}^2}c{n^3}{h^3}}}{{I_{\rm{0}}^2 \cdot {I_{\rm{u}}}}} + \frac{{2\left( {8{b^2} + 18bh - 16bd + 22ch + 13d - 40dh - 5{d^2}} \right)c{h^3}{n^2}}}{{{I_0} \cdot {I_{\rm{c}}} \cdot {I_{\rm{u}}}}} + }\\ {\left. {\frac{{\left( {27{{\left( {b - d} \right)}^2} + 4h\left( {15b - 27d + 12c} \right)n{h^4}} \right.}}{{{I_0} \cdot I_{\rm{c}}^2}} + \frac{{12{{\left( {b - d} \right)}^2}{n^2}{h^4}}}{{I_{\rm{0}}^2 \cdot {I_{\rm{c}}}}}} \right]} \end{array} $ |
| $ \begin{array}{*{20}{c}} {F = \left[ {\frac{{\left( {2c + 4b - 6d} \right){c^2}{h^3}{n^2}}}{{{I_{\rm{c}}} \cdot {I_{\rm{u}}}}} + \frac{{\left( {100c + 8b - 108d} \right)c{h^4}n}}{{I_{\rm{c}}^2}} + \frac{{24{h^5}\left( {5b + c - 6d} \right) \cdot {I_{\rm{u}}}}}{{I_{\rm{c}}^3}} + } \right.}\\ {\frac{{3{{\left( {b - d} \right)}^2}{c^2}{h^2}{n^3}}}{{{I_{\rm{0}}} \cdot {I_{\rm{u}}}}} + \frac{{\left[ {70{b^2} + 66{d^2} - 137bd - bc} \right]c{h^3}{n^2}}}{{{I_{\rm{0}}} \cdot {I_{\rm{c}}}}} + \frac{{\left( {111{b^2} + 105{d^2} - 21bd} \right)n{h^4} \cdot {I_{\rm{u}}}}}{{{I_{\rm{0}}} \cdot I_{\rm{c}}^2}} + }\\ {\left. {\frac{{3{{\left( {b - d} \right)}^2}bc{h^2}{n^2}}}{{I_0^2}} + \frac{{6{{\left( {b - d} \right)}^2}b{h^3}{n^2} \cdot {I_{\rm{u}}}}}{{I_0^2 \cdot {I_{\rm{c}}}}}} \right]} \end{array} $ |
| $ \begin{array}{*{20}{c}} {G = \left( {\frac{{4{c^2}\left( {c - b} \right){c^2}{h^2}{n^2}}}{{{I_{\rm{c}}} \cdot {I_{\rm{u}}}}} + \frac{{96\left( {c - b} \right)cn{h^3}}}{{I_{\rm{c}}^2}} - \frac{{{h^4}\left( {b - c} \right) \cdot I}}{{I_{\rm{c}}^3}} - \frac{{3\left( {{b^2} - 2bd - ch + {d^2} + dh} \right){c^2}h{n^3}}}{{{I_{\rm{0}}} \cdot {I_{\rm{u}}}}} + } \right.}\\ {\frac{{\left[ { - 73{b^2} + 7bc + 135bd + 61ch - 69{d^2} - 63dh + 2bh} \right]c{h^2}{n^2}}}{{{I_{\rm{0}}} \cdot {I_{\rm{c}}}}} + }\\ {\frac{{\left( { - 150{b^2} - 144{d^2} + 288bd + 54bh + 6cb - 144dh + 90ch} \right)n{h^3} \cdot {I_{\rm{u}}}}}{{{I_{\rm{0}}} \cdot I_{\rm{c}}^2}} - }\\ {\left. {\frac{{3\left( {{b^2} - 2bd - ch + {d^2} + dh} \right)bch{n^3}}}{{I_{\rm{0}}^2}} + \frac{{\left( { - 9{b^3} + 18{b^2}d + 8{b^2}h - 9b{d^2} - 18bdh + 6{d^2}h + 4cbh} \right){h^2}{n^2} \cdot {I_{\rm{u}}}}}{{I_{\rm{0}}^2 \cdot {I_{\rm{c}}}}}} \right)} \end{array} $ |
3) 横向弯曲应变能。
微元框架由外荷载P与剪力差T′s共同作用,则总的横向弯矩为M=MP+MT。横向弯曲应变能根据图乘法得到
| $ {\mathit{\Pi }_W} = \int_L {\int_S {\frac{{M_q^2}}{{2EI}}{\rm{d}}s{\rm{d}}z} } + \int_L {\int_S {\frac{{{M_q}{M_T}}}{{EI}}{\rm{d}}s{\rm{d}}z} } + \int_L {\int_S {\frac{{M_T^2}}{{2EI}}{\rm{d}}s{\rm{d}}z} } $ | (6) |
式中:
| $ \begin{array}{*{20}{c}} {\int_0^l {\int_s {\frac{{M_q^2}}{{2EI}} \cdot {\rm{d}}s{\rm{d}}z} } = \int_0^l {d\left[ {\left( {M_4^2 + M_5^2 + {M_4}{M_5}} \right)/\left( {6E{I_0}} \right) + \\\left( {b - d} \right)\left( {M_4^2 + M_1^2 + {M_4}{M_1}} \right)/\left( {6E{I_0}} \right) + } \right.} }\\ {a\left( {M_1^2 + M_2^2 + {M_1}{M_2}} \right)/\left( {3nE{I_c}} \right) + c\left( {M_2^2 + M_3^2 - {M_2}{M_3}} \right)/\left( {6E{I_u}} \right) + }\\ {\left. {2h\left( {M_3^2 + M_5^2 + {M_3}{M_5}} \right)/\left( {3nE{I_c}} \right)} \right]{\rm{d}}z} \end{array} $ |
| $ \begin{array}{*{20}{c}} {\int_0^l {\int_s {\frac{{M_T^2}}{{2EI}} \cdot {\rm{d}}s{\rm{d}}z} } = \int_0^l {d\left[ {\left( {M{'}_4^2 + M{'}_5^2 + {{M'}_4}{{M'}_5}} \right)/\left( {6E{I_0}} \right) +\\ \left( {b - d} \right)\left( {M{'}_4^2 + M{'}_1^2 + {{M'}_4}{{M'}_1}} \right)/\left( {6E{I_0}} \right) + } \right.} }\\ {a\left( {M{'}_1^2 + M{'}_2^2 - {{M'}_1}{{M'}_2}} \right)/\left( {3nE{I_c}} \right) + c\left( {M{'}_2^2 + M{'}_3^2 - {{M'}_2}{{M'}_3}} \right)/\left( {6E{I_u}} \right) + }\\ {\left. {2h\left( {M{'}_3^2 + M{'}_5^2 - {{M'}_3}{{M'}_5}} \right)/\left( {3nE{I_{\rm{c}}}} \right)} \right]{\rm{d}}z} \end{array} $ |
| $ \begin{array}{*{20}{c}} {\int_0^l {\int_s {\frac{{{M_q}{M_T}}}{{EI}} \cdot {\rm{d}}s{\rm{d}}z} } = \int_0^l {d\left[ {\left( {{M_4}\left( {2{{M'}_4} - {{M'}_5}} \right) +\\ {M_5}\left( {2{{M'}_5} - {{M'}_4}} \right)} \right)/\left( {12E{I_0}} \right) + \left( {b - d} \right)\left( {3{M_4}\left( {{{M'}_4} - {{M'}_1}} \right) + } \right.} \right.} }\\ {\left. {\left( {{M_1} - {M_4}} \right)\left( {{{M'}_4} - 2{{M'}_1}} \right)} \right)/\left( {12E{I_0}} \right) + a\left( {{M_1}\left( {2{{M'}_1} - {{M'}_2}} \right) +\\ {M_2}\left( {2{{M'}_2} - {{M'}_1}} \right)} \right)/\left( {6nE{I_c}} \right) + }\\ {c\left( { - {M_2}\left( {2{{M'}_2} + {{M'}_3}} \right) + {M_3}\left( {2{{M'}_3} + {{M'}_2}} \right)} \right)/\left( {6E{I_u}} \right) + }\\ {\left. {h\left( {{M_5}\left( {2{{M'}_5} + {{M'}_3}} \right) + {M_3}\left( {2{{M'}_3} + {{M'}_5}} \right)} \right)/\left( {6nE{I_c}} \right)} \right]{\rm{d}}z} \end{array} $ |
令
| $ {\lambda _{w1}} = \frac{{\int_0^l {\int_s {\frac{{M_q^2}}{{2EI}} \cdot {\rm{d}}s{\rm{d}}z} } }}{P},{\lambda _{w2}} = \frac{{\int_0^l {\int_s {\frac{{M_T^2}}{{2EI}} \cdot {\rm{d}}s{\rm{d}}z} } }}{{\Delta _T^2}},{\lambda _{w3}} = \frac{{\int_0^l {\int_s {\frac{{{M_q}{M_T}}}{{EI}} \cdot {\rm{d}}s{\rm{d}}z} } }}{{P\Delta _T^2}} $ | (7) |
取出一片微元框架,其实际的侧移变形如图 5所示。图中顶板侧移总和Δ等于顶板与底板的相对侧移量(由外荷载与板的剪力差作用产生),即
| $ \Delta \left( z \right) = {\Delta _0}\left( z \right) + {\Delta _u}\left( z \right) = {\Delta _q}\left( z \right) + {\Delta _T}\left( z \right) $ | (8) |

|
Download:
|
| 图 5 畸变位移图 Fig. 5 Distortion displacement | |
则用Δq (z)、ΔT (z)表示的纵向翘曲应变能计算为
| $ {\mathit{\Pi }_{\rm{q}}} = \int_L {\left\{ {W\left( z \right) \cdot {{\left[ {{{\Delta ''}_q}\left( z \right) + {{\Delta ''}_T}\left( z \right)} \right]}^2}} \right\}{\rm{d}}z} $ | (9) |
式中:
| $ \beta ' = \frac{{3 + \alpha _u^3\frac{{b \cdot {t_u}}}{{h' \cdot n \cdot {t_c}}}}}{{3 + \alpha _0^3\frac{{b \cdot {t_0}}}{{h' \cdot n \cdot {t_c}}}}} $ |
作用于结构上的反对称荷载实际上为以沿跨长的力偶P·d,由其产生的势能可取出微元框架分析,再沿跨长方向积分得到。
外部荷载势能
| $ \begin{array}{l} {\mathit{\Pi }_{\rm{p}}} = - \int_L {P \cdot d \cdot \theta {\rm{d}}z} = \\ - \int_L {{\psi _q}\left( z \right) \cdot {P^2}{\rm{d}}z} + \int_L {{\psi _T}\left( z \right) \cdot P \cdot {\Delta _T}\left( z \right){\rm{d}}z} \end{array} $ | (10) |
式中:
| $ \left\{ \begin{array}{l} {\psi _q} = - \frac{{{{\left( {b - d} \right)}^2}}}{{12PE{J_s}}}\left( {2{M_1} + {M_4}} \right) + \frac{{h\left( {b - d} \right)\left( {{M_1} - {M_2}} \right)}}{{2PE{J_h}}} + \\ \;\;\;\;\;\;\;\frac{{c\left( {b - d} \right)\left( {{M_3} + 2{M_2}} \right)}}{{12PE{J_x}}}\\ {\psi _T} = \left( {\left( {{{M'}_2} - {{M'}_1}} \right)h\left( {b - d} \right)/\left( {2nE{J_h}} \right) - } \right.\\ \left( {b - d} \right)\left( {{{M'}_3} + 2{{M'}_2}} \right)/\left( {12cE{J_x}} \right) - \\ \left. {\left( {b - d} \right)2\left( {{M_4} + 2{M_1}} \right)/\left( {12E{J_s}} \right)} \right)/{\Delta _T}\\ {J_s} = \frac{1}{{12}}{b^3}{t_0} + \frac{1}{6}b_{os}^3{t_o} + \frac{1}{2}{b_{os}}{t_o}{\left( {b + {b_{os}}} \right)^2} \end{array} \right. $ |
| $ {J_x} = \frac{1}{{12}}{c^3}{t_u} $ |
| $ {J_h} = \frac{1}{{12}}{h^3}{t_c} + \frac{1}{4}{h^3}{t_c}{\left( {\frac{{1 - \beta '}}{{1 + \beta '}}} \right)^2} $ |
通过以上三部分的推导,得到了体系各部分势能的计算表达式,体系的总势能为
| $ \mathit{\Pi } = {\mathit{\Pi }_{\rm{w}}} + {\mathit{\Pi }_{\rm{q}}} + {\mathit{\Pi }_{\rm{p}}} $ | (11) |
根据最小势能原理,等高度梁的总势能应满足δΠ=0,得出
| $ \begin{array}{*{20}{c}} {\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{z^2}}}\left[ {2W\left( z \right) \cdot {{\Delta ''}_T}\left( z \right)} \right] + 2{\lambda _2}\left( z \right) \cdot {\Delta _T}\left( z \right) = }\\ { - {\lambda _1}\left( z \right) \cdot q\left( z \right)} \end{array} $ | (12) |
式中:λ1(z)、λ2(z)分别为λ1=λω3-ψT,λ2=λω2。
由式(12)与弹性地基梁挠曲微分方程的相似性可求得ΔT(z);继而通过回代可得反对称荷载作用下加竖向链杆支撑的单箱双室横向弯矩分布图。
1.2 反对称荷载作用下支撑释放后的结构分析求出支反力后,将支反力反向施加于单箱双室箱梁上,结构将产生刚性扭转和畸变变形,仅畸变会产生横向内力。其具体计算过程同于剪力差作用下的内力分析,此处不再详述。最终将对称荷载作用下的内力图与反对称荷载作用下的内力图叠加即可得到波形钢腹板单箱双室箱梁的横向内力。
综上所述,采用能量法受力明确,计算方便,根据上述推导过程采用Matlab简单编程,即可得出波形钢腹板箱梁的横向内力分布。
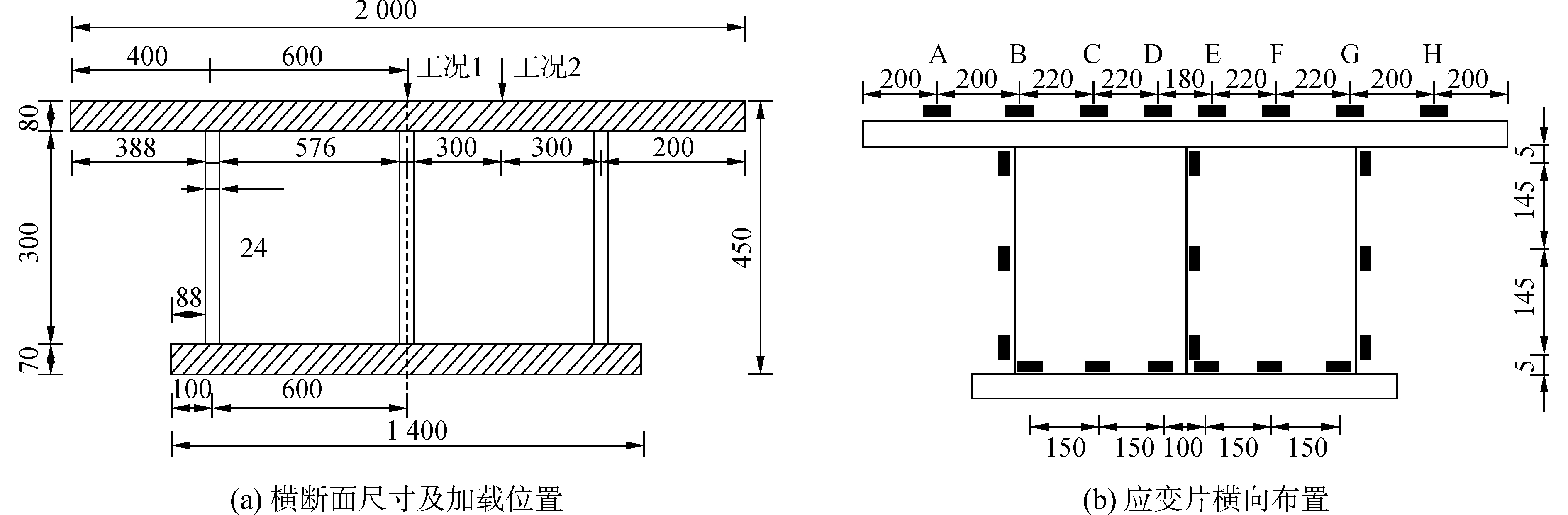
2 试验验证波形钢腹板试验简支梁全长3.5 m,截面形式、尺寸及加载工况见图 6。波形腹板采用Q235优质低碳钢,厚2 mm,水平面板宽40 mm,折叠角为37°,波高24 mm,波长144 mm。荷载分为对称加载(工况Ⅰ)和偏载(工况Ⅱ),两种工况在弹性阶段加载下的荷载值分别为40、25 kN,如图 6所示。
|
Download:
|
| 图 6 试验梁截面尺寸、加载位置及应变片布置 Fig. 6 Cross section, loading position and layout of strain gauges | |
两种作用工况下的桥面板横向内力值见表 1。由表 1可知,针对上述两种加载工况下的顶板横向内力值,所得到的能量法计算值与有限元值、实测值的误差绝大部分均在10%左右符合精度要求。说明采用能量法计算波形钢腹板单箱双室箱梁的横向内力是可行的。
| 表 1 顶板横向内力值 Tab.1 Transverse internal force of deck |
以中腹板厚度大于边腹板厚度来形成两者刚度差别的条件(中腹板的厚度增大4 mm),在试验梁尺寸基础上变换腹板高度,采用有限元法进行参数分析,荷载作用位置处的桥面板横向应力计算值见表 2。其中试验梁的中腹板与顶板相对刚度比为0.116。
| 表 2 不同的腹板与顶板线刚度比值条件下顶板的横向内力值 Tab.2 Transverse internal force of deck under different web and roof line stiffness ratio |
表 2中斜线前后的数据分别为中腹板厚度加大和原厚度两种情况下的横向内力值,通过比较发现上述两者在两种工况下的差别均约为15%。
图 7为按表 2绘制的中腹板厚度增加后试验梁顶板的横向弯矩值曲线。

|
Download:
|
| 图 7 中腹板厚度增加后不同线刚度比条件下顶板横向内力变化图 Fig. 7 Transversal internal force change under different line stiffness ratio after the increase in web thickness | |
由图 7可知,波形钢腹板箱梁的混凝土顶板横向弯矩值随腹板线刚度变化基本呈直线变化;随着腹板与顶板线刚度比值的增加,顶板的横向弯矩值随之减小,与单箱单室波形钢腹板箱梁的变化规律相同[8]。
4 结论1) 采用能量法可以较好地计算波形钢腹板单箱双室箱梁桥面板的横向内力,与试验结果及有限元结果吻合较好。
2) 对于波形钢腹板箱梁,其腹板对顶板的约束程度直接影响到顶板的横向受力,顶板横向应力值随腹板与顶板线刚度比变化基本呈线性变化;中腹板厚度变化对箱梁顶板横向内力的影响不可忽略。
本文着重研究了波形钢腹板单箱双室箱梁腹板间的桥面板横向内力,忽略了悬臂板的影响。随着大跨宽箱梁的发展,大悬臂问题愈加突出,波形钢腹板支撑下的大悬臂箱梁横向内力和悬臂合理尺寸还有待于进一步研究。
| [1] |
陈宜言. 波形钢腹板预应力混凝土桥设计与施工[M]. 北京: 人民交通出版社, 2009: 1-10. CHEN Yiyan. Design and construction of prestressed concrete bridge with corrugated steel webs[M]. Beijing: China Communications Press, 2009: 1-10. (  0) 0)
|
| [2] |
刘玉擎. 组合结构桥梁[M]. 北京: 人民交通出版社, 2005: 35-50. LIU Yuqing. Composite structure bridge[M]. Beijing: China Communications Press, 2005: 35-50. (  0) 0)
|
| [3] |
ELGAALY M, SESHADRI A. Girders with corrugated webs under partial compressive edge loading[J]. Journal of the Structural Division, ASCE, 1997, 122(4): 783-791. (  0) 0)
|
| [4] |
聂建国, 朱力, 唐亮. 波形钢腹板的抗剪强度[J]. 土木工程学报, 2013, 46(6): 97-109. NIE Jianguo, ZHU Li, TANG Liang. Shear strength of trapezoidal corrugated steel webs[J]. China civil engineering journal, 2013, 46(6): 97-109. (  0) 0)
|
| [5] |
彭鲲, 李立峰, 肖小艳, 等. 波形钢腹板组合箱梁疲劳性能试验与理论分析[J]. 中国公路学报, 2013, 26(4): 94-101. PENG Kun, LI Lifeng, XIAO Xiaoyan, et al. Experimental and theoretical analysis of fatigue performance of composite box girder with corrugated steel webs[J]. China journal of highway and transport, 2013, 26(4): 94-101. (  0) 0)
|
| [6] |
张阳, 邱俊峰, 唐重玺. 部分波形钢腹板预应力连续组合梁性能分析[J]. 湖南大学学报, 2013, 40(12): 14-20. ZHANG Yang, QIU Junfeng, TANG Chongxi. Analysis of behaviors of prestressed steel-concrete continuous composite beam with partial corrugated steel webs[J]. Journal of Hunan University, 2013, 40(12): 14-20. (  0) 0)
|
| [7] |
贾慧娟, 戴航, 张建东. 波形钢腹板组合梁桥横向受力研究[J]. 工程力学, 2014, 31(12): 76-82. JIA Huijuan, DAI Hang, ZHANG Jiandong. Research on transverse internal forces in box-girder bridge with corrugated steel webs[J]. Engineering mechanics, 2014, 31(12): 76-82. (  0) 0)
|
| [8] |
袁卓亚, 李立峰, 刘清, 等. 波形钢腹板组合箱梁横向内力分析及试验研究[J]. 中国公路学报, 2015, 28(11): 73-81. YUAN Zhuoya, LI Lifeng, LIU Qing, et al. Analysis and experimental study of transverse internal force in composite box-girder with corrugated steel webs[J]. China journal of highway and transport, 2015, 28(11): 73-81. (  0) 0)
|
| [9] |
赵品, 荣学亮, 叶见曙. 波形钢腹板组合箱梁横向受力有效分布宽度研究[J]. 湖南大学学报, 2016, 43(7): 105-110. ZHAO Pin, RONG Xueliang, YE Jianshu. Research on the lateral effective width of composite box-girders with corrugated steel webs[J]. Journal of Hunan University, 2016, 43(7): 105-110. (  0) 0)
|
| [10] |
方志, 郑辉, 刘双阳. 基于塑性分析的钢筋混凝土箱梁悬臂板横向受力有效分布宽度[J]. 土木工程学报, 2012, 45(3): 35-41. FANG Zhi, ZHENG Hui, LIU Shuangyang. Plastic analysis of the lateral effective width of cantilever slabs of reinforced concrete box-girders[J]. Journal of China civil engineering, 2012, 45(3): 35-41. (  0) 0)
|
| [11] |
李立峰, 侯立超, 孙君翠. 波形钢腹板抗剪性能的研究[J]. 湖南大学学报, 2015, 42(11): 56-63. LI Lifeng, HOU Lichao, SUN Juncui. Research on shear mechanical property of corrugated steel webs[J]. Journal of Hunan University, 2015, 42(11): 56-63. DOI:10.3969/j.issn.1674-2974.2015.11.008 (  0) 0)
|
| [12] |
李立峰, 王芳, 刘志才. 体外预应力波形钢腹板组合箱梁徐变性能研究[J]. 湖南大学学报, 2008, 35(5): 1-5. LI Lifeng, WANG Fang, LIU Zhicai. Study on the creep behavior of externally prestressed composite beam with corrugated steel webs[J]. Journal of Hunan University, 2008, 35(5): 1-5. (  0) 0)
|
| [13] |
聂建国. 钢-混凝土组合梁结构:试验、理论与应用[M]. 北京: 科学出版社, 2005: 43-99. NIE Jian-guo. Steel concrete composite bridges[M]. Beijing: China Communications Press, 2005: 43-99. (  0) 0)
|
| [14] |
徐向锋, 张峰, 韦成龙. 预应力混凝土箱梁开裂后的刚度损伤评估[J]. 工程力学, 2015, 32(7): 95-102. XU Xiangfeng, ZHANG Feng, WEI Chenglong. Stiffness damage assement of prestressed concrete box-girder after cracking[J]. Engineering mechanics, 2015, 32(7): 95-102. (  0) 0)
|
| [15] |
郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 2版. 北京: 人民交通出版社, 2008: 138-175. GUO Jinqiong, FANG Zhenzheng, ZHENG Zhen. Design theory of box girder[M]. Beijing: China Communications Press, 2008: 138-175. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


