2. 华南理工大学 电力学院, 广东 广州 510640
2. School of Electric Power, South China University of Technology, Guangzhou 510640, China
配电网是电力系统的重要组成部分,其供电的安全可靠程度直接影响着国民经济的发展和人民生活水平的提升[1]。进一步提升配网的供电可靠性,不仅可以最大限度满足电力用户的用电需求,同时也有利于促进电网建设的进一步完善和发展[2]。我国自1992年以后城市供电可靠性进入了迅速发展阶段,供电可靠性达到了99%以上。近几年供电可靠性水平有了显著提升,越来越多的地区供电可靠率达到99.9%。
如何开展供电可靠性评估是目前可靠性领域的重要研究方向。宋云亭等[3]从供电可靠性水平、指标体系、管理机制等3个方面对比国内城市配电网的情况,为提高我国城市配电网供电可靠性提供参考。曹伟[4]提出基于分块等值改进的故障模式-后果分析方法(failure mode effect analysis,FMEA)的中压配电系统可靠性评估快速算法,可适用于配电网规划中诸多待选择方案可靠性的评估。谷群辉等[5]介绍了一种基于实际运行参数的供电可靠性预测模型,采用故障率、设备修复时间等一些实际运行参数,对规划设计好的配电网络进行可靠性指标预测。
近年来,配网供电可靠性工作由被动管理转化为主动预防,宋云亭等[6]提出了基于BP神经网络对城市供电可靠性进行预测的方法,将人工神经网络应用到供电可靠性研究当中。但其考虑的影响因素具有一定的局限性,且BP神经网络算法需要设置大量网络训练参数,训练速度较慢且容易陷入局部最优解。叶航超[7]介绍了一种基于支持向量机(support vector machine,SVM)的城市电网可靠性影响因素分析模型,选用6种影响可靠性的因素,利用遗传算法对SVM进行优化。但其考虑的影响供电可靠性的因素主要集中于配网资产数据方面,涉及因素较少且不全面。此外,遗传算法无记忆性,收敛速度提升较困难。刘亚南等[8]提出了基于相关向量机(relevance vector machine,RVM)的电网供电可靠性预测模型,并采用主成分分析对样本集进行特征抽取。相关向量机训练时间长且模型输入变量的选取主要为电网供应能力方面,对于配网网架结构及配网运行维护方面的指标较少。
本文对影响供电可靠性的因素进行较为全面的总结,并在某大型电网实地调研数据的基础上提出基于粒子群算法(particle swarm optimization,PSO)优化极限学习机(extreme learning machine,ELM)的配网供电可靠性预测模型,其方法是利用主成分分析(principal component analysis,PCA)融合多方面影响供电可靠性的特征指标以消除特征间的冗余性和相关性,同时采用粒子群优化算法对初始输入权值和隐含层阈值进行优化,进一步利用ELM训练供电可靠性预测模型。
1 配网供电可靠性预测模型 1.1 主成分分析主成分分析(PCA)是一种重要的数据统计方法,其设法将原来众多具有一定相关性的数据指标,通过线性组合得到新的综合变量,这些综合变量不仅保留了原始变量的绝大部分信息,而且彼此之间互不相关[9]。PCA可以分为以下6个步骤:
1) 构成变量采样的原始数据矩阵Xn×p:
| $ {\mathit{\boldsymbol{X}}_{n \times p}} = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1p}}}\\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2p}}}\\ \cdots&\cdots&\cdots&\cdots \\ {{x_{n1}}}&{{x_{n2}}}& \cdots &{{x_{np}}} \end{array}} \right] $ | (1) |
式中:n为样本数,p为样本中的指标数。
2) 对变量采样原始数据矩阵进行标准化处理得到标准化矩阵Xn×p*。
3) 对标准化矩阵Xn×p*求解相关系数矩阵R。
相关系数的计算公式如下:
| $ {r_{ij}} = \frac{{\sum\limits_{k = 1}^n {\left( {{x_{ki}} - {{\bar X}_i}} \right)\left( {{x_{kj}} - {{\bar X}_j}} \right)} }}{{\sqrt {\sum\limits_{k = 1}^n {{{\left( {{x_{ki}} - {{\bar X}_i}} \right)}^2}} \sum\limits_{k = 1}^n {{{\left( {{x_{kj}} - {{\bar X}_j}} \right)}^2}} } }} $ | (2) |
式中:rij表示xi与xj之间的相关系数,且rij=rji。
4) 求解样本相关系数矩阵R的特征方程得到特征值和特征向量。求解特征方程与特征向量,首先计算特征方程|λE-R|=0,λi(i=1, 2, …, p),将p个特征值按由大到小的顺序排列,即λ1≥λ2≥λ3…≥λp≥0。然后计算(λiE-R)X=0,分别λi求出对应的X。
5) 求出累计贡献率,初步估计主成分个数,所选取的主成分个数应使累计贡献率达到85%~95%。选取主成分的个数取决于主成分的累积贡献率,主成分的贡献率Qi和累计贡献率Q∑(m)的计算公式分别为
| $ {Q_i} = \frac{{{\lambda _i}}}{{\sum\limits_{k = 1}^p {{\lambda _k}} }} \times 100\% \left( {i = 1,2, \cdots ,p} \right) $ | (3) |
| $ {Q_\Sigma }\left( m \right) = \sum\limits_{k = 1}^m {{Q_k}\left( {m = 1,2, \cdots ,p} \right)} $ | (4) |
6) 计算主成分载荷以及主成分得分。
主成分载荷即指每个主成分对应的载荷系数, 主成分载荷的计算公式为
| $ {l_{ij}} = \sqrt {{\lambda _i}} {e_{ij}}\left( {i,j = 1,2, \cdots ,p} \right) $ | (5) |
将原始样本数据或标准化后的样本数据代入上述主成分的表达式中即可计算出主成分得分,其计算公式为
| $ \left\{ \begin{array}{l} {F_1} = {l_{11}}\left( {{X_1} - {{\bar X}_1}} \right) + {l_{12}}\left( {{X_2} - {{\bar X}_2}} \right) + \cdots + \\ \;\;\;\;\;\;\;{l_{1p}}\left( {{X_p} - {{\bar X}_p}} \right)\\ {F_2} = {l_{21}}\left( {{X_1} - {{\bar X}_1}} \right) + {l_{22}}\left( {{X_2} - {{\bar X}_2}} \right) + \cdots + \\ \;\;\;\;\;\;\;{l_{2p}}\left( {{X_p} - {{\bar X}_p}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {F_m} = {l_{m1}}\left( {{X_1} - {{\bar X}_1}} \right) + {l_{m2}}\left( {{X_2} - {{\bar X}_2}} \right) + \cdots + \\ \;\;\;\;\;\;\;{l_{mp}}\left( {{X_p} - {{\bar X}_p}} \right) \end{array} \right. $ | (6) |
极限学习机对于单隐层前馈神经网络训练效果十分显著,目前已广泛应用于电网故障预测、电力负荷预测、风电功率预测等场合。该算法随机产生输入层和输出层之间的权值和阈值,且在训练的过程中无需调整,只要设置隐含层神经元个数,便可以获得预测误差最小的唯一解[10]。
由于ELM初始输入权值和阈值是随机确定,训练的精度和时间都会受随机性的影响,因此采用PSO对ELM初始输入权值和阈值进行优化。PSO算法是将问题的搜索空间比作鸟群飞行空间,将每只鸟抽象为一个粒子,用于表示寻优问题的一个待选解,优化得到的最优解等同于鸟群寻找的食物。所有粒子都有自身的位置及速度参数,其中速度用于决定飞行的距离和方向,速度根据其自身经验及群体经验进行动态调整。在每一次迭代中,确定每个粒子所经过的最佳位置pbest以及群体所发现的最佳位置gbest,通过跟踪更新这两个最佳位置,更新粒子的速度和位置可表示为[11]
| $ \begin{array}{*{20}{c}} {{v_{i,j}}\left( {t + 1} \right) = {v_{i,j}}\left( t \right) + {c_1}{r_1}\left[ {{p_{i,j}} - {x_{i,j}}\left( t \right)} \right] + }\\ {{c_2}{r_2}\left[ {{p_{g,j}} - {x_{i,j}}\left( t \right)} \right]} \end{array} $ | (7) |
| $ {x_{i,j}}\left( {t + 1} \right) = {x_{i,j}}\left( t \right) + {v_{i,j}}\left( {t + 1} \right),j = 1,2, \cdots ,D $ | (8) |
式中:c1和c2为学习因子,分别表示自身经验和集体经验,又称加速常数;r1和r2为0~1随机数;D为搜索维度,即需要优化的参数个数。
PSO-ELM预测评估模型需要初始化粒子群体,即确定粒子群的大小及搜索维度,种群过小容易陷入局部最优,种群过大又会影响优化时间。将每个粒子对应的输入层权值和隐含层阈值代入ELM训练算法中。第i个粒子的适应度函数fi用均方误差的倒数表示。对每个粒子将其当前适应度fi与f(pbest)对比,若fi>f(pbest)说明当前的适应度更高,则将用当前位置更新个体历史最佳位置pbest,否则保持pbest不变。同理比较当前适应值fi与f(gbest),当fi>f(gbest)更新全局最佳位置gbest。然后,根据式(7)及(8)更新每个粒子的速度与位置。当迭代次数达到最大迭代次数或最佳适应度达到设定阈值即停止寻优过程。通过PSO算法得到的最优输入权值ω和阈值b后,利用ELM训练算法,代入公式β=H+T,即可计算出模型预测值[12]。
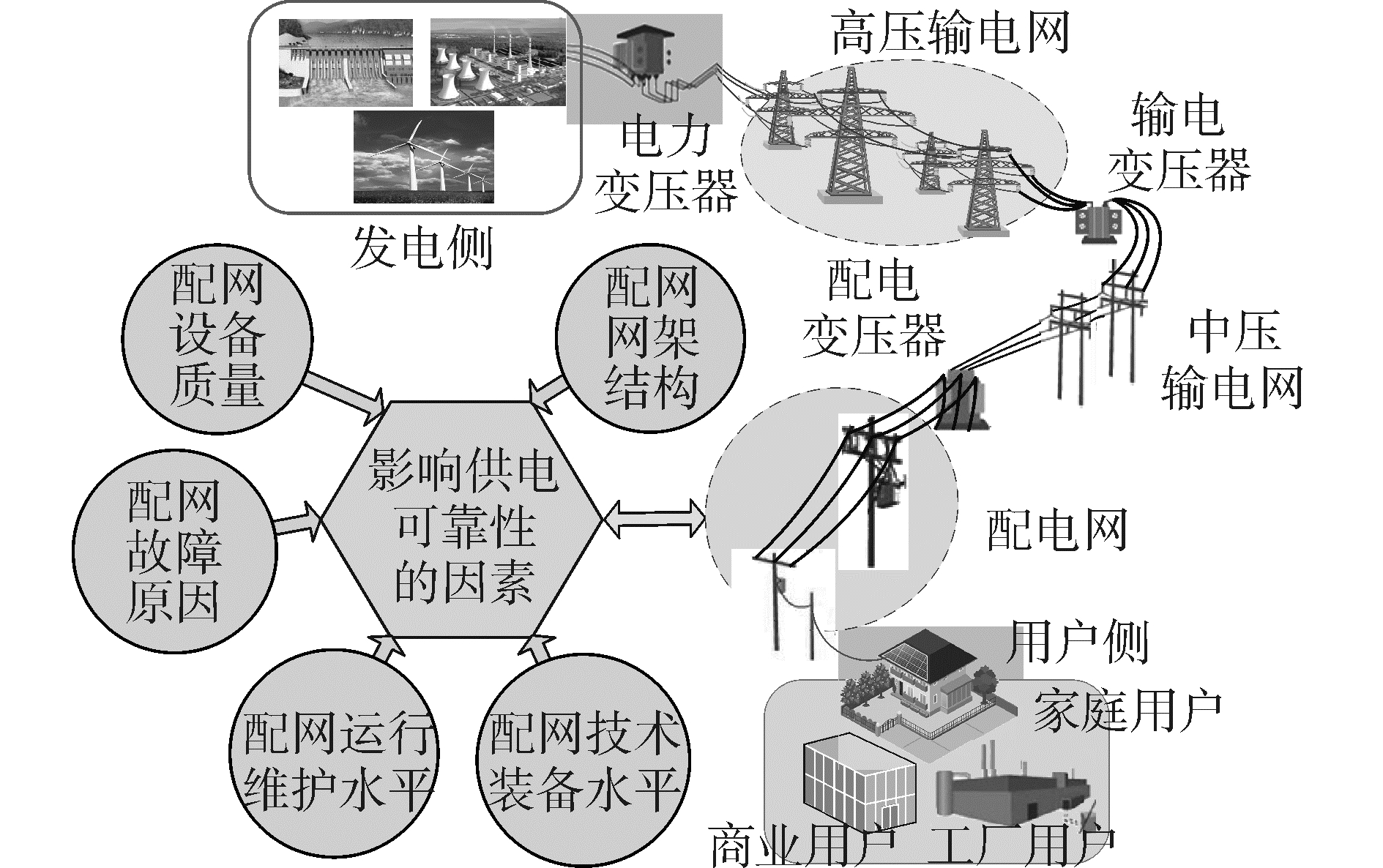
1.3 供电可靠性影响因素及评价指标的选取 1.3.1 供电可靠性影响因素为保证对供电可靠性分析的全面性,从配网的网架结构、配网的技术装备水平、配网设备质量、配网故障原因以及配网运行维护水平等五个方面选取30个影响供电可靠性指标,作为PCA-PSO-ELM供电可靠性预测模型输入变量。图 1为供电可靠性指标分类,表 1供电可靠性影响因素[13]。
|
Download:
|
| 图 1 供电可靠性指标分类 Fig. 1 Classification of reliability index of power supply | |
| 表 1 供电可靠性影响因素 Tab.1 Factors of affecting the power supply reliability |
目前我国采用的供电可靠性评价指标主要有以下五种:供电可靠率、用户平均停电时间、用户平均停电次数、用户平均短时停电次数(ATITC)、系统停电等效小时(SIEH)。除主要供电可靠性评价指标以外,有多种可靠性参考指标[14]。采取熵权法对各个评价指标的权重进行客观赋值,从而得到较为综合的评价指标,并作为配网供电可靠性预测模型输出变量。设有M个评价样本,N个供电可靠性评价指标,熵权法原理表示为
| $ \left\{ \begin{array}{l} {p_{ij}} = {V_{ij}}/\sum\limits_{j = 1}^M {{V_{ij}}} \\ {e_i} = - \frac{1}{{\ln M}}\sum\limits_{j = 1}^M {{p_{ij}}\ln {p_{ij}}} \\ {D_i} = 1 - {e_i}\\ {x_i} = {D_i}\sum\limits_{i = 1}^N {{D_i}} \end{array} \right. $ | (9) |
式中:pij表示样本j在指标i中所占的特征比重,ei表示指标i的熵值,Di表示指标i的差异系数,xi表示指标i的客观权重值。为使评价模型更符合规划人的意志,引入主观权重值yi,形成综合主观权重和客观权重的综合评价方案:
| $ {w_i} = {k_1}{x_i} + {k_2}{y_i} $ | (10) |
式中:wi表示指标i的综合权重值,k1为客观权重系数,k2为主观权重系数。由此,可得样本j的供电可靠性综合评价值为
| $ {p_i} = \sum\limits_{i = 1}^N {{w_i}{V_{ij}}} $ | (11) |
图 2为配网供电可靠性预测模型流程图。基于PCA-PSO-ELM的预测模型包括两个层次:1)分析与选取多种影响供电可靠性的指标因素;2)构建配网供电可靠性预测模型。

|
Download:
|
| 图 2 算法求解流程图 Fig. 2 Flow chart of the proposed algorithm | |
本文以某大型电网2015年47个供电局样本纵向建立基于PCA-PSO-ELM的配网供电可靠性预测模型。30个影响供电可靠性的因素作为输入变量,供电可靠性综合评价值作为输出变量。仿真分析在SPSS及Matlab软件环境下实现。
利用SPSS数据处理软件[15]对47个样本30个影响因素进行主成分分析。30个影响因素对应产生30个综合指标,如表 2所示,其中12个主成分累计贡献率为85.703%,已达到了85%,因此选取表 2中12个综合指标作为主成分。
| 表 2 方差及主成分贡献率 Tab.2 Eigenvalue and principle component contribution rates |
提取主成分之后,比较每一个主成分对应的各个原始指标的载荷,载荷越大,对应的主成分反映的该原始指标的信息量就越大。
采用熵权法对47个供电局的5个配网供电可靠性评价指标的权值客观赋值,如表 3所示,得到供电可靠性综合评价值。客观权重系数与主观权重系数均为0.5,可确定出人工神经网络的输出变量。
| 表 3 指标权重 Tab.3 Index weight |
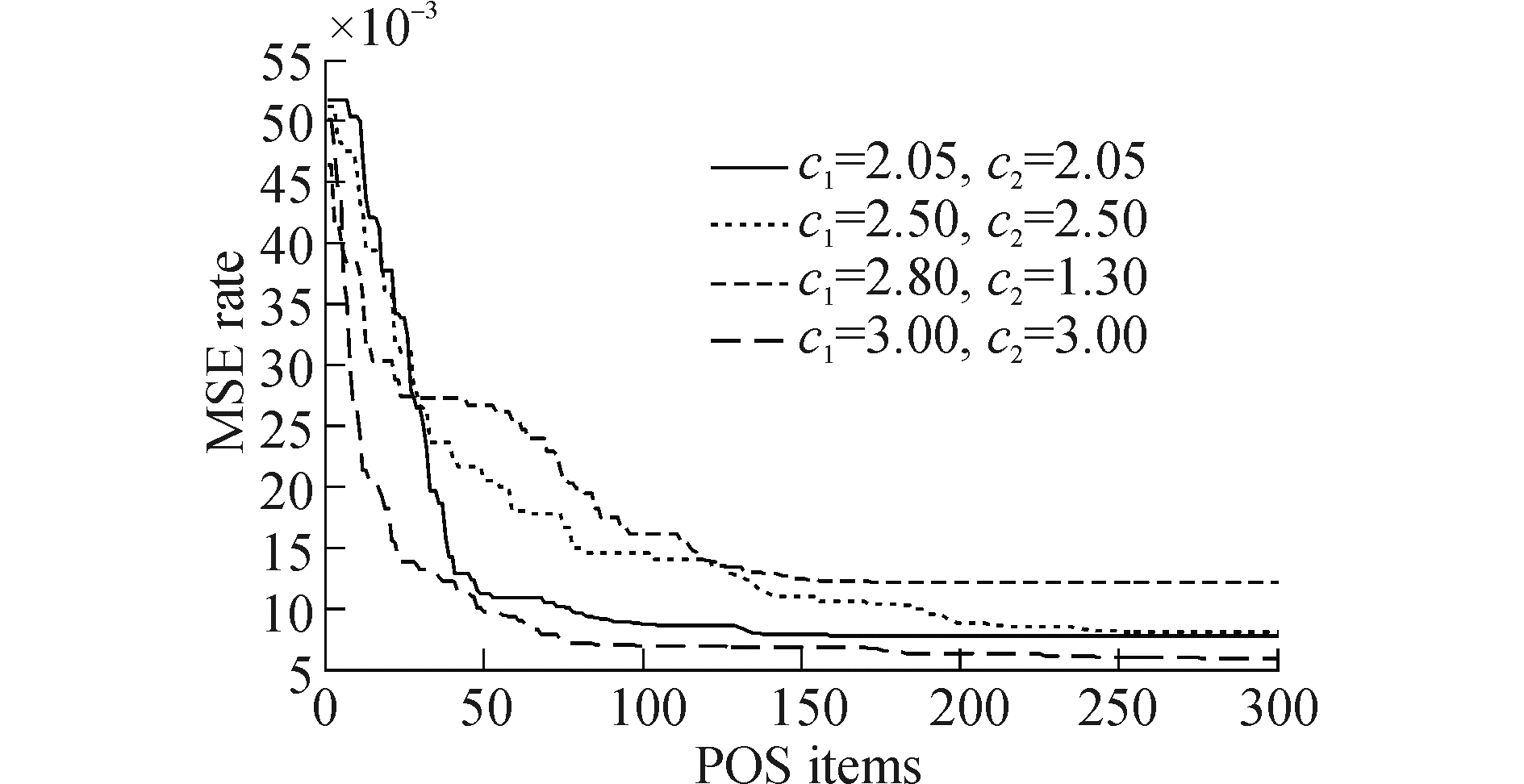
在Matlab环境下,利用PSO-ELM算法训练神经网络,以样本集中39个供电局样本作为训练样本,8个样本作为测试样本。选择应用最为广泛的3层单向前馈型神经网络,输入层神经元个数为12,隐含层神经元个数为7,输出层神经元个数为1,激活函数选择S型函数。为研究学习因子对于PSO-ELM训练人工神经网络效果的影响,分别测试PSO学习因子的以下4种情况:c1=2.05 c2=2.05;c1=2.5 c2=2.5;c1=2.8 c2=1.3;c1=3 c2=3。
图 3为迭代曲线,对比4种学习因子设置对应的迭代曲线,c1=2.05,c2=2.05时收敛速度及精度较低。c1=2.5,c2=2.5与c1=2.8,c2=1.3相比收敛速度较快,但两者适应度达到精度相似。c1=3,c2=3时收敛速度最快,适应度达到的精度较高。
|
Download:
|
| 图 3 PSO-ELM优化迭代图 Fig. 3 Optimal iteration graph of PSO-ELM | |
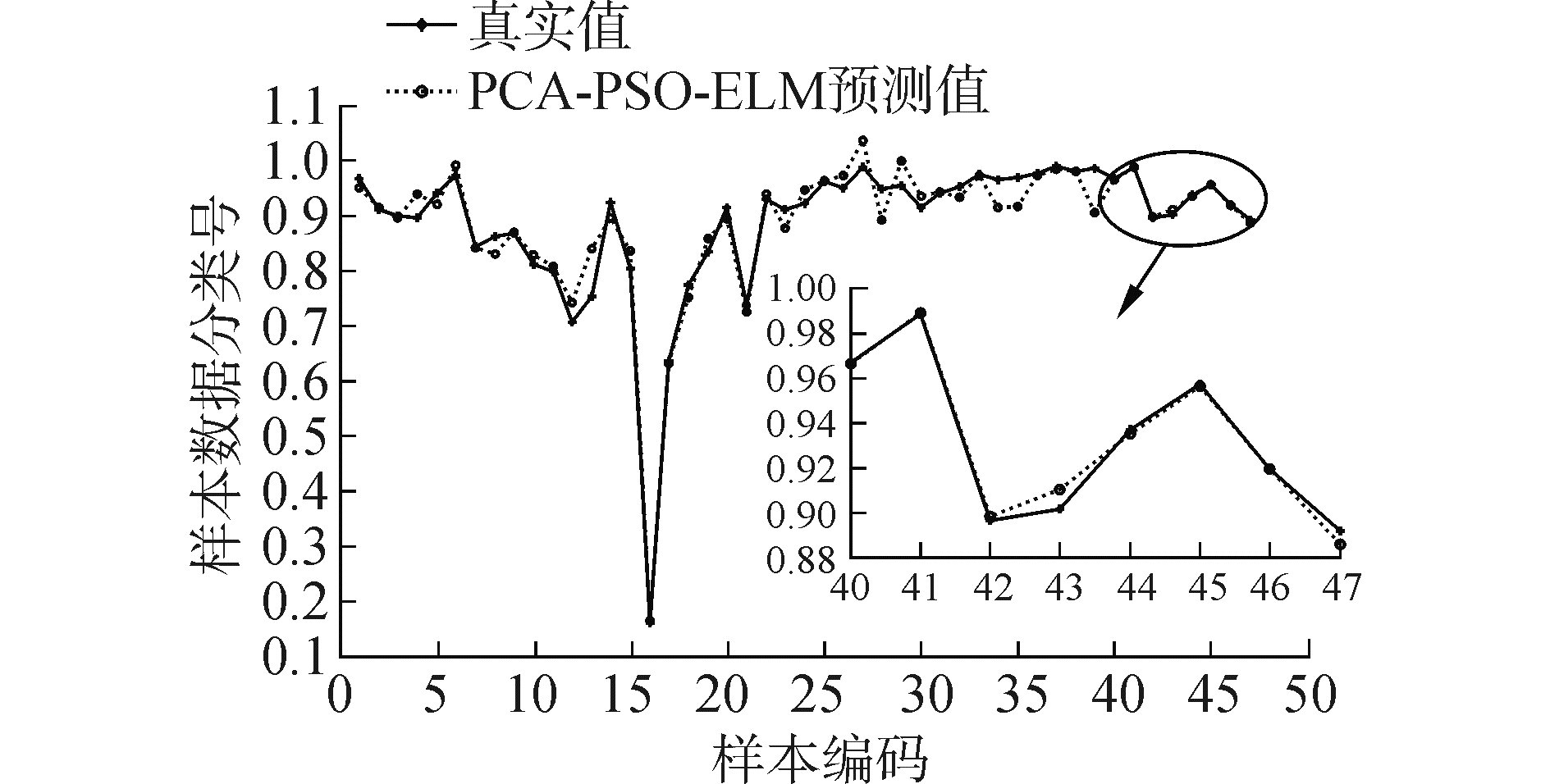
图 3为PCA-PSO-ELM模型全部样本数据供电可靠综合性指标真实值与仿真预测值对比,可知测试样本预测值与真实值的拟合程度较高。训练样本预测曲线与真实曲线趋势相同,存在一定误差,但误差较小。
|
Download:
|
| 图 4 PCA-PSO-ELM模型拟合曲线 Fig. 4 Fitting curve of PCA-PSO-ELM Model | |
为进一步验证本文模型在配网供电可靠性预测模型中有较强的性能,将PCA-PSO-ELM算法与PCA-ELM算法以及未经过PCA数据预处理的ELM算法、PSO-ELM算法进行对比试验。由于单纯的ELM训算法初始输入权值和阈值是随机确定的,因此针对ELM及PCA-ELM两种训练算法,以预测值和真实值的绝对误差及决定系数R2作为精度判断条件,反复循环训练,当绝对误差及测试集决定系数满足条件时完成训练过程。
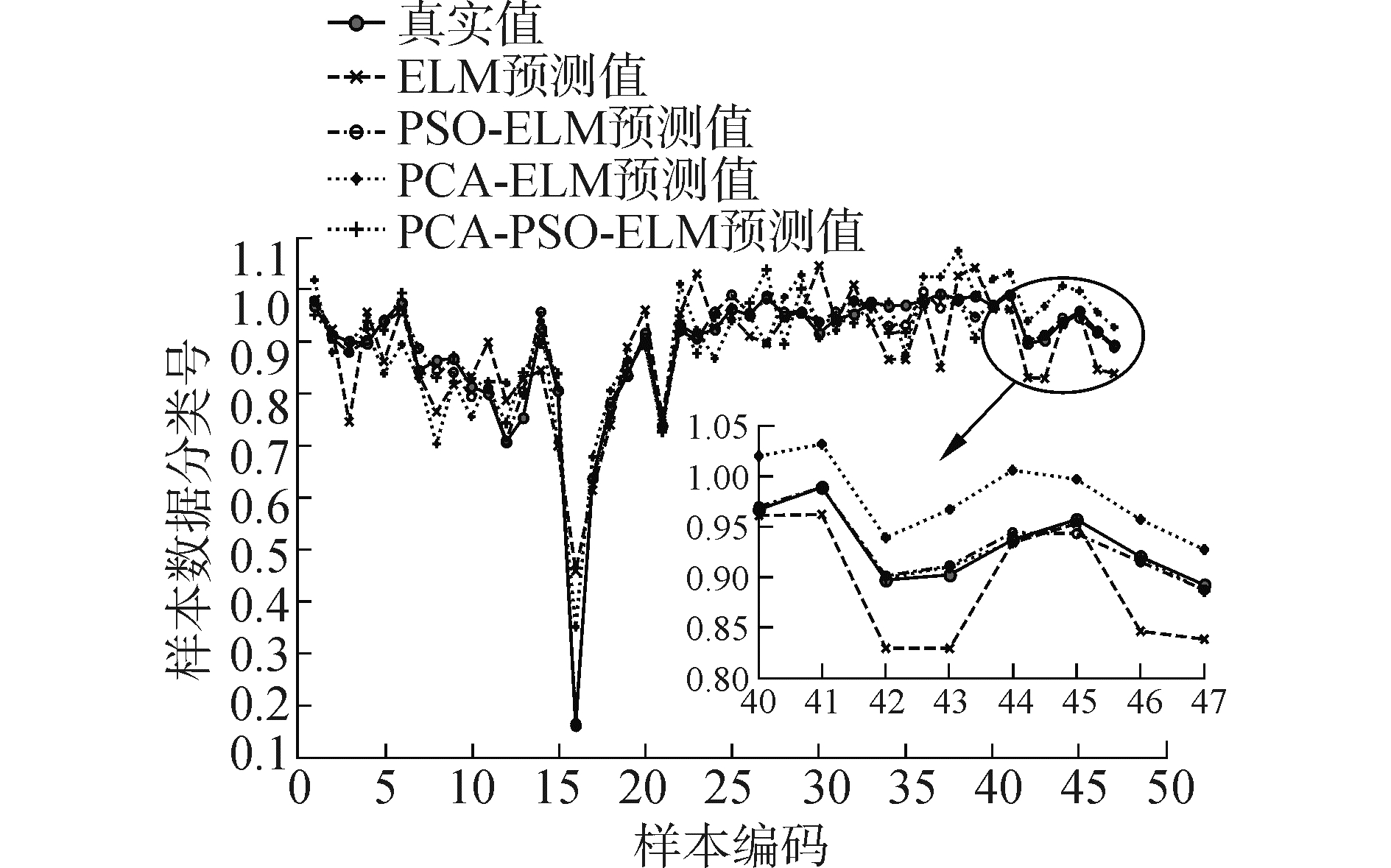
图 5为4种模型全部样本数据的供电可靠性综合指标真实值与仿真预测值对比,给出了4种算法的拟合曲线情况。表 4为测试集的真实值与预测值之间的对比,给出了两者之间的相对误差。
|
Download:
|
| 图 5 多种模型拟合曲线 Fig. 5 Fitting curves of various models | |
| 表 4 多种模型测试集真实值与预测值对比 Tab.4 Comparison between real value and predictive value of various model |
根据图 5所示拟合曲线,ELM模型和PCA-ELM模型与真实值差距较大,PCA-ELM模型拟合曲线的趋势与真实值相同,ELM模型拟合曲线的偏差较大且预测结果的精度很不稳定。PSO-ELM模型以及PCA-PSO-ELM模型预测值与真实值的拟合程度较高且偏差较小。
由表 4对比4种模型的相对误差,ELM模型测试集相对误差变化较大,测试集相对误差在0.5%~8%变动,预测结果稳定性较差。PCA-ELM模型测试集相对误差在3%~7%。PSO-ELM模型测试集相对误差均小于1.5%,PCA-PSO-ELM模型测试集相对误差小于1%,因此,PCA-PSO-ELM模型预测精度更高且拟合更好。
本算例采用决定系数R2及训练时间评价预测模型拟合程度及高效性,其中R2为[0, 1]评价指标,且越接近1表明模型拟合性能越好,接近于0表明模型拟合性能较差。
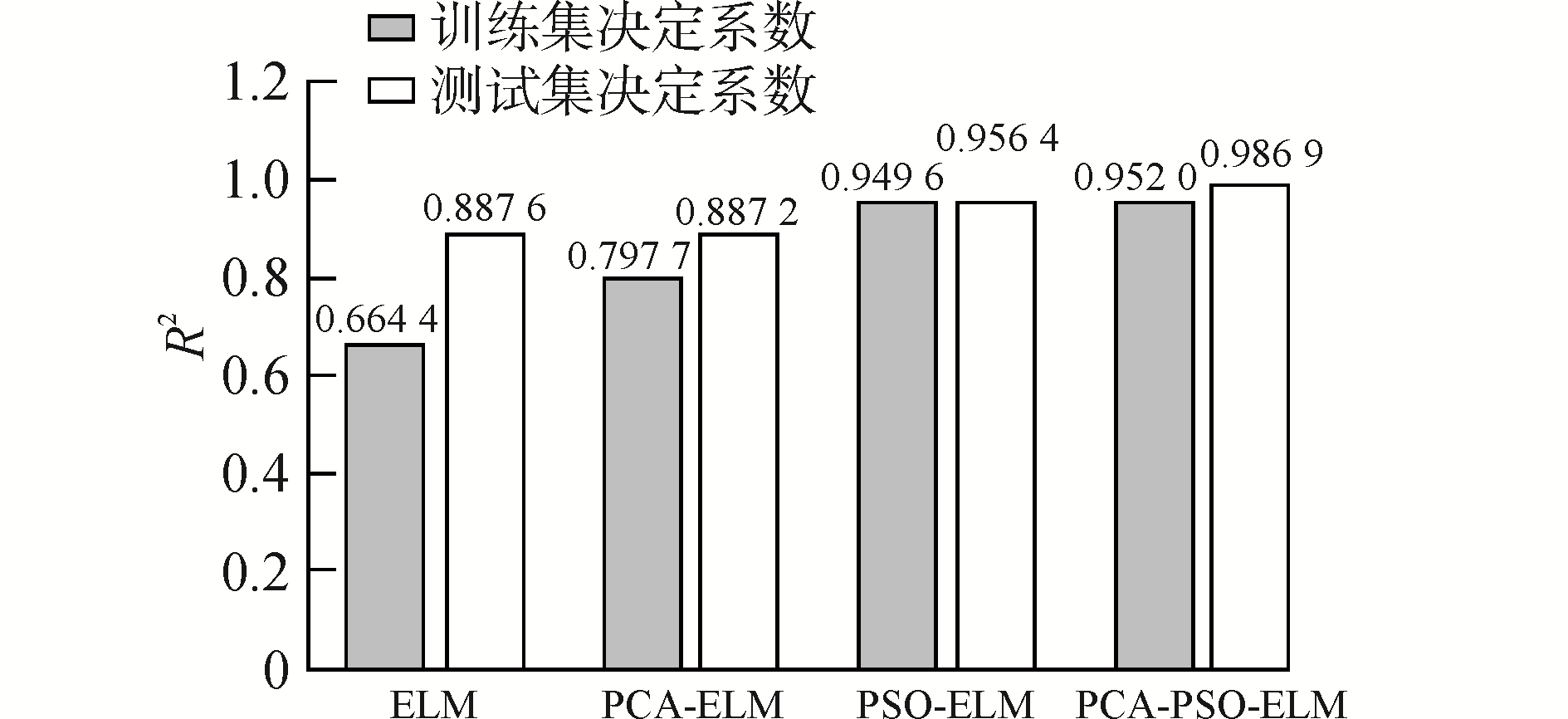
图 6为4种模型训练集及测试集决定系数的对比,PCA-PSO-ELM模型测试集决定系数及训练集决定系数均接近于1,有较高拟合程度。PCA-ELM模型训练集决定系数较高,但测试集决定系数不理想。ELM及PCA-ELM模型训练集决定系数较低。
|
Download:
|
| 图 6 多种模型决定系数对比 Fig. 6 Comparison decision coefficients of various model | |
图 7为4种模型训练时间对比,经过PSO优化后的ELM训练时间为203.89 s,而单纯的ELM训练时间要长3倍,产生训练时间上的差距主要由于单纯的ELM训练过程中输入权值和阈值是随机的,为提升预测结果的精度和决定系数,需要反复训练寻找满足要求的参数。这种较为盲目随机的训练方法增长了训练时间。

|
Download:
|
| 图 7 多种模型训练时间对比 Fig. 7 Comparison of training times of various model | |
由上述模型对比试验可知,通过PCA对原始数据的预处理,消除变量之间的冗余性和相关性,较大程度上为人工神经网络的训练奠定较好的数据基础,有利于提升训练结果的精度和稳定性。而粒子群优化算法避免了初始输入权值和阈值的随机性,通过对神经网络的初始输入权值和阈值进行优化后使得ELM模型具有了更高的预测精度,同时减少盲目寻找产生的训练时间的延长,使得供电可靠性预测模型有更好的泛化性能。故表明,基于PCA-PSO-ELM的配网供电可靠性预测模型可以对供电可靠性的预测进行快速高效的预测。
3 结论1) 可以充分考虑多方面多角度的供电可靠性影响因素,适用于多输入变量的情况,有利于对供电可靠性更加全面的分析预测。
2) 对输入的原始数据进行主成分分析的预处理,有效地实现了输入数据的降维,并去除各指标之间的相关性,提升了极限学习机训练模型的预测精度和稳定性。
3) 利用粒子群优化算法对神经网络的输入权值和阈值进行优化,有效减少预测模型的训练时间和预测精度。
4) 根据训练好的模型对影响供电可靠性指标的相关因素进行灵敏度分析可以获得对供电可靠性指标较敏感的相关特征量。
算例分析及多种回归拟合算法的对比试验表明,在样本数据准确的情况下,利用PCA-PSO-ELM模型的拟合精度和稳定性较高。此方法可以充分考虑多方面的供电可靠性影响因素,适用于多输入变量的情况。可为供电企业制定可靠性提升策略提供科学有效的参考依据。
| [1] |
国家电网公司. 电力可靠性管理培训教材.操作篇.供电系统用户供电可靠性工作指南[M]. 北京: 中国电力出版社, 2012. National Electric Net Ltd. Electric power reliability management training materials. Operating papers. User power supply reliability of power supply system[M]. Beijing: China Electric Power Press, 2012. (  0) 0)
|
| [2] |
BILLINTON R, ALLAN R N. Reliability evaluation of engineering systems:concepts and techniques[M]. 2nd ed. New York: Plenum Press, 1992.
(  0) 0)
|
| [3] |
宋云亭, 张东霞, 吴俊玲, 等. 国内外城市配电网供电可靠性对比分析[J]. 电网技术, 2008, 32(23): 13-18. SONG Yunting, ZHANG Dongxia, WU Junling, et al. Comparison and analysis on power supply reliability of urban power distribution network at home and abroad[J]. Power system technology, 2008, 32(23): 13-18. (  0) 0)
|
| [4] |
曹伟. 10kV配电网规划的供电可靠性评估和应用[D]. 长沙: 湖南大学, 2009. CAO Wei. Reliability assessment in 10kV distribution power network planning and its application[D]. Changsha: Hunan University, 2009. 10kV配电网规划的供电可靠性评估和应用 (  0) 0)
|
| [5] |
谷群辉, 罗安, 王击, 等. 一种实用的供电可靠性预测评估算法[J]. 电网技术, 2003, 27(12): 76-79. GU Qunhui, LUO An, WANG Ji, et al. A practicable algorithm to forecast and evaluate reliability of power supply[J]. Power system technology, 2003, 27(12): 76-79. DOI:10.3321/j.issn:1000-3673.2003.12.017 (  0) 0)
|
| [6] |
宋云亭, 吴俊玲, 彭冬, 等. 基于BP神经网络的城网供电可靠性预测方法[J]. 电网技术, 2008, 32(20): 56-59. SONG Yunting, WU Junling, PENG Dong, et al. A BP neural network based method to predict power supply reliability of urban power network[J]. Power system technology, 2008, 32(20): 56-59. (  0) 0)
|
| [7] |
叶航超. 支持向量机在电力系统可靠性分析中的应用研究[D]. 杭州: 浙江大学, 2013. YE Hangchao. The research of power system reliability analysis basins on SVM[D]. Hangzhou: Zhejiang University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013178178.htm (  0) 0)
|
| [8] |
刘亚南, 卫志农, 钟淋涓, 等. 基于PCA和RVM的电网供电可靠性预测模型研究[J]. 电力系统保护与控制, 2012, 40(20): 101-105, 112. LIU Ya'nan, WEI Zhinong, ZHONG Linjuan, et al. Study on the forecasting model of power supply reliability based on PCA and RVM[J]. Power system protection and control, 2012, 40(20): 101-105, 112. DOI:10.7667/j.issn.1674-3415.2012.20.018 (  0) 0)
|
| [9] |
赵春晖, 胡春梅, 石红. 采用选择性分段PCA算法的高光谱图像异常检测[J]. 哈尔滨工程大学学报, 2011, 32(1): 109-113. ZHAO Chunhui, HU Chunmei, SHI Hong. Anomaly detection for a hyperspectral image by using a selective section principal component analysis algorithm[J]. Journal of Harbin engineering university, 2011, 32(1): 109-113. (  0) 0)
|
| [10] |
HUANG Guangbin, WANG Dianhui, LAN Yuan. Extreme learning machines:a survey[J]. International journal of machine learning and cybernetics, 2011, 2(2): 107-122. DOI:10.1007/s13042-011-0019-y (  0) 0)
|
| [11] |
虞英杰. 基于PSO算法的BP神经网络模型对水体富营养化预测的研究[D]. 广州: 暨南大学, 2011. YU Yingjie. Prediction of eutrophication by BP neural network model based on PSO algorithm[D]. Guangzhou: Jinan University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10559-1011128015.htm (  0) 0)
|
| [12] |
付华, 王馨蕊, 王志军, 等. 基于PCA和PSO-ELM的煤与瓦斯突出软测量研究[J]. 传感技术学报, 2014, 27(12): 1710-1715. FU Hua, WANG Xinrui, WANG Zhijun, et al. Research on the soft sensor of coal and gas outburst based on PCA and PSO-ELM[J]. Chinese journal of sensors and actuators, 2014, 27(12): 1710-1715. DOI:10.3969/j.issn.1004-1699.2014.12.023 (  0) 0)
|
| [13] |
Std. IEEE. IEEE Std 1366-2012, IEEE Guide for electric power distribution reliability indices[S]. New York: IEEE, 2012: 1-40.
(  0) 0)
|
| [14] |
瞿海妮, 刘建清. 国内外配电网供电可靠性指标比较分析[J]. 华东电力, 2012, 40(9): 1566-1570. QU Haini, LIU Jianqing. Comparison and analysis on power supply reliability indicators of distribution network at home and abroad[J]. East China electric power, 2012, 40(9): 1566-1570. (  0) 0)
|
| [15] |
CHEN Hongming, XIAO Xiaocan. The application of SPSS factor analysis in the evaluation of corporate social responsibility[J]. Journal of software, 2012, 7(6): 1258-1264. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


