2. 南京理工大学 自动控制系, 南京 210094
2. Department of Automatic control, Nanjing University of Science and Technology, Nanjing 210094, China
惯性导航系统以其自主性、实时性和全导航参量的优点在各类车辆中应用广泛,但INS的定位误差随时间而积累,必须引入其他的辅助手段来对INS进行校正,常用方法有全球定位系统(global positioning system, GPS)、地图匹配及航位推算等。现阶段,数字地图的精度已经可以达到米级,甚至更高,因此用地图匹配方法来辅助INS进行导航已经成为热点。地图匹配方法有多种,如权值法[1]、概率统计法[2]、模糊逻辑法[3]、拓扑结构法[4]、D-S推理法[5]、Kalman滤波法[6]及贝叶斯法[7]等,但上述方法大部分都是针对GPS数据的,而针对INS数据的极少。ZHAO等提出了基于曲率半径的地图匹配算法[8];龚柏春等提出了基于移动相关的最小二乘地图匹配算法[9];LUO H等在基于权重地图匹配算法的基础上,针对道路搜索提出了二次网格划分的搜索方法[10]。文献[8]是通过曲率计算INS轨迹与道路的匹配度,进而选择最优匹配道路。文献[9]是利用最小二乘法计算INS轨迹与道路的相关性,再选择最优匹配道路。虽然文献[8-9]可以消除INS沿着道路的纵向位置误差,但是文献[8-9]提出的地图匹配算法都是在车辆的航向角发生较大变化时才有效,并且计算量较大。而文献[10]提出了加快道路搜索的方法,但不能够消除INS沿道路的纵向位置误差。
为了能够消除INS与道路垂直的横向位置误差和沿着道路的纵向位置误差,同时有更高的匹配效率和匹配精度,本文提出了一种新的基于INS信息的地图匹配算法。与文献[8]相比,本文采用基于动态权值的道路选择方法,具有更高的效率。在此基础上,引入平移向量,利用平移向量对当前时刻INS数据的偏移进行补偿,进而实现对与道路垂直的横向位置误差和沿着道路的纵向位置误差的修正。
1 惯导/地图匹配算法 1.1 基于平移向量的道路搜索方法INS的误差主要包括三种形式的周期振荡:舒拉周期振荡、地球周期振荡和付科周期振荡。对于装载纯INS的车载导航系统,虽然这种周期振荡会导致导航位置出现偏差,但它的位置依然是连续变化的。因此,对于INS来说,可以引入一个平移向量,在每次进行匹配候选道路搜索之前,都对当前INS输出的位置进行补偿,使补偿之后的位置更加接近真实的位置,进而缩小搜索候选道路的范围,节省时间,提高效率。另外,候选道路的选择范围和INS返回的速率相关,速率大,选择范围变大;速率小,选择范围变小。
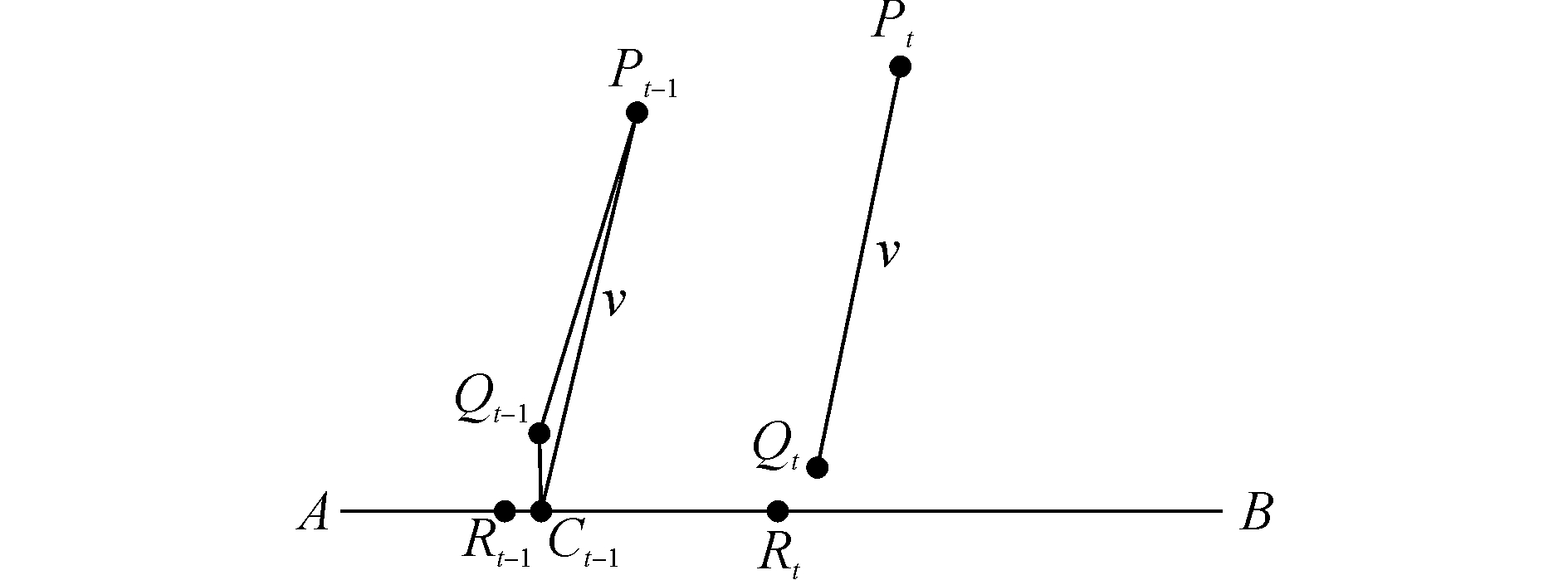
如图 1所示,其中AB为道路,点Pt-1、Qt-1、Ct-1和Rt-1分别为t-1时刻INS输出位置点、经过平移向量补偿后的INS位置点、地图匹配后的位置点和车辆真实位置点。定义平移向量:v=Pt-1Ct-1,在t时刻,相应的点为Pt、Qt和Rt。在选取候选道路之前,用平移向量v对INS位置点Pt进行补偿,得到补偿之后的位置点Qt,公式为Qt=v+Pt。
|
图 1 平移向量对INS位置的补偿 Fig.1 Compensation of location based on translation vector |
容易看出,点Qt比点Pt更接近于真实位置Rt。即,如果平移向量选取适当,只要选取很小范围内的路段作为候选道路即可。
1.2 基于动态权值的道路选择方法下面具体分析影响候选道路选择的因素:
因素1:INS位置与候选道路的距离d。
如图 2所示,其中AB为道路,点Q1、Q2和Q3代表经过平移向量补偿后INS可能输出的三种不同情况位置点。为了区分三种情况,引入辅助变量γ,设INS补偿后的位置点Q(Q1或Q2或Q3)的坐标为(x, y),道路上点A为(x1, y1),点B为(x2, y2)。则辅助变量γ的计算公式为
| $\gamma = \frac{{(x - {x_1})({x_2} - {x_1}) + (y - {y_1})({y_2} - {y_1})}}{{{{({x_1} - {x_2})}^2} + {{({y_1} - {y_2})}^2}}}$ | (1) |

|
图 2 距离d与γ的定义 Fig.2 The definition of distance d and γ |
当INS位置点在区域Ⅰ中,即γ < 0时,定义距离d=|Q1A|;当INS位置点在区域Ⅱ中(包括边界),即0≤γ≤1时,定义距离d=|Q2C|;当INS位置点在区域Ⅲ中,即γ>1时,定义距离d=|Q3B|。
因素2:INS航向与道路方向的夹角。
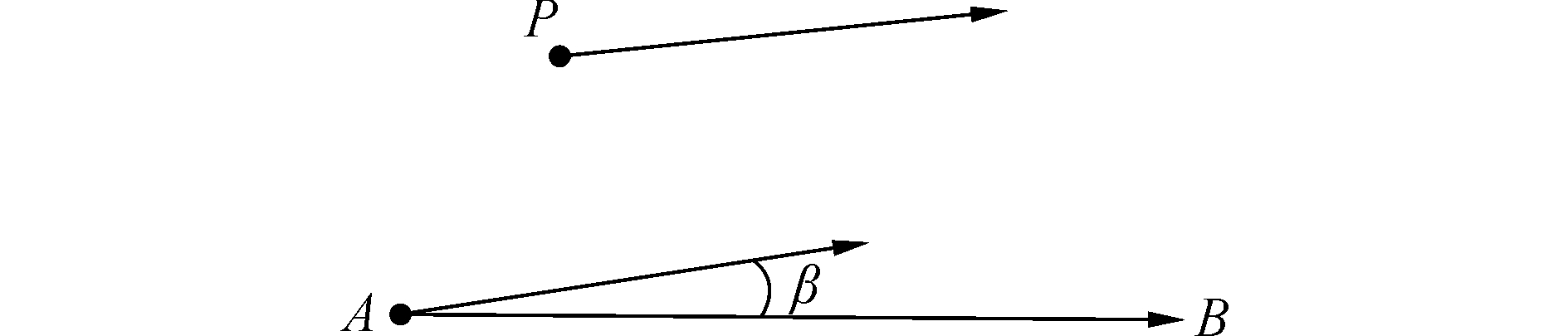
如图 3所示,其中AB为道路,P为INS输出位置点,以P为起点的向量为载体的航向角向量,平移航向角向量,使点P与点A重合,β即为载体航向与道路矢量的夹角。定义β余弦值的绝对值为θ,即θ=|cos β|。
|
图 3 INS航向与道路的夹角β Fig.3 Angle β between INS and road |
由于载体的航向角在道路转弯处会发生连续的变化,如果采用变化中的航向角作为加权因素之一,可能产生错误的结果。因此,道路转弯处可加入一个延迟环节,即当载体的航向角稳定后,再进行计算。
判断载体是否进入转弯阶段方法:根据载体航向角的变化率和经过地图匹配算法后的载体位置点与交叉路口点的距离可以判断载体是否进入转弯阶段,即当载体航向角的变化率越大,地图匹配后的位置点与交叉路口点的距离越短时,载体进入转弯的可能性越大。
因素3:道路网络的拓扑结构。
即车辆在道路上行驶,当前时刻t车辆所在的道路一定与前一时刻t-1车辆所在的道路相同或者相邻(假设两个时刻间隔足够短)。
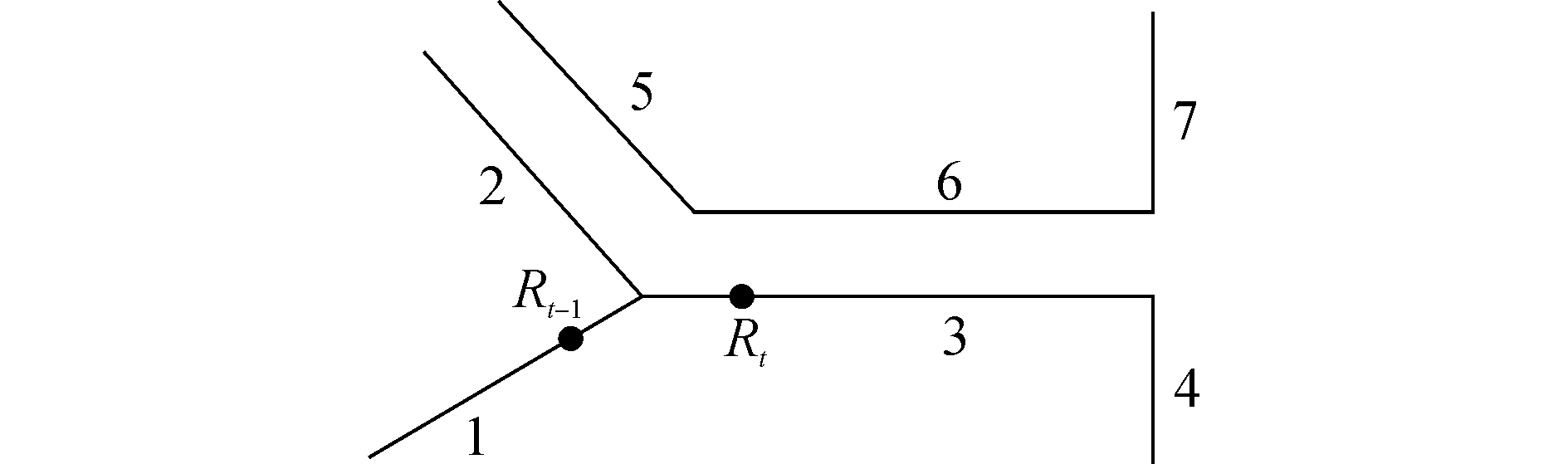
如图 4所示,其中有7段道路,分别为1~7。点Rt-1和Rt分别为t-1时刻和t时刻对应的载体位置点。假设t-1时刻载体在Rt-1位置,即在道路1上,那么t时刻,载体行驶的可能道路为1~3。当t时刻载体在Rt位置,即在道路3上时,那么t+1时刻载体行驶的可能道路为1~4,而不可能为道路5~7。为了加快选择速度,减少计算时间,在计算加权值之前,可利用道路的拓扑性排除不符合的候选道路,进而减少后续的计算量。
|
图 4 道路网络的拓扑结构 Fig.4 Topological structure of road network |
最后,加权公式为
| ${f_i} = {\omega _1}\left( {\sum\limits_{k = 1}^n {{d_k} - {d_i}} } \right)/\sum\limits_{k = 1}^n {{d_k} + {\omega _2}{\theta _i}} $ | (2) |
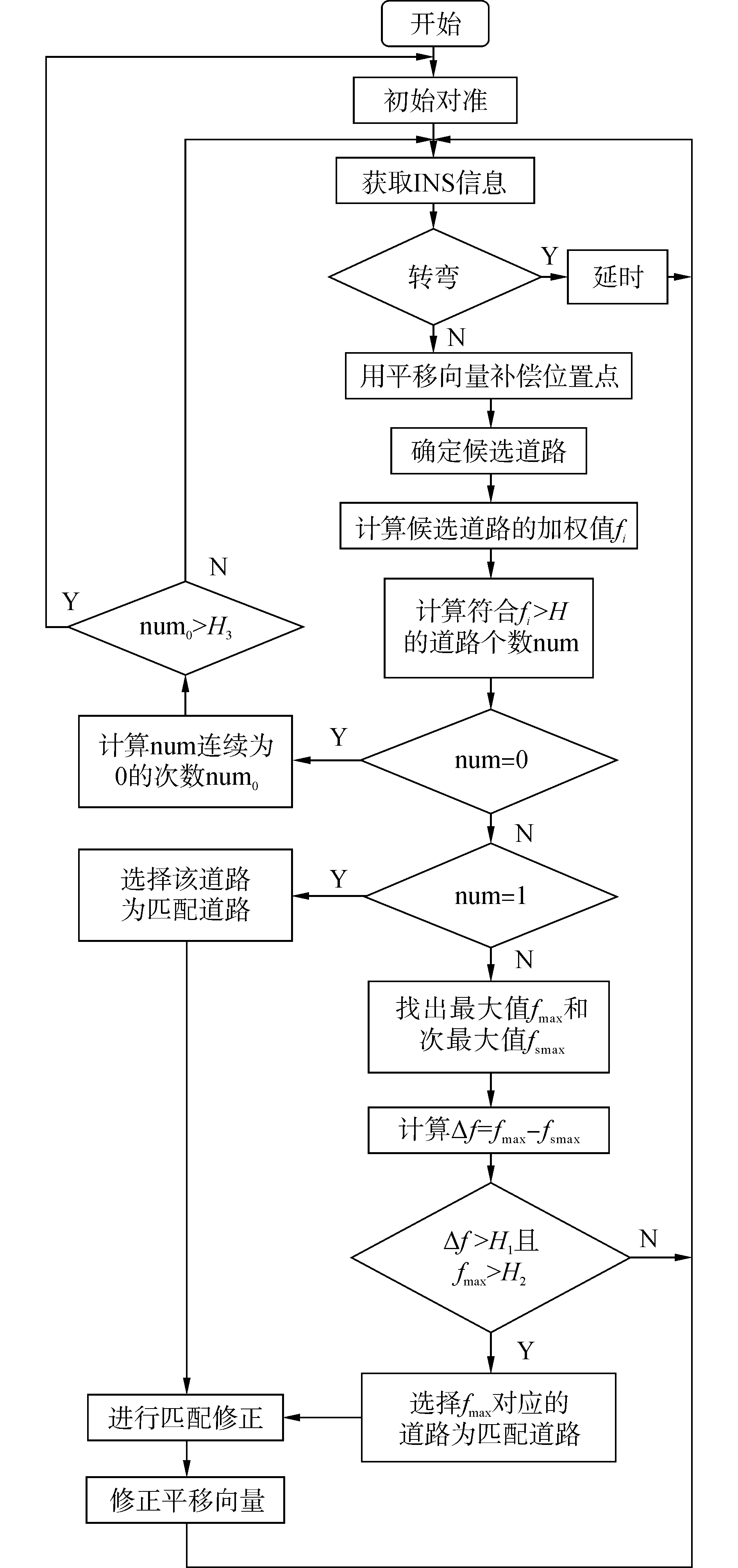
式中:fi是道路i的加权值,di是INS补偿后的位置点Q与道路i的距离,θi是INS航向角与道路i夹角余弦值的绝对值。当fi越大时,表明道路i的可信度越大,反之越小。ω1和ω2可以根据位置点所在的道路网络结构进行动态调整。调整规则如下:当候选道路较少,路网比较简单时,取ω1=0.6,ω2=0.4;当候选道路较多,路网比较复杂时,取ω1=0.4,ω2=0.6;当载体离道路的交叉点比较近,即可能发生转弯时,取ω1=0.35,ω2=0.65。统计fi大于阈值H的个数,如果候选道路个数为0,则等待下一个INS信息重新开始。如果候选道路个数连续为0的个数大于H3,则进行初始对准,重新开始。如果候选道路个数为1,则选择该道路为匹配道路;如果候选道路个数大于1,则判断最大加权值fmax和次大加权值fsmax的差值是否大于阈值H1,即fmax-fsmax>H1,并且判断fmax>H2是否成立,如果是则选择最大加权值fmax对应的道路作为匹配道路,否则等待下一个INS信息重新开始。其中H、H1、H2和H3取值分别为0.9、0.03、0.95和8,可根据道路实际情况进行动态调整。
1.3 基于平移向量的INS位置修正方法在候选道路中选出匹配道路后,采用平移向量补偿后的位置点Q进行投影匹配。参考图 2,使用辅助变量γ,当γ < 0时,即在区域Ⅰ中,位置点Q1投影到A点,投影点C与A重合;当0≤γ≤1,即在区域Ⅱ中时(包括边界),位置点Q2投影到点C;当γ>1,即在区域Ⅲ中时,点Q3投影到点B,投影点C与B重合。当0≤γ≤1时,设Q2点的坐标为(x, y),A的坐标为(x1, y1),B的坐标为(x2, y2),投影点C的坐标为(xi, yi),则
| $\begin{array}{l} {x_i} = \frac{{({x_2} - {x_1})[x({x_2} - {x_1}) + y({y_2} - {y_1})] + ({y_2} - {y_1})({x_1}{y_2} - {x_2}{y_1})}}{{{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}}\\ {y_i} = \frac{{({y_2} - {y_1})[x({x_2} - {x_1}) + y({y_2} - {y_1})] - ({x_2} - {x_1})({x_1}{y_2} - {x_2}{y_1})}}{{{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}} \end{array}$ | (3) |
得到投影点C之后,修正平移向量,即v=PC。由惯性导航系统输出位置信息的连续性可以推出,相邻的两个平移向量应满足|vt-vt-1| < H4。其中H4根据载体所在经纬度和车速进行动态调整。
算法流程图如图 5所示。
|
图 5 算法流程图 Fig.5 Flow chart of algorithm |
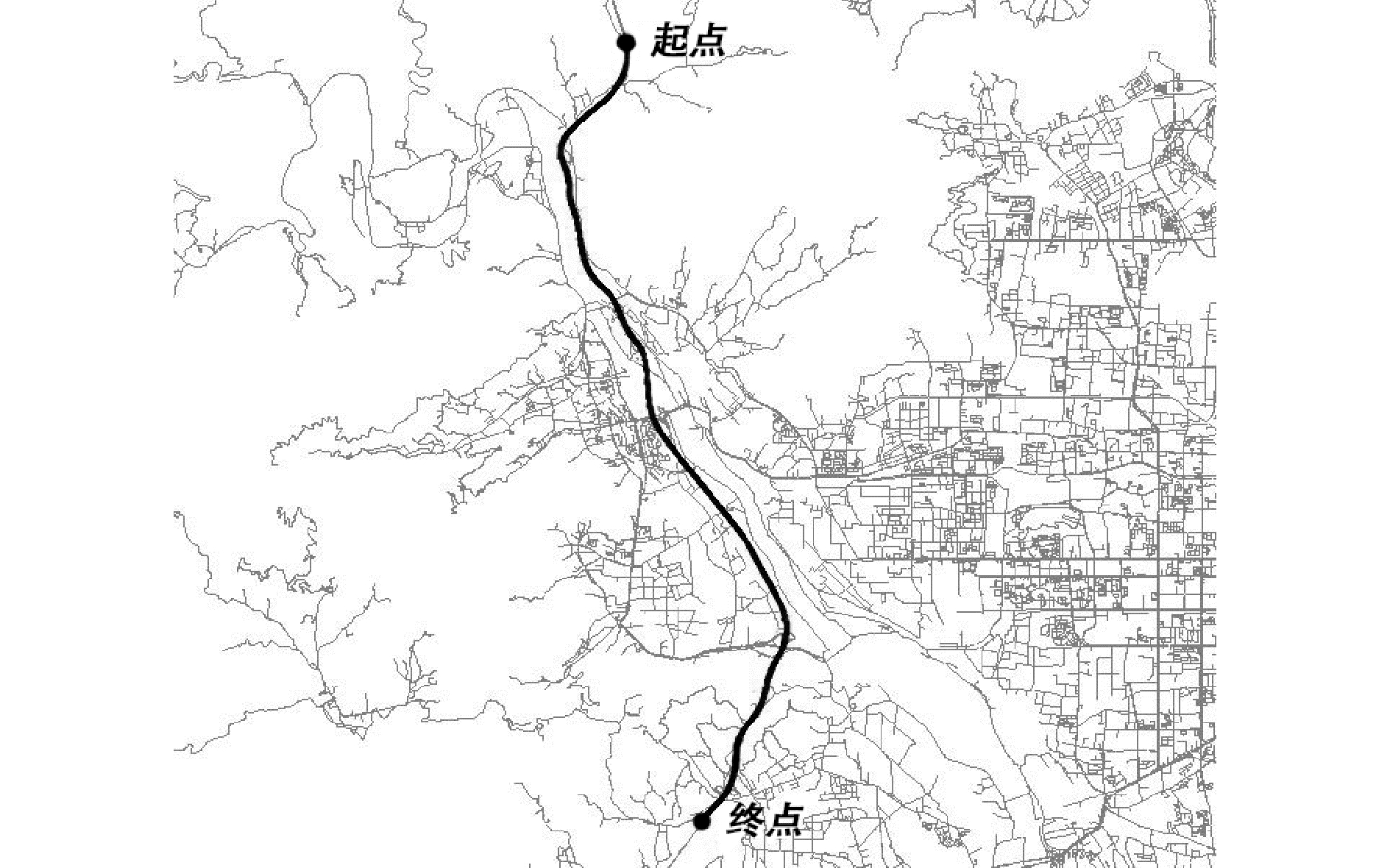
为了验证算法的有效性,用实地跑车数据进行了检验。实地跑车采用某型号SINS,陀螺的漂移为0.02(°)/h,加速度计的零偏为50 μg。使用INS和GPS组合导航输出的位置作为车辆的真实参考位置,精度优于0.1 m。地图选用MapInfo格式的北京市电子地图,精度为1 m。实际跑车起点为北京市门头沟区军庄镇西杨坨村北,终点为北京市丰台区长辛店镇大灰厂村东,全程约20 km,耗时约30 min,平均速度约为40 km/h,整段路程路况复杂,包括直行路段、丁字路口、多叉路口、平行路段等。路线如图 6中粗线所示。
|
图 6 跑车线路图 Fig.6 Route of driving car |
图 6为跑车结果及终点附近局部放大图。其中1线为INS返回的载体位置点,2线为地图匹配的位置点, 3线为GPS和INS组合导航返回的载体精确位置点(载体参考位置点)。从图 7中可以看出,INS位置点经过地图匹配算法后,可以得到更加准确的载体位置。(地图匹配位置点和参考位置点基本重合)

|
图 7 跑车试验结果 Fig.7 Experimental result of driving car |
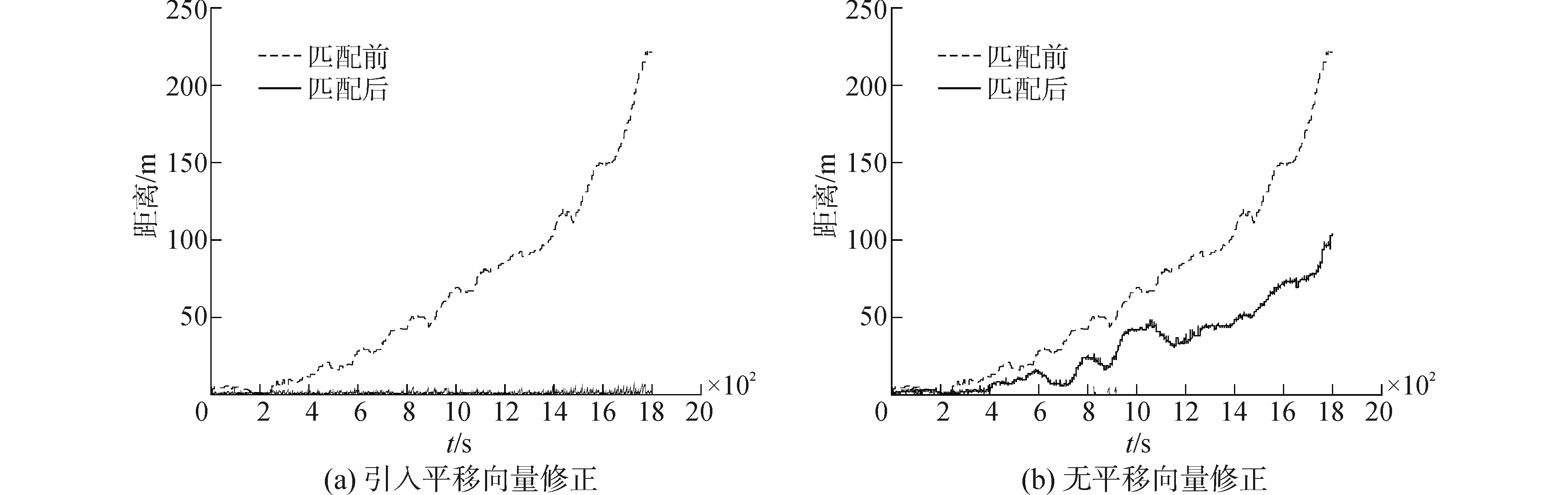
整段路程INS位置点相对于参考位置点的距离和地图匹配后INS位置点相对于参考位置点的距离随时间的变化如图 8(a)所示。作为对比,去掉平移向量后,INS位置点相对于参考位置点的距离和地图匹配后INS位置点相对于参考位置点的距离随时间的变化如图 8(b)所示。
|
图 8 地图匹配前INS位置相对于参考位置的距离和地图匹配后INS位置相对于参考位置的距离 Fig.8 Distance before MM between INS and reference position and distance after MM between INS and reference position |
从图 8中可以看出,车辆在行驶一段时间后,INS位置点相对于参考位置点的距离出现了明显的误差,最大距离约为220 m,这个误差包括与道路垂直的横向位置误差和沿着道路的纵向位置误差。而经过有平移向量的地图匹配算法后,INS位置点与参考位置点之间的距离明显缩小,约为1.5 m。而去掉平移向量之后,经过地图匹配算法的INS位置点相对于参考位置点之间的最大距离由220 m减小到约100 m,虽然误差得到了修正,但效果并不明显。
3 结论1) 多动态权值的道路选择方法、改进的投影修正方法、平移向量和转弯延迟的引入,使地图匹配算法不仅可以消除INS与道路垂直的横向位置误差和沿着道路的纵向位置误差,且在车辆航向角变化较小的情况下,仍然具有很高的匹配精度,这为基于地图匹配信息的INS的误差校正奠定了基础。
2) INS可以输出车辆的高度信息和姿态信息,如何利用该信息辅助地图匹配算法,提高匹配精度和效率,可以作为本文进一步研究的重点。
| [1] |
LI L, QUDDUS M, LIN Z. High accuracy tightly-coupled integrity monitoring algorithm for map-matching[J]. Transportation research part C:emerging technologies, 2013, 36: 13-26. DOI:10.1016/j.trc.2013.07.009 ( 0) 0)
|
| [2] |
BIERLAIRE M, CHEN J, NEWMAN J. A probabilistic map matching method for smartphone GPS data[J]. Transportation research part C:emerging technologies, 2013, 26: 78-98. DOI:10.1016/j.trc.2012.08.001 ( 0) 0)
|
| [3] |
REN M, KARIMI H A. Movement pattern recognition assisted map matching for pedestrian/wheelchair navigation[J]. The journal of navigation, 2012, 65(4): 617-633. DOI:10.1017/S0373463312000252 ( 0) 0)
|
| [4] |
BLAZQUEZ C, MIRANDA P, PONCE A. Performance of a new enhanced topological decision-rule map-matching algorithm for transportation application[J]. Journal of applied research and technology, 2012, 10(6): 929-940. ( 0) 0)
|
| [5] |
NASSREDDINE G, ABDALLAH F, DENOEUX T. Map matching algorithm using analysis and Dempster-Shafer theory[C]//2009 IEEE Intelligent Vehicles Symposium, 2009:494-499.
( 0) 0)
|
| [6] |
CHU H J, TSAI G J, CHIANG K W, et al. GPS/MEMS INS data fusion and map matching in urban areas[J]. Sensors, 2013, 13(9): 11280-11288. DOI:10.3390/s130911280 ( 0) 0)
|
| [7] |
SMAILI C, EI NAJJAR M E B, CHARPILLET F. A hybrid Bayesian framework for map matching formulation using switching kalman filter[J]. Journal of intelligent & robotic systems, 2014, 74(3): 725-743. ( 0) 0)
|
| [8] |
ZHAO C Z, LI S L, LENG Y X. A new map matching algorithm for In-vehicle Inertial Navigation Systems[C]//2010 Second ⅡTA International Conference on Geoscience and Remote Sensing. Shandong, China, 2010:590-592.
( 0) 0)
|
| [9] |
龚柏春, 罗建军, 李岁劳, 等. 基于移动相关的最小二乘法地图匹配新算法[J]. 中国惯性技术学报, 2012, 20(4): 435-439. GONG Baichun, LUO Jianjun, LI Suilao, et al. Novelmap-matching algorithm based on moving-related least squares[J]. Journal of Chinese inertial technology, 2012, 20(4): 435-439. (  0) 0)
|
| [10] |
LUO H, DENG Z H, FU M Y, et al. A map matching algorithm for Inertial Navigation Systems based on the adaptive projection method[C]//2014 Seventh International Symposium on Computational Intelligence and Design. Hangzhou, China, 2014:304-308.
( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


