2. 哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
21世纪以来,面对常规能源日益枯竭、环境恶化的局面,人类对可持续、无污染的可再生能源的开发利用刻不容缓。其中潮流能由于没有明显的丰枯年以及季节的大幅度能量变化,具有可持续、能量密度大、可预测、同时不占有陆地面积等优势,越来越受到人们的青睐[1]。潮流能水轮机[2]是潮流能电站的关键部件,它的水动力性能直接关系到电站的效益。目前水轮机水动力性能研究的主要数值方法有:流管法(BEM)[3-4]、涡方法[5]和黏性计算流体动力学(computational fluid dynamics, CFD)方法[6]。CFD方法由于能够提供详细的流场信息, 而得到广泛应用。
目前对垂直轴水轮机[7-8]定轴转动的研究已趋于完善,但对于垂直轴水轮在波浪中水动力性能影响还处于探索阶段。漂浮式是潮流能电站载体的重要形式,在实际漂浮式[9]潮流电站中,漂浮式载体由于海浪的存在会产生运动响应,从而导致水轮机跟随漂浮式载体一起运动,而水轮机水动力主要和叶片的相对运动速度有关,进而影响水轮机的水动力载荷。盛其虎等[10]对水轮机的纵荡和横荡做了简单分析。在此基础上,王凯等[11]对水轮机的艏摇运动做了简单计算,发现水轮机水动力载荷发生较大的波动。但对于水轮机摇荡运动的研究还停留在固定偏角,对于变偏角水轮机摇荡运动的研究尚未开展[12-14]。对于主动控制式变偏角水轮机而言,偏角的变化规律是在均匀来流中匀速旋转条件下优化得到的,因此当水轮机随漂浮式载体发生波浪响应运动时,改变了水轮机旋转平面处的速度分布,从而使水轮机的水动力特性发生变化。因此,本文以主动控制式变偏角水轮机为对象,采用CFD方法建立均匀来流中旋转和艏摇耦合运动模型,研究水轮机旋转和艏摇耦合运动时的流场和水动力特性,并阐明不同艏摇频率和艏摇幅值对水动力特性的影响规律。
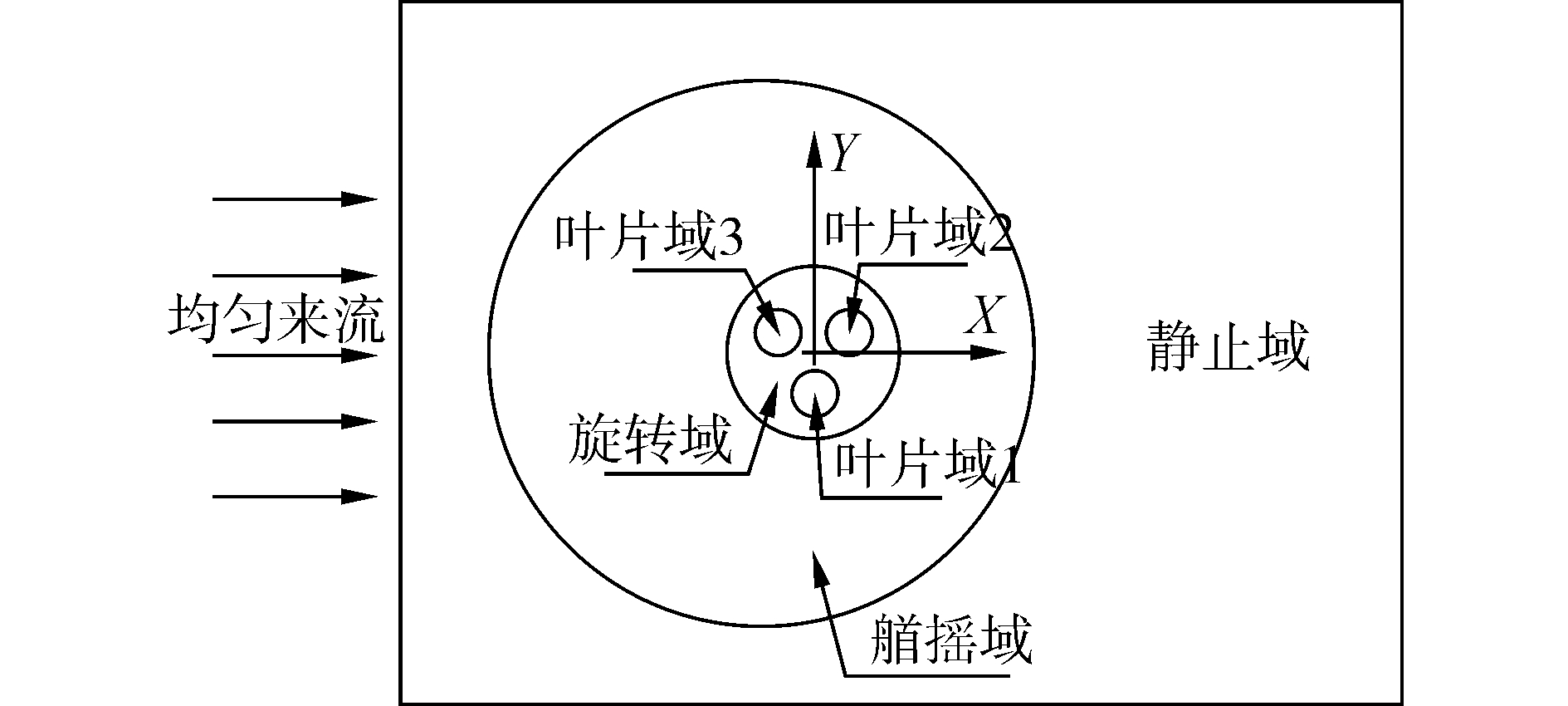
1 CFD数值模拟王凯等[15-17]已验证了ANSYS CFX模拟垂直轴潮流能水轮机水动力特性的有效性和准确性,因此本文采用ANSYS CFX进行模拟。在模拟时,由于垂直轴水轮机叶片展弦比(叶片展长与弦长的比值)较大,因此采用二维模型来模拟水轮机旋转和艏摇耦合运动。水轮机直径为0.8 m,叶片数为3,各叶片弦长均为0.12 m,叶片翼型为NACA0018。数值模拟时需要同时模拟水轮机的旋转运动、叶片绕自身转轴的旋转运动(叶片偏角控制,偏角运动规律根据文献[18]得到)和艏摇运动(a=Asin(ωt),A为艏摇幅值,ω为艏摇频率,艏摇中心距水轮机旋转中心D/2)。因此,为了保持计算过程中网格的质量,从而提高计算精度,将整个计算域分为6个区域:3个叶片域、旋转域、艏摇域及静止域,各区域之间通过交界面连接,计算域划分如图 1所示。整个计算域长32D,宽16D,且速度入口距水轮机中心8D。各区域的网格全部采用六面体的网格。
|
Download:
|
| 图 1 计算域示意图 Fig. 1 Calculation domain schematic | |
变偏角水轮机艏摇运动过程中,叶片的运动可由三个旋转运动组成:绕艏摇中心轴的旋转运动、绕水轮机中心轴的旋转运动及绕自身转轴的旋转运动,因此采用动网格来实现叶片运动的控制,即给出各个时刻网格节点的位置。具体运动控制如下:艏摇域整体设定艏摇运动,即整体绕艏摇域中心轴旋转,网格不发生变形;旋转域整体设定艏摇运动和绕自身中心轴的旋转运动,网格也不发生变形;叶片域整体设定艏摇运动、绕旋转域中心轴的旋转运动以及绕自身中心轴的旋转运动,网格也不发生变形;静止域网格保持静止。其他边界条件设置如下:设定大气压为参考气压;将进口边界设为速度进口,给定来流速度大小和湍流参数;出口边界采用压力出口边界条件;流体计算域的侧面设定为自由滑动墙面;叶片表面为无滑移壁面;各区域之间通过交界面连接。计算中湍流模型采用SST模型,求解器为瞬态求解器,时间步长为水轮机旋转3°所用的时间。
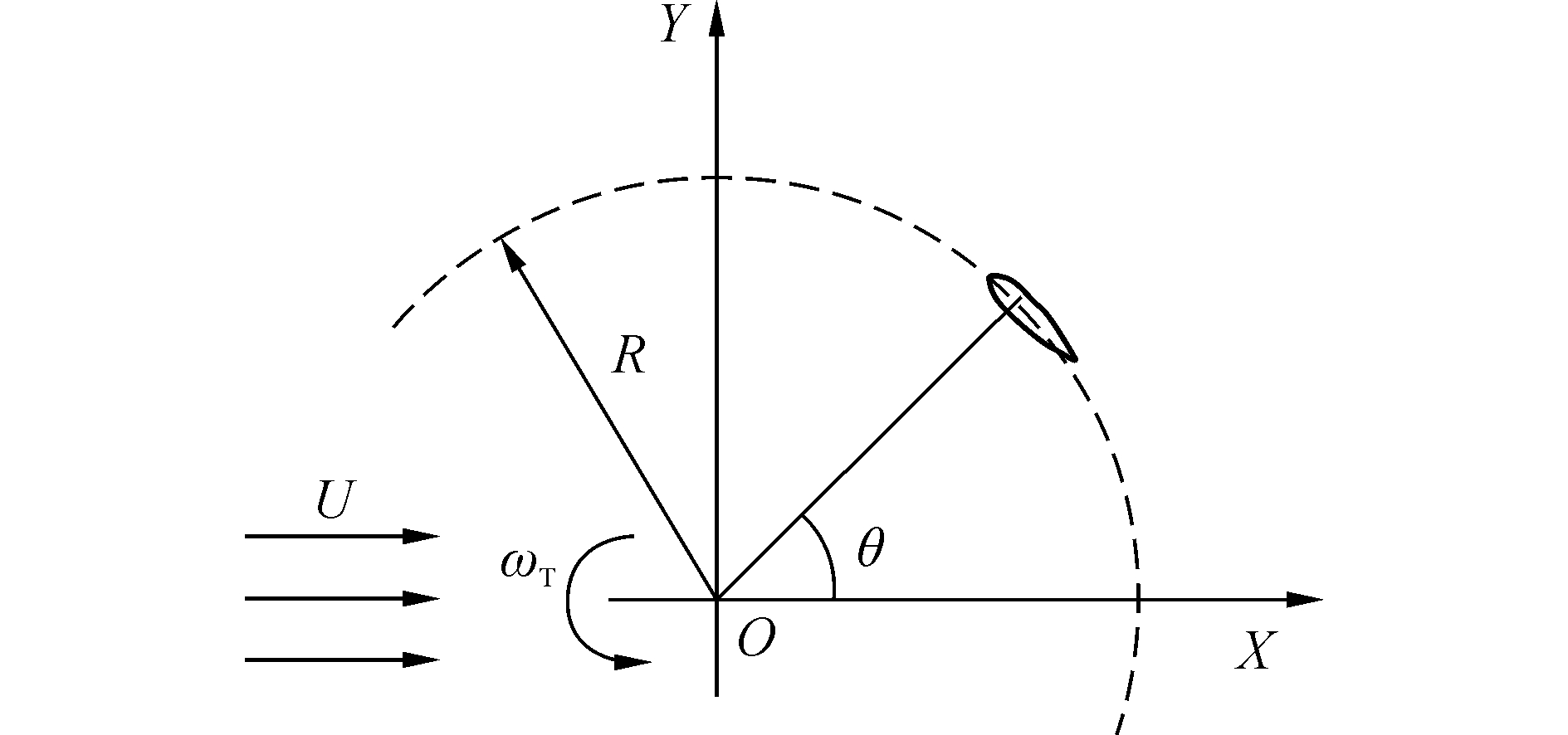
2 计算结果分析为方便后续分析,建立计算坐标系如图 2所示。坐标系O-XYZ,选取水轮机转轴中心为坐标原点O,来流方向为X轴,垂直于来流的方向为Y轴;假设在均匀来流U中,水轮机将以恒定的旋转角速度ωT,绕中心轴O旋转,其半径为R,θ为叶片方位角。叶片1的起始位置在Y轴负方向,即θ=270°的位置。叶尖速比、水轮机推力系数、水轮机侧向力系数及水轮机转矩系数分别为λ、CFx、CFy及CTz,定义如下:
| $ \lambda = \frac{{{\omega _T}R}}{U} $ | (1) |
| $ {C_{Fx}} = \frac{{{F_X}}}{{0.5\rho {U^2}Db}} $ | (2) |
| $ {C_{Fy}} = \frac{{{F_Y}}}{{0.5\rho {U^2}Db}} $ | (3) |
| $ {C_{Tz}} = \frac{{{T_Z}}}{{0.5\rho {U^2}DbR}} $ | (4) |
|
Download:
|
| 图 2 计算模型坐标系 Fig. 2 Coordinate system of model | |
式中:ρ为介质密度,b为叶片展长,FX为水轮机推力,FY为水轮机侧向力,TZ水轮机主轴转矩。
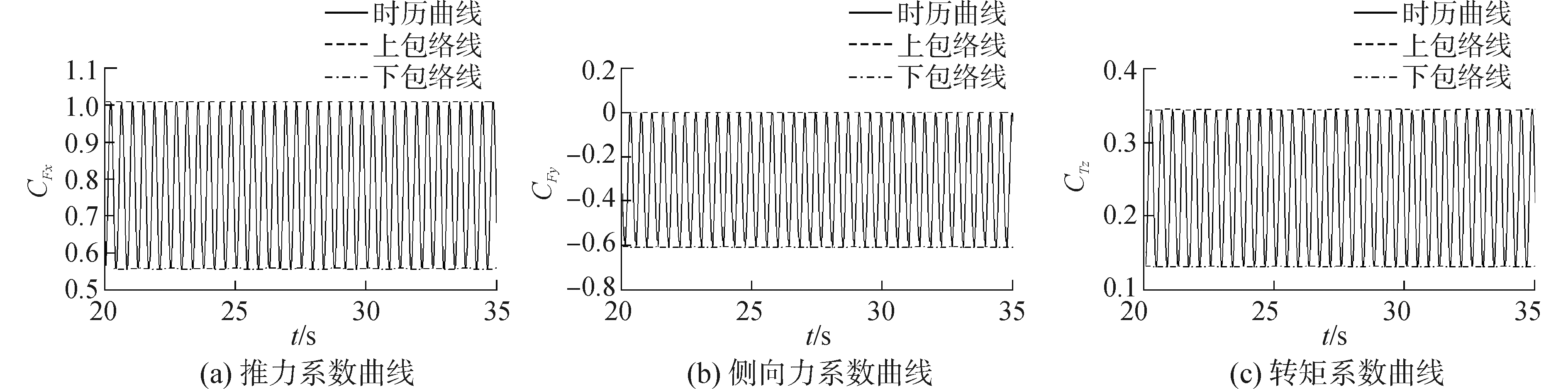
2.1 水轮机受力分析水轮机旋转一个周期内,主轴的瞬时载荷呈周期性波动,波动频率与叶片数NωT有关。水轮机载荷波动对水轮机叶片及轮辐的结构强度和疲劳寿命具有重要影响,直接关系到水轮机长期运行时的安全及稳定性。在均匀来流中仅做旋转运动时水轮机水动力载荷时历曲线如图 3所示,水动力载荷发生基于3倍旋转频率的波动,但载荷峰值基本上不发生改变,即峰值包络线近似为一条平坦的直线。
|
Download:
|
| 图 3 水动力载荷系数时历曲线 Fig. 3 The history data of hydrodynamic force coefficient | |
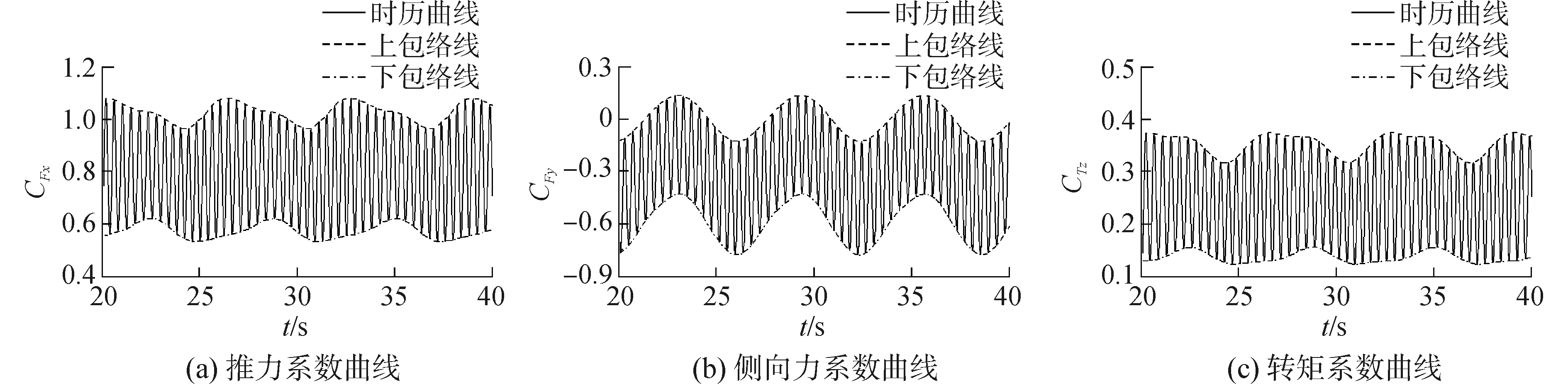
图 4为水轮机发生旋转和艏摇耦合运动(ω=1 rad/s,A=10°,λ=2)时的水动力载荷时历曲线,此时载荷峰值明显发生波动。将水动力载荷峰值连接成包络线,峰值包络线发生基于艏摇频率的波动,水轮机水动力载荷仍按3倍旋转频率在峰值包络线内波动。为了便于后续分析,定义峰值包络线均值和波动范围两个概念:峰值包络线均值是指上峰值包络线与下峰值包络线数值的平均值;波动范围是指上峰值包络线与下峰值包络线数值之差。从图中还能看出,侧向力系数上峰值和下峰值包络线在同一艏摇位置达到极值,而推力系数和转矩系数上峰值和下峰值包络线达到极值点的位置有偏移。
|
Download:
|
| 图 4 艏摇时水动力载荷系数时历曲线 Fig. 4 The history data of hydrodynamic force coefficient with yawing motion | |
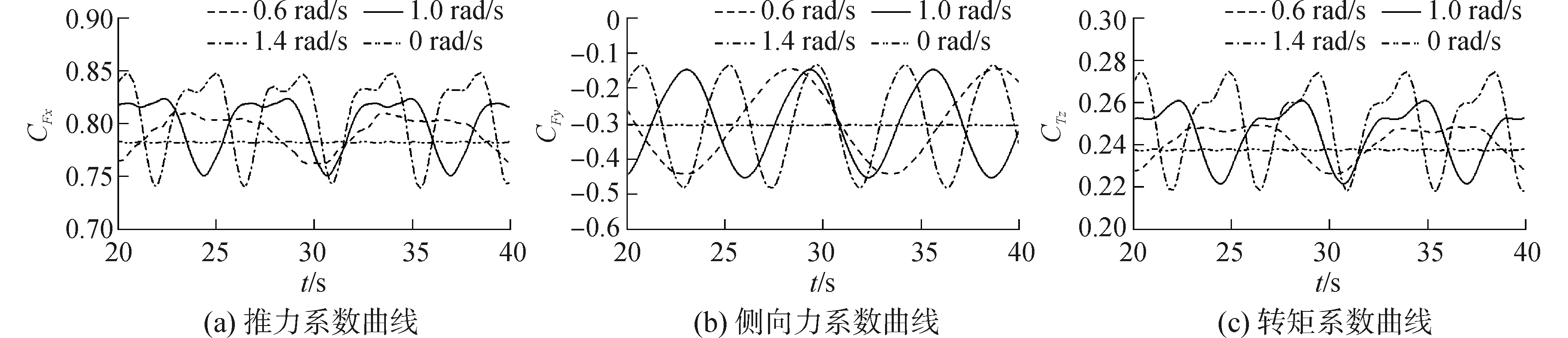
为了研究艏摇频率对水轮机水动力的影响规律,保持水轮机旋转频率(λ=2)和艏摇幅值(A=10°)不变,选取三个不同艏摇频率ω(0.6 rad/s、1.0 rad/s、1.4 rad/s)进行计算,峰值包络线均值对比如图 5所示。
|
Download:
|
| 图 5 不同艏摇频率下峰值包络线均值曲线 Fig. 5 The mean value of peak envelope under different yaw frequencies | |
从图中可以看出,峰值包络线均值随时间发生波动,波动频率与艏摇频率相等,且推力系数和转矩系数波动幅值随频率的增加有明显增大,但侧向力系数波动幅值增加不明显;推力系数和转矩系数峰值包络线均值的时均值比仅旋转时的平均值有所增加,而侧向力系数峰值包络线均值的时均值与仅旋转时的平均值相当。转矩系数时均值增加有利于提高水轮机能量转换效率,但推力系数时均值增加对水轮机的结构安全提出更高要求。
不同频率下,载荷波动范围的最大值和最小值如表 1所示,从表中可知,随着的艏摇频率的增加,推力系数和侧向力系数波动范围的上限值逐渐增加,而不限值逐渐减小;转矩系数波动范围上限值逐渐增加,而下限值基本不发生变化。这相当于随着频率的增加,水动力载荷波动加剧。就水轮机推力系数CFx而言,当艏摇频率为1.4 rad/s时,波动范围上限值达到水轮机仅旋转时的124%。原因是艏摇改变了水轮机旋转平面处的速度分布,相当于来流速度的大小和方向时刻发生变化,从而使水轮机载荷产生波动,随着艏摇频率的增加,在艏摇周期内来流速度变化范围增加,从而使载荷波动幅值增加。因此,在实际海洋环境中,当遭遇高频波浪时,水轮机载荷将发生高频率、高幅值波动,这对水轮机的电能输出的稳定性及结构安全可靠性来说是非常不利的。
| 表 1 不同艏摇频率下波动范围极值表 Tab.1 Extreme value of fluctuation range under different yaw frequencies |
为了研究艏摇幅值对水轮机水动力的影响规律,保持水轮机旋转频率(λ=2)和艏摇频率(ω=1 rad/s)不变,选取三个不同艏摇幅值A(5°、10°、15°)进行计算,峰值包络线均值对比如图 6所示。

|
Download:
|
| 图 6 不同艏摇幅值下包络线均值曲线 Fig. 6 The mean value of peak envelope under different yaw amplitudes | |
从图 6中可以看出,艏摇幅值越大,峰值包络线均值的波动幅值逐渐增加;推力系数和转矩系数包络线均值的时均值比仅旋转时的平均值有所增加。不同幅值下,载荷波动范围的最大值和最小值如表 2所示,由表 2可知,随着艏摇幅值的增加,波动范围的最大值逐渐增加,而最小值逐渐减小。这意味着随着幅值的增加,水轮机载荷波动逐渐加剧。就水轮机推力系数CFx而言,当艏摇幅值为15°时,波动范围最大值达到水轮机仅旋转时的124%。原因是随着艏摇幅值的增加,相当于来流速度大小和方向变化范围增加,从而使载荷波动幅值增加。在实际潮流电站中水轮机运动与浮体平台的运动是相互耦合的,因此在潮流电站的设计中尽可能减小运动幅度对水轮机的结构是非常有利的。
| 表 2 不同艏摇幅值下波动范围极值表 Tab.2 Extreme value of fluctuation range under different yaw amplitudes |
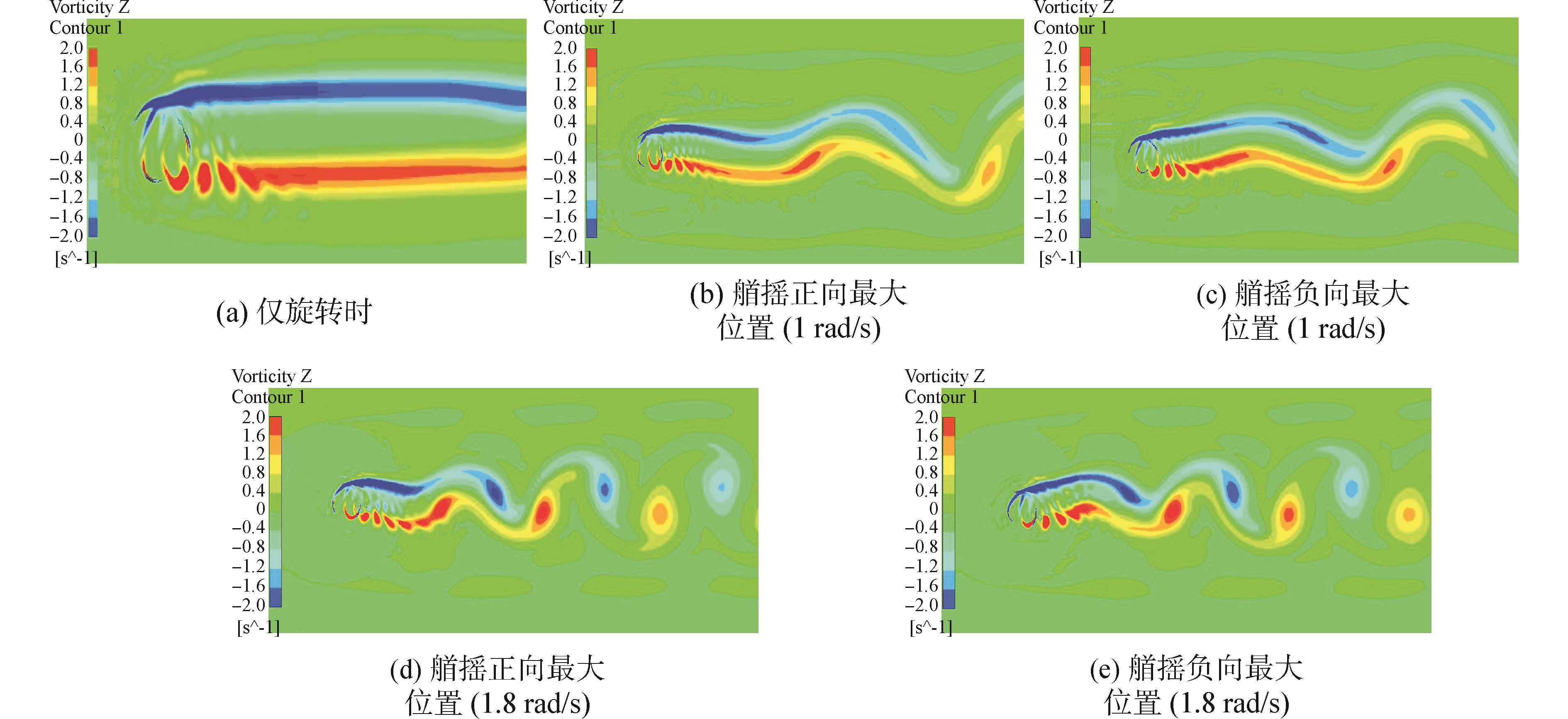
图 7给出了XOY平面Z方向的涡量分布图,其中图 7(a)是仅旋转时的涡量分布图;图 7(b)和7(c)是艏摇频率为1 rad/s时,水轮机分别位于艏摇正向最大位置和负向最大位置时的涡量分布图;图 7(d)和7(e)是艏摇频率为1.8 rad/s时,水轮机分别位于艏摇正向最大位置和负向最大位置时的涡量分布图。
|
Download:
|
| 图 7 涡量分布云图 Fig. 7 The contour of vortex distributions | |
从图 7中可以看出,艏摇时,水轮机出现类似卡门涡街的艉迹,且艉迹发生上下摆动。随着艏摇频率的增加,涡间距逐渐减小,艉涡影响增加,导致水轮机峰值包络线均值波动频率增加,波动幅值增大,这与前面的水轮机载荷曲线相对应。因此水轮机艏摇时,载荷发生波动是由于艉涡随艏摇位置的变化而发生变化。
3 结论1) 水轮机在艏摇情况下,出现类似卡门涡街的艉迹,且艉迹随艏摇位置发生变化。涡间距随艏摇频率的增加而减小,从而导致水动力载荷发生较大范围内的波动。
2) 艏摇对水轮机侧向力的时均值影响较小,但使推力和转矩的时均值有所增加。
3) 水轮机艏摇时,载荷波动加大,波动范围的最大值随艏摇频率和艏摇幅值的增加逐渐增加,而最小值却逐渐减小。
4) 水轮机艏摇时,载荷峰值包络线均值发生基于艏摇频率的规则波动,且波动幅值随艏摇频率和艏摇幅值的增加而增加,这对水轮机的结构安全、疲劳寿命产生不利影响,在结构设计中需要特别考虑。
| [1] |
WANG Shujie, YUAN P, LI D, et al. An overview of ocean renewable energy in China[J]. Renewable and sustainable energy reviews, 2011, 15(1): 91-111. DOI:10.1016/j.rser.2010.09.040 (  0) 0)
|
| [2] |
LEE J H, PARK S, KIM D H, et al. Computational methods for performance analysis of horizontal axis tidal stream turbines[J]. Applied energy, 2012, 98: 512-523. DOI:10.1016/j.apenergy.2012.04.018 (  0) 0)
|
| [3] |
BATTEN W M J, BAHAJ A S, MOLLAND A F, et al. The prediction of the hydrodynamic performance of marine current turbines[J]. Renewable energy, 2008, 33(5): 1085-1096. DOI:10.1016/j.renene.2007.05.043 (  0) 0)
|
| [4] |
YANG B, LAWN C. Fluid dynamic performance of a vertical axis turbine for tidal currents[J]. Renewable energy, 2011, 36(12): 3355-3366. DOI:10.1016/j.renene.2011.05.014 (  0) 0)
|
| [5] |
LI Ye, ÇALIŞAL S M. A discrete vortex method for simulating a stand-alone tidal-current turbine:modeling and validation[J]. Journal of offshore mechanics and arctic engineering, 2010, 132(3): 1-9. (  0) 0)
|
| [6] |
CHOI H J, ZULLAH M A, ROH H W, et al. CFD validation of performance improvement of a 500 kW Francis turbine[J]. Renewable energy, 2013, 54: 111-123. DOI:10.1016/j.renene.2012.08.049 (  0) 0)
|
| [7] |
XIAO Q, LIU W D, INCECIK A. Flow control for VATT by fixed and oscillating flap[J]. Renewable energy, 2013, 51: 141-152. DOI:10.1016/j.renene.2012.09.021 (  0) 0)
|
| [8] |
LI Y, ÇALIŞAL S M. Numerical analysis of the characteristics of vertical axis tidal current turbines[J]. Renewable energy, 2010, 35: 435-42. DOI:10.1016/j.renene.2009.05.024 (  0) 0)
|
| [9] |
马勇, 张亮, 盛其虎, 等. 漂浮式潮流能发电装置水动力特性试验研究[J]. 华中科技大学学报(自然科学版), 2012, 40(10): 123-127. MA Yong, ZHANG Liang, SHENG Qihu, et al. The test study on hydrodynamic characteristics of floating tidal power generation devices[J]. Journal of huazhong university of science and technology (natural science edition), 2012, 40(10): 123-127. (  0) 0)
|
| [10] |
盛其虎, 周念福, 张学伟, 等. 二维垂直轴水轮机强迫振荡水动力性能分析[J]. 哈尔滨工程大学学报, 2015, 36(1): 41-45. SHENG Qihu, ZHOU Nianfu, ZHANG Xuewei, et al. Hydrodynamic performance analysis of a 2D vertical current turbine with forced oscillation[J]. Journal of Harbin Engineering University, 2015, 36(1): 41-45. (  0) 0)
|
| [11] |
王凯, 孙科, 张亮, 等. 艏摇对立轴潮流能水轮机的水动力性能影响[J]. 上海交通大学学报, 2016, 50(4): 563-568, 574. WANG Kai, SUN Ke, ZHANG Liang, et al. Hydrodynamic performance of vertical axis tidal turbine under yawing motion[J]. Journal of Shanghai Jiao Tong University, 2016, 50(4): 563-568, 574. (  0) 0)
|
| [12] |
张学伟, 王树齐, 庞程燕, 等. 潮流能自由变偏角水轮机自启动特性分析[J]. 天津大学学报(自然科学与工程技术版), 2014, 47(5): 389-394. ZHANG Xuewei, WANG Shuqi, PANG Chengyan, et al. Self-Starting characteristics of free variable-pitch vertical axis tidal turbine[J]. Journal of Tianjin University (science and technology), 2014, 47(5): 389-394. (  0) 0)
|
| [13] |
ZHANG Xuewei, WANG Shuqi, WANG Feng, et al. The hydrodynamic characteristics of free variable pitch vertical axis tidal turbine[J]. Journal of hydrodynamics, 2012, 24(6): 834-839. DOI:10.1016/S1001-6058(11)60310-7 (  0) 0)
|
| [14] |
张学伟, 张亮, 李志川, 等. 潮流能自由变偏角水轮机限位角优化方法[J]. 哈尔滨工程大学学报, 2012, 33(11): 1341-1345, 1393. ZHANG Xuewei, ZHANG Liang, LI Zhichuan, et al. Optimization of limit angle for free variable-pitch vertical axis tidal turbine[J]. Journal of Harbin engineering university, 2012, 33(11): 1341-1345, 1393. (  0) 0)
|
| [15] |
王凯, 孙科, 张亮. 不同密实度垂直轴潮流能水轮机的相位干扰[J]. 哈尔滨工业大学学报, 2016, 48(8): 179-184. WANG Kai, SUN Ke, ZHANG Liang. Impaction of initial phase angle on performance of the vertical axis tidal turbines with different density[J]. Journal of Harbin Institute of Technology, 2016, 48(8): 179-184. DOI:10.11918/j.issn.0367-6234.2016.08.030 (  0) 0)
|
| [16] |
SHENG Qihu, JING Fengmei, ZHANG Liang, et al. Study of the hydrodynamic derivatives of vertical-axis tidal current turbines in surge motion[J]. Renewable energy, 2016, 96: 366-376. DOI:10.1016/j.renene.2016.04.074 (  0) 0)
|
| [17] |
WANG Kai, SUN Ke, SHENG Qihu, et al. The effects of yawing motion with different frequencies on the hydrodynamic performance of floating vertical-axis tidal current turbines[J]. Applied ocean research, 2016, 59: 224-235. DOI:10.1016/j.apor.2016.06.007 (  0) 0)
|
| [18] |
侯卫松. 竖轴潮流能水轮机偏角运动规律优化[D]. 哈尔滨: 哈尔滨工程大学, 2013. HOU Weisong. Blade motion optimization of active variable-pitch vertical axis turbine for tidal energy conversion[D]. Harbin: Harbin Engineering University, 2013. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


