硬岩掘进机(tunnel boring machine, TBM)广泛应用在城市饮水工程、地下隧洞工程,以及公路、铁路的建设中。相比传统的钻爆法,使用TBM进行施工具有自动化程度高、掘进速度快、施工质量高、环境影响小、安全性好的特点。根据设备的结构特点,TBM一般应用在硬岩的地质条件中,其刀盘要承受硬岩破碎的巨大变载荷,通过机架、液压缸和撑靴,最终传递到岩壁表面。因为外部载荷引起的TBM掘进波动较大,严重时甚至发生偏航、堵转等情况,因此通过建立推进机械系统的动力学模型,研究TBM推进系统在刀盘变载荷和变支撑刚度条件下的动力学特性有重要意义。
随着国内高铁、地铁和隧道工程的大量开工建设,TBM的推进系统的动力学研究近来已经成为热点。谢启江等研究了岩石变形和不同撑靴支撑刚度下TBM直线和曲线推进时动态特性响应,发现曲线推进时撑靴与岩石的接触刚度变化对运动特性影响较大[1]。周小磊等应用AMESim软件对TBM推进系统进行了建模,模拟了推进液压缸快速回收和高压直线推进过程,其响应曲线和实际分析基本相符[2]。张良贵对TBM推进系统进行了简化,计算了复合地质条件下所需的推力和扭矩[3]。Huo等建立了整机多自由度模型,通过仿真和现场测试,得到了TBM整机在扭转、倾覆和摆动方向的响应[4]。Sun等对TBM的刀盘系统和旋转驱动系统,建立了多自由度非线性动力学模型,分析了内外部耦合激励条件下的刀盘动力学响应[5-6]。Xia等通过滚刀实验台的破岩实验和数值仿真,对刀盘受力进行了分析和预测[7-8]。Gong等研究了TBM掘进贯入参数和岩石特性之间的关系,通过对实测数据库的分析,建立了掘进贯入度预测模型[9]。相近的研究还包括对土压平衡型掘进机推进系统的研究, 其研究方法可以部分借用到硬岩掘进机的推进系统。刘杰等对土压平衡型掘进机推进系统,建立了五自由度无阻尼动力学模型,计算了该模型的响应[10]。王洪新等通过理论结合实验分析了土压平衡盾构机推进系统的平衡控制方法[11]。霍军周等建立了多关节面TBM刀具系统的多自由度耦合动力学模型,并实验证明接头表面对刀具系统的振动性能有很大的影响[19]。
在之前的研究工作中,有一些因素并没有深入考虑,例如撑靴支撑液压缸和撑靴与岩壁变刚度因素,以及在不同初始条件下,动态特性的响应等。本文将综合考虑以上因素,通过对TBM推进系统多自由度动力学模型的建立和分析计算,得到一些更加具体的结论。
1 TBM推进系统动力学建模敞开式TBM主机结构如图 1所示,由刀盘、驱动装置,主机架、推进液压缸、支撑液压缸、撑靴和扭矩液压缸组成。其中刀盘在驱动装置的扭矩驱动下,进行旋转运动,实现滚刀对岩石的滚动切割;推进液压缸用来推进主机架和刀盘做直线进给运动,实现滚刀对岩石的贯入切割,两侧的推进液压缸可以实现不同长度的伸缩,以实现盾构机向左右不同方向的偏航,用来完成隧道转弯处的施工。

|
图 1 TBM部件结构图 Fig.1 The component diagram of TBM |
盾构机的推进系统由推进液压缸,支撑液压缸、扭矩液压缸和撑靴组成。其中扭矩液压缸只用来抵消盾构机刀盘旋转的扭转力矩,在推进过程中把它和主机架看成一体。在推进过程中,推进千斤顶的推进速度很小,可以近似为静态。在正常掘进过程中,可以认为推力系统的载荷是平稳的。因此,进行以下假设:1)刀盘、主机架和扭矩液压缸可以看成一体,作为一个刚体处理;2)相对于整机和撑靴的质量,液压缸质量被忽略不计,并且近似为弹簧。
简化的盾构机模型如图 2所示。刀盘、主机架和扭矩液压缸简化为质量块
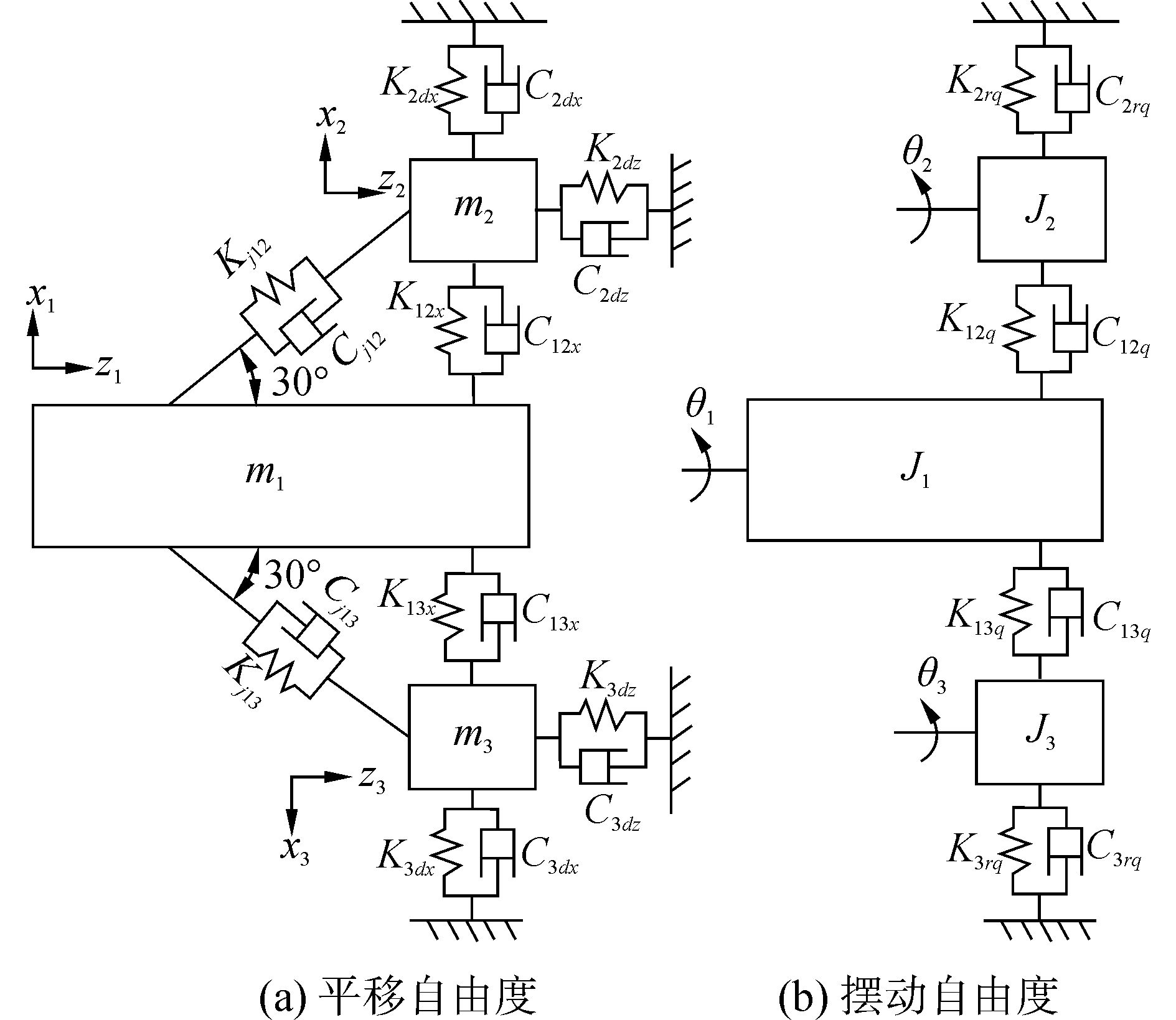
|
图 2 TBM动力学模型 Fig.2 The dynamic model of TBM |
多自由度系统的受迫振动方程式为[12]
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{M\ddot q}} + \mathit{\boldsymbol{C\dot q}} + \mathit{\boldsymbol{Kq}} = \mathit{\boldsymbol{F}}\\ \mathit{\boldsymbol{J\ddot \theta }} + \mathit{\boldsymbol{C\dot \theta }} + \mathit{\boldsymbol{K\theta }} = \mathit{\boldsymbol{T}} \end{array} \right. $ | (1) |
式中:
通过拉格朗日方程可以建立TBM系统的动力学模型。其中推进系统的动能为
| $ \begin{array}{*{20}{c}} {T = \frac{1}{2}{m_1}\dot x_1^2 + \frac{1}{2}{m_1}\dot z_1^2 + \frac{1}{2}{m_2}\dot x_2^2 + \frac{1}{2}{m_2}\dot z_2^2 + }\\ {\frac{1}{2}{m_3}\dot x_3^2 + \frac{1}{2}{m_3}\dot z_3^2 + \frac{1}{2}{J_1}\dot \theta _1^2 + \frac{1}{2}{J_2}\dot \theta _2^2 + \frac{1}{2}{J_3}\dot \theta _3^2} \end{array} $ | (2) |
推进系统的势能为
| $ \begin{array}{*{20}{c}} {U = \frac{1}{2}{k_{j12}}{{\left( {\frac{{{z_2} - {z_1}}}{{\sin {{30}^ \circ }}}} \right)}^2} + \frac{1}{2}{k_{j13}}{{\left( {\frac{{{z_3} - {z_1}}}{{\sin {{30}^ \circ }}}} \right)}^2} + }\\ {\frac{1}{2}{k_{12x}}\left( {{x_2} - {x_1}} \right)2 + \frac{1}{2}{k_{2dx}}x_2^2 + \frac{1}{2}{k_{2dz}}z_2^2 + }\\ {\frac{1}{2}{k_{13x}}\left( {{x_3} - {x_1}} \right)2 + \frac{1}{2}{k_{3dx}}x_3^2 + \frac{1}{2}{k_{3dz}}z_3^2 + }\\ {\frac{1}{2}{k_{12q}}{{\left( {{{\dot \theta }_2} - {{\dot \theta }_1}} \right)}^2} + \frac{1}{2}{k_{2rq}}\dot \theta _2^2 + }\\ {\frac{1}{2}{k_{13q}}{{\left( {{{\dot \theta }_3} - {{\dot \theta }_1}} \right)}^2} + \frac{1}{2}{k_{3rq}}\dot \theta _3^2} \end{array} $ | (3) |
推进系统的能量耗散函数为
| $ \begin{array}{*{20}{c}} {D = \frac{1}{2}{C_{j12}}{{\left( {\frac{{{{\dot z}_2} - {{\dot z}_1}}}{{\sin {{30}^ \circ }}}} \right)}^2} + \frac{1}{2}{C_{j13}}{{\left( {\frac{{{{\dot z}_3} - {{\dot z}_1}}}{{\sin {{30}^ \circ }}}} \right)}^2} + }\\ {\frac{1}{2}{C_{2dx}}\dot z_2^2 + \frac{1}{2}{C_{3dx}}\dot z_3^2 + \frac{1}{2}{C_{12x}}{{\left( {{{\dot x}_2} - {{\dot x}_1}} \right)}^2} + }\\ {\frac{1}{2}{C_{2dx}}x_2^2 + \frac{1}{2}{C_{13x}}{{\left( {{{\dot x}_3} - {{\dot x}_1}} \right)}^2} + \frac{1}{2}{C_{3dx}}x_3^2 + }\\ {\frac{1}{2}{C_{12q}}{{\left( {{{\dot \theta }_2} - {{\dot \theta }_1}} \right)}^2} + \frac{1}{2}{C_{2rq}}\dot \theta _2^2 + }\\ {\frac{1}{2}{C_{13q}}{{\left( {{{\dot \theta }_3} - {{\dot \theta }_1}} \right)}^2} + \frac{1}{2}{C_{3rq}}\dot \theta _3^2} \end{array} $ | (4) |
拉格朗日方程:
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial T}}{{\partial {{\dot q}_i}}} - \frac{{\partial T}}{{\partial {q_i}}} + \frac{{\partial U}}{{\partial {q_i}}} + \frac{{\partial D}}{{\partial {{\dot q}_i}}} = {F_i}\left( t \right) $ | (5) |
式中:
| $ \begin{array}{*{20}{c}} {{m_1}{{\ddot x}_1} + \left( {{k_{12x}} + {k_{13x}}} \right){x_1} - {k_{12x}}{x_2} - {k_{13x}}{x_3} + }\\ {\left( {{c_{12x}} + {c_{13x}}} \right){{\dot x}_1} - {c_{12x}}{{\dot x}_2} - {c_{13}}{{\dot x}_3} = {F_x}} \end{array} $ | (6) |
| $ \begin{array}{*{20}{c}} {{m_2}{{\ddot x}_2} - {k_{12x}}{x_1} + \left( {{k_{2dx}} + {k_{12x}}} \right){x_2} - {c_{12x}}{{\dot x}_1} + }\\ {\left( {{c_{2dx}} + {c_{12x}}} \right){{\dot x}_2} = 0} \end{array} $ | (7) |
| $ \begin{array}{*{20}{c}} {{m_3}{{\ddot x}_3} - {k_{13x}}{x_1} + \left( {{k_{13x}} + {k_{3dx}}} \right){x_3} - {c_{13x}}{{\dot x}_1} + }\\ {\left( {{c_{13x}} + {c_{3dx}}} \right){{\dot x}_3} = 0} \end{array} $ | (8) |
| $ \begin{array}{*{20}{c}} {{m_1}{{\dot z}_1} + 4\left( {{k_{j12}} + {k_{j13}}} \right){z_1} - 4{k_{j12}}{z_2} - 4{k_{j13}}{z_3} + }\\ {4\left( {{c_{j12}} + {c_{j13}}} \right){{\dot z}_1} - 4{c_{j12}}{{\dot z}_2} - 4{c_{j13}}{{\dot z}_3} = {F_z}} \end{array} $ | (9) |
| $ \begin{array}{*{20}{c}} {{m_2}{{\ddot z}_2} - 4{k_{j12}}{z_1} + \left( {{k_{j13}} + {k_{2dx}}} \right){z_2} - 4{c_{j12}}{{\dot z}_1} + }\\ {\left( {4{c_{j13}} + {c_{2dz}}} \right){{\dot z}_2} = 0} \end{array} $ | (10) |
| $ \begin{array}{*{20}{c}} {{m_3}{{\ddot z}_3} - 4{k_{j13}}{z_1} + \left( {4{k_{j13}} + {k_{3dz}}} \right){z_3} - 4{c_{j13}}{{\dot z}_1} + }\\ {\left( {4{c_{j13}} + {c_{3dz}}} \right){{\dot z}_3} = 0} \end{array} $ | (11) |
| $ \begin{array}{*{20}{c}} {{J_1}{{\ddot \theta }_1} + \left( {{k_{12q}} + {k_{13q}}} \right){\theta _1} - {k_{12q}}{\theta _2} - {k_{13q}}{\theta _3} + }\\ {\left( {{c_{12q}} + {c_{13q}}} \right){{\dot \theta }_1} - {c_{12q}}{{\dot \theta }_2} - {c_{13q}}{{\dot \theta }_3} = {T_y}} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {{J_2}{{\ddot \theta }_2} - {k_{12q}}{\theta _1} + \left( {{k_{12q}} + {k_{2rq}}} \right){\theta _2} - {c_{12q}}{{\dot \theta }_1} + }\\ {\left( {{c_{12q}} + {c_{2rq}}} \right){{\dot \theta }_2} = 0} \end{array} $ | (13) |
| $ \begin{array}{*{20}{c}} {{J_3}{{\ddot \theta }_3} - {k_{13q}}{\theta _1} + \left( {{k_{13q}} + {k_{3rq}}} \right){\theta _2} - {c_{13q}}{{\dot \theta }_1} + }\\ {\left( {{c_{13q}} + {c_{3rq}}} \right){{\dot \theta }_2} = 0} \end{array} $ | (14) |
在设计TBM时,根据不同的土壤环境会采用不同的滚刀分布。常见的滚刀分布如图 3所示,其中部布置中心滚刀,周围布置正滚刀,边缘布置边滚刀。

|
图 3 滚刀布置图 Fig.3 Arrangement drawing of cutter |
通过滚刀的受力分析[13],破岩过程中的滚刀受力可以表示为:正推力
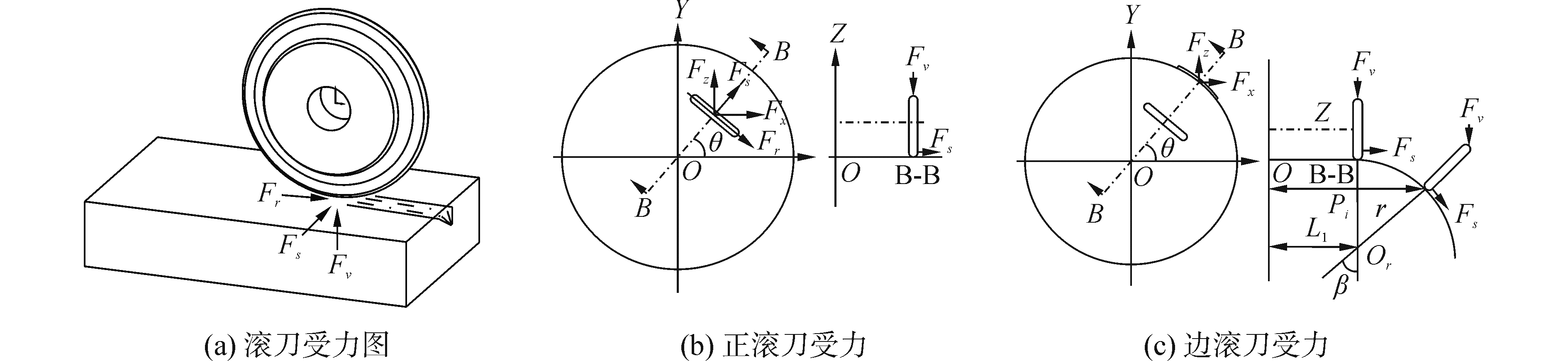
|
图 4 正滚刀和边滚的受力 Fig.4 Forces acting on a normal cutter and a gauge cutter |
根据单个滚刀的受力关系和滚刀的位置分布,可以列出主机受外部载荷的受力公式:
| $ {F_x} = {F_{vx\Sigma }} + {F_{rx\Sigma }} + {F_{sx\Sigma }} $ | (15) |
| $ {F_z} = \sum\limits_{i = 1}^n {{F_{vi}}} + \sum\limits_{j = 1}^m {{F_{vj}}} + \sum\limits_{k = 1}^p {\left( {{F_{vk}} + {F_{sk}}\sin {\beta _k}} \right)} $ | (16) |
| $ {T_y} = \sum\limits_{i = 1}^n {{F_{vi}}{l_{yi}}} + \sum\limits_{j = 1}^m {{F_{vj}}{l_{yj}}} $ | (17) |
式中:
TBM掘进过程中,撑靴和岩石表面的摩擦力提供驱动力和扭转反向力。由于刀盘阻力和推进载荷具有较大波动,所以撑靴和岩石截面间的接触刚度特性对其动力学特性非常重要。
隧道岩石的粗糙面可以认为是由很多小凸体随机分布,小凸体在受到法向载荷和切向载荷作用时,其变形和力的加载路径有关。通过使用修正各向同性三维分形表面方法来表征撑靴和岩壁的粗糙度,从而计算出撑靴和岩石之间的方向刚度和切向刚度[15]。
| $ \begin{array}{*{20}{c}} {{k_x} = \frac{4}{{3\sqrt {2{\rm{\pi }}} }}E\frac{{\left( {4 - D} \right)\left( {D - 1} \right)}}{{\left( {3 - D} \right)\left( {2 - D} \right)}}\left( {\alpha _L^{'1/2} - } \right.}\\ {\left. {\alpha _L^{'\left( {D - 1} \right)/2}\alpha _c^{'\left( {2 - D} \right)/2}} \right)} \end{array} $ | (18) |
| $ \left\{ \begin{array}{l} {k_z} = \frac{{8Gr'}}{{\left( {2 - v} \right)}}{\left[ {\mu \frac{{{\rm{d}}P}}{{{\rm{d}}Q}} + \left( {1 - \frac{{{\rm{d}}P}}{{{\rm{d}}Q}}} \right){{\left( {1 - \frac{Q}{{\mu P}}} \right)}^{ - 1/3}}} \right]^{ - 1}},\\ \;\;\;\;\;\;\;\;\;\;0 \le \frac{{{\rm{d}}P}}{{{\rm{d}}Q}} \le \frac{1}{\eta }\\ {k_z} = \frac{{8Gr'}}{{\left( {2 - v} \right)}},\;\;\;\;\;\frac{{{\rm{d}}P}}{{{\rm{d}}Q}} \ge \frac{1}{\eta } \end{array} \right. $ | (19) |
式中:
在重载荷慢动作过程中,液压缸的刚度成为系统的重要影响因素。液压缸的刚度计算不仅需要考虑缸内液压油的体积,还必须考虑液压管路中的液压油。通过文献[16]可以得到液压缸的刚度计算公式为
| $ {k_j} = E\left( {\frac{{A_1^2}}{{{V_{L1}} + {V_1}}} + \frac{{A_2^2}}{{{V_{L2}} + {V_2}}}} \right) $ | (20) |
式中:
系统中各部件之间均为固体表面的滑移接触,所以通过以下公式计算:
| $ c = 2\xi \sqrt {{m_e}{k_e}} $ | (21) |
式中:ξ为阻尼比,一般取值0.02~0.05,本文中取值0.02;
本文使用的Newmark-β法是一种隐式积分方法,是无条件稳定的方法。假定在时间间隔[t, t+Δt]内加速度呈线性变化,基本假定为
| $ {{\dot x}_{t + \Delta t}} = {{\dot x}_t} + \left[ {\left( {1 - \delta } \right){{\ddot x}_t} + \delta {{\ddot x}_{t + \Delta t}}} \right]\Delta t $ | (22) |
| $ {x_{t + \Delta t}} = {x_t} + {{\dot x}_t}\Delta t + \left[ {\left( {\frac{1}{2} - \beta } \right){{\ddot x}_t} + \beta {{\ddot x}_{t + \Delta t}}} \right]\Delta {t^2} $ | (23) |
式中δ、β是按积分精度和稳定性要求可以调整的参数。
根据式(22)~(23),可以用
| $ {{\dot x}_{t + \Delta t}} = \frac{1}{{\beta \Delta {t^2}}}\left( {{x_{t + \Delta t}} - {x_t}} \right) - \frac{1}{{\beta \Delta {t^2}}}{{\dot x}_t} - \left( {\frac{1}{{2\beta }} - 1} \right)\Delta t{{\ddot x}_t} $ | (24) |
| $ {{\ddot x}_{t + \Delta t}} = \frac{\delta }{{\beta \Delta t}}\left( {{x_{t + \Delta t}} - {x_t}} \right) + \left( {1 - \frac{\delta }{\beta }} \right){{\dot x}_t} + \left( {1 - \frac{\delta }{{2\beta }}} \right)\Delta t{{\ddot x}_t} $ | (25) |
每步积分应该满足
| $ M{{\ddot x}_{t + \Delta t}} + C{{\dot x}_{t + \Delta t}} + K{x_{t + \Delta t}} = {R_{t + \Delta t}} $ | (26) |
将式(23)~(24)代入式(25)可得关于
| $ \dot K{x_{t + \Delta t}} = {{\dot R}_{t + \Delta t}} $ | (27) |
式中:
| $ \dot K = K + \frac{\delta }{{\beta \Delta t}}C + \frac{1}{{\beta \Delta {t^2}}}M $ | (28) |
| $ \begin{array}{l} {{\dot R}_{t + \Delta t}} = {R_{t + \Delta t}} + M\left[ {\frac{1}{{\beta \Delta {t^2}}}{x_t} + \frac{\delta }{{\beta \Delta t}}{{\dot x}_t} + \left( {\frac{1}{{2\beta }} - 1} \right){{\ddot x}_t}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;C\left[ {\frac{\delta }{{\beta \Delta t}}{x_t} + \left( {\frac{\delta }{\beta } - 1} \right){{\dot x}_t} + \left( {\frac{\delta }{{2\beta }} - 1} \right)\Delta t{{\ddot x}_t}} \right] \end{array} $ | (29) |
以辽宁大伙房水库施工的地质条件和采用的Robins盾构机为研究对象,其参数如表 1所示。
| 表 1 盾构及岩石参数 Tab.1 Tunneling and rock parameters |
对滚刀和岩石的作用过程进行有限元数值仿真,并利用实测数据进行校正[17-18]。通过式(15)~(17)的计算,可以得到如图 5的主机外部时程载荷图。
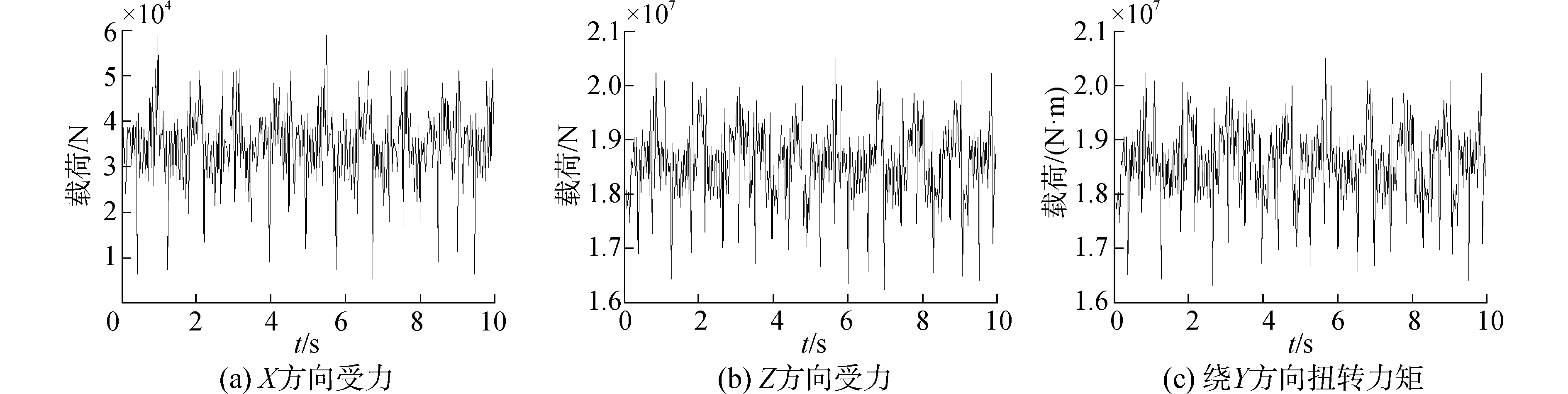
|
图 5 时程载荷图 Fig.5 Loads times history |
将载荷以及计算得到的刚度和阻尼代入动力学方程,应用Newmark-β法对微分方程组进行求解,可以得到系统的响应。图 6是各个方向的响应。

|
图 6 系统的响应 Fig.6 Dynamic responses of system |
在盾构机掘进过程中,控制系统会不断矫正推进路线,使盾构机按照规划路径前进,因此盾构机的初始位移就很小。选取如下的初始位移:0≤x1≤0.01 m,0≤x2≤0.01 m,0≤z1≤0.01 m,0≤z2≤0.01 m,0≤θ1≤0.1°,0≤θ2≤0.1°。为了能够清楚地比较不同初始条件下,主机位移和角度响应变化。按照如下公式定义敏感系数
| $ \left\{ \begin{array}{l} {v_{11}}\left( t \right) = \frac{{{x_1}\left( t \right)}}{{{x_0}\left( t \right)}},{v_{12}}\left( t \right) = \frac{{{x_2}\left( t \right)}}{{{x_0}\left( t \right)}}\\ {v_{21}}\left( t \right) = \frac{{{z_1}\left( t \right)}}{{{z_0}\left( t \right)}},{v_{22}}\left( t \right) = \frac{{{z_2}\left( t \right)}}{{{z_0}\left( t \right)}}\\ {v_{31}}\left( t \right) = \frac{{{\theta _1}\left( t \right)}}{{{\theta _0}\left( t \right)}},{v_{32}}\left( t \right) = \frac{{{\theta _2}\left( t \right)}}{{{\theta _0}\left( t \right)}} \end{array} \right. $ | (30) |
图 7为敏感系数时程图。在X方向,实线是主机在初始位移0.01 m时,刀盘的敏感系数时程曲线,虚线是撑靴在初始位移为0.01 m时,刀盘敏感系数时程曲线。主机在X方向的偏航位移对刀盘的影响要远大于撑靴的偏置影响。主机在X方向偏航0.01 m,会导致刀盘在随后的最大波动幅值达到0.18 m。在Z方向,实线是主机在初始位移为0.01 m时,刀盘敏感系数时程曲线,虚线是撑靴在初始位移为0.01 m时,刀盘敏感系数时程曲线。主机在Z方向的敏感度差值平均为0.16,差值较小,该方向对偏航不会产生影响,仅影响每次进给量的误差。在绕Y轴摆动方向,实线是主机角度为1°时,刀盘的敏感系数时程曲线,虚线是撑靴在初始条件为1°时,刀盘的敏感系数时程曲线。在初始状态下,主机偏航1°,会导致刀盘在随后的最大波动幅值达到1.4°;而撑靴偏航1°,会导致刀盘的偏航幅度达到1.08°。
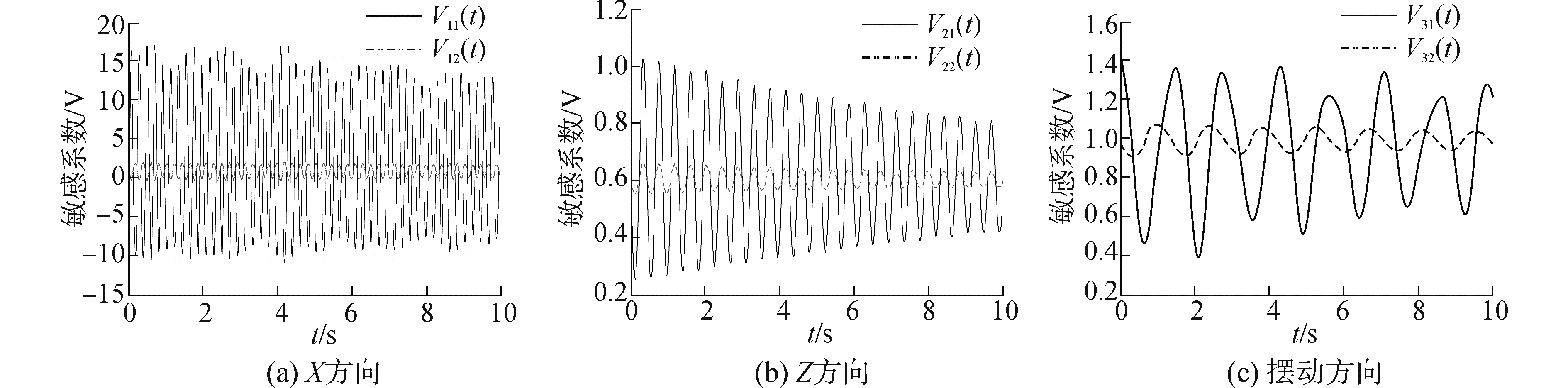
|
图 7 系统的敏感度时程图 Fig.7 Times history chart of sensitivity |
1)推进系统的稳态响应具有明显的周期性,并且Z方向响应周期短于摆动方向的周期。
2)主机在X方向和绕Y方向的偏航会导致刀盘波动幅值的较大变化,从而导致掘进过程出现较大误差。
3)撑靴在初始条件下的偏航位移和偏转角度对整机的影响较小,整机的角度调节仍要以调整两侧推进液压缸为主。
| [1] |
谢琦江, 于海东, 郑慧, 等. 变约束条件下硬岩掘进机推进系统动态特性研究[J]. 机械设计与研究, 2015, 31(3): 152-155. XIE Qijiang, YU Haidong, ZHENG Hui, et al. Dynamic characteristics of propulsion system of hard rock roadheader under variable constraint[J]. Mechanical design and research, 2015, 31(3): 152-155. (  0) 0)
|
| [2] |
周小磊, 贺飞, 张瑜峰. 主梁式TBM推进系统基于AMESim的仿真分析[J]. 装备制造技术, 2015(1): 31-34. ZHOU Xiaolei, HE Fei, ZHANG Yufeng. Main beam TBM thrust system AMESim simulation and analysis[J]. Equipment manufacturing technology, 2015(1): 31-34. (  0) 0)
|
| [3] |
张良贵. 双护盾TBM主推进系统的研究[D]. 秦皇岛: 燕山大学, 2013. ZHANG Lianggui. Research on double shield TBM main propulsion system[D]. Qinhuangdao:Yanshan University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10216-1013028613.htm (  0) 0)
|
| [4] |
HUO J, WU H, LI G, et al. The coupling dynamic analysis and field test of TBM main system under multipoint impact excitation[J]. Shock & vibration, 2015(1): 1-14. ( 0) 0)
|
| [5] |
SUN Wei, DING Xin, WEI Jing, et al. Hierarchical modeling method and dynamic characteristics of cutter head driving system in tunneling boring machine[J]. Tunneling and underground space technology, 2016, 52: 99-110. DOI:10.1016/j.tust.2015.11.022 ( 0) 0)
|
| [6] |
SUN Wei, LING Jingxiu, HUO junzhou, et al. Dynamic characteristics study with multidegree-of-freedom coupling in TBM cutterhead system based on complex Factors[J]. Mathematical problems in engineering, 2013(3): 657-675. ( 0) 0)
|
| [7] |
TANG Q, XU Z, XIA Y, et al. Numerical study on mode of breaking rock by TBM cutter in two cutting orders[J]. Journal of Central South University, 2012, 43(3): 940-946. ( 0) 0)
|
| [8] |
XIA Y, YANG T, ZHANG X, et al. Mechanical model of breaking rock and force characteristic of disc cutter[J]. Journal of Central South University, 2012, 19(7): 1846-1852. DOI:10.1007/s11771-012-1218-8 ( 0) 0)
|
| [9] |
GONG Q. M, ZHAO J. Development of a rock mass characteristics model for TBM penetration rate prediction[J]. International journal of rock mechanics & mining sciences, 2009, 46(4): 8-18. ( 0) 0)
|
| [10] |
刘杰, 卿启湘, 文桂林. EPM盾构机推进系统振动响应分析[J]. 工程设计学报, 2013, 20(6): 489-493. LIU Jie, QING Qixiang, WEN Guilin. Research on vibration response of EPB thrust system[J]. Chinese journal of engineering design, 2013, 20(6): 489-493. (  0) 0)
|
| [11] |
王洪新, 傅德明. 土压平衡盾构机平衡控制理论及实验研究[J]. 土木工程学报, 2007, 40(5): 61-68. WANG Hongxin, FU Deming. Theoretical and test studies on balanced control of EPB shields[J]. China civil engineering journal, 2007, 40(5): 61-68. (  0) 0)
|
| [12] |
闻邦椿, 刘树英, 陈照波, 等. 机械振动理论及应用[M]. 北京: 高等教育出版社, 2009: 86-90.
( 0) 0)
|
| [13] |
ENTACHER M, WINTER G, BUMBERGER T, et al. Cutter force measurement on tunnel boring machines[J]. Tunneling and underground space technology, 2012, 31(5): 97-106. ( 0) 0)
|
| [14] |
HUO Junzhou, WU Hangyang, YANG Jing, et al. Multi-directional coupling dynamic characteristics analysis of TBM cutterhead system based on tunneling field test[J]. Journal of mechanical science and technology, 2015, 29(8): 3043-3058. DOI:10.1007/s12206-015-0701-1 ( 0) 0)
|
| [15] |
余海东, 郝培, 赵勇, 等. 硬岩掘进装备支撑系统界面接触刚度非线性[J]. 机械工程学报, 2014, 50(11): 54-59. YU Haidong, HAO Pei, ZHAO Yong, et al. Non-linear behavior of normal contact stiffness of tunnel surface and supporting system of tunnel boring machines[J]. Journal of mechanical engineering, 2014, 50(11): 54-59. (  0) 0)
|
| [16] |
戴云飞. 液压缸液压刚度的计算[J]. 有色金属设计, 1999, 26(1): 61-62. DAI Yunfei. The cylinder hydraulic stiffness calculation[J]. Nonferrous metals design, 1999, 26(1): 61-62. (  0) 0)
|
| [17] |
李辉, 王树林, 汪加科. TBM盘形滚刀受力分析[J]. 现代隧道技术, 2012, 49(3): 193-196. LI Hui, WANG Shulin, WANG Jiake. Force analysis of the disc cutter on TBM[J]. Modern tunneling technology, 2012, 49(3): 193-196. (  0) 0)
|
| [18] |
张魁, 夏毅敏, 朱宗铭, 等. 不同地质工况条件下TBM刀具破岩模式研究[J]. 哈尔滨工程大学学报, 2015, 36(9): 1240-1245. ZHANG Kui, XIA Yimin, ZHU Zongming, et al. Rock-breaking modes of TBM cutters under different working conditions[J]. Journal of Harbin Engineering University, 2015, 36(9): 1240-1245. (  0) 0)
|
| [19] |
HUO Junzhou, HOU Nan, WEI Sun, et al. Analyses of dynamic characteristics and structure optimization of tunnel boring machine cutter system with multi-joint surface[J]. Nonlinear Dynamics, 2016. ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


