偏导射流式伺服阀由力矩马达、偏导射流前置级及功率滑阀三部分组成,从射流管伺服阀发展而来[1-2],具有抗污染能力强、动态性能好、可靠性高等优点,在航空、航天及工业领域中均有广泛应用。
相对于国内外对滑阀与喷嘴挡板阀的长期研究,目前针对偏导射流式伺服阀的研究较少,尚没有可供借鉴的成熟理论。王传礼等建立了偏导射流前置级的节流模型,推导了其线性化流量方程[3];訚耀保等总结了供油压力、接收器通道夹角等因素对阀压力特性的影响,并提出了改善前置级气穴现象的方法[4-5];杨月花对不同几何形状的前置级流场进行了数值模拟及可视化试验验证,得出了在射流盘两接收器入口间使用平劈结构更易导流的结论[6];江林秋提出了基于紊动冲击射流理论对偏转射流前置级流场进行分析的创新思路,优化了前置级结构参数[7];SANGIAH等提出了一类基于双压电晶片的新型偏转射流式伺服阀,改善了此类阀的性能[8];ZHU等设计了一种应用超磁致伸缩材料驱动偏转板位移的新型偏转射流式伺服阀,该结构的应用使此类阀具有更快的响应速度[9]。
但在上述研究中,前置级模型均基于射流管阀结构进行推导,与实际的偏导阀结构不符;仅应用节流理论对形状微小复杂的紊动射流流场进行简化分析,无法准确表征该流场的复杂状态变化,得出的某些结论与流场实际现象不符,也未对影响前置级流场状态及阀特性的因素进行探讨。本文以某型偏导射流式力反馈伺服阀为研究对象,基于文献[7]的分析方法,结合附壁射流理论与偏导射流式伺服阀的实际尺寸结构,将油液由射流盘口流入至最终回油的完整运动过程分四个流动阶段进行分析计算,量化油液在射流盘V型槽中的附壁特性,并在文献[3-5]的基础上,推导前置级压力增益理论表达式,由此建立精确的偏导射流式前置级流场模型,用以表征流体的复杂状态变化;应用Matlab与Fluent分别对流场附壁特性及前置级压力特性进行仿真计算与数值模拟,并设计可间接获得前置级压力增益的试验方法,用以验证理论模型的正确性,获得影响前置级内部流场与压力增益变化的关键结构参数。
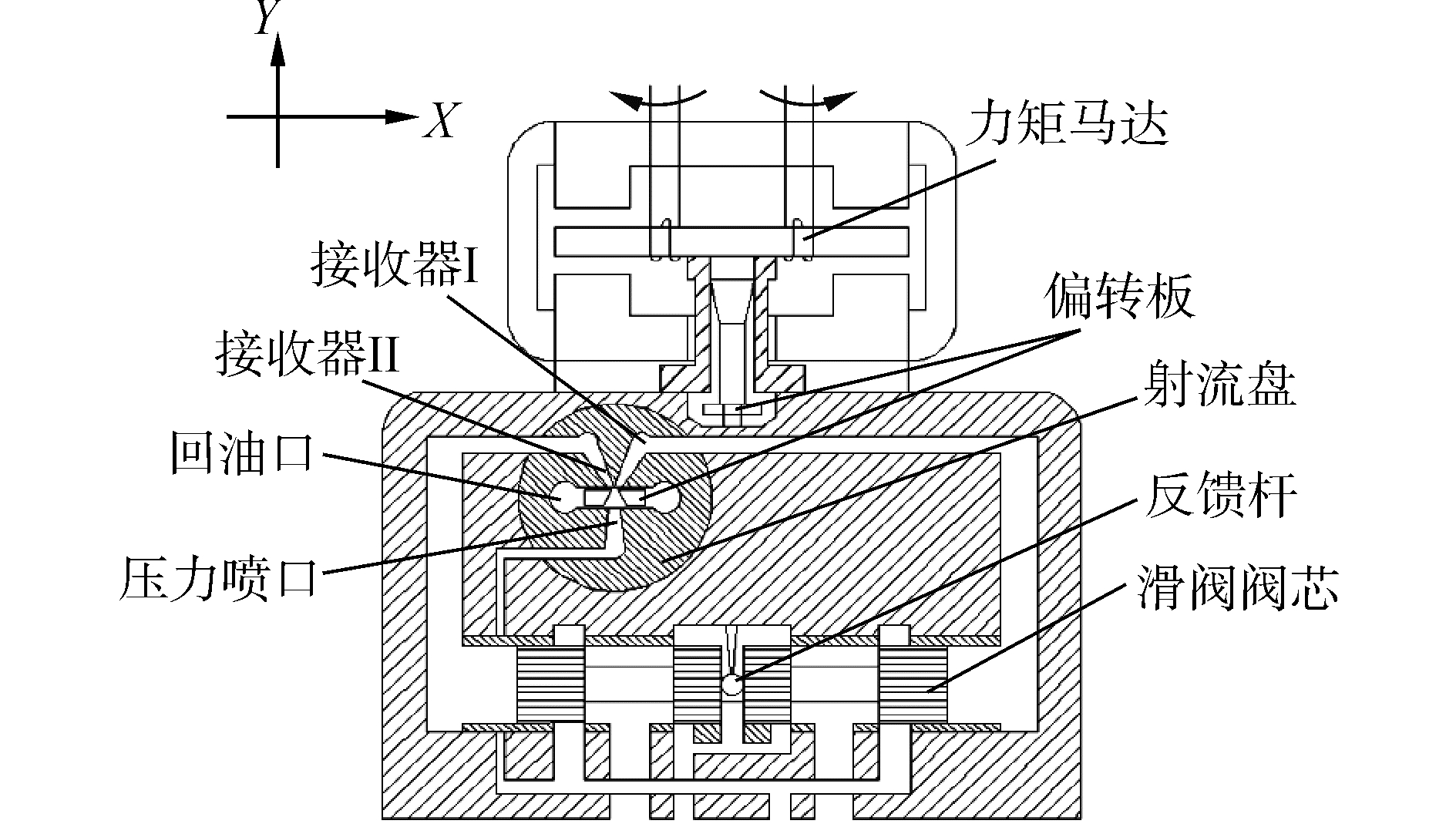
1 偏导射流式伺服阀工作原理偏转射流式伺服阀的结构如图 1所示。其中,偏导射流前置级为伺服阀的核心部件,由偏转板与射流盘构成。射流盘为圆形薄片,其上设计加工有“大”字形孔,孔各端分别为供油口、回油口以及接收器,供油口与油源相连,两接收器分别与滑阀左、右两腔相连;偏转板为一开有V型导流槽的薄片,插入射流盘喷口与接收器之间的通道内。偏导阀工作时,偏转板沿X方向发生偏移,通过其V型导流槽将油液导入不同的接收器中,进而在滑阀阀芯两端产生压差,实现控制滑阀阀芯换向的功能。
|
图 1 偏导射流式伺服阀结构原理图 Fig.1 Structural schematics of deflector jet servo valve |
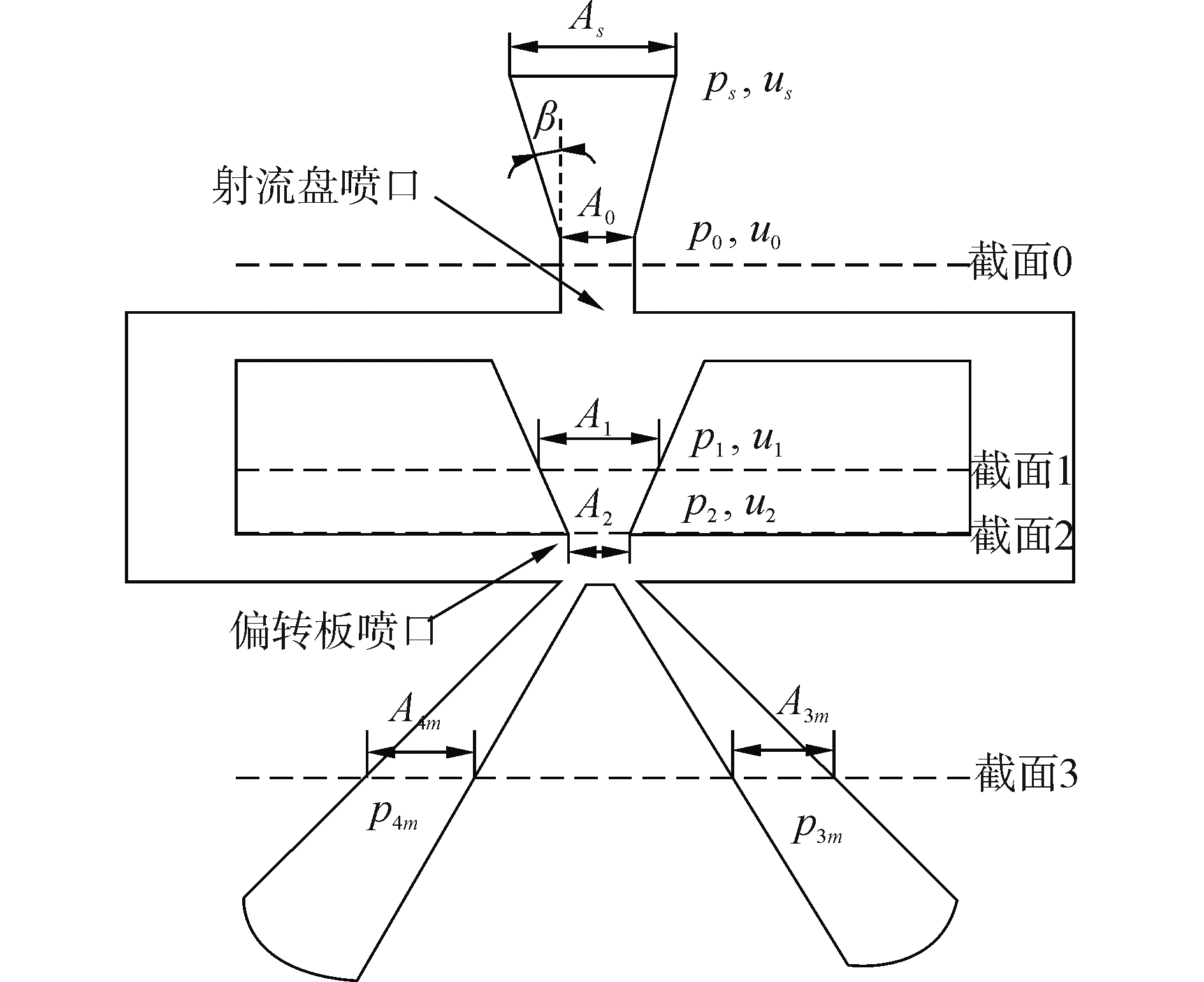
假设油液为不可压缩粘性流体。在偏导射流前置级的流场中选取四个截面,如图 2所示,分析各截面处的油液流速及压力。其中,射流盘入口截面积为
|
图 2 偏导射流前置级压力截面 Fig.2 Definition of pressure sections in deflector jet pilot stage |
如图 2所示,油液进入射流盘,并流至截面0处,根据理想伯努利方程[10]有
| $\frac{p_s} {ρg}+\frac{u^2_s} {2g}+z_s=\frac{p_0} {ρg}+\frac{u^2_0} {2g}+z_0+Δh_0$ | (1) |
式中:
| $\frac{Δp} {ρg}=(1+ζ_0)\frac{u_0^2} {2g}$ | (2) |
取Δp=16 MPa,经计算可知,射流盘压力喷口处的雷诺数为3 066.6,远大于射流临界雷诺数[11],前置级流场中的射流为紊动射流。
2.2 前置级流场附壁特性分析油液由截面0流至截面1的过程。射流发生在薄片状结构的射流盘内,且上下装有密封盖板,故可将其近似看作二维射流。当油液射入偏转板V型槽的有限空间内时,与侧壁发生干涉,并对周围的流体产生卷吸作用,最终附着于一侧壁面继续流动,称为射流的附壁效应。基于文献[12-13]中的假设条件,对前置级射流流场附壁特性进行描述。
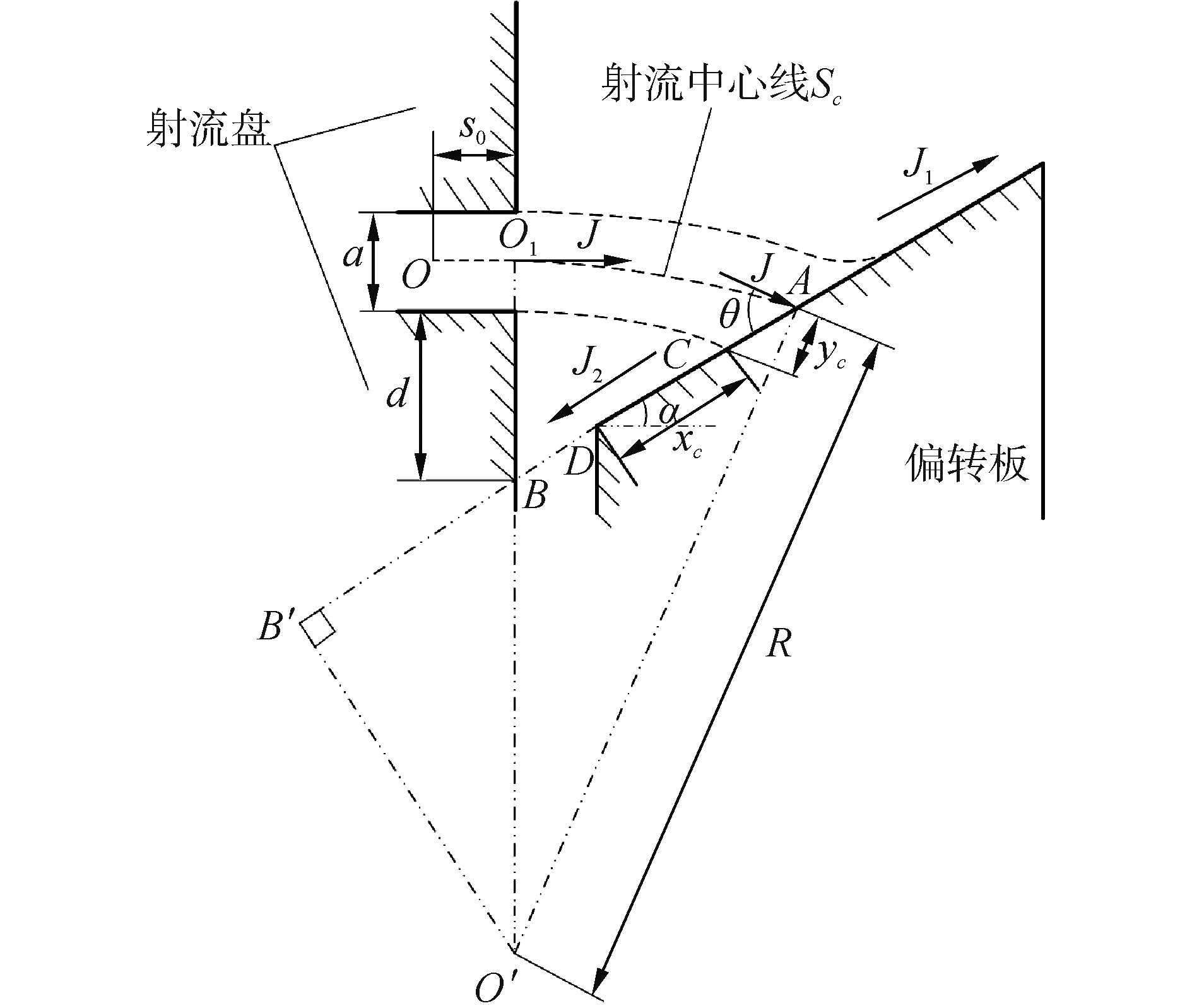
前置级流场的附壁射流示意图如图 3所示。其中,射流盘喷口宽度为
|
图 3 前置级附壁射流几何模型 Fig.3 Geometry model of the wall attached jet in pilot stage |
考虑有限宽度的射流盘喷口,采用Goertler二维自由紊动射流模型描述前置级射流流场的主体段,则流场的速度分布可表示为
| $u=u_m\text{sech}^2\left(\frac{σy} {s+s_0}\right)$ | (3) |
| $u_m=\left(\frac{3Jσ} {4ρ(s+s_0)}\right)^{1/2}$ | (4) |
式中:
| ${∫\limits^{+∞} _{-∞}u·\text dy}\left|_{s=0}=u_0a\right.$ | (5) |
射流盘喷口处油液动量可表示为
| $s_0=\frac{σa} {3}$ | (6) |
射流未附壁前,不受外力作用,故保持动量守恒,根据冲量定理可得
| $J\cosθ=J_1-J_2$ | (7) |
经碰撞后,油液的顺流动量
| $J_1=∫\limits^{y_c} _{-∞}ρu^2\text dy$ | (8) |
| $J_2=∫\limits^∞ _{y_c}ρu^2\text dy$ | (9) |
将式(3)、(4) 分别代入式(8)、(9) 中,得到碰撞点
| $J_1=\frac{3} {4}J\left(\frac{2} {3}+\tan \text h\frac{σy_c} {s_c+s_0}-\frac{1} {3}\tan h^3\frac{σy_c} {s_c+s_0}\right)$ | (10) |
| $J_1=\frac{3} {4}J\left(\frac{2} {3}-\tan \text h\frac{σy_c} {s_c+s_0}+\frac{1} {3}\tan h^3\frac{σy_c} {s_c+s_0}\right)$ | (11) |
射流流线上任一点处的流量可表示为
| $Q={∫\limits^∞ _0u\text dy}\left|_{s=s′}\right.$ | (12) |
式中:
| $s_c=\frac{σa} {3}\left(\frac{1} {4{\cos}^2\frac{θ+π} {3}}-1\right)$ | (13) |
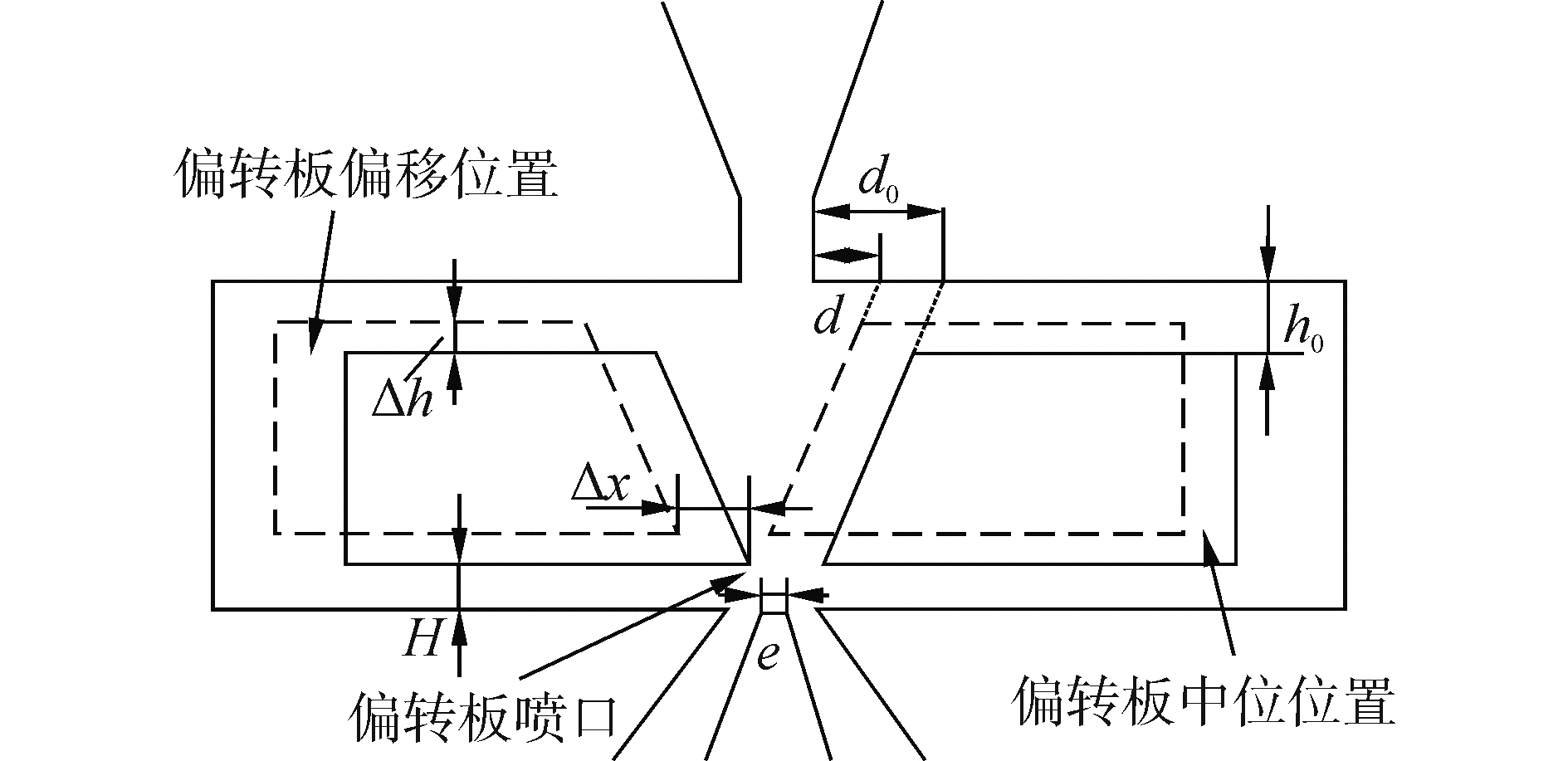
而附壁位差
|
图 4 偏转板位置偏移示意图 Fig.4 Schematic diagram of deflector offsets |
| $d=d_0-Δx+Δh/\tanα$ | (14) |
由图 3中的几何关系,有
| $s_c=R(θ-α)$ | (15) |
| $d+a/2=\overline{O_1B}=R(1-\cosθ/\cosα)$ | (16) |
综合式(13)~(16),得到射流碰撞角θ所应满足的等式:
| $\left(\frac{d_0} {a}-\frac{Δx} {a}+ \frac{Δh} {a·\tanα}+\frac 1 2\right)\frac{\cosα(θ-α)} {\cosα-\cosθ}=\\ \frac σ 3\left(\frac 1 {4{\cos}^2\frac{θ+π} 3}-1\right)$ | (17) |
式中:
由式(6)、(7)、(10)、(11) 与(13) 可得,碰撞处射流中心线到射流内边界的垂直距离为
| $y_c=\frac a 3·\frac 1 {4{\cos}^2\frac{θ+π} 3}·\text{arctanh}\left(2\cos\frac{θ+π} 3\right)$ | (18) |
根据图 3中几何关系有
| $\overline{AB}=\overline{AB′}-\overline{BB′}=R·(\sinθ-\cosθ·\tanα)$ | (19) |
| $\overline{AC}=y_c/\sinθ$ | (20) |
由式(14)、(16)、(18)~(20),可得射流的碰撞距离为
| $x_c=\overline{CD}=\left(d_0-Δx+\frac{Δh} {\tanα}+\frac a 2\right)\frac{\sin(θ-α)} {\cosα-\cosθ}-\\ \frac a 3\frac{\text{arctanh}\left(2\cos\frac{θ+π} 3\right)} {4\sinθ{\cos}^2\frac{θ+π} 3}-\frac{h_0+Δh} {\cosα}$ | (21) |
由式(21) 可知,碰撞距离受碰撞角θ、侧壁倾角α、射流盘喷嘴宽度
射流与偏转板侧壁碰撞后,部分油液沿侧壁继续向下流动至偏转板喷口,即由截面1流至截面2,如图 2所示。忽略势能影响,考虑偏转板V型导流槽的方形渐缩损失水头[10],由伯努利方程可表示为
| $\frac{p_2-p_1} {ρg}=\left[1-(1+ζ_2){\left(\frac{A_1} {A_2}\right)}^2\right]\frac{u^2_1} {2g}$ | (22) |
式中:
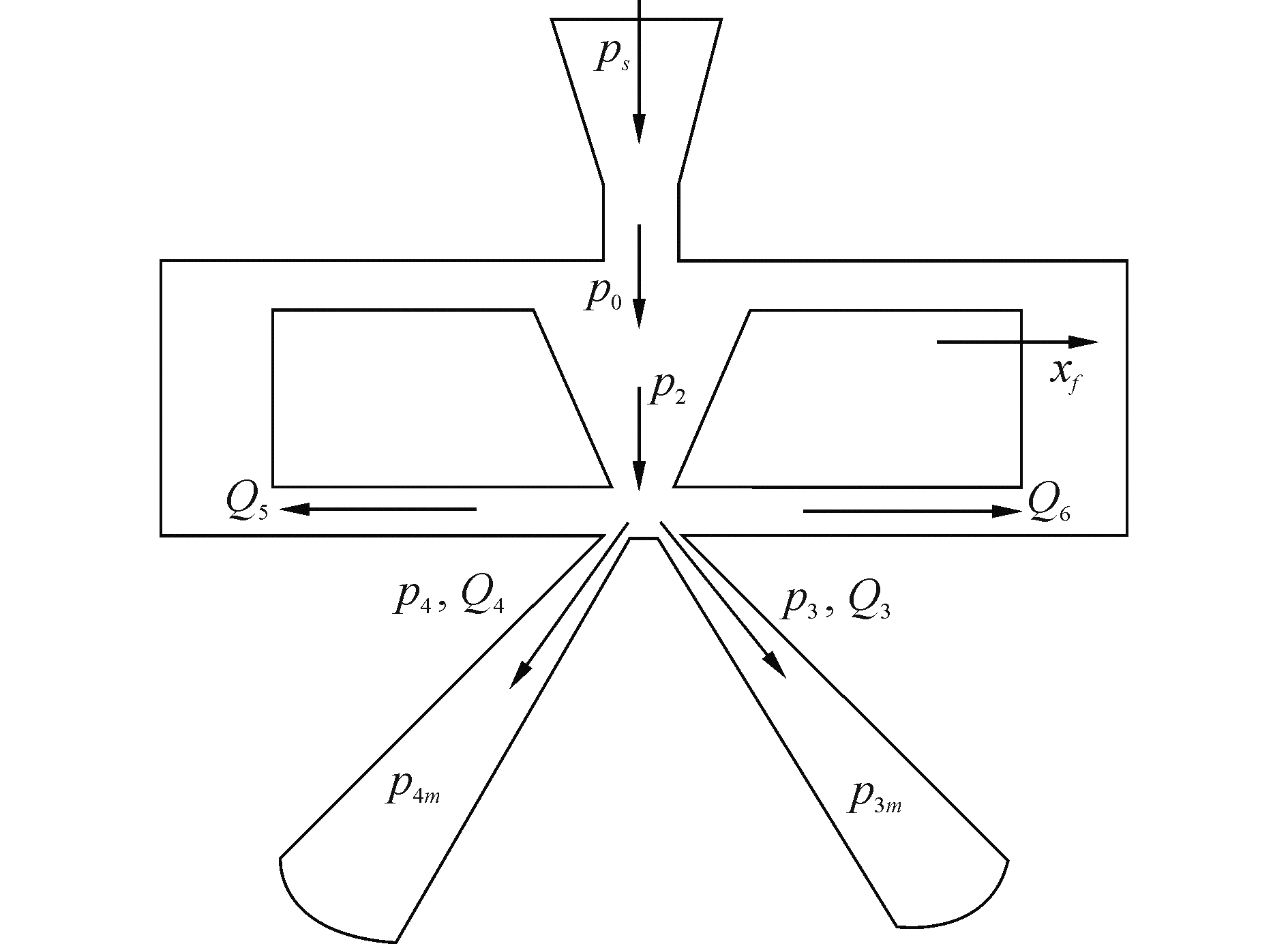
分析油液从截面2流至截面3的过程。前置级液流分布如图 5所示。其中,
|
图 5 偏转射流前置级液流分布示意图 Fig.5 Schematic diagram of the flow distribution in pilot stage |
假定阀匹配对称,供油压力恒定,温度和密度均为常数,则流入射流盘两接收器及偏转板与射流盘两侧缝隙的流量计算如下
| $Q_3=C_dA_3(x_f)\sqrt{\frac 2 ρ(p_2-p_3)}$ | (23) |
| $Q_4=C_dA_4(x_f)\sqrt{\frac 2 ρ(p_2-p_4)}$ | (24) |
| $Q_5=C_dA_5(x_f)\sqrt{\frac 2 ρp_4}$ | (25) |
| $Q_6=C_dA_6(x_f)\sqrt{\frac 2 ρp_3}$ | (26) |
式中:

|
图 6 偏转板喷口与射流盘接收器入口相对位置截面图 Fig.6 Relative position between the nozzle of deflector and the receiver of the jet plate |
| $A_3(x_f)=b\left[\frac 1 2(B-e)+x_f\right]$ | (27) |
| $A_4(x_f)=b\left[\frac 1 2(B-e)-x_f\right]$ | (28) |
| $A_5(x_f)=b\left[c-\frac 1 2(B-e)+x_f\right]$ | (29) |
| $A_6(x_f)=b\left[c-\frac 1 2(B-e)-x_f\right]$ | (30) |
负载流量
| $Q_L=Q_3-Q_6=Q_5-Q_4$ | (31) |
当偏转板中位时,负载流量为零,两接收器入口压力相等,即
| $p_3=p_4=\frac 1 {1+{(K-1)}^2}p_2$ | (32) |
式中:令
当油液进入接收器后,由于末端不通,流速降低,压力增大至恢复压力,由伯努利方程有
| $p_{3m}=ρ\left[1-{\left(\frac{A_3} {A_{3m}}\right)}^2-ζ_3\right]\frac{u^2_3} 2+p_3$ | (33) |
| $p_{4m}=ρ\left[1-{\left(\frac{A_4} {A_{4m}}\right)}^2-ζ_4\right]\frac{u^2_4} 2+p_4$ | (34) |
式中:
| $Δp_L=p_{3m}-p_{4m}$ | (35) |
负载流量
| $ΔQ_L={\frac{\partial Q_L} {\partial x_f}}\left|_{x_f=0}·Δx_f+{\frac{\partial Q_L} {\partial p_L}}\right|_{x_f=0}·Δp_L$ | (36) |
由式(27)~(32) 计算得到
| $ΔQ_L=C_db(K-2)\sqrt{\frac 2 ρ\frac{p_2} {1+{(K-1)}^2}}·Δx_f+\frac 1 2C_db·\\ \frac{(K-1)c+ \left(1-\frac K 2\right)(B-e)} {K-1}\sqrt{\frac{1+{(K-1)}^2} {2ρp_2}}·Δp_L$ | (37) |
式(37) 结合
| $K_p=\frac{K_{q0}} {K_{c0}}=\\ \frac{4(K-1)(K-2)} {\left[(K-1)c+\frac{1-K} 2 (B-e)\right][1+{(K-1)}^2]}p_2$ | (38) |
由式(38) 可知,压力增益系数受偏转板喷口压力、射流盘两接收器入口宽度及间距、偏转板尺寸等结构因素影响,与射流盘厚度无关。当负载流量为零时,由式(36) 可得,负载压力的表达式为
| $Δp_L=p_{3m}-p_{4m}=K_p·Δx_f$ | (39) |
由式(39) 可知,伺服阀负载压力与偏转板偏移量呈线性关系,且压力增益系数越大,对负载压力的控制灵敏度越高。
3 偏导射流前置级特性仿真验证 3.1 前置级射流流场附壁特性仿真验证 3.1.1 前置级流场附壁特性的Matlab仿真计算基于第2.2节对附壁射流特性参数的推导,仿真分析前置级流场附壁特性,所需参数如表 1所示。
| 表 1 附壁特性Matlab仿真参数 Tab.1 The parameters for Matlab simulation of the wall attachment properties |
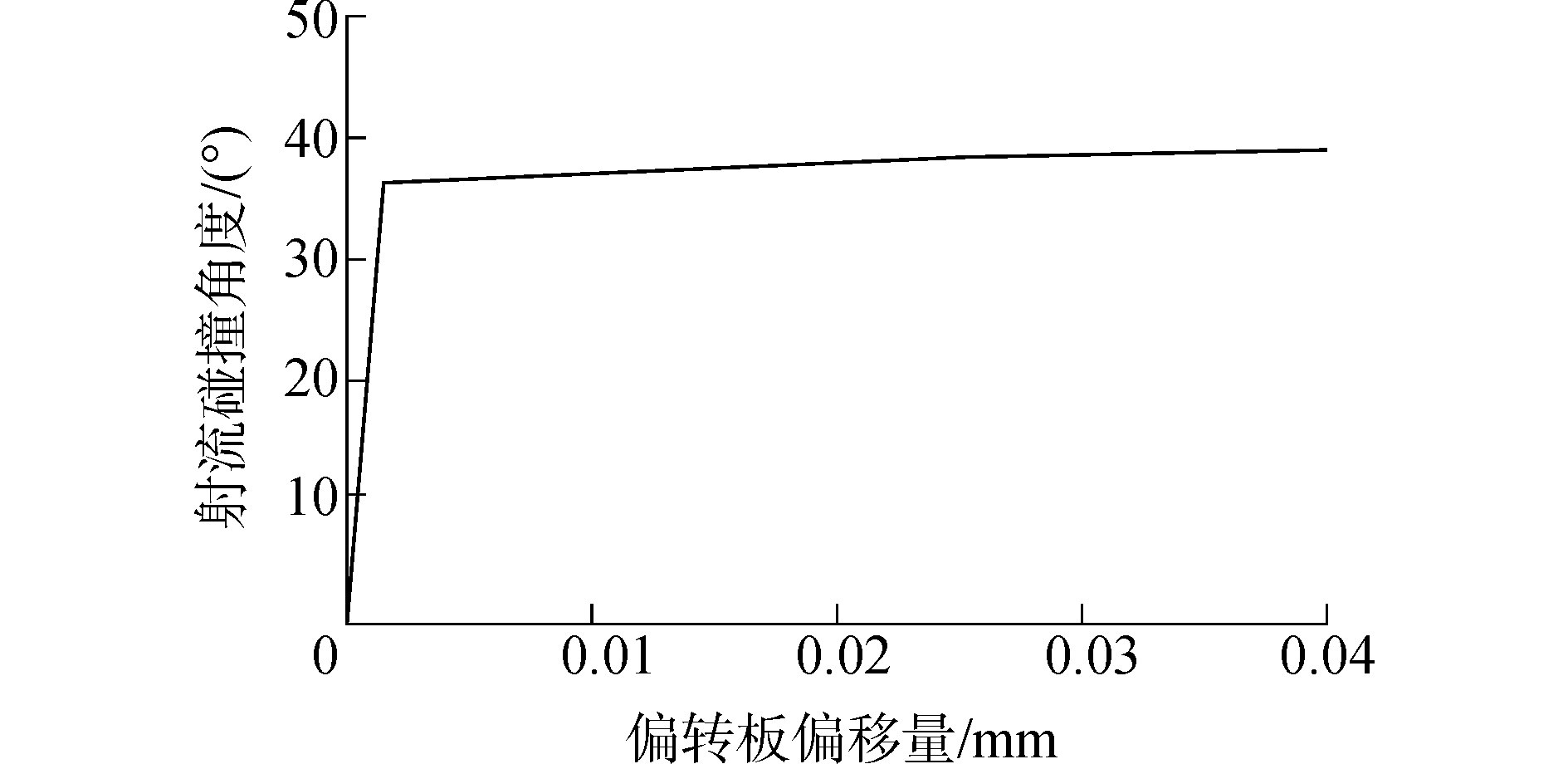
偏转板处于中位时无附壁现象。由于结构对称,向左或向右偏移时引起的射流现象亦对称,故选取偏转板向左偏移的情况进行讨论,偏移范围[0, 0.04] mm。仿真得到射流碰撞角θ与碰撞距离
|
图 7 受偏转板位移影响的射流碰撞角变化曲线 Fig.7 Jet impact angle variation affected by deflector offsets |
|
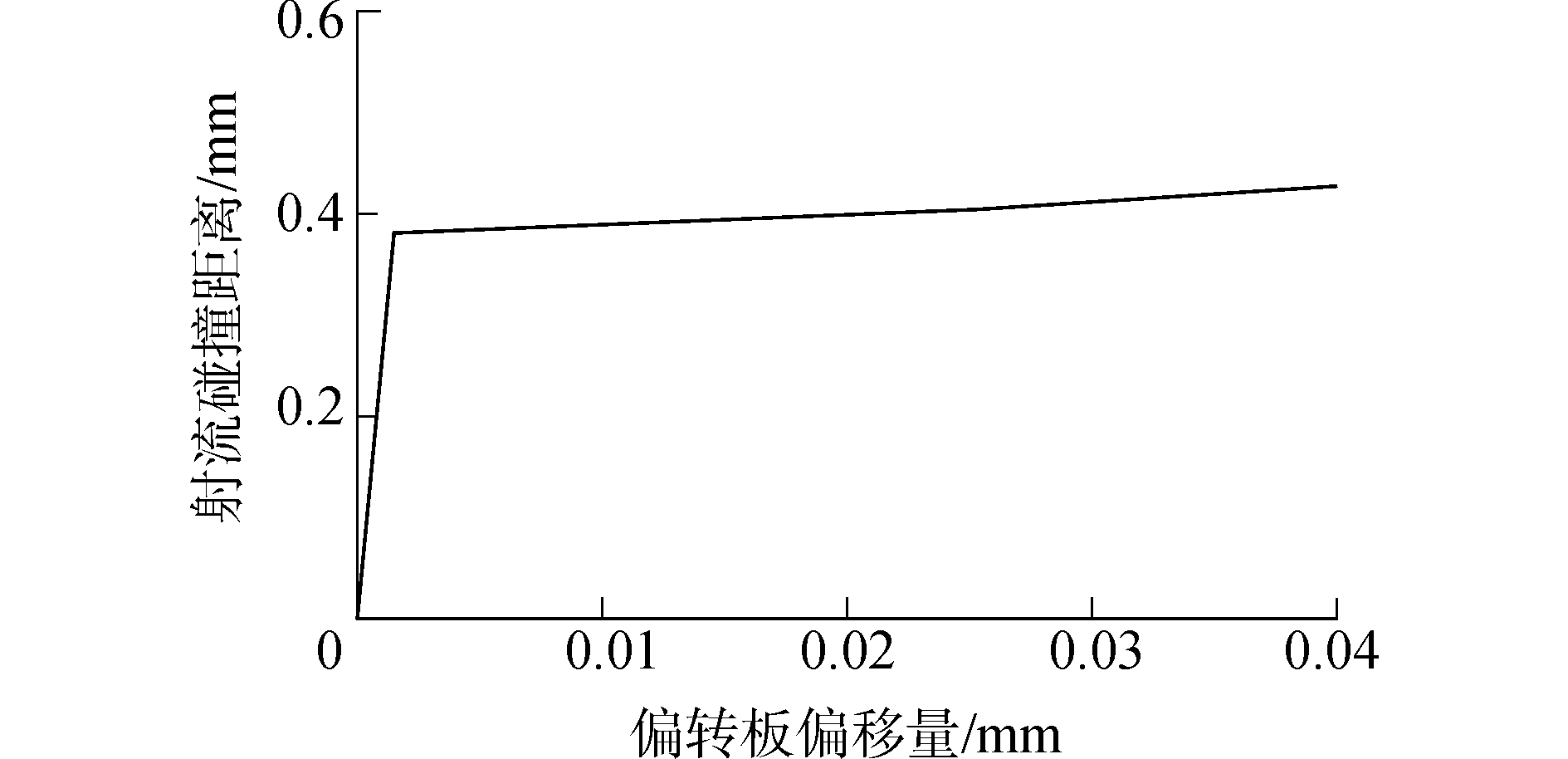
图 8 受偏转板位移影响的碰撞距离变化曲线 Fig.8 Collision distance variation affected by deflector offsets |
由图 7、8可知,偏转板向左偏移,右侧壁位差减小,射流与右侧壁碰撞,碰撞角θ随偏移量的增大而逐渐增加,变化范围36°~40°;碰撞距离亦逐渐增大,变化范围为0.37~0.45 mm。碰撞角和碰撞距离的变化受偏转板位移影响不大,原因在于:1)偏转板可偏移范围较小;2)偏转板导流槽楔形结构对射流产生约束,壁面与液流之间的干涉作用缩短了可自由射流的行程,抑制了其扩散。
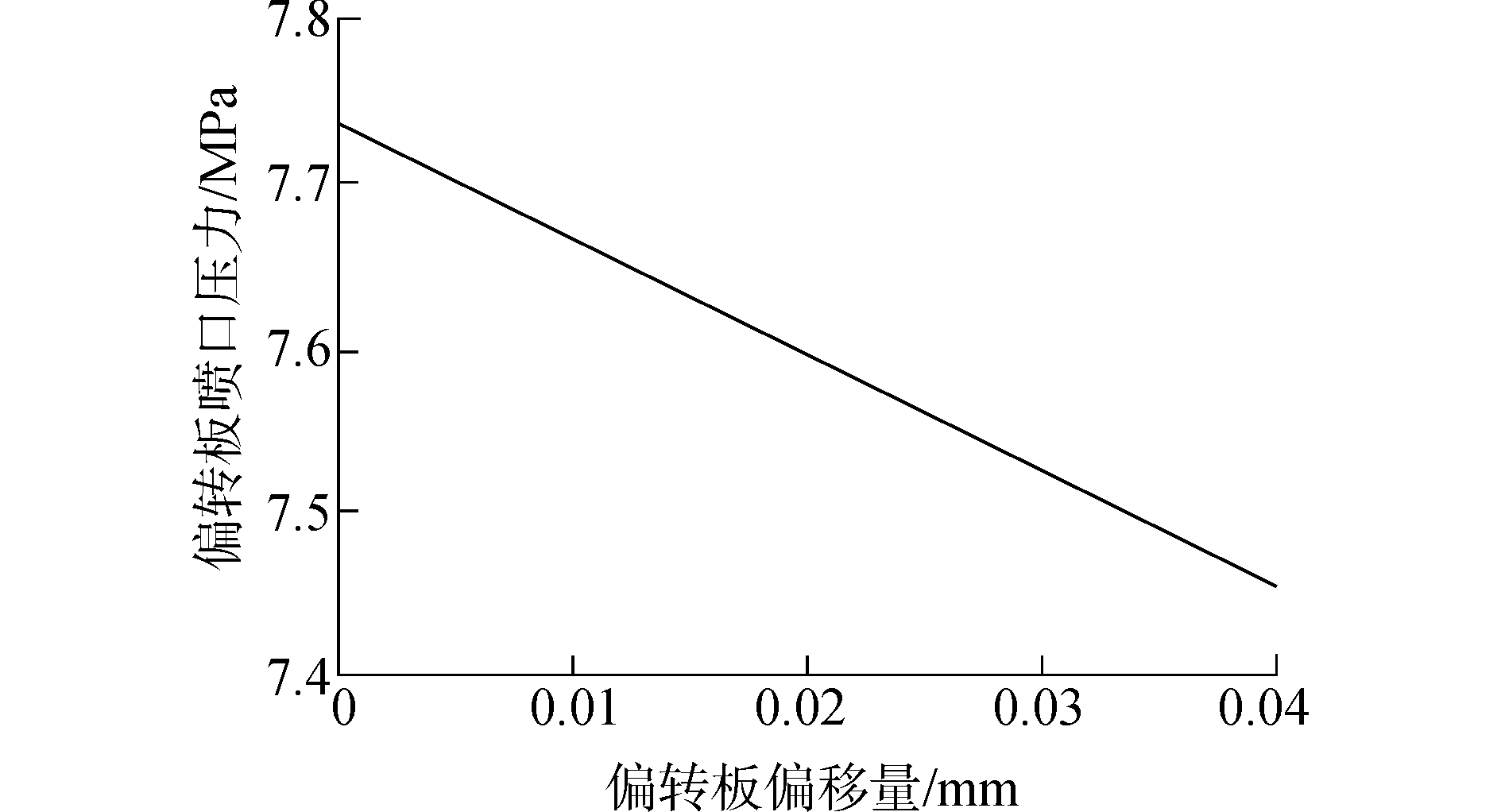
偏转板喷口压力
由图 9~10可知,偏转板处于中位时,其喷口压力为7.74 MPa;随着偏转板向左偏移,其喷口与左侧射流盘接收器入口的重合面积不断增加,油液进入射流盘接收器的阻力减小,偏转板喷口压力以约0.067 MPa/0.01 mm的速率下降,偏转板喷口处的油液平均流速也随之减小。
|
图 9 受偏转板位移影响的偏转板喷口压力变化曲线 Fig.9 Deflector pressure variation affected by deflector offsets |

|
图 10 受偏转板位移影响的偏转板喷口流速变化曲线 Fig.10 Deflector fluid velocity variation affected by its offsets |
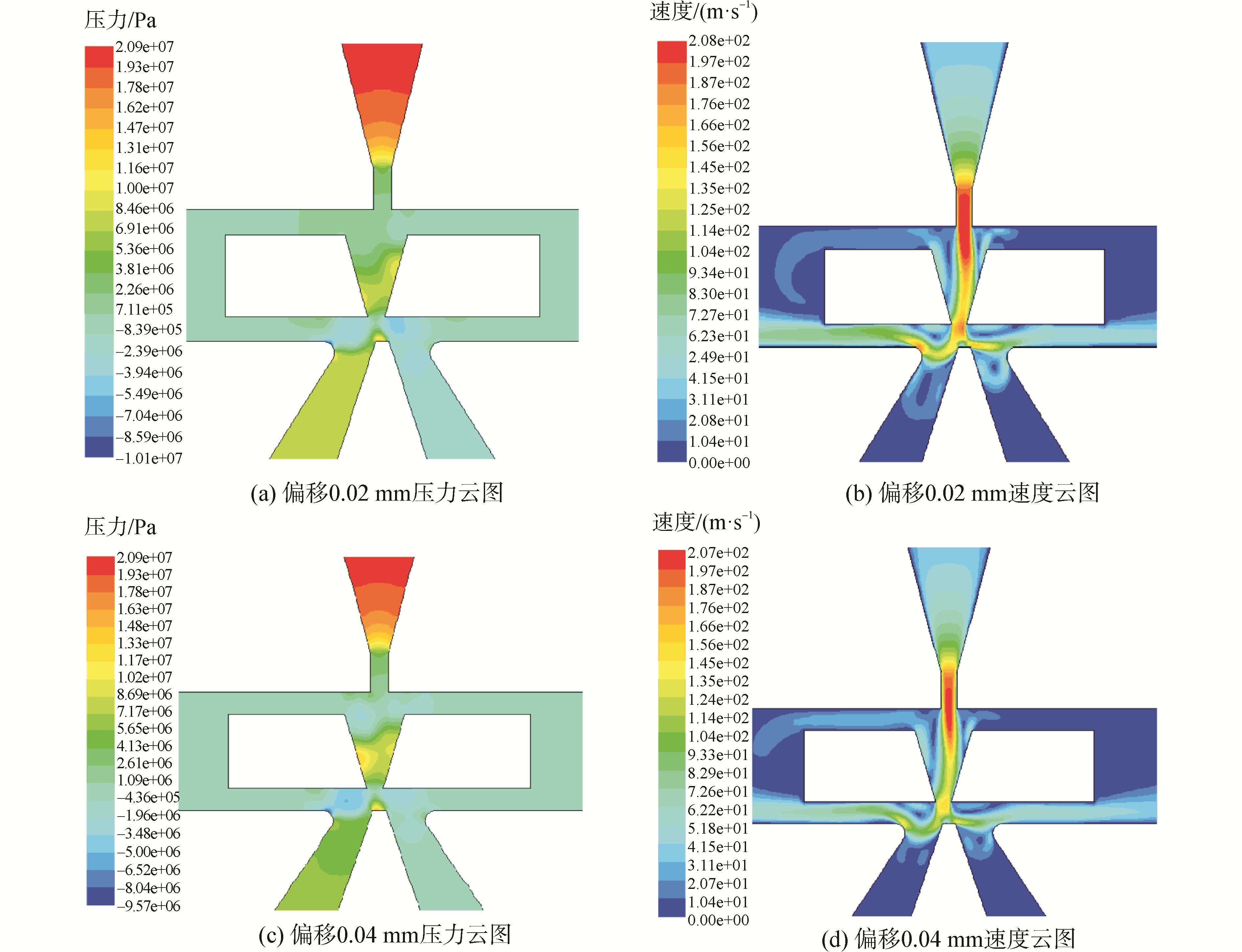
应用Fluent对前置级的附壁特性进行数值模拟。在Gambit中建立偏转板偏移量为0、0.02、0.04 mm时的前置级流场二维网格模型[14]。并在Fluent中设置如下参数:供油压力21 MPa,油液密度870 kg/m3,运动粘度0.008 7 kg/ms,其余参数默认。当偏转板位于中位时,射流无附壁现象。偏转板偏移量为0.02、0.04 mm时的油液压力分布及速度云图如图 11所示。
|
图 11 不同偏转板偏移时的前置级压力与速度分布云图 Fig.11 Pressure and velocity contours of the flow in pilot stage with different deflector offsets |
由图 11可知,当偏转板向左偏移,右侧位差减小,射流向右侧偏转弯曲,末端与偏转板侧壁碰撞,流迹线形状近似于弧型,原因在于:射流对其附近的流体具有卷吸作用,位差较小的一侧从其余流体处得到的介质补充更快,故该侧压力小于位差较大的一侧,致使射流向该侧偏转。碰撞后,少部分油液出现回流,并经偏转板与射流盘间缝隙流至两侧回油口,其余依附侧壁继续向下流动,射流下端由于受到导流槽楔形侧壁的限制,压力上升,到达偏转板喷口后再次出射,上述现象与2.2节中提出的附壁射流模型对射流的描述一致,且侧壁的存在对于改善紊动射流的流向稳定性具有显著效果。
根据Fluent仿真数据,得出随偏转板偏移,其喷口平均压力与平均流速、射流碰撞角及碰撞距离的变化,如表 2所示。
| 表 2 受偏转板偏移影响的前置级流场附壁特性表 Tab.2 Wall attachment characteristics of pilot stage flow distribution affected by deflector offsets |
由表 2可知,随偏移量增大,射流碰撞角小幅增加,碰撞点向下移动,逐渐靠近偏转板喷口,偏转板喷口平均压力减小,平均流速略有减小。
对比Matlab仿真计算与Fluent数值模拟结果,相对误差如表 3所示。
| 表 3 Matlab仿真与Fluent数值模拟结果相对误差 Tab.3 Relative errors of results between Matlab and Fluent |
由表 3可知,偏转板喷口平均压力与流速计算误差较小,两种模型结果符合较好;而由数值模拟得出的射流碰撞角与碰撞距离为观测估计值,故与理论计算结果相比存在一定误差,但以上误差均处于合理范围内,两种模型所得数据基本一致,验证了基于附壁射流理论的前置级射流模型的合理性。
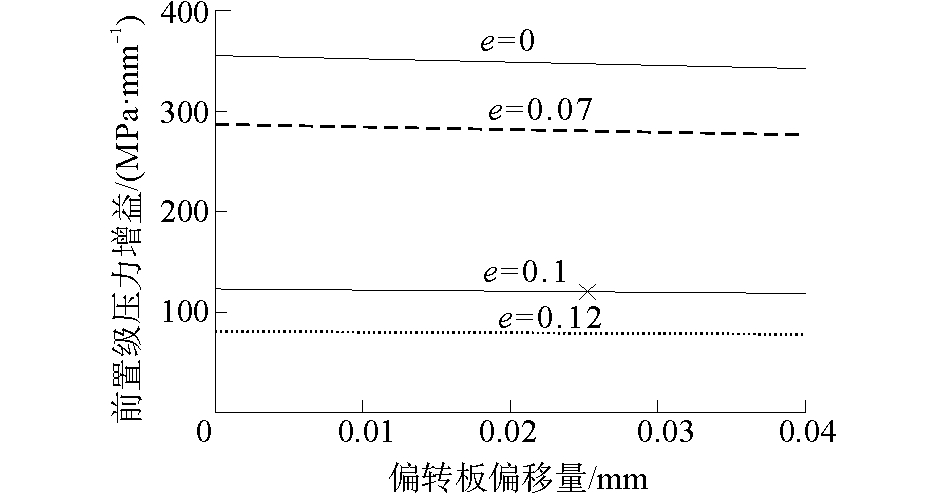
3.2 前置级结构参数对伺服阀压力增益影响基于2.3节推导可知,当供油压力一定时,压力增益系数大小仅由前置级尺寸结构决定。根据不同接收器入口间距
|
图 12 接收器入口间距变化对压力增益系数的影响 Fig.12 Influence of the distance variation between receiver inlets on pressure gain coefficient |
由图 12可知,当e=0时, 射流盘接收器处为尖劈型结构,此时压力增益最大,随两接收器入口间距增大,压力增益系数减小,但其变化不呈线性,且压力增益系数几乎不受偏转板位移的影响,可近似为常数。采用尖劈结构虽能够获得较大的压力增益,但当劈距H较小时,不易获得射流的稳定附壁,将影响整阀响应的快速性,故射流盘接收器入口间宜采用平劈型结构,此处设计间距为e=0.1 mm。
偏转板尺寸改变亦对压力增益产生影响。采用不同偏转板导流槽侧壁倾角的压力增益曲线如图 13所示。

|
图 13 偏转板导流槽侧壁倾角变化对压力增益系数的影响 Fig.13 Influence of the inclination angle variation of deflector flow channel on pressure gain coefficient |
由图 13可知,侧壁倾角减小5°,平均压力增益系数随之减小约15~20 MPa/mm;偏转板位移对压力增益系数略有影响。这里设计采用的侧壁倾角为α=15°,此时压力增益为122 MPa/mm。
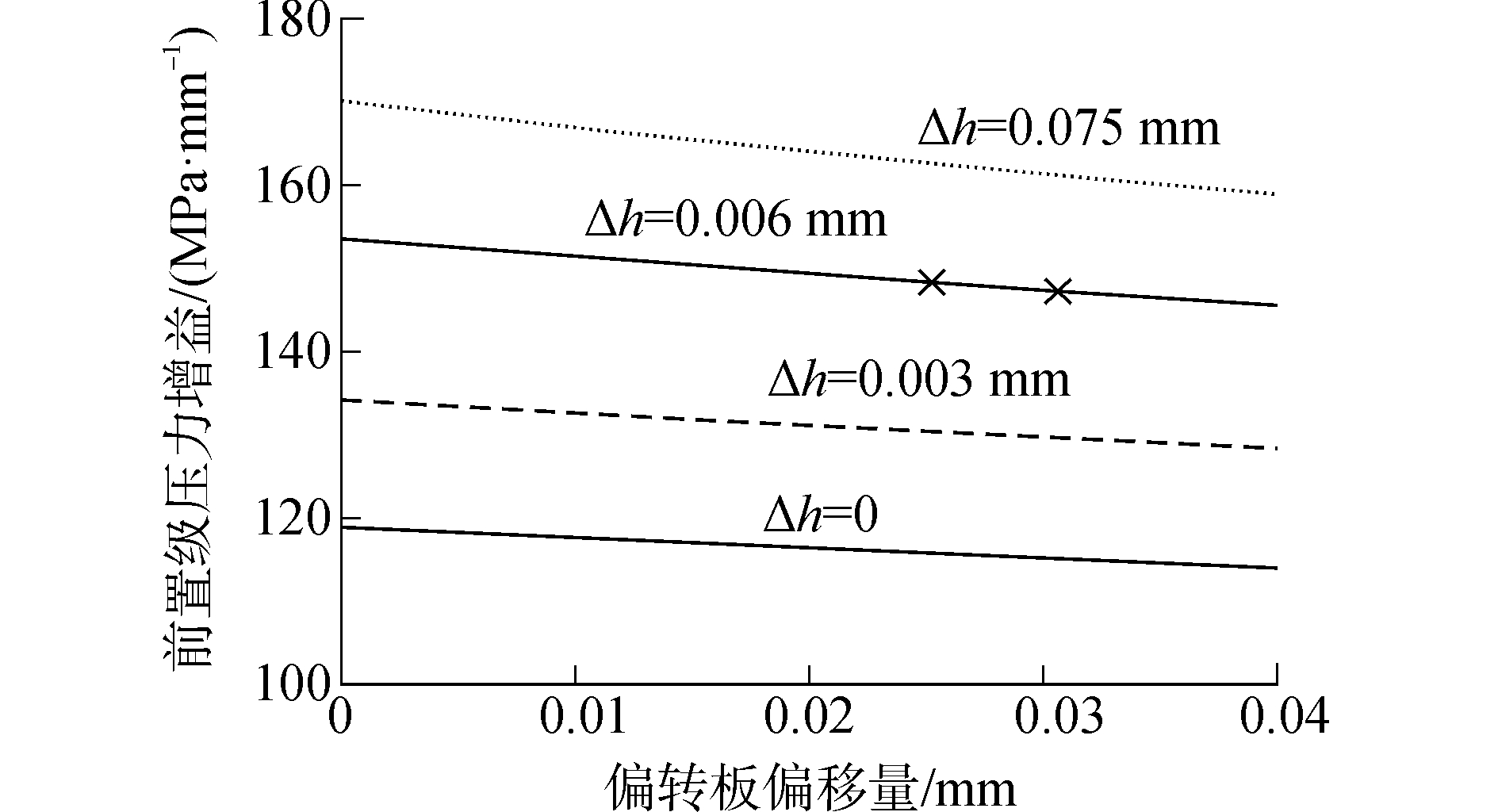
对伺服阀进行组装调试时,会引起偏转板与射流盘喷口所在侧壁的间距
|
图 14 偏转板与射流盘喷口侧间距变化对压力增益的影响 Fig.14 Influence of the distance variation between deflector and jet plate nozzle on pressure gain coefficient |
由图 14可知,当偏转板与射流盘处于初始间距h0=0.2 mm时,平均压力增益为122 MPa/mm,偏转板靠近射流盘喷口所在侧移动,压力增益随之增大,但不受偏转板偏移量影响。由此可见,将偏转板靠近射流盘喷口安装,或减小偏转板与射流盘喷口一侧的设计间距,可相应提高整阀压力增益。
综上所述,设计采用适当的前置级结构参数,如接收器入口间距、偏转板侧壁倾角,选取恰当的偏转板安装位置,或缩小偏转板与射流盘喷口侧设计间距,不仅能有效提高伺服阀压力增益,还能增强射流的附壁稳定性,缩短射流方向切换时间,由此提高整阀的响应速度和灵敏度,改善整阀性能。
4 偏导射流前置级压力增益测试试验及结果分析 4.1 前置级压力测试试验设计在射流盘供油口、偏转板喷口及射流盘接收器内分别安装压力传感器,用于测定供油压力
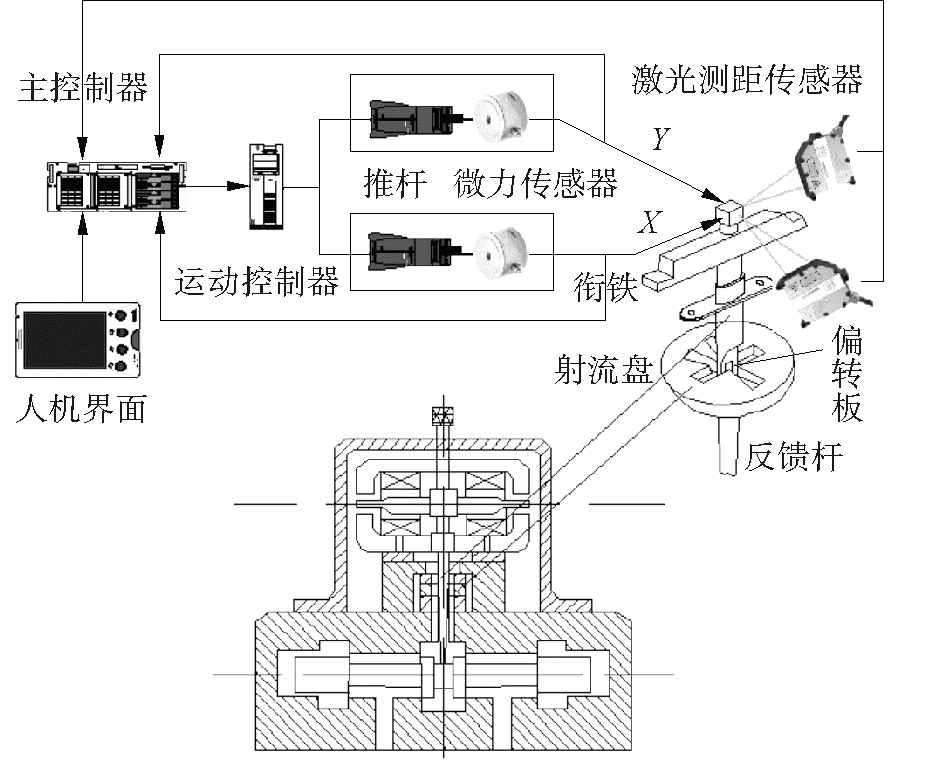
设计偏转板微位移检测装置,原理图如图 15。
|
图 15 偏转板微位移检测原理示意图 Fig.15 Diagram of deflector′s micro displacement detection |
该装置用于推动偏转板以实现其精确微位移并检测该值。将电动推杆垂直安装于伺服阀衔铁上方的测试工装中,可在X与Y向上对力矩马达上端的机械反馈装置实施恒力推动。在测试过程中,主控制器为衔铁组件施加精确的位置信号,使其运动到相应偏转角度,通过两个激光传感器测量同一水平面内X与Y向的力矩马达微小位移,并反馈给主控制器,构成精确的位置闭环系统。基于所测力矩马达位移量,根据前置级结构参数可折算得到偏转板的位移。偏转板微位移检测装置如图 16所示。

|
图 16 偏转板微位移检测装置 Fig.16 Device for micro displacement detection of deflector |
根据上述试验所测恢复压力数据
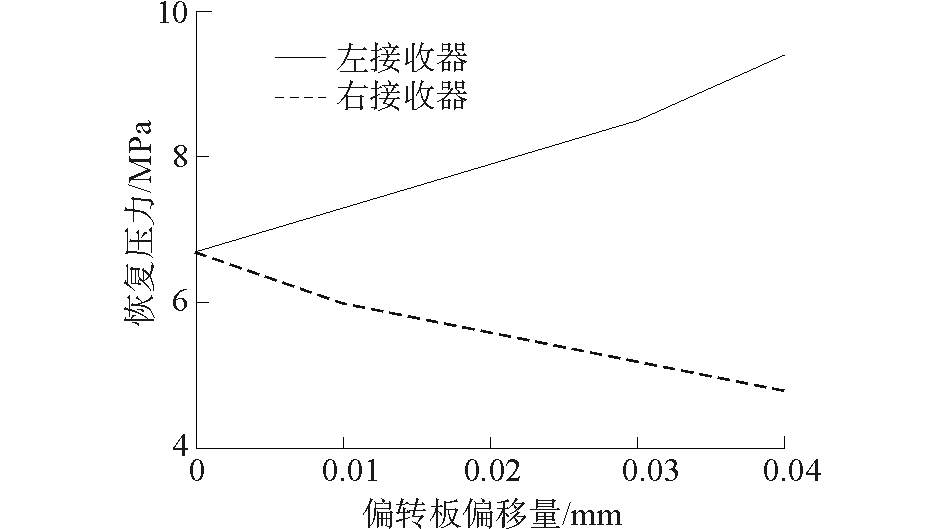
设置供油压力为21 MPa,改变伺服阀线圈控制电流,使偏转板由中位偏转至0.04 mm处,测得不同偏移位置时的两接收器内恢复压力变化如图 17。
|
图 17 射流盘接收器内的恢复压力变化曲线 Fig.17 Recovery pressure variation at the jet plate receivers |
由图 17可知,偏转板中位时,两接收器内恢复压力试验值均为6.7 MPa,由式(32)~(34) 计算可知,恢复压力理论值为7.14 MPa,误差为6.16%,此时两侧无压差,阀芯静止;随偏转板向左位移,左侧恢复压力近似线性升高,右侧压力则线性下降,负载压力表现为偏转板位移的线性函数,与理论公式(39) 一致。基于试验数据,代入式(39) 可得,前置级平均压力增益试验值为118 MPa/mm,而根据理论模型计算得到的压力增益值为122 MPa/mm,相对误差为3.28%。分析理论计算的误差,推断主要来源于:前置级机构的加工误差及现有射流理论对于分析复杂流态的局限性等。试验表明,理论计算结果与试验结果基本一致,基于附壁射流理论建立的流场模型合理,且压力增益理论表达式正确。
5 结论1)提出的基于附壁射流理论的偏导射流前置级流场精确数学模型,可完整描述射流在前置级有限空间约束下的复杂流动状态,为后续研究前置级内部流场影响下的整阀特性变化规律提供理论支持。
2)基于实际前置级结构推导得出的前置级压力增益理论表达式,经仿真与试验验证,具有合理性。由此确定:射流盘接收器入口间距、偏转板侧壁倾角及其相对于射流盘喷口侧的间距,为影响伺服阀压力增益的关键结构参数,为设计优化前置级结构,改善此类伺服阀的整体性能提供了理论依据。
3)所设计的伺服阀压力增益测试方案,能够间接测得前置级压力增益,且结论与理论计算、仿真模拟一致,证明了该方案的可行性,为伺服阀的动态性能检测提供了工程指导。
本文的研究结果对于偏导类伺服阀前置级流场精确完整模型的建立、结构改进及特性测试试验的设计均具有参考价值。而受到前置级微小结构约束的复杂射流形态,后续仍需进一步研究与探讨。
| [1] |
卢长耿, 李金良. 液压控制系统的分析与设计[M]. 北京: 煤炭工业出版社, 1992: 10-45.
( 0) 0)
|
| [2] |
方群, 黄增. 电液伺服阀的发展历史、研究现状及发展趋势[J]. 机床与液压, 2007, 35(11): 162-164. FANG Qun, HUANG Zeng. Developing process, research actuality and trend of electrohydraulic servo valve[J]. Machine tool & hydraulics, 2007, 35(11): 162-164. DOI:10.3969/j.issn.1001-3881.2007.11.053 (  0) 0)
|
| [3] |
王传礼, 丁凡, 李其朋, 等. 射流盘伺服阀控电液位置系统的动态特性[J]. 重庆大学学报, 2003, 26(11): 11-15. WANG Chuanli, DING Fan, LI Qipeng, et al. Dynamic characteristics of electro-hydraulic position system controlled by jet-pan servo valve[J]. Journal of Chongqing University, 2003, 26(11): 11-15. DOI:10.11835/j.issn.1000-582X.2003.11.003 (  0) 0)
|
| [4] |
訚耀保, 张鹏, 张阳. 偏转板伺服阀压力特性研究[J]. 流体传动与控制, 2014, 65(4): 10-15. YIN Yaobao, ZHANG Peng, ZHANG Yang. Analysis of the pressure characteristics of deflector jet servo valve[J]. Fluid power transmission and control, 2014, 65(4): 10-15. (  0) 0)
|
| [5] |
訚耀保, 张鹏, 岑斌. 偏转板射流伺服阀前置级流场分析[J]. 中国工程机械学报, 2015, 13(2): 1-7. YIN Yaobao, ZHANG Peng, CEN Bin. Prestage flow field analysis on deflector jet servo valves[J]. Chinese journal of construction machinery, 2015, 13(2): 1-7. (  0) 0)
|
| [6] |
杨月花. 伺服阀前置级射流流场分析及实验研究[D]. 哈尔滨: 哈尔滨工业大学, 2006. YANG Yuehua. Analysis and experimental research of prestage jet flow field in hydraulic servo valve[D]. Harbin:Harbin Institute of Technology, 2006. http: //cdmd. cnki. com. cn/Article/CDMD-10213-2006171319. htm (  0) 0)
|
| [7] |
江林秋. 新型偏转板射流液压伺服阀的设计与研究[D]. 南京: 东南大学, 2013. JIANG Linqiu. Design andresearch on a new type of deflection plate jet servo valve[D]. Nanjing:Southeast University, 2013. http: //d. wanfangdata. com. cn/Thesis/Y2511490 (  0) 0)
|
| [8] |
SANGIAH D K, PLUMMER A R, BOWEN C R, et al. Modelling and experimental validation of a novel piezohydraulic servovalve[C]//Proceedings of the ASME 2011 Dynamic Systems and Control Conference. Arlington, USA, 2011:343-350.
( 0) 0)
|
| [9] |
ZHU Yuchuan, LI Yuesong. Development of a deflector-jet electrohydraulic servovalve using a giant magnetostrictive material[J]. Smart materials and structures, 2014, 23(11): 1-19. ( 0) 0)
|
| [10] |
日本机械学会. 流体力学[M]. 祝宝山, 张信荣, 王世学译. 北京: 北京大学出版社, 2013: 89-107.
( 0) 0)
|
| [11] |
董志勇. 射流力学[M]. 北京: 科学出版社, 2005: 15-17.
( 0) 0)
|
| [12] |
原田正一, 尾崎省太郎. 射流工程学[M]. 陆润林, 郭秉荣, 译.北京: 科学出版社, 1977: 104-137.
( 0) 0)
|
| [13] |
LEVIN S G, MANION F M. Jet attachment distance as a function of adjacent wall offset and angle[J]. Advances in fluidics, 1962(9): 1087-1099. ( 0) 0)
|
| [14] |
张仁徽, 陈宇里, 耿钊. 网格尺寸对Delft3D有限元水流场仿真精度影响的分析[J]. 应用科技, 2015, 42(1): 57-61. ZHANG Renhui, CHEN Yuli, GENG Zhao. Influence analysis of the mesh size on the precision of flow field simulation of the Delft3D finite element[J]. Applied science and technology, 2015, 42(1): 57-61. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


