2. 吉林大学 符号计算与知识工程教育部重点实验室, 吉林 长春 130012;
3. 吉林大学 应用技术学院, 吉林 长春 130012
2. Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun 130012, China;
3. Applied Technology College, Jilin University, Changchun 130012, China
智能交通系统(intelligent transportation system,ITS)是集信息、通信、控制及网络等技术于一体的综合研究学科,可以提供全方位、实时、准确以及高效的服务信息,ITS是有潜力的研究方向,进一步说将成为未来相关研究领域的热点[1]。动态路径诱导系统(dynamic route guidance system,DRGS)是ITS一个重要的分支,利用计算机、通信等现代技术,为出行者提供实时交通信息以及最优路径。在DRGS中,路径选择模型可以确立DRGS的目标[2]。
路径诱导模型分为静态模型和动态模型,静态模型以假设出行者获知路网信息为前提,并以随机期望效用理论或积累前景理论为基础。而动态模型包含一些信息获取和学习的过程,以随机虚拟理论或增强学习理论作为指导[3]。目前,在国内路径诱导模型的研究主要还是集中在静态模型且取得了阶段性的成果。基于期望效用理论的模型是在确定性框架下,以几何路径或者出行时间为效用值,以期望获得效用最大化评价各备选方案的优劣。孟梦等针对不同的出行时间,提出了组合出行工具的路径选择模型,以组合出行工具的模式下为出行者提供最优路径[4]。刘艳秋等构建了交通堵塞下基于实时交通信息的路径选择模型[5]。相反,积累前景理论是不确定性情况下的决策行为,决策者以财富的变化量而不是最终量作为参考依据进行决策[6],针对交通信息不确定的特性,诸多学者以积累前景理论为基础提出了路径选择模型[7-9]。但是,目前提出的模型大多仅针对路段行程时间构建的单目标路径选择模型[6],显然,与实际存在很大的偏差。在实时环境下,交通畅通、拥挤情形下路阻的产生形式有所差异,因此,分别以交通畅通、拥挤下的路阻构建了基于时间最短的路径选择模型,进而提高了模型的可靠性。
Erel Avineri等提出时间是影响路径抉择最重要的因素,但不能确切地表述所有出行者的意愿[10]。由此可见,在实时环境下,路径优化是多目标组合优化问题[11],例如,时间、费用、环境等因素。因此,仅从时间上考虑构建路径选择模型并不合理而建立基于多目标的路径选择模型是有必要的。因此,分别从时间、费用两个角度出发,构建了实时环境下基于多目标的路径选择模型。
在处理多准则优化问题时,一般采取单目标类和多目标类的策略[12]。单目标类将多目标优化问题转化为单目标优化问题,转化过程使用目标聚合或目标标准策略对其结果进行组合。而多目标类是以目标向量间的关系来定义决策向量之间的优劣关系,一般可获得均匀分布的Pareto最优前端。但在高维度下,多标准Pareto最优路径算法运行效率极低甚至无法运行[13]。然而,在实时信息下,对反应速度的要求却十分苛刻,由此可见多目标类在动态实时路网中并不实用。评价函数中加权求和函数属于单目标类,加权求和函数是解决多目标函数优化问题比较常见的方式之一。它采用目标聚合策略即将多维空间中的数据对象聚集转化为单目标空间的优化问题。处理过程相对比较简单,但组合权重的意义及结果的优劣至关重要。聚合过程中,由于不同的计量方式,各个目标函数间具有不同的值域。相应地,当映射到加权求和目标函数时,决策变量间具有不同的阈值。在这种情形下,阈值大的决策变量对组合函数的支配大,反之支配小[14]。所以,本文在使用加权求和函数前,对各个目标函数值进行了预处理,即对其进行类似的量值处理,从而保证支配能力的均衡即可获取最优路径。
1 基于多目标的路径选择模型设计 1.1 问题描述及分析路径优化问题相当于图理论模型中最优路径的查找问题,但又存在差异。在动态路径诱导系统中含有静态属性和动态属性[15],静态属性是路网信息相对固定的部分,例如:地理位置信息、路段间距以及路段的基本通行能力等。而动态属性可以反映实时信息状况,例如,车流量、行车速度等。所以,路网数据对象具有多样、复杂以及实时的特性。
以图论为基础,同时结合动态路网信息的特性,路径优化问题的定义形式:
| $P=\{G,W_{ij},S_\text{start},S_\text{end}\}$ | (1) |
式中:G=(V,Rij)是静态属性,表示路网结构;V是从起始点到结束点间的结点集合;Rij是当前Sstart到Send所有无环路集合,其定义形式为
| $\{R_{ij}|i,j∈V∧i\ne j\}$ | (2) |
式中:Wij是体现了动态路径诱导系统中的动态属性,Wij对应(i,j)间的权重值,并以此为优化准则;Sstart是出发节点且随着车辆的不断行驶动态更新,Send表示目标节点。
1.2 基于时间最短的路径选择模型在实时交通信息下,影响路阻的因素多样化。例如:天气、ITS系统故障、交通事故等偶然事件,也包含一些不确定因素,例如车速、车流量等。所以,仅以单一的车辆行程时间为路阻并不合理,交通畅通或者拥挤的情形下产生路阻的方式有所差异。在交通畅通情形下以行驶时间及交叉口转向延误产生的时间为路阻;而在交通拥挤的状态下,产生路阻最主要的是延误时间而行程时间可忽略不计。所以,基于时间最短的路径选择模型的定义形式为
| $\min∑\limits_{i\in V}∑\limits_{\substack{j\in V\\i\ne j}}R_{ij}\{K(t_{ij}+\partial D_{ij})+\\ (1-K)(d_{ij}+D_{ij})\}^{(t)}$ | (3) |
其约束条件为
| $R_{ij}=\left\{\begin{align} 1,i\ne j \\ 0,i=j \end{align}\right.$ | (4) |
| $K=\left\{\begin{align}&1,Q_{ij}/C_{ij}∈[0,1]\\ &0,(2C_{ij}-Q_{ij})/C_{ij}∈(1,2)\end{align}\right.$ | (5) |
| $\partial=\left\{\begin{align}&0,(0<D_{ij}(t)<t_n)\\ &1,(t_n≤D_{ij}(t)≤nt_n)\end{align}\right.$ | (6) |
式中:(i,j)均属于V集合且互异。式(4) 是无环路控制。式(5) 为道路饱和度[16]并约束路阻的计算方式,Qij表示当前路段交通量,Cij为路段基本通行能力,当Qij/Cij比值在[0, 1]范围时,道路属于畅通状态,而(2Cij-Qij/Cij)比值在(1, 2) 范围内时,道路交通处于拥挤状态。针对交通拥挤以及畅通情形下路阻计算方式的不同:式(3) 中,在约束系数K为1时,tij及Dij表示车辆的行程时间和交叉口等待时间;在约束系数K为0时,dij及Dij代表车辆间相互影响产生的延误时间及交叉口延误时间。式(6) 在道路畅通的情况下,交叉口有可能出现小范围的等待红灯时间。当在一个有效绿灯时长tn通过交叉口时,系数
通常情况下,燃油费是最主要的费用,而在一些欧洲国家采用缴纳拥挤税的方式缓解拥挤地区的交通压力,拥挤税的计费方式是一天中仅第一次进入拥挤区域时收取费用,但多次或未进入时不计费用,基于费用最低的路径选择模型的定义形式为
| $\min\sum\limits_ {i∈V}\sum\limits_ {\substack{j∈V\\i\ne j}}F{(i,j)}^{(t)}$ | (7) |
式中:(i,j)均属于V结点集合且互异;F(i,j)表示(i,j)两结点间的费用总和,费用的计算方式为
| $F(i,j)=F_h(i,j)+γF_c(i,j)$ | (8) |
式中:Fh(i,j)表示燃油费用;Fc(i,j)代表拥挤区域缴纳拥挤费,约束拥挤费的计算方式为
| $γ=\left\{\begin{align}&1,\text{first time}∧K∈(1,2)\\ &0,\text{other}\end{align}\right.$ | (9) |
式(9)表示:当且仅当第一次进入拥挤区域时缴纳拥挤费,即γ=1,否则γ=0。
1.4 组合优化函数模型针对出行者出行需求的多样化,采用加权求和最小化方法处理基于多目标的路径选择模型更加合理且易实现。出行者可以预设出行需求,例如设置费用最低、时间最短或自设权重大小。所以,本文以加权求和函数值作为优化准则,组合优化函数模型的定义形式为
| $\min W_{ij}=ω_zZ(i,j)+ω_cF(i,j)$ | (10) |
式中:wz、wc分别代表路阻、费用的权重系数且和为1,Z(i,j)和F(i,j)分别为(i,j)路段间的路阻及费用。为均衡各决策变量在组合权重函数中的控制权限,对Z(i,j)及F(i,j)均采用迭代取最高有效位的策略进行类似的量值处理,从而使各个决策变量的阈值限定在指定范围内。
2 基于多目标的路径选择模型求解在实时交通信息下,动态路径优化中“动”主要体现在各路段中评价值会随着时间的变化而发生变更,而最优路径也会随之发生变化,因此,动态地为出行者提供优化方案。针对交通信息的不可控性、随机性以及不确定性等因素,显然一步寻优与实时状况相背离,而逐步寻优更加合理。换言之,动态路径优化是一种逐步寻优的搜索过程,而最终目的是降低费用、减少污染或节省时间等。
为验证实时环境下基于多目标的路径选择模型,采用广义自适应A*算法[17]实现并获取最优路径及评价参数值。
2.1 采用广义自适应A*算法的合理性分析广义自适应A*算法被认为是A*算法的迭代过程,同样在算法中,采用open表保存所有已生成而未考察的节点,closed表存储已访问过的节点。但存在两方面的差异,一方面每完成一次A*搜索后,修改closed表中所有状态的h值,从而使启发值更明智。另一方面,当发现某条边的权重减少时,在搜索空间中需修改某些状态h值,即重构h值的一致性。这两点体现广义自适应A*算法在动态环境中的适用性。
在动态路径优化中,一方面,随着距离目标越来越近,结点不断减少,起始点Sstart在不断的发生变化。因此,起始点Sstart需动态的调整;另一方面,在实时环境下,路段的权值动态的变化。本文以组合权重值Wij为算法的启发式h值,实时环境下,决策变量路阻、时间在不断发生变化,Wij有可能减小。在这种情形下,需重构Wij的一致性。重构后,调用A*算法进而得到当前信息下的最优路径,重复此过程直到Sstart=Send算法结束。
2.2 算法应用过程 2.2.1 实现过程在本文中,广义自适应A*算法具体实现过程如图 1所示。

|
图 1 广义自适应A*算法实现过程 Fig.1 Generalized adaptive A* algorithm implementation process |
1) 初始化Sstart、Send,加载Sstart和Send间地图的静态数据并获取当前实时动态信息,进而初始化组合权重Wij,执行步骤2。
2) 若Sstart!= Send,首先调用A*算法,若不存在路径,返回NULL程序结束;反之,则返回目标结点Send,进而转向步骤3。
3) 修改closed表中所有的启发式值Wij,并以Send为参数构造Sstart与Send间的路径,执行步骤4。
4) 以当前路径的下一结点为Sstart,并更新实时动态数据,重新检测以Sstart的Wij启发式值是否减小,若减小,则重构Wij的一致性,重构完成后,跳出步骤4,执行步骤2;若不变或增加,则继续执行步骤4;若Sstart=Send时,跳出步骤4,执行步骤2。
2.2.2 控制策略1) 拥挤区域控制策略:调用A*算法过程中,采用K约束设置open表优先级的策略,即当K=1时的优先级高于K=0时的优先级,从而可以优先扩展畅通区域的结点。设定open表优先级过程:首先将open表定义以Wij为优先的队列;进而,判断K值,若K=0,则该结点插入临时优先队列,否则插入open表;优先扩展畅通区域的结点,当open表为空且未找到目标节点时,进而扩展临时优先队列。在道路拥挤的情形下,有效避免进入拥挤区域,从而节省时间、减少费用也可以缓解拥挤区域的交通压力。
2) 组合优化函数中各决策变量的控制策略:采用迭代循环将各决策变量的阈值限定在(0, 0.1) 内。因此,有效保证各个决策变量在组合优化函数模型中的均衡支配。从而,使得组合权重与优化结果的映射保持一致性。
3 实验仿真及结果分析为验证在实时环境下基于多目标的路径选择模型的合理性及有效性,采用C++编程仿真实验环境。以随机读入文本的形式模拟实时环境,即车流量以文本流的形式更新。
3.1 参数设置在交通信息中,车流量是实时变化的,车流量Qij与密度kij间存在函数关系:
| $Q_{ij}=v_f\left(k_{ij}-\frac{k^2_{ij}} {k_f}\right)$ | (11) |
式中:vf、kf分别为畅通速度及阻塞密度,参考城市道路函数模型,在实验中设置vf=77.4,kf=124。
行驶时间以BPR函数计算,路阻系数α和β采用交通流分配程序中的取值,即α=0.15,β=4。由于速度的随机性、不可控性,在不考虑人为主观因素的前提下,同时考虑城市道路限速。本文将其理想化处理,即假设路段(i,j)以均速行驶。由车流量、密度、速度三者间的关系确定速度:
| $v_{ij}=Q_{ij}/k_{ij}$ | (12) |
在交通拥挤情形下,车辆间相互影响产生延迟时间的计算方式[5]为
| $d_{ij}=\frac{θ_{ij}L_{ij}} {Q_{ij}L_c}$ | (13) |
式中:θij代表单位小时内当前路段车辆的时间密集度,Lij表示当前路段长度,Lc为有效检测器长度与平均车长的距离之和。
形式化交叉口等待时间为
| $D_{ij}=\left\{\begin{align}&n\frac{t_n} {λ},K\in [0,1]\\ &\text{int}\lfloor \frac{d_{ij}} {t_n}\rfloor \frac{t_n} {λ},K\in (1,2)\end{align}\right.$ | (14) |
式(14) 表示道路畅通及拥挤的情形下,交叉口的等待时间Dij的计算方式。在实验中,n设置为1,即在交通畅通下,出行者可接受在交叉口的延迟为一个有效红绿灯的时间,λ为绿信比。
影响燃油费用Fh(i,j)与车辆运行相关的外部因素多样化,例如平均速度、加速度、车辆行驶工况等[18]。为简化及理想化处理,本文仅从平均速度上考虑燃油费。计算方法采用隗海林等构建的平峰期和高峰期车速-油耗的模型[19],其计算形式为
| $F_h(i,j)=\left\{\begin{align}&(L_{ij}/v_{ij})M_\text{flat}p^\text{pre}_\text{oil},K∈[0,1]\\ &(L_{ij}/v_{ij})M_\text{rush}p^\text{pre}_\text{oil},K∈(1,2)\end{align}\right.$ | (15) |
式中:Mflat、Mrush分别为平峰期、高峰期油耗模型,
| $F_c(i,j)=\left\{\begin{align}&\text{cost},γ=1\\ &0,γ=0\end{align}\right.$ | (16) |
式中:cost表示当车辆第一次(γ=1) 进入拥挤区域时缴纳拥挤税,否则,无需缴纳拥挤税。
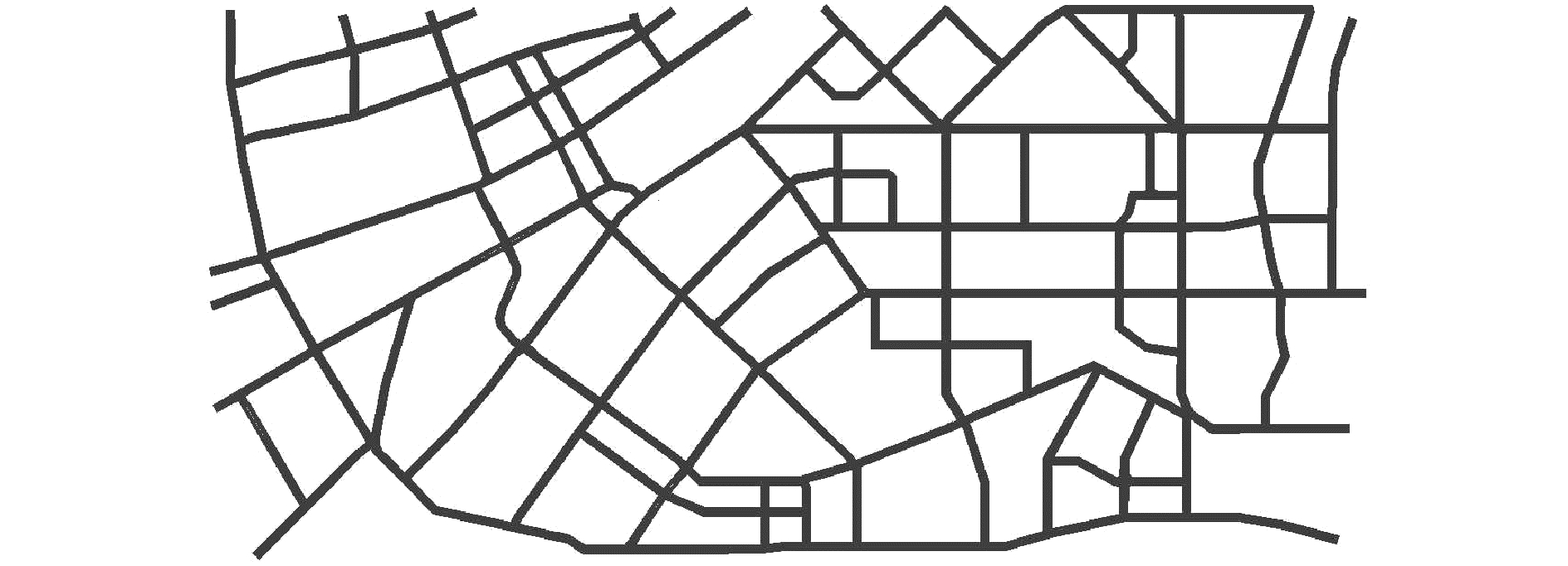
3.2 实验仿真数据利用某城市实际道路网络结构进行路径寻优仿真实验,VISSIM仿真将真实地图映射为如图 2所示的路网结构。
|
图 2 VISSIM仿真图 Fig.2 Map using VISSIM simulation |
在图 2中有101个测试结点和291条测试路段,实验数据以VISSIM仿真数据并结合实际进行了合理假设。车流量采用VISSIM仿真数据并以文本的形式实时读入。速度、燃油费、时间等结合实际道路情况进行了合理的设定和计算。
3.3 评价指标到目前为止,针对路径选择模型的评价没有统一的标准。而目前普通汽车上安装的商用导航系数大多是基于几何最短路径或可通达路径的静态路径为优化路径。为验证模型的合理性及实用价值,与基于几何距离最短的路径选择模型分别以时间、费用、距离等参数进行了对比实验。实验结果证明了在实时环境下,几何最短路径并非最优路径,而基于多目标的路径选择模型更加合理且具有一定的实用价值。
3.4 实例及结果分析本文在仿真实时环境下进行了多组实验,分别从道路畅通及拥挤情形下,以基于几何最短路径与本文模型进行了对比实验。为形象地显示实验结果,本文分别以最优路径对比图以及评价参数的对比结果加以诠释。
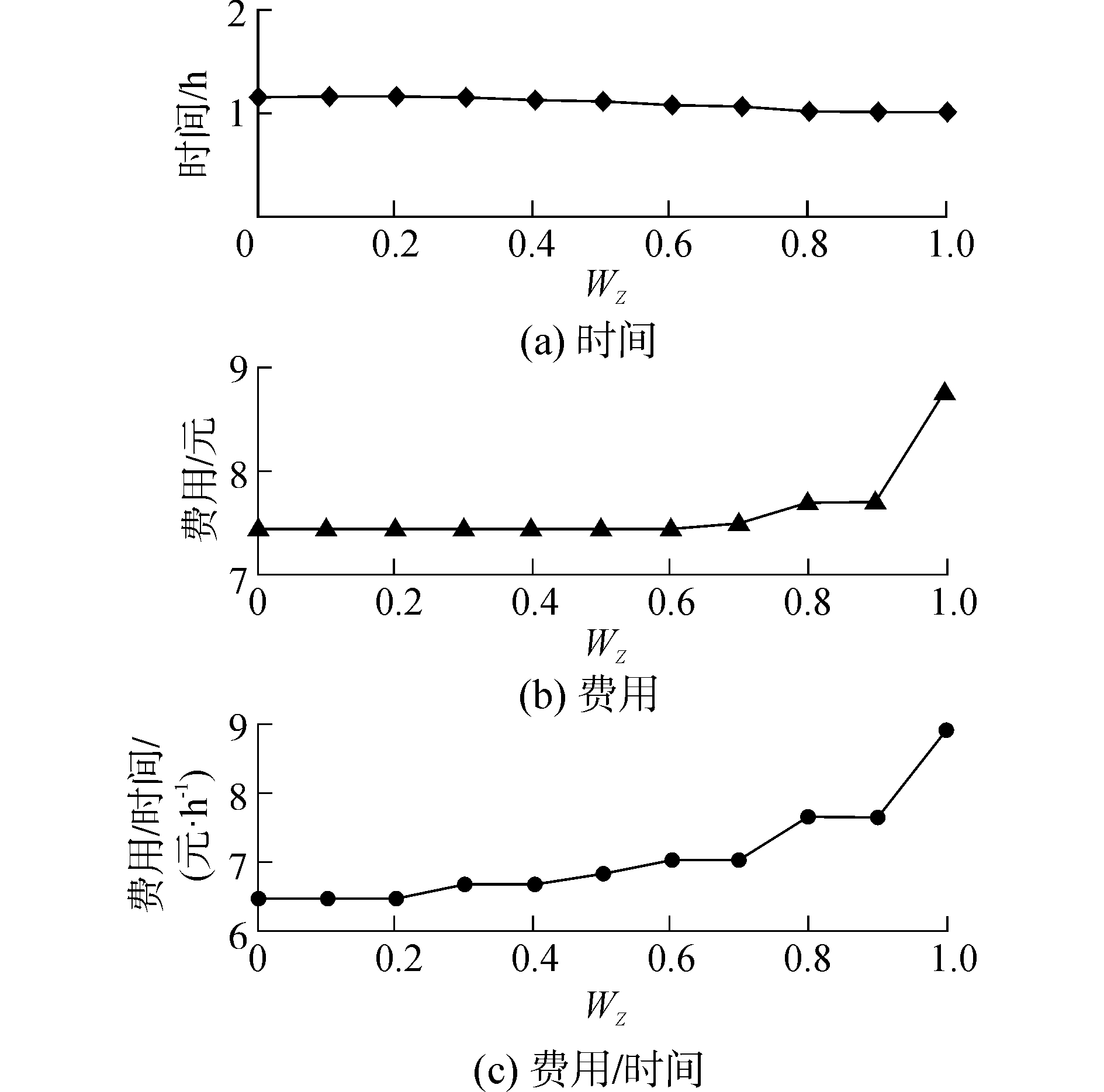
3.4.1 道路畅通情形下的对比实验在交通畅通的情形下,以结点1~100为一组实例进行分析。为验证本文组合优化函数模型的有效性,基于该实例下,以同等实验环境,时间权重系数wz分别在0~1以0.1为间隔取值。在不同wz下,最优路径所对应的时间、费用以及两者比值(费用/时间)如图 3所示,体现了组合权重与优化结果间的映射关系。
|
图 3 道路畅通情形下组合权重与优化结果映射关系 Fig.3 The mapping relationship between combination weights and the optimization results under the smoother of road traffic |
由图 3可知,随着时间权重系数增加,时间逐渐减少,而费用越来越大。由于wz的增加,时间决策变量在组合优化函数中的支配力越来越大,与此同时,费用决策变量的支配力变小。所以,优化结果趋向于时间越来越少而费用逐渐变大。在图 3中,费用与时间比值逐渐增大但在某些相邻点间的比值相同,例如:时间权重系数分别为0、0.1、0.2时。这种情况下,由不同的权重系数得到相同的优化结果属于结果重合,结果重合的意义在于当前最优路径唯一化。进一步分析图 3可知,曲线为上升趋势,优化结果符合加权求和函数的一般规律,即组合权重与优化结果间的映射具有一致性。因此,可以证明本文的组合优化函数模型的合理性及有效性。而且在不同权重系数下存在不同的优化结果,则最优路径的结果集合具有多样性的特点,从而可以满足出行者多样化的需求。
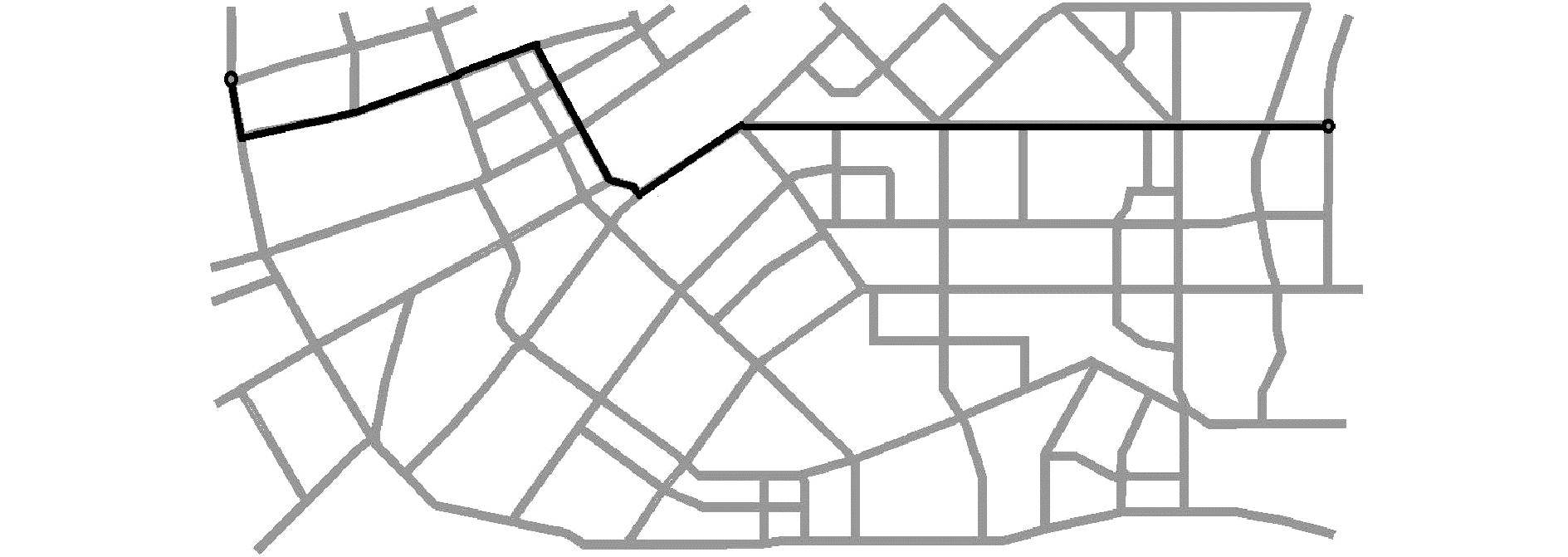
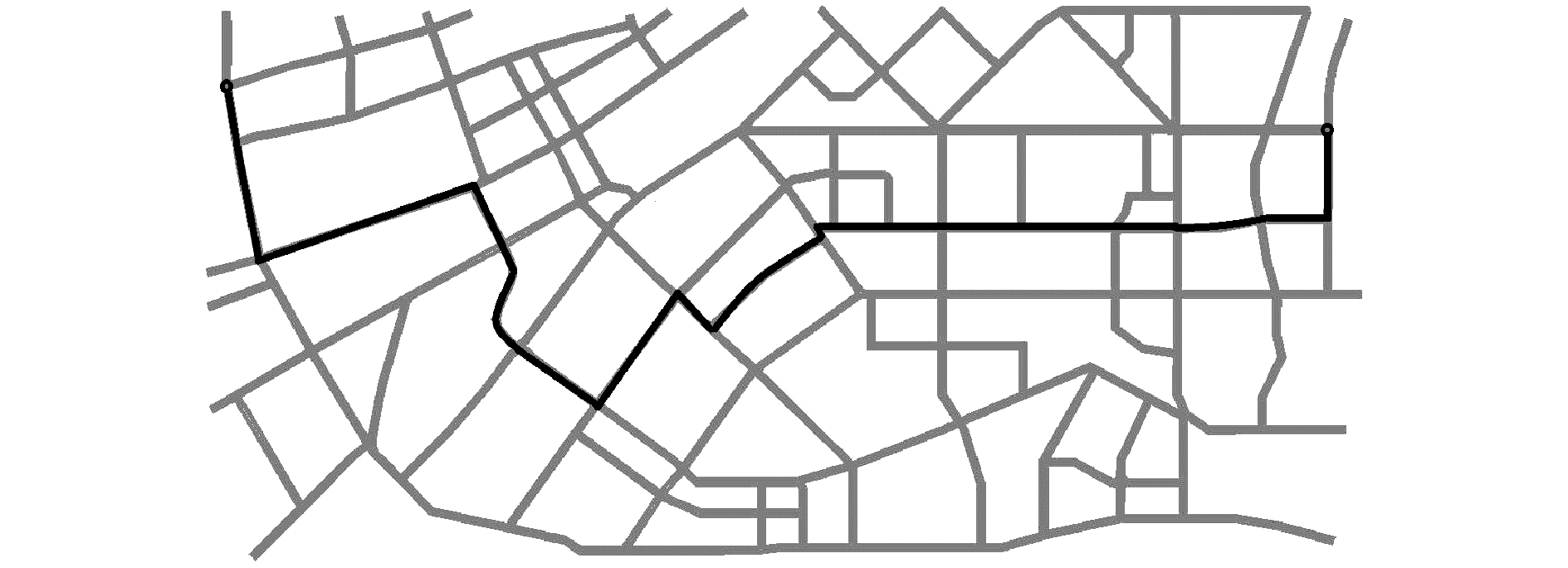
为进一步验证本模型的优势,在同等实验环境下,本文模型分别以不同时间权重系数下的最优路径与基于几何最短的最优路径进行了对比实验,如图 4~6中图例所示。其中,图 4为几何最短路径示意图,图 5、6是时间权重系数分别为1和0.5的最优路径。
|
图 4 道路畅通情形下的几何最短路径 Fig.4 Geometric shortest path under the smoother of road traffic |
|
图 5 道路畅通情形下wz=1的基于多目标的路径选择模型的最优路径 Fig.5 The optimal path of wz =1 based on multi-objective under smoother of road traffic |
|
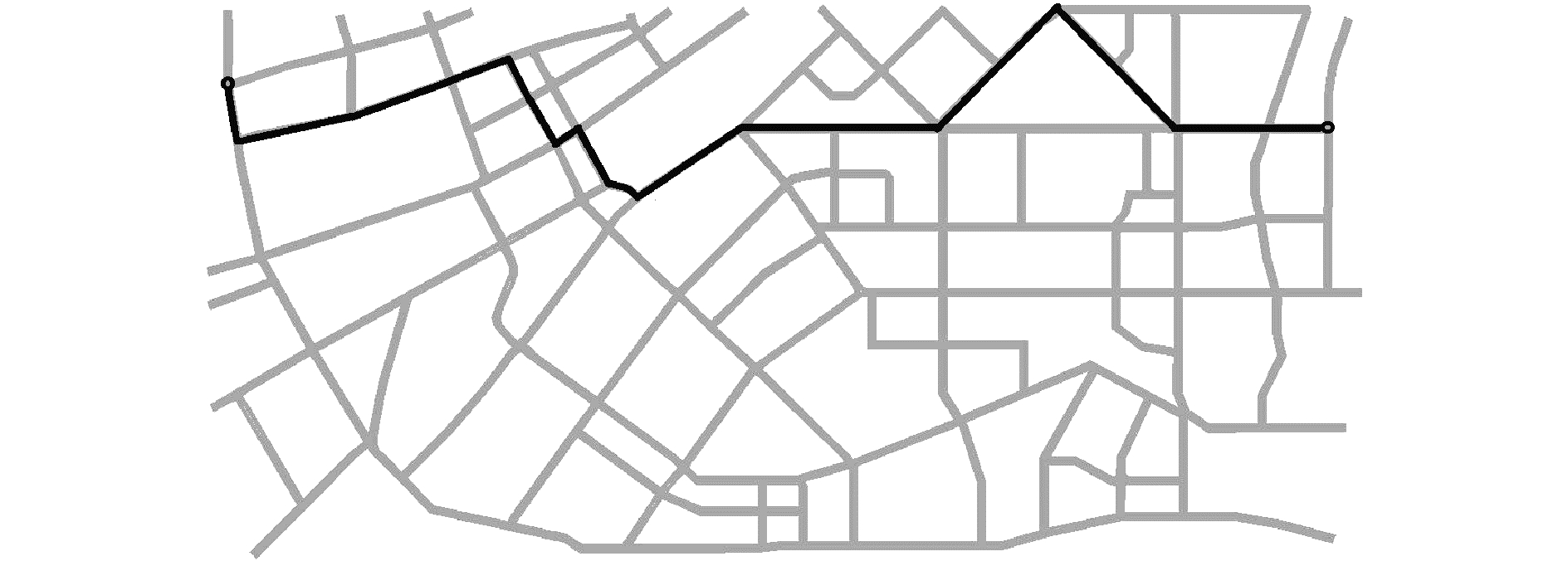
图 6 道路畅通情形下wz=0.5的基于多目标的路径选择模型的最优路径 Fig.6 The optimal path of wz=0.5 based on multi-objective under smoother of road traffic |
由图 4~6可知,几何最短路径的距离明显优于多目标模型。为进一步说明上述结果,本文分别从距离、时间、费用等参数进行了对比实验,其结果如表 1所示。
| 表 1 道路畅通情形下的对比实验 Tab.1 Contrast experiment under smoother of road traffic |
对比表 1列出的基于两种模型下最优路径的距离,可以进一步验证上述图 4~6结果。针对基于几何距离最短的路径选择模型而言,优化是以距离最短为目标。所以,基于几何距离最短的模型下,最优路径的距离最短。
尽管基于几何距离最短的路径选择模型在距离上占优多目标模型,但由表 1中时间、费用等参数可以看出,多目标模型在时间、费用上均优于对比模型。其原因是由于影响路阻的因素多样化,如行驶时间、交叉口等待时间等。在道路畅通但未达到拥挤如交通密度达到临界的情形下,在交叉口等红灯的几率明显增加,相应的延误时间就会增加,而行驶速度相对较慢导致行驶时间增加,因而路阻增加。而且,燃油费用与距离、速度密切相关,其距离与速度间存在正相关的特性,因此费用也增加。所以,在实时环境下,当图 4所示的最优路径上的车流量增加时,车辆在交叉口的等待时间及行驶时间均增加,而行驶速度减小导致费用的增加。由此可见,在实时环境下,以最短距离作为优化目标并不合理,而建立基于多目标的路径选择模型具有更高的实用价值。
为进一步验证组合优化函数模型的有效性,在本实例中,分别以时间权重系数为1(如图 5)和0.5(如图 6)对比实验。图 5的距离大于图 6的距离且与实例结果如表 1相一致,但由表 1中可以看出随着时间权重系数的减少,费用权重系数的增加,权重系数为1的最优路径的路阻占优于图 6所示的路径,但费用劣于时间权重系数为0.5的最优路径。由于各权重系数的变化产生不同的优化结果是组合权重的目的,因此,实验结果符合加权求和函数的意义。从而,进一步证明了本文的组合权重函数模型的合理性、易实现性以及在实时环境下可满足出行者需求的多样化。
3.4.2 道路拥挤情形下的对比实验为进一步验证基于多目标的路径选择模型的性能,在道路阻塞的情形下,对多目标模型进行了对比实验。在反复多组实验的基础上,选取结点1~39为一组实例进行实验分析。为验证组合优化函数的有效性,在本实例下,同样地,时间权重系数wz以0.1为间隔在0~1取值。在相同的实验环境下,组合权重与优化结果的映射关系(以费用与时间的比值为优化结果)如图 7所示。
|
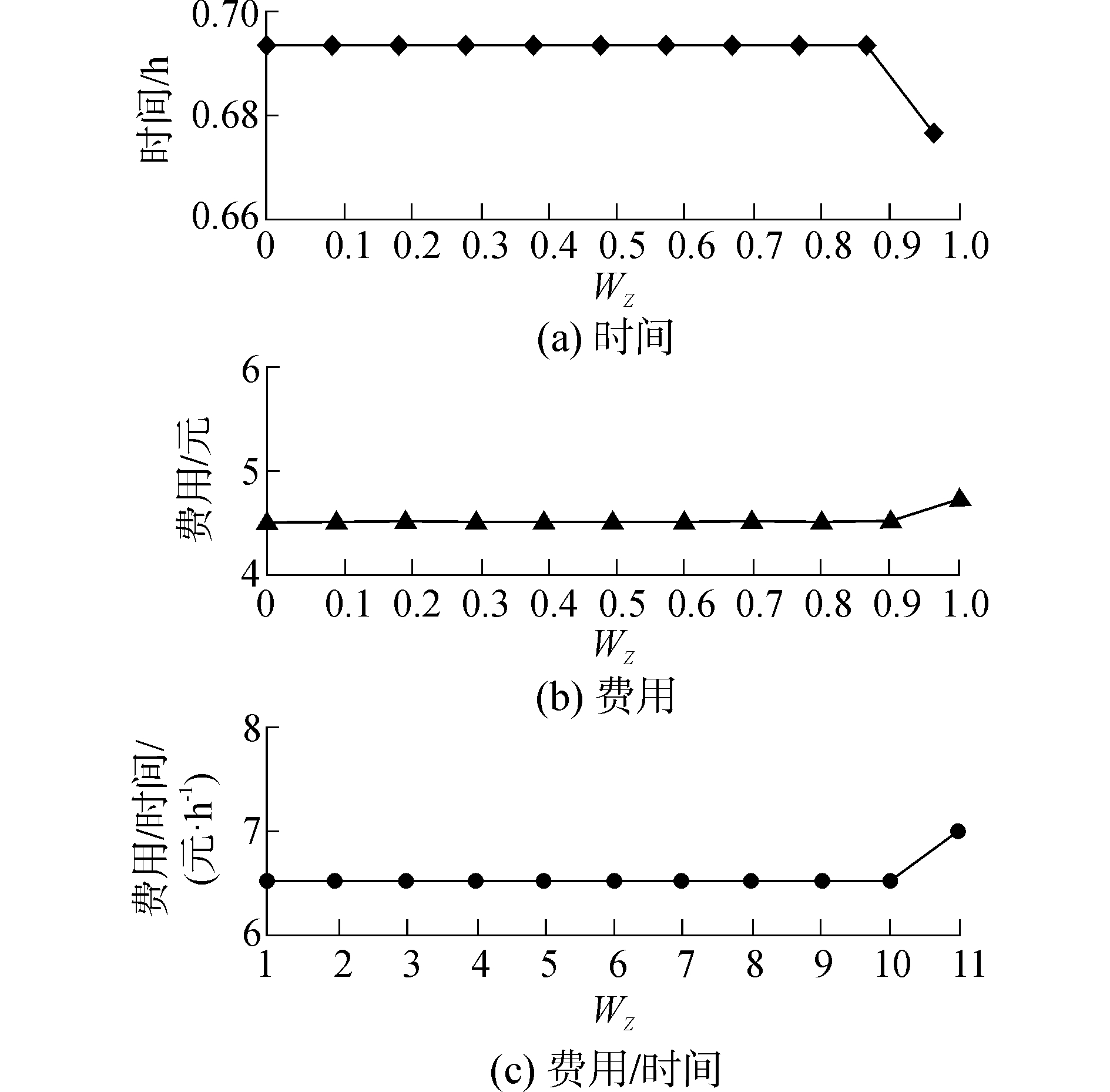
图 7 道路拥挤情形下组合权重与优化结果映射关系 Fig.7 The mapping relationship between combination weights and the optimization results under congestion of road traffic |
由图 7中可知,权重系数在0~0.9的费用、时间以及两者比值持平,仅在0.9~1间费用及两者比值处于上升趋势而时间略有减少。由于K系数的约束控制,优先扩展畅通区域而拥挤区域结点被保存在临时队列中。因此,与道路畅通情形下相比,其可扩展的区域明显减小,从而导致结果重合的概率增大。解集的多样性受到影响,但有效避免进入拥挤区域,从而提高出行的可靠性,缓解交通压力以及减少环境污染。但在图 7中,费用与时间的比值整体是上升趋势,符合加权求和函数的一般规律。因此,在拥挤情形下,组合优化函数模型符合加权求和函数的意义。
为进一步诠释本模型的合理性,在相同实验环境下,基于多目标的路径选择模型分别以时间权重系数为0.8和0的最优路径如图 8、9所示与几何最短路径如图 10进行了对比实验。图示中黑色加重为最优路径,矩形标注为拥挤区域。
|
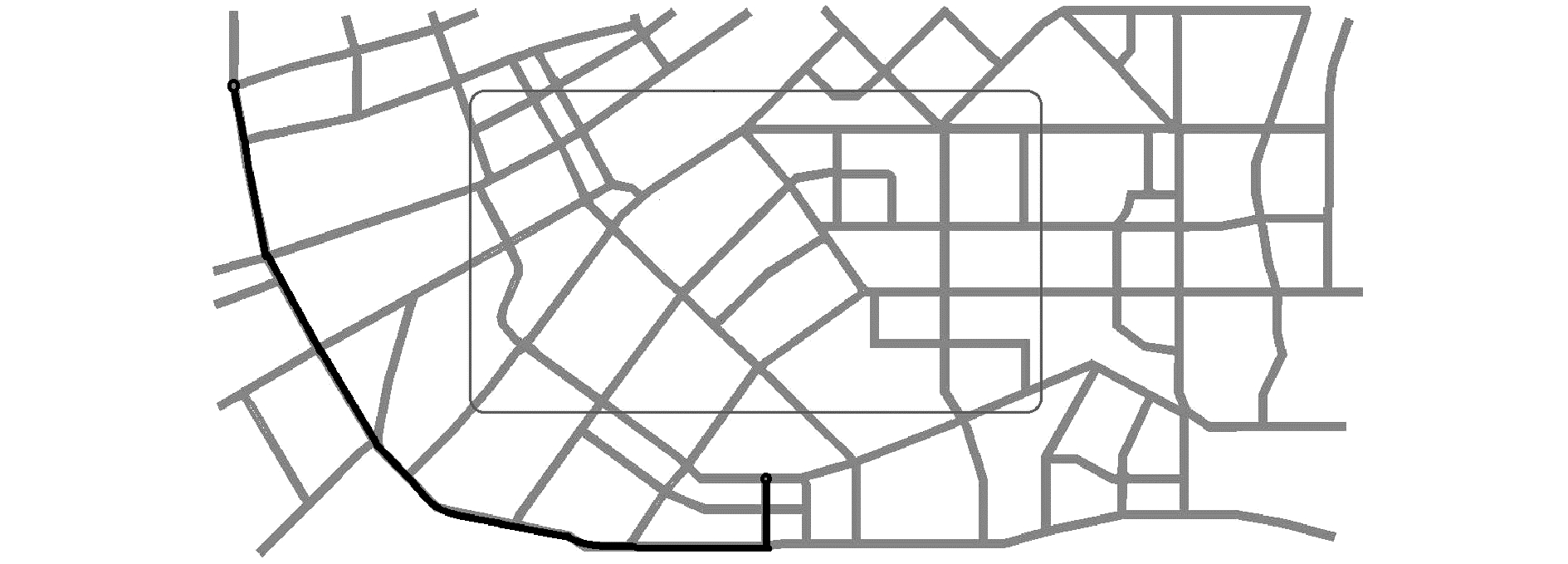
图 8 拥挤情形下wz=0.8基于多目标的路径选择模型的最优路径 Fig.8 The optimal path of wz=0.8 based on multi-objective under congestion of road traffic |
|
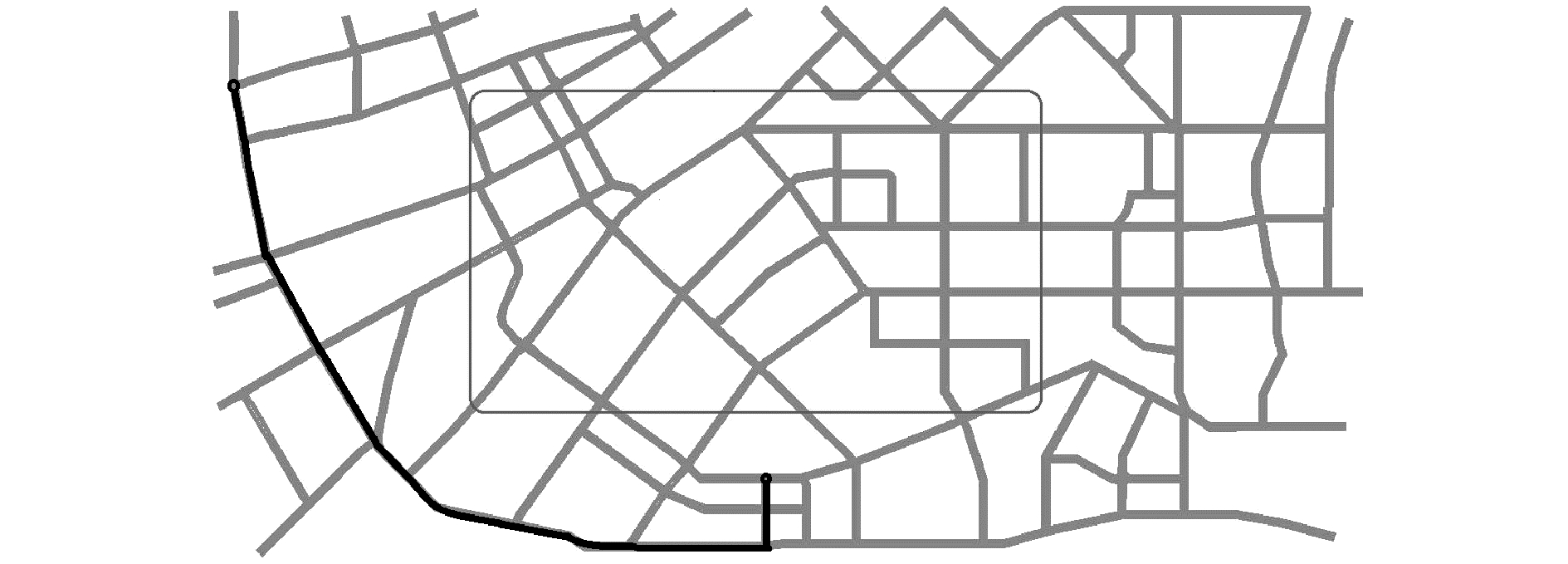
图 9 拥挤情形下wz=0基于多目标的路径选择模型的最优路径 Fig.9 The optimal path of wz=0 based on multi-objective under congestion of road traffic |

|
图 10 道路拥挤情形下的几何最短路径 Fig.10 Geometric shortest path under the congestion of road traffic |
在道路拥挤的情形下,采用约束系数K的控制策略,基于多目标的路径选择模型得到的最优路径均有效避免拥挤区域,但距离略长于基于几何距离的路径选择模型。而当权重系数分别为0.8和0时,图 8、9的最优路径相同。当各权重系数不同而结果相同时,产生原因有两种:一种是各决策变量的阈值相差大,组合权重函数对权重系数不敏感;而另一种就是当前最优路径是唯一的,即不同权重系数的组合产生了同样的结果。在求解算法中,针对各决策变量的阈值进行了预处理且已证明其有效性,所以原因归结于结果重合。为更充分地说明问题,以距离、时间、费用等为参数进行了对比实验,其结果如表 2所示。
| 表 2 道路拥挤情形下的对比实验 Tab.2 Contrast experiment under the congestion of road traffic |
由表 2中同时列出的基于两种不同模型给出的最优路径的距离、时间以及费用等指标。实验结果表明,基于几何路径最短的模型下的最优路径距离最短,但基于多目标的路径选择模型在时间、费用上均甚优于最短距离。由于在交通拥挤的情形下,车辆间的相互延误导致行驶速度缓慢,尤其,当交通达到堵塞时,交通滞留导致行驶速度为0。因此,当最短路径在拥挤区域时,延误时间增加导致路阻明显增加;速度迟缓也导致燃油费增加,且当处于拥挤区内时拥挤费增加,从而导致费用的明显增加。而多目标模型在系数K的约束控制下,有效避免了进入拥挤区域,从而时间、费用均明显占优于最短路径。但若目标结点处于拥挤区域时,由于本文以组合权重为优化目标,即以时间和费用组合的权重为诱导因素,且在求解中采用临时优先队列保存拥挤区域结点的策略。所以,基于多目标的模型得到的最优路径在时间、费用上均占优于最短路径。因此,可得到以下结论:在道路拥挤的情形下,基于多目标的路径选择模型比基于几何最短的路径选择模型更具有实用价值。
4 结论1) 采用迭代取最高位的策略,对组合优化函数中的决策变量进行类似的量值处理后,组合权重与最优解之间的映射更符合要求且结果优于未预处理的解。所以,基于多目标的路径选择模型能满足出行者多样化的需求。
2) 在道路畅通的情形下,基于多目标的路径选择模型的路径在时间、费用上均优于基于几何最短模型的路径。
3) 在道路拥挤的情形下,由于K系数的约束可以有效避免车辆进入拥挤区域。所以,基于本文模型的最优路径在时间、费用上均明显甚优于几何最短距离。
总之,基于多目标的路径选择模型比基于几何最短的路径选择模型更具有实用价值。
| [1] |
KIM G, ONG Y S, HENG C K, et al. City vehicle routing problem (city vrp):A review[J]. IEEE transactions on intelligent transportation systems, 2015, 16(4): 1654-1666. DOI:10.1109/TITS.2015.2395536 ( 0) 0)
|
| [2] |
郑祖舵. 动态路径优化关键技术研究[D]. 长春: 吉林大学, 2006: 5-7. ZHENG Zuduo. Research on key technologies of the dynamic route optimization[D]. Changchun:Jilin University, 2016:5-7. http://cdmd.cnki.com.cn/Article/CDMD-10183-2006108847.htm (  0) 0)
|
| [3] |
AVINERI E, PRASHKER J N. Sensitivity to travel time variability:travelers' learning perspective[J]. Transportation research part C:emerging technologies, 2005, 13(2): 157-183. DOI:10.1016/j.trc.2005.04.006 ( 0) 0)
|
| [4] |
孟梦, 邵春福, 曾靖静, 等. 考虑出发时间的组合出行动态路径选择模型[J]. 中南大学学报:自然科学版, 2014, 45(10): 3676-3684. MENG Meng, SHAO Chunfu, ZENG Jingjing, et al. Dynamic route choice model with departure time in combined trip[J]. Journal of Central South University:science and technology, 2014, 45(10): 3676-3684. (  0) 0)
|
| [5] |
刘艳秋, 刘博. 交通拥堵下基于实时交通信息的路径选择模型[J]. 沈阳工业大学学报, 2014, 36(4): 426-430. LIU Yanqiu, LIU Bo. Route selection model based onreal-time traffic information under traffic congestion[J]. Journal of Shenyang University of Technology, 2014, 36(4): 426-430. DOI:10.7688/j.issn.1000-1646.2014.04.13 (  0) 0)
|
| [6] |
吴磊. 车辆自组织网络环境下动态路径诱导系统的建模与优化策略研究[D]. 济南: 山东大学, 2014: 22-24. WU Lei. Modeling and optimization of dynamic route guidance system under vehicular Ad-Hoc networks[D]. Jinan:Shandong University, 2014:22-24. http://cdmd.cnki.com.cn/Article/CDMD-10422-1015532010.htm (  0) 0)
|
| [7] |
刘玉印, 刘伟铭, 吴建伟. 基于累积前景理论的出行者路径选择模型[J]. 华南理工大学学报:自然科学版, 2010, 38(7): 84-89. LIU Yuyin, LIU Weiming, WU Jianwei. A route selection model based on cumulative prospect theory[J]. Journal of South China University of Technology:natural science edition, 2010, 38(7): 84-89. (  0) 0)
|
| [8] |
吴磊, 杨立才. 基于前景理论的实时路径选择模型[J]. 控制理论与应用, 2013, 30(7): 916-921. WU Lei, YANG Licai. Prospect theory-based route choice model in dynamic route guidance system[J]. Control theory & applications, 2013, 30(7): 916-921. (  0) 0)
|
| [9] |
张波, 隽志才, 林徐勋. 基于累积前景理论的随机用户均衡交通分配模型[J]. 西南交通大学学报, 2011, 46(5): 868-874. ZHANG Bo, JUN Zhicai, LIN Xuxun. Stochastic user equilibrium model based on cumulative prospect theory[J]. Journal of Southwest Jiaotong University, 2011, 46(5): 868-874. (  0) 0)
|
| [10] |
AVINERI E, PRASHKER J N. Sensitivity to travel time variability:travelers' learning perspective[J]. Transportation research part C:emerging technologies, 2005, 13(2): 157-183. DOI:10.1016/j.trc.2005.04.006 ( 0) 0)
|
| [11] |
WAHLE J, ANNEN O, SCHUSTER C, et al. A dynamic route guidance system based on real traffic data[J]. European journal of operational research, 2001, 131(2): 302-308. DOI:10.1016/S0377-2217(00)00130-2 ( 0) 0)
|
| [12] |
徐鹤鸣. 多目标粒子群优化算法的研究[D]. 上海: 上海交通大学, 2013: 45-46. XU Heming. Research on Multi-objective particle swarm optimization algorithms[D]. ShangHai:Shanghai Jiao Tong University, 2013:45-46. http://cdmd.cnki.com.cn/Article/CDMD-10248-1013020723.htm (  0) 0)
|
| [13] |
杨雅君, 高宏, 李建中. 多维代价图模型上最优路径查询问题的研究[J]. 计算机学报, 2012, 35(10): 2147-2158. YANG Yajun, GAO Hong, LI Jianzhong. Optimal path query based on cost function over multi-cost graphs[J]. Chinese journal of computers, 2012, 35(10): 2147-2158. (  0) 0)
|
| [14] |
MARLER R T, ARORA J S. The weighted sum method for multi-objective optimization:new insights[J]. Structural and multidisciplinary optimization, 2010, 41(6): 853-862. DOI:10.1007/s00158-009-0460-7 ( 0) 0)
|
| [15] |
WAHLE J, ANNEN O, SCHUSTER C, et al. A dynamic route guidance system based on real traffic data[J]. European journal of operational research, 2001, 131(2): 302-308. DOI:10.1016/S0377-2217(00)00130-2 ( 0) 0)
|
| [16] |
王素欣, 王雷震, 高利, 等. BPR路阻函数的改进研究[J]. 武汉理工大学学报:交通科学与工程版, 2009, 33(3): 446-449. WANG Suxin, WANG Leizhen, et al. Improvement of BPR path resistance function[J]. Journal of Wuhan University of Technology:transportation science & engineering, 2009, 33(3): 446-449. (  0) 0)
|
| [17] |
SUN X, KOENIG S, YEOH W. Generalized adaptive A*[C]//Proceedings of the 7th international joint conference on Autonomous agents and multiagent systems-Volume 1. International Foundation for Autonomous Agents and Multiagent Systems, 2008:469-476.
( 0) 0)
|
| [18] |
冯雨芹. 基于交通流状态的城市道路燃油经济性模型研究[D]. 哈尔滨: 哈尔滨工业大学, 2011: 31-32. FENG Yuqin. Research on fuel economy model of urban road based on traffic flow status[D]. Harbin:Harbin Institute of Technology, 2011:31-32. http://cdmd.cnki.com.cn/Article/CDMD-10213-1012000492.htm (  0) 0)
|
| [19] |
隗海林, 王劲松, 王云鹏, 等. 基于城市道路工况的汽车燃油消耗模型[J]. 吉林大学学报:工学版, 2009, 39(5): 1146-1150. KUI Hailin, WANG Jinsong, WANG Yunpeng, et al. Vehicle fuel consumption model based on urban road operations[J]. Journal of Jilin University:engineering and technology edition, 2009, 39(5): 1146-1150. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


