近年来,非线性系统的研究备受关注。特别是针对一类具有严格反馈形式的非线性系统,已经取得了很多研究成果。其中,反步法是解决这类系统控制器设计问题的重要方法,以及与自适应等相结合的反步法技术已经比较成熟[1-3]。但对于高阶系统而言,反步法存在缺陷,对虚拟控制量求导的过程中会出现“微分爆炸”现象。韩京清提出了自抗扰控制器,介绍了自抗扰控制器的应用。验证了自抗扰控制器的适应性和鲁棒性,并给出了自抗扰控制器的最大特点[4]。Swaroop对传统反步法进行了改进,提出了动态面控制算法[5],该方法在非线性系统中得到了广泛的应用。文献[6]将动态面控制方法应用到了船舶的航向控制中,并验证了该控制方法的有效性。文献[7]针对201起重船装载作业过程中模型参数不确定及存在未知扰动问题设计了动态面自抗扰控制器,验证了该算法具有强抗干扰能力及对模型参数变化具有强鲁棒性。
基于以上的研究成果,本文采用动态面自抗扰控制技术对具有严格反馈形式的非线性系统进行控制器设计。该控制器避免了传统反步法中出现的“微分爆炸”现象,并对系统的未建模部分或者未知部分进行实时估计,然后根据估计量的大小对系统的实际控制量进行相应的补偿,使得控制器具有更强的鲁棒性。同时,该控制器的设计具有一般标准形式,对于类似的非线性系统均适用,因此,该控制器体现了很强的工程实用价值。
1 动态面自抗扰控制器设计 1.1 系统描述考虑如下单输入单输出系统:
| $ \left\{ \begin{array}{l} {{\dot x}_i} = {x_{i + 1}},\;\;\;i = 1,2, \cdots ,n - 1\\ {{\dot x}_n} = f\left( {{x_1},{x_2}, \cdots ,{x_n}} \right) + bu\\ y = {x_1} \end{array} \right. $ | (1) |
式中:xi(i=1, 2, …, n-1) 为系统的状态变量;f(·)为系统的非线性部分,表示系统的未建模部分或者系统的不确定性;y和u分别为系统的输入和输出,b为输入增益。该系统的控制目标是实现系统的状态跟踪,即设计控制律u使得系统的输出y跟踪上期望信号yd,这里假设期望信号yd是n阶可微并且有界的函数。
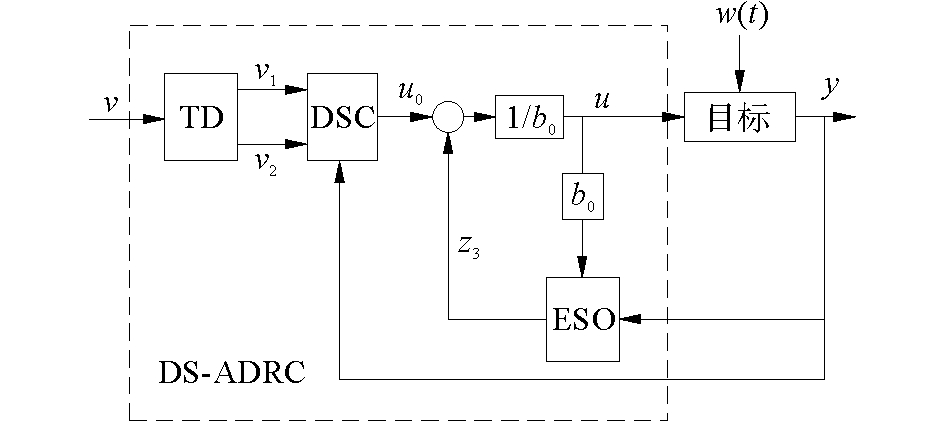
1.2 控制器设计动态面自抗扰控制器由四部分组成,分别为跟踪微分器(tracking differentiator, TD)、扩张状态观测器(extended state observer, ESO)、动态面控制律(dynamic surface control, DSC)、动态扰动补偿(dynamic compensation, DC)。控制器的原理如图 1所示。
|
图 1 动态面自抗扰控制器原理 Fig.1 Principle of dynamic surface autodisturbance rejection controller |
TD的主要作用是安排过渡过程,其设计思路是利用一个惯性环节来尽快(通常选取较小的时间常数即可实现,但不宜过小,需根据系统的实际要求)地跟踪上期望信号,并获取期望信号的微分值,即一边尽快地跟踪上期望,同时给出其近似微分。
对于上述系统,根据系统的期望信号yd,安排系统的跟踪过渡过程v1,并提取其微分信号v2。为了计算方便,该算法通常选用离散形式,具体表达式为
| $ \left\{ \begin{array}{l} {f_h} = {f_h}\left( {{v_1}\left( k \right) - {y_d}\left( k \right),{v_2}\left( k \right),r,h} \right)\\ {v_1} = \left( {k + 1} \right) = {v_1}\left( k \right) + h{v_2}\left( k \right)\\ {v_2} = \left( {k + 1} \right) = {v_2}\left( k \right) + h{f_h} \end{array} \right. $ | (2) |
式中:fh(x1, x2, r, h)为最速控制综合函数,动态面自抗扰控制算法如下:
| $ \left\{ \begin{array}{l} d = rh\\ {d_0} = hd\\ y = {x_1} + h{x_2}\\ {a_0} = \sqrt {{d^2} + 8r\left| y \right|} \\ a = \left\{ \begin{array}{l} {x_2} + \frac{{\left( {{a_0} - d} \right)}}{2}{\rm{sign}}\left( y \right),\;\;\;\;\left| y \right| > {d_0}\\ {x_2} + \frac{y}{h},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| y \right| \le {d_0} \end{array} \right.\\ {f_h} = \left\{ \begin{array}{l} - r\;{\rm{sign}}\left( a \right),\;\;\;\;\left| a \right| > d\\ - r\frac{a}{d},\;\;\;\;\;\;\;\;\;\;\;\;\left| a \right| \le d \end{array} \right. \end{array} \right. $ | (3) |
式中:参数r为跟踪速度的速度因子,参数r选取的越大,跟踪期望信号的速度就越快,反之,则跟踪期望信号的速度就越慢;参数h为TD的积分步长。
1.2.2 扩张状态观测器设计对于控制系统中存在的扰动,如果这种扰动不能从被控对象的输出观测到,或者说这种扰动不能控制被控输出,那么在控制系统的设计中可以不用考虑这部分扰动;反之,如果这种扰动可以在被控对象的输出观测到,那么在控制系统的设计过程中必须考虑扰动对系统的影响,并尽可能的消除扰动的影响。ESO将系统的总扰动扩张成新的一维系统状态,并对其进行观测。
针对上述系统(1),现将该系统的未知非线性函数f(x1, x2, …, xn)扩张成新的一维状态,设xn+1=f(x1, x2, …, xn),则上述系统可写成
| $ \left\{ \begin{array}{l} {{\dot x}_i} = {x_{i + 1}},\;\;i = 1, \cdots ,n - 1\\ {{\dot x}_n} = {x_{n + 1}} + bu\\ {{\dot x}_{n + 1}} = \zeta \left( t \right)\\ y = {x_1} \end{array} \right. $ | (4) |
对于上述系统,设计状态观测器,对系统的状态xi, i=1, 2, …, n+1进行观测,设观测值为zi, i=1, 2, …, n+1,扩张观测器的离散形式为
| $ \left\{ \begin{array}{l} e\left( k \right) = {z_1}\left( k \right) - y\left( k \right)\\ {z_1}\left( {k + 1} \right) = {z_1}\left( k \right) + h\left( {{z_2}\left( k \right) - {\beta _1}e\left( k \right)} \right)\\ {z_2}\left( {k + 1} \right) = {z_2}\left( k \right) + h\left( {{z_3}\left( k \right) - } \right.\\ \;\;\;\;\;\;\;\left. {{\beta _2}{\rm{fal}}\left( {e\left( k \right),\frac{1}{2},\delta } \right)} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {z_n}\left( {k + 1} \right) = {z_n}\left( k \right) + h\left( {{z_{n + 1}}\left( k \right) - } \right.\\ \;\;\;\;\;\;\;\;\left. {{\beta _n}{\rm{fal}}\left( {e\left( k \right),\frac{1}{{{2^{n - 1}}}},\delta } \right) + bu\left( k \right)} \right)\\ {z_{n + 1}}\left( {k + 1} \right) = {z_{n + 1}}\left( k \right) + \\ \;\;\;\;\;\;\;h\left( { - {\beta _{n + 1}}{\rm{fal}}\left( {e\left( k \right),\frac{1}{{{2^n}}},\delta } \right)} \right) \end{array} \right. $ | (5) |
式中:β1, β2, …, βn+1分别为扩张观测器的待设计参数,函数fal(e, α, δ)为原点附近具有线性段的连续的幂次函数,其具体算法表示为
| $ {\rm{fal}}\left( {e,\alpha ,\delta } \right) = \left\{ \begin{array}{l} \frac{e}{{{\delta ^{1 - \alpha }}}},\;\;\;\;\;\;\;\;\left| e \right| \le \delta \\ {\left| e \right|^\alpha }{\rm{sign}}\left( e \right),\;\;\;\;\left| e \right| > \delta \end{array} \right. $ | (6) |
式中:δ为线性区间的长度。
1.2.3 动态面控制器设计对于系统(1),为了动态面控制器设计,假设u0=f(x1, x2, …, xn)+bu或者bu0=f(x1, x2, …, xn)+bu,则系统(1) 可转化为如下系统:
| $ \left\{ \begin{array}{l} {{\dot x}_i} = {x_{i + 1}},\;\;\;i = 1, \cdots ,n - 1\\ {{\dot x}_n} = {u_0}/{{\dot x}_n} = b{u_0}\\ y = {x_1} \end{array} \right. $ | (7) |
对于上述系统,进行动态面控制器设计:
1) 对于第一个子系统
首先,定义第一个动态面:
| $ {S_1} = {x_1} - {y_d} $ | (8) |
对其求导,并结合式(7) 可以得到:
| $ {{\dot S}_1} = {{\dot x}_1} - {{\dot y}_d} $ | (9) |
为了镇定式(9) 选取x2为虚拟控制量,设计虚拟控制律α2:
| $ {{\bar \alpha }_2} = - {k_1}{S_1} + {{\dot y}_d} $ | (10) |
式中:k1为待设计的参数,且有k1>0。结合动态面的设计思路,引入一个一阶低通滤波器:
| $ {\tau _2}{{\dot \alpha }_2} + {\alpha _2} = {{\bar \alpha }_2},\;\;{\alpha _2}\left( 0 \right) = {{\bar \alpha }_2}\left( 0 \right) $ | (11) |
式中:τ2为待设计滤波器的时间常数,且有τ2>0;α2为滤波器的输出。
2) 对于第二个子系统
这里定义第二个动态面:
| $ {S_2} = {x_2} - {\alpha _2} $ | (12) |
对其求导,并结合式(7) 可以得到:
| $ {{\dot S}_2} = {x_3} - {{\dot \alpha }_2} $ | (13) |
为了镇定式(13),选取x3为虚拟控制量,设计虚拟控制律α3:
| $ {{\bar \alpha }_3} = - {k_2}{S_2} + {{\dot \alpha }_2} $ | (14) |
式中:k2为待设计参数,且有k2>0。根据动态面的设计思想,再次引入一个一阶低通滤波器:
| $ {\tau _3}{{\dot \alpha }_3} + {\alpha _3} = {{\bar \alpha }_3},\;\;{\alpha _3}\left( 0 \right) = {{\bar \alpha }_3}\left( 0 \right) $ | (15) |
式中:τ3为待设计的滤波器时间常数,且有τ3>0;α3为滤波器的输出。
| $ {S_i} = {x_i} - {\alpha _i} $ | (16) |
对其求导,并结合式(7) 可以得到:
| $ {{\dot S}_i} = {x_{i + 1}} - {{\dot \alpha }_i} $ | (17) |
为了镇定式(17),选取xi+1为虚拟控制量,设计虚拟控制律αi+1:
| $ {{\bar \alpha }_{i + 1}} = - {k_i}{S_i} + {{\dot \alpha }_i} $ | (18) |
式中:ki为待设计参数,且有ki>0。根据动态面的设计思想,这里再次引入一个一阶低通滤波器:
| $ {\tau _{i + 1}}{{\dot \alpha }_{i + 1}} + {\alpha _{i + 1}} = {{\bar \alpha }_{i + 1}},\;\;{\alpha _{i + 1}}\left( 0 \right) = {{\bar \alpha }_{i + 1}}\left( 0 \right) $ | (19) |
式中:τi+1为待设计的滤波器时间常数,且有τi+1>0,αi+1为滤波器的输出。
n)对于最后一个子系统
这里定义第n个动态面:
| $ {S_n} = {x_n} - {\alpha _n} $ | (20) |
对其求导,并结合式(7) 可以得到:
| $ {{\dot S}_n} = {u_0} - {{\dot \alpha }_n} $ | (21) |
镇定式(21),从而得到控制律u0:
| $ {u_0} = - {k_n}{S_n} + {{\dot \alpha }_n} $ | (22) |
式中:kn为待设计参数,且有kn>0。
1.3 扰动补偿设计为了保证在所设计的控制律作用下,系统在扰动过程中仍然能跟踪上期望信号,需要对上述独立设计的控制律进行相应的扰动补偿。本文中将由状态扩张观测器观测到的扰动值补偿到动态面控制律中。针对上述系统,系统的扰动值为zn+1,补偿到动态面控制律u0中,最终决定实际控制律u,表达式为
| $ u = {u_0} - {z_{n + 1}}/b\;或者\;u = \left( {{u_0} - {z_{n + 1}}} \right)/b $ | (23) |
式中:b是系统的补偿参数,即上述系统中的控制输入增益。
2 稳定性分析 2.1 扩张状态观测器稳定性分析对于扩张状态观测器(5) 的稳定性分析,类似于一阶系统的分析,为了分析方便,现考虑如下一阶非线性系统:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = f\left( {{x_1}} \right) + bu\\ y = {x_1} \end{array} \right. $ | (24) |
式中:f(x1)为非线性部分。
对该系统建立扩张观测器,得到观测器的误差模型为
| $ \left\{ \begin{array}{l} {e_1} = {z_1} - {x_1}\\ {e_2} = {z_2} - {x_2}\\ {{\dot e}_1} = {e_2} - {\beta _1}{e_1}\\ {{\dot e}_2} = \zeta \left( t \right) - {\beta _2}{f_e} \end{array} \right. $ | (25) |
式中:ζ(t)为f(x1)的导数,并且有ζ(t)≤w0,w0为一常数fe=fal(e, a, δ)。
根据式(25),对(e1, e2)进行划分,如图 2所示。

|
图 2 (e1, e2)划分图 Fig.2 (e1, e2)partition area |
图 2中,
| $ \left\{ \begin{array}{l} {A_0} = \left\{ {\left( {{e_1},{e_2}} \right)\left| {\left| {{e_1}} \right| < {c_0},\frac{{{\beta _1}}}{2}\left( {{e_1} - {c_0}} \right) \le {e_2} \le } \right.} \right.\\ \left. {\frac{{{\beta _1}}}{2}\left( {{e_1} + {c_0}} \right)} \right\}\\ {A_1} = \left\{ {\left( {{e_1},{e_2}} \right)\left| {{e_1} > {c_0},0 \le {e_2} \le {\beta _1}{e_1}} \right.} \right\}\\ {A_2} = \left\{ {\left( {{e_1},{e_2}} \right)\left| {{e_2} > 0,{e_2} \ge \frac{{{\beta _1}}}{2}\left( {{e_1} + {c_0}} \right),} \right.} \right.\\ \left. {{e_2} \ge {\beta _1}{e_1}} \right\}\\ {A_3} = \left\{ {\left( {{e_1},{e_2}} \right)\left| {{e_1} < - {c_0},0 \ge {e_2} \ge {\beta _1}{e_1}} \right.} \right\}\\ {A_4} = \left\{ {\left( {{e_1},{e_2}} \right)\left| {{e_2} < 0,{e_2} \le \frac{{{\beta _1}}}{2}\left( {{e_1} - {c_0}} \right),} \right.} \right.\\ \left. {{e_2} \le {\beta _1}{e_1}} \right\} \end{array} \right. $ | (26) |
对于误差模型,为了证明其稳定性,即需证明图 2中区域A0是稳定的。根据非连续系统的多李亚普洛夫稳定性定理,只需证明图 2中区域Ai, i=1, 2,3, 4,均存在正定的李亚普洛夫函数Vi(e1, e2), i=1, 2,3, 4,并且有
| $ \left\{ \begin{array}{l} {V_1}\left( {{e_1},{e_2}} \right) = \frac{{{\beta _1}}}{2}\left( {{e_1} - {c_0}} \right),\;\;\left( {{e_1},{e_2}} \right) \in {A_1}\\ {V_2}\left( {{e_1},{e_2}} \right) = {e_2} - \frac{{{\beta _1}}}{2}\left( {{e_1} + {c_0}} \right),\;\;\left( {{e_1},{e_2}} \right) \in {A_2}\\ {V_3}\left( {{e_1},{e_2}} \right) = - \frac{{{\beta _1}}}{2}\left( {{e_1} + {c_0}} \right),\;\;\left( {{e_1},{e_2}} \right) \in {A_3}\\ {V_4}\left( {{e_1},{e_2}} \right) = - {e_2} + \frac{{{\beta _1}}}{2}\left( {{e_1} - {c_0}} \right),\;\;\left( {{e_1},{e_2}} \right) \in {A_4} \end{array} \right. $ | (27) |
对以上各李亚普洛夫函数求偏导,则有
| $ \left\{ \begin{array}{l} \left( {\frac{{\partial {V_1}}}{{\partial {e_1}}},\frac{{\partial {V_1}}}{{\partial {e_2}}}} \right) = \left( {\frac{{{\beta _1}}}{2},0} \right),\\ \left( {\frac{{\partial {V_2}}}{{\partial {e_1}}},\frac{{\partial {V_2}}}{{\partial {e_2}}}} \right) = \left( { - \frac{{{\beta _1}}}{2},1} \right)\\ \left( {\frac{{\partial {V_3}}}{{\partial {e_1}}},\frac{{\partial {V_3}}}{{\partial {e_2}}}} \right) = \left( { - \frac{{{\beta _1}}}{2},0} \right),\\ \left( {\frac{{\partial {V_4}}}{{\partial {e_1}}},\frac{{\partial {V_4}}}{{\partial {e_2}}}} \right) = \left( {\frac{{{\beta _1}}}{2}, - 1} \right) \end{array} \right. $ | (28) |
在区域A1中,有
| $ {{\dot V}_1}\left( {{e_1},{e_2}} \right) = \frac{{\partial {V_1}}}{{\partial {e_1}}}{{\dot e}_1} + \frac{{\partial {V_1}}}{{\partial {e_2}}}{{\dot e}_2} = \frac{{{\beta _1}}}{2}\left( {{e_2} - {\beta _1}{e_1}} \right) $ | (29) |
对于区域A1,有e2 < β1e1,即有
| $ {{\dot V}_1}\left( {{e_1},{e_2}} \right) < 0 $ | (30) |
在区域A3中,同理可得
对于区域A2,有
| $ \begin{array}{*{20}{c}} {{{\dot V}_2}\left( {{e_1},{e_2}} \right) = \frac{{\partial {V_2}}}{{\partial {e_1}}}{{\dot e}_1} + \frac{{\partial {V_2}}}{{\partial {e_2}}}{{\dot e}_2} = }\\ { - \frac{{{\beta _1}}}{2}\left( {{e_2} - {\beta _1}{e_1}} \right) + \left[ {\zeta \left( t \right) - {\beta _2}fe} \right]} \end{array} $ | (31) |
当|e1|>δ时,则有fe=|e1|0.5sign(e1),对于任意c>c0,在直线段e2=
| $ \begin{array}{*{20}{c}} {{{\dot V}_2}\left( {{e_1},{e_2}} \right) = \frac{{{\beta _1}}}{2}\left( {{e_2} - {\beta _1}{e_1}} \right) + \left[ {\zeta \left( t \right) - {\beta _2}fe} \right] = }\\ {\frac{{{\beta _1}}}{4}{e_1} - {\beta _2}{\rm{sign}}\left( {{e_1}} \right){{\left| {{e_1}} \right|}^{0.5}} + \zeta \left( t \right) - \frac{{\beta _1^2}}{4}c} \end{array} $ | (32) |
欲证
| $ \frac{{{\beta _1}}}{4}{e_1} - {\beta _2}{\rm{sign}}\left( {{e_1}} \right){\left| {{e_1}} \right|^{0.5}} + {w_0} - \frac{{\beta _1^2}}{4}c < 0 $ | (33) |
又因为|e1|≤c,故只需c满足:
| $ c > \max \left\{ {\frac{{4{w_0}}}{{\beta _1^2}},{{\left| {\frac{{{w_0}}}{{{\beta _2}}}} \right|}^2},\frac{1}{4}{{\left( {\frac{{4{\beta _2}}}{{\beta _1^2}}} \right)}^2} + \frac{{4{w_0}}}{{\beta _1^2}}} \right\} $ | (34) |
即可实现
当|e1|≤δ时,则有fe=
| $ c > \frac{4}{{\beta _1^2}}\left( {{w_0} - {\beta _2}{\delta ^\alpha }} \right) + \delta $ | (35) |
在区域A4中,同理可得在一定条件下
因此,对于上述扩张观测器模型,根据多李亚普洛夫理论可以证明该系统是稳定的,并且最终会收敛到区域A0中。
2.2 动态面稳定性分析定义误差变量e2=α2-α2,结合式(10)、(11),则有
| $ {e_2} = - {\tau _2}{{\dot \alpha }_2} $ | (36) |
对于动态面S1有
| $ {{\dot S}_1} = {S_2} + {\alpha _2} - {{\dot y}_d} $ | (37) |
结合式(35),则有:
| $ {{\dot S}_1} = {S_2} + {e_2} - {k_1}{S_1} $ | (38) |
再次定义误差变量ei=αi-αi,则有
| $ {e_i} = - {\tau _i}{{\dot \alpha }_i},i = 1, \cdots ,n - 1 $ | (39) |
同理可得
| $ {{\dot S}_i} = {S_{i + 1}} + {e_{i + 1}} - {k_i}{S_i} $ | (40) |
当i=n时,有
| $ {{\dot S}_n} = - {k_n}{S_n} $ | (41) |
结合式(18)、(19)、(20) 可以得到:
| $ \left\{ \begin{array}{l} {{\dot e}_2} = {{\dot \alpha }_2} + {k_1}{{\dot S}_1} - {{\ddot y}_d} = \\ \;\;\;\; - \frac{{{e_2}}}{{{\tau _2}}} + {g_1}\left( {{S_1},{S_2},{e_2},{k_1},{y_d},{{\dot y}_d},{{\ddot y}_d}} \right)\\ {{\dot e}_i} = {{\dot \alpha }_i} + {k_i}{{\dot S}_i} + \frac{{{e_{i - 1}}}}{{{\tau _{i - 1}}}} = \\ \;\;\;\; - \frac{{{e_i}}}{{{\tau _i}}} + {g_i}\left( {{S_1}, \cdots ,{S_{i + 1}},{e_2} \cdots {e_i},{k_1}, \cdots ,{k_i},{\tau _2},} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. { \cdots ,{\tau _i},{y_d},{{\dot y}_d},{{\ddot y}_d}} \right),i = 2,3, \cdots ,n \end{array} \right. $ | (42) |
其中, g1=k1
定义:
| $ {V_{is}} = \frac{{S_i^2}}{2},i = 1,2, \cdots ,n $ | (43) |
| $ {V_{ie}} = \frac{{e_i^2}}{2},i = 2,3, \cdots ,n $ | (44) |
结合式(39)、(40) 可以得到:
| $ \left\{ \begin{array}{l} {{\dot V}_{is}} = {S_i}\left( {{S_{i + 1}} + {e_{i + 1}} - {k_i}{S_i}} \right) = \\ \;\;\;\; - {k_i}S_i^2 + {S_i}{S_{i + 1}} + {S_i}{e_{i + 1}},i = 1, \cdots ,n - 1\\ {{\dot V}_{ns}} = - {k_n}S_n^2 \end{array} \right. $ | (45) |
结合式(41) 可以得到:
| $ {{\dot V}_{ie}} = - \frac{{e_i^2}}{{{\tau _i}}} + {e_i}{g_i},i = 2,3, \cdots ,n $ | (46) |
这里定义李亚普洛夫函数:
| $ V = \sum\limits_{i = 1}^n {{V_{is}}} + \sum\limits_{j = 2}^n {{V_{je}}} $ | (47) |
在此,不妨做如下假设:
| $ S_1^2 + e_2^2 + \cdots + S_{n - 1}^2 + e_n^2 + S_n^2 \le 2p $ | (48) |
| $ {g_i} \le C $ | (49) |
式中:p为任何正数,C为函数gi的最大值。
取控制器增益参数ki=2+a,一阶低通滤波器的时间常数为τi=1+(C2/2ε)+a,则有
| $ \begin{array}{l} \dot V \le \left. { - \left( {2 + a} \right)\sum\limits_{i = 1}^n {S_i^2} } \right) + \sum\limits_{i = 1}^{n - 1} {\left[ {\frac{{2S_i^2 + S_{i + 1}^2 + e_{i + 1}^2}}{2} + } \right.} \\ \;\;\;\;\;\;\left. {\left( {1 + \frac{{{C^2}}}{{2\varepsilon }} + a} \right)e_{i + 1}^2 + \frac{{{C^2}e_{i + 1}^2}}{{2\varepsilon }}\frac{{g_i^2}}{{{C^2}}}} \right] + \frac{{\left( {n - 1} \right)\varepsilon }}{2} \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - 2aV + \frac{{\left( {n - 1} \right)\varepsilon }}{2} \end{array} $ | (50) |
当V=p,且a满足a>((n-1)ε)/2p,则有
| $ \dot V < 0 $ | (51) |
由此证明过程可知,当选择合适的控制增益ki和一阶滤波器的时间常数τi,能够保证整个控制系统最终收敛。
3 UUV的特性及其仿真研究 3.1 UUV的数学模型| $ \left\{ \begin{array}{l} {{\dot u}_r} = \left( { - {d_{11}}{u_r} + {\tau _u}} \right)/{m_{11}}\\ {{\dot v}_r} = \left( {A{m_{66}} - B{m_{26}}} \right)/\left( {{m_{22}}{m_{66}} - m_{26}^2} \right)\\ \dot r = \left( {B{m_{22}} - A{m_{26}}} \right)/\left( {{m_{22}}{m_{66}} - m_{26}^2} \right)\\ \dot x = u\cos \psi - v\sin \psi \\ \dot y = u\sin \psi + v\cos \psi \\ \dot \psi = r \end{array} \right. $ | (52) |
式中:[x y ψ]T为UUV的位置向量,[u v r]T为UUV的速度向量,[uc vc 0]T为海流的速度向量,[ur vr r]T为UUV相对海流的速度,[τu 0 τr]T为UUV的控制力和力矩,A=-d22vr+(d26-urc26-muc)r,B=(d62-urc62)vr-d66r+τr,并且有
| $ \left\{ \begin{array}{l} {m_{11}} = m - {X_{\dot u}}\;\;\;{d_{11}} = {X_{{u_r}}} + {X_{\left| {{u_r}} \right|{u_r}}}\left| {{u_r}} \right|\\ {m_{22}} = m - {Y_{\dot v}}\;\;\;\;{d_{22}} = {Y_{{v_r}}} + {Y_{\left| {{v_r}} \right|{v_r}}}\left| {{v_r}} \right|\\ {m_{26}} = - {Y_{\dot r}}\;\;\;\;\;\;\;\;{d_{26}} = {Y_r}\\ {m_{66}} = {I_z} - {N_{\dot r}}\;\;\;{d_{62}} = {N_{{v_r}}}\\ {c_{26}} = m - {X_{\dot u}}\;\;\;\;{d_{66}} = {N_r} + {N_{\left| r \right|r}}\left| r \right|\\ {c_{62}} = {X_{\dot u}} - {Y_{\dot v}} \end{array} \right. $ | (53) |
式(53) 中相关参数及其水动力系数为m=40,
UUV循迹过程中,由视线导引法[10-11]提供实时期望艏向vψ,纵向速度为定常值。根据动态面自抗扰控制器的设计思路,分别设计该UUV的艏向控制器和纵向速度控制器。
1) 艏向控制器设计:
| $ \left\{ \begin{array}{l} e = {v_{11}} - {v_\psi }\\ {f_h} = {f_h}\left( {e,{v_{12}},r,h} \right)\\ {v_{11}} = {v_{11}} + h{v_{12}}\\ {v_{12}} = {v_{12}} + h \cdot fh\\ {e_1} = {z_{11}} - {y_1}\\ fe = {\rm{fal}}\left( {{e_1},0.5,\delta } \right),f{e_1} = {\rm{fal}}\left( {{e_1},0.25,\delta } \right)\\ {z_{11}} = {z_{11}} + h\left( {{z_{12}} - {\beta _{11}}{e_1}} \right)\\ {z_{12}} = {z_{12}} + h\left( {{z_{13}} - {\beta _{12}} \cdot fe + {b_{10}}{u_1}} \right)\\ {z_{13}} = {z_{13}} + h\left( { - {\beta _{13}} \cdot f{e_1}} \right)\\ {s_{11}} = {x_{11}} - {v_{11}}\\ {{\bar \alpha }_{11}} = {v_{12}} - {k_{11}}{s_{11}},{\tau _{11}}{{\dot \alpha }_{11}} + {\alpha _{11}} = {{\bar \alpha }_{11}},\\ {\alpha _{11}}\left( 0 \right) = {{\bar \alpha }_{11}}\left( 0 \right)\\ {s_{12}} = {x_{12}} - {\alpha _{11}}\\ {u_{10}} = {{\dot \alpha }_{11}} - {k_{12}}{s_{12}}\\ {u_1} = \left( {{u_{10}} - {z_{13}}} \right)/{b_{10}} \end{array} \right. $ | (54) |
式中:h为仿真步长,r为跟踪微分器的调节因子,y1为UUV实时艏向,u1为控制力矩,β1i为扩张状态观测器待设计参数,k1i为动态面待设计参数,τ11为滤波器时间常数。
2) 纵向速度控制器设计:
| $ \left\{ \begin{array}{l} e = {v_{21}} - {v_u}\\ {f_h} = {f_h}\left( {e,{v_{22}},r,h} \right)\\ {v_{21}} = {v_{21}} + h{v_2}\\ {v_2} = {v_2} + h \cdot {f_h}\\ {e_{21}} = {z_{21}} - {y_2}\\ fe = {\rm{fal}}\left( {{e_1},\alpha ,\delta } \right)\\ {z_{21}} = {z_{21}} + h\left( {{z_{22}} - {\beta _{21}}{e_1} + {b_{20}}{u_2}} \right)\\ {z_{22}} = {z_{22}} + h\left( { - {\beta _{22}} \cdot fe} \right)\\ {s_{21}} = {x_{21}} - {v_{21}}\\ {u_{20}} = {v_{22}} - {k_{21}}{s_{21}}\\ {u_2} = \left( {{u_{20}} - {z_{22}}} \right)/{b_{20}} \end{array} \right. $ | (55) |
相关参数的含义与艏向控制器中类似。
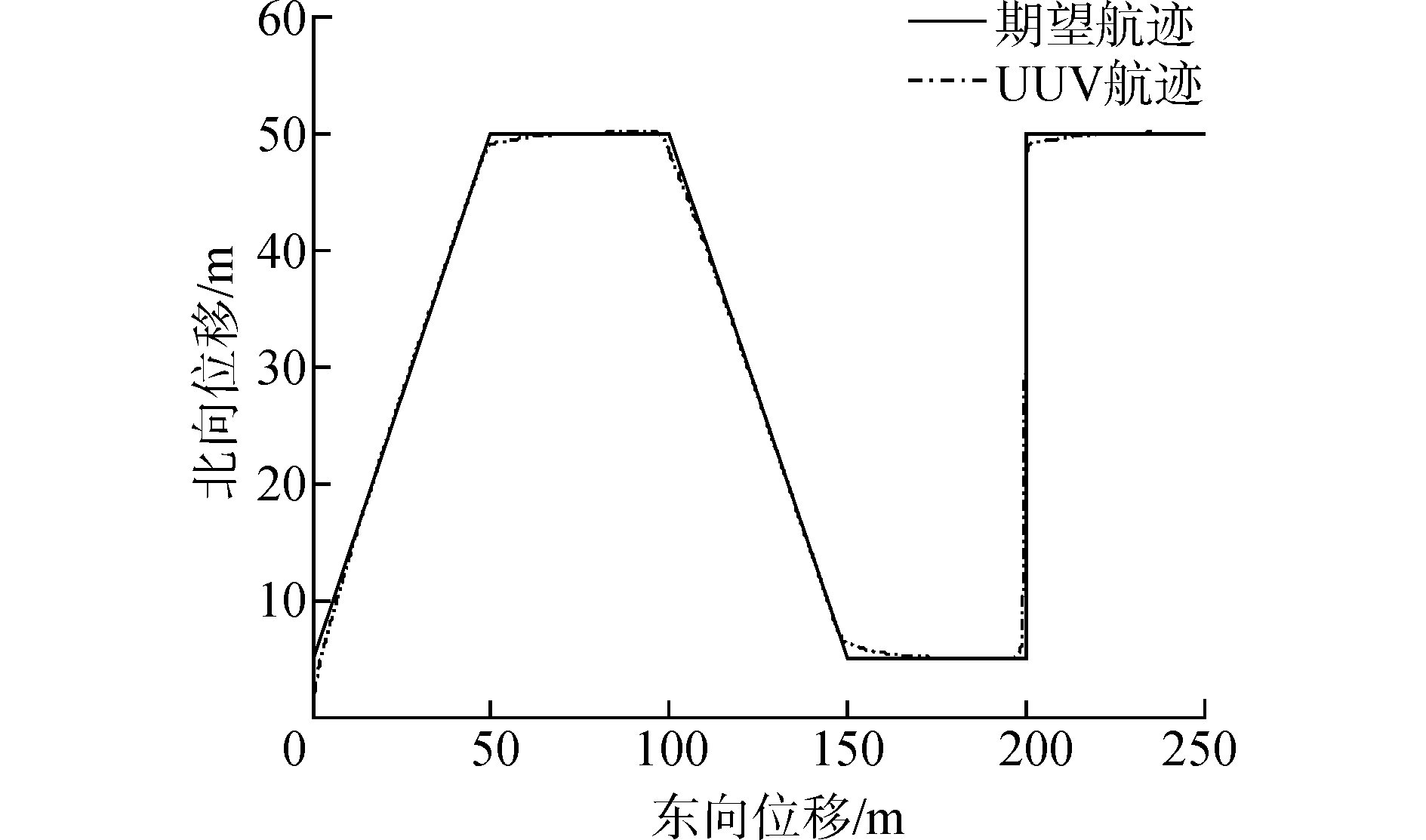
3.3 UUV循迹仿真在北东坐标系下,假设UUV的期望航迹为P={(5, 0), (50, 50), (50, 100), (5, 150), (5, 200), (50, 200), (50, 250)},期望速度为1 m/s。海流大小为0.5 m/s方向为π/4。并在UUV的艏向和横向分别加幅值为0.2、0.18 N·m,周期均为20π的外界扰动。相关参数分别为r=0.8,h=0.02,δ=0.1,β11=100,β12=300,β13=1 000,β21=50,β22=800,k11=1,k12=1,k13=1,k21=5,τ11=0.1,b10=0.025,b20=0.06。仿真结果如3~6图所示。
|
图 3 UUV航迹图 Fig.3 UUV track map |
|
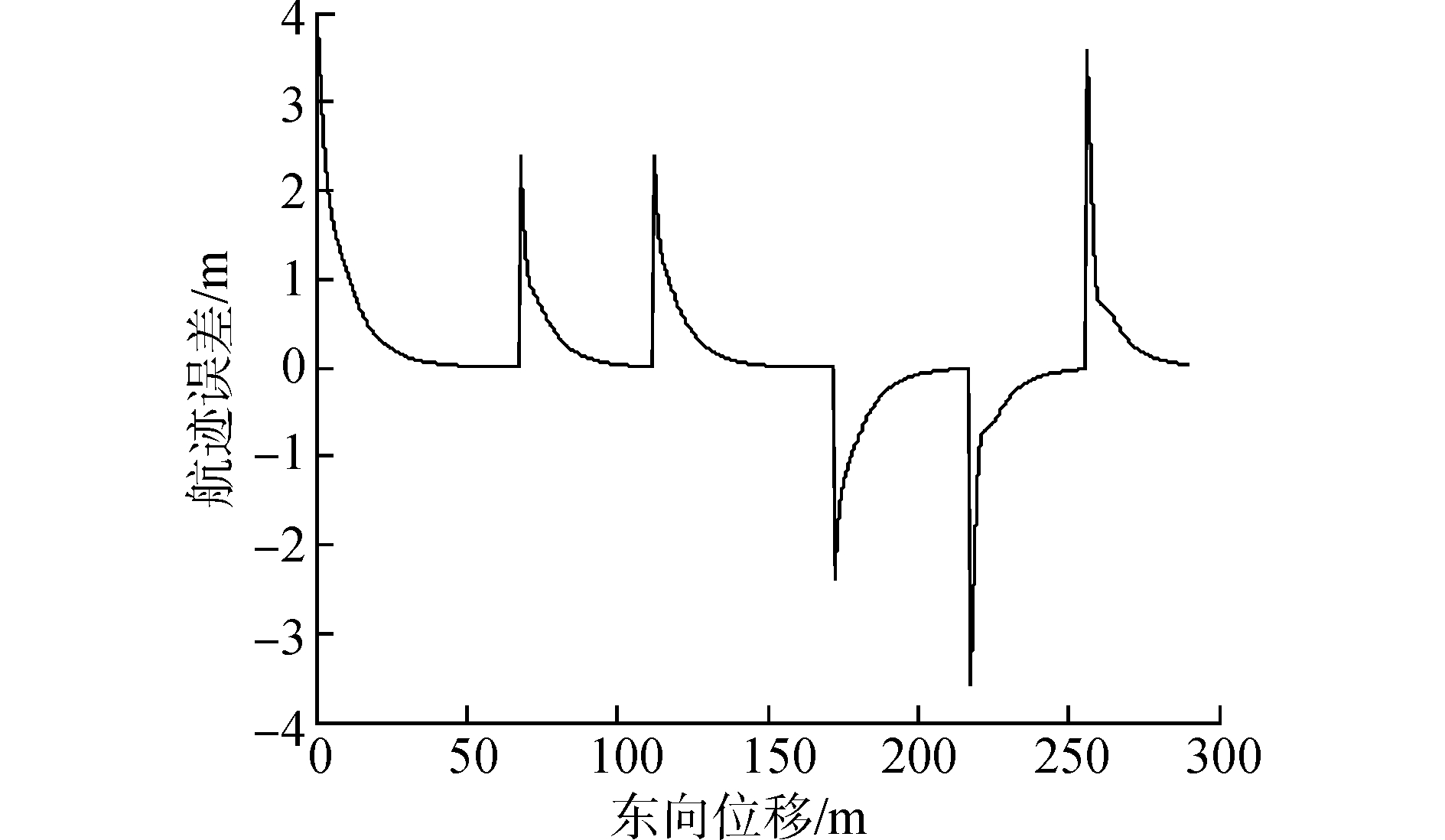
图 4 UUV航迹误差图 Fig.4 UUV track error chart |
|
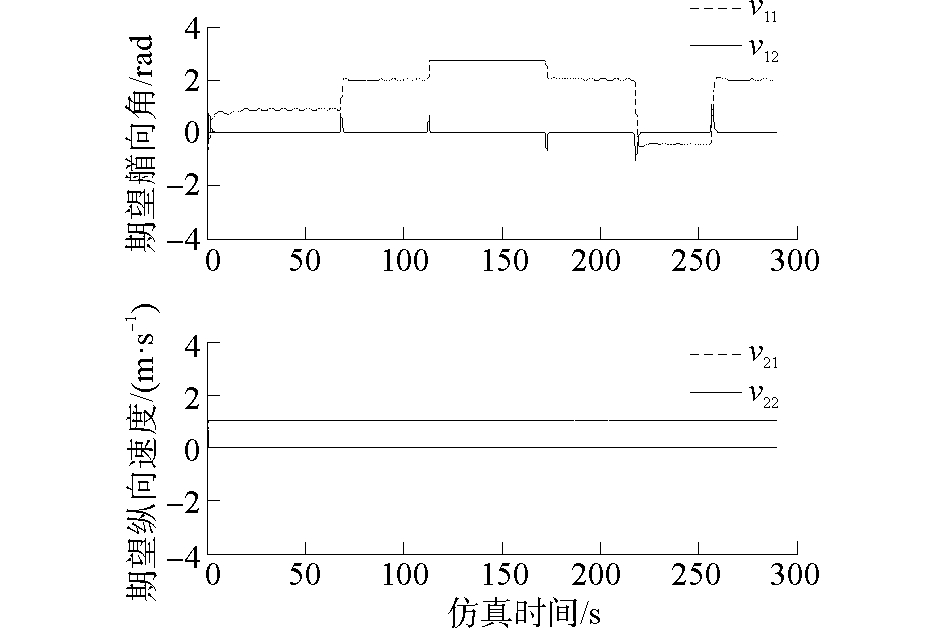
图 5 跟踪微分器的输出信号 Fig.5 Output signal of tracking differentiator |
|
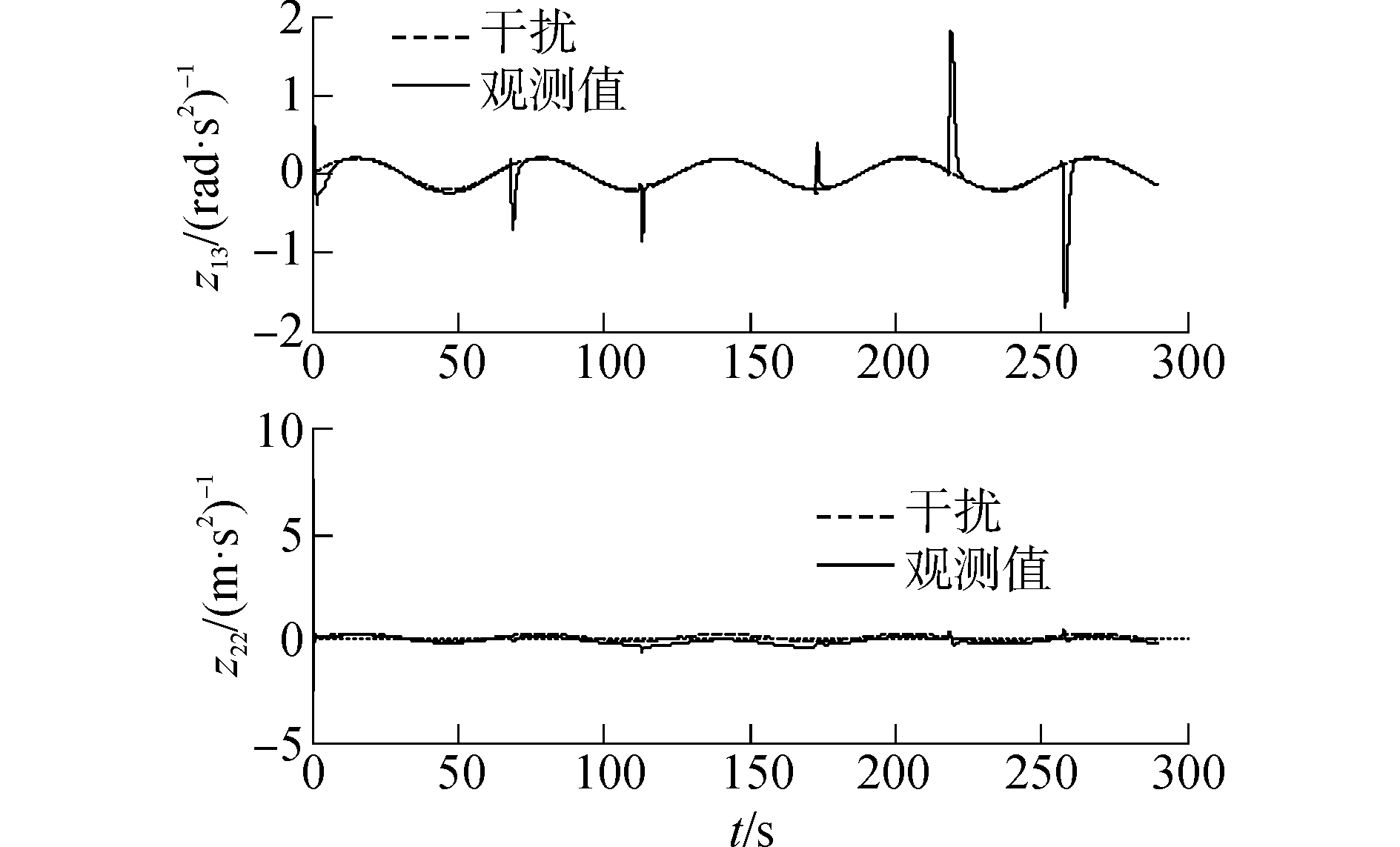
图 6 扩张状态观测器的观测值 Fig.6 Observed value of extended state observer |
结合图 3和图 4可以看出,在有外界干扰的情况下,UUV能够跟踪上期望航迹,并使得航迹误差较快趋于零;图 5给出动态面自抗扰控制器中艏向和纵向跟踪微分器的输出值;图 6是状态扩张观测器的观测值与实际值的对比图,可以看出观测器能够很好的估计外界扰动。
4 结论1) 该控制算法成功避免了反步法对虚拟控制量求导的过程中会出现“微分爆炸”的现象,对系统的未建模部分或者未知部分进行实时估计,然后根据估计量的大小对系统的实际控制量进行相应的补偿,使得控制器具有更强的鲁棒性。
2) 该控制算法对UUV航迹跟踪、UUV纵向速度和艏向速度估计以及估计外界扰动具有很好的效果。
| [1] |
刘燕斌, 陆宇平. 基于反步法的高超音速飞机纵向逆飞行控制[J]. 控制与决策, 2007, 22(3): 313-317. LIU Yanbin, LU Yuping. Longitudinal inverse flight control of hypersonic aircraft based on back-stepping method[J]. Control and decision making, 2007, 22(3): 313-317. (  0) 0)
|
| [2] |
向峥嵘, 向伟铭. 基于反步法的一类非线性切换系统控制器设计[J]. 控制与决策, 2007, 22(12): 1373-1376. XIANG Zhengrong, XIANG Weiming. Design of class of nonlinear switching system controller based on back-stepping method[J]. Control and decision making, 2007, 22(12): 1373-1376. DOI:10.3321/j.issn:1001-0920.2007.12.010 (  0) 0)
|
| [3] |
何朕, 王广雄, 杨文哲. 一类欠驱动系统的频域反步法设计[J]. 电机与控制学报, 2012, 16(2): 71-76. HE Zhen, WANG Guangxiong, YANG Wenzhe. Design of frequency-domain back-stepping for a class of underactuted systems[J]. Journal of electric machines and control, 2012, 16(2): 71-76. (  0) 0)
|
| [4] |
韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19-23. HAN Jingqing. Active disturbance rejection controller and its application[J]. Control and decision making, 1998, 13(1): 19-23. (  0) 0)
|
| [5] |
SWAROOP D, HEDRICK J K, YIP P P, et al. Dynamic surface control for a class of nonlinear systems[J]. IEEE transactions on automatic control, 2000, 45(10): 1893-1899. DOI:10.1109/TAC.2000.880994 ( 0) 0)
|
| [6] |
孙红英, 于风卫. 船舶航向非线性系统自适应动态面控制器设计[J]. 中国航海, 2008, 31(3): 236-239. SUN Hongying, YU Fengwei. Design of adaptive dynamic surface controller for ship course nonlinear system[J]. China sailing, 2008, 31(3): 236-239. (  0) 0)
|
| [7] |
付明玉, 彭海军, 徐玉杰, 等. 基于动态面自抗扰技术的起重船动力定位控制[J]. 新型工业化, 2014, 4(10): 10-17. FU Mingyu, PENG Haijun, XU Yujie, et al. Dynamic positioning control of crane based on dynamic surface auto-disturbance rejection technology[J]. New industrialization, 2014, 4(10): 10-17. DOI:10.3969/j.issn.2095-6649.2014.10.02 (  0) 0)
|
| [8] |
ERLING J, REFSNES G. Nonlinear model-based control of slender body AUVs[D]. Trondheim:Norwegian University of Science and Technology, 2007.
( 0) 0)
|
| [9] |
REFSNES J E, SORENSEN A J, PETTERSEN K Y. Model-based output feedback control of slender-body under actuated AUVs:theory and experiments[J]. IEEE transactions on control systems technology, 2008, 16(5): 930-946. DOI:10.1109/TCST.2007.916347 ( 0) 0)
|
| [10] |
FREDRIKSEN E, PETTERSEN K Y. Global k-exponential way-point maneuvering of ships[C]//43rd IEEE Conference on Decision and Control.[S.l.], 2004:5360-5367.
( 0) 0)
|
| [11] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M].[S.l.]:Norwegian University of Science and Technology, 2011:248-252.
( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


