电液伺服振动台具有响应速度快、控制精度高、控制方式灵活等优点,使得其在航天、汽车、建筑等许多领域得到广泛的应用。振动试验是把试件固定在试验台上,通过模拟该试件受载时的情况,来研究载荷对试件的影响、试件的可靠性和抗震、减振与避振措施[1-2]。电液伺服振动台主要由机械、液压和电子3个子系统构成,存在着诸如死区、摩擦、间隙等各种非线性。由于上述的非线性因素,当电液伺服振动台作正弦振动激励时,系统加速度响应会出现高次谐波,信号失真比较严重。这不仅降低了系统的动态跟踪能力,也影响了系统的控制精度。
谐波辨识对于电液振动台谐波抑制有着重要的指导作用, 但是目前对于谐波辨识的研究主要集中在电力系统领域。为了对电力系统中的谐波进行检测、抑制和补偿,研究人员提出了很多方法。傅里叶变换是最常用的谐波检测法,它需要一定时间的电流值,且需要进行两次变换,计算量大,从而使得检测时间较长,检测结果的实时性较差,并且在采样过程中,当信号频率与采样频率不一致时,将产生频谱泄漏和栅栏效应,使辨识出的幅值和相位不准确,尤其是相位的误差很大,无法满足辨识精度的要求[3]。小波分析作为时域分析的重要工具,克服了FFT在频域完全局部化而在时域完全无局部化的缺点,对含有谐波的信号进行正交小波分解,利用多分辨率的概念,将高尺度上的结果看作不含谐波的基波分量。但算法需要软件实现,计算量大,实时性难以保证,且辨识精度比较低。人工神经网络算法原理简单,实现方便,具有自适应性,可以实时的跟踪信号,但需知道相位初值,且需训练样本;随着测量范围的增加,样本和网络规模随之增加。近年来,一些智能优化算法如遗传算法、模拟退火算法、粒子群算法和蚁群算法被应用到了谐波辨识领域, 但这些算法的收敛速度受初始参数的影响,并且计算量比较大,因此未能广泛应用[4-7]。
电液伺服振动台谐波辨识与电力系统谐波辨识不同的是,前者要求具有良好的实时性能、计算量小、辨识精度高。梯度下降法是一种最优化算法,它是求解无约束优化问题最简单的方法之一。本文采用梯度算法,设计电液伺服振动台谐波辨识策略,并用试验验证其有效性。
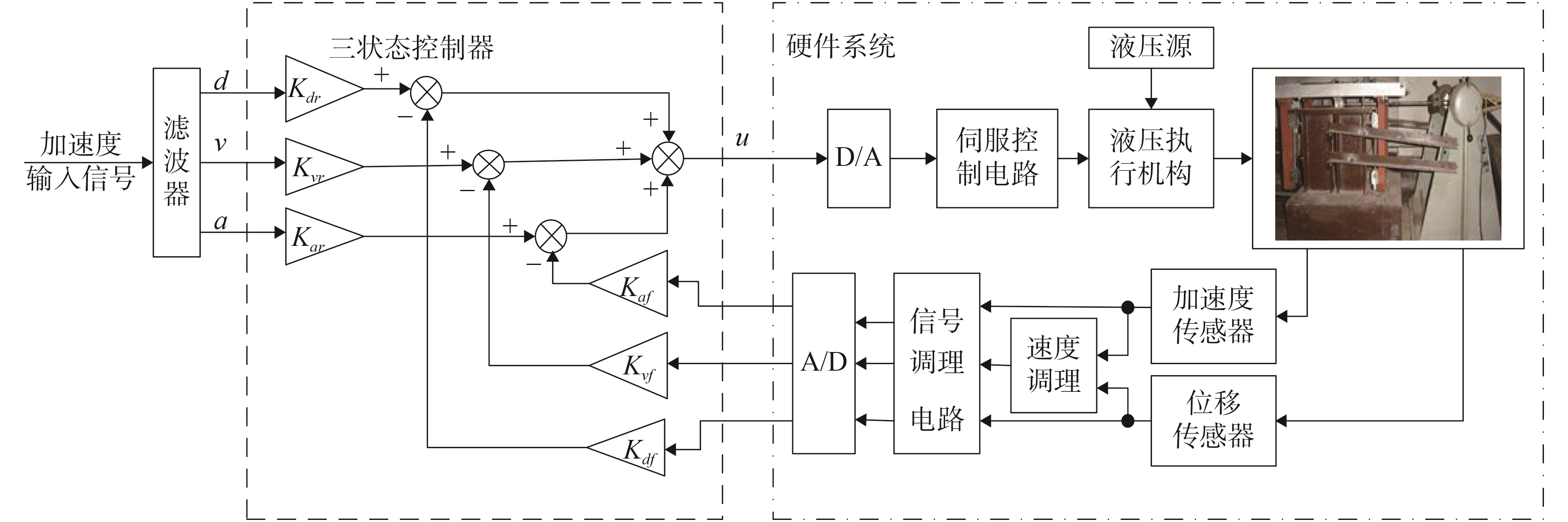
1 电液伺服振动台试验用的电液伺服振动台为单自由度振动台,其控制系统如图 1所示,基本控制策略为三状态(位移、速度和加速度)控制器[8]。输入信号经过滤波器获得三输入状态,利用加速度传感器和位移传感器获得振动台的加速度和位移,经速度调理后获得速度,由此获得三状态反馈。经过调理电路放大和滤波处理后的三状态反馈通过A/D转换器与三输入状态在控制器的作用下,产生偏差信号u。偏差信号u经D/A转换器后经过伺服控制电路产生伺服控制信号。控制信号通过控制伺服阀的往复运动使高压油交替进入激振器的油腔,利用油压推动活塞运动,从而带动振动台台面运动,以实现期望加速度信号。该振动台的主要技术指标如表 1所示。
|
图 1 电液伺服振动台控制系统 Fig.1 The control system of the electro-hydraulic servo shaking table |
| 表 1 振动台主要技术参数 Tab.1 Main parameters of shaking table |
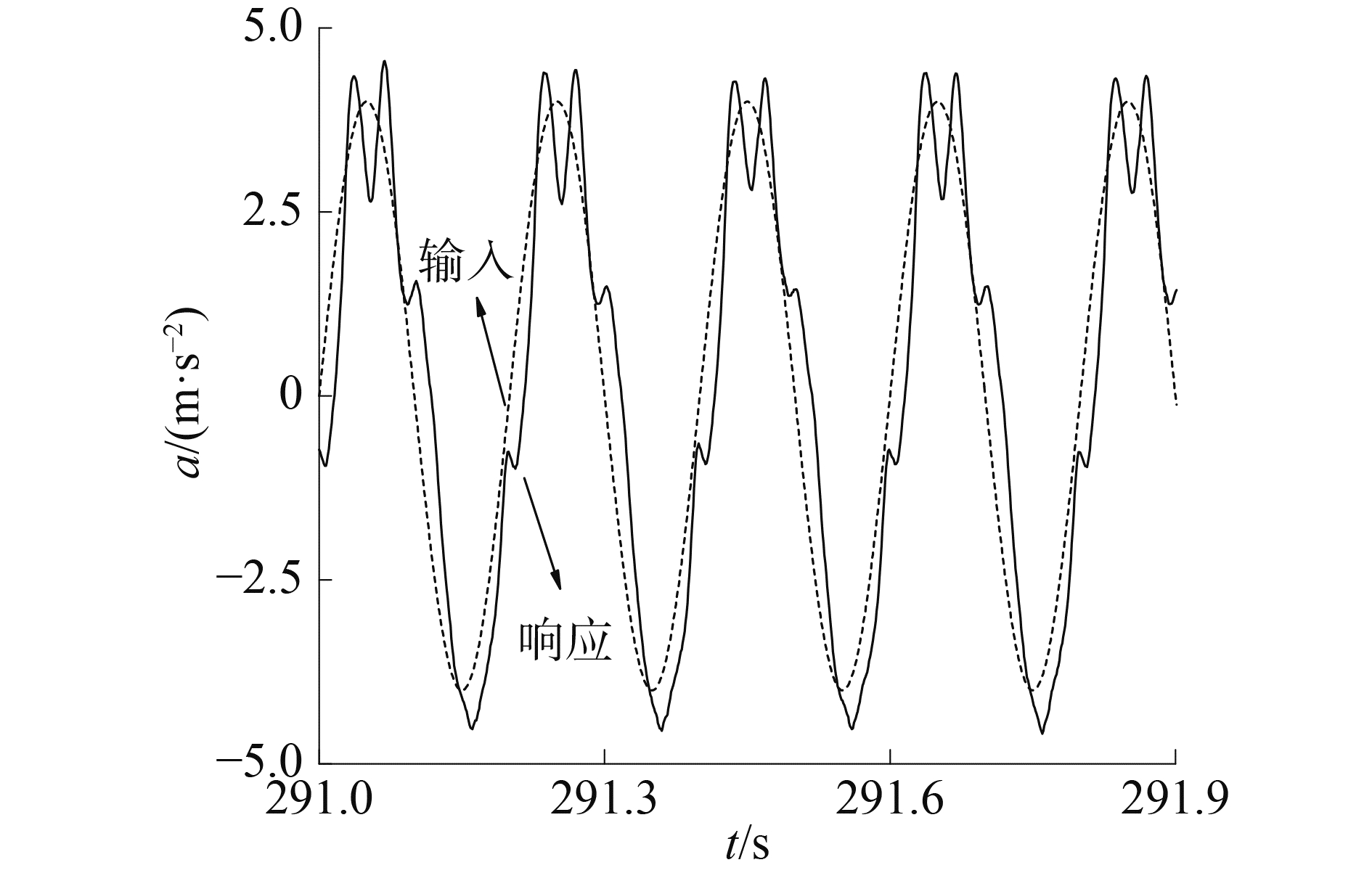
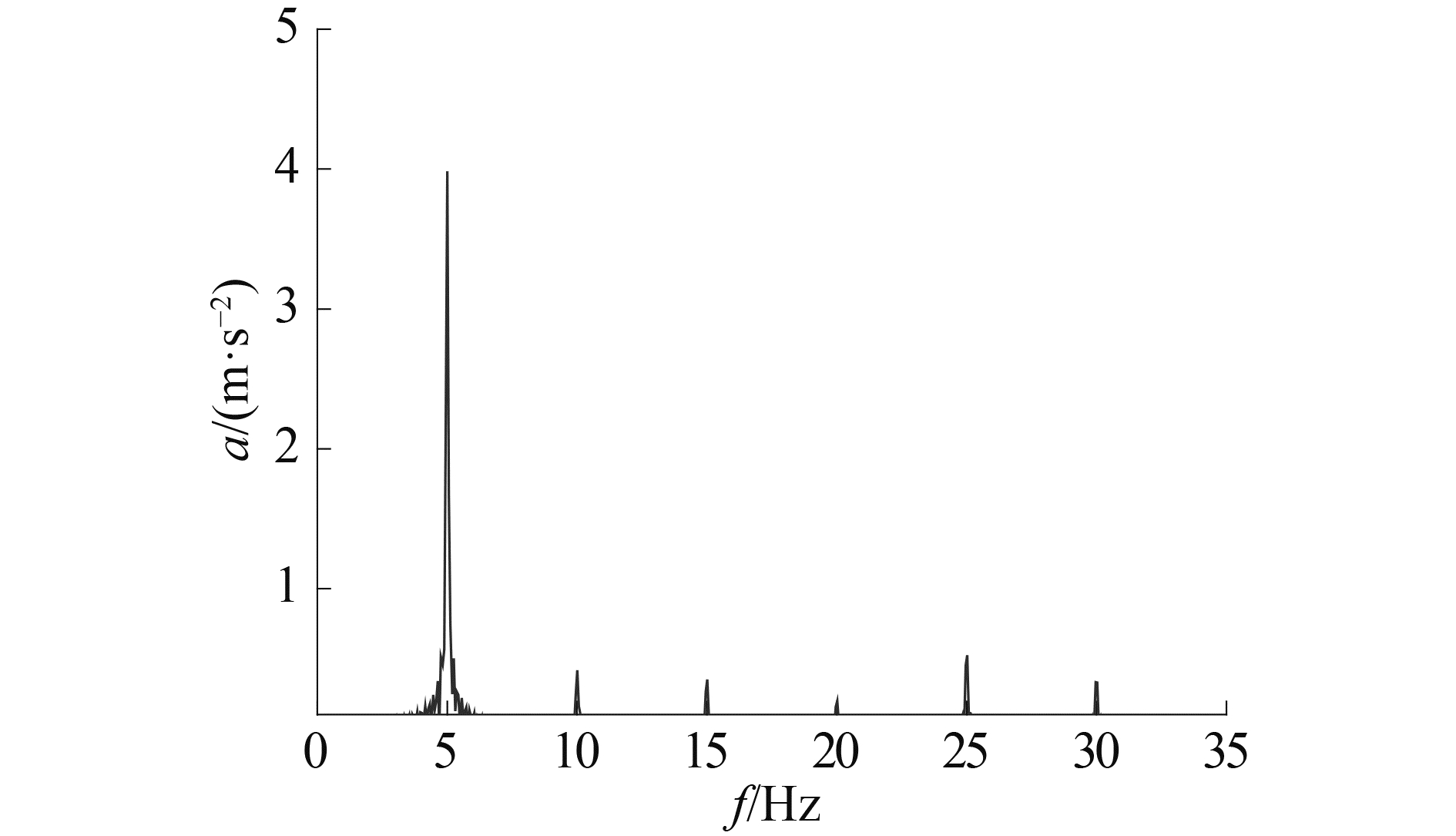
正弦振动试验是力学试验中经常被采用的一种试验方法,也是最基本的振动试验方法,可以模拟周期振动。对图 1所示的振动台系统,当输入的正弦加速度信号为4sin(10πt)m/s2时,其时域响应如图 2所示,从图中可以看出,由于系统的非线性因素,导致加速度响应信号严重失真。对应的频域响应如图 3所示,从图中可以看出加速度响应信号存在高次谐波现象。FFT(fast Fourier transformation)离线辨识的基频响应和各次谐波的幅值分别为4.002,0.418, 0.368,0.209, 0.576, 0.375 m·s-2。高次谐波的幅值中五次谐波最大,四次谐波最小,三次谐波和六次谐波相差不大。
|
图 2 时域响应 Fig.2 The response in the domain |
|
图 3 频域响应 Fig.3 The frequency spectrum |
对于电液伺服振动台的正弦振动试验,往往用总的谐波失真度(total harmonic distortion, THD)来衡量信号失真程度。谐波失真度是各次谐波的幅值相对基频响应幅值而言, 其值越低则谐波分量越少,谐波失真程度越小,振动台复现信号的能力就越强。其计算表达式为
| $ {\rm{THD}} = \frac{{\sqrt {A_2^2 + A_3^2 + A_4^2 + \cdots A_N^2} }}{{{A_1}}} \times 100\% $ | (1) |
式中:A1为基频响应幅值, A2、A3、…AN为各次谐波幅值,N为总的谐波的次数。利用式(1)计算THD值为22.71%,失真程度比较严重。
3 梯度算法时不变单输入单输出系统用差分方程描述为
| $ \begin{array}{*{20}{c}} {y\left( k \right) = {a_1}y\left( {k - 1} \right) + \cdots + {a_n}y\left( {k - n} \right) = }\\ {{b_1}u\left( {k - 1} \right) + \cdots {b_m}u\left( {k - m} \right)} \end{array} $ | (2) |
式中:y、u为系统输出、输入量,m、n为系统阶次。
记
| $ \mathit{\boldsymbol{h}}\left( k \right) = {\left[ { - y\left( {k - 1} \right) \cdots - y\left( {k - n} \right)u\left( {k - 1} \right) \cdots u\left( {k - m} \right)} \right]^{\rm{T}}} $ | (3) |
| $ \mathit{\boldsymbol{\theta }}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{a_1}}&{{a_2} \cdots {a_n}}&{{b_1}}&{{b_2} \cdots {b_m}} \end{array}} \right]^{\rm{T}}} $ | (4) |
则可得到
| $ y\left( k \right) = {\mathit{\boldsymbol{h}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{\theta }}\left( k \right) $ | (5) |
梯度算法的基本思想就是利用h(k)和y(k),确定参数θ在k时刻的估计值
| $ J\left( {\mathit{\boldsymbol{\hat \theta }}} \right) = \frac{1}{2}{e^2}\left( {\mathit{\boldsymbol{\hat \theta }},k} \right) $ | (6) |
其中
梯度校正参数辨识方法的递推形式为
| $ \mathit{\boldsymbol{\hat \theta }}\left( {k + 1} \right) = \mathit{\boldsymbol{\hat \theta }}\left( k \right) - \mathit{\boldsymbol{K}}\left( k \right){\rm{grad}}\left[ {J\left( {\mathit{\boldsymbol{\hat \theta }}} \right)} \right] $ | (7) |
式中:K(k)为加权阵,它是对称阵;
| $ \begin{array}{*{20}{c}} {{\rm{grad}}\left[ {J\left( {\mathit{\boldsymbol{\hat \theta }}} \right)} \right] = \frac{d}{{{\rm{d \mathsf{ θ} }}}}\left[ {\frac{1}{2}{e^2}\left( {\mathit{\boldsymbol{\hat \theta }},k} \right)} \right] = }\\ { - \left[ {y\left( k \right) - {\mathit{\boldsymbol{h}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{\hat \theta }}\left( k \right)} \right]\mathit{\boldsymbol{h}}\left( k \right)} \end{array} $ | (8) |
则式(7)改为
| $ \mathit{\boldsymbol{\hat \theta }}\left( {k + 1} \right) = \mathit{\boldsymbol{\hat \theta }}\left( k \right) + \mathit{\boldsymbol{K}}\left( k \right)\mathit{\boldsymbol{h}}\left( k \right)\left[ {y\left( k \right) - {\mathit{\boldsymbol{h}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{\hat \theta }}\left( k \right)} \right] $ | (9) |
权矩阵的选择很重要,且输入数据向量h(k)的各分量h(k)将直接影响参数的估计值。权矩阵取:
| $ \mathit{\boldsymbol{K}}\left( k \right) = \frac{1}{{{\mathit{\boldsymbol{h}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{h}}\left( k \right)}} = \frac{1}{{r\left( k \right)}} $ | (10) |
此时梯度辨识算法的递推式变为
| $ \mathit{\boldsymbol{\hat \theta }}\left( {k + 1} \right) = \mathit{\boldsymbol{\hat \theta }}\left( k \right) + \frac{{\mathit{\boldsymbol{h}}\left( k \right)}}{{r\left( k \right)}}\left[ {y\left( k \right) - {\mathit{\boldsymbol{h}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{\hat \theta }}\left( k \right)} \right] $ | (11) |
虽然梯度辨识算法的计算量比较小,参数估计是一致收敛的,但收敛速度很慢。为了加快随机梯度算法的收敛速度,引入遗忘因子λ。带遗忘因子随机梯度辨识算法的递推公式变为[9-10]
| $ \mathit{\boldsymbol{\hat \theta }}\left( {k + 1} \right) = \mathit{\boldsymbol{\hat \theta }}\left( k \right) + \frac{{\mathit{\boldsymbol{h}}\left( k \right)}}{{r\left( k \right)}}\left[ {y\left( k \right) - {\mathit{\boldsymbol{h}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{\hat \theta }}\left( k \right)} \right] $ | (12) |
| $ r\left( {k + 1} \right) = \lambda r\left( k \right) + {\mathit{\boldsymbol{h}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{h}}\left( k \right) $ | (13) |
式中:0≤λ≤1, r(0)=1。
4 谐波辨识策略由频域响应的分析结果可知,振动台正弦振动试验的加速度响应中高次谐波的频率均为基频的整数倍。采样得到加速度响应是一个离散信号,且是各次谐波线性叠加的结果[11],故k时刻的加速度响应可以表示为
| $ a\left( k \right) = \sum\limits_{i = 1}^N {{A_i}\sin \left( {{\rm{i}}\omega k + {\phi _i}} \right)} $ | (14) |
式中:ω为输入信号的圆频率,
为了能够应用梯度算法辨识谐波,式(14)变为
| $ \begin{array}{*{20}{c}} {a\left( k \right) = \sum\limits_{i = 1}^N {{a_i}\left( k \right)} = }\\ {\sum\limits_{i = 1}^N {{A_i}\cos {\phi _i}\sin \left( {{\rm{i}}\omega k} \right) + {A_i}\sin {\phi _i}\cos \left( {{\rm{i}}\omega k} \right)} } \end{array} $ | (15) |
令xi1=Aicos
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{h}}\left( k \right) = \left[ {\sin \left( {\omega k} \right)\cos \left( {\omega k} \right) \cdots \sin \left( {{\rm{i}}\omega k} \right)} \right.}\\ {{{\left. {\cos \left( {{\rm{i}}\omega k} \right) \cdots \sin \left( {N\omega k} \right)\cos \left( {N\omega k} \right)} \right]}^{\rm{T}}}} \end{array} $ | (16) |
| $ \mathit{\boldsymbol{\theta }}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}&{{x_{21}}}&{{x_{22}} \cdots {x_{N1}}}&{{x_{N2}}} \end{array}} \right]^{\rm{T}}} $ | (17) |
则第i次谐波的幅值和相位可计算为
| $ \left\{ \begin{array}{l} {A_i} = \sqrt {x_{i1}^2 + x_{i2}^2} \\ {\phi _i} = \arctan \left( {\frac{{{x_{i2}}}}{{{x_{i1}}}}} \right) \end{array} \right. $ | (18) |
而辨识得到的第i次谐波
| $ {{\hat a}_i}\left( k \right) = {x_{i1}}\sin \left( {{\rm{i}}\omega k} \right) + {x_{i2}}\cos \left( {{\rm{i}}\omega k} \right) $ | (19) |
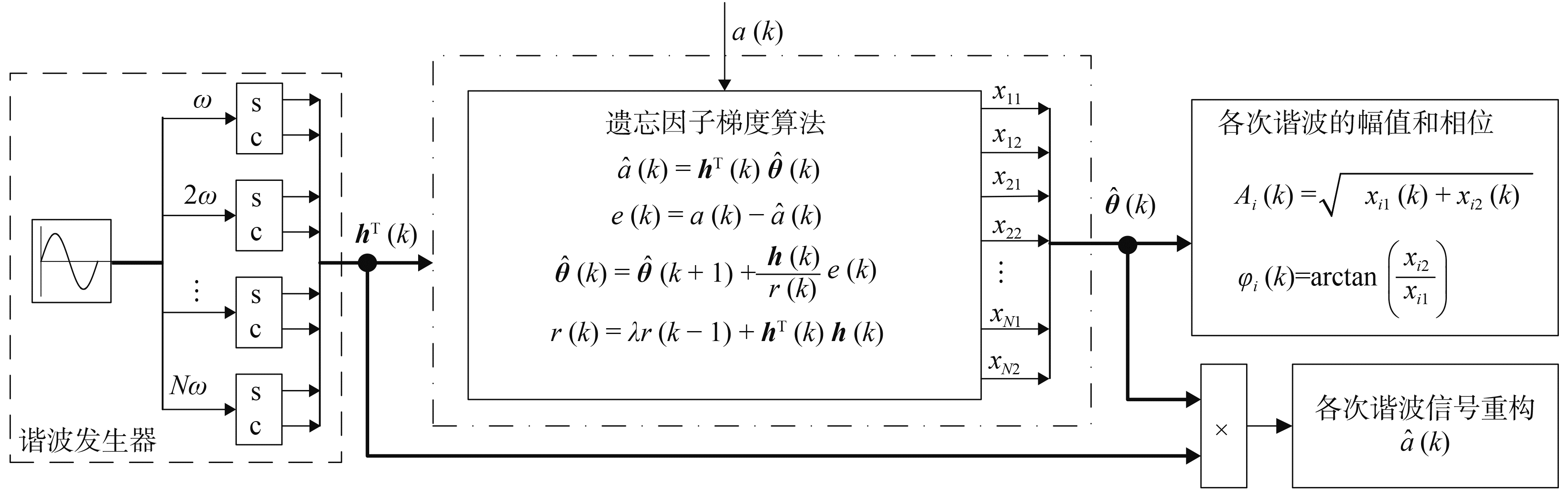
基波频率和谐波次数确定后,谐波向量便可确定,若能求得参数向量θ(k),通过式(18)、(19)便可确定各次谐波的幅值和相位。加速度谐波辨识原理如图 4所示,s和c分别表示正弦函数和余弦函数,谐波发生器产生输入向量hT(k)。正弦加速度响应a(k)为期望信号,该期望信号与辨识得到的加速度信号
|
图 4 加速度谐波辨识方框图 Fig.4 Block diagram of the acceleration harmonic identification |
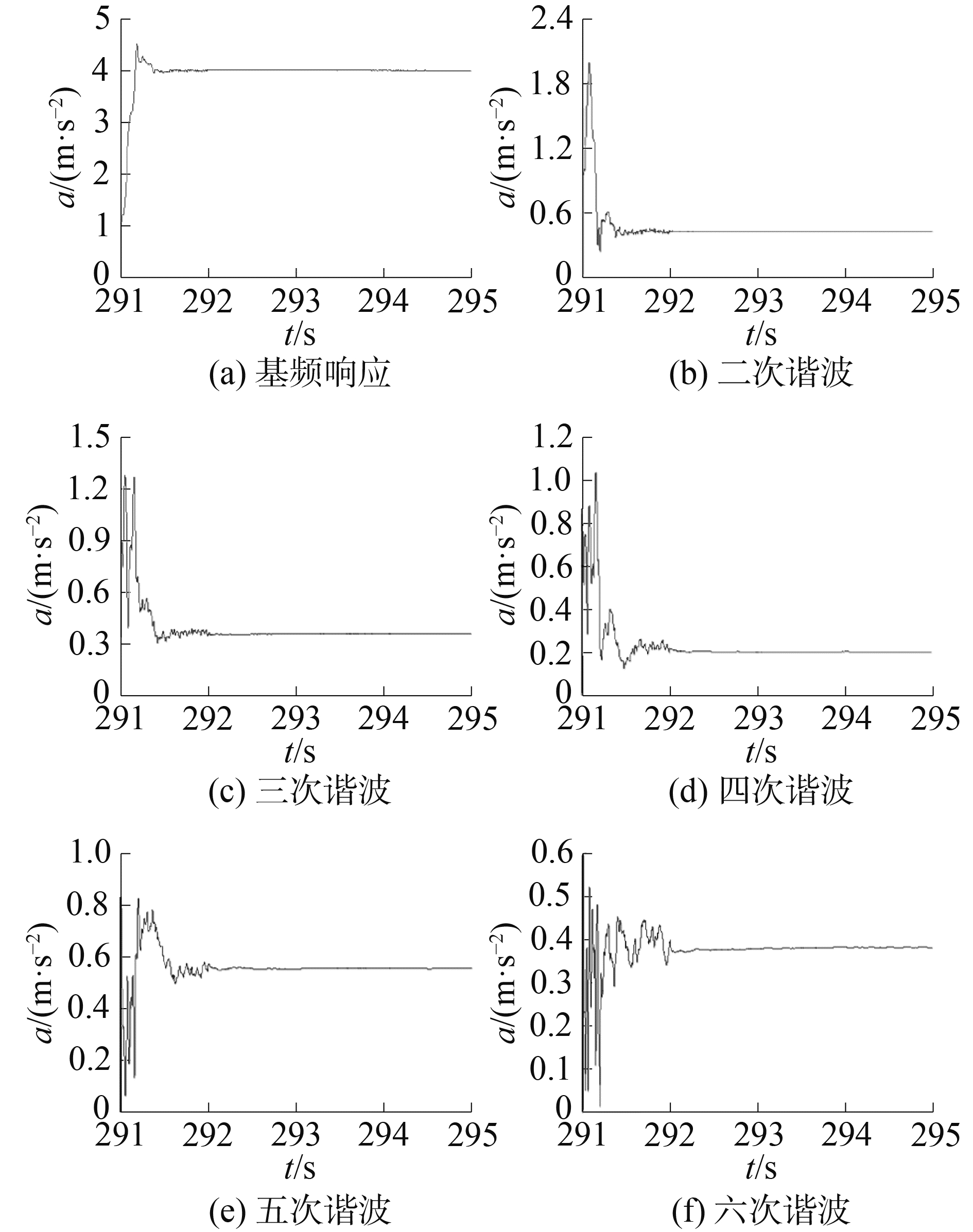
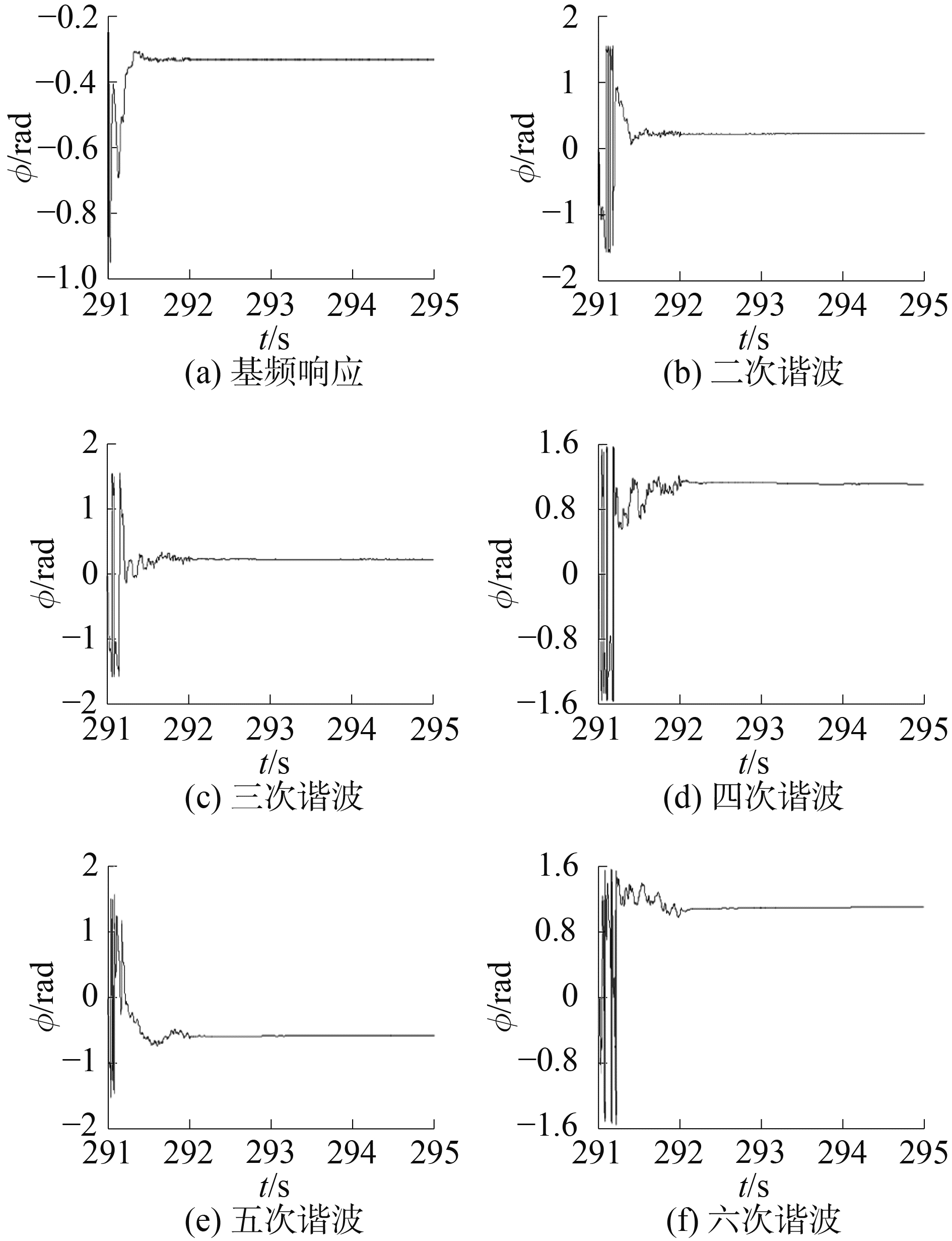
利用图 4的加速度谐波辨识原理图辨识图 2所示的加速度响应信号中的各次谐波。为了加快收敛速度,当前1 000次采样时λ取0.8,之后λ取0.99。幅值和相位的辨识过程如图 5、6所示,从图中可以看出幅值和相位经过短暂波动后,迅速收敛于稳定状态。由于基频在各次谐波中占主导地位,基频响应的收敛速度明显快于其他谐波。表 3是各次谐波达到稳定状态后的幅值和相位,稳定后各次谐波的幅值与表 2中经FFT分析得到的幅值非常接近,这说明梯度算法对谐波幅值的辨识精度比较高。
|
图 5 各次谐波的幅值 Fig.5 The identified each harmonic′s amplitude |
|
图 6 各次谐波的相位 Fig.6 The identified each harmonic′s phase |
| 表 3 辨识谐波的幅值和相位 Tab.3 The amplitudes and phases of all times harmonic |
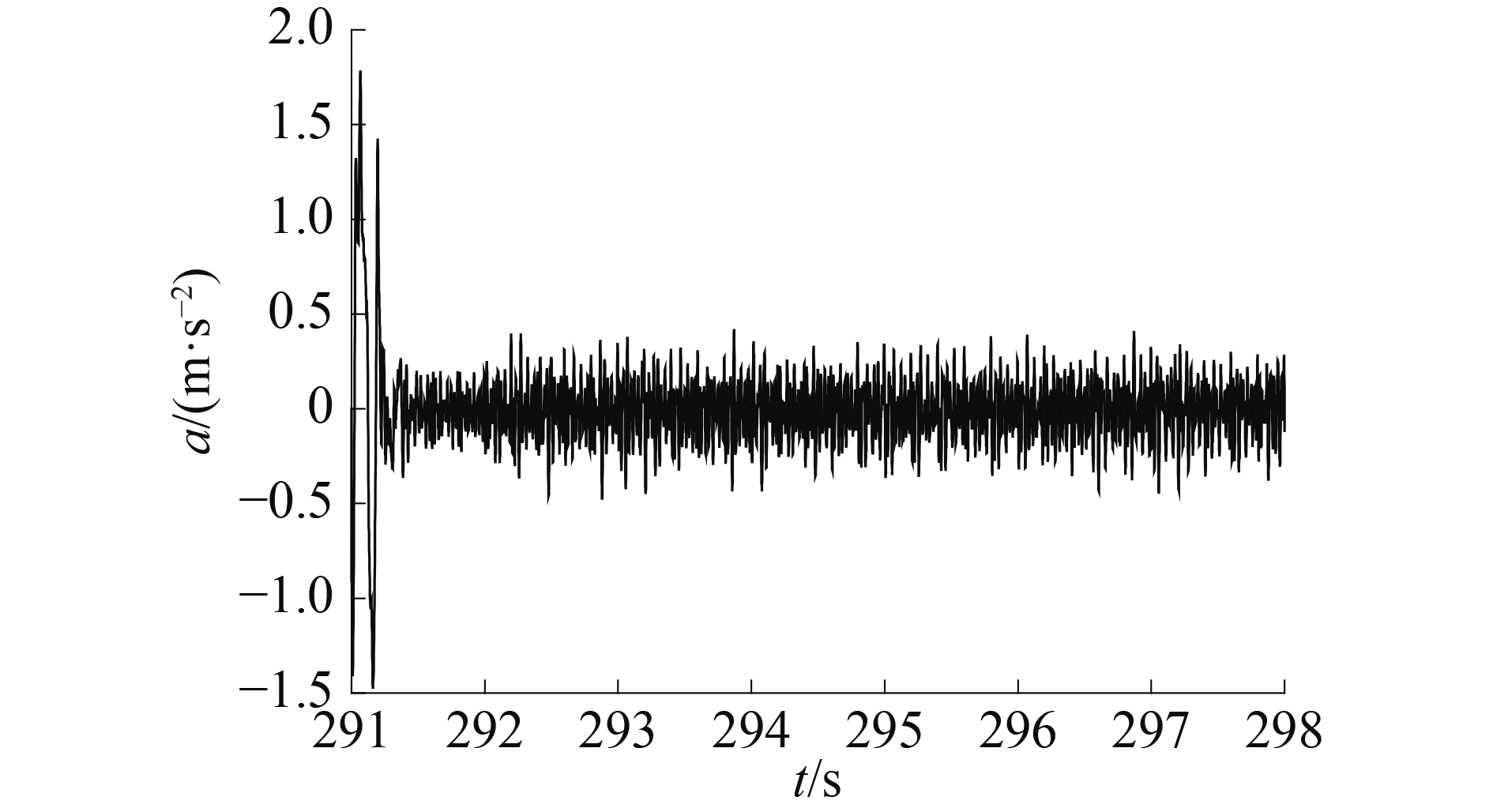
辨识误差如图 7所示,从图中可以看出跟踪误差在算法起始阶段衰减的比较快,在0.5 s内就达到了收敛状态。之后虽有波动,但波动幅度在±0.4 m/s2以内,这说明梯度算法对谐波幅值和相位的辨识精度比较高。
|
图 7 辨识误差 Fig.7 Estimated error |
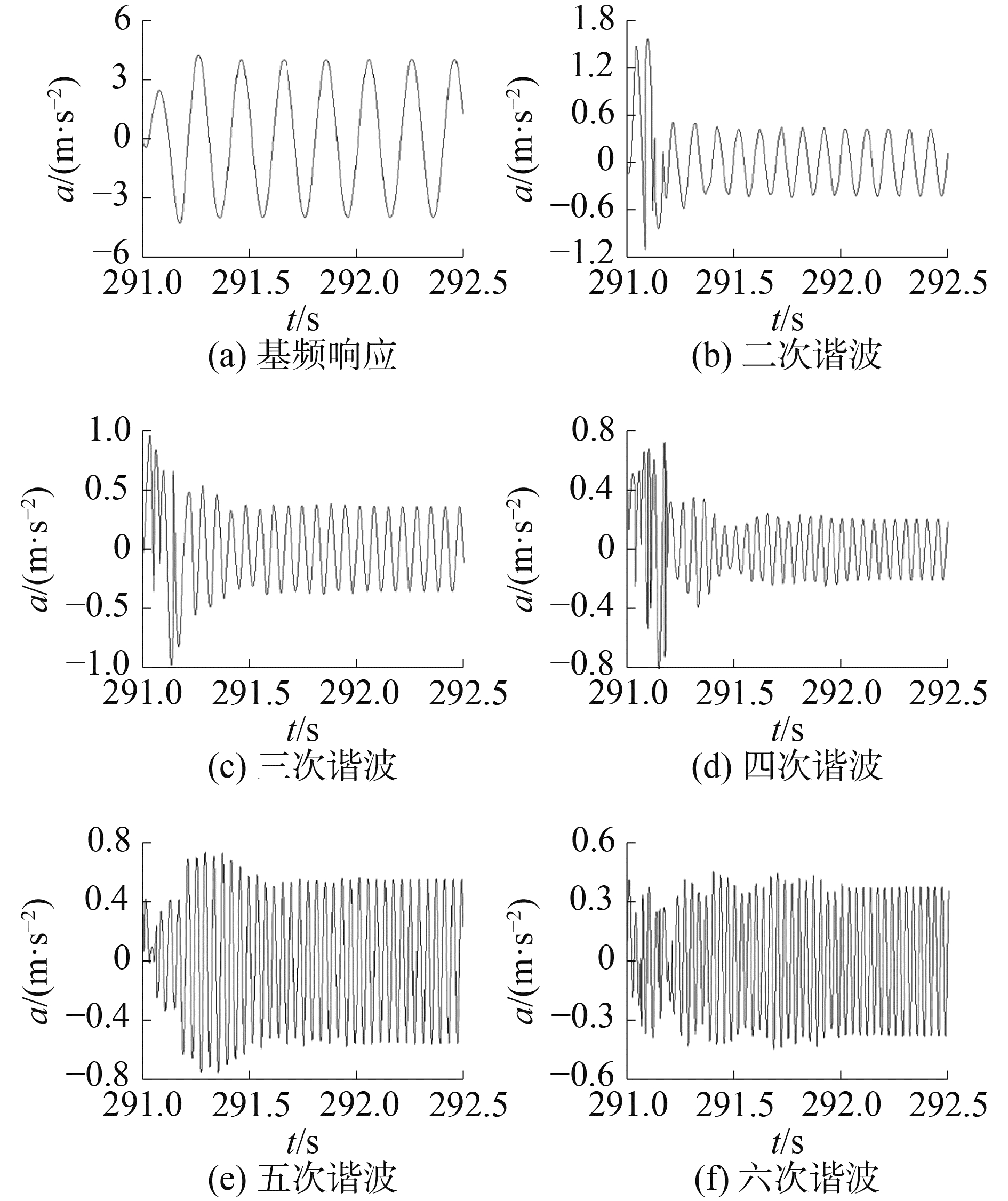
由式(19)可以直接构造出各次谐波,各次谐波的结果如图 8所示,从图中可以看出算法开始阶段高次谐波波动剧烈,但在0.4 s后趋于稳定,辨识得到的各次谐波可以作为谐波抑制的依据。
|
图 8 各次谐波分量的波形 Fig.8 The waveform of each harmonic component |
1) 电液伺服振动台是集机、电、液于一体的非线性系统,在正弦信号激励下,加速度响应由于系统的非线性因素存在波形失真。基于梯度算法的辨识模型,容易与振动台原有控制策略结合,确保所有的操作都可以在计算机上实时运行。
2) 该辨识算法不但能辨识各次谐波的幅值和相位,而且能直接得到各次谐波。辨识策略结构简单,辨识速度快,且具有很好的动态跟踪能力,且无需知道系统的先验知识。
3) 为了加快收敛速度,引入了遗忘因子λ的概念。λ越小,算法收敛速度越快,但谐波参数波动大;λ越大,虽然参数估计平稳,但算法的跟踪速度较慢。故一般在算法开始阶段选择较小的λ值,之后再选择较大的λ值,既可提高算法的收敛速度,又可减小谐波参数的波动,从而提高辨识的精度。
4) 实验结果与FFT分析结果进行了比较,但是FFT分析是离线多点计算得到,而所用的辨识算法是实时在线进行。辨识结果表明遗忘因子梯度算法的谐波辨识算法具有较快的收敛速度和较高的辨识精度,其得到的辨识结果可以作为电液伺服振动台谐波抑制的依据。
| [1] |
赵勇. 液压振动台高精度正弦振动的控制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2009: 1-3. ZHAO Yong. Control strategy of high accuracy sinusoidal vibration for the hydraulic shaking table[D]. Harbin:Harbin Institute of Technology, 2009:1-3. (  0) 0)
|
| [2] |
SHEN Gang, LVG M, YEZ M, et al. Implementation of electrohydraulic shaking table controllers with a combined adaptive inverse control and minimal control synthesis algorithm[J]. Iet control theory & applications, 2011, 5(13): 1471-83. (  0) 0)
|
| [3] |
HABROUK M E, DARWISH M K. Design and implementation of a modified Fourier analysis harmonic current computation technique for power active filters using DSPs[J]. Electric power applications, 2001, 148(1): 21-28. DOI:10.1049/ip-epa:20010014 (  0) 0)
|
| [4] |
汤胜清, 程小华. 一种基于多层前向神经网络的谐波检测方法[J]. 中国电机工程学报, 2006, 26(18): 90-94. TANG Shengqing, CHENG xiaohua. A harmonic detection method based on themulti-layer forward neural network[J]. Proceedings of the CSEE, 2006, 26(18): 90-94. DOI:10.3321/j.issn:0258-8013.2006.18.016 (  0) 0)
|
| [5] |
李圣清, 朱英浩, 周又庆, 等. 电网谐波检测方法的综述[J]. 高电压技术, 2004, 30(3): 39-43. LI Shenqing, ZHU Yinghao, ZHOU Youqing, et al. Review of power grid harmonic detection method[J]. High voltage technique, 2004, 30(3): 39-43. (  0) 0)
|
| [6] |
DASH P K, PANDA S K, MISHRA B, et al. Fast estimation of voltage and current phasors in power networks using an adaptive neural network[J]. IEEE transactions on power system, 1997, 12(4): 1491-1499. (  0) 0)
|
| [7] |
VENKADESAN A, RAMAN K S, CHANDRASEKARAN K, et al. Artificial neural network based harmonics estimator for a power electronics converter[J]. Indian journal of Saience & technology, 2016, 42(9): 1-5. (  0) 0)
|
| [8] |
TAGAWA Y, KAJIWARA K. Controller development for the E-defense shaking table[J]. Proceedings of the institution of mechanical engineers Part Ⅰ journal of systems & control engineering, 2007, 221: 171-181. (  0) 0)
|
| [9] |
刘金琨, 沈晓蓉, 赵龙. 系统辨识理论及MATLAB仿真[M]. 北京: 电子工业出版社, 2013: 45-55. LIU Jinkun, SHEN Xiaorong, ZHAO Long. System identification theory and MATLAB simulation[M]. Beijing: Publishing House of Electronics Industry, 2013: 45-55. (  0) 0)
|
| [10] |
ZHANG Zhening, JIA Jie, DING Ruifeng. Hirarchical least squares based iterative parameter estimation algorithm for multivariable Box-Jenkins-like system using the auxiliary model[J]. Applied mathematical computation, 2012, 218(9): 5580-5587. DOI:10.1016/j.amc.2011.11.051 (  0) 0)
|
| [11] |
DING Feng, CHEN Tao. Gradient based iterative algorithm for soling a class of matrix equations[J]. IEEE transactions on automatic control, 2005, 50(8): 1216-1221. DOI:10.1109/TAC.2005.852558 (  0) 0)
|
| [12] |
YAO Jianjun, DI Duotao, JIANG Guilin, et al. Acceleration amplitude-phase regulation for electro-hydraulic servo shaking table based on LMS adaptive filtering algorithm[J]. International journal of control, 2010, 85(10): 1581-1592. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


