群桩系统的共同作用研究一直是岩土工程中的热点问题。目前较有效的方法有两种:一种是使用有限单元法(finite element method)或完全离散条件下的边界元法(boundary element method)来研究桩筏基础的共同作用[1-2](该方法严谨,结果精确,尽管过于复杂,至今作为主要方法应用于桩基工程领域);另一种是建立在弹性理论叠加原理基础上桩基相互作用系数法[3]。该方法建立在弹性力学理论和叠加原理基础上的桩基相互作用系数法,因边界条件和力学模型的简化而变得更加实用。然而,在群桩变形分析中,因传统的桩基相互作用系数法不能很好地考虑桩基与临近桩位的土体位移场的相互影响,使得桩基相互作用系数计算值会高于实测值,从而低估了群桩抵抗变形的刚度[4]。随着国内大型群桩基础在超高层建筑的工程建设中应用日趋广泛,很多学者对群桩变形计算中加筋效应影响进行了深入的研究,取得了丰富的研究成果[5-12],然而现有的分析方法一方面计算较为复杂,近似假定给理论方法的工程应用造成难度,另一方面群桩分析过程中并未充分考虑群桩基础中桩基相互加筋效应对群桩变形的影响,因此群桩变形理论研究上仍有较大改进和完善的空间。群桩基础的抗拔作用作为在地下室施工阶段的超高层建筑的基础体现形式和抵抗地下水浮力的主要措施,抗拔群桩的变形理论研究更待完善和深入。鉴于以上背景,本文对考虑加筋效应的抗拔群桩变形理论计算进行了深入研究,基于薄壁同心圆筒剪切变形模式和弹性叠加原理,推导得到能同时考虑抗拔群桩中桩基相互加筋效应的理论解析解答。
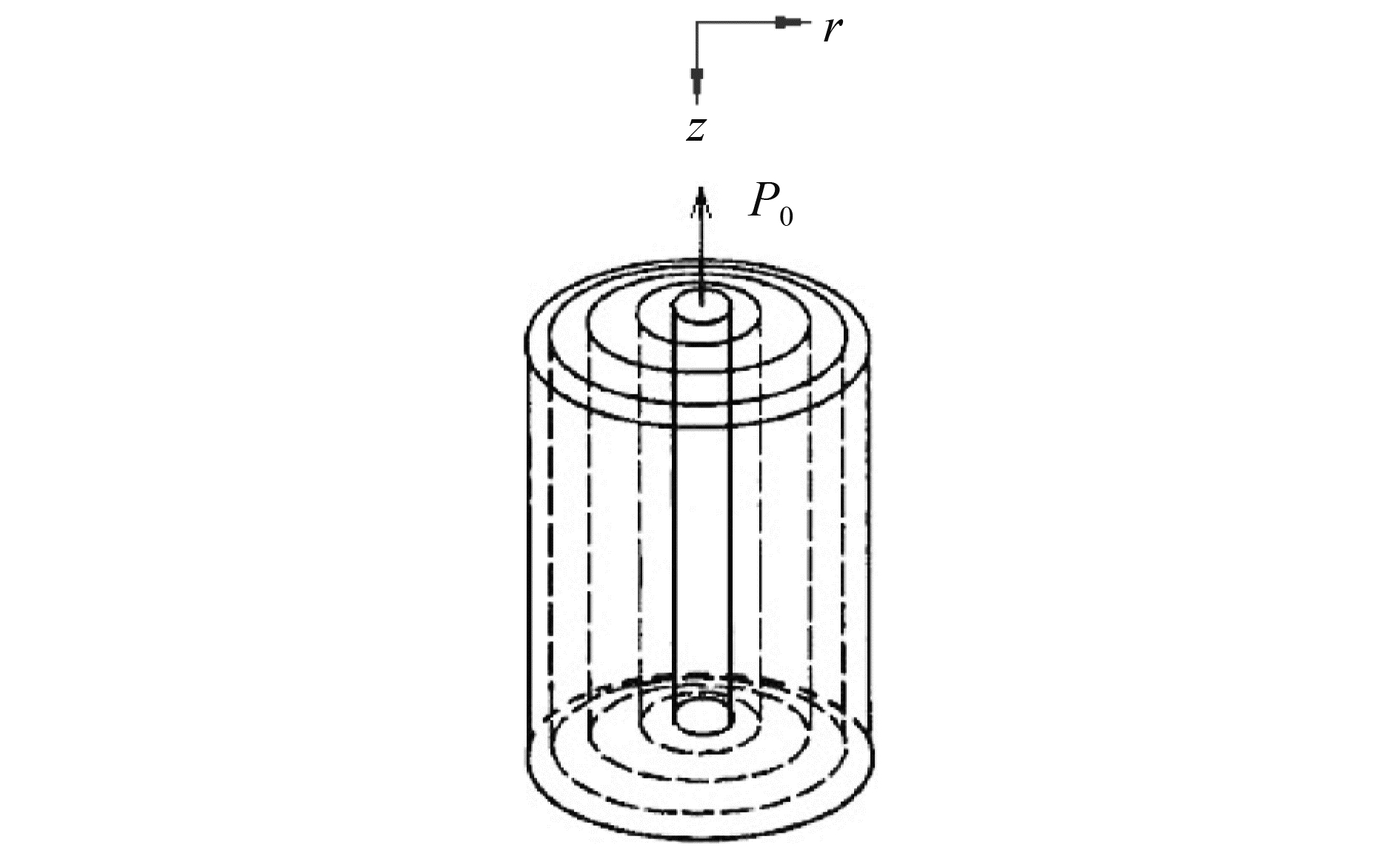
1 抗拔桩薄壁同心圆筒剪切变形模式Randolph等在等截面抗压桩的研究中,对桩周土的变形机理进行了研究[13],以桩体为轴心的土体剪切变形模式被试验结果所证实。根据该思路,这里将等截面抗拔单桩的桩周土体变形也理想化为桩周土体薄壁同心圆筒的剪切变形,桩体被视作倒插在圆筒中心轴线上的弹性体,如图 1所示。图中z方向为沿桩长方向,r方向为沿桩径方向,P0为桩顶上拔荷载。
|
图 1 薄壁同心圆筒剪切变形模式 Fig.1 The shear deformation mode of thin walled concentric cylinder |
距桩轴r处上单元的剪应变为
| $ \gamma = \frac{{{\rm{d}}S\left( {r,z} \right)}}{{{\rm{d}}r}} $ | (1) |
式中:S(r, z)为深度z处桩侧土体的竖向变形。
等截面抗拔单桩在桩顶上拔力作用下,桩体本身会产生拉伸变形,沿桩身剪应力τ为变化的数值。τ应与径向距离r、深度z有关,则
| $ \tau \left( {r,z} \right) = {G_s}\gamma = {G_s}\frac{{{\rm{d}}S\left( {r,z} \right)}}{{{\rm{d}}r}} $ | (2) |
式中:Gs为土的剪切模量。
根据平衡条件有
| $ \tau \left( {r,z} \right) = \frac{{{\tau _0}\left( {{r_0},z} \right){r_0}}}{r} $ | (3) |
式中:τ0(r0, z)= τ(r, z)|r=ro,r0为抗拔桩的半径。
将式(3)代入式(2)得
| $ {\rm{d}}S\left( {r,z} \right) = \frac{{\tau \left( {r,z} \right)}}{{{G_s}}}{\rm{d}}r = \frac{{{\tau _0}\left( {{r_0},z} \right){r_0}}}{{{G_s}}}\frac{{{\rm{d}}r}}{r} $ | (4) |
在均质土中,式(4)变形为
| $ \left\{ \begin{array}{l} S\left( {r,z} \right) = \frac{{{\tau _0}\left( {{r_0},z} \right){r_0}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{r}} \right),{r_0} \le r \le {r_m}\\ S\left( {r,z} \right) = 0,r > {r_m} \end{array} \right. $ | (5) |
令r=r0,将式(5)简化为
| $ S\left( z \right) = \xi \frac{{{\tau _0}\left( z \right){r_0}}}{{{G_s}}} $ | (6) |
式中:S(z)= S(r, z)|r=ro,τ0(z)= τ(r, z)|r=ro, ξ=ln(rm/r0)。
根据Randolph等的研究[13],rm表达式为
| $ {r_m} = 2.5\left( {1 - {\mathit{\boldsymbol{v}}_s}} \right)l $ | (7) |
式中:vs为桩侧土体的泊松比,l为桩长。但对于桩身刚度较小、桩长过短或过长时,如采用式(7)来考虑rm会产生一定的误差[8]。
根据弹性力学,在深度z处桩身变形与轴力的关系为
| $ \frac{{\partial S\left( z \right)}}{{\partial z}} = - \frac{{P\left( z \right)}}{{{\rm{ \mathsf{ π} }}r_0^2{E_p}}} $ | (8) |
式中:Ep为桩的弹性模量。
根据剪应力平衡条件,得
| $ \frac{{{\partial ^2}S\left( z \right)}}{{\partial {z^2}}} = \frac{{ - 1}}{{{\rm{ \mathsf{ π} }}r_0^2{E_p}}}\frac{{\partial P\left( z \right)}}{{\partial z}} = \frac{2}{{{r_0}{E_p}}}{\tau _0}\left( z \right) $ | (9) |
由式(8)和(9)可得
| $ \frac{{{\partial ^2}S\left( z \right)}}{{\partial {z^2}}} = \frac{{ - 1}}{{{\rm{ \mathsf{ π} }}r_0^2{E_p}}}\frac{{\partial P\left( z \right)}}{{\partial z}} = \frac{2}{{{r_0}{E_p}}}{\tau _0}\left( z \right) $ | (10) |
将式(7)代入式(10),得到控制微分方程为
| $ \frac{{{\partial ^2}S\left( z \right)}}{{\partial {z^2}}} = \frac{{2S\left( z \right)}}{{r_0^2\xi \lambda }} $ | (11) |
式中:λ=Ep/Gs。
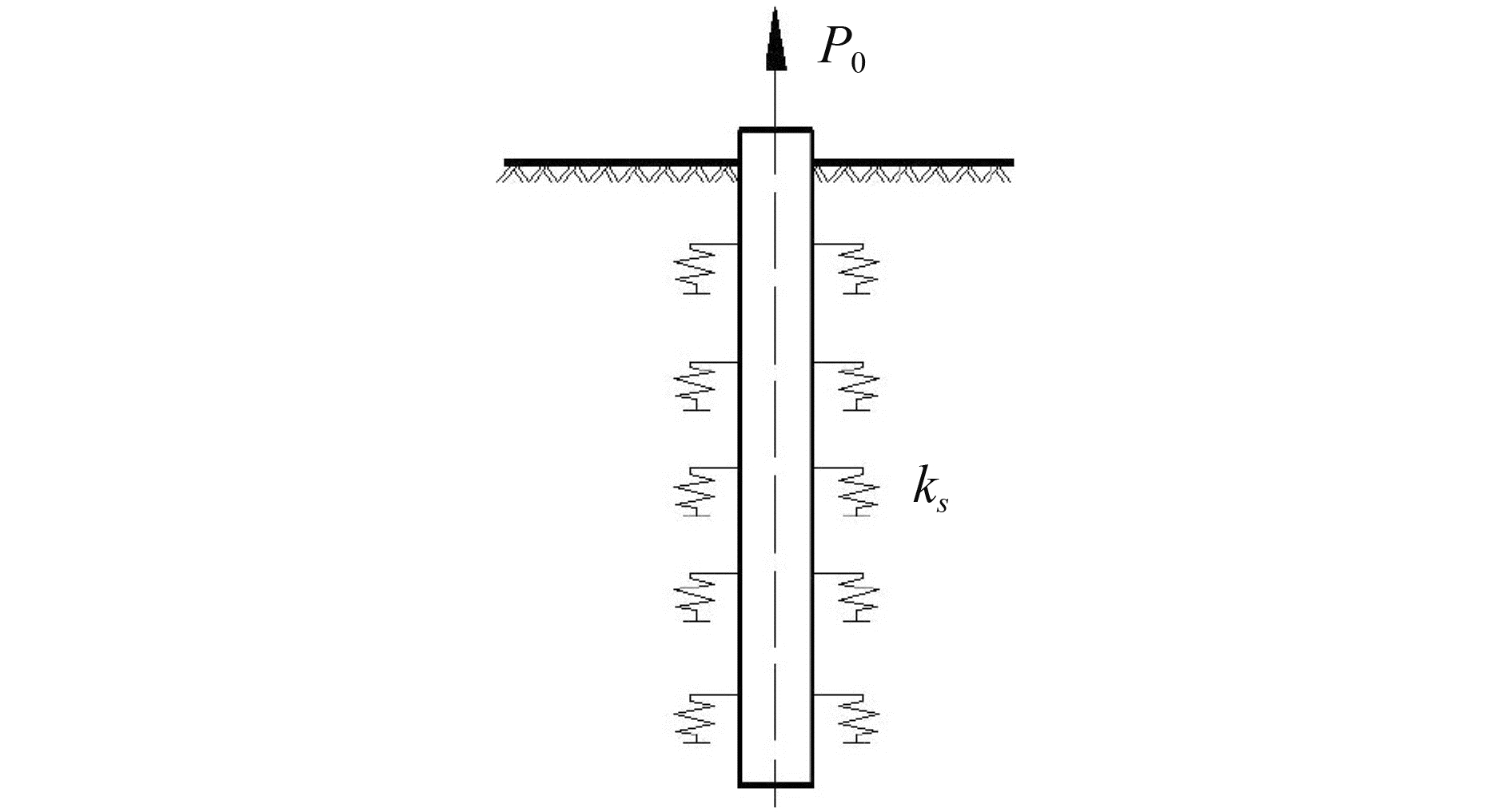
2 桩土弹簧刚度为等截面抗拔单桩基于荷载传递函数法的解析推导,假定桩体为弹性材料,桩在上拔力作用下会产生对应变形,如图 2所示。图中ks为桩土弹簧刚度。
|
图 2 桩土弹簧示意图 Fig.2 Schematic diagram of spring between pile and soil |
从抗拔桩身任意位置选取桩单元,根据力的平衡有
| $ {\rm{d}}P\left( z \right) = {U_m}{k_s}S\left( z \right){\rm{d}}z $ | (12) |
式中:Um为桩身周长。
桩身轴力和变形关系式为
| $ P\left( z \right) = {E_p}{A_p}\frac{{{\rm{d}}S\left( z \right)}}{{{\rm{d}}z}} $ | (13) |
将式(13)微分得
| $ \frac{{{\rm{d}}P\left( z \right)}}{{{\rm{d}}z}} = {E_p}{A_p}\frac{{{{\rm{d}}^2}S\left( z \right)}}{{{\rm{d}}{z^2}}} $ | (14) |
联合式(12)和式(14),可得
| $ {E_p}{A_p}\frac{{{{\rm{d}}^2}S\left( z \right)}}{{{\rm{d}}{z^2}}} - 2{\rm{ \mathsf{ π} }}{r_0}{k_s}S\left( z \right) = 0 $ | (15) |
通过分析式(11)和式(15)可知,2种基于弹性理论的解析解答的求解原理不同,但求解结果的本质相同。为利用2种求解方法联合求解桩基变形问题,令:
| $ {k_s} = \frac{{{G_s}}}{{{r_0}\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right)}} $ | (16) |
抗拔群桩基础中,选取任意桩(如i桩)的,其上拔位移的组成为:
1) i桩桩顶作用上拔荷载Pi时,而且j桩不存在时,i桩自身产生上拔主动位移Sii;
2) i桩无荷载状态下,j桩承受荷载Pj作用,j桩的上拔主动位移Sjj将使i桩产生上拔被动位移Sij。Sjj计算方法同Sii;
3) i桩桩顶作用上拔荷载Pi时,j桩存在但桩顶无荷载,考虑j桩对i桩的加筋效应,将对i桩的上拔主动位移Sii产生阻碍位移Sij1,i桩的实际位移为S′ii;同时,考虑i桩对j桩的加筋效应,对j桩的上拔被动位移Sji产生阻碍位移Sji1,将使j桩的实际上拔被动位移为Sji;
4) 在上述2)情况下,考虑i桩对j桩的加筋效应,将对j桩的上拔主动位移Sjj产生阻碍位移Sji,考虑加筋效应后j桩的实际位移为Sjj;同时,考虑j桩对i桩的加筋效应,对i桩的上拔被动位移Sij产生阻碍位移Sij1,将使i桩的实际上拔被动位移为Sij。
由上述位移分析可知,抗拔群桩中i桩的最终位移为
| $ \begin{array}{*{20}{c}} {{S_i}\left( z \right) = {{S'}_{ii}}\left( z \right) + \sum\limits_{j = 1,j \ne i}^n {{{S'}_{ij}}\left( z \right)} = }\\ {{{S'}_{ii}}\left( z \right) + \sum\limits_{j = 1,j \ne i}^n {{\xi _{ij}}{{S'}_{ij}}\left( z \right)} } \end{array} $ | (17) |
式中:
| $ {{S'}_{ii}}\left( z \right) = {S_{ii}}\left( z \right) - {S_{ij1}}\left( z \right) $ | (18) |
| $ {{S'}_{ij}}\left( z \right) = {S_{ij}}\left( z \right) - {{S'}_{ij}}\left( z \right) $ | (19) |
| $ {\xi _{ij}} = {{S'}_{ij}}/{{S'}_{jj}} $ | (20) |
同理,抗拔群桩中j桩的最终位移为
| $ \begin{array}{*{20}{c}} {{S_j}\left( z \right) = {{S'}_{jj}}\left( z \right) + \sum\limits_{i = 1,i \ne j}^n {{{S'}_{ji}}\left( z \right)} = }\\ {{{S'}_{jj}}\left( z \right)\sum\limits_{i = 1,i \ne j}^n {{\xi _{ji}}{{S'}_{ii}}\left( z \right)} } \end{array} $ | (21) |
式中:
| $ {{S'}_{jj}}\left( z \right) = {S_{jj}}\left( z \right) - {S_{ji}}\left( z \right) $ | (22) |
| $ {{S'}_{jj}}\left( z \right) = {S_{ji}}\left( z \right) - {{S'}_{ji1}}\left( z \right) $ | (23) |
| $ {\xi _{ji}} = {{S'}_{ji}}/{{S'}_{ii}} $ | (24) |
上述i桩的位移计算中,式(21)的计算相对比较完善[3, 13-14]。文献[11-12]中对桩基相互加筋效应进行了深入的理论研究,但位移SijV求解中未能考虑因i桩对j桩的加筋效应引起的桩土弹簧刚度影响;同时未考虑“i桩无荷载状态下,j桩承受荷载Pj作用”时,j桩对i桩的加筋效应引起i桩处土体位移场的影响(即:“i桩无荷载状态下,j桩承受荷载Pj作用”时,考虑j桩对i桩的加筋效应,对i桩的上拔被动位移Sij产生阻碍位移S′ii1,将使i桩的实际上拔被动位移为S′ii)。
4 抗拔群桩变形解析解 4.1 计算模型如图 1所示,设抗拔桩群由n根等截面抗拔单桩组成,桩身位于均质土中,群桩中各桩基的材料、直径、间距和入土深度均相同。
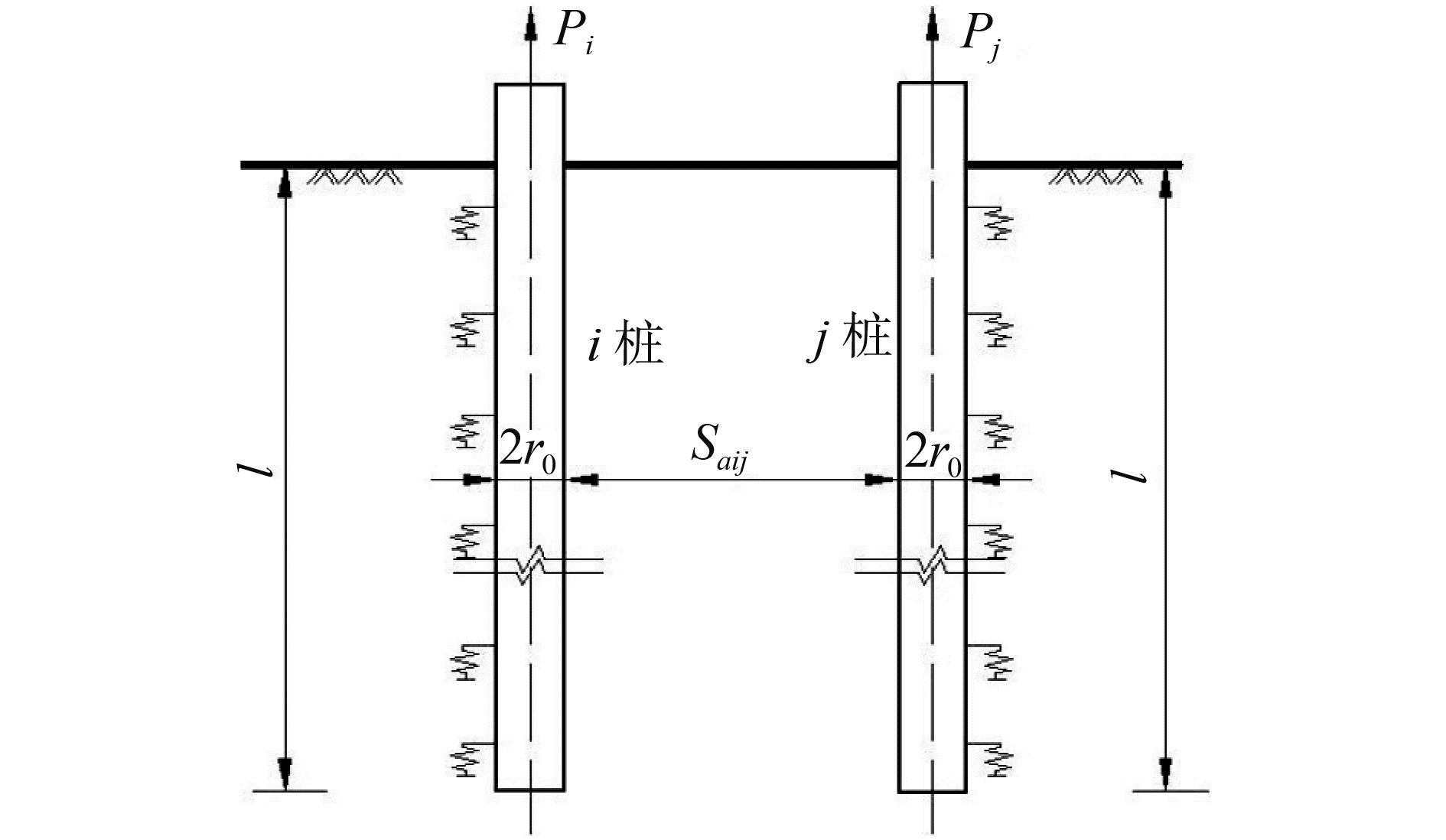
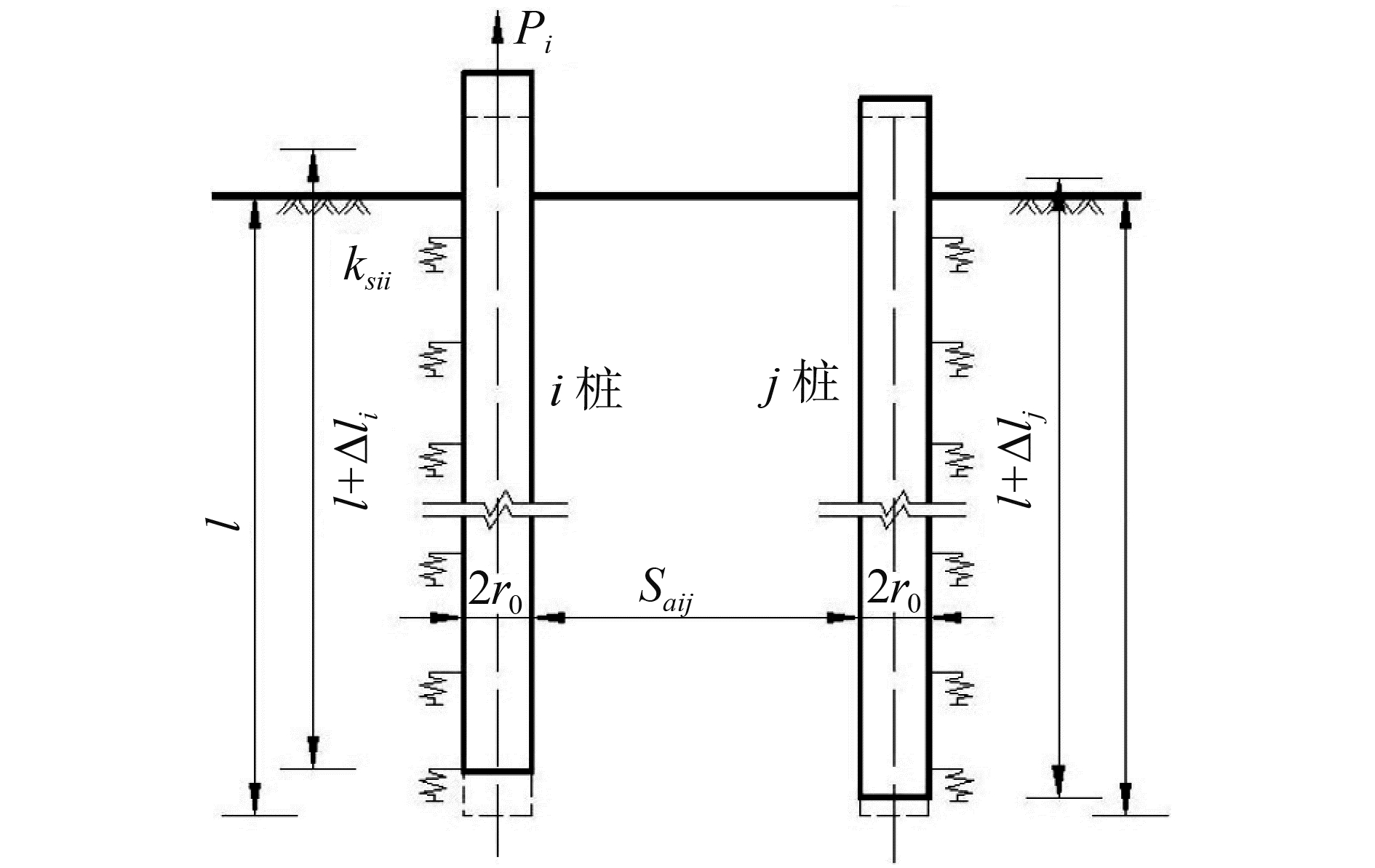
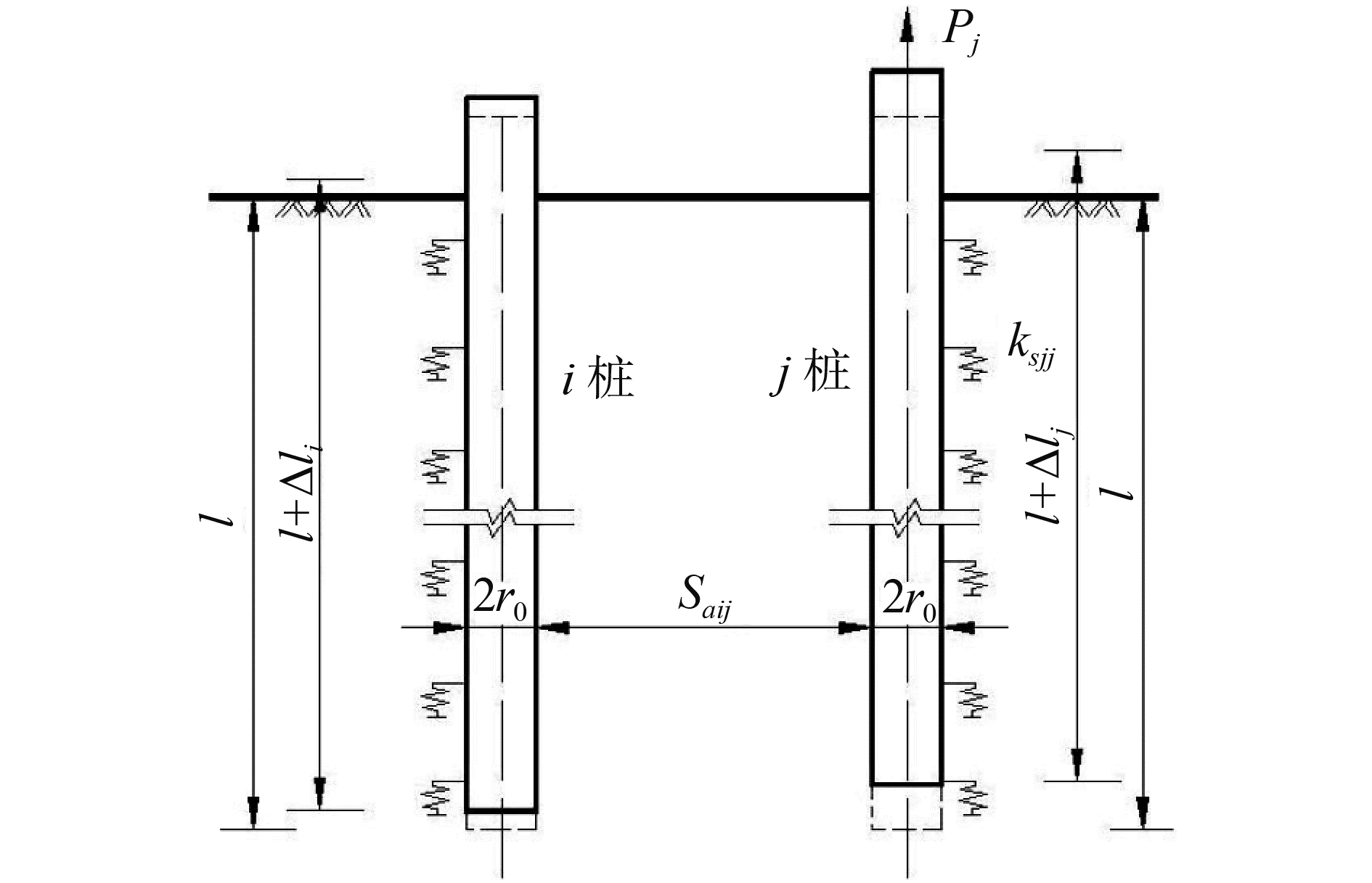
为便于分析抗拔桩基间的加筋效应,由上述分析可知,任取抗拔群桩中两桩,以i桩为例,i桩的位移Si由SiiV和S′ij组成。这里S′ii、SijV均充分考虑i桩、j桩间的相互加筋效应。计算模型见图 3~5。图中:Saij为i桩与j桩间净距;Δli、Δlj分别为SiiV计算工况时i桩、j桩在i桩上拔荷载Pi作用下产生的桩身变形量;ΔlVi、Δl′j分别为S′ij计算工况时i桩、j桩在j桩上拔荷载Pj作用下产生的桩身变形量。
|
图 3 抗拔桩群分析模型 Fig.3 Analytical model of uplift group piles |
|
图 4 S′ii计算模型 Fig.4 Calculating model of S′ii |
|
图 5 S′ij计算模型 Fig.5 Calculating model of S′ij |
如图 4所示工况,设i桩周土体z深度处的摩阻力为τi0,τi0在深度z处引起的土体位移场为
| $ \left\{ \begin{array}{l} {S_{ii}}\left( z \right) = \frac{{{\tau _{i0}}{r_0}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{r}} \right),\;\;\;r < {r_m}\\ {S_{ii}}\left( z \right) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;r \ge {r_m} \end{array} \right. $ | (25) |
据薄壁同心圆筒剪切变形模式,i桩桩周土体中的摩阻力τi0以剪应力方式沿径向传递,在j桩的同一深度处为
| $ {\tau _{ji}} = \frac{{{\tau _{i0}}{r_0}}}{{{S_{aij}}}} $ | (26) |
式中:τji为i桩引起的j桩桩周的向上的侧摩阻力,此时j桩桩周也会产生与τji方向相反、大小相等的侧摩阻力τ′ji。式(26)代入式(6),可得τ′ji在i桩周土体中引起的位移场为
| $ \left\{ \begin{array}{l} {S_{ij1}}\left( z \right) = \frac{{{r_0}{\tau _{i0}}}}{{{S_{aij}}}}\frac{{{r_0}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{r}} \right),\;\;\;r < {r_m}\\ {S_{ij1}}\left( z \right) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;r \ge {r_m} \end{array} \right. $ | (27) |
考虑i桩、j桩的相互加筋效应后,i桩桩顶荷载Pi引起的深度z处的位移为
| $ \begin{array}{*{20}{c}} {{{S'}_{ii}}\left( z \right) = {S_{ii}}\left( z \right) - {S_{ij1}}\left( z \right) = }\\ {\frac{{{\tau _{i0}}{r_0}}}{{{G_s}}}\left[ {\ln \left( {\frac{{{r_m}}}{r}} \right) - \sum\limits_{j = 1,j \ne i}^n {\frac{{{r_0}}}{{{S_{aij}}}}\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right)} } \right]} \end{array} $ | (28) |
根据式(16),i桩桩周单位厚度的桩土弹簧刚度为
| $ {k_{sii}} = \frac{{{G_s}}}{{\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right) - \sum\limits_{j = 1,j \ne i}^n {\frac{{{r_0}}}{{{S_{aij}}}}\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right)} }} $ | (29) |
对于图(4)荷载工况,i桩微分控制方程为
| $ {E_p}{A_p}\frac{{{{\rm{d}}^2}{{S'}_{ii}}\left( z \right)}}{{{\rm{d}}{z^2}}} - 2{\rm{ \mathsf{ π} }}{k_{sii}}{{S'}_{ii}}\left( z \right) = 0 $ | (30) |
根据桩顶和桩端受力情况,得式(30)的边界条件为
| $ \left\{ \begin{array}{l} {E_p}{A_p}\frac{{{\rm{d}}{{S'}_{ii}}\left( z \right)}}{{{\rm{d}}z}}\left| {_{z = 0}} \right. = {P_i}\\ {E_p}{A_p}\frac{{{\rm{d}}{{S'}_{ii}}\left( z \right)}}{{{\rm{d}}z}}\left| {_{z = l}} \right. = 0 \end{array} \right. $ | (31) |
其解为
| $ {{S'}_{ii}}\left( z \right) = {c_1}{{\rm{e}}^{{\lambda _{ii}}z}} + {c_2}{{\rm{e}}^{ - {\lambda _{ii}}z}} $ | (32) |
其中:
| $ {\lambda _{ii}} = \sqrt {\frac{{{k_{sii}}}}{{{E_p}{A_p}}}} ,{c_1} = \frac{{ - {P_i}{{\rm{e}}^{ - {\lambda _{ii}}l}}}}{{2{E_p}{A_p}{\lambda _{ii}}\sinh \left( {{\lambda _{ii}}l} \right)}}, $ |
| $ {c_2} = \frac{{ - {P_i}{{\rm{e}}^{{\lambda _{ii}}l}}}}{{2{E_p}{A_p}{\lambda _{ii}}\sinh \left( {{\lambda _{ii}}l} \right)}} $ |
同理,根据图 5所示工况可得考虑i桩、j桩间的相互加筋效应后,j桩桩顶上拔力Pj引起的深度z处的位移为
| $ {{S'}_{jj}}\left( z \right) = {c_3}{{\rm{e}}^{{\lambda _{jj}}z}} + {c_4}{{\rm{e}}^{ - {\lambda _{jj}}z}} $ | (33) |
其中:
| $ {\lambda _{jj}} = \sqrt {\frac{{{k_{sjj}}}}{{{E_p}{A_p}}}} ,{c_3} = \frac{{ - {P_j}{{\rm{e}}^{ - {\lambda _{jj}}l}}}}{{2{E_p}{A_p}{\lambda _{jj}}\sinh \left( {{\lambda _{jj}}l} \right)}}, $ |
| $ {c_4} = \frac{{ - {P_j}{{\rm{e}}^{{\lambda _{jj}}l}}}}{{2{E_p}{A_p}{\lambda _{jj}}\sinh \left( {{\lambda _{jj}}l} \right)}}, $ |
| $ {k_{sjj}} = \frac{{{G_s}}}{{\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right) - \sum\limits_{i = 1,i \ne j}^n {\frac{{{r_0}}}{{{S_{aij}}}}\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right)} }} $ |
引入系数ξij,其物理意义为:“i桩无荷载状态下,j桩承受荷载Pj作用”工况时,考虑i桩和j桩的相互加筋效应后,在相同深度处i桩与j桩的位移之比,即ξij=S′ij/S′jj。该系数的引入解决了文献[11-12]中位移S′ij求解中未考虑因i桩对j桩的加筋效应引起的桩土弹簧刚度影响,和未考虑j桩对i桩的加筋效应引起对i桩的上拔被动位移Sij产生阻碍位移S′ij1的不足。
如上述图 5所示,根据Randolph和Worth的方法,当j桩受桩顶荷载Pi作用时,在桩侧产生侧摩阻力τi0,其在某一深度z处产生的自由位移场为
| $ \left\{ \begin{array}{l} {S_{jj}}\left( z \right) = \frac{{{\tau _{j0}}{r_0}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{r}} \right),\;\;\;r < {r_m}\\ {S_{jj}}\left( z \right) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;r \ge {r_m} \end{array} \right. $ | (34) |
由式(34)可知:τi0在深度z处的j桩、i桩位置上产生的位移分别为
| $ \left\{ \begin{array}{l} {S_{jj}}\left( z \right) = \frac{{{\tau _{j0}}{r_0}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right),\;\;\;r \le {r_m}\\ {S_{ij}}\left( z \right) = \frac{{{\tau _{j0}}{r_0}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right),\;\;r \le {r_m} \end{array} \right. $ | (35) |
式中:Sij(z)为考虑j桩对i桩的加筋效应,将使i桩产生的上拔被动位移。
根据薄壁同心圆筒剪切变形模式,桩侧摩阻力τi0由桩周土以剪应力形式沿径向向外传递时,传递到i桩桩周同一深度处变为
| $ {\tau _{ij}} = \frac{{{\tau _{j0}}{r_0}}}{{{S_{aij}}}} $ | (36) |
当侧摩阻力传递到i桩处,i桩的存在将会对j桩传递来的效应产生被动的相互作用,这种作用阻碍j桩周土体的剪切变形,便产生与桩周土体剪切变形方向相反的力τ′ii,其大小与τii相等,方向相反。τ′ii在土中深度z处的i桩、j桩位置上产生的位移分别为
| $ \left\{ \begin{array}{l} {{S'}_{ij1}}\left( z \right) = \frac{{{r_0}{\tau _{j0}}}}{{{S_{aij}}}}\frac{{{r_0}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right),\;\;\;r \le {r_m}\\ {S_{ji}}\left( z \right) = \frac{{{r_0}{\tau _{j0}}}}{{{S_{aij}}}}\frac{{{r_0}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right),\;\;r \le {r_m} \end{array} \right. $ | (37) |
因此,充分考虑到i桩与j桩相互加筋效应后,则有j桩在深度z处产生的实际位移为Sii和Sii的叠加:
| $ \begin{array}{*{20}{c}} {{{S'}_{jj}} = {S_{jj}}\left( z \right) - {S_{ji}}\left( z \right) = }\\ {\frac{{{r_0}{\tau _{j0}}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right) - \frac{{{r_0}{\tau _{j0}}}}{{{S_{aij}}}}\frac{{{r_0}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right)} \end{array} $ | (38) |
同理可得i桩在深度z处产生的位移S′jj为Sii和S′ii1的叠加
| $ \begin{array}{*{20}{c}} {{{S'}_{jj}} = {S_{jj}}\left( z \right) - {S_{ij1}}\left( z \right) = }\\ {\frac{{{r_0}{\tau _{j0}}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right) - \frac{{{r_0}{\tau _{j0}}}}{{{S_{aij}}}}\frac{{{r_0}}}{{{G_s}}}\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right)} \end{array} $ | (39) |
根据上述相互作用系数定义,由式(38)和式(39)可得
| $ \begin{array}{*{20}{c}} {{\xi _{ij}} = \frac{{{{S'}_{ij}}\left( z \right)}}{{{{S'}_{jj}}\left( z \right)}} = \frac{{\frac{{{r_0}{\tau _{j0}}}}{{{G_s}}}\left[ {\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right) - \frac{{{r_0}}}{{{S_{aij}}}}\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right)} \right]}}{{\frac{{{r_0}{\tau _{j0}}}}{{{G_s}}}\left[ {\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right) - \frac{{{r_0}}}{{{S_{aij}}}}\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right)} \right]}} = }\\ {\frac{{\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right) - \frac{{{r_0}}}{{{S_{aij}}}}\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right)}}{{\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right) - \frac{{{r_0}}}{{{S_{aij}}}}\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right)}},\;\;\;\;r \le {r_m}} \end{array} $ | (40) |
式(39)即为在考虑桩的相互加筋效应时,推导求得的相互作用系数的具体表达式。
4.4 抗拔群桩位移解答考虑抗拔群桩中各桩基相互加筋效应后,可得到i桩的位移为
| $ \begin{array}{*{20}{c}} {{S_i}\left( z \right) = {{S'}_{ii}}\left( z \right) + \sum\limits_{j = 1,j \ne i}^n {{\xi _{ij}}{{S'}_{jj}}\left( z \right)} = }\\ {{{S'}_{ii}}\left( z \right) + \sum\limits_{j = 1,j \ne i}^n {\frac{{\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right) - \frac{{{r_0}}}{{{S_{aij}}}}\ln \left( {\frac{{{r_m}}}{{{r_0}}}} \right)}}{{\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right) - \frac{{{r_0}}}{{{S_{aij}}}}\ln \left( {\frac{{{r_m}}}{{{S_{aij}}}}} \right)}}{{S'}_{jj}}\left( z \right)} } \end{array} $ | (41) |
若承台顶部抗拔力P已知,当桩基承台为柔性承台时,将下列方程代入式(41)得到各桩位移(r0 < Saij < rm):
| $ \left\{ \begin{array}{l} {P_i} = \frac{P}{n},\;\;\;1 \le i \le n\\ z = 0 \end{array} \right. $ | (42) |
当桩基承台为刚性承台时,利用下列方程得到各桩位移(r0 < Saij < rm):
| $ \left\{ \begin{array}{l} {S_i}\left( {z = 0} \right) = {S_j}\left( {z = 0} \right),\;\;\;\;1 \le i \le n\\ \sum\limits_{i = 1}^n {{P_i} = P} \end{array} \right. $ | (43) |
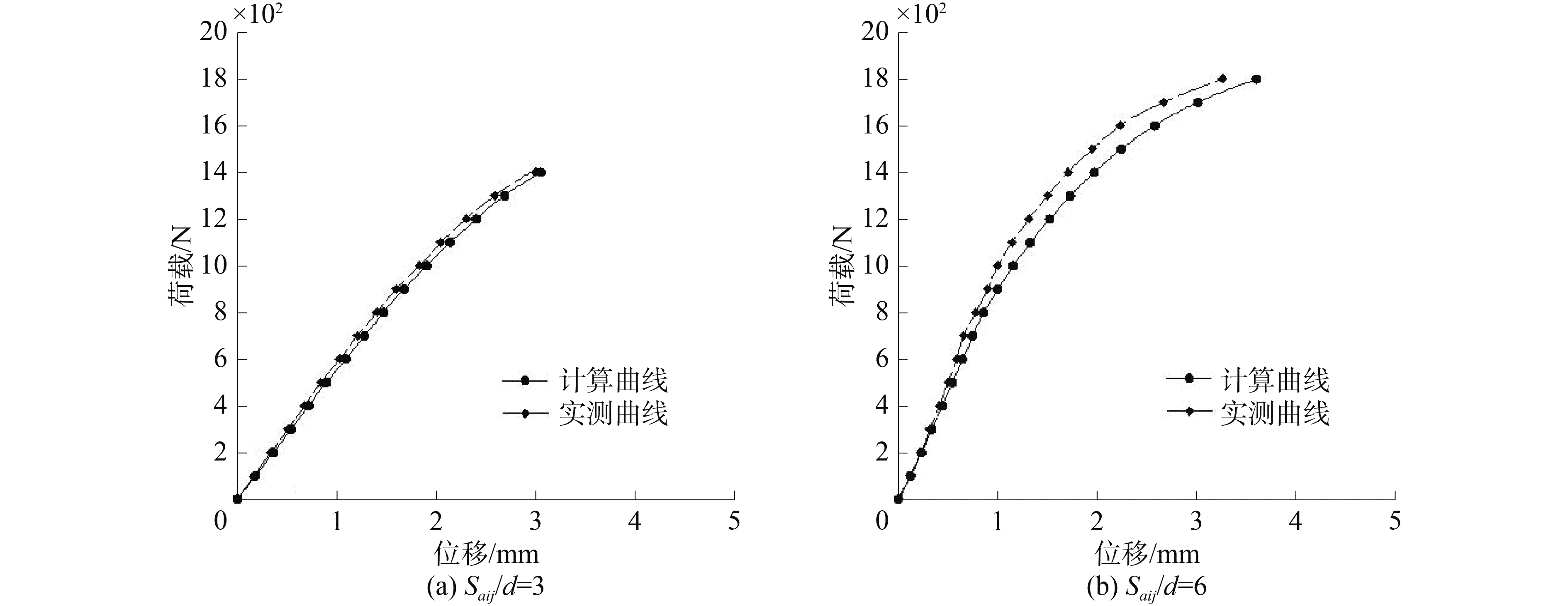
文献[15]对砂土中的抗拔群桩进行了模型试验研究。模型群桩的承台材料为铝板,其厚度为30 mm。试验模型分别对表面光滑和表面粗糙的铝合金管模型桩的桩基间共同作用进行了研究,这里选择与工程实际情况符合的表面粗糙模型桩试验结果与本文理论解进行比较,得到相关结论。模型试验参数如下:砂土为均匀干砂,砂土的单位重度为16.4 kN/m3,剪切模量Gs=500 kPa,泊松比vs=0.4。模型桩为铝合金管。桩的外直径为19 mm,壁厚0.81 mm。根据模型材料、厚度情况,本文假定承台为为刚性承台,桩身弹性模量Ep取为7×104 MPa。文献中给出了距径比为3倍桩径和距径比为6倍桩径下群桩变形曲线,与本文解析解得到的群桩变形曲线进行对比,如图 6所示。
|
图 6 实测曲线与理论曲线比较 Fig.6 Comparison between Calculated and measured Load-settlement curves |
分析可知,桩基间距对群桩变形的影响与算例2中的规律一致。因桩基间相互加筋效应,随着桩距变大,同一荷载作用下群桩变形较小,群桩的荷载变形曲线变缓,桩距对桩基的变形性能有明显的改善。在上拔力较小时,理论计算结果与变形实测值非常接近,但随着荷载增大,两者表现出一定差别,这是因为理论计算没有考虑砂土的剪胀效应引起的桩砂界面剪应力变化的影响,同时桩周砂粒密实度的改变引起了土体参数变化。
5.2 算例2某匀质饱和粘性土地基土上建筑物基础采用群桩基础,各桩均为抗拔桩兼作抗压桩。桩基采用直径为800 mm的等截面钻孔灌注桩。桩身采用C35混凝土,其养护满足28 d的龄期要求。为计算抗拔群桩的变形,这里仅考虑地下室施工阶段,即群桩作为抗拔桩出现这一工况。假定桩侧土体弹性模量分别为10、15、20 MPa,理论计算根据Gs=Ec/2(1+vs)可得到土体剪切模量。为方便研究抗拔群桩变形,这里假定承台为完全刚性,厚度为2 m。当然也可假定承台完全柔性,而将群桩中的各桩的理论位移与有限元结果进行比较分析。有限元计算中不考虑桩身泥皮效应对桩基变形的影响。实际上,工程中满足桩基对承台冲切验算时的承台在一般情况下接近刚性假定情况。
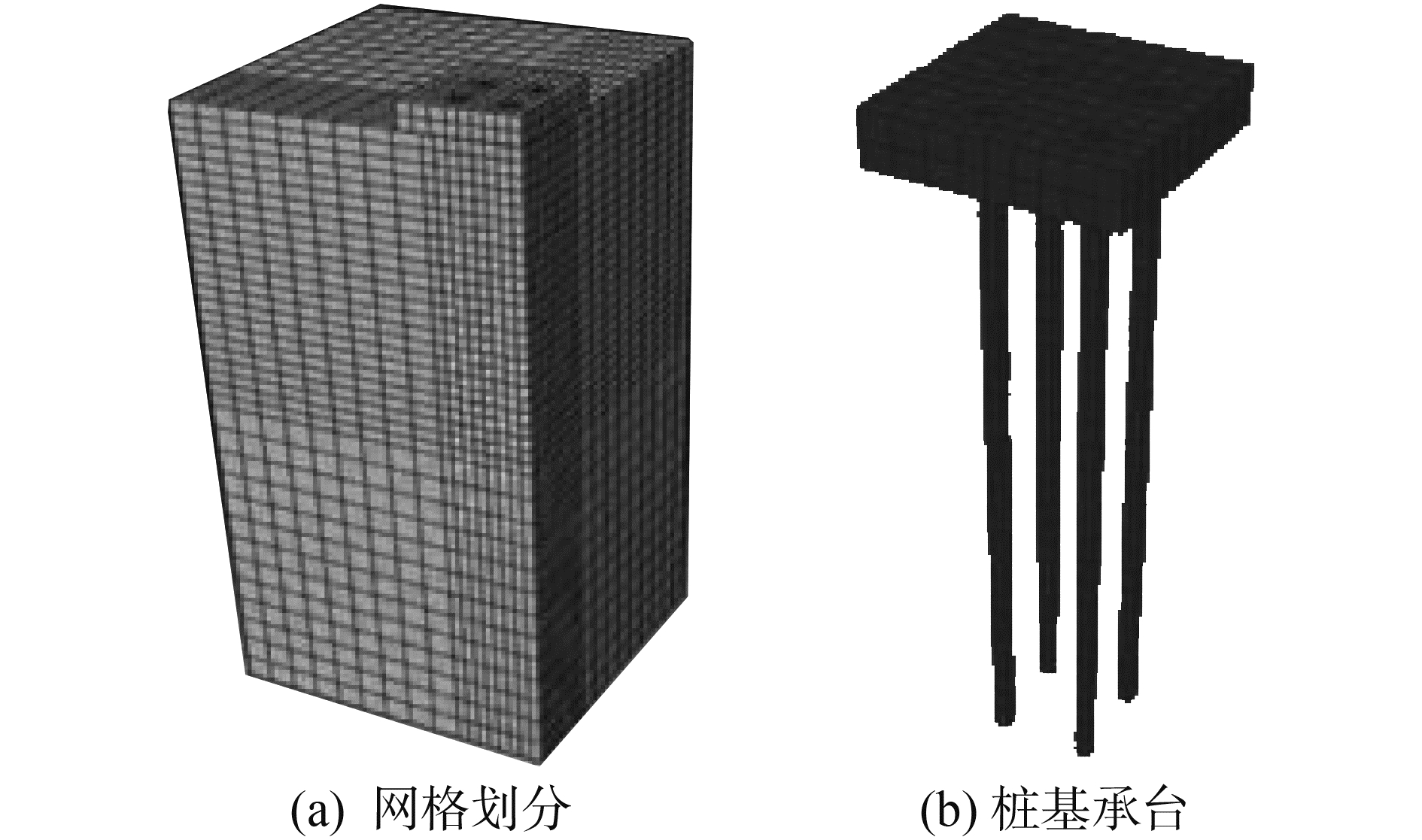
有限元分析模型的大小选取:取空间的1/4区域,水平方向取3倍承台宽度的范围,桩端向下延伸半倍桩长作为模型区域边界。模型边界约束:上表面为自由面,下表面约束竖向位移,对称面上取相应对称轴的对称约束,其他2个侧面分别约束其垂直方向上的位移。ABAQUS中的有限元建模及其网格划分如图 7所示。土体本构模型采用Mohr-Coulomb模型,桩体为线弹性体。桩体直径D=0.8 mm,弹性模量Ep=31.5 GPa,重度rp=25 kN/m3, 泊松比vp=0.17,土体重度rs=17.4 kN/m3,粘聚力c=19 kPa,内摩擦角φ=25°,泊松比vs=0.5。
|
图 7 三维有限元分析模型 Fig.7 3-D finite element analysis model |
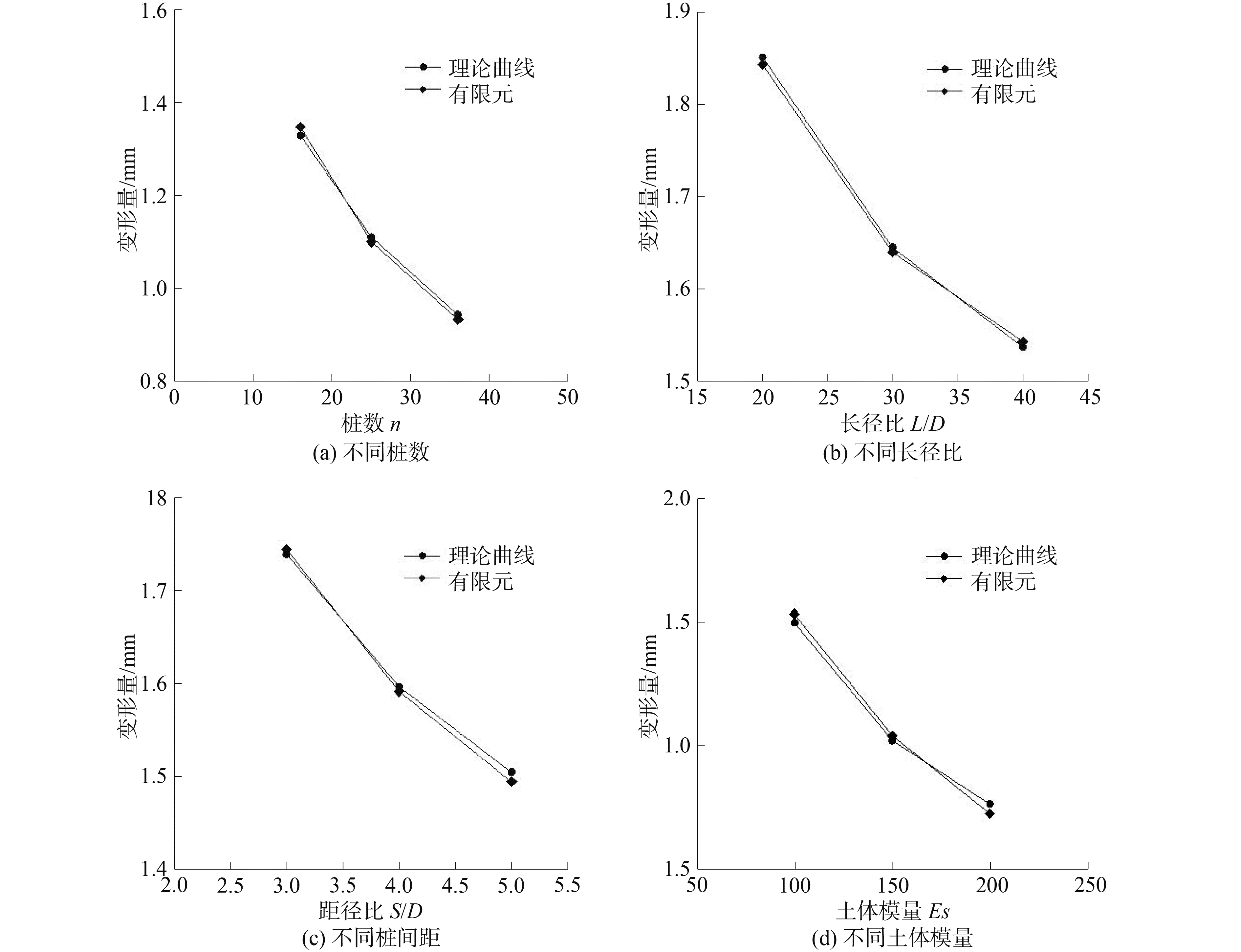
在上述既定上拔力情况下,解析解理论结果与有限元计算得到的结果如图 8所示。
|
图 8 不同桩数、长径比、桩间距、土体模量时变形计算结果 Fig.8 Calculated results of displacement with different n, L/d, S/D, Es |
本例中理论结果与有限元结果相当接近,重要因素是弹性理论计算方法和有限元法两种方法均是考虑抗拔群桩弹性阶段的分析结果。其实现阶段抗拔群桩设计过程中,受桩身强度、裂缝计算和群桩顶部变形控制设计三者的影响,认为群桩基础中各桩基处于弹性工作阶段是合适的。该方法充分考虑了群桩系统中桩基间的相互加筋效应,在群桩设计实践中有很好的应用前景。
由图 8(a)可知,群桩的变形随着桩数的增加而减少,增加桩数可以明显改善抗拔群桩的变形。但桩数增多到一定数量,对变形的改善效果并没有桩数较少时增加桩数时明显。因为对刚性承台承受特定的上拔荷载,增加的桩基会参与分摊上拔荷载,而且对群桩中任意一桩,随着远距离桩基加筋效应弱化,对抗拔变形有利影响也会减弱。这说明设计中应考虑在桩基抗拔强度完全发挥的前提下选择合适的桩数。由图 8(b)可知,长桩比短桩控制群桩变形的效果更加明显,但桩长到一定程度后,其对于群桩变形的改善效果并不明显。因为对抗拔桩来讲,随着桩长增大桩身拉伸量同时增大,桩顶变形达到变形控制值时桩端摩阻力可能还未发挥。尤其是现行规范[16]还要求桩身裂缝计算也要参与控制设计。抗拔群桩的桩长过长对工程意义不大,造成不必要的浪费。由图 8(c)可知,对特定的桩数、桩长、桩径,抗拔群桩基础中桩基间距对群桩变形的影响比较明显,增大桩间距明显改善群桩变形性能。桩间距增大后,各桩基间的相互加筋效应弱化,对抗拔群桩的有利作用增强。由图 8(d)可知,土体性能的改善对抗拔群桩变形影响比较明显,土质对桩基相互加筋效应的传递发挥一定的作用。这说明抗拔群桩设计中,作为抗拔桩,应根据现场的土体物理情况,在桩身强度、裂缝计算和群桩顶部变形控制设计的前提下,确定合理的桩数、桩长、桩间距,才可能成为最优方案。
6 结论1) 提出能同时考虑群桩基础中桩基相互加筋效应的理论解析解答。解析解理论计算结果与有限元分析和模型实测结果吻合较好。
2) 抗拔群桩承受工作荷载过程中,受桩身强度、裂缝计算和群桩顶部变形控制设计等因素的影响,桩基在工作荷载下一般处于弹性工作阶段,计算群桩相互作用符合群桩系统工程实际情况,因此本文理论方法具有很高的理论和实际工程价值,在大规模群桩的变形分析和设计实践中具有很好的应用前景。
| [1] |
BATTERFIELD R, BANERIEE P K. The elastic analysis of compressible piles and pile groups[J]. Geotechnique, 1971, 21(1): 43-60. DOI:10.1680/geot.1971.21.1.43 (  0) 0)
|
| [2] |
OTTAVIANI M. Three dimensional finite element analysis of vertically loaded pile groups[J]. Geotechnique, 1975, 25(2): 159-174. DOI:10.1680/geot.1975.25.2.159 (  0) 0)
|
| [3] |
POULOS H G, DAVIS E H. Pile foundation analysis and design[M]. New York: John Wiley and Sons, 1980: 71-142.
(  0) 0)
|
| [4] |
董建国, 赵锡宏. 高层建筑地基基础:共同作用理论与实践[M]. 上海: 同济大学出版社, 1997. DONG Jianguo, ZHAO Xihong. Theory and practice about interaction of high building foundation[M]. Shanghai: Tongji University Press, 1997. (  0) 0)
|
| [5] |
石名磊, 邓学钧, 刘松玉. 群桩间"加筋与遮帘"相互作用[J]. 东南大学学报, 2003, 33(3): 343-347. SHI Minglei, DENG Xuejun, LIU Songyu. Study of restrain effect among piles[J]. Journal of Southeast University, 2003, 33(2): 343-347. (  0) 0)
|
| [6] |
庞锋, 顾小安, 卢明康, 等. 群桩加筋效应机理研究[J]. 东南大学学报, 2004, 34(3): 390-392. PANG Feng, GU Xiaoan, LU Mingkang, et al. Study on reinforcing effect of grouped piles[J]. Journal of Southeast University, 2004, 34(3): 390-392. DOI:10.3969/j.issn.1001-0505.2004.03.025 (  0) 0)
|
| [7] |
石名磊, 战高峰. 群桩荷载位移特性研究[J]. 岩土力学, 2005, 26(10): 1607-1611. SHI Minglei, ZHAN Gaofeng. Research on load displacement characteristics of pile group[J]. Rock and soil mechanics, 2005, 26(10): 1607-1611. DOI:10.3969/j.issn.1000-7598.2005.10.016 (  0) 0)
|
| [8] |
梁发云, 陈龙珠, 李镜培. 加筋效应对群桩相互作用系数的影响[J]. 岩土力学, 2005, 26(11): 1757-1760. LIANG Fayun, CHEN Longzhu, LI Jingpei. Analysis of piles reinforced effects on interaction coefficients of piles[J]. Rock and soil mechanics, 2005, 26(11): 1757-1760. DOI:10.3969/j.issn.1000-7598.2005.11.012 (  0) 0)
|
| [9] |
吴晓峰, 王浩, 文新伦. 软土中已打入桩对土体位移的遮帘作用研究[J]. 岩土力学, 2006, 27(12): 2208-2212. WU Xiaofeng, WANG Hao, WEN Xinlun. Analysis of sheltering effects of previously driven piles on soil displacements in soft soils[J]. Rock and soil mechanics, 2006, 27(12): 2208-2212. DOI:10.3969/j.issn.1000-7598.2006.12.023 (  0) 0)
|
| [10] |
高盟, 高广运, 杨成彬. 层状地基群桩沉降计算的剪切位移解析算法[J]. 岩土力学, 2010, 31(4): 1072-1077. GAO Meng, GAO Guangyun, YANG Chengbin. Analytical solution for settlement of group piles in layered ground based on shear displacement method[J]. Rock and soil mechanics, 2010, 31(4): 1072-1077. (  0) 0)
|
| [11] |
赵明华, 邹丹, 邹新军. 基于荷载传递法的高承台桩基沉降计算方法研究[J]. 岩石力学与工程学报, 2005, 24(13): 2310-2314. ZHAO Minghua, ZOU Dan, ZOU Xinjun. Settlement calculation of pile foundations with elevated caps by load transfer method[J]. Chinese journal of rock mechanics and engineering, 2005, 24(13): 2310-2314. DOI:10.3321/j.issn:1000-6915.2005.13.019 (  0) 0)
|
| [12] |
赵明华, 邹丹, 邹新军. 群桩沉降计算的荷载传递法[J]. 工程力学, 2006, 23(7): 119-123. ZHAO Minghua, ZOU Dan, ZOU Xinjun. Settlement calculation of pile groups by load transfer method[J]. Engineering mechanics, 2006, 23(7): 119-123. (  0) 0)
|
| [13] |
RANDOLPH M F, WROTH C P. Analysis of deformation of vertically loaded piles[J]. Journal of geotechnical engineering, ASCE, 1978, 104(12): 1465-1489. (  0) 0)
|
| [14] |
RANDOLPH M F, WROTH C P. An Analysis of vertical deformation of pile groups[J]. Gebtechnique, 1979, 29(4): 423-439. DOI:10.1680/geot.1979.29.4.423 (  0) 0)
|
| [15] |
PATRA N R, PISE P J. Uplift capacity of pile groups in sand[J]. Electronic journal of geotechnical engineering, 2002, 8 Bundle B: 1-1. (  0) 0)
|
| [16] |
中华人民共和国行业标准. GB 50007-2011, 建筑地基基础设计规范[S]. 北京: 中国建筑工业出版社, 2012. Industry standard of People's Republic of China. GB 50007-2011, Building foundation design code[S]. Beijing:China Building Industry Press, 2012. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


