2. 哈尔滨工程大学 航天与建筑工程学院, 黑龙江 哈尔滨 150001
2. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China
地下商场、地下停车场、船舶储货舱等扁平型大空间内一旦发生火灾,会表现出一些独有的规律特性,并且极易造成群死群伤和巨大的财产损失。而且有些用于存储货物的扁平型空间内一般无人长期值守,所以更多地依赖于火灾自动探测报警系统,若能较好掌握扁平型空间内的火灾特性,则可以采取有针对性的多传感器融合探测等技术进行火灾初期的准确自动探测报警。为此,众多学者对扁平型空间的火灾特性和防排烟技术开展了相关研究,Zhang等对扁平型的地下停车场火灾进行了数值模拟[1];Huo等通过实验和数值模拟对地下扁平型空间火灾特性进行了研究[2];陈颖等采用理论计算和计算机模拟对扁平型大空间火灾烟气填充规律进行了研究[3];伍卫军等通过实验研究了机械排烟系统在扁平型大空间火灾中的有效性[4];李炎锋等探讨了扁平型地下车库内诱通风辅助排烟技术的适用性和应用价值[5]。然而,对于有通风的扁平型空间火灾形成的顶棚射流特性则鲜有报道。鉴于火灾探测器一般都被安装于空间上壁面并依靠火灾产生的顶棚射流触发,而空间内的通风是影响顶棚射流参数变化规律的重要影响因素,从而影响火灾自动探测报警能力,因此本文利用实验和数值模拟方法对一扁平型空间内火灾时顶棚射流特性进行研究,重点考察空间内通风带来的影响,所得结果对于深入理解扁平型空间内火灾特性以及此类空间内的火灾自动探测技术改进具有一定的指导意义。
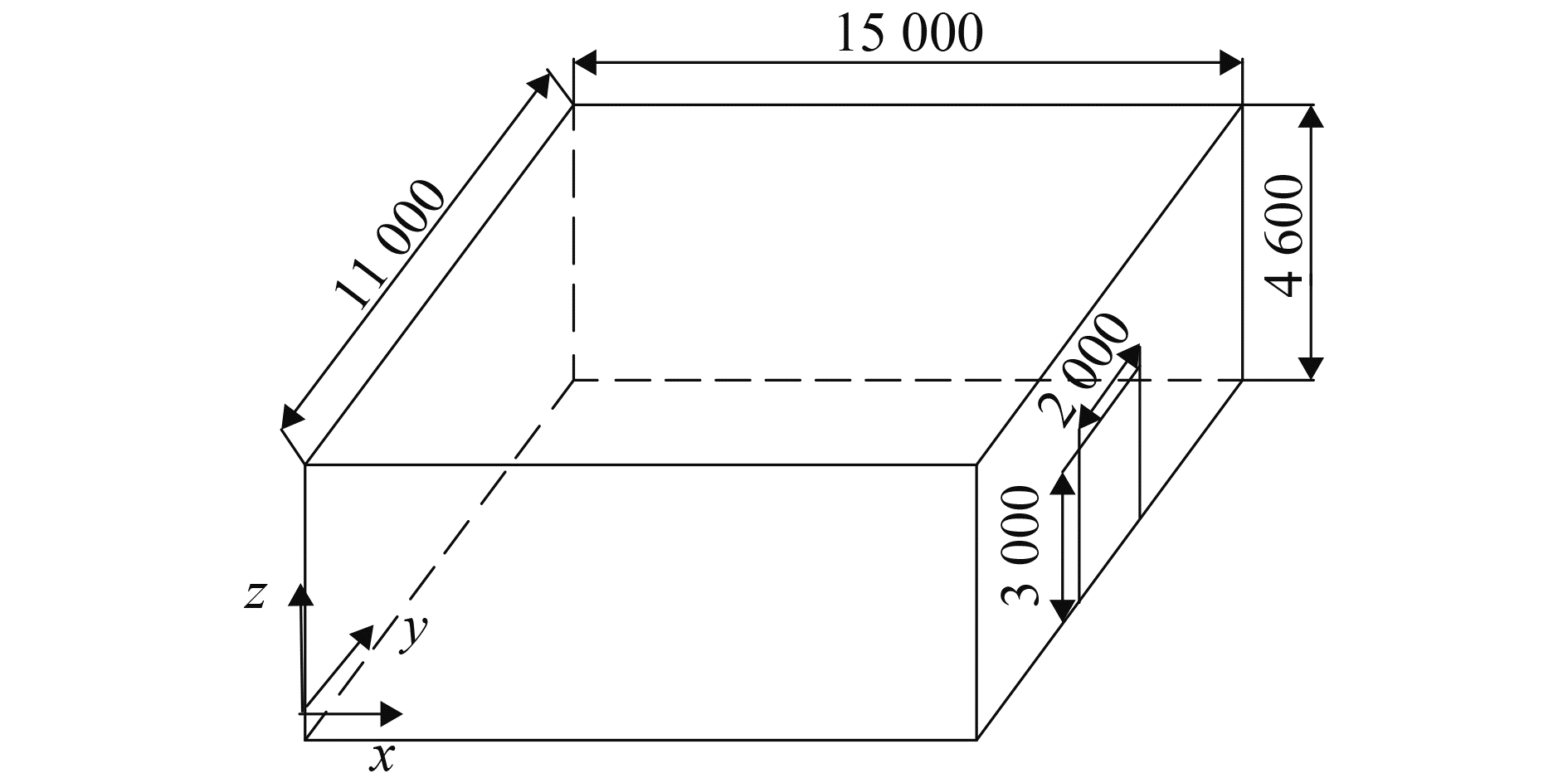
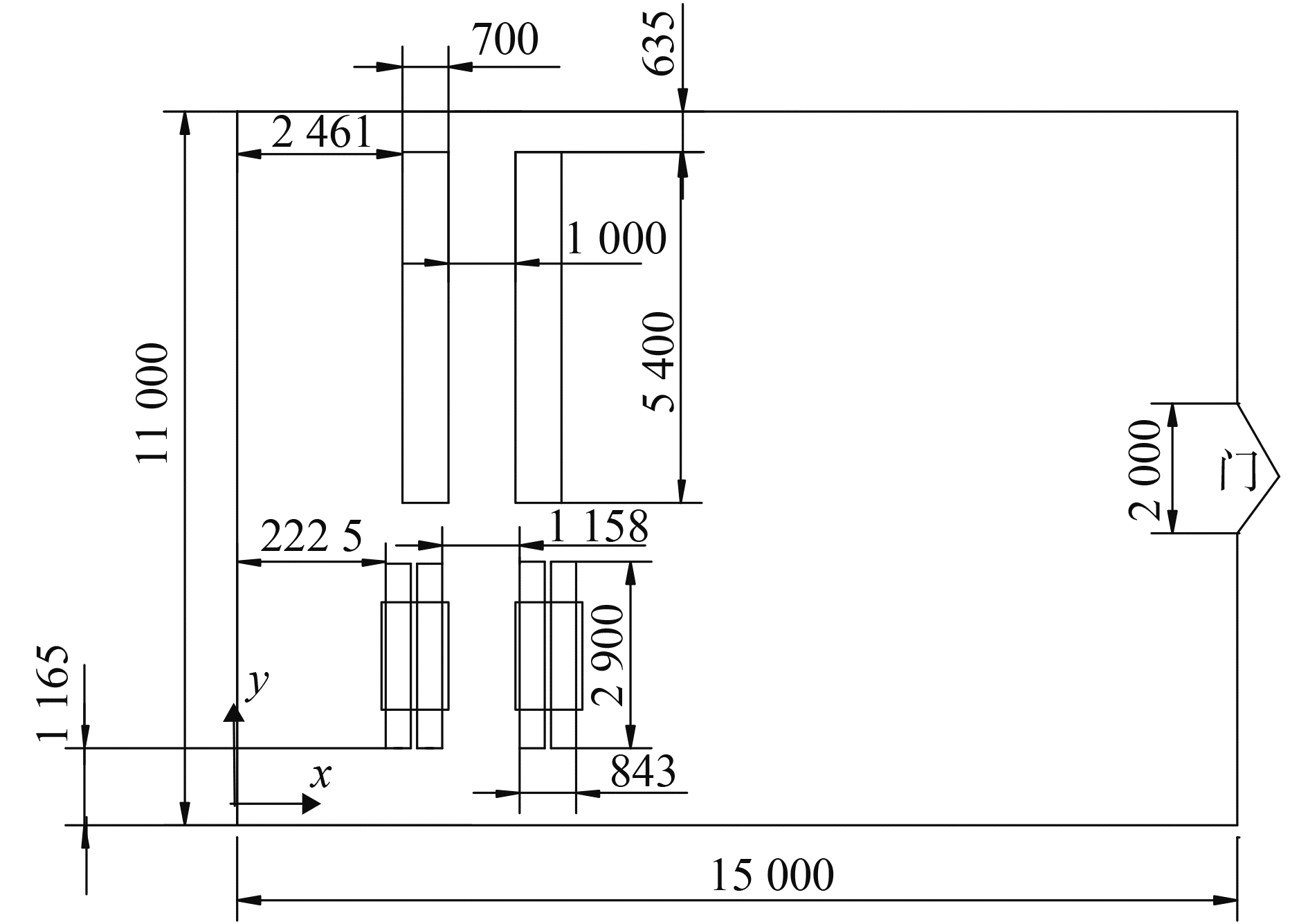
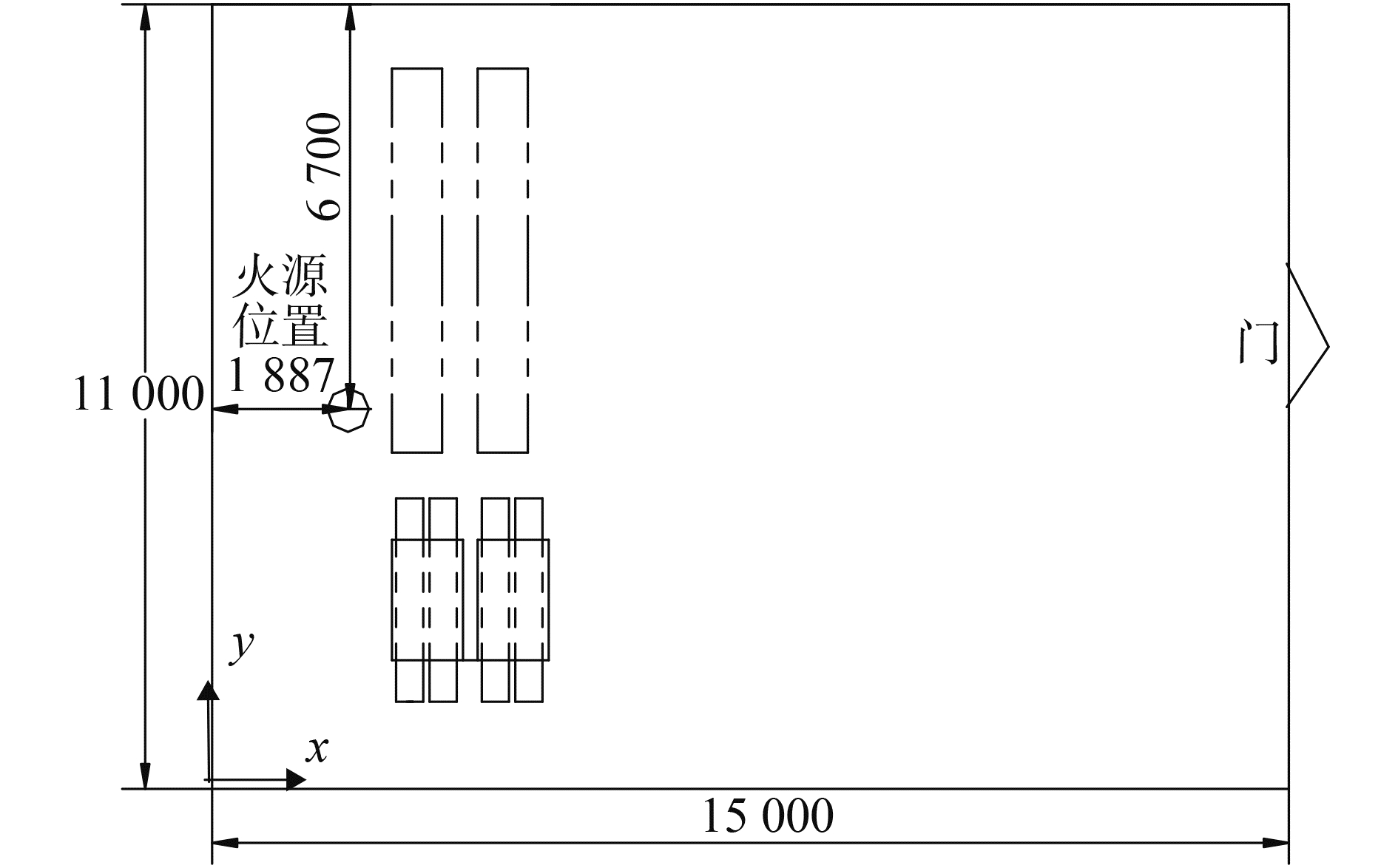
1 有通风扁平空间火灾顶棚射流布置研究对象为一长15 m(x轴),宽11 m(y轴),高4.6 m(z轴)的扁平型空间,有一个宽2 m,高3 m的门与外界环境相通,如图 1所示。空间内布置有模拟真实环境中摆放物品的障碍物,所有障碍物均摆放于空间地面上,高度均为2 m,位置如图 2所示。
|
图 1 扁平型实验空间结构尺寸 Fig.1 Size of experimental flat space |
|
图 2 实验空间内的障碍物布置 Fig.2 Obstructions arrangement in the experimental space |
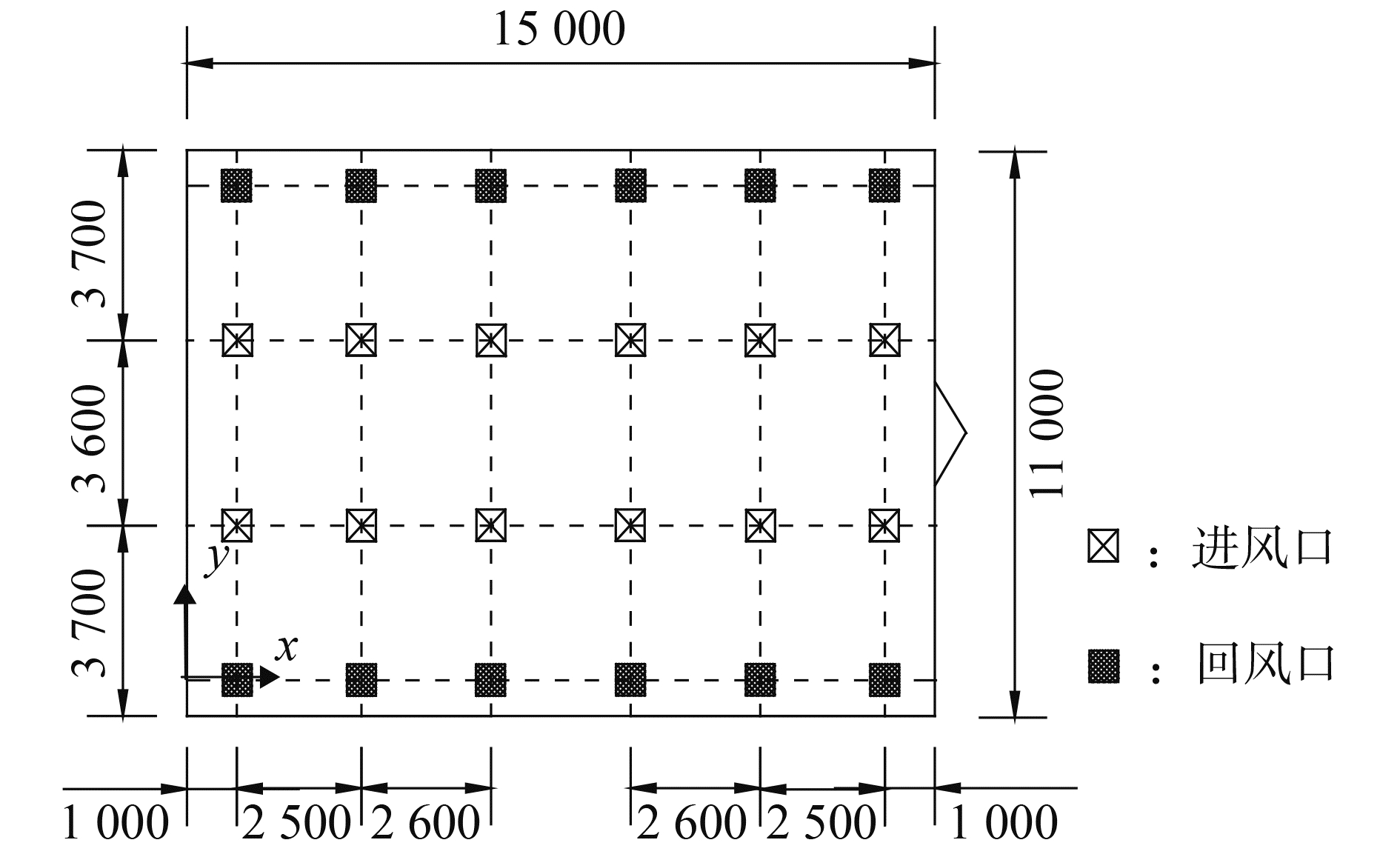
空间上壁面上布置有24个通风口,如图 3所示,其中12个为进风口,主要位于空间上壁面的中部区域,另12个为回风口,主要分布于空间内靠近侧壁的边沿区域,所有风口均可以根据需要关闭或开启机械通风,所有风口均位于空间上壁面上,开口为水平方向,通风方向均为竖直方向。
|
图 3 空间上壁面通风口布置 Fig.3 Vents arrangement on the ceiling |
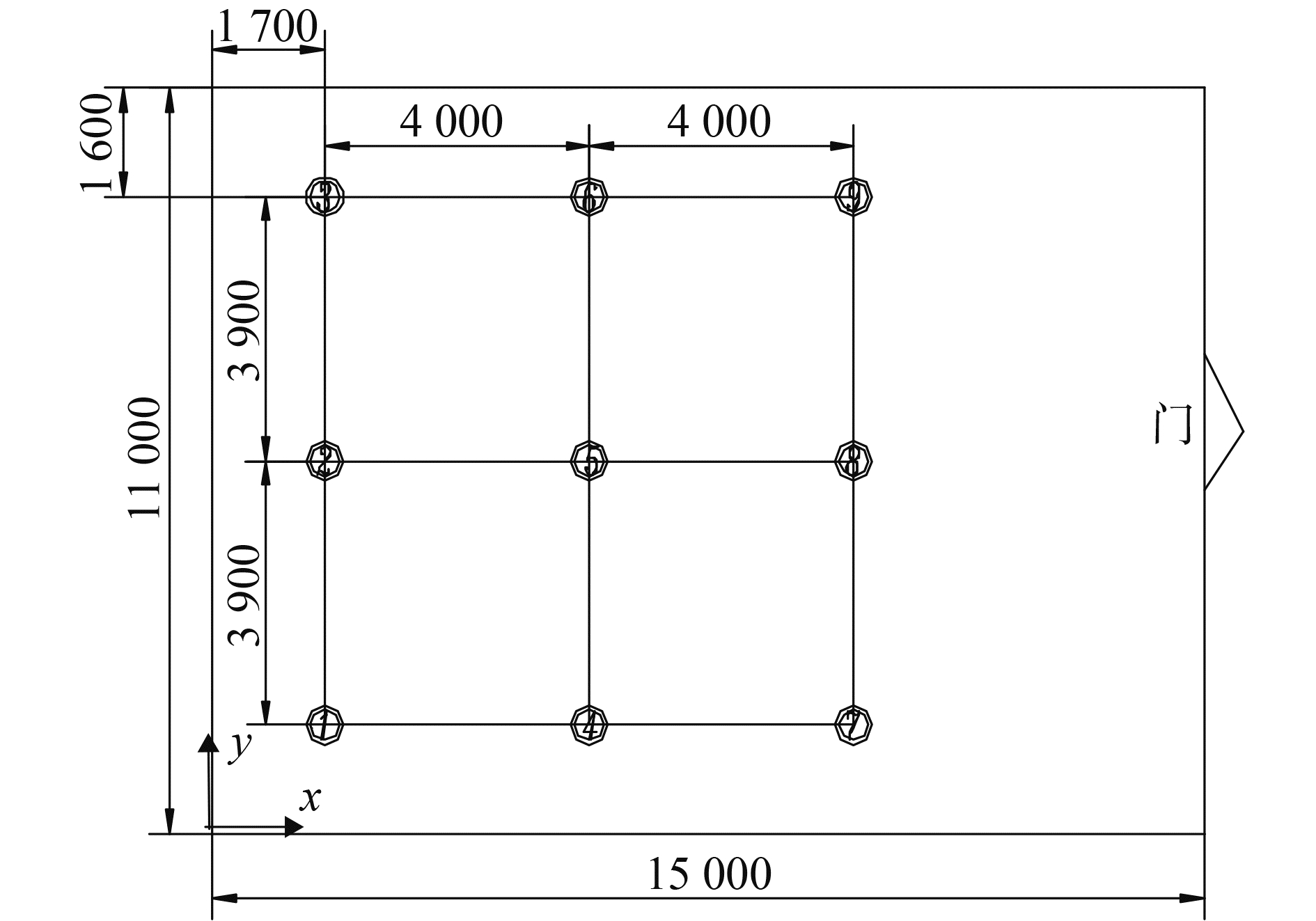
在空间内上壁面以下0.3 m高度(距地面4.3 m高)平面上布置有9个温度测点C1~C9,使用直径2 mm铠装热电偶测量各位置处的温度变化,测点分布位置如图 4所示。
|
图 4 空间近上壁面区域的温度测点布置 Fig.4 Temperature measuring points arrangement near the ceiling |
在空间远离门开口的里端地面上设置一尺寸0.5 m×0.5 m的方形燃料池,位置如图 5所示,此位置距离门开口较远,而且被空间内的障碍物遮挡,所以在实际情况中属于难以被发现的代表性火源位置。火灾实验时,先开启通风,待空间内流场稳定后,使用1 500 ml正庚烷液体燃料形成火灾场景,燃料被点燃后可持续燃烧约210 s,环境温度28 ℃。
|
图 5 火源位置示意图 Fig.5 Fire location schematic |
火灾热流场控制方程主要包括连续性方程、组分方程、动量方程、速度散度约束方程、状态方程分别为
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \mathit{\boldsymbol{V}}} \right) = 0 $ | (1) |
| $ \frac{{\partial \left( {\rho {Y_l}} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho {Y_l}\mathit{\boldsymbol{V}}} \right) = \nabla \cdot \left( {\rho {D_l}\nabla {Y_l}} \right) $ | (2) |
| $ \begin{array}{l} \;\;\;\;\;\frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial t}} - V\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} + \nabla \left( {\frac{{{{\left| V \right|}^2}}}{2} + \frac{{\tilde \rho }}{\rho }} \right) = \\ \frac{1}{\rho }\left[{\left( {\rho-{\rho _\infty }} \right)\mathit{\boldsymbol{g}} + \nabla \cdot \tau } \right] + \tilde P\nabla \left( {\frac{1}{\rho }} \right) \end{array} $ | (3) |
| $ \begin{array}{l} \nabla \cdot \mathit{\boldsymbol{V}} = \frac{1}{{\rho {C_P}T}}\left[{\dot q-\mathit{\boldsymbol{V}} \cdot \nabla \left( {\rho {h_s}} \right) + \nabla \cdot \left( {k\nabla T} \right) + } \right.\\ \;\;\;\;\;\left. {\nabla \cdot \left( {\sum\limits_l {{h_{s, l}}\rho {D_l}\nabla {Y_l}} } \right)-\nabla \cdot {\mathit{\boldsymbol{q}}_r} + w{\rho _0}{g_z}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{\rho }\sum\limits_l {\left( {\frac{{\overline {{M_l}} }}{{{M_l}}} - \frac{{{h_l}}}{{{C_P}T}}} \right)} \left[{\nabla \cdot } \right.\rho {D_l}\nabla {Y_l}-\\ \;\;\;\;\;\;\;\;\left. {V \cdot \nabla \left( {\rho {Y_l}} \right) + {{\dot m'''}_l}} \right] + \left( {\frac{1}{{\rho {C_P}T}} - \frac{1}{{{P_0}}}} \right)\frac{{\partial {P_0}}}{{\partial t}} \end{array} $ | (4) |
| $ {P_0}\left( t \right) = \rho T\mathit{\boldsymbol{R}}\sum\limits_l {\frac{{{Y_l}}}{{{M_l}}}} $ | (5) |
式中:ρ为气体的密度, Yl为组分l的质量分数,
整个计算区域的固体边界均假设为绝热条件,为了准确捕捉火羽流信息并满足网格独立性要求的基础上,最终确定火源区域采用边长为0.05 m的立方体网格对计算空间进行划分,确保火源有10个网格覆盖[6],除火源外的其他区域采用边长为0.1 m的网格划分,整个计算空间总网格数为887 800。数值计算过程中,湍流模型采用基于Deardorff亚格子模型的大涡模拟(large eddy simulation, LES)技术求解[7],热辐射采用100个离散角的有限体积法(finite volume method, FVM)进行计算,变量的时间微分项以显性二阶预测/校正机制进行离散迭代,使用CFL条件保证整个迭代过程的稳定性。数值计算采用美国国家标准与技术研究院(national institute of standards and technology, NIST)开发的火灾模拟软件FDS(fire dynamics simulator, version 6.1.1)为平台[8-9]。
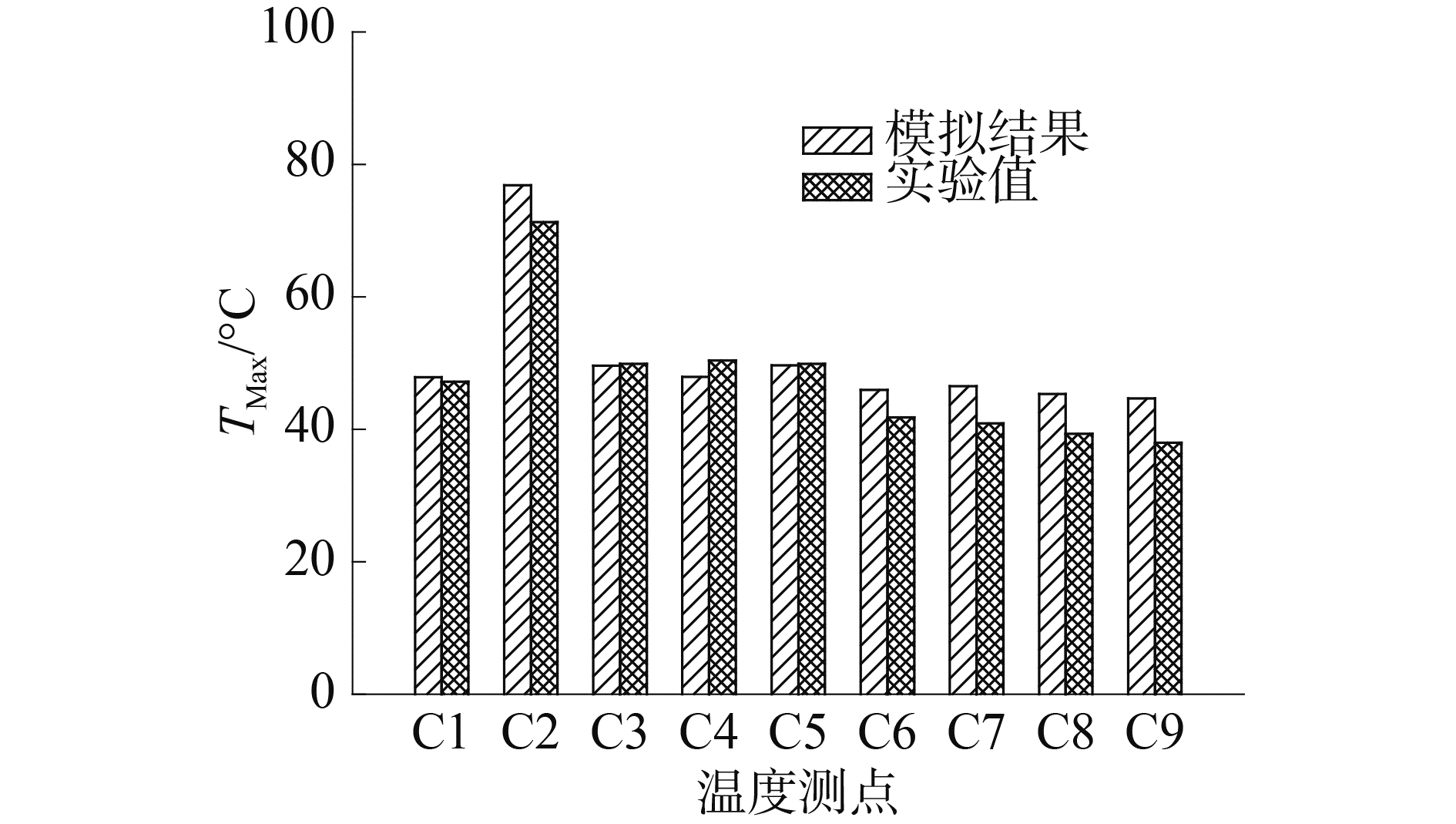
2.2 数值模拟有效性验证根据实验使用燃料属性,其燃烧热值为44 000 kJ/kg,燃料纯度和燃烧效率为95%,则可由实验所用的燃料消耗量和燃烧耗时情况估算实验火源的平均热释放率约为200 kW,以此为基础进行火灾热流场数值模拟,待流场稳定后,由实验和数值模拟得到的空间上壁面C1~C9各测点处的最高温度值TMax比较结果如图 6所示。
|
图 6 实验与数值模拟结果比较 Fig.6 Experimental and numerical comparison results |
由图 6中结果可以看出实验值与数值模拟结果在整体上吻合较好,最大偏差在15%以内,说明即使在有通风条件下,采用的数学模型和数值模拟方法也可以在一定程度上较好地反应实验结果。由此,基于实验的空间结构和通风条件,利用数值方法对火源热释放率(heat release rate, HRR)为100~500 kW时的火灾场景进行了模拟。
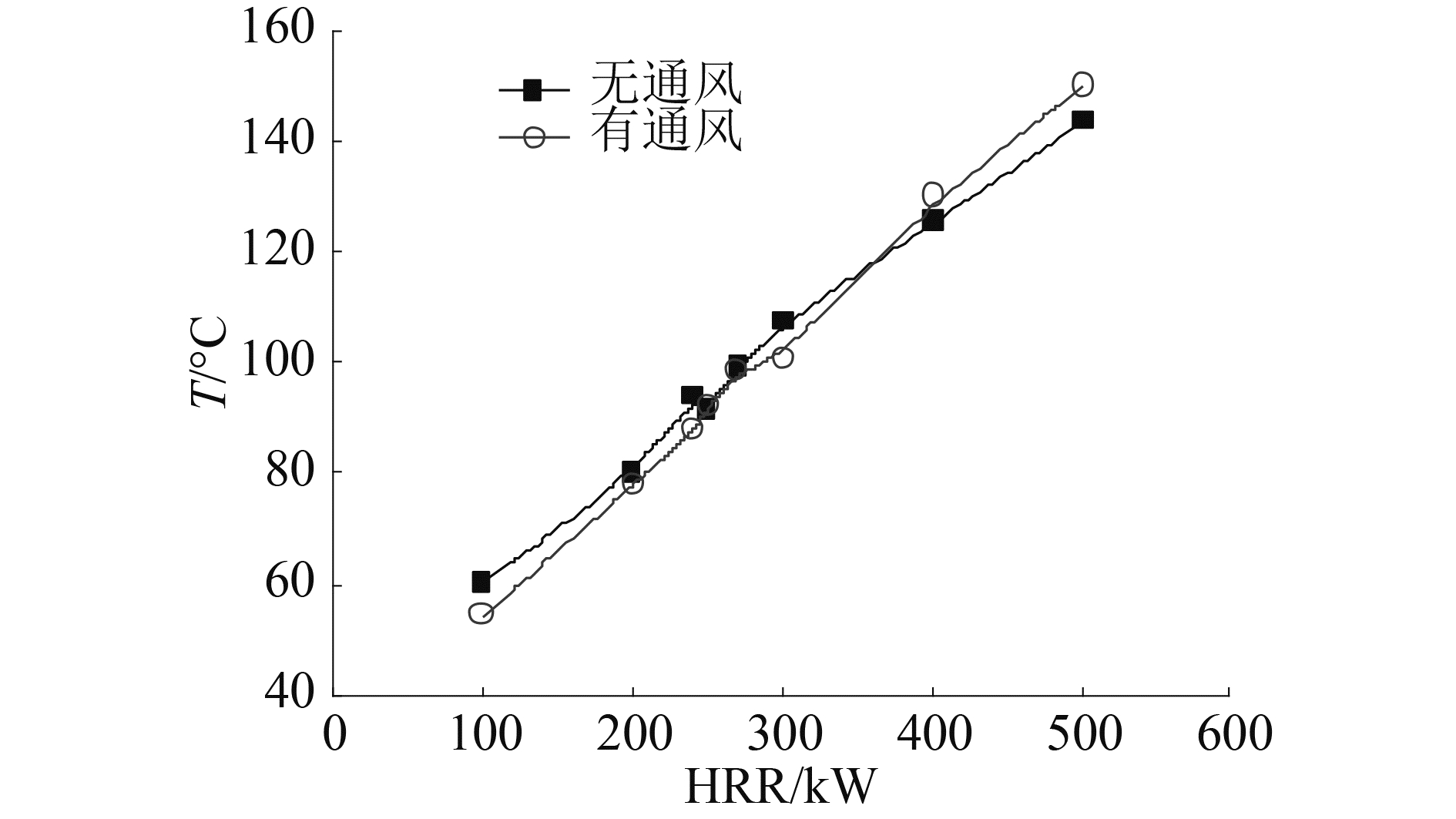
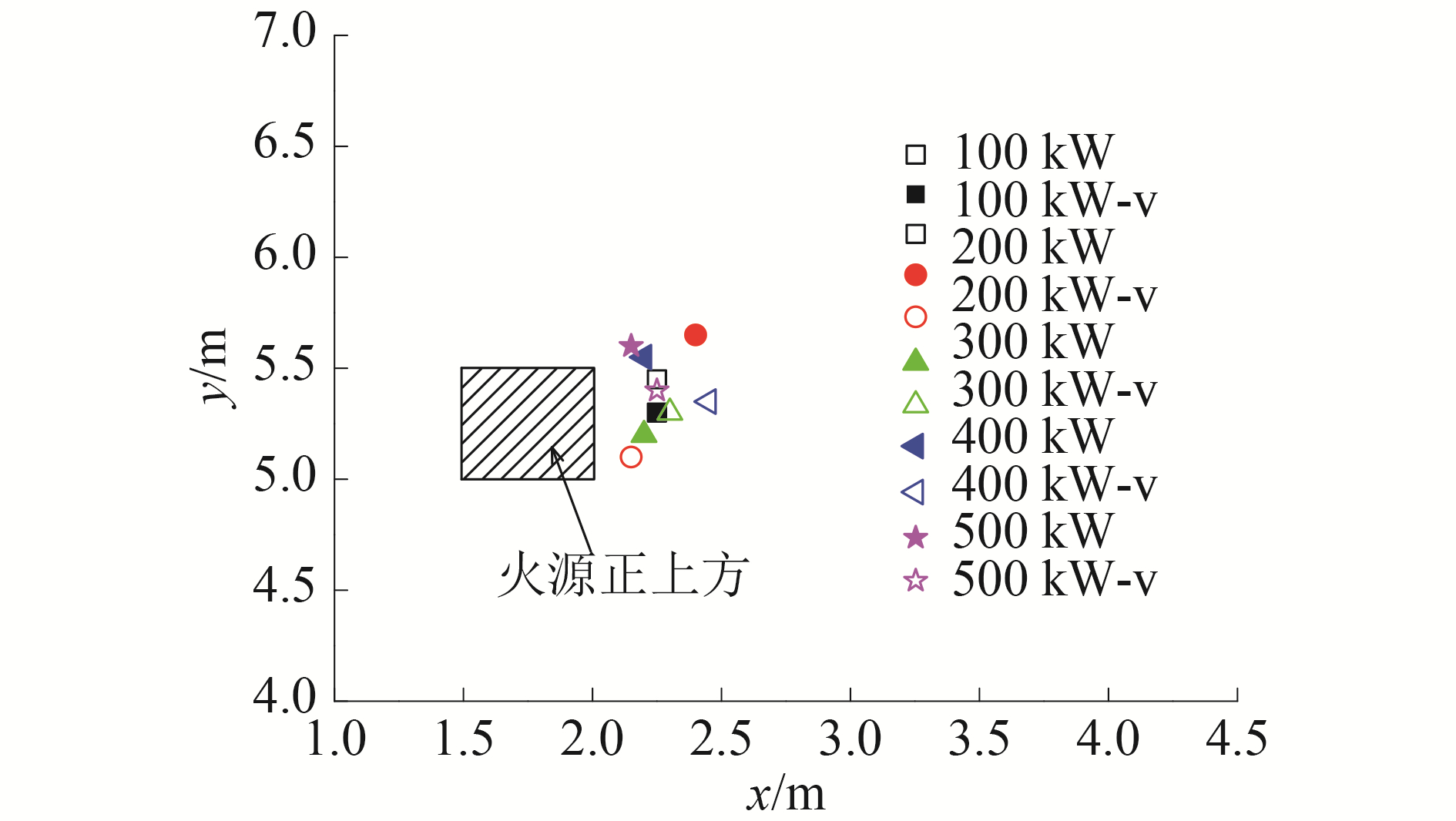
3 顶棚射流温度特性火源热释放率为100~500 kW时,当火灾流场达到稳态后,空间上壁面以下0.3 m高度的整个平面上所能达到的最高温度如图 7所示,对应最高温度所在位置见图 8,图中“-v”表示有通风。由图 7中可以看出,无论是否存在通风,空间内上壁面附近所能达到的最高温度均随着火源热释放率增加而增大,当火源热释放率小于350 kW时,空间内通风的降温作用会使上壁面附近所能达到的最高温度值有所降低,然而火源热释率大于350 kW后,由于通风可在一定程度上加剧上壁面附近的热烟气流动,所以反而使上壁面附近所能达到的最高温度较无通风时稍有升高。同时,由图 8的最高温度所在位置可以看出,由于火源附近障碍物和空间门开口的综合影响,致使最高温度所在位置并不是火源正上方,而是在火源正上方稍偏向门开口方向一侧附近,而且无论空间内是否有通风的影响,最高温度所在的位置并没有明显的差别,说明本文所研究的通风条件对上壁面附近温度最高点的位置影响不明显。
|
图 7 上壁面以下0.3 m高度平面上所能达到的最高温度 Fig.7 The highest temperature on the plane 0.3 m below ceiling |
|
图 8 上壁面以下0.3 m高度平面上最高温度所在位置 Fig.8 Location of the highest temperature on the plane 0.3 m below ceiling |
火灾流场达到稳态时,空间上壁面以下0.3 m高度平面上,温度测点所在区域的温度值如图 9所示。由图中可以看出,无论是否存在通风的影响,火源正上方附近区域都是温度最高的局部区域,距离火源正上方位置较远区域的温度相对较低并且温度值接近。当空间内无通风时,随着火源热释率增加,上壁面附近温度测点所在区域的温度值相应均匀增加,而有通风时,对于热释放率为100 kW和200 kW的火灾场景,由于火源热释放率值相对较小,产生的热烟气温度较低,所以上壁面附近温度测点所在区域的温度值在通风的影响下被明显降低,火源热释放率大于300 kW时,虽然温度值也较无通风时有所降低,但由于此时火源热释放率值相对较大,所以温度降低的幅度要稍小一些,致使火源热释放率在200 kW和300 kW之间有个明显偏大的温度跳跃。另外,由于受火焰热羽流持续不断的影响,火源正上方附近区域温度可以维持较高水平,因此通风对此区域的降温作用较弱,而远离火源的区域由于温度相对较低,所以受通风的降温作用影响则更为明显。

|
图 9 上壁面下0.3 m高度平面上温度测点所在区域的温度 Fig.9 Temperature of zone where the temperature measuring points on the plane 0.3 m below ceiling |
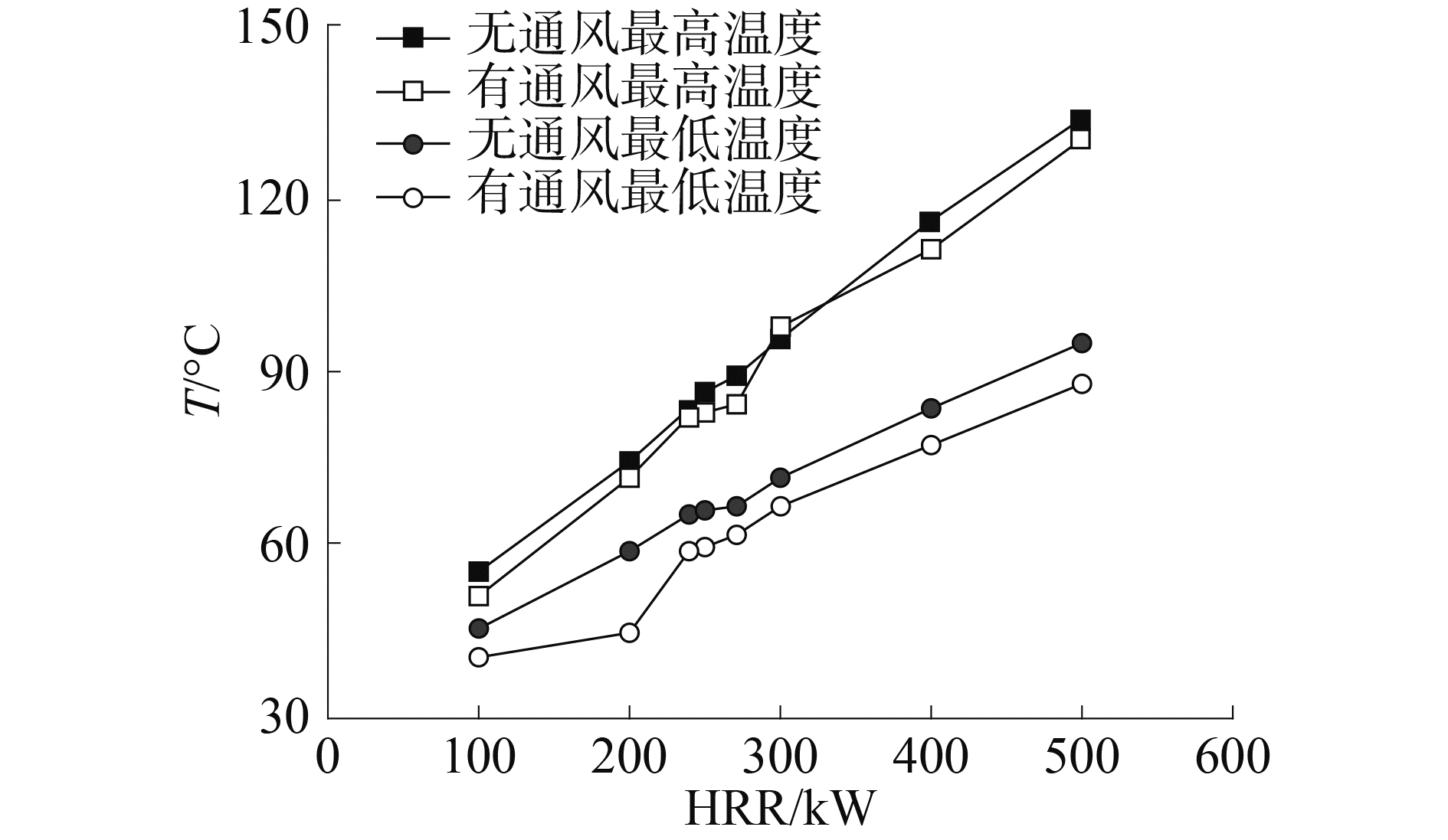
对于火源热释放率为100~500 kW的火灾场景,当空间内热流场达到稳定状态时,由上壁面附近的温度测点C1~C9各测点所得到温度值中最高温度和最低温度见图 10,图 10中的最高温度都是由火源正上方最近测点C2得到的,而最低温度都是与火源直线距离最远的测点C9得到的。由图 10中结果可以看出,随着火源热释放率增加,由温度测点所得到的最高温度和最低温度之间的温度差值逐渐增加,而且空间内的通风对于温度测点所得到的最低温度值起到了明显的降低作用,而对于最高温度影响则相对较小。
|
图 10 各温度测点的最高温度和最低温度 Fig.10 Maximum and minimum temperatures of the temperature measuring points |
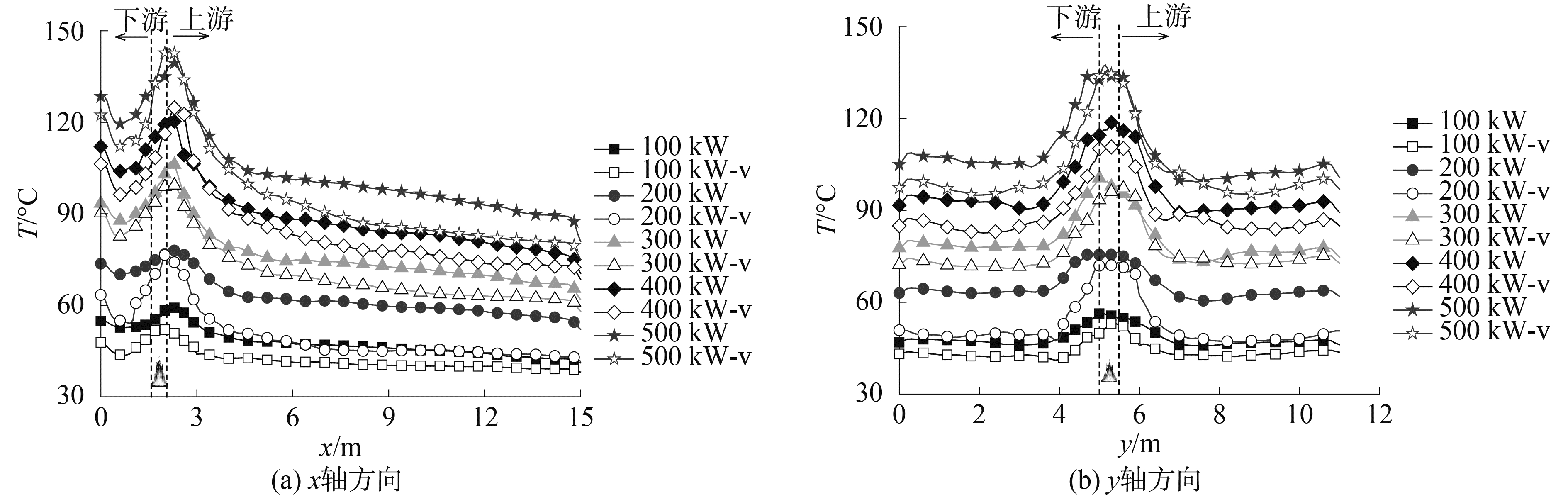
火源热释放率为100~500 kW时的稳态流场,空间上壁面以下0.3 m高度平面上,过火源正上方投影中心分别沿x轴方向和y轴方向的温度分布情况如图 11所示,图中“-v”表示有通风。由图中结果可以看出,不论是沿x轴还是沿y轴方向,由火源正上方的高温区域向远离火源的两侧低温区域均按指数形式降低变化;对于火源热释放率较小的火灾场景,空间内通风使整个平面上的温度值均降低,而对于火源热释放率较大时,通风对火源正上方附近的高温区域的温度影响相对较小,仅对于远离火源的区域起到明显降温作用;另外,由于温度沿y轴方向不像沿x轴方向那样受到空间侧壁、障碍物和门开口的影响,所以温度曲线的对称性相对较好,火源正上方中心位置是温度最高点。
|
图 11 上壁面以下0.3 m高度平面上沿x轴和y轴温度分布 Fig.11 Temperature distribution along the x-axis and y-axis on the plane 0.3 m below ceiling |
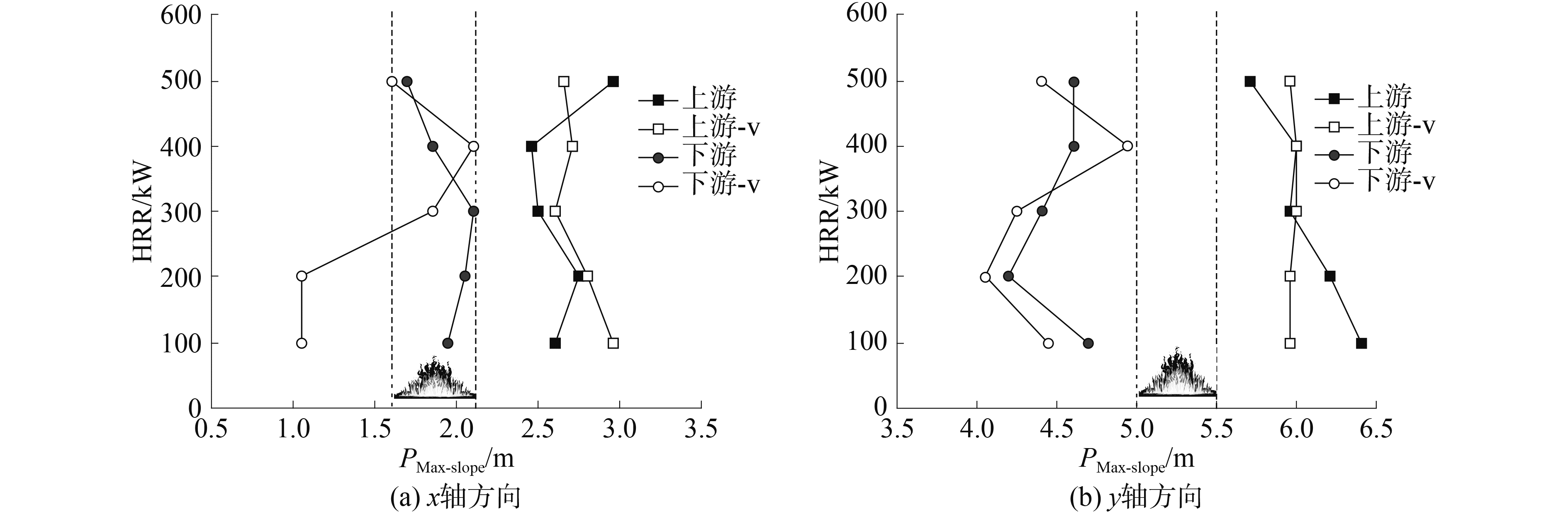
若以火源为中心,向火源两侧方向分别定义为温度变化的“上游”和“下游”,则对应“上游”和“下游”温度曲线降低过程的最大斜率位置Pmax-slope如图 12所示, “-v”表示有通风。由图中可以看出,沿x轴方向由于整个温度曲线与火源位置发生偏移,最大斜率位置也相应向上游一侧偏移,所以并没有像沿y轴方向那样“上游”和“下游”最大斜率位置近似均匀的位于火源正上方的两侧。同时,当火源热释放率小于300 kW时,在通风的影响下,沿x轴方向的温度曲线最大斜率位置明显向远离火源方向移动,而对于火源热释放率较大和沿y轴方向的结果则影响相对较小。
|
图 12 上壁面以下0.3 m高度平面上沿x轴和y轴温度变化最大斜率位置 Fig.12 Location of the maximum slope of temperature change along the x-axis and y-axis on the plane 0.3 m below ceiling |
由于图 11中温度曲线近似按指数形式变化,所以若单独考虑上壁面附近温度沿x轴或y轴方向的变化过程,则可以将其近似为温度的一维变化过程,针对高度远小于平面上长度和进深的扁平型空间,若不考虑侧壁面的影响,则其与长通道型空间近似,由此,根据文献[10-13]中对顶棚射流的推导,可将顶棚射流无量纲温度随无量纲运动距离的变化公式表示为
| $ {T^ * } = {{\rm{e}}^{ - K{d^ * }}} $ | (6) |
式中:无量纲温度T*=(T-T0)/(Tr-T0),无量纲距离d*=(d-dr)/(dmax-dr)。其中Tr为对应温度曲线在火源正上方附近的最高温度值,对应位置为dr;T0为环境温度,d为与dr的距离,dmax为距离最高温度值所在位置两侧的最大距离。
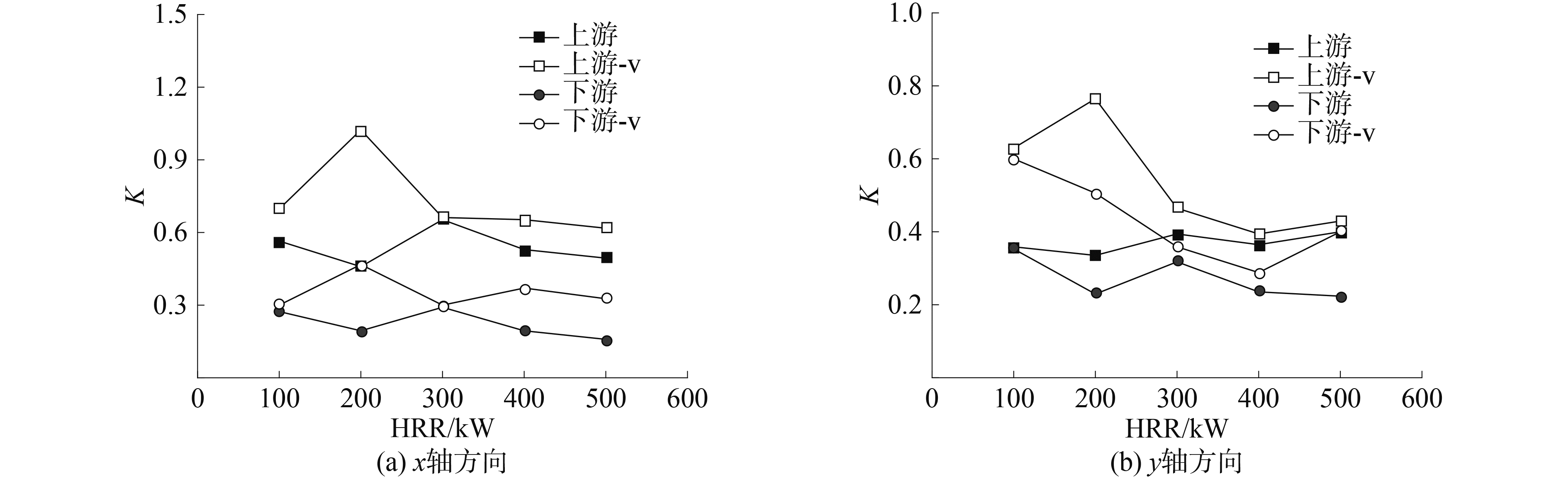
以式(6)为基础,分别对上壁面以下0.3 m高度平面上沿x轴和y轴的温度变化曲线进行拟合,取dmax=1 m,则对于不同火源热释放率的火灾场景得到的温度衰减系数K结果如图 13所示。由图中可以看出,通风的作用使系数K值增大,说明通风加剧了温度的下降过程。沿y轴方向由于受障碍物和门开口的影响较小,而且是空间内通风的气体流动方向,因此在火源热释放率较小时通风的作用更为明显,使系数K值最大提高了近2倍。而沿x轴由于受到空间内障碍物和门开口的影响,而且与通风的气体流动方向垂直,所以受到的扰动较大,虽在整体上表现出通风使衰减系数K值增加,但其变化规律要较沿y轴复杂得多。
|
图 13 上壁面以下0.3 m高度平面上沿x轴和y轴温度变化曲线拟合系数 Fig.13 Temperature variation curve fit factor along the x-axis and y-axis on the plane 0.3 m below ceiling |
1) 通风的降温作用会在一定程度上降低上壁面附近的温度,然而当火源热释率大于350kW后,由于通风可在一定程度上加剧上壁面附近的热烟气流动,所以反而使上壁面附近所能达到的最高温度较无通风时稍有升高,但通风对上壁面附近最高温度所在位置并没有明显的影响。
2) 通风对火源正上方的高温区域降温作用较弱,对于远离火源区域的降温作用更为明显。同时,对于火灾初期或阴燃等火源热释放率相对较小时,通风的降温作用更为明显,可导致其温度下降曲线最大斜率位置向远离火源方向移动。
3) 扁平型空间上壁面附近温度由火源正上方附近的高温区域向周围以近似指数形式降低,通过对温度曲线下降过程结果拟合得到,通风可加速温度的下降,最大可使温度衰减系数K值提高近2倍。
4) 除通风外,空间内障碍物和门开口位置也会对顶棚射流温度变化特性产生影响,使其产生复杂的变化规律。
| [1] |
ZHANG X G, GUO Y C, CHAN C K, et al. Numerical simulations on fire spread and smoke movement in an underground car park[J]. Building and environment, 2007, 42(10): 3466-3475. DOI:10.1016/j.buildenv.2006.11.002 (  0) 0)
|
| [2] |
HUO Y, GAO Y, WU H M. The characteristics of smoke spreading of fires in a flat underground building in cities[C]//International Conference on Management and Service Science, MASS 2009. Wuhan, China, 2009.
(  0) 0)
|
| [3] |
陈颖, 安翠. 扁平大空间建筑烟气填充规律研究[J]. 武警学院学报, 2008, 24(12): 9-11. CHEN Ying, AN Cui. The disscussion on smoke filling characteristics in flat large space[J]. Journal of Chinese People Sarmed Police Force Academy, 2008, 24(12): 9-11. DOI:10.3969/j.issn.1008-2077.2008.12.002 (  0) 0)
|
| [4] |
伍卫军, 徐亮, 陶李华, 等. 扁平大空间机械排烟全尺寸试验研究[J]. 消防科学与技术, 2012, 31(10): 1038-1040. WU Weijun, XU Liang, TAO Lihua, et al. Study on effectiveness of smoke exhaust in large flat space using hot smoke experiment[J]. Fire science and technology, 2012, 31(10): 1038-1040. DOI:10.3969/j.issn.1009-0029.2012.10.006 (  0) 0)
|
| [5] |
李炎锋, 常琳, 冯霄, 等. 地下车库诱导通风辅助排烟系统研究[J]. 消防科学与技术, 2015, 34(3): 315-318. LI Yanfeng, CHANG Lin, FENG Xiao, et al. Study on smoke control system assistant by impulse ventilation in underground garage[J]. Fire science and technology, 2015, 34(3): 315-318. (  0) 0)
|
| [6] |
WANG H Y. Numerical study of under-ventilated fire in medium-scale enclosure[J]. Building and environment, 2009, 44(6): 1215-1227. DOI:10.1016/j.buildenv.2008.09.011 (  0) 0)
|
| [7] |
DEARDORFF J W. Numerical investigation of neutral and unstable planetary boundary layers[J]. Journal of atmospheric sciences, 1972, 29: 91-115. DOI:10.1175/1520-0469(1972)029<0091:NIONAU>2.0.CO;2 (  0) 0)
|
| [8] |
MCGRATTAN K, HOSTIKKA S, MCDERMOTT R, et al. Fire dynamics Simulator user's guide Special Publication 1019[R]. Gaithersburg:National Institute of Standards and Technology, 2014. http://ascelibrary.org/doi/10.1061/%28ASCE%29MT.1943-5533.0001311
(  0) 0)
|
| [9] |
MCGRATTAN K, HOSTIKKA S, MCDERMOTT R, et al. Fire dynamics Simulator technical reference guide volume 1:mathematical model Special Publication 1018[R]. Gaithersburg:National Institute of Standards and Technology, 2014.
(  0) 0)
|
| [10] |
DELICHATSIOS M A. The flow of fire gases under a beamed ceiling[J]. Combustion and flame, 1981, 43: 1-10. DOI:10.1016/0010-2180(81)90002-X (  0) 0)
|
| [11] |
EVERS E, WATERHOUSE A. A complete model for analyzing smoke movement in buildings BRE CP 69/78[R]. Watford:Building Research Establishment, 1981.
(  0) 0)
|
| [12] |
胡隆华. 隧道火灾烟气蔓延的热物理特性研究[D]. 合肥: 中国科学技术大学, 2006. Hu Longhua. Stuidies on thermal physics of smoke movement in tunnel fires[D]. Hefei:University of Sicence and Technology of China, 2006. (  0) 0)
|
| [13] |
霍岩, 赵建贺. 有限长度倾斜通道内火灾近上壁面区域温度特性[J]. 哈尔滨工程大学学报, 2015, 36(4): 461-466. HUO Yan, ZHAO Jianhe. Temperature characteristics near the ceiling of an inclined channel with finite length in case of fire[J]. Journal of Harbin Engineering Univeristy, 2015, 36(4): 461-466. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


