海洋立管是海洋平台进行海底油气输送的重要设施和关键部分,它是连接海底管线或海底井口与海洋平台之间的输送管道。立管内部一般有高温、高压的油气流过,外部承受波浪、海流及风等环境载荷的作用[1]。在内外流的作用下立管有可能产生流固耦合振动,当立管固有频率与外界激励力频率接近时,就会发生振动“锁定”现象,使得振幅显著加大,从而导致立管的疲劳破坏,造成立管失效。因此,立管的振动特性研究对结构的性能分析、动态设计具有重要意义。
模态分析是进行复杂动力学问题分析的前提和基础[2-3]。由于海洋立管位于海洋环境中,因此计算需要考虑立管周围流体对海洋立管动态特性的影响,也就是湿模态特性[4-5]。海洋环境对海洋立管振动特性的影响主要来自于流体水动力载荷作用于立管表面引起的预应力效应,以及流体随同立管振动引起的附加质量效应[6-7]。
自20世纪70年代以来,随着计算机技术和数值模拟技术的迅猛发展,基于计算流体力学(computational fluid dynamics, CFD)理论的数值模拟已成为研究复杂流场的重要手段。目前,CFD技术已具备模拟三维粘性流场绕流的能力,为海洋立管三维圆柱绕流提供精确的海洋环境流体响应载荷,成为研究海洋立管涡激振动的重要工具[8-10]。
本文对立管的流场环境进行了计算。基于尺度自适应模拟(scale-adaptive simulation, SAS),分别计算了将立管视为刚体和柔性体两种情况下的流体载荷响应。分析了水动力载荷和水深对立管振动特性的影响。
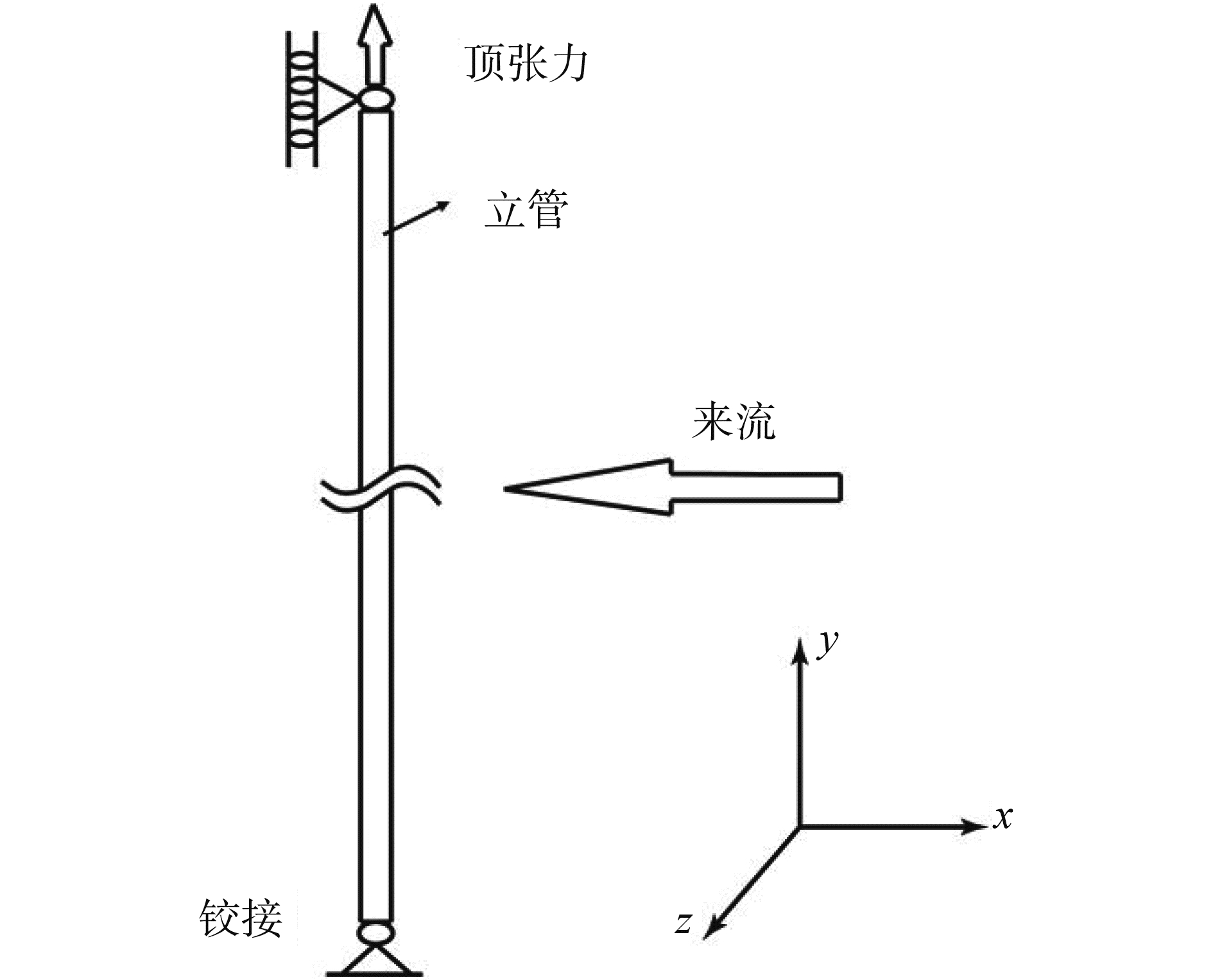
1 湿模态计算模型 1.1 几何模型及参数本文以Bijan Sanaati的实验模型为研究对象[13]。立管的两端边界为铰-铰约束,同时立管顶端顶张力大小为T,如图 1所示。PVC管结构参数、周围流体环境参数、内部流体介质参数见文献[13]。
|
图 1 三维立管模型 Fig.1 3D model of the riser |
当海洋立管处于真空中时,计算出的模态为干模态,而当海洋立管位于海洋环境中时,需要考虑立管内外水介质对立管振动特性的影响,因此必须采用湿模态法对其动力特性进行分析。声-固耦合模型中,水为无粘不可压缩流体,并且通过Kinsler假定,将流体的动量方程(Navier-Stokes)和连续性方程简化为声波方程:
| $ \frac{1}{{{c^2}}}\frac{{{\partial ^2}P}}{{\partial {t^2}}} - {\nabla ^2}P = 0 $ | (1) |
式中:c为流体介质的声速,
将声波方程离散化[14], 得到
| $ {\mathit{\boldsymbol{M}}_f}\mathit{\boldsymbol{\ddot P}} + {\mathit{\boldsymbol{K}}_f}\mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{F}}_f} + {\rho _0}{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{\ddot U}} $ | (2) |
结构本身的动力学方程为
| $ {\mathit{\boldsymbol{M}}_s}\mathit{\boldsymbol{\ddot U}} + {\mathit{\boldsymbol{K}}_s}\mathit{\boldsymbol{U}} = {\mathit{\boldsymbol{F}}_s} + \mathit{\boldsymbol{RP}} $ | (3) |
将式(2)、(3)联立:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_s}}&0\\ {{\rho _0}{\mathit{\boldsymbol{R}}^{\rm{T}}}}&{{\mathit{\boldsymbol{M}}_f}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot U}}}\\ {\mathit{\boldsymbol{\ddot P}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_s}}&{ - \mathit{\boldsymbol{R}}}\\ 0&{{\mathit{\boldsymbol{K}}_f}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{U}}\\ \mathit{\boldsymbol{P}} \end{array}} \right] = \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_s}}\\ {{\mathit{\boldsymbol{F}}_f}} \end{array}} \right\} $ | (4) |
式中:s代表结构,f代表流体;M、K分别表示质量矩阵、刚度矩阵;P为声学压力矩阵,F为力的矩阵,U为位移矩阵,R为流固耦合界面的耦合矩阵,代表流固界面上每个节点处的有效面积,它将界面上的流体压力转换成结构的载荷。湿模态计算由Ansys软件完成。
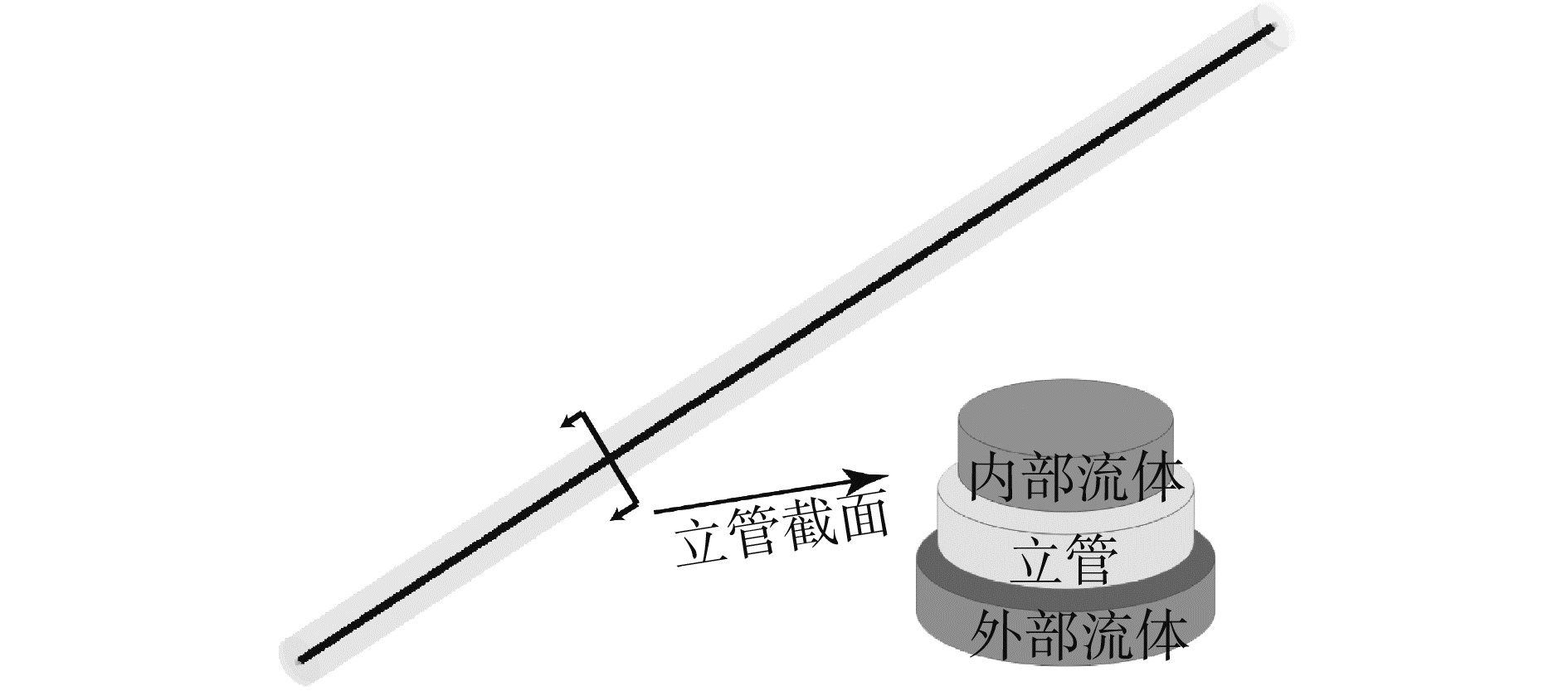
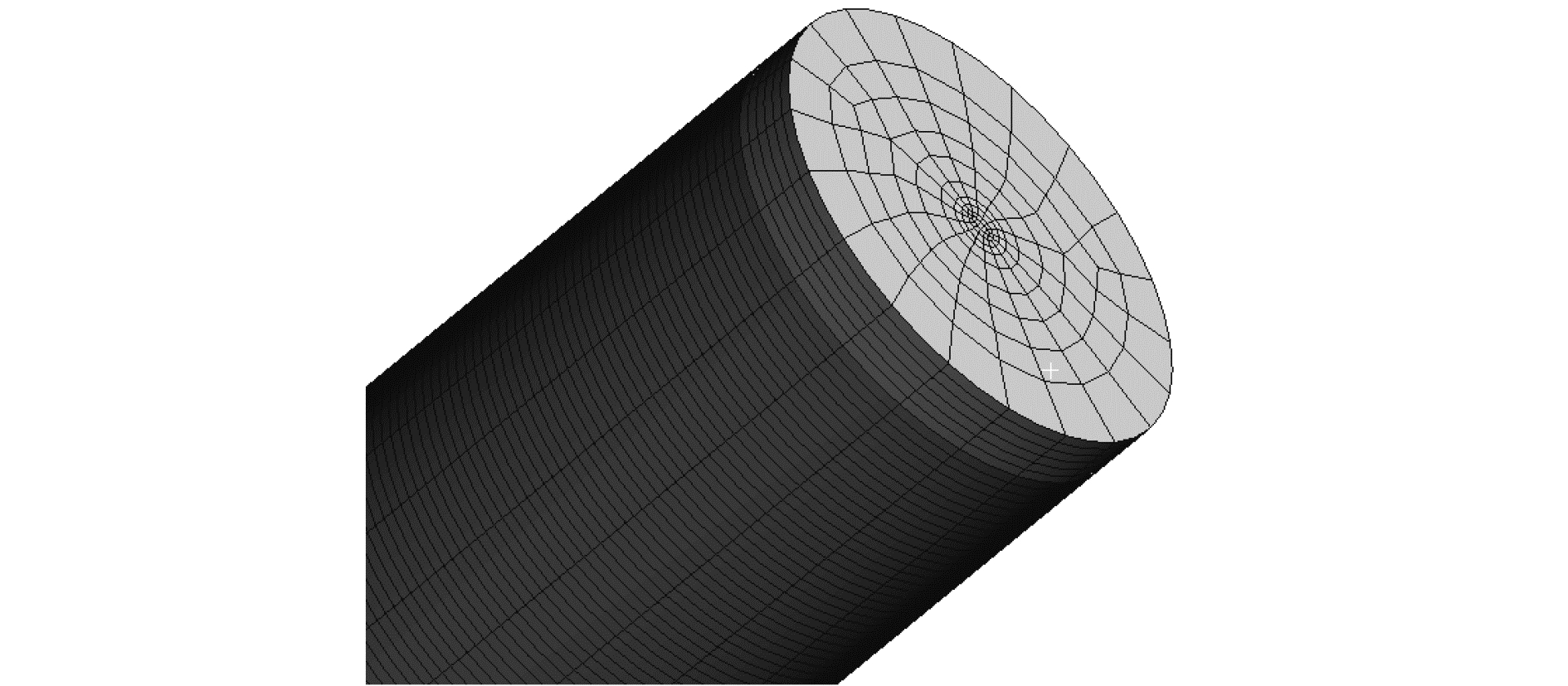
几何模型由3部分组成,如图 2所示,分别是立管外部流体介质、立管内部流体介质和立管本身。立管周围流体介质采用圆柱形,以方便画网格时候,采用切块和扫略方法能够生成较好的网格。图 3为立管与立管内外流体介质网格局部放大图。其中PVC管采用18 734个SOLID 186单元,PVC管内部流体介质采用的是34 510个FLUID 220单元,PVC管外部流体采用的是85 061个FLUID 220单元。FLUID 220是高阶20节点,每节点具有3个位移、一个压力共4个自由度的声学实体单元。只有流固交界面上的位移自由度才有效,所以对于该单元的节点,除了落在交界面上的随结构移动之外,其他都是固定在空间一点的。流固耦合交界面上的流体单元被定义为耦合单元,流固耦合交界面上的所有节点被定义为流固耦合(fluid structure interaction,FSI)载荷的作用点。在材料库中定义了水的密度和水中声速,以及立管内部介质的密度和该介质中声速。
|
图 2 立管与立管内外流体介质几何模型 Fig.2 Geometric model of the riser and its internal and external fluid |
|
图 3 网格局部图 Fig.3 Partial part of mesh diagram |
为计算考虑立管顶张力情况下的湿模态。首先,对立管进行顶张力作用下的静力学分析,并以静力学计算结果更新数值模型的刚度和质量矩阵,然后进行湿模态分析。计算流体载荷和水深对立管湿模态的影响,也采用同样的方法。
2 流-固双向耦合模型 2.1 流体域模型Menter借鉴DES模型中长度尺度的思路[15],基于剪切应力传输(shear stress transfer,SST)湍流模型提出了一种尺度自适应模拟方法(scale-adaptive simulation,SAS),它是一种新的(reynolds average navier-stokes/large eddy simulation, RANS/LES)混合模型,SAS模型长度尺度不依赖于计算单元的大小,可以依靠流动状态动态自适应调整湍流黏性,并克服了RANS/LES交界面问题,且SAS模型远场处耗散小,从而可以自适应的分辨湍流结构。
SST-SAS湍流模型实际上只在标准SST湍流模型的基础上修改其ω方程,在Lvk方程的源项中增加一项QSAS[16]。
| $ \begin{array}{*{20}{c}} {{Q_{{\rm{SAS}}}} = \max \left[ {\rho {\zeta _2}\kappa {S^2}{{\left( {\frac{L}{{{L_{vk}}}}} \right)}^2} - } \right.}\\ {\left. {C\frac{{2\rho k}}{{{\sigma _\varphi }}}\max \left( {\frac{{{{\left| {\nabla \omega } \right|}^2}}}{{{\omega ^2}}},\frac{{{{\left| {\nabla k} \right|}^2}}}{{{k^2}}}} \right),0} \right]} \end{array} $ | (5) |
| $ {L_{{\rm{vk}}}} = \frac{{\kappa \sqrt {2{S_{ij}}{S_{ij}}} }}{{\sqrt {{{\left( {{\nabla ^2}u} \right)}^2} + {{\left( {{\nabla ^2}v} \right)}^2} + {{\left( {{\nabla ^2}w} \right)}^2}} }} $ | (6) |
| $ L = \sqrt k /\left( {c_\mu ^{1/4}\omega } \right) $ | (7) |
式中:Lvk和L分别为von Karman尺度和模化湍流力尺度,具体动力学模型方程、模型常数ζ2、κ、C、σφ、Cμ见文献[14-15]。
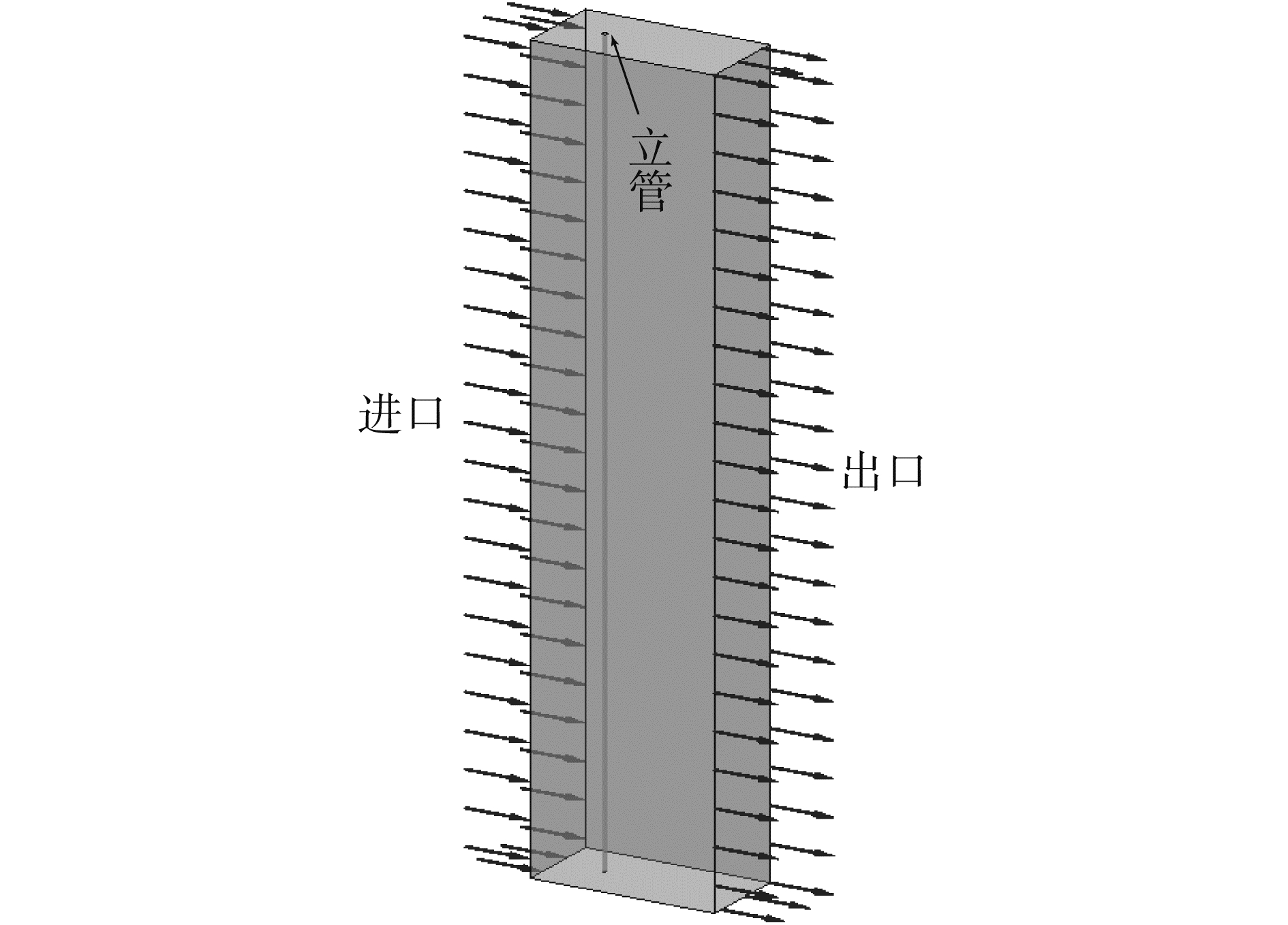
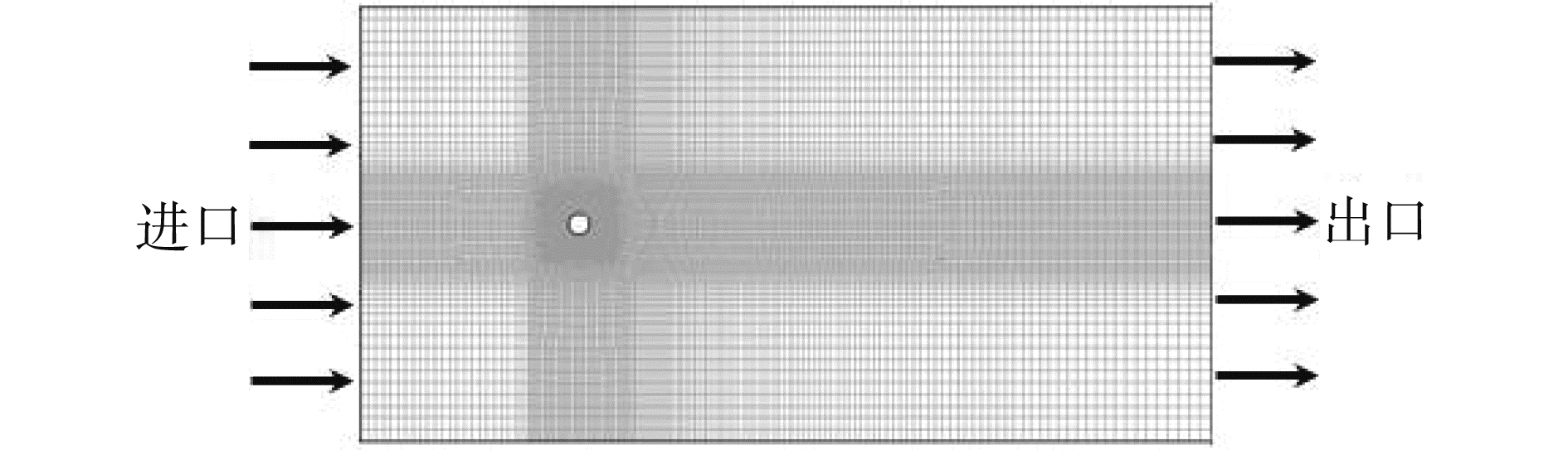
建立PVC立管的外流场,其中PVC管的直径为D。入口处来流到立管的距离为10D,两边到立管的距离也为10D,出口处到立管的距离为30D。进口处采用速度进口边界条件,出口处采用开放性边界条件,其他面都采用对称边界条件。流体域模型如图 4所示。
|
图 4 流体域模型 Fig.4 Fluid domain model |
流体与壁面间相互作用,很多因变量具有较大的梯度,而且粘度对传输过程有很大的影响。采用SST-SAS湍流模型要求近壁处有y+ < 1。计算网格如图 5所示,在沿着管长方向分布了100个节点。网格数量为2 776 653。
|
图 5 流体域计算网格 Fig.5 Grid of fluid domain |
立管的动力学方程为
| $ \mathit{\boldsymbol{M\ddot x}} + \mathit{\boldsymbol{C\dot x}} + \mathit{\boldsymbol{Kx}} = \mathit{\boldsymbol{F}} $ | (8) |
式中:M为质量矩阵,C为阻尼矩阵,K为刚度矩阵。x、
式(8)中F为作用在立管表面的流体力,由基于SST-SAS的计算流体力学方法计算得到。F随着时间变化,根据具体的物理作用,F(x, y, z, t)= Ff+ FFSI,Ff为来流引起的水动力;FFSI为立管振动加速度和速度引起的辐射力,以及立管振动位移引起的回复力;FFSI可以写为
| $ {\mathit{\boldsymbol{F}}_{{\rm{FSI}}}} = - \mathit{\boldsymbol{\bar M\ddot x}} - \mathit{\boldsymbol{\bar C\dot x}} - \mathit{\boldsymbol{\bar Kx}} $ | (9) |
式中:M、C、K分别表示流体附加质量、阻尼和刚度矩阵。因此,水弹性方程可以写为
| $ \left( {\mathit{\boldsymbol{M}} + \mathit{\boldsymbol{\bar M}}} \right)\mathit{\boldsymbol{\ddot x}} + \left( {\mathit{\boldsymbol{C}} - \mathit{\boldsymbol{\bar C}}} \right)\mathit{\boldsymbol{\dot x}} + \left( {\mathit{\boldsymbol{K}} - \mathit{\boldsymbol{\bar K}}} \right)\mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{F}}_f} $ | (10) |
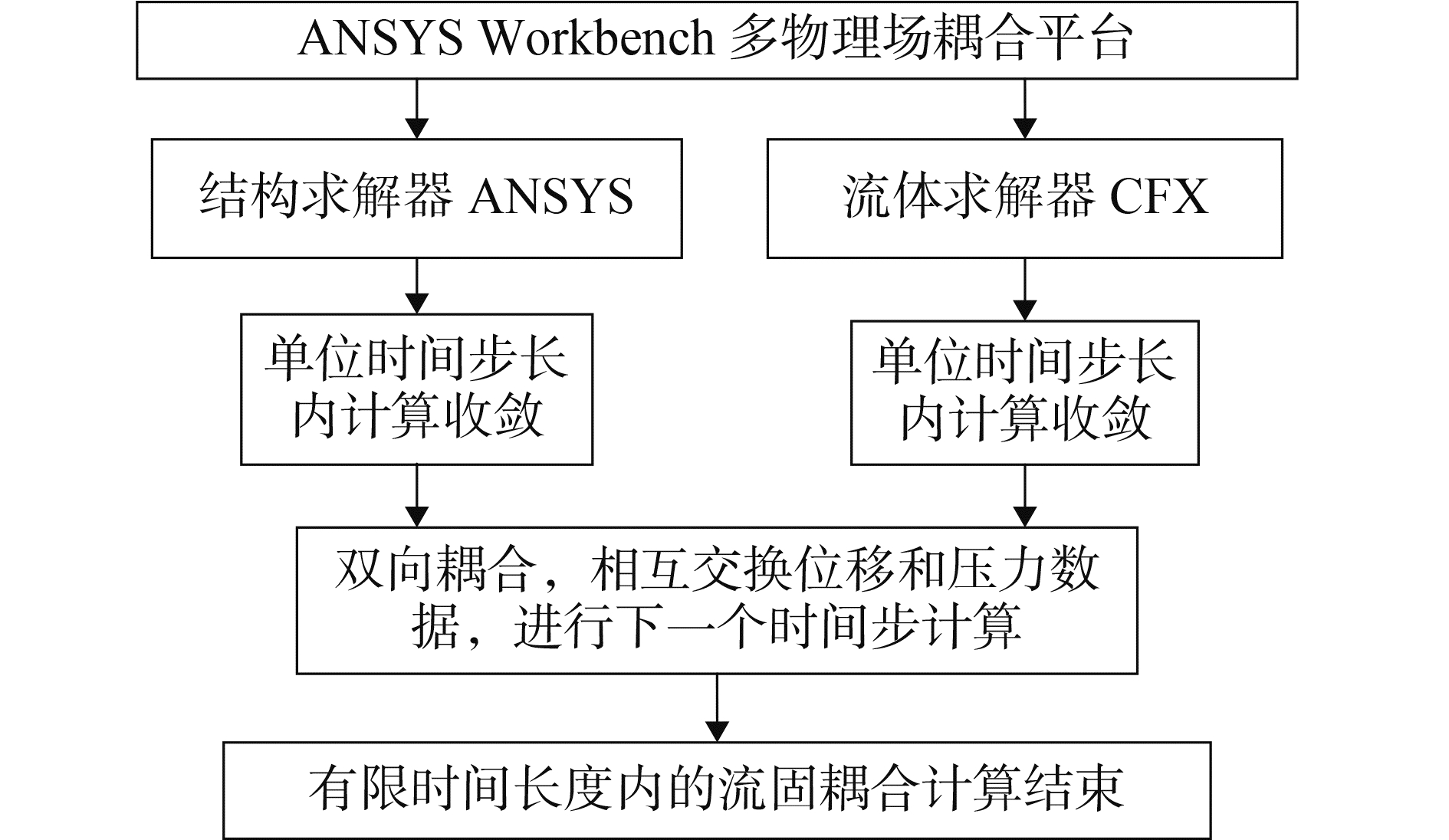
采用任意拉格朗日欧拉(arbitrary Lagrange-Euler,ALE)法来解决耦合作用问题中由于坐标不统一所带来的运动界面协调问题。ALE的基本思想是在流体域采用欧拉单元,在固体域内使用拉格朗日单元,并在统一的ALE坐标系下进行求解。ALE法的优点是可以实现欧拉网格的移动,这样可以使流体网格根据固体的变形而发生改变。网格运动通过弹簧比拟法实现,为了避免流场中心域和环绕域之间的变形过于迅速造成计算失败, 采取小体积网格单元部分网格刚度系数大,主要靠大体积网格吸收变形的做法。双向流固耦合流程图如图 6所示。
|
图 6 双向耦合流程图 Fig.6 The flow chart of two-way coupling |
简支梁频率的理论计算公式为
| $ {f_n} = \left( {\frac{{{n^2}{\rm{ \mathsf{ π} }}}}{{2{L^2}}}} \right)\sqrt {\frac{{EI}}{{M + m}}} \sqrt {1 + \frac{{T{L^2}}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}EI}}} ,n = 1,2,3 \cdots $ | (11) |
式中:m为单位长度的流体介质附加质量,工程上一般将圆柱形立管的附加质量简化为立管外径对应的圆柱排开流体介质的质量; T为顶张力,M为单位长度的PVC管质量,L为立管长度,E为立管的弹性模量,I为立管的截面惯性矩。该公式只能计算横向或者纵向的振动频率,圆柱形立管属于对称结构,所以横向振动频率与纵向振动频率一致。
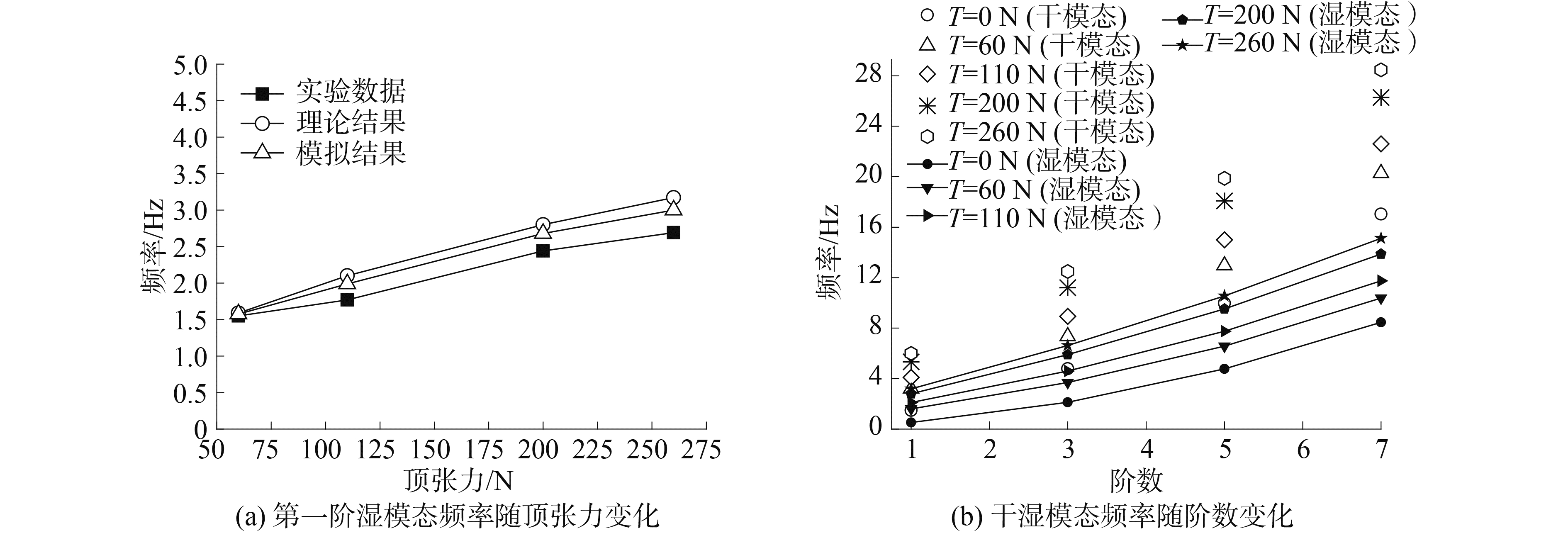
基于声-固耦合模型,首先计算了铰-铰约束、立管顶端不同顶张力情况下的干、湿模态。从图 7(a)可以看出,第一阶湿模态频率比理论公式计算值略小,但更接近于文献[13]中的实验数据。但随着顶张力的加大,和实验数据相比,误差增大。由于立管是完全对称的模型,立管的振动频率都是每两阶相等的。图 7(b)为三维立管的1、3、5、7阶干、湿模态频率分布。从图中可以看出,湿模态频率几乎都是干模态频率的一半,随着立管顶张力的加大,干、湿模态频率都显著提高。
|
图 7 铰-铰约束情况下模拟结果 Fig.7 The simulation results in the condition of hinge-hinge constraint |
CFD求解流场参数的原理是,先对流场进行求解,得到流场每一个网格上的速度、密度、压力等参数,然后通过计算公式求出水动力系数。来流绕过圆柱体,会使得圆柱体产生阻力,同时,流体绕过圆柱体,由于漩涡脱落,使得圆柱横向产生速度差,从而产生压力差,导致圆柱横向产生升力。阻力系数和升力系数的计算公式为
| $ {C_L} = \frac{{2{F_L}}}{{\rho {U^2}DL}} $ | (12) |
| $ {C_D} = \frac{{2{F_D}}}{{\rho {U^2}DL}} $ | (13) |
式中:CL、CD分别为升力系数、阻力系数,FL, FD分别为升力、阻力,L是立管的长度,D为PVC管的外径,U为来流速度。
描述圆柱绕流现象的一个重要参数是斯特鲁哈数St,St数代表流体的非定常性质。St与漩涡脱落的频率fs的关系式为
| $ St = \frac{{{f_s}D}}{U} $ | (14) |
式中:fs为漩涡脱落的频率,通过对升力系数时间响应作快速傅里叶(FFT)变换得到。
所有系数的计算公式采用CFX的二次开发CEL语言编写成CCL文件导入CFX软件。
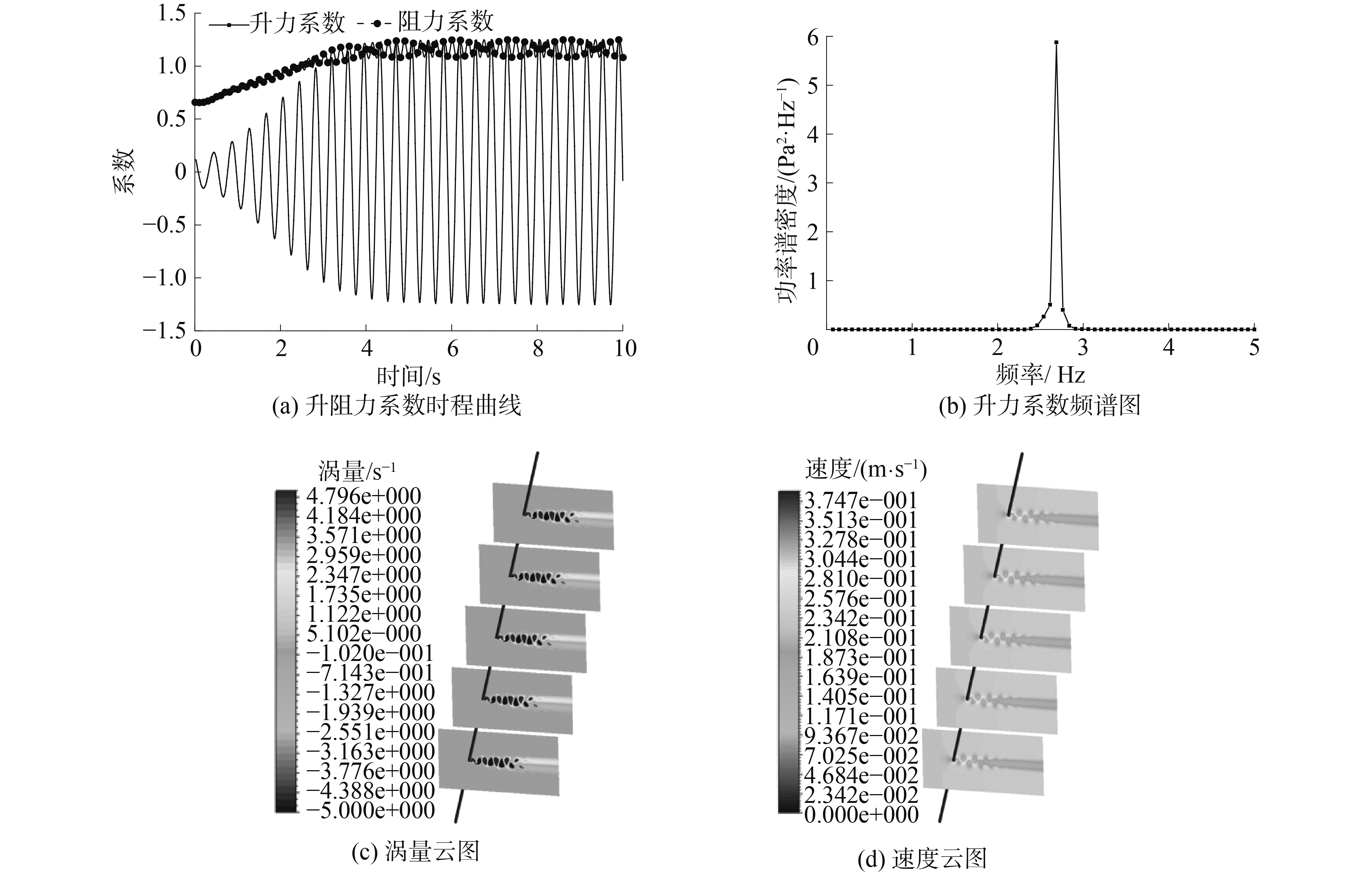
首先计算了雷诺数Re为3 900情况下的三维PVC管圆柱绕流流场。计算得到升力系数、阻力系数时程曲线如图 8(a)所示,将升力系数时程曲线作FFT变换得到Re为3 900时的漩涡脱落频率,如图 8(b)所示。
|
图 8 雷诺数Re=3 900时的计算结果 Fig.8 Simulation result of Re=3 900 situation |
图 8(c)、(d)分别为Re=3 900时候的涡量云图及速度云图。从图中可以看到漩涡的脱落。利用式(14)计算得到斯特鲁哈数St。文献[17]中, 得到的平均阻力系数为0.99,St为0.209;文献[18]中得到的平均阻力系数为1.26,St为0.22;与本文计算结果阻力系数1.13,St为0.22较为接近,说明计算结果较好,验证了本文CFD流场模拟的精确性。
3.2.2 基于CFD/CSD双向耦合求解瞬态流场载荷基于CFD/CSD双向流固耦合方法,分别计算立管顶张力为60 N和260 N时立管动态响应。约化速度
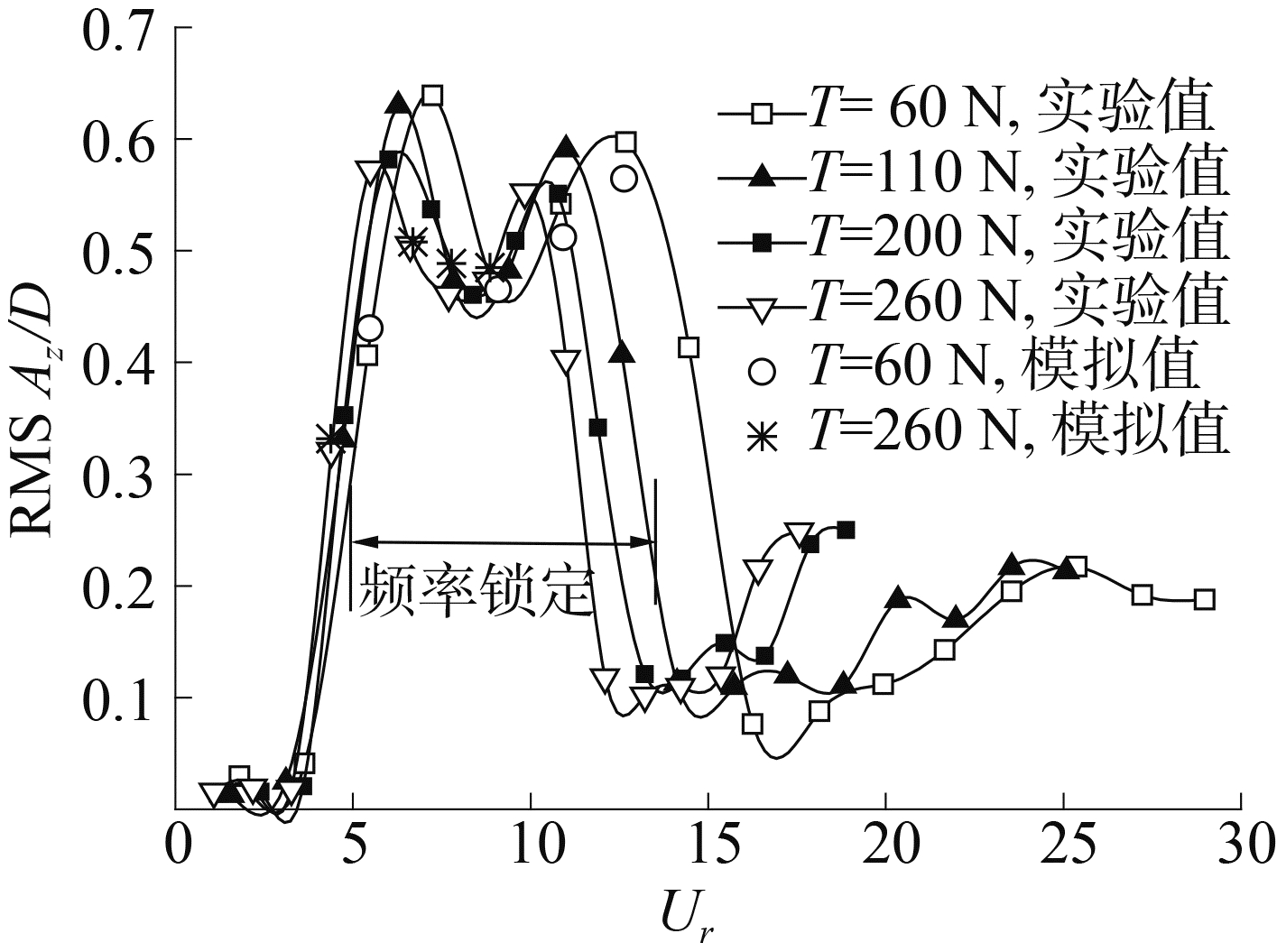
横向振幅的均方根与立管直径的比值RMS AZ/D(root mean square of amplitude in Z direction devide D)随着约化速度的变化结果如图 9所示,计算了8组结果,从图中可以看出,数值模拟的结果与文献[13]实验数据对比,误差值较小。说明基于尺度自适应模拟的双向流固耦合仿真精度较高。Ur=4.39~12.67之间为本文PVC立管的频率锁定区间,该区间内负值相对周围区间有显著的增大。本文数值模拟的计算结果都位于锁定区间。
|
图 9 立管Z方向幅值均方根随着约化速度变化图 Fig.9 Variation of root mean square of ampitude in Z direction with reduced velocity |
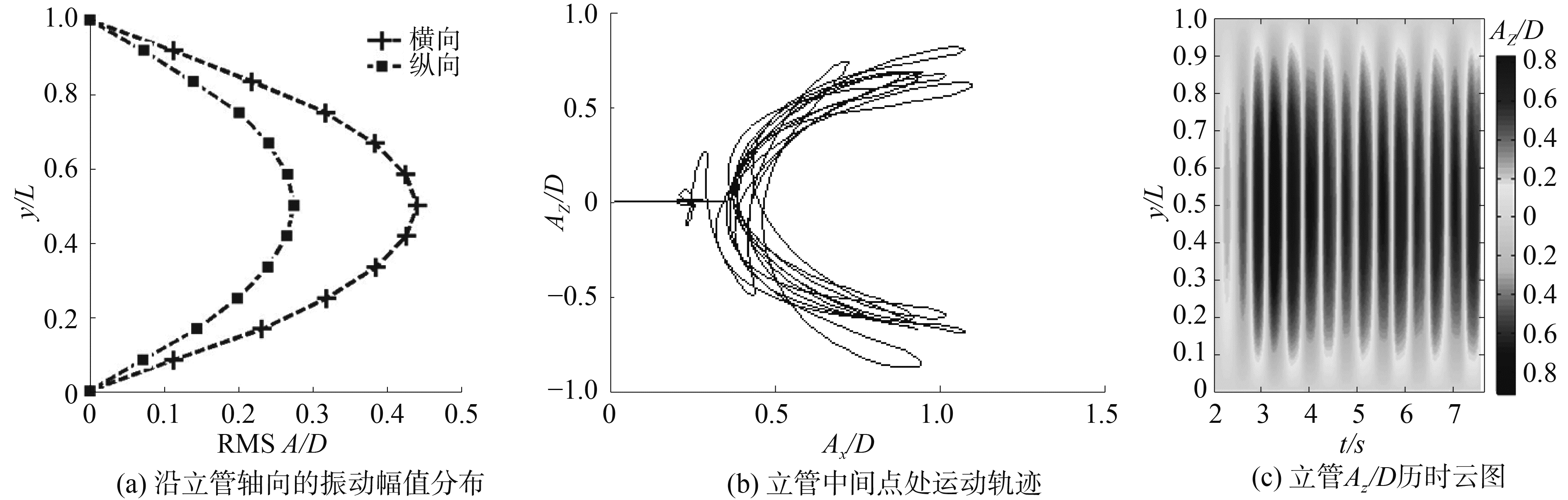
图 10为T=60 N, U=0.15 m/s时的部分仿真结果,图 10(a)为立管横向和纵向的振动幅值的无量纲量的均方根(root mean square, RMS)沿着立管长度方向(立管上的位置与立管长度的比值,y/L)的分布,从图中可以看出,横向振幅大于来流向振幅,立管最大幅值发生在立管中部,幅值无量纲量为0.42,与Ur=5.43处实验数据很接近。图 10(b)为立管中间点处的运动轨迹,从图中可以看出,运动轨迹比较杂乱,横向和来流向的振动位移响应都比较大,因此单方面只考虑横向振动的模型不能准确反映立管实际振动情况。图 10(c)为立管横向振动幅值无量纲量的历时云图,从图中可以看出,该流速情况下,立管主要是以第一阶模态振动。
|
图 10 T=60 N, U=0.15 m/s情况下的仿真结果 Fig.10 Simulation results of T=60 N, U=0.15 m/s situation |
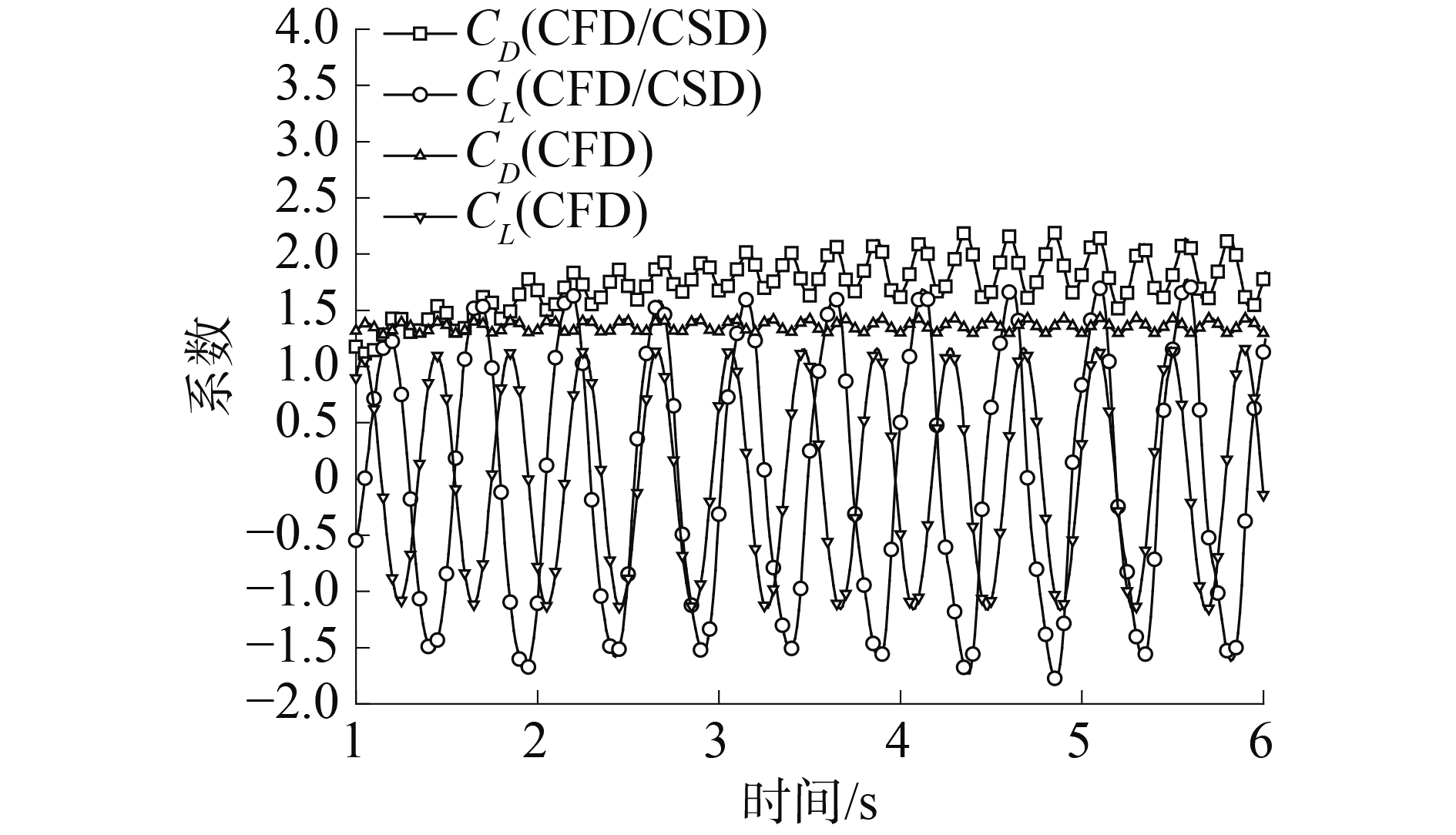
图 11为顶张力T=260 N,来流速度为0.2 m/s时候的三维立管升力系数和阻力系数的时间历程图。从图中可以看出,将立管视为柔性体,基于CFD/CSD双向耦合方法求得的系数的振幅要比将立管视为刚体情况下的大。立管为柔性体,双向耦合情况下计算出来的瞬态流场更接近实际情况。
|
图 11 升阻力系数时程曲线 Fig.11 Variation of drag and lift coefficient with time |
以公式P=ρgh计算沿着立管长度方向的静水压力分布,施加在立管外表面,然后对立管进行静水压力作用下的静力学分析,并以静力学计算结果更新数值模型的刚度和质量矩阵,然后进行湿模态计算。计算了不同顶张力情况下,静水压力对湿模态的影响。计算结果表明,考虑静水压力后,湿模态频率都会略微变大,变化幅度很小。表 3为顶张力等于0 N和260 N情况下,考虑和不考虑静水压力的湿模态频率计算结果,从表中可以看出,考虑静水压力后,湿模态频率略微增大。
| 表 3 水深对湿模态频率的影响 Tab.3 The influence of water depth on wet modal frequency |
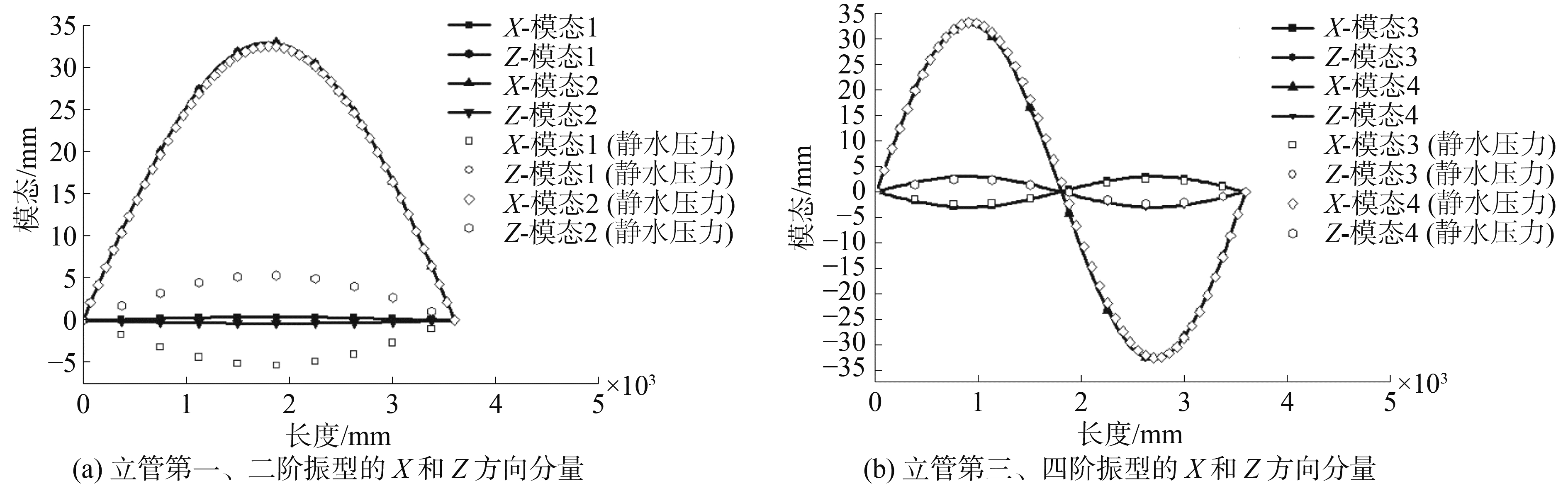
分别计算三维PVC柔性立管考虑和不考虑静水压力情况下的振型。计算结果表明,立管的振型主要表现在X和Z两个方向上。振型的数值比较大的为主振型,数值小的为次振型。考虑静水压力对该柔性立管低阶振型有影响,这种影响主要体现在次振型上,对主振型几乎没有影响。对高阶振型的主振型和次振型都没有影响。图 12中,original one标识不考虑水深影响的立管湿模态振型,hydro pressure表示考虑水深影响情况下的立管湿模态振型。图中可以看出,第一、二阶的次振型在考虑静水压力情况下弯曲幅度要比不考虑静水压力的情况下大。而考虑和不考虑静水压力对第三、四阶振型没有影响。
|
图 12 T=0 N情况下的振型 Fig.12 Mode shape of T=0 Nsituation |
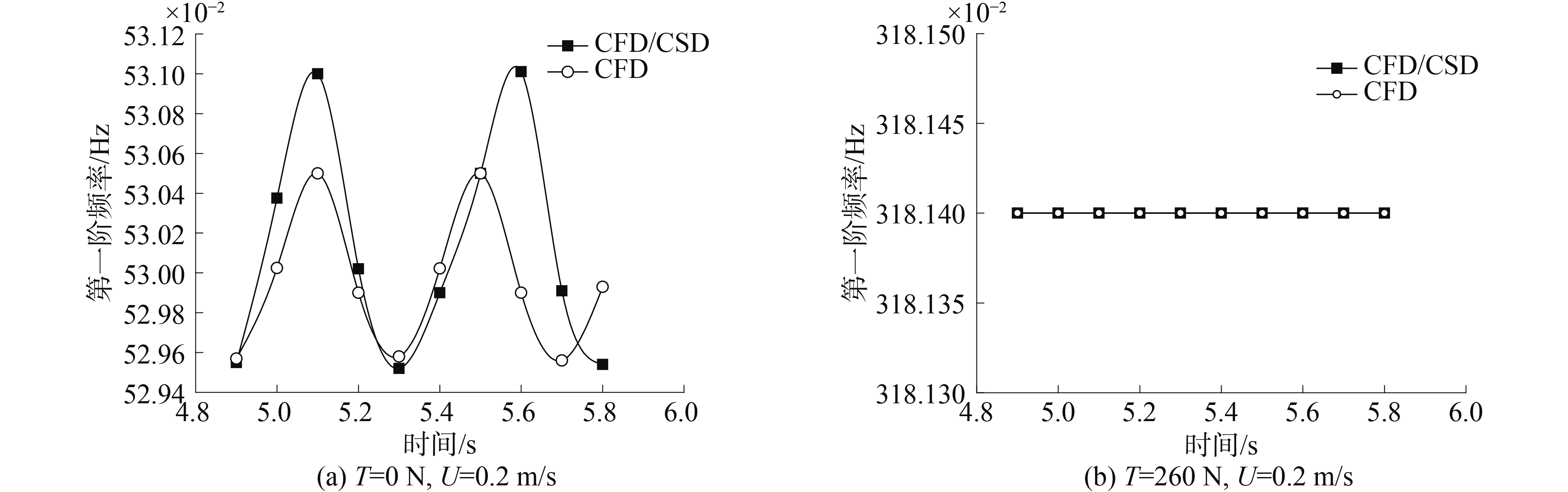
将前文计算出的瞬态流场载荷插值到三维柔性PVC立管的外表面的有限单元节点上,先进行静力学分析,再进行湿模态计算。图 13(a)、(b)分别是来流速度为0.2 m/s,顶张力为0 N和260 N时的第一阶频率随时间变化图。从图中可以看出,在瞬态流场作用下,湿模态频率呈周期性变化,这是由于漩涡脱落引起流体载荷呈周期变化引起的。考虑瞬态流场载荷后,湿模态频率相对不考虑流场载荷的情况下略微变大,变大幅度极小。随着顶张力的增加,频率变化更小。如图 13(b)所示,两种方法计算出来的瞬态流场载荷(第一种:立管视为刚体计算出的瞬态流场载荷;第二种:立管视为柔性体,双向耦合计算出的瞬态流场载荷)对湿模态频率几乎没有影响。如图 13(a)所示,采用双向耦合法计算出的瞬态流场载荷对立管的湿模态频率影响相比立管视为刚体计算出来的瞬态流场载荷对立管湿模态频率影响大。将立管视为柔性体,该情况下计算出的瞬态流场载荷对立管湿模态频率影响的计算结果更符合实际。
|
图 13 第一阶频率随时间变化趋势 Fig.13 Variation of the first mode frequency with time |
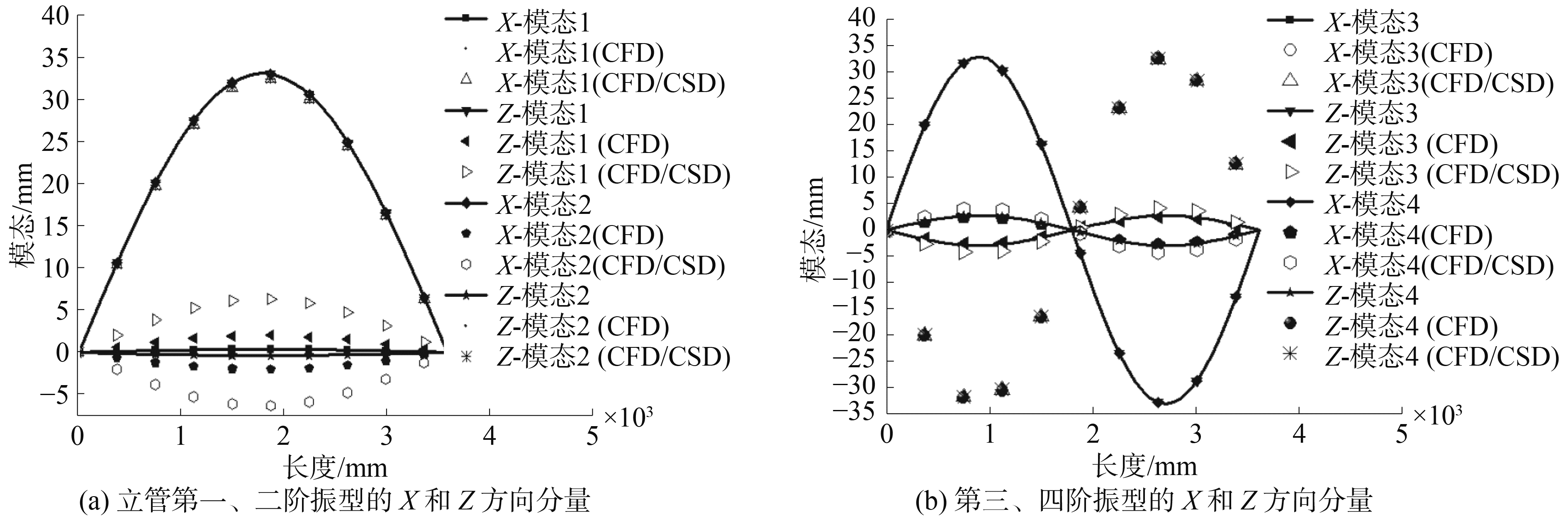
图 14为T=260 N、U=0.2 m/s、t=5.6 s时的湿模态振型的前四阶计算结果。从图 14(a)中可以看出,考虑瞬态流场载荷主要对第一、二阶的次振型有影响,对主振型都没有影响。采用双向耦合方法计算出的第一、二阶次振型弯曲幅度相比不考虑耦合方法计算出的第一、二阶次振型弯曲幅度大。从图 14(b)中可以看出,瞬态流场载荷对第三、四阶的主振型和次振型都几乎没有影响。此结果与水深对立管湿模态振型的影响结果类似。
|
图 14 T=260 N, U=0.2 m/s时的振型 Fig.14 Mode shape of T=260 N, U=0.2 m/s situation |
1) 立管各阶模态频率相比干模态频率有较大降低,降幅在30%~50%左右。随着立管顶端的顶张力的增大,立管出现明显的应力刚化现象,使得立管湿模态频率有大幅度的增加。
2) 考虑静水压力使得立管湿模态频率略微增加。同时,考虑静水压力对该柔性立管低阶振型有影响,对高阶振型没有影响。
3) 分别计算出立管视为刚体和柔性体两种情况下的瞬态流场载荷,将瞬态流场载荷插值到立管有限单元节点上,进行湿模态分析。湿模态频率相比不考虑瞬态流场载荷影响的要略微变大,且随时间呈周期性变化。两种情况下计算出的瞬态流场载荷对立管的湿模态频率影响极小,但对湿模态的低阶振型影响较大。
| [1] |
刘德辅, 王树青, 郭海燕. 海洋立管综合环境条件设计标准研究[J]. 海洋工程, 2011, 19(2): 13-17. LIU Defu, WANG Shuqing, GUO Haiyan. Study on combined design criteria for marine risers conveying flowing fluid[J]. The ocean engineering, 2011, 19(2): 13-17. (  0) 0)
|
| [2] |
顾海明, 周勇军. 机械振动理论与应用[M]. 南京: 东南大学出版社, 2007. GU Haiming, ZHOU Yongjun. Theory and application of mechanical vibration[M]. Nanjing: Southeast University Press, 2007. (  0) 0)
|
| [3] |
闻邦椿, 刘树英, 陈照波, 等. 机械振动理论及应用[M]. 北京: 高等教育出版社, 2009. WEN Bangchun, LIU Shuying, CHEN Zhaobo, et al. Theory and application of mechanical vibration[M]. Beijing: Higher Education Press, 2009. (  0) 0)
|
| [4] |
CHEN Y F, CHEN W J, HE Y L, et al. Dry and wet modal analysis and evaluation of influencing factors for flexible airship envelop[J]. Journal of Shanghai Jiaotong University, 2014, 48(2): 1002-1023. (  0) 0)
|
| [5] |
姜峰, 郑运虎, 梁瑞, 等. 海洋立管湿模态振动分析[J]. 西南石油大学学报, 2015, 37(5): 159-166. JIANG Feng, ZHENG Yunhu, LIANG Rui, et al. An analysis of the wet modal vibration of marine riser[J]. Journal of Southwest Petroleum University, 2015, 37(5): 159-166. DOI:10.11885/j.issn.1674-5086.2013.11.11.03 (  0) 0)
|
| [6] |
张光法. 潜深对半潜器附加质量影响分析[J]. 舰船电子工程, 2012(11): 9-10. ZHANG Guangfa. Analysis ofinfluence of submerged depth on adds mass of semmi-submerged device[J]. Ship electronic engineering, 2012(11): 9-10. DOI:10.3969/j.issn.1627-9730.2012.11.004 (  0) 0)
|
| [7] |
CHEN D Y, ABBAS L K, RUI X T, et al. Dynamic modeling of sail mounted hydroplanes system-Part Ⅰ:modal characteristics from a transfer matrix method[J]. Ocean engineering, 2017, 130: 629-644. DOI:10.1016/j.oceaneng.2016.12.020 (  0) 0)
|
| [8] |
HUANG K. Riser VIV and its numerical simulation[J]. Engineering sciences, 2013(4): 55-60. (  0) 0)
|
| [9] |
ZHU H, YAO J, MA Y, et al. Simultaneous CFD evaluation of VIV suppression using smaller control cylinders[J]. Journal of fluids & structures, 2015, 57: 66-80. (  0) 0)
|
| [10] |
ZHU H, YAO J. Numerical evaluation of passive control of VIV by small control rods[J]. Applied ocean research, 2015, 51: 93-116. DOI:10.1016/j.apor.2015.03.003 (  0) 0)
|
| [11] |
缪旭弘, 钱德进, 姚熊亮, 等. 基于ABAQUS声固耦合法的水下结构声辐射研究[J]. 船舶力学, 2009(2): 319-324. MIAO Xuhong, QIAN Dejin, YAO Xiongliang, et al. Sound radiation of underwater structure based on coupledacoustic-structural analysis with ABAQUS[J]. Journal of ship mechanics, 2009(2): 319-324. (  0) 0)
|
| [12] |
田红莉, 刘志峰, 张乃龙, 等. 箱体结构的声固耦合有限元分析[J]. 机械设计与制造, 2007(7): 24-26. TIAN Hongli, LIU Zhifeng, ZHANG Nailong. Solid box on the acoustic coupling finite element analysis[J]. Machinery design & manufacture, 2007(7): 24-26. (  0) 0)
|
| [13] |
SANAATI B, KATO N. Vortex-induced vibration (VIV) dynamics of a tensioned flexible cylinder subjected to uniform cross-flow[J]. Journal of marine science and technology, 2013, 18(2): 247-261. DOI:10.1007/s00773-012-0204-z (  0) 0)
|
| [14] |
CUI X Y, HU X, WANG G, et al. An accurate and efficient scheme for acoustic-structure interaction problems based on unstructured mesh[J]. Computer methods in applied mechanics & engineering, 2017, 317: 1122-1145. (  0) 0)
|
| [15] |
LUCIUS A, BRENNER G. Unsteady CFD simulations of a pump in part load conditions using scale-adaptive simulation[J]. International journal of heat & fluid flow, 2010, 31(6): 1113-1118. (  0) 0)
|
| [16] |
王翔宇, 李栋. SST-SAS在小分离流动数值模拟中的表现测试[J]. 西北工业大学学报, 2014(3): 337-340. WANG Xiangyu, LI Dong. Behavior of SST-SAS for mild airfoil trailing-edge separation[J]. Journal of Northwestern Polytechnical University, 2014(3): 337-340. (  0) 0)
|
| [17] |
FRANKE J, FRANK W. Large eddy simulation of the flow past a circular cylinder at Re=3900[J]. Journal of wind engineering and industrial aerodynamics, 2002, 90: 1191-1206. DOI:10.1016/S0167-6105(02)00232-5 (  0) 0)
|
| [18] |
詹昊, 李万平, 方秦汉, 等. 不同雷诺数下圆柱绕流仿真计算[J]. 武汉理工大学学报, 2008, 30(12): 129-132. ZHAN Hao, LI Wanping, FANG Qinhan, et al. Numerical simulation of the flow around a cricular cylinder at varies reynolds number[J]. Journal of Wuhan University of Techonlogy, 2008, 30(12): 129-132. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


