RV减速器以其体积小、速比大、运动精度高、回转误差小等优点被广泛应用于机器人的关节处。作为RV减速器重要组成部分的摆线针轮传动机构,对于RV减速器整体性能,尤其是传动精度的影响是不容忽视的。摆线针轮传动机构是由摆线轮与若干针齿相互啮合传动,在传动过程中会产生摩擦热,进而产生热变形,从而对整体的传动精度产生影响,甚至在啮合处发生热胶合。所以对摆线针轮传动部分进行相关热分析,对于提高RV减速器的整体传动精度是十分必要的。
目前国内外对于摆线针轮传动机构热分析的相关研究还少有报道,但是对于齿轮以及行星齿轮系的温度场及热分析已经有学者进行了相关的研究,方法主要有解析法[1]、试验方法[2-4]、有限元法[5-6]。解析法做了一定简化,与工程实际往往相差较大;试验法虽然可以得出比较准确的温度值,但对设备要求较高,成本较大,适合科学研究,但缺乏通用性。有限元法仿真结果取决于准确的摩擦热流量和对流边界条件的施加,简单有效。本文将在此基础上,运用有限元的方法,将其应用于摆线针轮传动机构上,通过理论计算分析得出温度场,从而为后续的相关研究奠定基础。
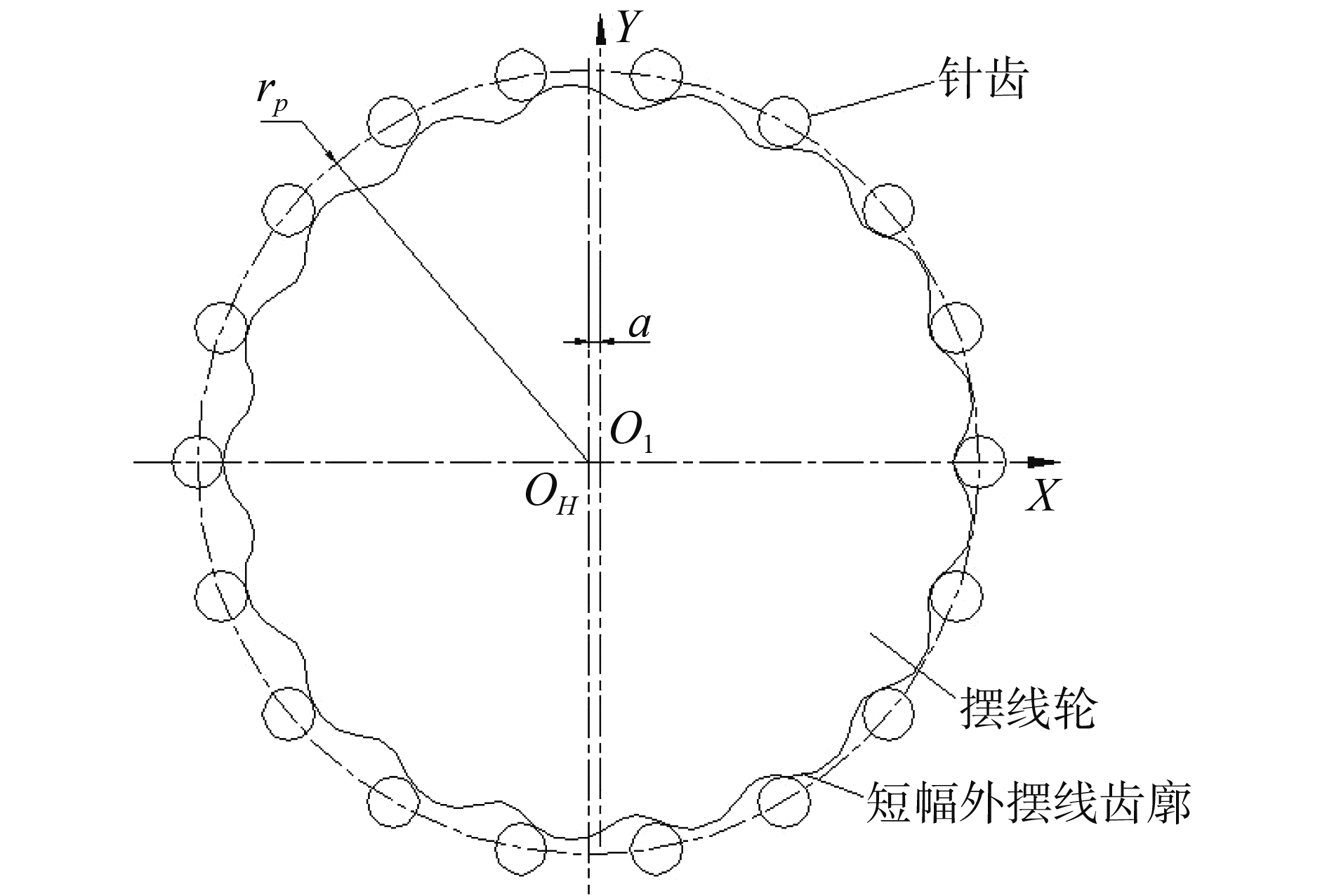
1 摆线针轮传动原理及摆线轮齿廓的形成RV减速器中摆线针轮传动机构的传动原理如图 1所示,摆线轮安装在有一定偏心距的输入轴上。当输入轴转动时,摆线轮不仅绕其自身自转,同时还会随着输入轴一起绕着针齿轮中心公转。所以在行星轮系中,把摆线轮称为行星轮,而把相对固定的针齿轮称为中心轮或太阳轮。针齿轮是由若干个针齿销均匀分布固定在半径为rp的圆周上,针齿销上套有针齿套共同组成了针齿,摆线轮齿数比针齿数少一个,图中针齿数为18个。

|
图 1 摆线针轮传动机构 Fig.1 The transmission of pin-cycloid planetary gearing |
以摆线轮的几何中心为原点,通过原点并以摆线轮齿槽的对称轴所在直线为x轴,建立坐标系,可得摆线轮齿廓(即:短幅外摆线齿廓)的标准齿形方程式为[7]
| $ \left\{ \begin{array}{l} x = \left( {{r_p} - {r_{rp}}{s^{ - \frac{1}{2}}}} \right)\cos \left[ {\left( {1 - i} \right)j} \right] - \\ \;\;\;\;\;\;\frac{a}{{{r_p}}}\left( {{r_p} - {z_p}{r_{rp}}{s^{ - \frac{1}{2}}}} \right)\cos \left( {ij} \right)\\ y = \left( {{r_p} - {r_{rp}}{s^{ - \frac{1}{2}}}} \right)\sin \left[ {\left( {1 - i} \right)j} \right] + \\ \;\;\;\;\;\;\frac{a}{{{r_p}}}\left( {{r_p} - {z_p}{r_{rp}}{s^{ - \frac{1}{2}}}} \right)\sin \left( {ij} \right) \end{array} \right. $ | (1) |
式中:i为摆线轮和针齿的相对传动比,
s=1+K12-2K1cosj,
|
图 2 短幅外摆线齿廓 Fig.2 The curtate epicycloid tooth profile |
在摆线轮与针齿啮合传动中,它们的啮合面处会产生大量的摩擦热,这会导致摆线轮齿的温度逐渐升高;然而又由于齿面润滑油和空气等其他因素,使摆线轮齿同时会散失热量。最终,传动中的摆线轮齿会达到一个热平衡状态,此时的温度将不再发生剧烈的变化,称为摆线轮齿的稳态温度(也叫本体温度)。
本文将通过有限元的方法模拟三维摆线轮在传动过程中,轮齿啮合处摩擦热的产生及传递过程,并在相应位置施加对流边界条件,进而求解计算获得整个摆线轮齿的稳态温度场分布。所选取的摆线针轮传动模型参数如表 1所示。
| 表 1 模型主要参数 Tab.1 Main parameters of the model |
由于在传动过程中,摆线轮齿每个齿的受载和传热、散热情况基本相同,因此各个齿的稳态温度场分布差别不大,所以可以建立单齿模型来分析整个摆线轮齿的稳态温度场。
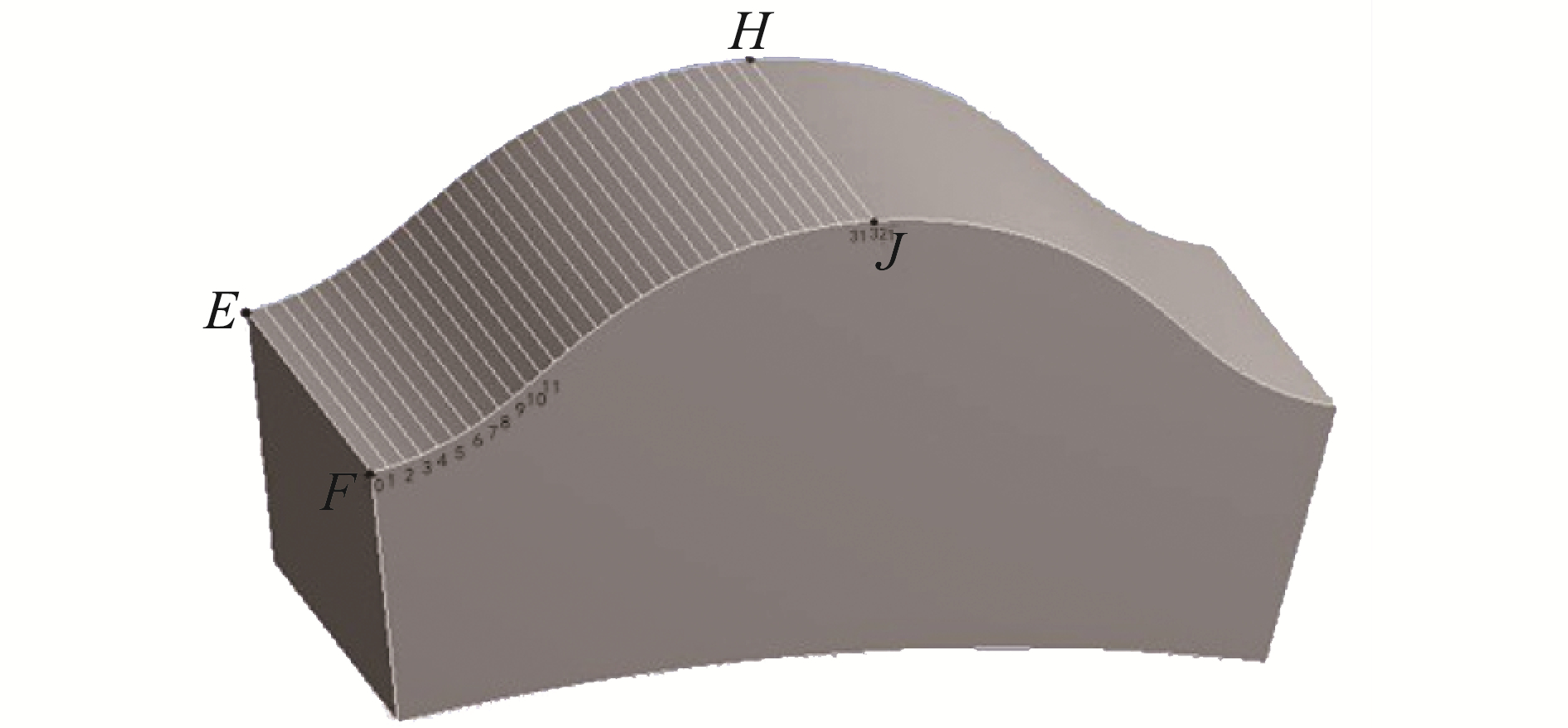
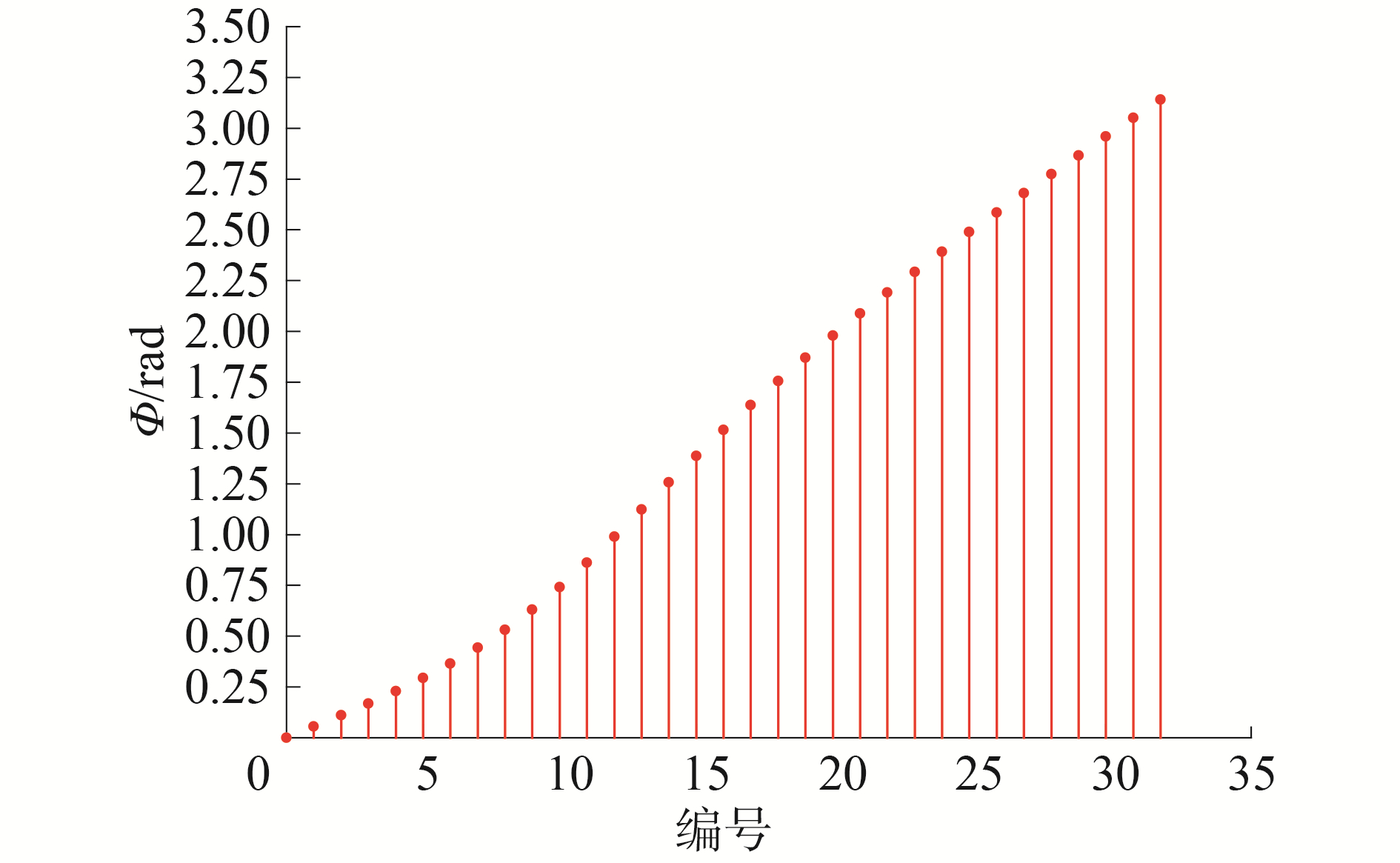
从摆线轮模型上切出一个轮齿如图 3,其接触区域为轮齿的一半齿面[8](区域EFJH)。将接触区域沿齿宽方向等分出若干条形区域并编号(0、1、2…31、32),这里分出32个条形区域。其中的每一条等分线即为摆线轮齿与针齿在不同啮合位置处的理论啮合线,而每一条啮合线的位置由上文中提到的啮合相位角φ来决定(其对应关系如图 4),啮合线上的每一点即为它们的啮合点。
|
图 3 摆线轮齿模型 Fig.3 The model of cycloidal gear tooth |
|
图 4 不同啮合位置处的啮合相位角 Fig.4 The phase angles of meshing for different engaging positions |
由摆线针轮传动机构的传动原理可知,摆线轮与针齿套接触,针齿套与针齿销接触,它们两两之间均存在相对滑动和滚动。为了便于计算,这里假设针齿套与针齿销固结在一起(下文统称针齿,其半径用rrp表示,即针齿半径等于针齿套半径)。因此,摆线轮齿与针齿啮合处的摩擦热主要由它们之间的相对滑动产生。
摆线轮齿与针齿不同啮合处的摩擦热流量q由它们之间的接触应力σp、相对滑动速度vr、摩擦系数f和能量转化系数γ决定[5, 9-10],计算公式为
| $ q = {s_p}{v_r}fg $ | (2) |
对于σp、vr和f的求解过程将在下文中介绍,γ为摩擦能转化为热能的能量转化系数,一般取0.9~0.95[6, 11]。
2.1 平均接触应力σp针齿齿廓为圆,摆线轮齿廓为曲线,摆线轮齿廓上各点的曲率半径都不一样。当针齿与摆线轮齿接触并传动时,可近似认为是两个瞬时圆柱体在接触。所以,摆线轮齿与针齿间的最大接触应力σH及接触区产生的宽度L可以根据Hertz公式来近似计算[8, 12], 其平均接触应力σp为最大接触应力σH的π/4倍[5, 13-14]。
| $ {s_H} = 0.418\sqrt {\frac{{{E_c}{P_i}}}{{B{\rho _{ei}}}}} $ | (3) |
| $ L = \sqrt {\frac{{8{P_i}{\rho _{ei}}\left( {1 - {u^2}} \right)}}{{pB{E_c}}}} $ | (4) |
| $ {s_p} = \frac{p}{4}{s_H} = \frac{p}{4} \times 0.418\sqrt {\frac{{{E_c}{P_i}}}{{B{\rho _{ei}}}}} $ | (5) |
式中:Pi为摆线轮齿与针齿啮合处的法向应力(i=0,1,2…32);Ec为摆线轮齿与针齿啮合处的当量弹性模量;B为摆线轮齿宽度;υ为摆线轮齿与针齿的泊松比(这里取0.3);ρei为摆线轮齿与针齿啮合处的当量曲率半径(i=0,1,2…32)。
为了求得摆线轮齿与针齿啮合的平均接触应力σp,还需要求出它们在不同位置处的法向应力Pi、当量弹性模量Ec和当量曲率半径ρei。
2.1.1 当量曲率半径ρei摆线轮标准齿形的理论齿廓曲线的曲率半径ρ0i,由微积分公式可求得[8]
| $ {\rho _{0i}} = \frac{{{{\left( {1 + K_1^2 - 2{K_1}\cos {j_i}} \right)}^{\frac{3}{2}}}{r_p}}}{{{K_1}\left( {1 + {z_p}} \right)\cos {j_i} - \left( {1 + {z_p}K_1^2} \right)}} $ | (6) |
φi同上文φ,即不同的啮合位置处(i=0,1,2…32)。实际齿廓曲线的曲率半径ρi为[12]
| $ {\rho _i} = {\rho _{0i}} + {r_{rp}} = \frac{{{{\left( {1 + K_1^2 - 2{K_1}\cos {j_i}} \right)}^{\frac{3}{2}}}{r_p}}}{{{K_1}\left( {1 + {z_p}} \right)\cos {j_i} - \left( {1 + {z_p}K_1^2} \right)}} + {r_{rp}} $ | (7) |
针齿与摆线轮齿接触点的当量曲率半径ρei为[12]
| $ \frac{1}{{{\rho _{ei}}}} = \left| {\frac{1}{{{r_{rp}}}} - \frac{1}{{{\rho _i}}}} \right| = \left| {\frac{{{\rho _i} - {r_{rp}}}}{{{r_{rp}}{\rho _i}}}} \right| = \left| {\frac{{{\rho _{0i}}}}{{{r_{rp}}\left( {{\rho _{0i}} + {r_{rp}}} \right)}}} \right| $ | (8) |
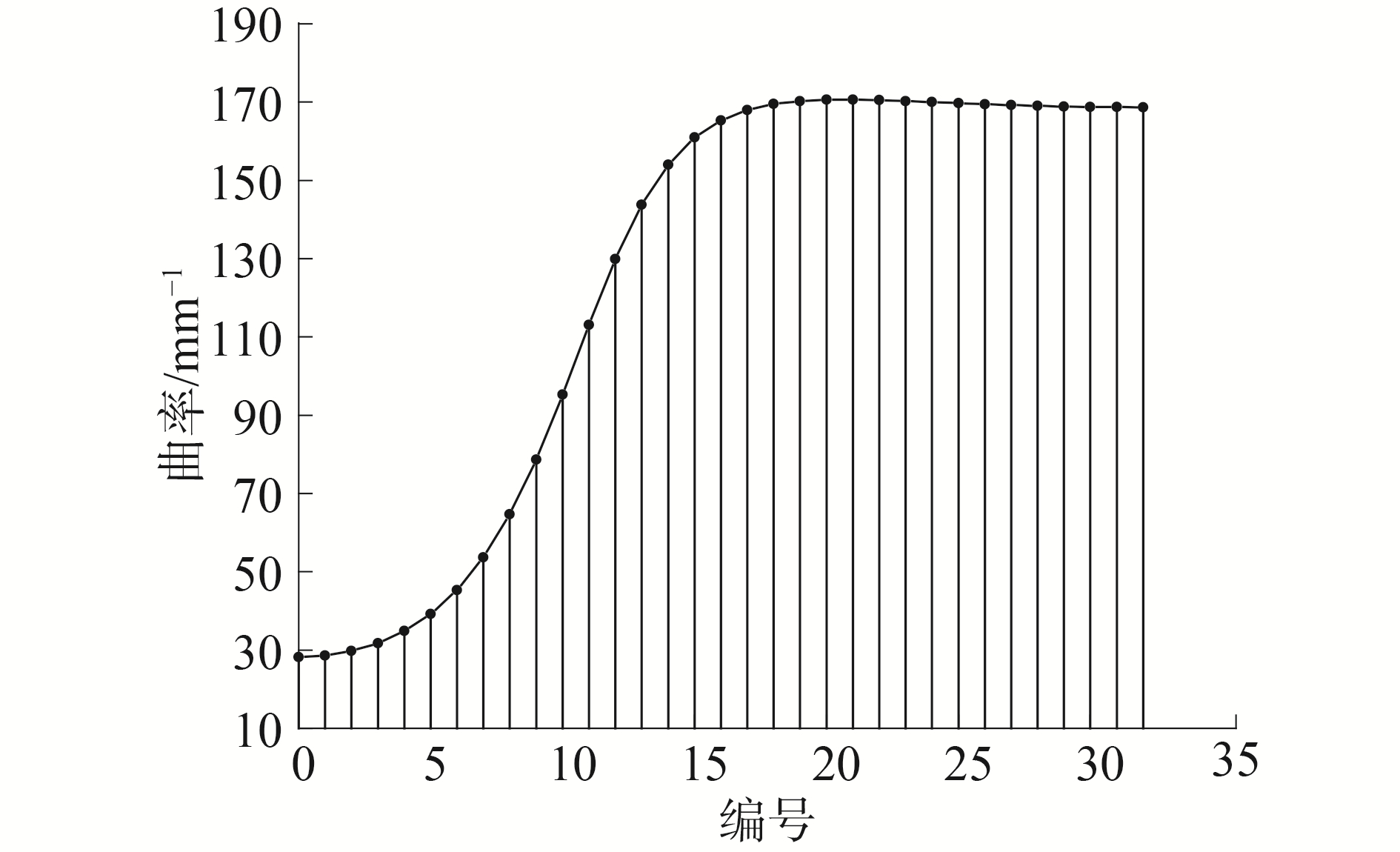
由式(8)可知,当量曲率半径的值是随着φ的变化而变化,而φ值对应着摆线轮齿沿齿廓方向的啮合位置,并且在相同的位置沿齿宽方向的值相同。摆线轮齿接触区域的等分线处的当量曲率值可由图 5表示。
|
图 5 不同啮合位置处的当量曲率 Fig.5 The equivalent curvatures for different engaging positions |
| $ {E_c} = \frac{{2{E_1}{E_2}}}{{{E_1} + {E_2}}} $ | (9) |
式中:E1、E2分别为摆线轮与针齿的弹性模数[12]。在摆线针轮传动中,摆线轮与针齿(套)材料相同,且均为轴承钢,所以有
| $ {E_c} = {E_1} + {E_2} = 2.06 \times {10^5}\;{\rm{MPa}} $ | (10) |
Pi为标准齿形下的摆线轮与针齿啮合时的瞬时法向接触压力,其值为
| $ {P_i} = \frac{{2.2{M_v}}}{{{K_1}{z_c}{r_p}}}\frac{{\sin {\varphi _i}}}{{{s^{\frac{1}{2}}}}} $ | (11) |
式中:Mv为摆线针轮传动部分的输出轴阻力矩。由式(11)可知,Pi的值也是随着啮合位置(即φ的值)的变化而变化,可由图 6表示。
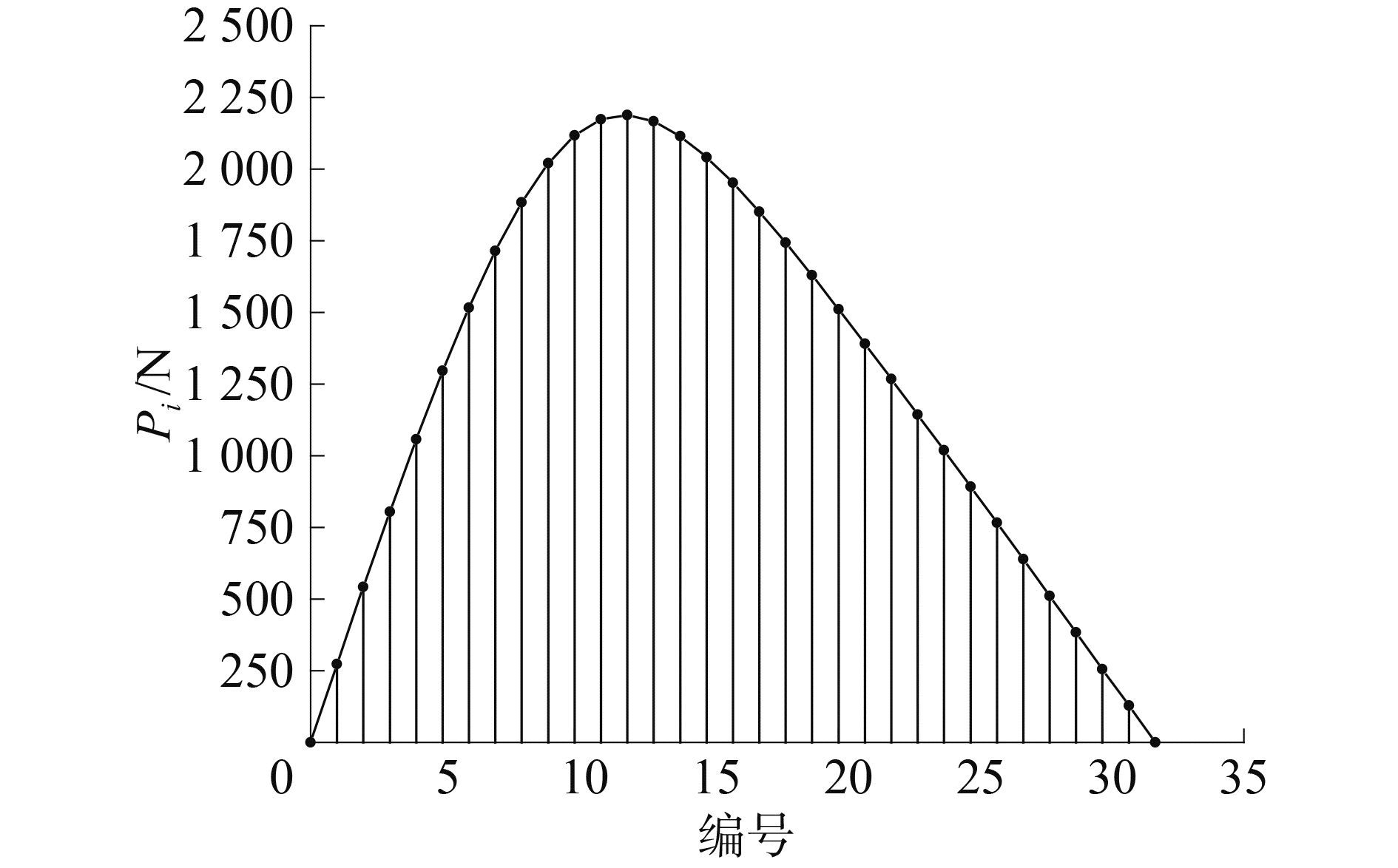
|
图 6 不同啮合位置处的法向接触压力 Fig.6 The normal contact pressure for different engaging positions |
最终求出的在摆线轮齿接触区域的平均接触应力σp沿齿廓方向的值如图 7所示。其值沿摆线轮齿宽方向不发生变化,只是随着啮合线位置的不同,沿齿廓方向发生变化。
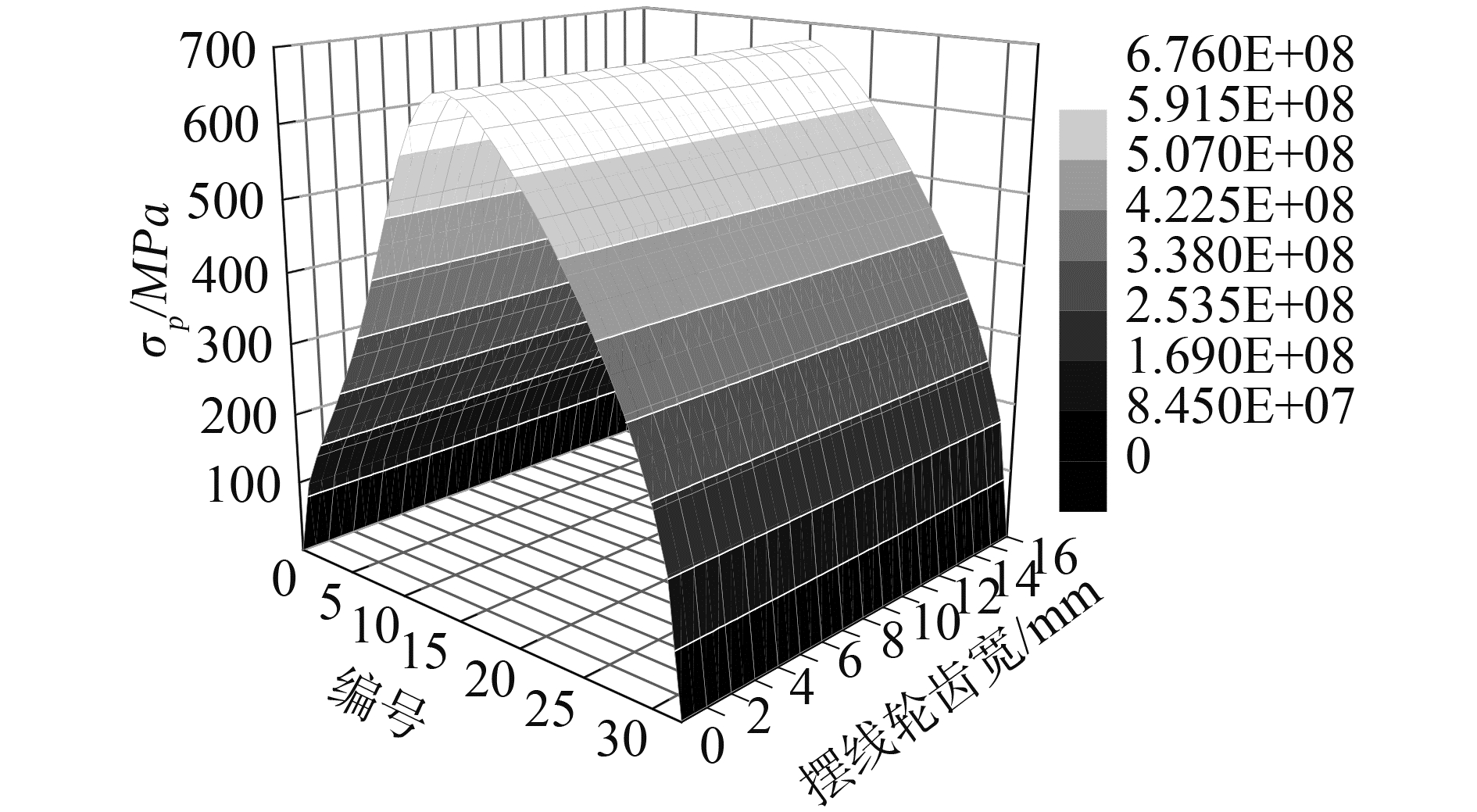
|
图 7 不同啮合位置处的平均接触应力 Fig.7 The average contact stress for different engaging positions |
在摆线轮与针齿啮合传动过程中,摆线轮齿与针齿在啮合线切线方向有相对滑动,产生相对滑动速度vr。本文已假设针齿套与针齿销固结在一起并统称针齿,所以针齿认为是固定不动的。正是因为vr的存在造成了摆线轮齿上摩擦热的产生,其值如下[16-17]
| $ \left\{ \begin{array}{l} - {v_r} = {r_p}{s^{\frac{1}{2}}} - {r_{rp}}\frac{{{w_H}}}{{{z_c}}}\\ {w_H} = \frac{{2{\rm{ \mathsf{ π} }}{n_H}}}{{60}} \end{array} \right. $ | (12) |
式中:wH为摆线针轮传动部分输入轴的角速度;nH为摆线针轮传动部分输入轴转速。负号表明摆线轮与输入轴(转臂)的转向相反。
2.3 摩擦系数f摆线轮齿与针齿接触处的摩擦系数f会受很多因素的影响,如材料、粗糙度、润滑油特性等。所以可以采用实验的方法具体测定某工作条件下的摩擦系数f。根据国内和国际上在齿轮胶合强度计算中采用的方法[9, 18],摆线轮齿与针齿啮合位置处的摩擦系数f可表示为
| $ \begin{array}{l} f = 0.002{\left( {\frac{{{P_{ti}}}}{{B \times 0.001}}} \right)^{0.2}} \cdot \\ {\left( {\frac{2}{{0.001{\rho _{ei}}{v_n}\cos \alpha }}} \right)^{0.2}}{\eta ^{ - 0.05}}X \end{array} $ | (13) |
式中:X为摆线轮齿与针齿啮合处的粗糙度因子;ρei为啮合处的当量曲率半径;η为润滑油的动力粘度系数;Pti为啮合处的切向载荷;vn为切向速度。
其中粗糙度因子X可表示为
| $ X = 21.4{\left( {\frac{{{S_1} + {S_2}}}{{2d}}} \right)^{0.25}} $ | (14) |
式中:S1、S2分别为摆线轮齿与针齿的表面粗糙度;d为摆线轮齿分度圆直径。
为了得出摆线轮齿面的摩擦热流量,分析计算其所需的各种参数,所得出的摩擦热流量q的值如图 8所示。
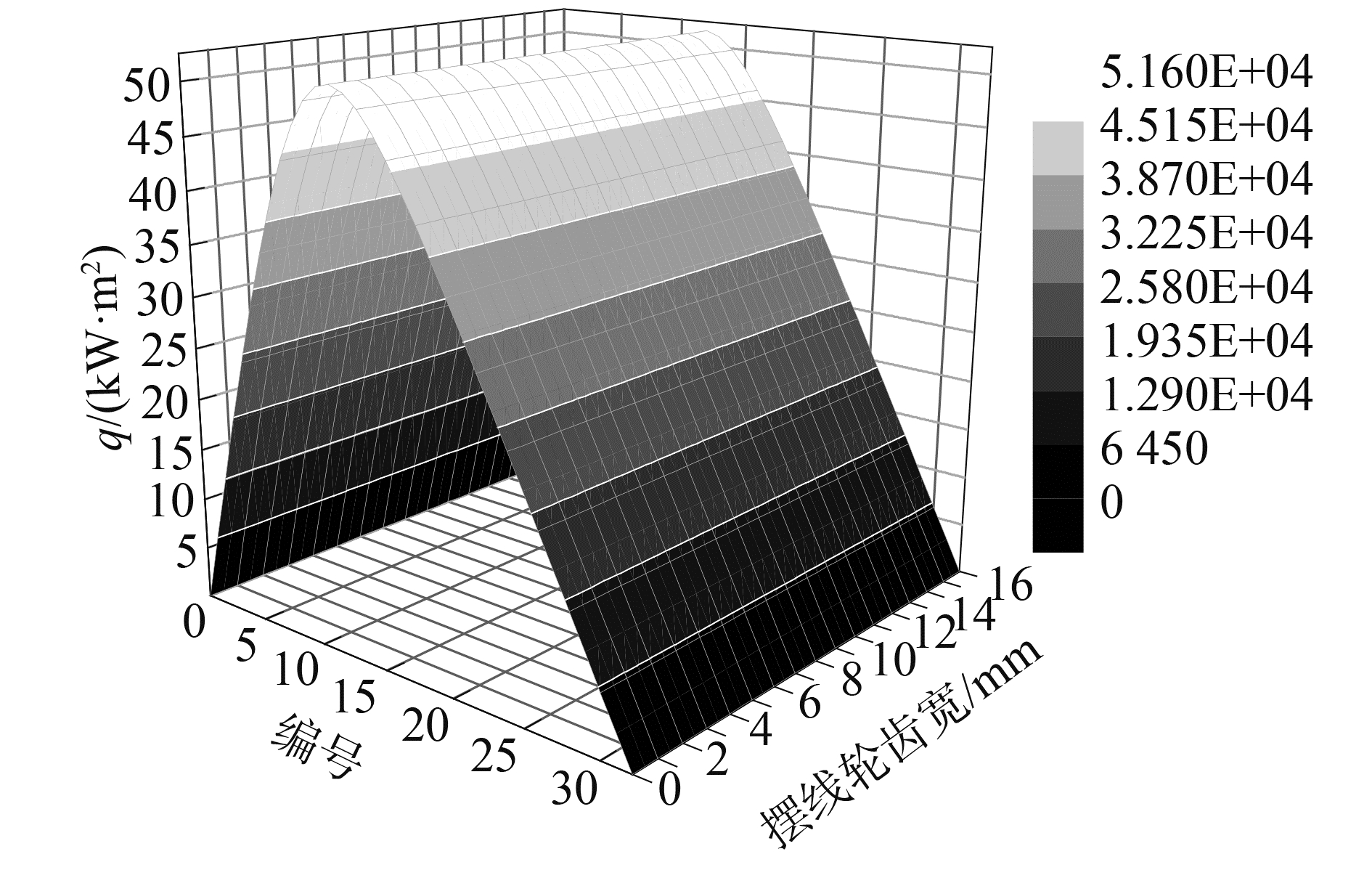
|
图 8 接触齿面摩擦热流量的分布 Fig.8 The distribution of friction heat flux for contact tooth surface |
在摆线轮与针齿啮合传动中,摆线轮齿同时和润滑油以及空气发生对流换热而散失一部分热量,其对流换热系数的分析和计算目前还不是十分成熟,没有一个较为精确的计算方法。由于摆线轮齿面和端面的对流换热系数差别不大,在这里取它们相同,均以齿面与润滑油及空气的对流换热系数h代替。h的计算方法可以参考对于齿轮齿面对流换热系数的求法[9]。采用与参考文献相同的润滑油,其性能参数见表 2。
| $ h = 0.664\lambda {P^{\frac{1}{3}}}{\left( {\frac{w}{v}} \right)^{\frac{1}{2}}} $ | (15) |
| 表 2 润滑油性能参数 Tab.2 Lubricating oil performance parameters |
式中:λ为导热率,P为普朗特数,w为摆线轮自转的角速度,v为运动粘度。
4 摆线轮齿温度场有限元分析 4.1 摆线轮齿模型的建立和导入用三维绘图软件Solidworks根据摆线轮齿廓的标准齿形方程式建立摆线轮的三维模型,并切出一个摆线轮齿导入到Ansys Workbench中,再进行摆线轮齿接触区域条形区域的划分,如第2章所述。同时在Workbench的此工程项目中设置好材料参数,并对此单齿模型进行网格划分,如图 9所示。

|
图 9 摆线轮齿的网格划分 Fig.9 The mesh generation of the cycloidal gear tooth |
对于摆线轮齿,由文中摩擦热流量的求解过程可知,其值仅由于啮合位置的不同沿着摆线轮齿齿廓方向发生变化,而在同一啮合位置处沿齿宽方向没有变化。所以,可在齿面平行于齿宽方向等分出若干条形区域,并将每条等分线编号,如图 3所示。再分别将每个条形区域两侧的等分线上的摩擦热流量取平均值,将此平均值作为此条形区域的摩擦热流量来施加。(例如:如图 3所示,分别求出1处和2处的摩擦热流量,再取平均值,作为其间条形区域的摩擦热流量)此等分线其实就是摆线轮齿与针齿的理论啮合线,其上各点的摩擦热流量是相同的(沿齿宽方向没有变化),其值等于此啮合线上任一点的摩擦热流量,可由上文摩擦热流量的求解过程求出。
在这里需要特别注意的是,求出的摩擦热流量是摆线轮齿与针齿啮合传动时,啮合点在单位时间单位面积上产生的摩擦热量。但在实际传动中,此热量并不是一个随时间恒定不变的值,而是以一定时间t2为周期(此周期与摆线轮公转有关),周期性产生的。也就是说,在每一个周期内,摆线轮齿与针齿在每一条理论啮合线上的啮合点处只参与啮合一次,也只有在这个短暂的啮合时间段t1内,在此啮合点处产生热量q[6]。
在摆线轮与针齿的某处啮合位置,其齿面接触宽度L可由上文求得,所以在此位置产生摩擦热流量的时间t1为
| $ {t_1} = \frac{L}{{{v_r}}} $ | (16) |
式中:vr为上文中的相对滑动速度。
由摆线轮与针齿啮合传动的原理可知,摆线轮绕针齿分布中心公转的同时,也进行自转,类似于行星轮系中的行星轮,并且摆线轮齿数比针齿数少一个。所以某一个摆线轮齿距下一次啮合的时间周期t2等于摆线轮公转(zp-1)个针齿所用的时间,其中zp、wH的含义同上文(wH为输入轴角速度同时也是摆线轮绕针轮中心的公转角速度),则t2为
| $ {t_2} = \frac{1}{{{w_H}}}\left( {2g\frac{{{z_p} - 1}}{{{z_p}}}} \right) $ | (17) |
因此,在摆线轮齿面任意啮合位置(即任意条形区域)处,可施加的平均摩擦热流量q为
| $ \bar q = \frac{{{t_1}}}{{{t_2}}}q\mathit{\Lambda } $ | (18) |
式中:q为摆线轮齿条形区域的摩擦热流量;Λ为摆线轮与针齿啮合的热分配系数,这里近似取0.5[6]。针齿(销套)在获得热量后温度也会上升,但是由于其与摆线轮齿在某一啮合位置的啮合时间t1非常短暂,摆线轮齿的稳态温度场受到的影响相对较小。
4.3 摆线轮齿对流边界条件的设定在4.2节已经在接触面EFJH上进行了摩擦热流量的施加,这里再在齿廓曲面EFGI和轮齿的两个侧面FBCG、EADI上施加对流边界条件,如图 10所示,其对流换热系数值可由第3节求出。
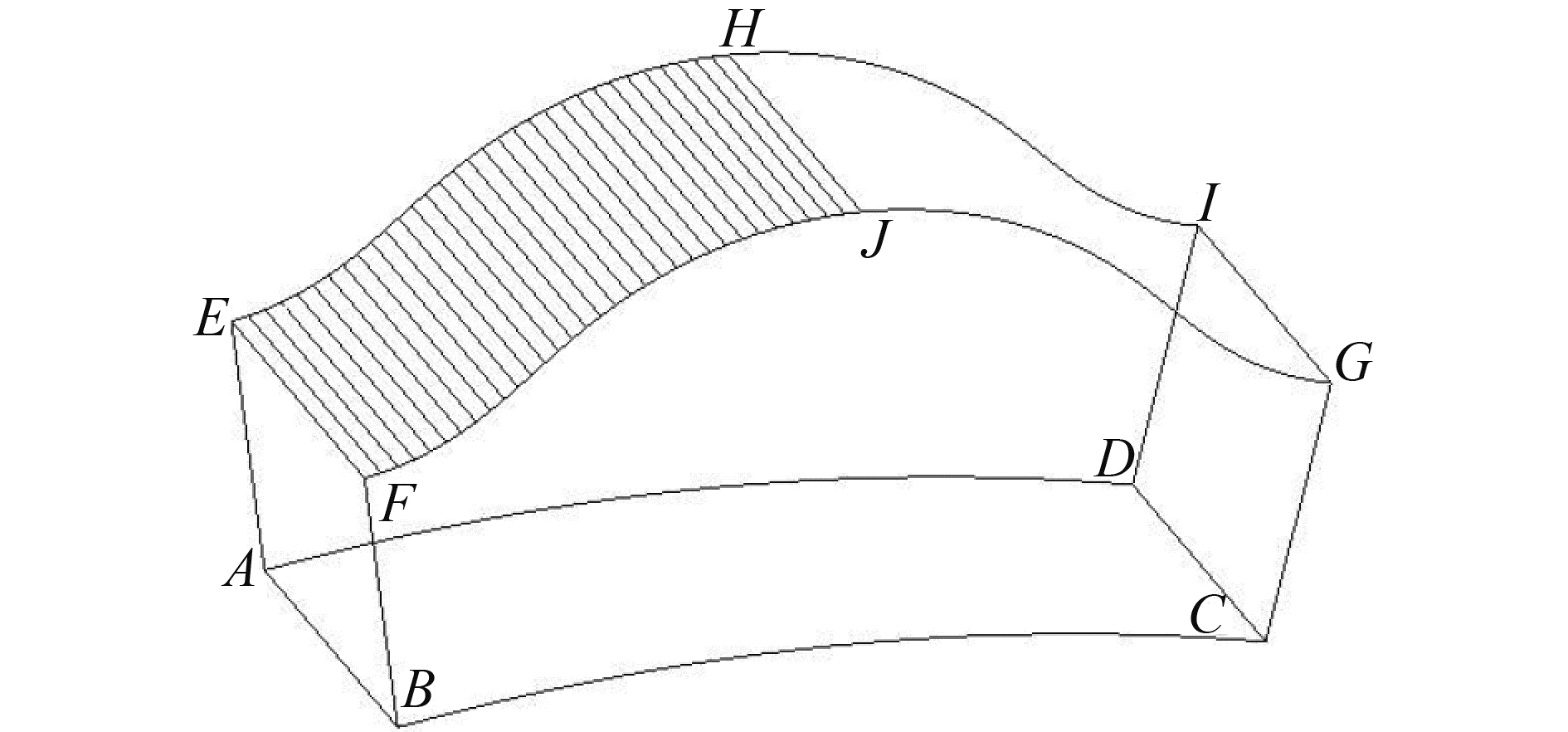
|
图 10 摆线轮齿 Fig.10 The cycloidal gear tooth |
当摆线针轮传动部分输入功率分别为7.5、11.25、15 kW时,分析计算出的摆线轮齿温度场分布如图 11所示。

|
图 11 当输入功率为7.5, 11.25, 15 kW时的温度场分布 Fig.11 The distribution of temperature fields when the input powers are 7.5, 11.25, 15 kW |
由图 11可以看出,随着输入功率的增加摆线轮齿整体温度上升,但摆线轮齿温度分布规律大致不变;摆线轮齿接触区域的最高温度随载荷的增加也显著提高。这是因为随着输入功率的增加,摆线轮齿与针齿之间的摩擦热流量也相应提高,导致温度上升;但是对流换热系数的影响相对较小,所以散热状况变化不大。这些均与实际情况相吻合。
摆线轮齿面从接触区域一侧到非接触区域,温度逐渐降低,形成了鲜明的温度梯度;并且在轮齿接触区域,齿面温度整体高于齿体温度。这是由于在接触区域产生摩擦热流量使齿面温度上升,而在非接触区域仅发生对流换热降低了温度所致。而正是这种温度分布的不均匀性,严重减低了摆线针轮传动部分以及整个RV减速器的传动精度和承载能力,引起冲击和振动,在实际传动中需要进行充分考虑。
摆线轮齿温度场沿齿宽方向呈对称分布,中间温度偏高、两端偏低,且最高温度均出现在接触区域靠中间的位置。这是由于在沿齿宽方向的啮合线上,摩擦热流量并未发生变化,它只是沿着齿廓方向随着啮合位置的不同而发生变化;并且摆线轮齿与润滑油及空气的对流边界条件沿齿宽方向对称分布,越靠近轮齿两侧对流换热状况越好,而越靠近中间状况越差;摆线轮齿中间位置摩擦热流量较大,散热较小,所以最高温度出现在摆线轮齿接触面一侧靠近中间的位置。而这种沿齿宽方向的温度变化所产生的热变形,将直接导致摆线轮齿与针齿啮合接触线长度的减少,降低传动精度及承载能力。
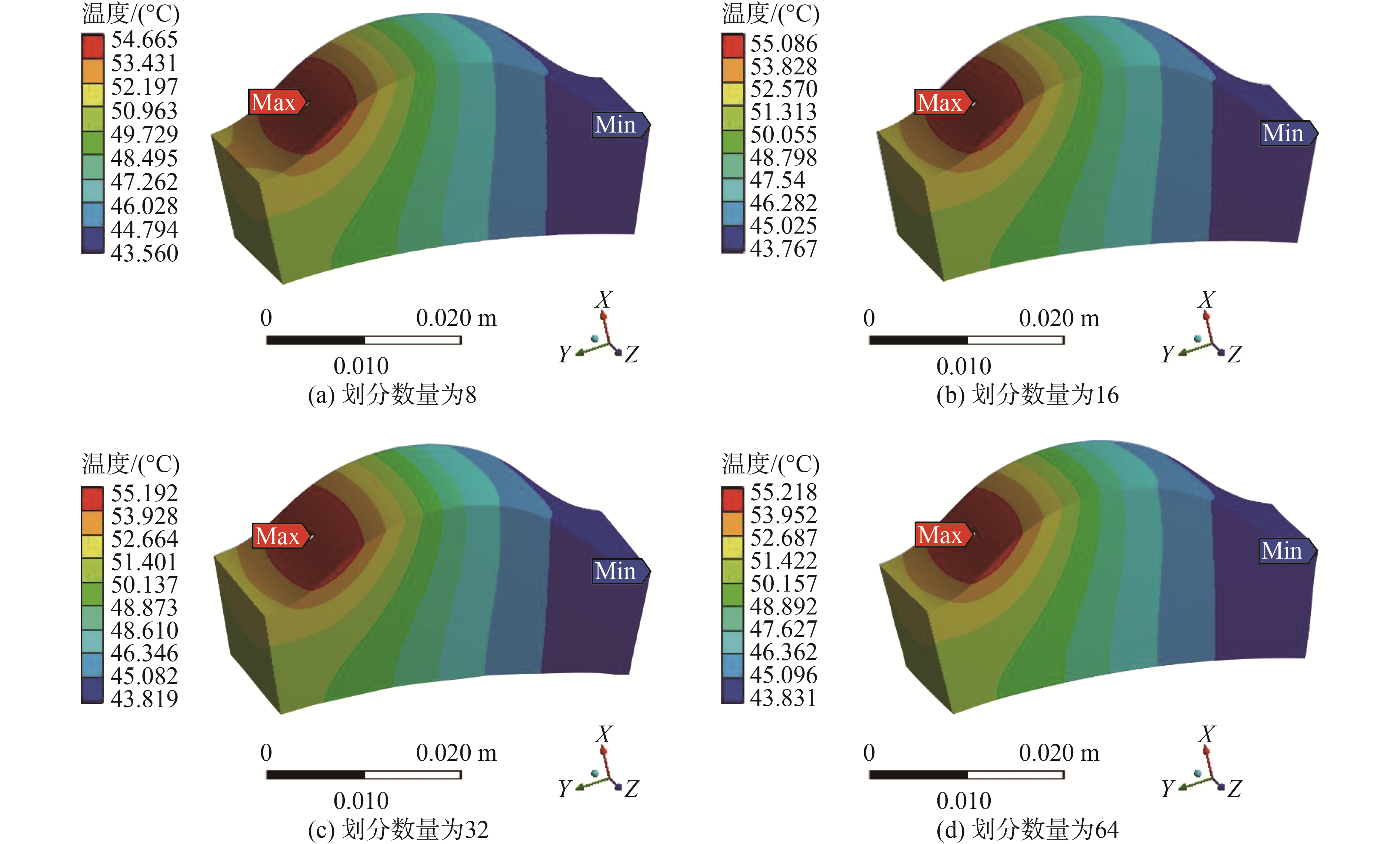
4.4.2 条形区域划分数量对结果精度的影响考虑到上文中摆线轮齿面接触区划分的条形区域数量对最终结果可能产生的影响,在输入功率为11.25 kW的情况下,分别划分条形区域数为8、16、32、64,按上文方法进行计算分析,所得出的温度场分布及最高温度值如图 12所示。
|
图 12 条形区域划分数量为8、16、32、64的温度场分布 Fig.12 The number of bar area division are 8, 16, 32, 64 |
由图 12可知,当摆线轮齿接触区域划分不同数量的条形区域时,温度场分布规律大致不变,但整体温度呈上升趋势,齿面最高温度和最低温度的数值是不同的,但是随着划分区域数量的增加,温度变化幅度越来越小,并且趋于平缓,其分布规律可由图 13表示。

|
图 13 不同条形区域划分时的温度变化规律 Fig.13 The temperature variation regularity for different bar area division |
由图 13温度分布规律可以看到,当条形区域数为32时,摆线轮齿面最高温度和最低温度的变化开始趋于平缓,并且趋于恒定的数值,这个数值可以认为就是摆线轮齿的稳态温度,因此所得出的温度场分布结果较为精确。
5 结论1) 本文通过计算RV减速器中摆线轮齿与针齿啮合过程中的摩擦热流量和各种所需参数,以及对流边界条件的施加,通过Ansys Workbench有限元分析,模拟出短幅外摆线轮齿在传动过程中的稳态温度场分布。验证了随着输入功率的变化,摆线轮齿温度场的变化规律与实际情况相吻合。
2) 为了更加接近实际情况,充分考虑了摩擦热流量的施加过程中,摆线轮齿接触区条形区域的划分数量对最终结果的影响,得出了更加准确的温度场分布结果。
本文研究内容为今后的提高机构传动精度、避免轮齿胶合、轮齿降温、轮齿修形等更为深入的研究奠定了基础。
| [1] |
MAO K. A numerical method for polymer composite gear flash temperature prediction[J]. Wear, 2007, 262(11): 1321-1329. (  0) 0)
|
| [2] |
SUTTER G, RANC N. Flash temperature measurement during dry friction process at high sliding speed[J]. Wear, 2010, 268(11): 1237-1242. (  0) 0)
|
| [3] |
LETZELTER E, GUINGAND M, VAUJANY J P, et al. A new experimental approach for measuring thermal behaviour in the case of nylon 6/6 cylindrical gears[J]. Polymer testing, 2010, 29(8): 1041-1051. DOI:10.1016/j.polymertesting.2010.09.002 (  0) 0)
|
| [4] |
赵建平, 杜鸿家. 舰船齿轮润滑状态研究[J]. 机械传动, 1996(1): 70-71. ZHAO Jianping, DU Hongjia. Research on lubrication modes of ship gears[J]. Journal of mechanical transmission, 1996(1): 70-71. (  0) 0)
|
| [5] |
肖望强, 李威, 韩建友. 非对称齿廓渐开线齿轮传动的热分析[J]. 农业机械学报, 2006, 37(12): 164-167. XIAO Wangqiang, LI Wei, HAN Jianyou. Thermal analysis of involute gear transmission with unsymmetric tooth profile[J]. Transactions of the Chinese society for agricultural machinery, 2006, 37(12): 164-167. DOI:10.3969/j.issn.1000-1298.2006.12.039 (  0) 0)
|
| [6] |
龙慧, 张光辉, 罗文军. 旋转齿轮瞬时接触应力和温度的分析模拟[J]. 机械工程学报, 2004, 40(8): 25-26. LONG Hui, ZHANG Guanghui, LUO Wenjun. Modeling and analysis of transient contact stress and temperature of involute gears[J]. Chinese journal of mechanical engineering, 2004, 40(8): 25-26. (  0) 0)
|
| [7] |
何卫东, 李力行. 高精度RV减速器中摆线轮齿形的优化修形[J]. 大连铁道学院学报, 1999, 20(2): 54-58. HE Weidong, LI Lixing. The optimized modification of cycloidal gear of high precision RV reducer[J]. Journal of Dalian Railway Institute, 1999, 20(2): 54-58. (  0) 0)
|
| [8] |
郑州工学院机械原理及机械零件教研室. 摆线针轮行星传动[M]. 北京: 科学出版社, 1978: 64, 74-75. Department of mechanical engineering and mechanical parts in Zhengzhou Institute of Technology. The pin-cycloid planetary gearing[M]. Beijing: Science Press, 1978: 64, 74-75. (  0) 0)
|
| [9] |
薛建华, 李威. 齿轮系统的温度场预测方法[J]. 北京科技大学学报, 2014(2): 18. XUE Jianhua, LI Wei. Prediction methods of gear system temperature fields[J]. Journal of University of Science and Technology Beijing, 2014(2): 18. (  0) 0)
|
| [10] |
LIN H T, LIN L K. Heat transfer from a rotating cone or disk to fluids of any Prandtl number[J]. International communications in heat and mass transfer, 1987, 14(3): 323-332. DOI:10.1016/0735-1933(87)90033-9 (  0) 0)
|
| [11] |
HANDSCHUH R F. Thermal behavior of spiral bevel gears[D]. Washington:Case Western Reserve University, 1993.
(  0) 0)
|
| [12] |
朱孝录, 何卫东, 李威, 等. 齿轮传动设计手册[M]. 北京: 化学工业出版社, 2004: 798, 772-773. ZHU Xiaolu, HE Weidong, LI Wei, et al. Handbook of gear design[M]. Beijing: Chemical Industry Press, 2004: 798, 772-773. (  0) 0)
|
| [13] |
BLOK H. The thermal network method for predicting bulk temperatures in gear transmissions[C]//Proc 7th Round Table Discussion on Marine Reduction Gears. Stal-Laval, Finspang, Sweden, 1969:3-25.
(  0) 0)
|
| [14] |
LONG H, LORD A, GETHIN D T, et al. Operating temperatures of oil-lubricated medium-speed gears:numerical models and experimental results[J]. Proceedings of the institution of mechanical engineers, Part G:Journal of aerospace engineering, 2003, 217(2): 87-106. DOI:10.1243/095441003765208745 (  0) 0)
|
| [15] |
张东生, 关天民. 摆线针轮传动动态受力分析理论[J]. 机械设计, 2006, 23(10): 35-37. ZHANG Dongsheng, GUAN Tianmin. Dynamic force bearing analytical theory of cycloidal pinwheel transmission[J]. Journal of machine design, 2006, 23(10): 35-37. DOI:10.3969/j.issn.1001-2354.2006.10.012 (  0) 0)
|
| [16] |
李充宁. 摆线针齿行星传动轮齿的相对运动及滑动系数[J]. 机械传动, 1998, 22(3): 19-21. LI Chongning. Relative motion and sliding coefficient of gear teeth ofpin-cycloid planetary gearing[J]. Journal of mechanical transmission, 1998, 22(3): 19-21. (  0) 0)
|
| [17] |
机械系机械基础实验室. 关于摆线针轮行星传动中几个问题的讨论[J]. 东北大学学报:自然科学版, 1976(2): 84. Mechanical basic laboratory. Discussion on several problems of thepin-cycloid planetary gearing[J]. Journal of Northeastern University:natural science, 1976(2): 84. (  0) 0)
|
| [18] |
BOBACH L, BEIICKE R, BARTEL D, et al. Thermal elastohydrodynamic simulation of involute spur gears incorporating mixed friction[J]. Tribology international, 2012, 48: 191-206. DOI:10.1016/j.triboint.2011.11.025 (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


