窄矩形加热通道凭借着换热面积大、临界热负荷高、换热设备结构紧凑等优点在船舶、航空航天、化工、微电子等领域得到广泛应用。关于窄矩形通道内的对流换热特性一直备受学者们关注,其大部分研究都是在强迫循环条件下进行的等[1-5]。
自然循环是仅依赖回路中流体的密度差形成的驱动力来实现的流动循环。其在工程领域中被普遍应用,如能源、化工、船舶、航天等。在核能工程领域,作为一种重要的非能动安全技术,自然循环已经成为众多先进反应堆系统及安全设计的重要选择[6]。在船用核动力装置中,良好的自然循环能力对于提高反应堆固有安全性、降低噪声和简化系统等都具有很重要的意义。关于自然循环系统下的单相水传热特性研究,主要集中在圆形截面通道。Siddiqui等对太阳能集水器内的单相水自然循环换热特性进行了实验研究,其研究结果表明自然循环系统中的单相水换热特性与浮升力有很大关系[7];Liu等对自然循环系统下,窄矩形通道内的超临界CO2传热特性进行了实验研究,提出了新的适用于自然循环条件下,超临界CO2的对流换热计算关联式[8-9];Yadav[10-11]等对自然循环条件下矩形通道内CO2对流换热特性进行数值分析和理论研究,提出了新的计算关联式。
由于单相自然循环系统中,系统循环流量较低,浮升力的作用较强,而现有的大部分单相强迫对流传热公式都没有考虑浮升力对传热特性的影响。单相自然循环系统被广泛应用于核反应堆余热排出系统中,其中窄矩形加热通道在船舶动力装置中应用较为普遍。基于该背景,本文以单相去离子水为介质,对自然循环系统下,单面加热窄矩形通道内的单相对流传热特性进行了实验研究。
1 实验回路及实验本体本文实验回路装置如图 1所示,该回路为自然循环回路,其本体主要由预热器、可视化加热实验段、冷凝器、辅助循环泵、稳压器、流量计以及相关的连接管道和阀门等组成。其中,流量计选用精度为0.2%,响应时间为5 ms的KROHNE电磁流量计(OPTIFLUX4300F)。实验段前的预热器可对入口水温进行自动反馈调节,确保进入实验段的温度为恒定值,实验过程中,通过预热器对入口欠热度进行控制。

|
图 1 闭式自然循环系统主回路 Fig.1 Main loop of closed-natural circulation system |
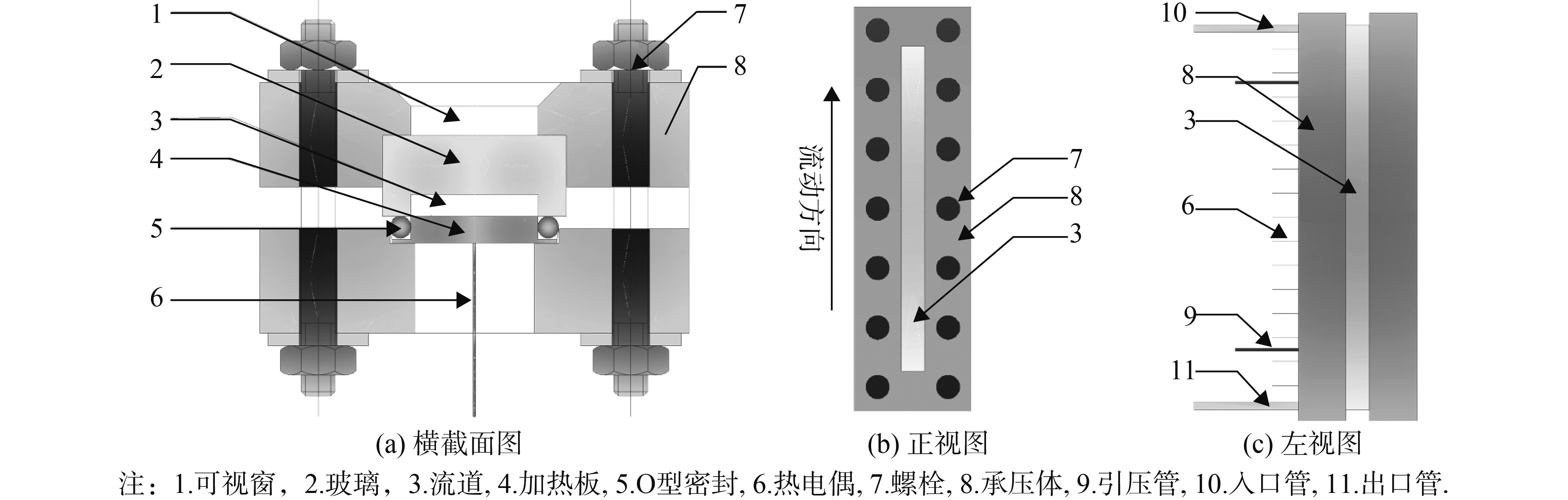
可视化单面加热实验段中有一当量直径为4 mm的窄矩形通道。该实验段简图如图 2所示。其中加热元件为一3 mm厚的316 L不锈钢板。可视化窗体为石英玻璃。在实验段进出口分别布置了精度为0.5级、直径为1 mm的N型热电偶,用于测量矩形通道进出口流体温度;在实验段加热板背部据入口无量纲距离(x/De)分别为6、18、30、42、54、66、78、90、102、114、126处焊接多根Ⅰ级精度的N型热电偶,用于测量加热板外壁温;实验段上安装有RoseMount公司生产的测量精度为0.075%,响应时间为100 ms的3051CD型差压变送器,用于测量测压段压降,计算Darcy摩擦阻力系数。
|
图 2 可视化单面加热实验段 Fig.2 Visual one-side heating test section |
在本实验中,对加热板导热问题进行一维、稳态、常物性、均匀内热源假设。根据实验测得的加热板外壁温来计算与流体接触的内壁温。
加热板内一维稳态常物性导热微分方程及其边界条件为
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}T}}{{\partial {y^2}}} + \frac{\mathit{\Phi }}{\lambda } = 0\\ \lambda \frac{{\partial T}}{{\partial y}}\left| {_{y = Y}} \right. = - q\\ T\left| {_{y = 0}} \right. = {T_{{\rm{w,out}}}} \end{array} \right. $ | (1) |
式中:T为温度,℃;Tw, out为外壁面温度,℃;y为据外壁面的距离,m;Y为加热板厚度,m;Φ为体积释热率,W/m3;λ为导热系数,W/(m ·K);q为热流密度,W/m2。
由式(1)可得稳态条件下加热板内的温度分布为
| $ T = {T_{{\rm{w,out}}}} - \frac{1}{2}\frac{\mathit{\Phi }}{\lambda }{y^2} $ | (2) |
局部换热系数h(W/m2 ·K)的计算关系式为
| $ h = \frac{q}{{{T_{{\rm{w,in}}}} - {T_{\rm{f}}}}} $ | (3) |
式中:Tw, in为外壁面温度,℃;Tf为主流水温,℃。
由于加热板均匀释热,局部流体主流温度计算采用进出口温度进行线性插值计算,具体为
| $ {T_{\rm{f}}} = {T_{{\rm{in}}}} + \frac{x}{{{L_0}}}\left( {{T_{{\rm{out}}}} - {T_{{\rm{in}}}}} \right) $ | (4) |
式中:Tin、Tout分别为实验段进出口流体温度,℃;x为距离加热元件底端的距离,m;L0为加热元件总长,m。
考虑到加热元件的热损失,在计算流体加热功率时,采用热平衡关系式来计算加热热流密度
| $ q = \frac{{M\left( {{i_{{\rm{out}}}} - {i_{{\rm{in}}}}} \right)}}{{{A_{\rm{h}}}}} $ | (5) |
式中:M为实验段质量流量,kg/s;iin、iout分别为实验段进、出口流体比焓,J/kg;Ah为换热面积,m2。
采用局部努塞尔数Nu来计算实验段不同位置的换热能力
| $ Nu = \frac{{h \cdot De}}{{{\lambda _{\rm{f}}}}} $ | (6) |
式中:De为流道当量直径,m;λf为流体导热系数,其定性温度取0.5(Tw, in+Tf)。
3 换热能力影响分析 3.1 单相自然循环实验在本文研究中,进行了不同系统压力,不同入口过冷度,不同加热功率下的单相自然循环实验。实验获得不同数下的平均Re数,结果如图 3、4所示。迄今为止,在强迫循环对流换热中,Gnielinski[12]公式被公认为计算准确度最高的单相对流换热公式
| $ \left\{ \begin{array}{l} Nu = \frac{{\left( {f/8} \right)\left( {Re - 1000} \right)\mathit{P}{\mathit{r}_{\rm{f}}}}}{{1 + 12.7\sqrt {f/8} \left( {\mathit{Pr}_{\rm{f}}^{2/3} - 1} \right)}}\left[ {1 + {{\left( {\frac{{De}}{l}} \right)}^{2/3}}} \right]{c_{\rm{t}}}\\ {c_{\rm{t}}} = {\left( {\frac{{\mathit{P}{\mathit{r}_{\rm{f}}}}}{{\mathit{P}{\mathit{r}_{{\rm{w,in}}}}}}} \right)^{0.01}} \end{array} \right. $ | (7) |
|
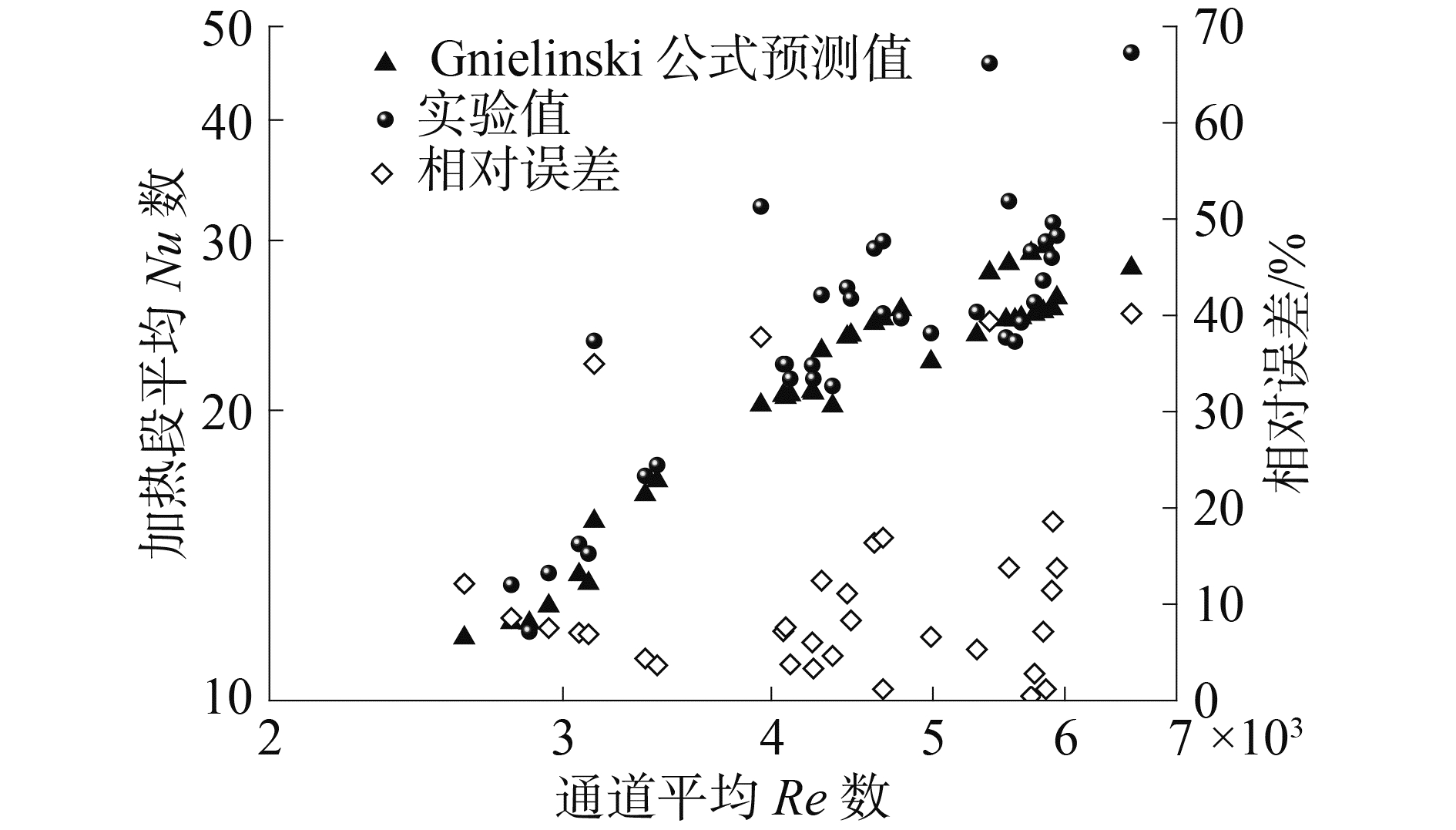
图 3 加热段平均Nu数与Gnielinski公式预测值对比 Fig.3 Comparison of average Nu with Gnielinski correlation predictions |
|
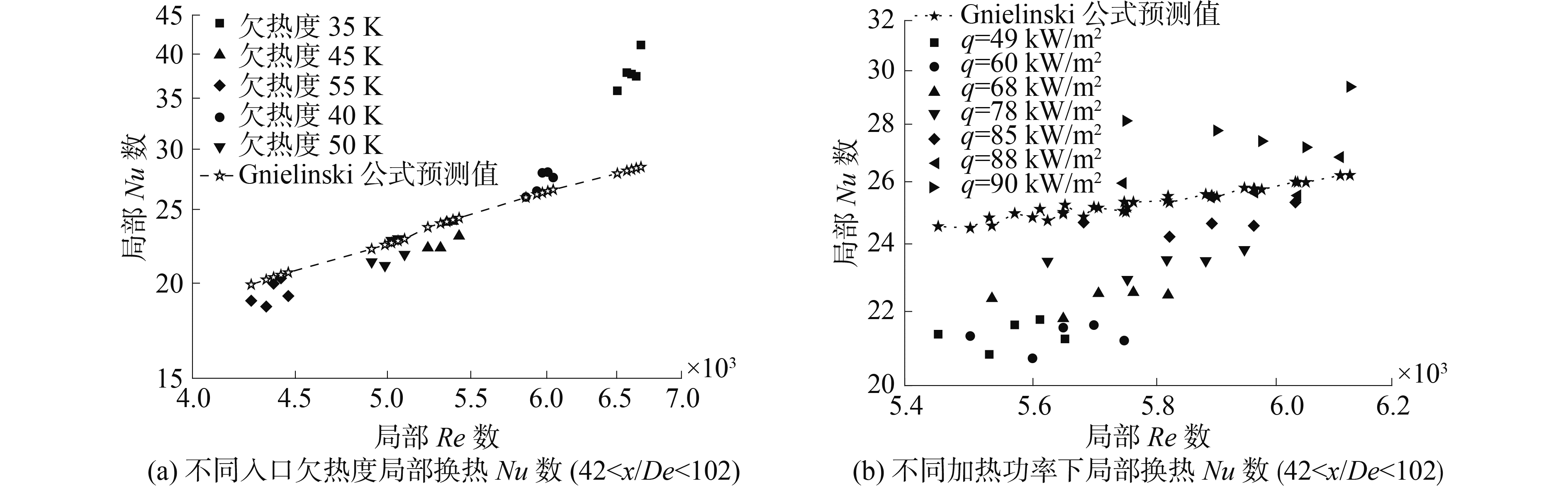
图 4 加热段局部Nu数与Gnielinski公式对比 Fig.4 Comparison of local Nu with Gnielinski correlation |
式中:f为达西阻力系数;Prf为以水温为定性温度的普朗特数,Prw, in为以内壁温为定性温度的普朗特数。由于本文实验研究工况包含了过渡流和湍流两种流态,且研究对象为单面加热窄矩形通道,现有的绝大部分阻力计算关系式都难以对其进行准确计算。因而,在本文中,通过实验段差压计测得的摩擦压降和达西公式,对阻力系数进行计算:
| $ f = \frac{{2De\Delta {P_{\rm{f}}}}}{{{{\bar \rho }_{{\rm{ch}}}}{u^2}{L_1}}} $ | (8) |
式中:L1为测压段长度,m;u为流速,m/s; ΔP为测压段压强,Pa; ρch为测压段平时密度,kg/m2。
图 3给出了实验结果与式(7)计算结果的对比,其中“Gnielinski公式预测值为相同流动参数和物性参数下,根据Gnielinski公式计算出的Nu数,对比结果表明:92%的数据与Gnielinski公式计算值的相对误差在20%以内,80%的数据相对误差在15%以内;且实验测得平均Nu数普遍高于Gnielinski公式计算值,这是由于实验段入口效应段的影响,使得换热系数变大。
图 3中有部分实验值高出Gnielinski公式预测值40%左右,经分析,该部分数据的加热热流密度较大或者入口欠热度较低。针对该现象,图 4分别给出了不同入口欠热度,以及不同加热功率下,入口效应较弱位置(42<x/De<102)的局部Nu数,该实验结果与Gnielinski公式计算值吻合较好,但随着入口欠热度的降低和加热功率的升高,实验测得局部Nu数与Gnielinski公式计算值之差逐渐升高。
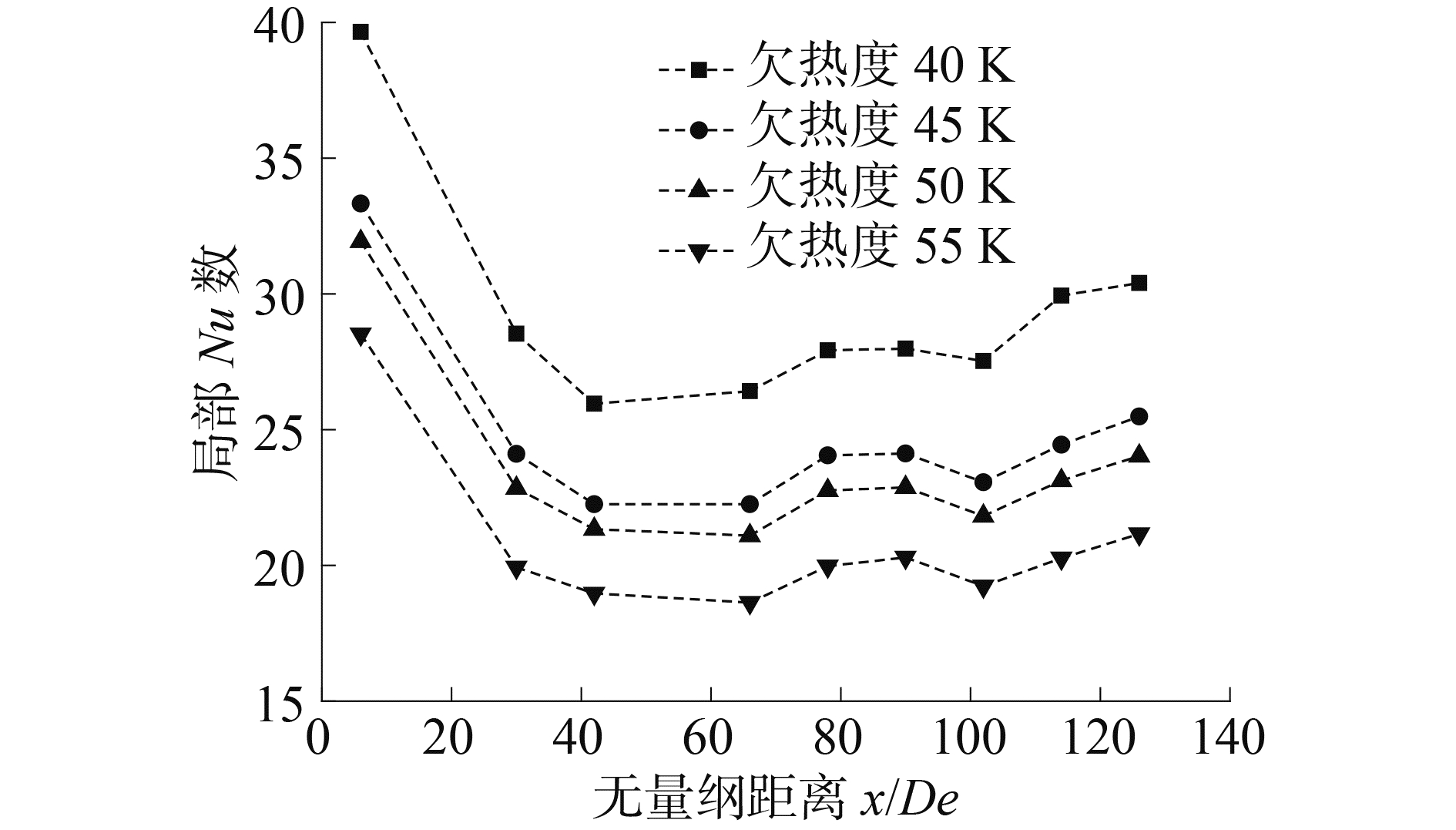
3.2 浮升力对换热能力影响图 5给出了系统压强0.3 MPa,加热功率43 kW ·m-2,Re数从4 000~7 000,不同入口欠热度条件下沿程局部Nu数。从图分析得,Nu数随着入口欠热度的增大而逐渐减小。另外,根据Nu数随轴向位置变化趋势可得,入口处的局部换热系数较高,且沿着通道轴向逐渐降低,最后在出口处小幅度上升。Hwang等[13]对两无限大平板间,入口段内层流换热特性进行了理论分析,其研究结果表明,由于入口段流动边界层较薄,因而热阻小,换热能力强,且入口段内的Nu数主要受Pr数和Gz数影响,其中Gz数定义为
| $ Gz = \frac{{\mathit{RePr}}}{{x/De}} $ | (9) |
|
图 5 不同入口欠热度下局部换热能力 Fig.5 Local heat transfer capability under different inlet sub-cooling |
在自然循环系统中,入口温度的增加会导致上升段平均密度下降,回路密度差增加,自然循环流量上升, 从而导致实验段雷诺数变大,使得换热系数增加。为消除了雷诺数对换热系数的影响,进一步分析其换热增强机理,引入局部St数对换热能力进行分析
| $ St = \frac{{Nu}}{{\mathit{RePr}}} $ | (10) |
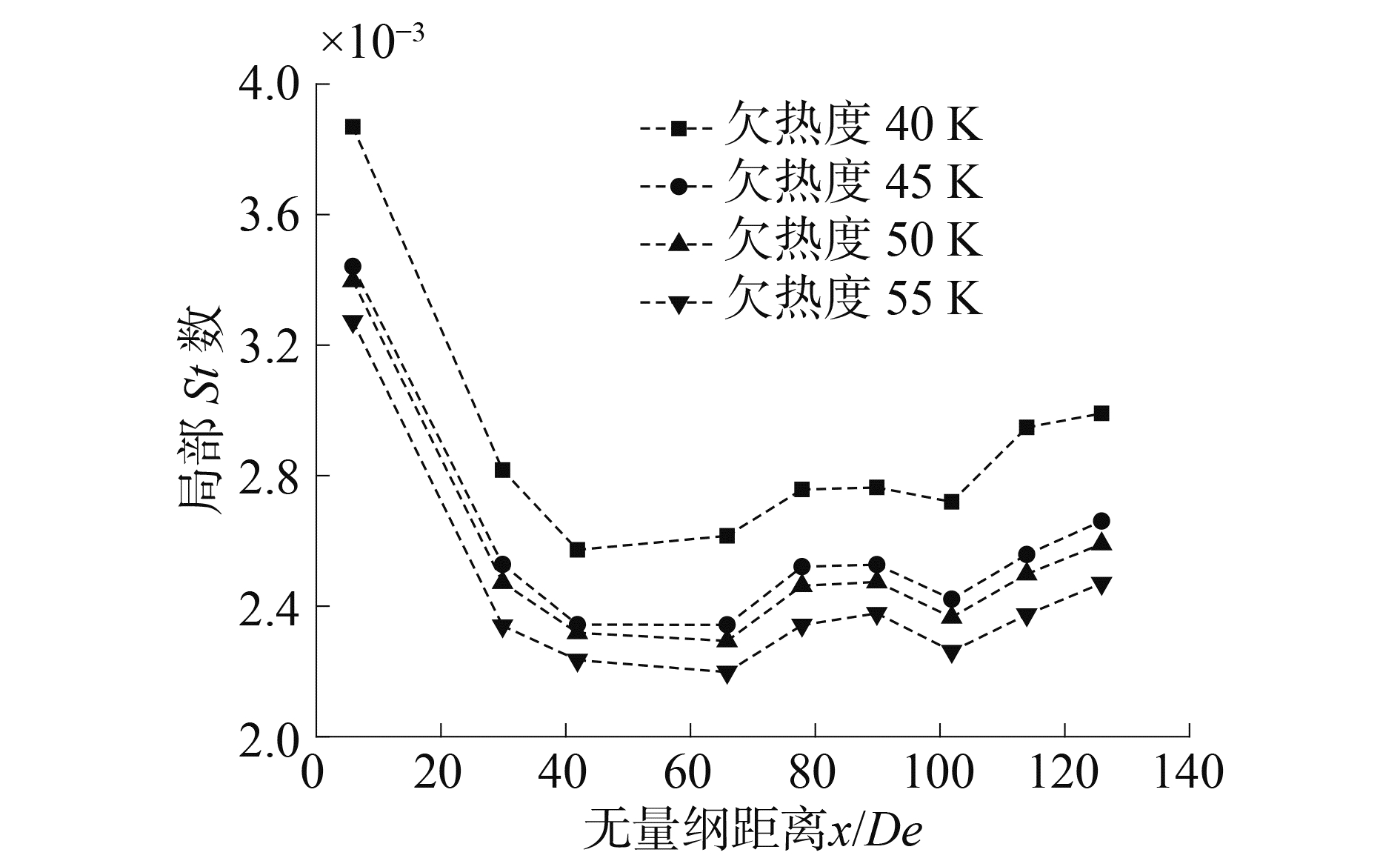
其结果如图 6所示。从图中可以发现,随着入口过冷度的增加,St数减小。该结果表明,除了Re数与Pr数外,尚有其他因素影响换热能力。
|
图 6 不同入口欠热度下的局部St数 Fig.6 St number under different inlet sub-cooling |
与传统强迫循环不同,自然循环不需要泵、风机和其他外力驱动流体流动,仅靠自身的浮力来驱动流体流动,因而其换热有可能受到浮升力的影响。本文引入Raδ数来对浮力的影响进行分析:
| $ R{a_\delta } = \frac{{g{\alpha _v}\Delta T{\delta ^3}}}{{{v^2}}}\mathit{Pr} $ | (11) |
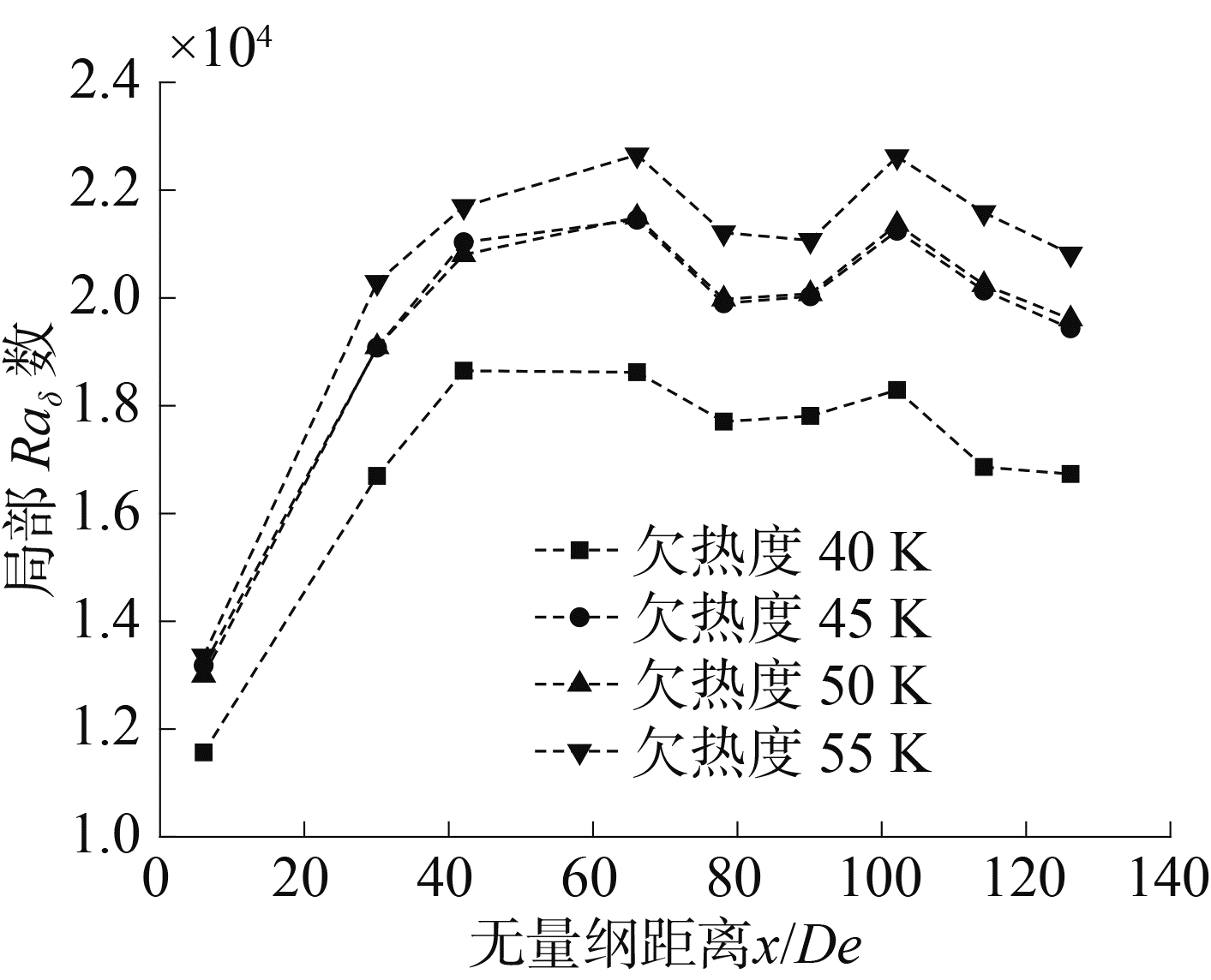
式中:ΔT=Tw, in-Tf,δ取矩形通道窄边长度。不同入口欠热度条件下的Raδ数沿流动方向的变化关系如图 7所示。图中结果显示,入口欠热度越高,Raδ数越大,即浮升力随着入口过冷度的增加而增加。
|
图 7 不同入口欠热度下局部Raδ数 Fig.7 Local Raδ number under different inlet sub-cooling |
由此可初步得出:自然循环系统中,浮升力的存在会使加热窄矩形通道内的换热能力减弱。这一结论在杨瑞昌等的研究结果中也有所体现[14]。
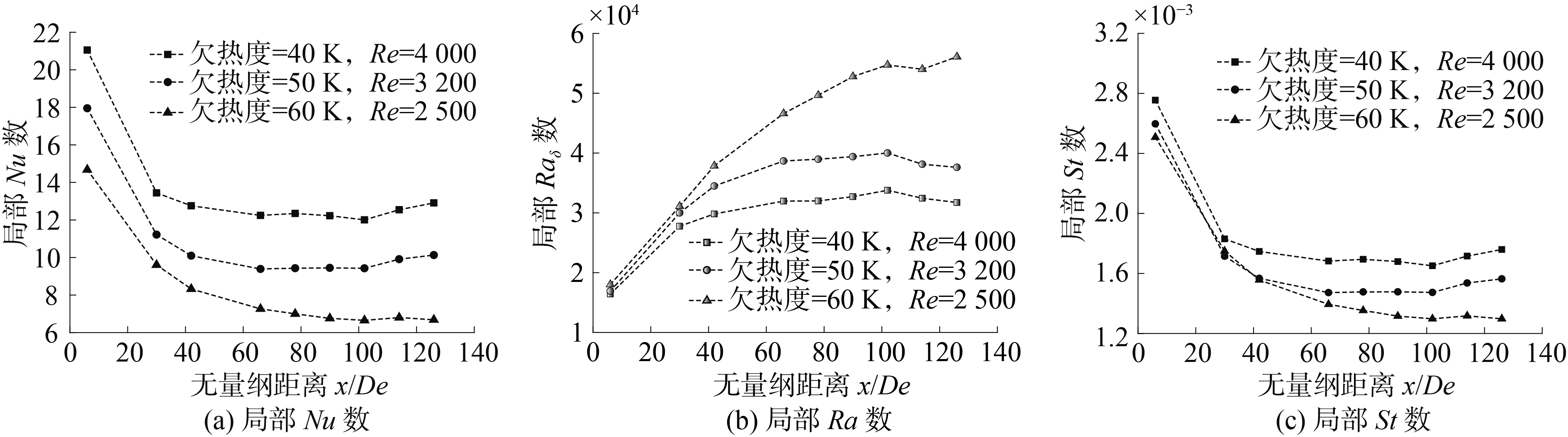
为探究低Re数下浮升力对换热的影响,进行了系统压强0.2 MPa,加热功率43 kW/m2,不同入口欠热段条件下的自然循环实验,其实验结果如图 8所示,与高Re数流动条件下结果相同,随着入口过冷度的升高,浮升力升高,St数降低,换热能力下降。
|
图 8 低Re数下入口欠热度对换热特性影响 Fig.8 Effect of inlet sub-cooling on heat transfer characteristics under low Re number |
该组实验中,入口欠热度为60 K的实验工况流态接近层流,根据Shah & London[15]理论解,对于长宽比为20的单面加热矩形通道,其层流Nu数解析解为5.2,而本实验中Nu数高出该理论解20%左右,实验值偏高的主要原因是实验值受入口段效应影响较为严重。
由于本实验中,流体向上流动,浮升力的作用方向与流动方向相同,这会使得流通截面内,径向速度梯度变小,流动边界层及热边界层变厚,最终导致流道内的流态呈现出一种层流化的趋势。由于热量在热边界层内的传递形式以导热为主,换热能力差,热边界层厚度的增加将直接导致换热能力的减弱。
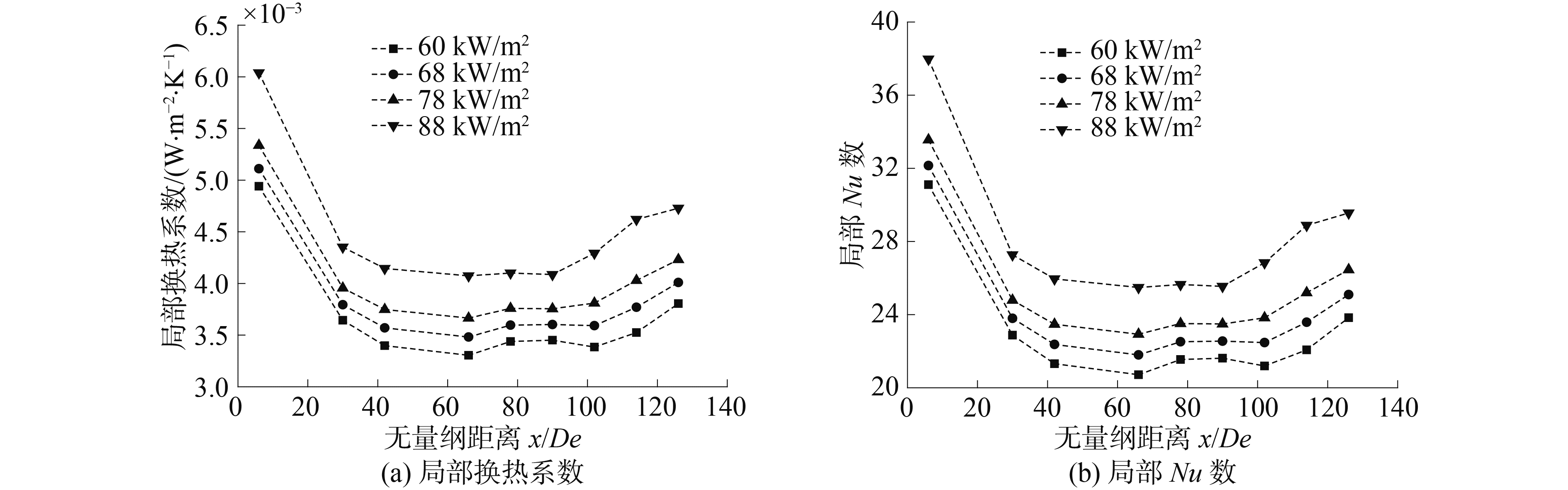
3.3 热驱动力对换热能力影响图 9为系统压力0.3 MPa,入口欠热度45 K,不同加热功率下,局部换热系数实验结果。实验表明随着加热功率的升高,换热系数变大。
|
图 9 不同加热功率下局部换热能力 Fig.9 Local heat transfer ability under different heat flux |
加热功率的升高亦会提高回路上升段的平均密度,从而提高回路驱动压头,增加循环流量。因此,引入St数来分析换热变化,其结果如图 10所示。St数随着加热功率的增加而变大。因而,换热能力会随着加热功率的增加而变大。
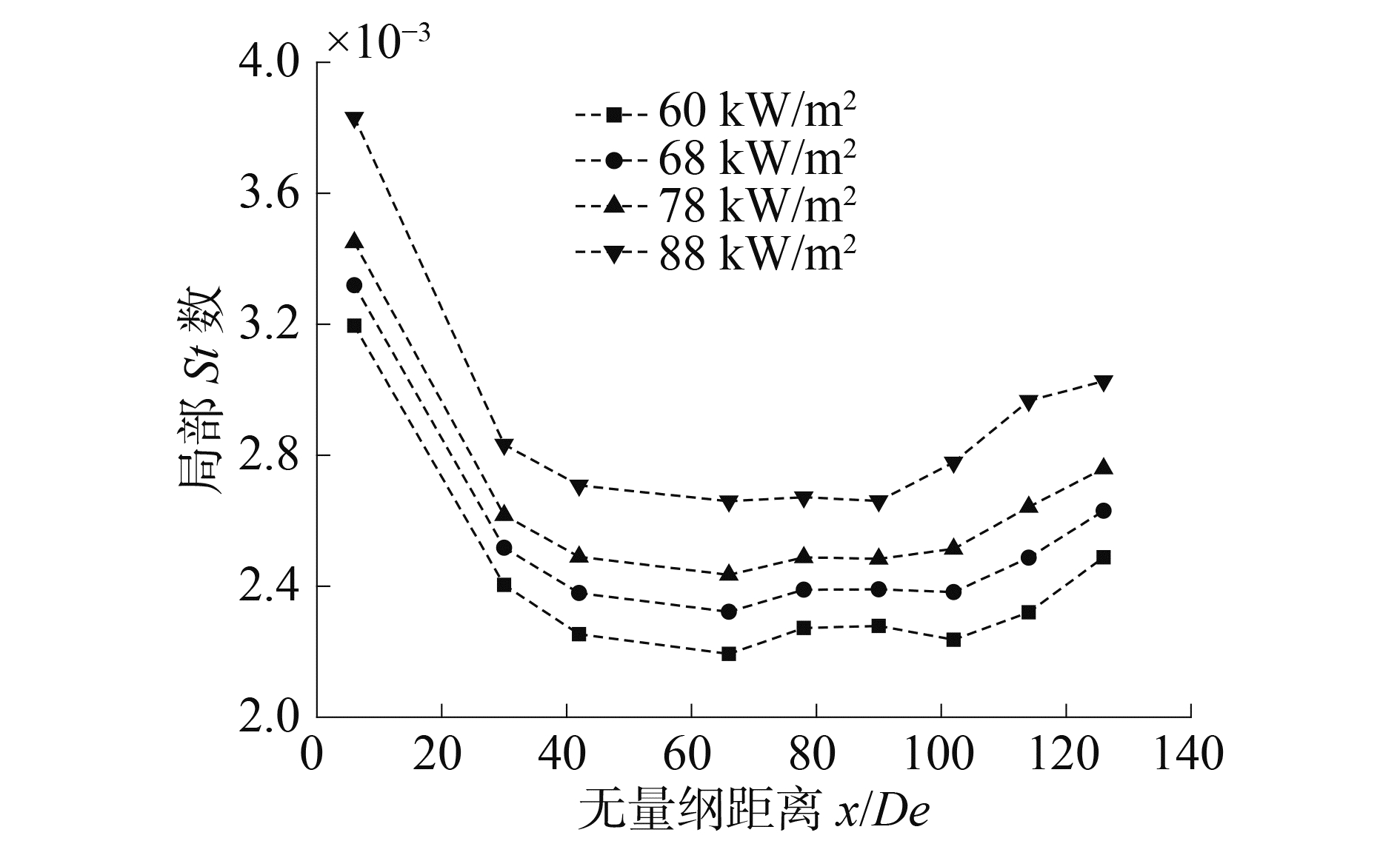
|
图 10 不同加热功率下St数 Fig.10 Local St number under different heat flux |
加热功率的增加会导致近壁面流体温度梯度增加和黏度减小,使得横向热驱动力增加,该热驱动力亦为一种横向浮升力,引入修正Grδ, q数[16]对其进行分析:
| $ \mathit{G}{\mathit{r}_{\delta ,q}} = \frac{{g{\alpha _v}q{\delta ^4}}}{{\lambda {v^2}}} $ | (12) |
其结果如图 11所示。从图中可以看出Grδ, q数随着加热功率的增加而变大,Grδ, q数的增大表明近壁面处的浮升力增大。
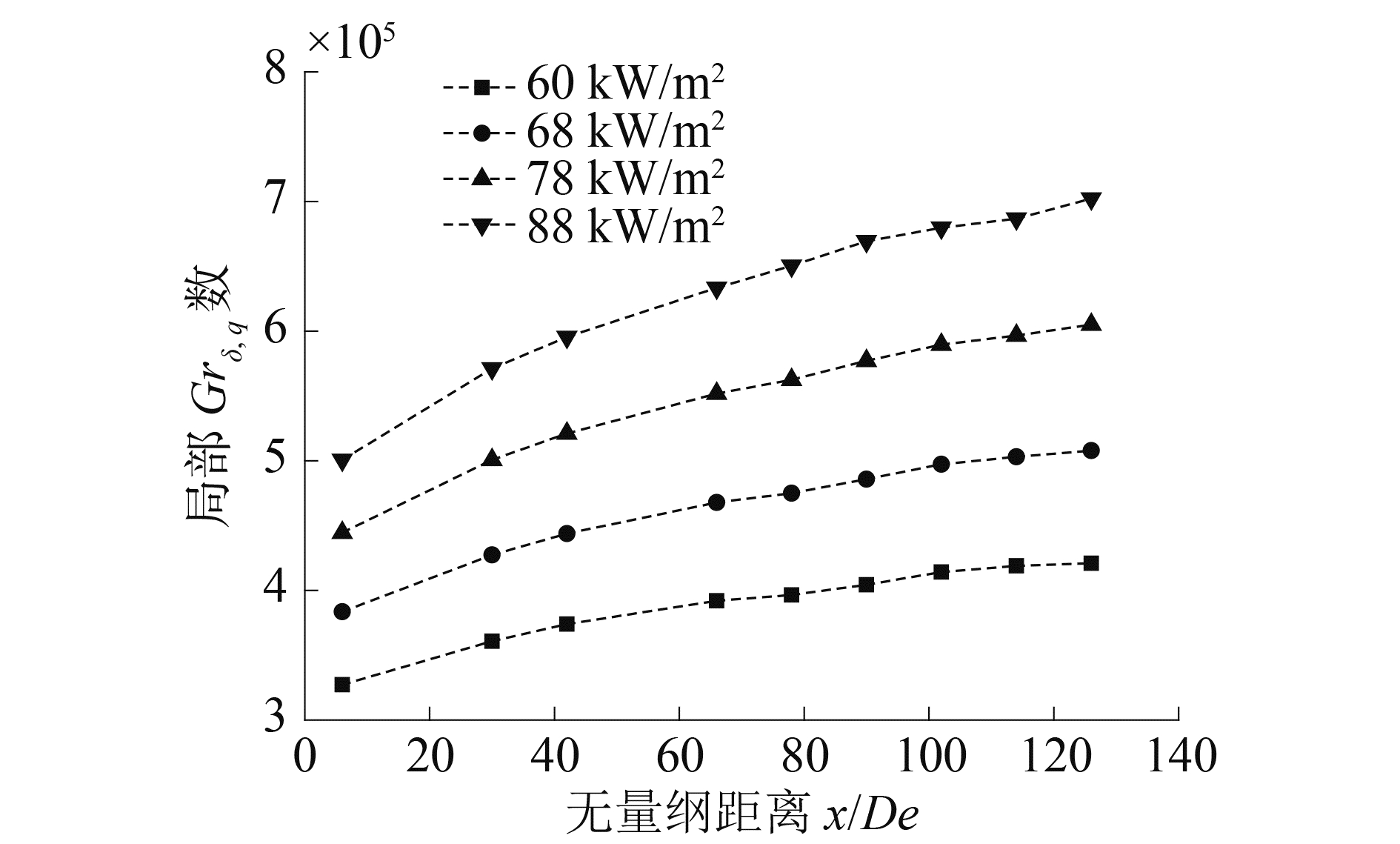
|
图 11 不同加热功率下局部Grδ, q数 Fig.11 Local Grδ, q number under different heat flux |
由于温度梯度增加而引起的密度差增加会使热驱动力(浮升力)增大,促进近壁面处的热致流动现象,使得热不稳定性增强,扰动热边界层,最终使边界层处流体呈现出局部湍流化的趋势,边界层湍流化使得换热增强。
4 结论1) 表征对流换热能力强度的局部St数会随着入口过冷度的增加而减小,且随着热流密度的增加而增加;
2) 沿流动方向的浮升力会引起的同向对流,从而导致近壁处表现出层流化的趋势,最终导致换热能力减弱;
3) 横向热驱动力引起的局部对流会增加流体的湍流度,使得换热能力增加。
| [1] |
GHIONE A, NOEL B, VINAI P, et al. On the prediction of single-phase forced convection heat transfer in narrow rectangular channels[C]//Proceedings of the 10th International Topical Meeting on Nuclear Thermal-Hydraulics, Operation and Safety (NUTHOS-10). Okinawa, Japan, 2014:14-18.
(  0) 0)
|
| [2] |
GHIONE A, NOEL B, VINAI P, et al. Assessment of thermal-hydraulic correlations for narrow rectangular channels with high heat flux and coolant velocity[J]. International journal of heat and mass transfer, 2016, 99(8): 344-356. (  0) 0)
|
| [3] |
马建, 黄彦平, 刘晓钟. 窄缝矩形通道单相流动及传热实验研究[J]. 核动力工程, 2012, 33(1): 39-45. MA Jian, HUANG Yanping, LIU Xiaozhong. Experimental study on single-phase flow and heat transfer in a narrow rectangular duct[J]. Nuclear power engineering, 2012, 33(1): 39-45. (  0) 0)
|
| [4] |
PENG X F, PETERSON G P. The effect of thermofluid and geometrical parameters on convection of liquids through rectangular microchannels[J]. International journal of heat and mass transfer, 1995, 38(4): 755-758. DOI:10.1016/0017-9310(95)93010-F (  0) 0)
|
| [5] |
JO D, AL-YAHIA O S, RAGA'I M A, et al. Experimental investigation of convective heat transfer in a narrow rectangular channel for upward and downward flows[J]. Nuclear engineering and technology, 2014, 46(2): 195-206. DOI:10.5516/NET.02.2013.057 (  0) 0)
|
| [6] |
ZVIRIN Y. A review of natural circulation loops in pressurized water reactors and other systems[J]. Nuclear engineering and design, 1982, 67(2): 203-225. DOI:10.1016/0029-5493(82)90142-X (  0) 0)
|
| [7] |
SIDDIQUI M A. Heat transfer and fluid flow studies in the collector tubes of a closed-loop natural circulation solar water heater[J]. Energy conversion and management, 1997, 38(8): 799-812. DOI:10.1016/S0196-8904(96)00097-0 (  0) 0)
|
| [8] |
LIU G, HUANG Y, WANG J, et al. Effect of buoyancy and flow acceleration on heat transfer of supercritical CO 2 in natural circulation loop[J]. International journal of heat and mass transfer, 2015, 91(9): 640-646. (  0) 0)
|
| [9] |
LIU G, HUANG Y, WANG J, et al. Heat transfer of supercritical carbon dioxide flowing in a rectangular circulation loop[J]. Applied thermal engineering, 2016, 98(4): 39-48. (  0) 0)
|
| [10] |
YADAV A K, GOPAL M R, BHATTACHARYYA S. CO 2 based natural circulation loops:new correlations for friction and heat transfer[J]. International journal of heat and mass transfer, 2012, 55(17): 4621-4630. (  0) 0)
|
| [11] |
CAO Y, ZHANG X R. Flow and heat transfer characteristics of supercritical CO 2 in a natural circulation loop[J]. International journal of thermal sciences, 2012, 58(4): 52-60. (  0) 0)
|
| [12] |
GNIELINSKI V. New equations for heat and mass transfer in the turbulent flow in pipes and channels[J]. NASA STI/recon technical report A, 1975, 75(2): 22028. (  0) 0)
|
| [13] |
HWANG C L, FAN L T. Finite difference analysis of forced-convection heat transfer in entrance region of a flat rectangular duct[J]. Applied scientific research, section A, 1964, 13(1): 401-422. DOI:10.1007/BF00382066 (  0) 0)
|
| [14] |
杨瑞昌, 刘若雷, 刘京宫, 等. 自然循环加热段内摩擦阻力及对流传热的实验研究[J]. 工程热物理学报, 2008, 29(1): 108-111. YANG Ruichang, LIU Ruolei, LIU Jinggong, et al. Investigation on friction and heat transfer in a tube with natural circulation[J]. Journal of engineering thermophysics, 2008, 29(1): 108-111. (  0) 0)
|
| [15] |
SHAH R K, LONDON L A. Laminar flow forced convective in ducts:A source book for compact heat exchanger analytical data[M]. New York: Academic Press, 1978.
(  0) 0)
|
| [16] |
SPARROW E M, CARLSON C K. Local and average natural convection Nusselt numbers for a uniformly heated, shrouded or unshrouded horizontal plate[J]. International journal of heat and mass transfer, 1986, 29(3): 369-379. DOI:10.1016/0017-9310(86)90207-3 (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


