流致振动(flow-induced motion, FIM)是指流体流经固体时会对固体表面施加交替相间的流体力,使得固体发生往复运动,而固体的往复运动又改变流体流态,进而改变作用于固体表面的流体力。流致振动现象广泛地存在于各类工程领域当中[1-4]。流致振动中最典型的两种运动为涡激振动(vortex-induced vibration, VIV)与驰振。其中,涡激振动是由于流体粘性作用使得其在绕流钝体后侧产生了交替脱涡的漩涡,从而引起钝体纵向的往复运动[5];而驰振则是由于钝体攻角的变化造成升力失稳,从而使得钝体发生纵向往复运动[6]。从15世纪中期,达芬奇通首次发现了VIV现象后,学者们纷纷投入到了流致振动的相关研究工作当中。Feng首次通过风洞试验得到了圆柱、D型柱的VIV响应规律[7]。随后Bearman等对绕流圆柱的理论模型及流体作用力的特点进行了深入分析,提出了预测绕流圆柱响应的振子模型[8-9]。20世纪中后期,Williamson等在水槽中进行了一系列的圆柱绕流试验,阐释了水流条件下圆柱响应的影响因素、受力特点及尾流模式,进一步完善了VIV的理论模型[10-13]。Den Hartog首次运用准静态方法(quasi-steady)预测了驰振的响应规律[14]。随后Parkinson等对三角形及正方形截面下振子的驰振特性进行了理论研究与响应预测[15-16]。
以往关于流致振动的研究大多集中在如何抑制振动以保证结构的安全[1-4]。近年来流致振动也逐渐成为了一种重要的能量转化来源之一。在众多的振动发电装置当中,压电俘能技术是最早运用空气流致振动进行能量转化的发电装置[17],成功的运用在各类微型、小型传感器及其他电子设备的供电系统上[18-19]。相对于压电俘能材料,另一种利用流致振动转化海流能源的发电设备(vortex induced vibration for aquatic clean energy,VIVACE)于2009年由密歇根大学的Bernitsas及其科研团队研制成功[20]。随后,马良等提出了改进的涡激与升力混合发电设备[21]。该类设备具有启动流速低、能量密度大、可扩展性强等特点,具有更加广阔的运用前景。自此,许多学者开始从发电理念出发,重新审视并研究流致振动的振动特性、影响因素及形成机理。Barrero-Gil等基于准静态理论的方法研究了驰振响应下能量转化效率[22-23]。Muhanmood等则通过理论分析及数值计算等方法对压电俘能转换机的能量转化及相应的负荷电压进行了深入研究[24-26]。丁林等则探讨了振动特性与能量转化的基本规律[27-29]。
目前,基于流致振动发电的研究大多集中于振子的振动特性,考虑实体发电机或将发电机及负荷参数引入振动体系的耦合研究相对较少。这在某种程度上制约了流致振动发电的实际运用前景。对于振动体系而言,发电机的影响在于阻碍振子的运动,一旦电机或负荷发生改变,发电机对振子的阻力必然发生改变,从而影响振子的振动响应,最终影响系统的发电功率与效率。可见,发电功率与流致振动响应、发电机参数及系统负荷存在强耦合关系。为此,本文首次建立了水力-振子-电机-负荷耦合模型系统(hydraulic, oscillator, generator and resistance, HOGR),分析了振子的受力特点与运动特点,推导得到了发电功率与效率的表达方程,揭示了效率的控制因素与影响机制。随后,基于效率的控制因素提出了最优发电效率的分析方法以及发电机选配的原则,并运用试验结果进行验证与说明。本文的研究旨在确定流固耦合发电系统的发电功率与效率及对应的控制因素,为后续的流致振动能量转换研究以及发电机的研发提供良好的参考。
1 HOGR耦合运动模型 1.1 运动与受力分析图 1为水力-振子-电机-负荷耦合系统的简化示意图,水流力迫使振子发生竖向振动,振子带动传动结构发生运动,并带动发电机动子运动进而发电,发电机发出的电能供给负荷电阻的电能消耗。图中,

|
图 1 水力-振子-电机-负荷耦合振动模型(HOGR)示意图 Fig.1 The combined model of hydraulic, oscillator, generator and resistance (HOGR) |
HOGR系统为单自由度振动体系,在运动过程中,振子除受到刚度力、阻尼力及惯性力外,还受到竖向的水流力Ffluid与发电机阻力Fgen。由此可得到HOGR系统的动力学方程为
| $ {m_{{\rm{osc}}}}\ddot y + c\dot y + Ky = {F_{{\rm{fluid}}}} + {F_{{\rm{gen}}}} $ | (1) |
| $ {m_{{\rm{osc}}}} = {m_{{\rm{cyl}}}} + {m_{{\rm{tra}}}} + {m_{{\rm{spr}}}}/3 $ | (2) |
式中:mcyl是振子质量、mtra是传动质量,mspr是弹簧质量之和。
1.2 水流力Khalak与Williamson的研究指出[10-13],作用于结构的水流力Ffluid包括惯性力Finviscid与粘性力Fviscous两个部分,表达式分别为
| $ {F_{{\rm{inviscid}}}} = - {m_{\rm{a}}}\ddot y $ | (3) |
| $ {F_{{\rm{viscous}}}} = \frac{1}{2}{c_y}\rho {U^2}Dl $ | (4) |
式中:ma为附加质量,cy为瞬时升力系数,ρ为流体密度,U为来流流速,D为振子的特征宽度(圆形截面振子为直径),l为振子的长度。
1.3 发电机外力由图 1可知,发电机动子运动速度
| $ {{\dot y}_{{\rm{gen}}}} = \alpha \dot y $ | (5) |
那么,发电机的感应电动势E为
| $ E = \alpha BL\dot y $ | (6) |
考虑到电流回路中的电机内阻R0与负荷电阻RL,由此即可得到发电机动子切割磁感线时受到的电磁力Felc为
| $ {F_{{\rm{elc}}}} = - \frac{{\alpha {B^2}{L^2}\dot y}}{{{R_0} + {R_{\rm{L}}}}} $ | (7) |
由于传动结构中转速比α的影响,HOGR系统上的发电机外力实际为动子切割磁感线受到外力的α倍,即
| $ {F_{{\rm{gen}}}} = \alpha {F_{{\rm{elc}}}} = - \frac{{\alpha {B^2}{L^2}\dot y}}{{{R_0} + {R_{\rm{L}}}}} $ | (8) |
根据水流力Ffluid及发电机阻力Fgen的表达,可进一步得到HOGR系统的耦合运动方程为
| $ {m_{{\rm{osc}}}}\ddot y + c\dot y + Ky = \frac{1}{2}{c_y}\rho {U^2}Dl - {m_{\rm{a}}}\ddot y - \frac{{\alpha {B^2}{L^2}\dot y}}{{{R_0} + {R_{\rm{L}}}}} $ | (9) |
显然,水流的惯性力Finviscid可视为振动系统质量的一部分,即附加质量ma;而系统受到的发电机阻力Fgen可视为振动总阻尼系数ctotal的一部分,可称为发电机阻尼cgen。由此,HOGR系统的运动方程可进一步简化为
| $ \left( {{m_{{\rm{osc}}}} + {m_{\rm{a}}}} \right)\ddot y + {c_{{\rm{total}}}}\dot y + Ky = \frac{1}{2}{c_y}\rho {U^2}Dl $ | (10) |
| $ {c_{{\rm{total}}}} = c + {c_{{\rm{gen}}}} = c + \frac{{\alpha {B^2}{L^2}}}{{{R_0} + {R_{\rm{L}}}}} $ | (11) |
此时,运动方程的解可用经典的谐振理论进行表达[4, 7]。谐振理论中,认为运动位移y与升力cy均随时间成简谐变化规律,即
| $ y = A\sin \left( {2{\rm{ \mathsf{ π} }}{f_{{\rm{osc}}}}t} \right) $ | (12) |
| $ {c_y} = {C_y}\sin \left( {2{\rm{ \mathsf{ π} }}{f_{{\rm{fluid}}}}t + \phi } \right) $ | (13) |
式中:A与fosc分别为系统的振动振幅与振动主频,Cy与ffluid分别为最大升力系数与升力主频,Ф则为运动位移与升力的相位差。
根据结构力学知识,在稳定振动中,HOGR系统的振动主频与升力主频相等,即
| $ {f_{{\rm{osc}}}} = {f_{{\rm{fluid}}}} $ | (14) |
关于流致振动响应的通解,Bearman等都给出了相应的解答[8, 10-13]。在此,考虑到后续功率及效率的分析,本文仅给出振幅与振动主频的乘积(Afosc)解为
| $ A{f_{{\rm{osc}}}} = \frac{{\rho Dl{U^2}{C_y}\sin \phi }}{{4{\rm{ \mathsf{ π} }}{c_{{\rm{total}}}}}} $ | (15) |
由此可见,HOGR系统中振幅与频率取决于振子物理参数、流速、升力、相位与阻尼。根据现有的研究结果[5-16],升力、相位取决于振子的攻角(形状、流速)、总阻尼比ζtotal因此,对于振子形状、刚度、质量都不变的HOGR系统,若流速恒定,(Afosc)必然决定于系统的总阻尼系数ctotal。
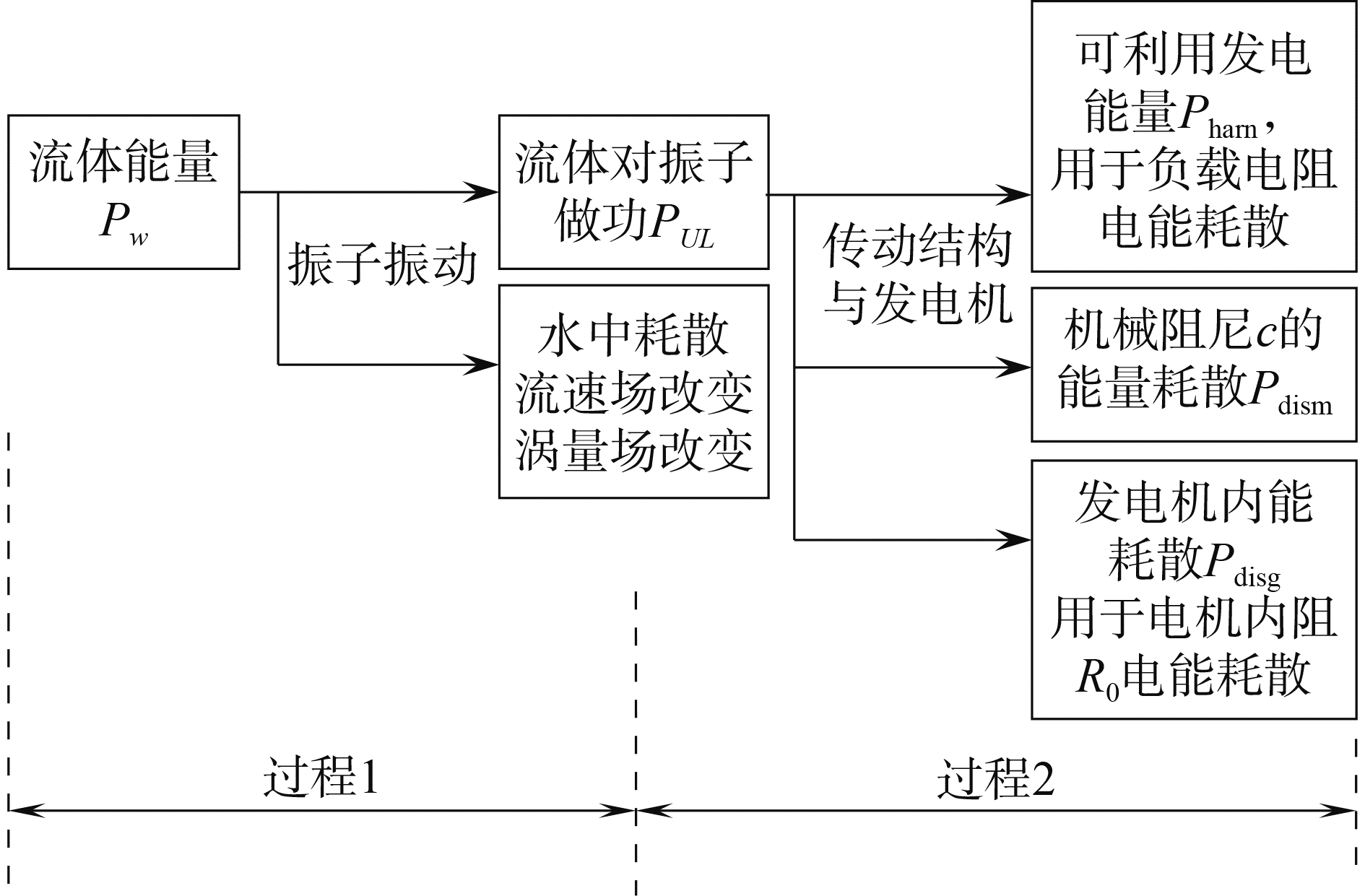
2 功率与效率 2.1 HOGR系统的能量汲取与分配对于HOGR系统而言,水流能量终转化为可利用的能量实际要经历2个基本过程,如图 2所示。
|
图 2 HOGR系统中水流能量的利用过程 Fig.2 The extracting processes of the kinetic energy of flow in HOGR |
1) 过程1:流体能量的其中一部分用于对振子做功,另一部分由于尾流场的变化而耗散在流体当中。振子尾流中,由于速度场及涡量场的改变,使得流体粒子不断碰撞、摩擦,这部分能量实际也来源于流体本身的能量。
2) 过程2:流体对振子所做的功中,一部分通过发电机转化成负荷电阻的电能消耗,一部分耗散于电机发电过程中自身产生的热量,还有一部分耗散于振子振动过程中的机械损耗。对于上述能量当中,发电机转化成为负荷电阻RL的电能消耗实际上即为整个系统当中可以利用的能量。因此,考察各个能量以及效率之间的关系是提高流致振动发电应用前景的关键因素。
2.2 流体功率由于HOGR系统为分布式的能量转换设备,其能量仅为流体动能。故总的流体功率为单位流量动能功率pT与水流的流量Q的乘积,即
| $ {P_w} = {p_T}Q $ | (16) |
其中
| $ {p_T} = \frac{1}{2}\rho {U^2} $ | (17) |
| $ Q = {A_w}U $ | (18) |
式中:Aw为过流面积。此处认为过流面积为振子在水流方向上的投影面积,即
| $ {A_w} = Dl $ | (19) |
那么,可得到流体功率为
| $ {P_w} = \frac{1}{2}\rho {U^3}Dl $ | (20) |
根据2.1节水流能量的利用过程可知,因发电机内能及机械损耗,使得水流对振子做功不能完全被利用。但在理想条件下,若使得发电机自身发热及传动阻尼力损耗为零,则可实现水流对振子所做功全部被利用。由此可见,对于HOGR系统而言,水流对振子的做功功率Pfluid即为系统可利用功率的上限,即上限功率PUL,Pfluid=PUL。
将式(10)右侧对位移在周期Tosc(Tosc=1/fosc)上进行积分,再除以周期Tosc,即可得到水流对振子的有效做功功率Pfluid为
| $ {P_{{\rm{fluid}}}} = \frac{1}{{{T_{{\rm{osc}}}}}}\int_0^{{T_{{\rm{osc}}}}} {\frac{1}{2}{c_y}\rho {U^2}Dl\dot y{\rm{d}}t} $ | (21) |
将位移y的表达式(12)与升力cy的表达式(13)代入式(21)即可解得上限功率的表达式为
| $ {P_{UL}} = {P_{{\rm{fluid}}}} = \frac{{{{\left( {\rho {U^2}Dl{C_y}\sin \varphi } \right)}^2}}}{{8{c_{{\rm{total}}}}}} $ | (22) |
另一方面,将式(10)左侧对位移在周期Tosc上进行积分,再除以周期Tosc,即可得到HOGR系统的总有效机械功率Pmech。需要说明的是,Pmech并不仅包含振子的机械运动功率,而是将发电机阻尼视为系统阻尼一部分前提下振子的总机械功率。其表达式为
| $ {P_{{\rm{mech}}}} = \frac{1}{{{T_{{\rm{osc}}}}}}\int_0^{{T_{{\rm{osc}}}}} {\left[ {\left( {{m_{{\rm{osc}}}} + {m_{\rm{a}}}} \right)\ddot y + {c_{{\rm{total}}}}\dot y + Ky} \right]\dot y{\rm{d}}t} $ | (23) |
根据能量守恒定律,水流对振子做功必然等于振子的总机械能量,即Pmech=Pfluid。进一步,将位移y的表达式(12)代入,即可解得HOGR系统的上限功率的另一表达式为
| $ {P_{UL}} = {P_{{\rm{mech}}}} = 2{{\rm{ \mathsf{ π} }}^2}{c_{{\rm{total}}}}{\left( {{f_{{\rm{osc}}}}A} \right)^2} $ | (24) |
事实上,式(24)与式(22)为相同的表达式,将(Afosc)的解(式(15))代入式(24)即可得到式(22)。
上限效率为上限功率与流体功率之比。根据上限功率PUL及流体功率Pw的表达式,即可获得到上限效率ηUL的表达式为
| $ {\eta _{UL}} = \frac{{2{{\rm{ \mathsf{ π} }}^2}{c_{{\rm{total}}}}{{\left( {{f_{{\rm{osc}}}}A} \right)}^2}}}{{\frac{1}{2}\rho {U^3}Dl}}\frac{{\rho UDl{{\left( {{C_y}\sin \phi } \right)}^2}}}{{4{c_{{\rm{total}}}}}} $ | (25) |
可见与(Afosc)类似,系统的上限效率ηUL决定于振子形状、特征宽度、刚度、质量、流速及系统总阻尼系数。当振子形状、特征宽度、刚度、质量及流速环境都不改变时,系统的机械功率必然取决于系统总阻尼系数ctotal。
2.4 系统发电功率与效率HOGR系统中,被利用的发电功率为单位时间内负荷电阻RL所消耗的电能能量。在发电回路系统中,电流I为感应电动势E与回路总电阻(发电机内阻R0与负荷电阻RL之和)的比值。结合式(6)即可得电流回路中到瞬时电流I(t)的表达式为
| $ I\left( t \right) = \frac{{\alpha BL\dot y\left( t \right)}}{{{R_0} + {R_{L}}}} $ | (26) |
那么,系统的瞬时发电功率Pharn(t)即为
| $ {P_{{\rm{harn}}}}\left( t \right) = {I^2}{R_L} = \frac{{{\alpha ^2}{B^2}{L^2}{R_L}}}{{{{\left( {{R_0} + {R_{L}}} \right)}^2}}}{{\dot y}^2}\left( t \right) $ | (27) |
由于HOGR系统中,位移y随时间t成正弦变化规律(式(12)),故发电功率Pharn(t)也随时间成正弦变化规律。因此,将式(27)在周期Tosc上进行积分,再除以周期Tosc,即可得到系统的有效发电功率Pharn为
| $ {P_{{\rm{harn}}}} = 2{{\rm{ \mathsf{ π} }}^2}\frac{{{\alpha ^2}{B^2}{L^2}{R_L}}}{{{{\left( {{R_0} + {R_{L}}} \right)}^2}}}{\left( {{f_{{\rm{osc}}}}A} \right)^2} $ | (28) |
此处,定义发电阻尼系数charn为
| $ {c_{{\rm{harn}}}} = \frac{{{\alpha ^2}{B^2}{L^2}{R_L}}}{{{{\left( {{R_0} + {R_{L}}} \right)}^2}}} $ | (29) |
则可得
| $ {P_{{\rm{harn}}}} = 2{{\rm{ \mathsf{ π} }}^2}{c_{{\rm{harn}}}}{\left( {{f_{{\rm{osc}}}}A} \right)^2} $ | (30) |
进一步,比较式(24)与式(30)不难发现,系统的发电功率Pharn与上限功率PUL的表达方程仅在阻尼系数上有所差异。因此,系统的发电功率Pharn与发电效率ηharn可表示为
| $ {P_{{\rm{harn}}}} = \frac{{{c_{{\rm{harn}}}}}}{{{c_{{\rm{total}}}}}}{P_{UL}} $ | (31) |
| $ {\eta _{{\rm{harn}}}} = \frac{{{c_{{\rm{harn}}}}}}{{{c_{{\rm{total}}}}}}{\eta _{UL}} $ | (32) |
可见,对于HOGR系统而言,最终可利用的发电效率ηharn(功率Pharn)除了取决于系统的上限效率ηUL(功率PUL)外,还取决于系统发电阻尼系数charn与总阻尼系数ctotal之比。
2.5 阻尼系数与功率、效率的关系与上限功率PUL及发电功率Pharn类似,由发电机内阻R0造成的内能耗散功率Pdis, g以及机械阻尼系数c造成的机械耗散功率Pdis, m可分别表示为
| $ {P_{{\rm{dis,g}}}} = 2{{\rm{ \mathsf{ π} }}^2}{c_{{\rm{dis,g}}}}{\left( {{f_{{\rm{osc}}}}A} \right)^2} $ | (33) |
| $ {P_{{\rm{dis,m}}}} = 2{{\rm{ \mathsf{ π} }}^2}c{\left( {{f_{{\rm{osc}}}}A} \right)^2} $ | (34) |
式中cdis, g为发电机内能耗散阻尼系数。
| $ {c_{{\rm{dis,g}}}}\frac{{{\alpha ^2}{B^2}{L^2}{R_L}}}{{{{\left( {{R_0} + {R_{L}}} \right)}^2}}} $ | (35) |
那么,可得HOGR系统中各阻尼系数之间的相互关系以及阻尼系数与功率、效率之间的关系为
| $ {c_{{\rm{total}}}} = c + {c_{{\rm{dis,g}}}} + {c_{{\rm{harn}}}} $ | (36) |
| $ \frac{{{c_{{\rm{total}}}}}}{{{P_{UL}}}} = \frac{c}{{{P_{{\rm{dis,m}}}}}} = \frac{{{c_{{\rm{dis,g}}}}}}{{{P_{{\rm{dis,g}}}}}} = \frac{{{c_{{\rm{harn}}}}}}{{{P_{{\rm{harn}}}}}} $ | (37) |
| $ \frac{{{c_{{\rm{total}}}}}}{{{\eta _{UL}}}} = \frac{c}{{{\eta _{{\rm{dis,m}}}}}} = \frac{{{c_{{\rm{dis,g}}}}}}{{{\eta _{{\rm{dis,g}}}}}} = \frac{{{c_{{\rm{harn}}}}}}{{{\eta _{{\rm{harn}}}}}} $ | (38) |
可见,HOGR系统中各个阻尼系数的大小决定了功率的大小及效率的大小。因此,确定系统中各阻尼系数之间的关系是分析系统效率的前提。
3 上限效率与上限能量利用率 3.1 负荷比与折合阻尼系数由前述分析可知,HOGR系统中的各项阻尼系数的相关关系是决定振子响应、系统发电功率与效率的关键性因素。为了掌握各项阻尼系数的相关关系以及其与发电机参数(α、B、L、R0)和负荷电阻RL之间的关系,此处引入2个无量纲参量——负荷比R*与折合阻尼系数c*。负荷比R*定义为外界负荷电阻值RL与发电机内阻值R0之比;折合阻尼系数c*则定义为发电系统在某负荷比R*下的总阻尼系数ctotal与机械阻尼系数c之比。其表达式分别为
| $ {R^ * } = \frac{{{R_L}}}{{{R_0}}} $ | (39) |
| $ {c^ * } = \frac{{{c_{{\rm{total}}}}}}{c} $ | (40) |
进一步,当系统断路时,总阻尼系数ctotal即为机械阻尼系数c,此时有c∞*=1;而当系统短路时,外界负荷比R*=0,此时有
| $ c_0^ * = \frac{{c + {c_{{\rm{gen}}}}\left| {_{{R^ * } = 0}} \right.}}{c} = 1 + \frac{{{\alpha ^2}{B^2}{L^2}}}{{c{R_0}}} $ | (41) |
将c∞*与c0*与式(11)代入式(41)中,可得到折合阻尼系数c*的无量纲表达式为
| $ {c^ * } = \frac{{c_0^ * + {R^ * }}}{{c_\infty ^ * + {R^ * }}} = \frac{{c_0^ * + {R^ * }}}{{1 + {R^ * }}} $ | (42) |
可见,HOGR系统的折合阻尼系数c*决定于2个因素,即负荷比R*与短路时的折合阻尼系数c0*。其中,负荷比R*为c*的外部影响因素,表征了负荷电阻值的差异;而短路时的折合阻尼系数c0*则为c*的内部影响因素,表征了发电机内部参数的配比差异。图 3给出不同c0*条件下c*随R*的变化规律。

|
图 3 不同c0*条件下的c*随R*的变化规律 Fig.3 The variation of c* against R* with different c0* |
由图 3可见,当R*→0时,c*→c0*;随着R*增大,c*逐渐减小;而当R*→∞时,c*→1。另外,而随c0*的增大,c*会逐渐增大;当c0*=∞时,任意R*下的c*≡∞;而当c0*=1时,任意R*下的c*≡1。
事实上,上述规律说明:当外界负荷无穷大时(R*=∞),HOGR系统断路,ctotal=c且charn=0,此时水流对系统做功全部用于机械阻尼耗散,系统没有能量利用;而当负荷为零时(R*=0),HOGR系统短路,ctotal=c+cdis, g且charn=0,此时水流对系统做功全部用于机械阻尼与发电机内能耗散,系统依然没有能量利用。由此可见,对于HOGR系统,必然存在一个特定的c*与特定的R*使得所利用的功率与效率达到最大。此外,若HOGR系统中c*≡1,说明始终没有发电能量可被利用,此时系统必然发生故障。可见,检验c*是否恒为1是判定HOGR系统是否正常工作的一条有效途径。若HOGR系统中c*≡∞,说明系统cdis, g=0,此为理想条件下的最优发电机。
3.2 上限效率的决定因素由式(24)可知,上限效率受制于振子的振幅与频率。故振子的形状、特征宽度、质量、刚度、总阻尼、水流流速等都是上限效率的变化规律的决定因素。实际上,振子各项参数的差异会使得响应差异十分显著。对于圆形截面振子,因其截面的轴对称特性,一般仅出现涡激振动响应,但当圆形截面振子配合被动湍流装置(passive turbulence control, PTC)后[30],则可能出现驰振响应,对应的振幅、频率必然会出现变化。即便圆形截面振子不出现驰振响应,其质量、直径及雷诺数Re的差异又会导致锁定区间、振动幅值及响应分支差异[7, 10-13, 27]。而对于其他有尖角的截面振子(如方形或三角形截面振子),由于攻角的变化,使得其或出现涡激振动响应,或出现驰振响应,或出现涡激振动与驰振的交替响应,响应分支的数量、涡激振动与驰振的转变点等也会因上述因素的差异存在较大的差异[6, 8-9, 27, 31]。
可见,由于响应规律的差异,使得很难运用某一特定的统一规律对任意振子的上限效率加以预测。文献[20、28、30、31]等是通过试验方法加以预测的,文献[4、24、26、27]等则通过数值方法加以预测,而文献[6、14、22、23、25]等则通过准静态理论对驰振响应加以预测的。
HOGR系统中,阻尼决定了功率与效率,故研究上限效率与总阻尼系数间关系是确定系统效率的必要条件。考虑到影响上限效率的各参数之间相互独立,故若保证其他参数不变,仅研究总阻尼系数ctotal与上限效率ηUL的关系是容易实现的。进一步,将折合阻尼系数c*代入式(24)可得到
| $ {\eta _{UL}} = \frac{{\rho UDl{{\left( {{C_y}\sin \phi } \right)}^2}}}{{4c{c^ * }}} $ | (43) |
因此,在确定其他参数不变的条件下,通过理论、数值或试验方法即可获得上限效率ηUL与折合阻尼系数c*的相关关系。
3.3 上限能量利用率由2.4节与2.5节的分析可知,发电阻尼系数charn与总阻尼系数ctotal的比值实际表明了HOGR系统中上限能量的利用率。此处,用符号η来表征这一比值。由此,可得到η的表达式为
| $ \eta = \frac{{{c_{{\rm{harn}}}}}}{{{c_{{\rm{total}}}}}} = \frac{{{\alpha ^2}{B^2}{L^2}{R_L}}}{{c{{\left( {{R_0} + {R_{L}}} \right)}^2} + {\alpha ^2}{B^2}{L^2}\left( {{R_0} + {R_{L}}} \right)}} $ | (44) |
显然,上限能量的利用率η与外界的负荷电阻RL以及电机的各项参数(机械阻尼系数c、减速比α、电机磁通量B、线圈长度L及电机内阻R0)有关,而与振子特征、刚度、流速U、升力系数Cy、相位差等并不相关。
进一步,将折合阻尼系数c*代入式(44)中,即得到上限能量利用率η与折合阻尼系数c*的相关关系为
| $ \eta = \frac{{\left( {c_0^ * - {c^ * }} \right)\left( {{c^ * } - 1} \right)}}{{{c^ * }\left( {c_0^ * - 1} \right)}} $ | (45) |
图 4给出了不同c0*条件下,上限能量利用率与折合阻尼系数的相关关系。可见,随着c*的增大,η从零逐渐增大,直到c*达到临界数值ccr, η*后,η达到最大ηmax。此外,随着c0*的增大,η也会逐渐增大。因此,c0*的提高必然有助于HOGR系统能量上限利用率的提高。需要说明的是,当c0*=∞时,η随c*会持续增大直至接近数值1。

|
图 4 不同c0*条件下的η随c*的变化规律 Fig.4 The variation of η against c* with different c0* |
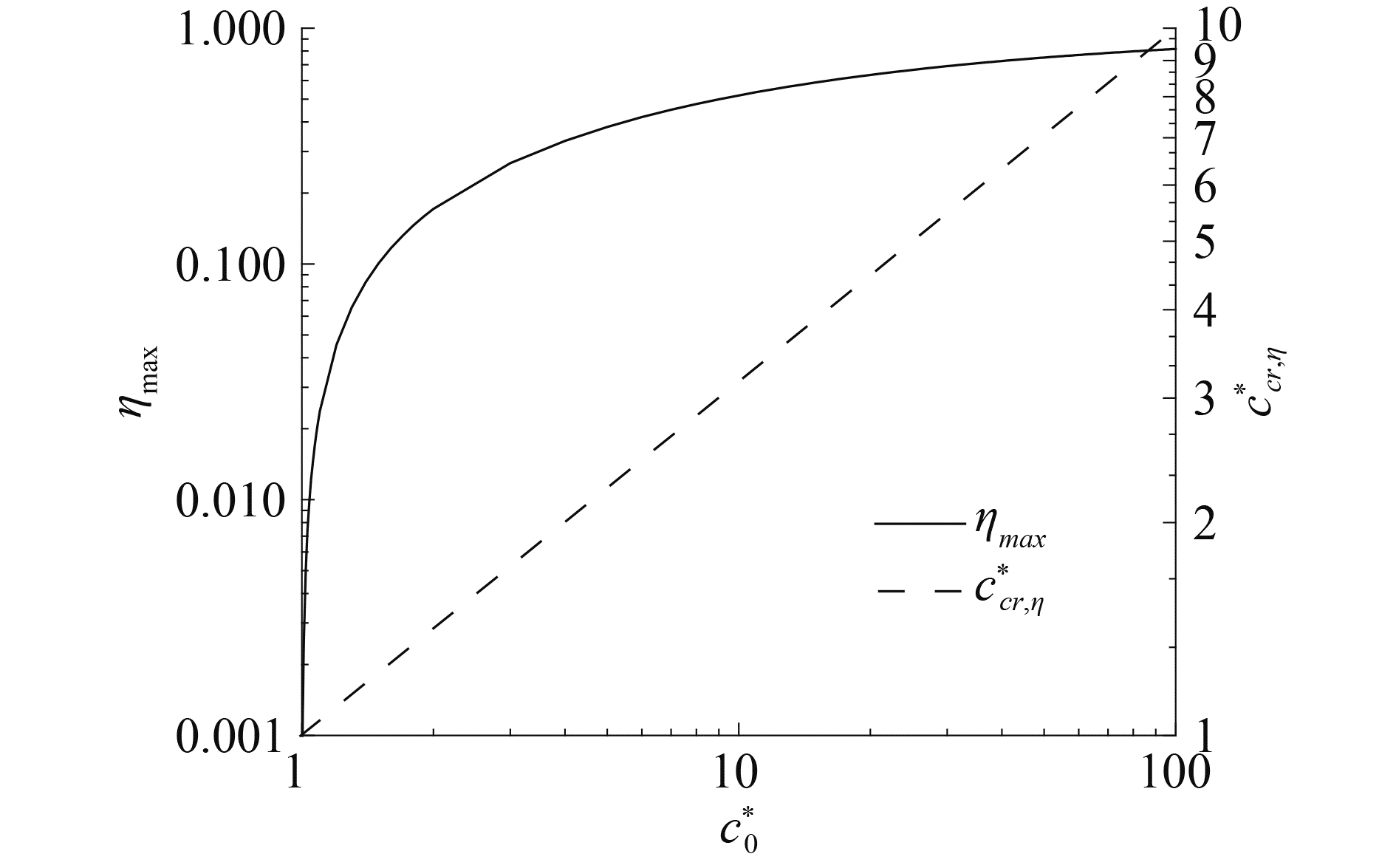
进一步,由图 4可知,不同的c0*必然存在不同的临界数值ccr, η*与最优的上限能量利用率ηmax。为此,将式(45)对c*求导并取零,即可得到ηmax与ccr, η*的表达式分别为
| $ {\eta _{\max }} = \frac{{\sqrt {c_0^ * } - 1}}{{\sqrt {c_0^ * } + 1}} $ | (46) |
| $ c_{cr,\eta }^ * = \sqrt {c_0^ * } $ | (47) |
显然,ηmax和ccr, η*与c0*密切相关。图 5给出了ηmax与ccr, η*随c0*的变化规律。可见,随着c0*的增大,ηmax和ccr, η*均有所增大。再次说明提高c0*有利提升上限能量利用率η。
|
图 5 ηmax与ccr, η*随不同c0*的变化规律 Fig.5 The variations of ηmax and ccr, η* against c0* |
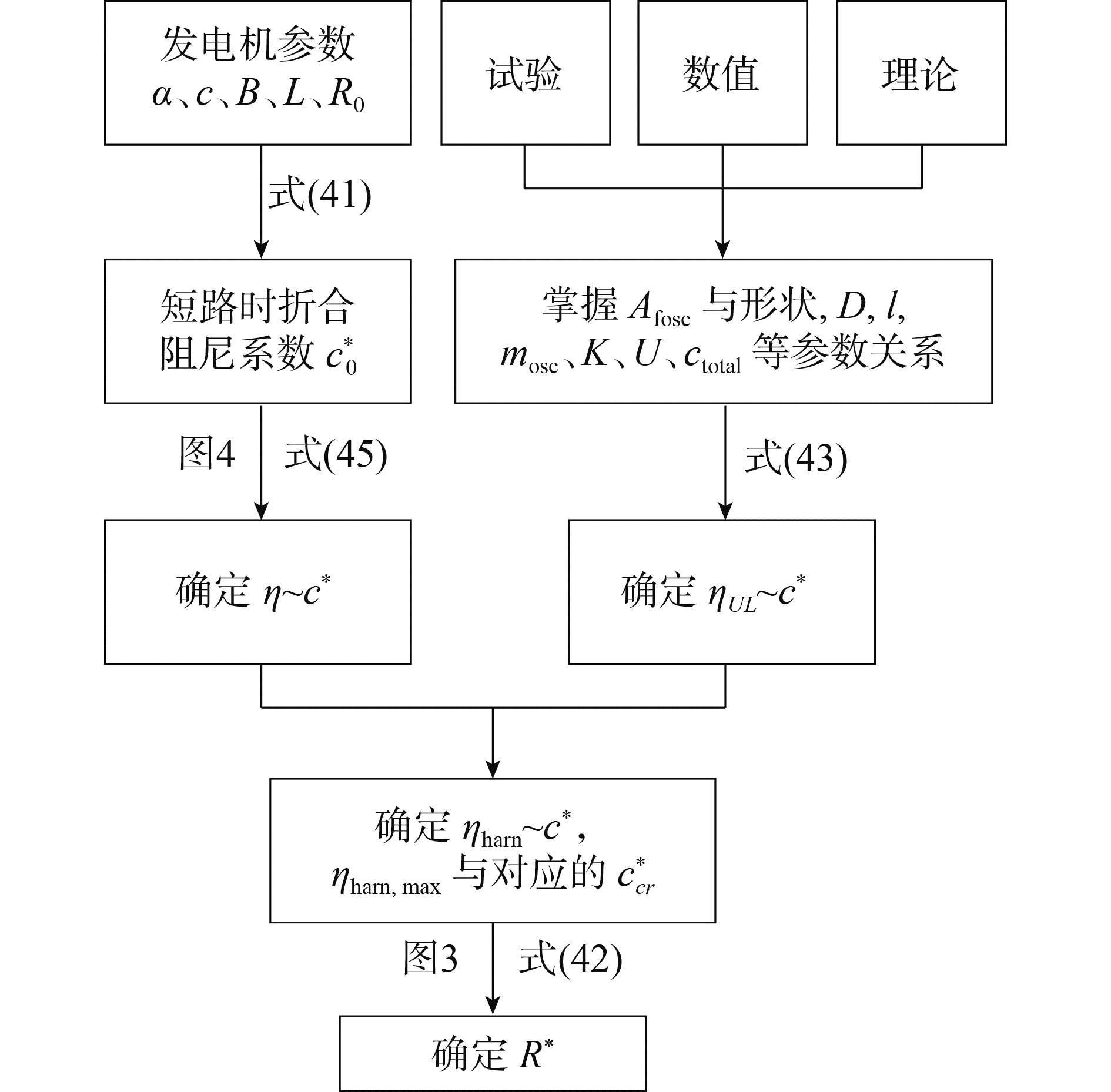
由2.4节分析可知,HOGR系统的发电效率ηharn决定于其上限效率ηUL与上限能量利用率η的乘积。第3节中已经分别阐述了上限效率ηUL与上限能量利用率η的变化规律及控制参数。那么,对于确定的发电机,HOGR系统最终的最优发电效率可通过如图 6途径加以确定。
|
图 6 HOGR系统最优效率的确定途径 Fig.6 The method to confirm the highest conversion efficiency in HOGR |
具体步骤为:1)确定发电机的各项参数(c、α、B、L、R0),并通过式(41)确定短路时的折合阻尼系数c0*,然后通过式(45)(或图 4)确定上限能量利用率与折合阻尼系数的相关关系η~c*;2)通过试验、数值或理论的方法掌握A与fosc的响应规律与振子参数、水流参数(形状、D、l、mosc、K、U、ctotal)的相关关系,并通过式(43)确定上限效率与折合阻尼系数的相关关系ηUL~c*;3)根据η~c*与ηUL~c*确定发电效率与折合阻尼系数之间的关系ηharn~c*,并确定最优发电效率ηharn, max与对应的ccr*;4)通过式(42)或图 3确定负荷比R*,最终确定最优发电效率下的负荷条件。
为了进一步证明上述方法的可靠性,此处采用文献[31]当中一组典型的圆柱体涡激振动试验结果进行验证。振子的直径D为0.089 m,振子长度L为0.914 m,振动质量mosc为8.88 kg,弹簧刚度K为1 600 N/m,总阻尼比ctotal为0.017。
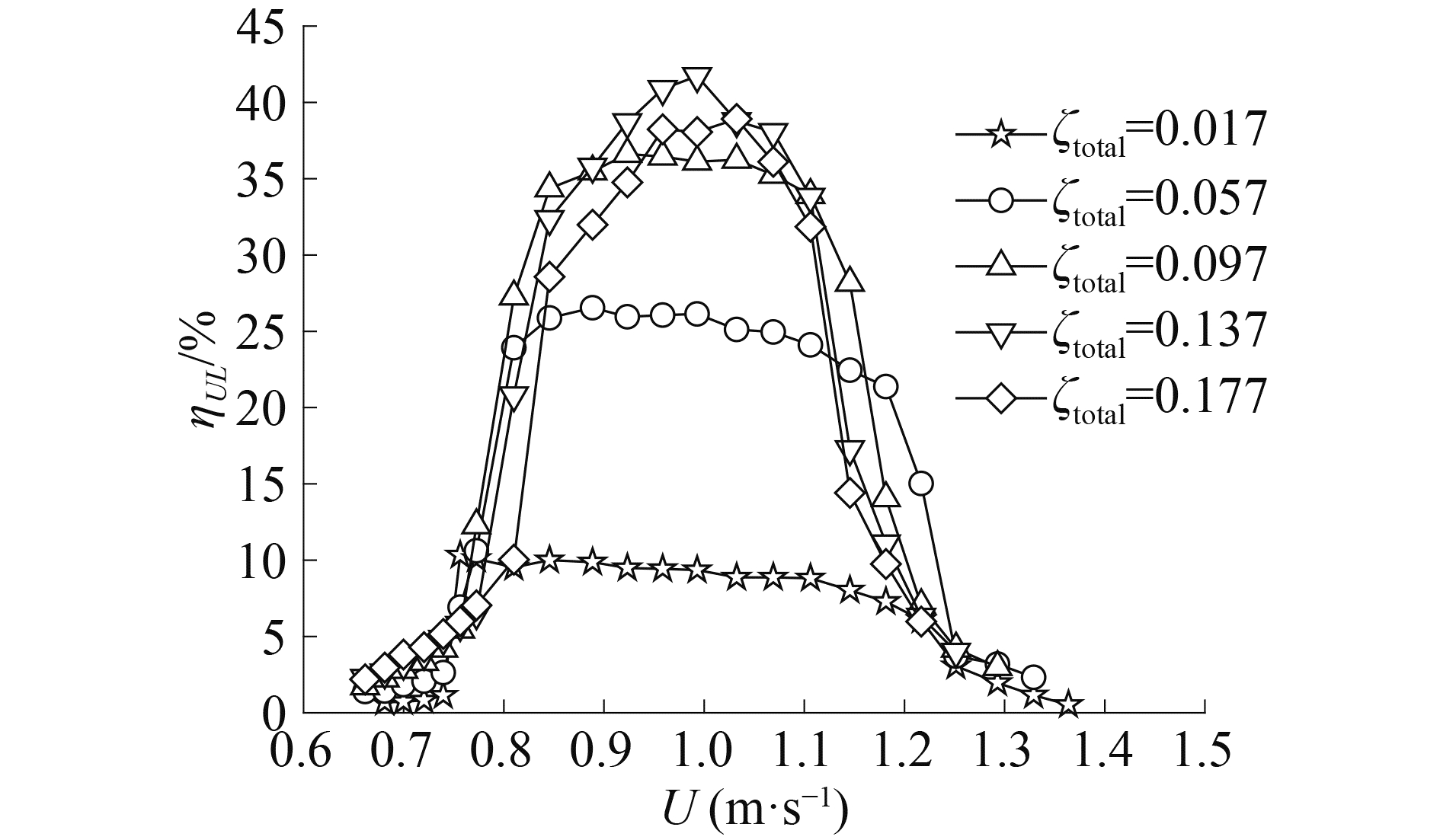
根据文献中不同总阻尼比条件下振幅A与频率fosc随流速U的响应规律,可得到上限效率ηUL随流速U的变化规律如图 7所示。可见,上限效率随总阻尼比并非呈现单调关系,且流速条件不同,上限效率ηUL随总阻尼的相关关系也不相同。此处,选择上限效率都较大的典型流速,U=0.993 m/s,并确定该流速下上限效率随折合阻尼系数的相关关系ηUL~c*,如图 8所示。
|
图 7 文献[31]中典型工况下上限效率随流速的变化关系 Fig.7 The typical variation of upper limit efficiency against the reduced velocity in Ref [31] |

|
图 8 最优发电效率确定的方法验证与说明 Fig.8 The verification and the illustration to confirm the optical harnessed efficiency |
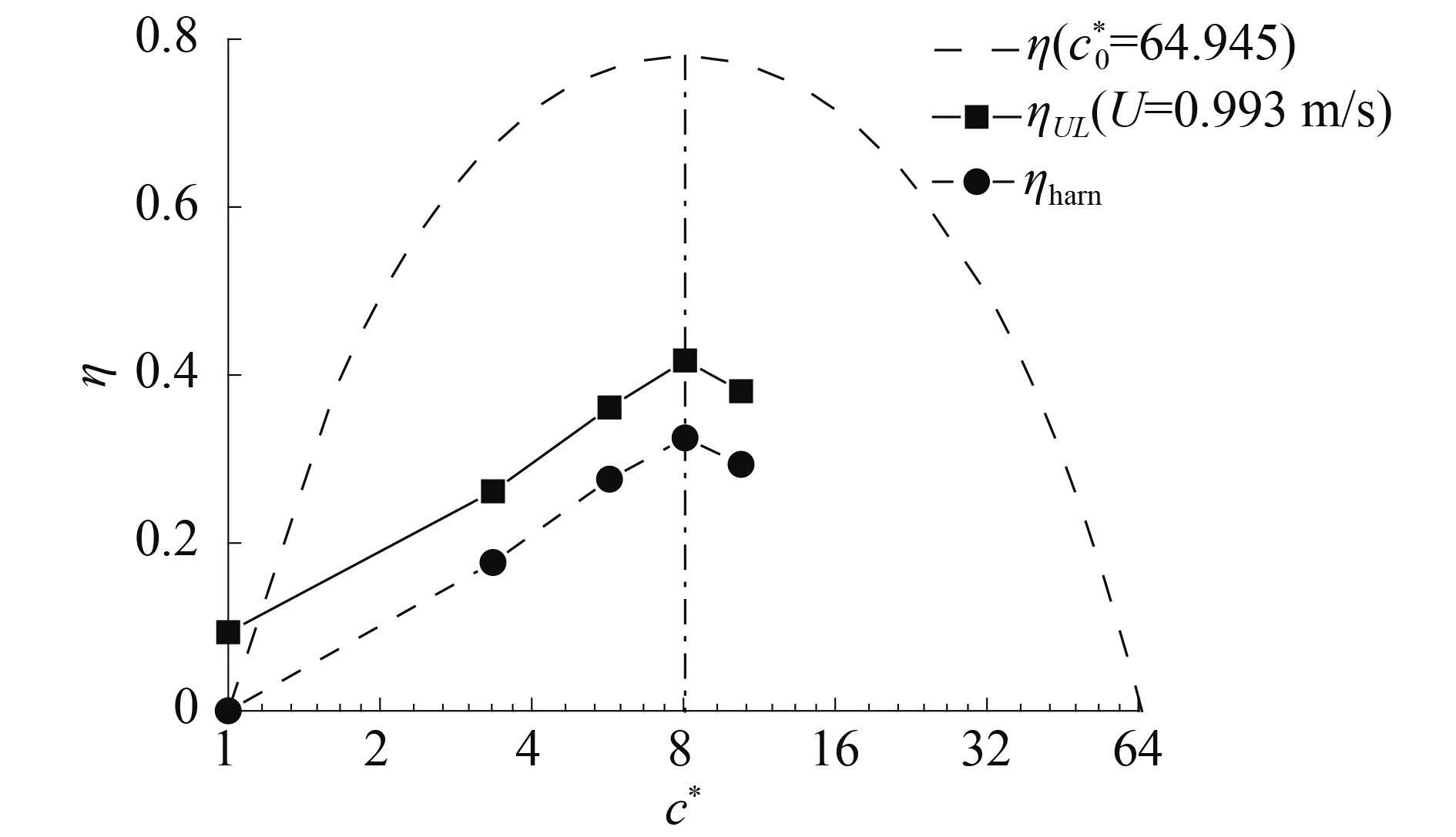
由于文献[31]中采用Vck模拟系统发电机,发电机无内能耗散(即R0=0)。此时,电机的短路折合阻尼系数c0*=∞,对应的η~c*关系如图 8所示。综合η~c*与ηUL~c*的关系,即可得到发电效率随折合阻尼系数之间的关系ηharn~c*,如图 9所示。进一步,将上述ηharn与文献[31]中测试得到的ηharn-mea进行对比可知,两者结果与规律基本一致。测试得到的ηharn-mea数值略小,原因可能在于文献[31]中忽略了某些系统的机械能的损耗。由此说明,本文对HOGR系统最优发电效率的确定方法是可靠的。
|
图 9 最优发电机下的效率规律 Fig.9 The regulation of efficiencies in the optimal convertor |
进一步,可得到该流速下(U=0.993 m/s)理想发电机的最优发电效率、对应折合阻尼系数以及最优负荷比分别为:ηharn, max=0.365;ccr*=8.059;R*=∞。
需要说明的是,上述结果是在理想的发电机条件下得到的。实际工程中,发电机必然存在内能损耗。此处,若假设实际电机的短路折合阻尼系数c0*=15,那么即可得到如图 8中的η~c*、ηUL~c*及ηharn~c*的相关关系。由此,也可获得该条件下最优发电效率、对应折合阻尼系数以及最优负荷比分别为:ηharn, max=0.198;ccr*=5.706;R*=1.975。
显然,发电机的差异必然造成最优发电效率的差异。因此,发电机的选配是最优发电效率的关键因素。
4.2 发电机的选配在HOGR系统中,若c0*较小且ccr, ηUL*大于ccr, η*(如图 8所示),则ηUL最大时的发电机η已过最大且正在减小,说明发电机容量不够,存在能量浪费。若c0*较大且ccr, ηUL*小于ccr, η*(图 8),则ηUL最大时的发电机η未达最大且正在增大,说明发电机容量过大,存在电机容量浪费。可见短路时的折合阻尼系数c0*在某种程度上表征了发电机的容量大小。另一方面,随着c0*的增大,η不断升高(图 4),因而发电效率必然有所提高。因此,理想发电机条件下的(无内能耗散,c0*=∞)发电效率必然最大。不过,c0*的升高实际为α、B、L的升高或c、R0的降低。而上述参数的变化,必然导致发电机的成本的提升。因此,对于发电机的选配,除了需考虑发电机对上限能量的利用率外,还应综合考虑其研制费用与维护费用,从而才能达到经济最优。
因此,综合上述两个方面,本文建议采用如下原则来选配发电机:水流做功最大时(ηUL最大),发电机上限能量转化能力最大(η最大)。由此,可得到
| $ c_{cr}^ * = c_{cr,{\eta _{UL}}}^ * = c_{cr,\eta }^ * $ | (48) |
| $ {\eta _{{\rm{harn,max}}}} = {\eta _{\max }}{\eta _{UL,\max }} $ | (49) |
此处,再采用文献[31]中相同的圆柱体涡激振动试验结果进行分析。结果表明U=0.993 m/s条件下,ccr, ηUL*=8.059。进一步,令ccr, η*=ccr, ηUL*=8.059,根据式(47)可计算得到此时的短路折合阻尼系数c0*=64.945。与4.1节过程类似,在得到η~c*、ηUL~c*关系后,可得到ηharn~c*关系(图 9)。由此,可确定最优发电效率下的各项参数为:ηharn, max=0.325;ccr*=8.059;R*=8.059。而此时的最优发电机参数配比满足c0*=64.945。
5 结论1) 发电机对振子的外力Fgen可视为系统总阻尼的一部分cgen。因此,HOGR系统运动方程的解可运用经典的谐振理论进行表达。
2) 系统中,各项阻尼系数的大小决定了各项功率与效率的大小。
3) HOGR系统的发电效率ηharn实际为系统的上限效率ηUL与上限能量利用率η的乘积;其中,上限效率ηUL决定于确定参数下的振子流致振动响应,而上限能量利用率η则决定于发电机参数配比与折合阻尼系数c*。
4) 最优发电效率的分析方法:①分别掌握上限效率ηUL及上限能量利用率η与折合阻尼系数c*的相关关系;②确定发电效率ηharn与折合阻尼系数c*的相关关系;③确定最优的发电效率ηharn, max与对应的折合阻尼系数ccr*;④基于折合阻尼系数c*与负荷比R*关系确定最优负荷条件。
5) 发电机的选配原则为保证发电机经济性的前提下,使最优上限效率ηUL, max与最优上限能量利用率ηmax对应的折合阻尼系数相等(ccr, ηUL*=ccr, η*)。
| [1] |
谢杰, 许劲松, 郁程. 圆柱绕流的流动分离控制[J]. 哈尔滨工程大学学报, 2011, 32(4): 401-406. XIE Jie, XU Jinsong, YU Cheng. A flow separation control on cylinder flow[J]. Journal of Harbin Engineering University, 2011, 32(4): 401-406. (  0) 0)
|
| [2] |
秦伟, 康庄, 宋儒鑫, 等. 深水钢悬链立管的双向涡致疲劳损伤时域模型[J]. 哈尔滨工程大学学报, 2013, 34(1): 26-33. QIN Wei, KANG Zhuang, SONG Ruxin, et al. Research on time domain model for vortex induced fatigue damage intwo-degree-of-freedom of deepwater steel catenary riser[J]. Journal of Harbin Engineering University, 2013, 34(1): 26-33. (  0) 0)
|
| [3] |
赵恩金, 拾兵, 曹坤. 导流板对海底管线涡激振动的影响[J]. 哈尔滨工程大学学报, 2016, 37(3): 320-325. ZHAO Enjin, SHI Bing, CAO Kun. Influence of reflectors onvortex-induced vibration of subsee pipelines[J]. Journal of Harbin Engineering University, 2016, 37(3): 320-325. (  0) 0)
|
| [4] |
丁林, 张力, 杨仲卿. 高雷诺数时分隔板对圆柱涡致振动的影响[J]. 机械工程学报, 2013, 49(14): 133-138. DING Lin, ZHANG Li, YANG Zhongqing. Effect of splitter plate on vortex-induced vibration of circular cylinder at high reynolds number[J]. Journal of mechanical engineering, 2013, 49(14): 133-138. (  0) 0)
|
| [5] |
白莱文斯. 流体诱发振动[M]. 吴恕三, 译. 北京: 机械工业出版社, 1981. BLENVINS R D. Flow-Induced Vibration[M]. WU Shusan, Trans. Beijing:China Machine Press, 1981. (  0) 0)
|
| [6] |
ALONSO G, MESEGUER J. A parametric study of the galloping stability of two dimensional triangular cross-section bodies[J]. Journal of wind engineering and industrial aerodynamics, 2006, 94: 241-53. DOI:10.1016/j.jweia.2006.01.009 (  0) 0)
|
| [7] |
FENG C C. The measurement of vortex induced effects in flow past stationary and oscillating circular and d-section cylinders[D]. Vancouver:University of British Columbia, 1968.
(  0) 0)
|
| [8] |
BEARMAN P W. Vortex shedding from oscillating bluff bodies[J]. Annual review of fluid mechanics, 1984, 16: 195-222. DOI:10.1146/annurev.fl.16.010184.001211 (  0) 0)
|
| [9] |
SARPKAYA T. Fluid forces on oscillating cylinders[J]. Journal of waterway port coastal and ocean division ASCE, WW4, 1978, 104: 275-290. (  0) 0)
|
| [10] |
KHALAK A, WILLIAMSON C H K. Fluid forces and dynamics of a hydroelastic structure with very low mass and damping[J]. Journal of fluids and structures, 1997, 11(8): 973-982. DOI:10.1006/jfls.1997.0110 (  0) 0)
|
| [11] |
KHALAK A, WILLIAMSON C H K. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping[J]. Journal of fluids and structures, 1999, 13(7-8): 813-851. DOI:10.1006/jfls.1999.0236 (  0) 0)
|
| [12] |
GOVARDHAN R, WILLIAMSON C H K. Modes of vortex formation and frequency response of a freely vibrating cylinder[J]. Journal of fluid mechanics, 2000, 420: 85-130. DOI:10.1017/S0022112000001233 (  0) 0)
|
| [13] |
WILLIAMSON C H K, GOVARDHAN R. Vortex Induced Vibrations[J]. Annual review of fluid mechanics, 2004, 36: 413-455. DOI:10.1146/annurev.fluid.36.050802.122128 (  0) 0)
|
| [14] |
DEN HARTOG J P. Mechanical vibrations[M]. 4th. New York: McGraw-Hill, 1956.
(  0) 0)
|
| [15] |
PARKINSON G V. Phenomena and modeling of flow-induced vibrations of bluff bodies[J]. Progress in aerospace sciences, 1989, 26(2): 169-224. DOI:10.1016/0376-0421(89)90008-0 (  0) 0)
|
| [16] |
BEARMAN P W, GARTSHORE I S, MAULL D J, et al. Experiments on flow-induced vibration of a square-section cylinder[J]. Journal of fluids and structures, 1987(1): 19-34. (  0) 0)
|
| [17] |
袁江波, 谢涛, 单小彪, 等. 压电俘能技术研究现状综述[J]. 振动与冲击, 2009, 28(10): 36-42. YUAN Jiangbo, XIE Tao, SHAN Xiaobiao, et al. A review of current situation for piezoelectric energy harvesting[J]. Journal of vibration and shock, 2009, 28(10): 36-42. DOI:10.3969/j.issn.1000-3835.2009.10.007 (  0) 0)
|
| [18] |
MURALT P. Ferroelectric thin films for micro-sensors and actuators:a review[J]. Journal of micromechanics and microengineering, 2000, 10(2): 136-146. DOI:10.1088/0960-1317/10/2/307 (  0) 0)
|
| [19] |
GURAV S P, KASYAP A, SHEPLAK M, et al. Uncertainty based design optimization of a micro piezoelectric composite energy reclamation device[C]//10th AIAA/ISSSMO Multidisciplinary Analysis and Optimization Conference. Albany, NY, 2004.
(  0) 0)
|
| [20] |
BERNITSAS M M, RAGHAVAN K, BEN-SIMON Y, et al. VIVACE (vortex induced vibration aquatic clean energy) A new concept in generation of clean and renewable energy from fluid flow[J]. Journal of offshore mechanics and arctic engineering, 2008, 130(4): 041101-1. DOI:10.1115/1.2957913 (  0) 0)
|
| [21] |
哈尔滨工程大学. 涡激振动与升力混合动力型水流发电装置: 中国, CN 102979660 A[P]. 2013. 03. 20.
(  0) 0)
|
| [22] |
BARRERO-GIL A, ALONSO G, SANZ-ANDRES A. Energy harvesting from transverse galloping[J]. Journal of sound and vibration, 2010, 329: 2873-2883. DOI:10.1016/j.jsv.2010.01.028 (  0) 0)
|
| [23] |
BARREROG A, PINDADO S, AVILA S. Extracting energy from vortex-induced vibrations:a parametric study[J]. Applied mathematical modelling, 2012, 36: 3153-3160. DOI:10.1016/j.apm.2011.09.085 (  0) 0)
|
| [24] |
MEHMOOD A, ABDELKEFI A, HAJJ M R, et al. Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder[J]. Journal of sound and vibration, 2013, 332: 4656-4667. DOI:10.1016/j.jsv.2013.03.033 (  0) 0)
|
| [25] |
DAI H L, ABDELKEFI A, WANG L. Theoretical modeling and nonlinear analysis of piezoelectric energy harvesting from vortex-induced vibrations[J]. Journal of intelligent material systems and structures, 2014, 25(14): 1861-1874. DOI:10.1177/1045389X14538329 (  0) 0)
|
| [26] |
DAI H L, ABDELKEFI A, WANG L. Piezoelectric energy harvesting from concurrent vortex-induced vibrations and base excitations[J]. Nonlinear dynamic, 2014, 77: 967-981. DOI:10.1007/s11071-014-1355-8 (  0) 0)
|
| [27] |
丁林, 张力, 姜德义. 高雷诺数范围内不同形状柱体流致振动特性研究[J]. 振动与冲击, 2015, 34(12): 176-181. DING Lin, ZHANG Li, JIANG Deyi. Flow-induced motion of bluff bodies with different cross sections in flow field with high Reynolds number[J]. Journal of vibration and shock, 2015, 34(12): 176-181. (  0) 0)
|
| [28] |
袁鹏, 陈东旺, 王树杰, 等. 涡激振动潮流能转换装置获能实验研究[J]. 中国海洋大学学报, 2015, 45(10): 114-120. YUAN Peng, CHEN Dongwang, WANG Shujie, et al. Experimental study onvortex-induced vibration tidal current energy conversion[J]. Periodical of Ocean University of China, 2015, 45(10): 114-120. (  0) 0)
|
| [29] |
李小超, 周熙林, 赵利平. 水流-圆柱-发电机动力相互作用量纲分析及实验装置[J]. 实验力学, 2017, 32(1): 49-56. LI Xiaochao, ZHOU Xilin, ZHAO Liping. On the dimensional analysis and experimental apparatus of interaction among water current-cylinder and generator[J]. Journal of experimental mechanics, 2017, 32(1): 49-56. DOI:10.7520/1001-4888-16-055 (  0) 0)
|
| [30] |
CHANG Chechun, KUMAR R A, BERNITSAS M M. VIV and galloping of single circular cylinder with surface roughness at 3.0×104 ≤ Re ≤ 1.2×105[J]. Ocean engineering, 2011, 38: 1713-1732. DOI:10.1016/j.oceaneng.2011.07.013 (  0) 0)
|
| [31] |
LEE J H, BERNITSAS M M. High-damping, high-reynolds VIV tests for energy harnessing using the VIVACE converter[J]. Ocean engineering, 2011, 38: 1697-1712. DOI:10.1016/j.oceaneng.2011.06.007 (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


