20世纪90年代,美国学者提出了基于性态的抗震设计思想[1]。随着相应理论和方法的不断发展,基于性态的抗震设计正逐渐为工程界所接受,但目前基于性态的抗震设计在我国尚未广泛推广应用。我国第一部基于性态的抗震设计技术标准:《建筑工程抗震性态设计通则》CECS160:2004(以下简称《通则》),从设防原则、设防目标、设防参数以及设防方法等方面给出了指导意见[2],为进一步完善基于性态的抗震设计理论、方法以及编制地方抗震性态设计规范起到了引领和导向作用[3]。
提及抗震性态抗震设计,人们普遍关心的问题是:性态设计与现行抗震设计究竟有何区别?结构的抗震性能能否提高?以及如何体现?基于此,本文在分析《通则》和现行《建筑抗震设计规范》(GB 50010-2010) (以下简称《规范》)相关条文规定的基础上,利用PKPM软件分别参照两种规范(通则)进行结构设计。根据设计结果,采用OpenSees软件分别建立依据两种抗震规范(通则)设计的不同层高的钢筋混凝土框架结构模型。并基于双线性需求模型以及贝叶斯理论进行不同框架结构的地震易损性分析,以更好的模拟结构在弹性和弹塑性阶段的响应。得到结构地震易损性曲线,探讨两种钢筋混凝土框架结构在抗震性能方面的差异。
1 结构模型建立和地震记录选取 1.1 模型的建立《通则》引入了基于性态的抗震设计思想,通过控制建筑结构在外部作用下的性态反应,使其能够达到设计所需求的性态水平,从而确保实现预期的使用功能[4]。《规范》和《通则》在设计原则、场地类别、场地设计谱、地震作用和结构抗震验算等方面差异显著,相关学者开展大量的工作,取得了一定的研究成果[5]。
钢筋混凝土框架结构,在我国广大地区应用广泛且在历次震害中破坏严重,因此备受重视[6]。本文分别参照《规范》和《通则》,并严格执行其他相关规范条款规定,分别设计完成2层、4层和6层,共计6个不同的钢筋混凝土框架结构模型,用于后续的研究分析。模型的主要抗震设计参数如下:设防烈度为7度,场地类别取Ⅱ类场地,地震分组按照设计地震第二组,框架抗震等级为三级,建筑使用分类为Ⅱ类使用功能建筑,与《通则》中丙类建筑相对应。鉴于轴压比对结构抗震能力有显著影响[7],考虑到本文的研究目的,在设计过程中对相同层高的结构采用相同的截面尺寸。同时,由于结构整体质量和侧向刚度分布较为均匀,故只需取一榀框架进行有限元建模分析,杨红等[8]的研究也表明该处理方法是合理的。
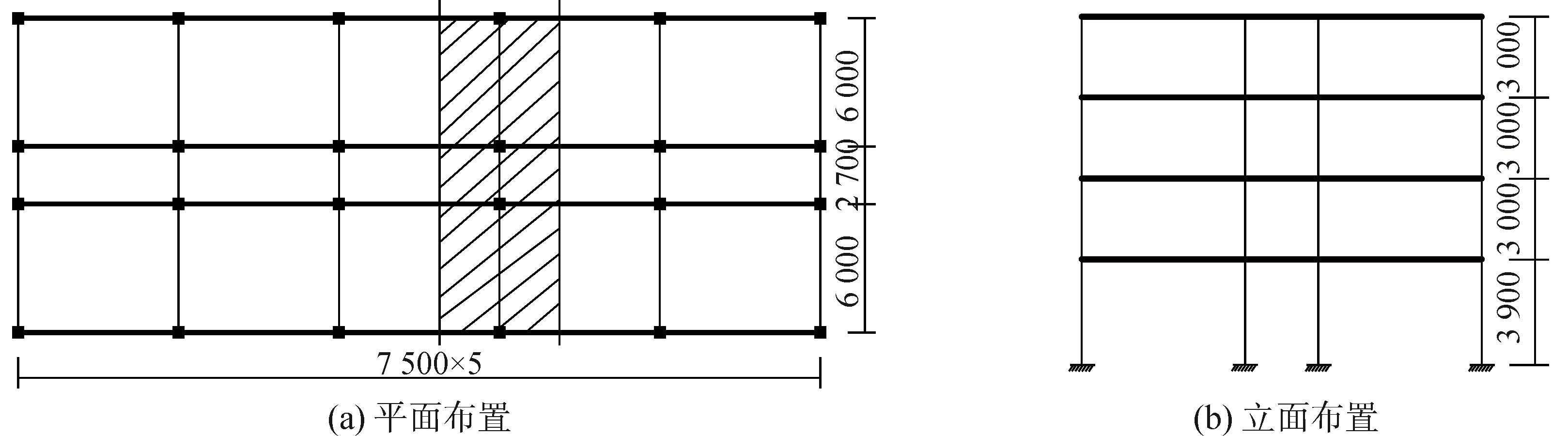
框架结构模型具体尺寸如下:首层层高为3.9 m,其他层层高为3.0 m;横向跨度为7.5 m,纵向边跨跨度为6.0 m,中间跨跨度取2.7 m,结构外形尺寸为37.5 m×14.7 m。沿横向边跨中间各布置一道次梁,以四层结构为例,结构布置如图 1所示。
|
Download:
|
| 图 1 结构布置 Fig. 1 Structural layout | |
依据PKPM的设计结果,利用OpenSees软件建立结构的有限元模型并进行非线性动力时程分析,得到结构在地震作用下的动力响应。在用两种软件进行建模设计过程中,以结构基本自振周期为标准量,通过结构的动力特性,校核两种模型的吻合程度。
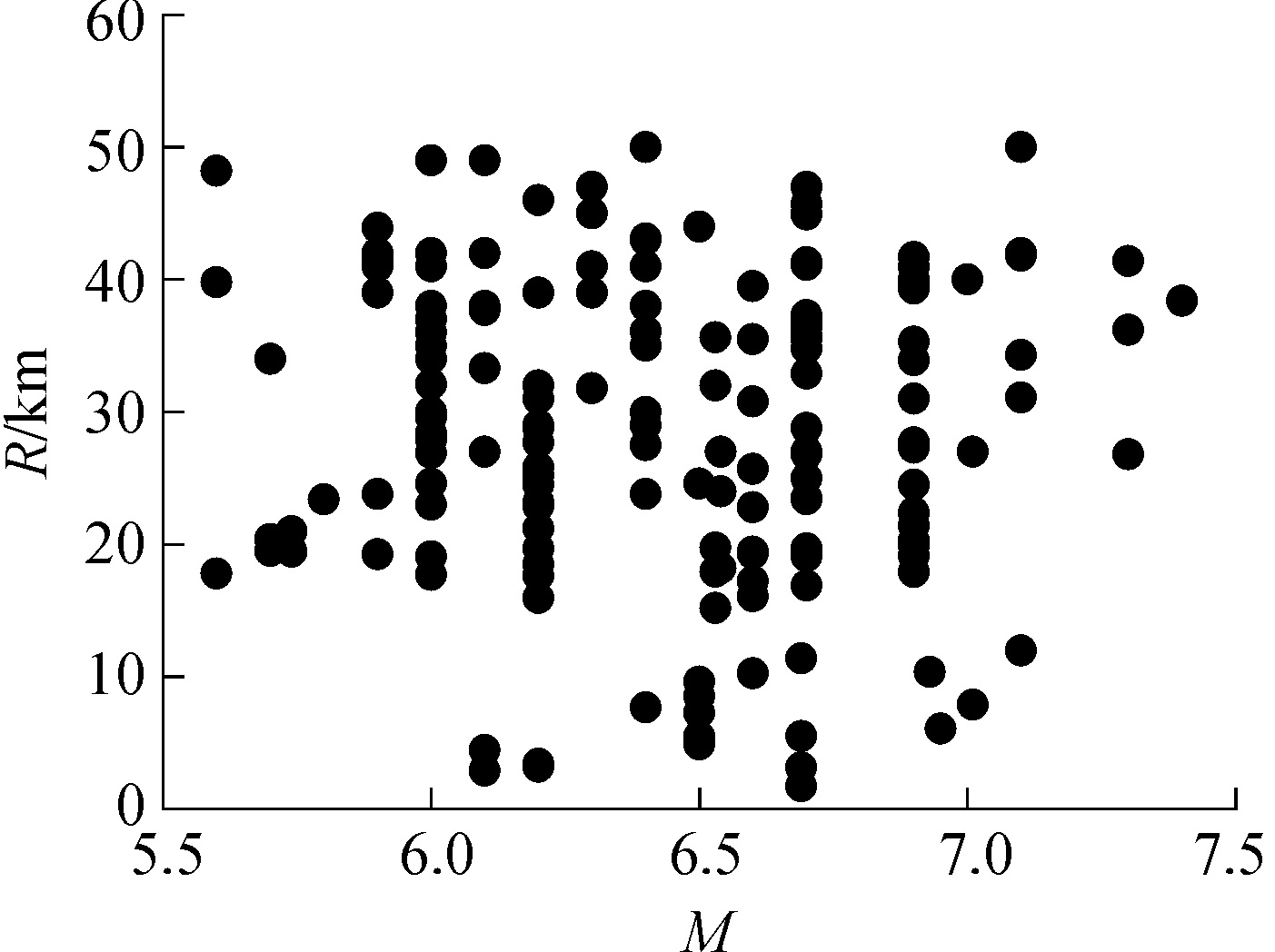
1.2 地震动记录的选取在结构非线性动力时程分析中,输入地震动的不确定性是导致其地震响应不确定性的最主要因素,对最终分析结果具有决定性作用[9]。地震动本身的复杂性,会导致不同输入的计算结果产生很大的差异。Shome和Cornell将地震动按照震级M、震中距R等进行划分,划分过程中考虑概率地震需求和标准衰减规律之间的关系[10]。本文参照该选取方法,以震级、震中距为依据,在尽可能宽的M-R范围内选取200条地震动,充分考虑不同场地类别,震级大小,以及远、近场地震等情况的影响,地震动散点分布图如图 2。
|
Download:
|
| 图 2 地震动散点分布图 Fig. 2 The ground motion scatter distribution | |
地震作用强度较为常用的表示方法有峰值加速度(PGA)和阻尼比为5%的结构基本周期对应的谱加速度(Sa(T1, 5%))。由于不同周期的结构受不同地震动参数的影响程度不尽相同,使得PGA的适用范围存在一定限制[11];相比于PGA,结构基本周期对应的谱加速度(Sa(T1, 5%))由于考虑了结构基本周期以及阻尼比等因素,能够有效的减小结果的离散性,得到相对比较集中的结果[12-13]。故此处选择Sa作为地震动强度参数。
2 结构易损性分析 2.1 概率地震需求模型地震需求模型与地震动强度参数和结构的性能参数均有较大的关联。以往采用较多的线性模型对于较大和较小的Sa估计得到的地震需求偏低,而对于适中的Sa值则会产生过高的估计值,无法做到对弹性和非弹性范围内的数据都有良好的拟合效果。为此本文研究采用双线性模型:
| $ \left\{ \begin{array}{l} D({S_a},\mathit{\Theta }) = {\rm{ln}}({\delta _D}) = {\theta _0} + {\theta _1}{\rm{ln}}({S_a}) + \\ \quad \quad \quad \quad {\sigma _1}{\varepsilon _1},{\rm{ln}}({S_a}) \le {\theta _{{S_a}}}\\ D({S_a},\mathit{\Theta }) = {\rm{ln}}({\delta _D}) = {\theta _0} + {\theta _1}{\theta _{{S_a}}} + \\ {\theta _2}[{\rm{ln}}({S_a}) - {\theta _{{S_a}}}] + {\sigma _2}{\varepsilon _2},{\rm{ln}}({S_a}) > {\theta _{{S_a}}} \end{array} \right. $ | (1) |
式中:δD表示最大层间位移;Θ=(θ0, θ1, θ2, θSa, σ1, σ2)为未知的模型参数,θ1、θ2分别为双线性模型各部分的斜率;σ1ε1和σ2ε2表示两部分的模型误差,σ1和σ2表征相应部分模型的标准差;ε1和ε2是均值为0、方差为1的随机正态分布。其中第一部分表示弹性范围,第二部分表示非弹性范围[14]。上述参数可通过非线性时程分析得到结构反应数据,应用极大似然估计方法得到。考虑到结构模型中存在误差,模型参数和分析方法等方面存在不确定性,考虑依据贝叶斯更新理论,在极大似然估计拟合结果的基础上进行校核[15]:
| $ f\left( \mathit{\Theta } \right) = \gamma L\left( \mathit{\Theta } \right)p\left( \mathit{\Theta } \right) $ | (2) |
式中:f(Θ)为后验分布,即最终校正后的参数结果;γ为正则化因子;L(Θ)为似然函数,即初步的数据分析结果;p(Θ)为先验分布,表示先前通过实验获得的对Θ的了解,亦或是其他研究人员得到的相关结果。本文研究中采用无信息先验分布。
贝叶斯更新理论中可以利用新的信息对未知参数的样本模型连续修正。在应用该理论时,这种不断更新修正的过程可以无限重复。因此,随着样本数目的增加,经过一定次数的更新修正之后,最初的先验分布对最终结果的影响便会越来越小。按照这种方法,本文经过多次修正,获得最终的模型参数Θ=(θ0, θ1, θ2, θSa, σ1, σ2),并以此作为后续分析的参数值。
2.2 结构抗震能力最大层间位移角由于与节点转动、楼层层间变形能力直接相关,故适用于表征框架结构的损伤变形情况[16];《规范》在多遇地震下结构的弹性承载力和变形验算以及罕遇地震作用下的薄弱层弹塑性变形验算规定中,也要求钢筋混凝土框架结构的弹性层间位移角限值取1/550、弹塑性位移角限值为1/50 [17]。本文中采用最大层间位移角表示结构体系的抗震能力,并参考相关文献的研究成果,确定框架结构不同性能水平所对应的最大层间位移角限值如表 1所示。
| 表 1 框架结构性能水平层间位移角限值 Tab.1 The story drift limit of RC structure performance level |
按照上述贝叶斯更新理论,分别得到基于《规范》和《通则》设计的2层结构的模型参数值,如下所示:Θ=(θ0, θ1, θ2, θSa, σ1, σ2)=(-4.202 9,1.051 9,1.223 1,-1.661 5,0.074 9,0.448 9)和Θ=(θ0, θ1, θ2, θSa, σ1, σ2)=(-4.266 5,1.033 6,1.197 6,-1.701 7,0.060 8,0.410 4)。按式(1)得到的双线性需求模型如图 3所示。

|
Download:
|
| 图 3 2层结构的双线性地震需求模型 Fig. 3 Bilinear seismic demand model of two-layer structure | |
从图 3双线性需求模型可以看出,两个结构的时程响应随着地震动强度的增加,都呈增加的趋势;并且图形后半部分数据点的排布比前半部分更为分散,表明随着地震强度等级的增大,结构进入非弹性阶段,数据的离散性也因此增大。
基于贝叶斯更新理论最终拟合出的参数,估计得到结构的易损性:
| $ F({S_a};\mathit{\Theta }) \cong 1 - \mathit{\Phi }\left( {\frac{{{\lambda _{\rm{C}}} - {\lambda _{D|{S_a}}}}}{{\sqrt {\sigma _C^2 + \sigma _{D|{S_a}}^2 + \sigma _m^2} }}} \right) $ | (3) |
式中:Φ(·)为标准正态累积分布函数;λC和λD|Sa分别表示结构抗震能力和地震需求取自然对数后的平均值;σC和σD|Sa则分别代表在估计抗震能力和地震需求中的不确定性;σm代表的则是建筑结构模型在非线性时程分析中的不确定性。按照Wen的建议,σC和σm均取为0.3[18]。由于前后两部分地震需求模型标准差存在差异(σ1 < σ2),导致在按照式(3)拟合地震易损性曲线时曲线中出现断点。为方便地震易损性曲线在实际工程中的应用,采用对数函数进行处理,以便在整个数据范围内得到一条连续的地震易损性曲线。对数函数为
| $ F({S_a};\mathit{\Gamma }) = \mathit{\Phi }\left( {\frac{{{\rm{ln}}({S_a}) - {\gamma _1}}}{{{\gamma _2}}}} \right) $ | (4) |
式中:F(Sa; Γ)为连续形式的易损性, Γ=(γ1, γ2)为对数函数中未知的参数向量,参数γ1和γ2通过最小二乘法拟合得到。由于估计概率分布函数F(Sa; Θ)时受各种不确定因素的影响,本文采用平均值一次二阶矩的方法予以考虑。
令:
| $ \beta ({S_a}) = {\left. {\frac{{{\lambda _C} - {\lambda _{D|{S_a}}}({S_a};\theta )}}{{\sqrt {\sigma _{D|{S_a}}^2 + \sigma _C^2 + \sigma _m^2} }}} \right|_{\mathit{\Theta } = {M_\mathit{\Theta }}}} $ | (5) |
通过将功能函数β(Sa)在随机变量Sa的平均值M处按照一阶泰勒级数展开,近似求得功能函数β(Sa)的方差:
| $ \sigma _\beta ^2({S_a}) \approx {\left. {{\pmb{\mathit{\nabla }} _\mathit{\Theta }}\beta ({S_a})} \right|_{\mathit{\Theta } = {M_\mathit{\Theta }}}}{\left. {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\mathit{\Theta \Theta }}}{\pmb{\mathit{\nabla }} _\mathit{\Theta }}\beta {{({S_a})}^{\rm{T}}}} \right|_{\mathit{\Theta } = {M_\mathit{\Theta }}}} $ | (6) |
式中:∇Θβ (Sa)|Θ=MΘ是功能函数β(Sa; Θ)的梯度行矩阵,ΣΘΘ表示功能函数的协方差矩阵。
易损性估计中,考虑的置信区间范围为
| $ \{ \mathit{\Phi }[ - \beta ({S_a}) - {\sigma _\beta }({S_a})\left] {,\mathit{\Phi }} \right[ - \beta ({S_a}) + {\sigma _\beta }({S_a})]\} $ | (7) |
基于上述方法,得到按两种规范(通则)设计的2层框架结构易损性曲线及两者的对比如图 4、5所示。

|
Download:
|
| 图 4 2层结构的地震易损性曲线 Fig. 4 Fragility curves of two-layer structure | |

|
Download:
|
| 图 5 2层结构地震易损性曲线对比 Fig. 5 Comparison of seismic fragility curves of two-layer structures | |
从图 4中不难发现,两个结构易损性曲线的变化均呈现出如下特点:1)随着地震作用的强度的提高,结构发生各个等级破坏的超越概率均逐渐增大;2)随着破坏严重程度的增大,易损性曲线的置信区间范围均逐渐变大。对比按照不同规范(通则)设计的二层结构的地震易损性曲线,可以发现两者轻微破坏的曲线近乎重合,发生中等破坏的概率差别也并不明显,而按照《通则》设计的结构发生严重破坏和倒塌的超越概率则都要小于基于《规范》设计的二层结构。
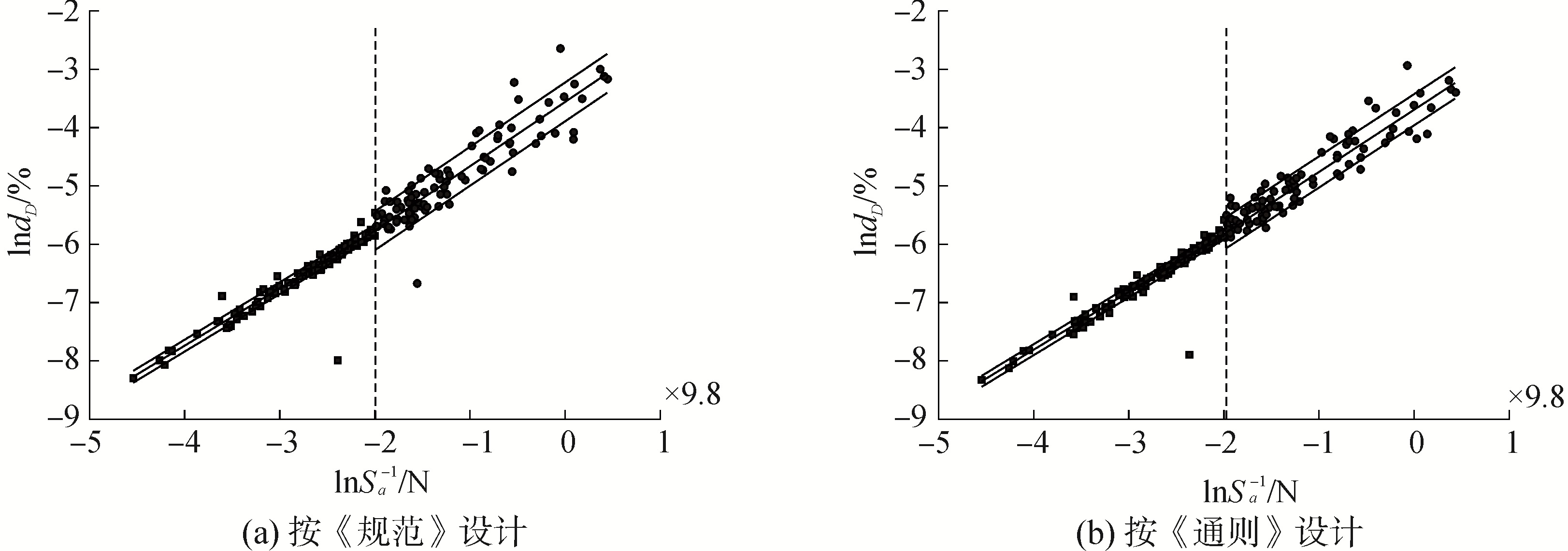
3.2 4层结构模型易损性分析对于按照《规范》和《通则》设计的4层结构,同样按照上述方法进行拟合,得到的最终拟合结果分别为:Θ=(θ0, θ1, θ2, θSa, σ1, σ2)=(-3.795 4,0.984 2, 1.102 5,-1.994 7,0.101 5,0.333 3)和Θ=(θ0, θ1, θ2, θSa, σ1, σ2)=(-3.848 9,0.989 7,1.064 8,-1.970 3,0.094 0, 0.267 6)。按式(1)得到的双线性需求模型如图 6所示。
|
Download:
|
| 图 6 4层结构的双线性地震需求模型 Fig. 6 Bilinear seismic demand model of four-layer structure | |
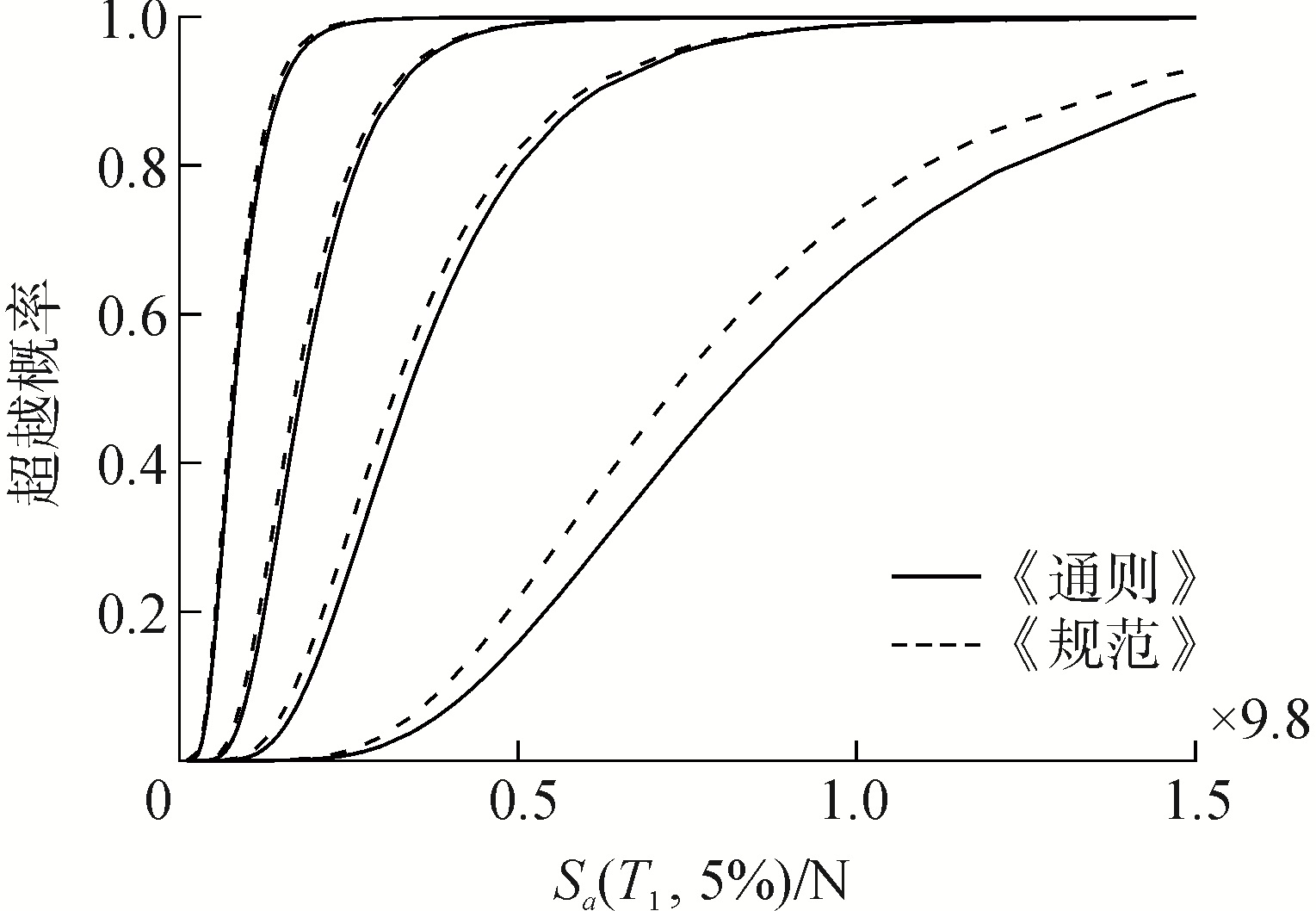
按照连续的易损性计算方法,分别计算得到按照规范(通则)设计的4层结构的易损性曲线如图 7所示,两者易损性之间的对比如图 8所示。

|
Download:
|
| 图 7 4层结构的地震易损性曲线 Fig. 7 Fragility curves of four-layer structure | |
|
Download:
|
| 图 8 4层结构地震易损性曲线对比 Fig. 8 Comparison of seismic fragility curves of four-layer structures | |
从图 7和图 8中可以看出:1)在包含置信区间的地震易损性曲线上,按照《通则》设计结构的置信区间范围要明显小于基于《规范》设计的结构,表明该种结构在不同地震作用下,其动力响应的变化较小,抗震性能较为稳定;2)对比按照不同规范设计结构的地震易损性曲线,两者的轻微破坏和中等破坏曲线是几乎重合的,按照《通则》设计的4层结构发生中等破坏超越概率要低于《规范》,而两者抗倒塌性能之间的差异则更为明显。
3.3 六层结构模型易损性分析对于按照《规范》和《通则》设计的6层结构,最终拟合出的参数值分别为:Θ=(θ0, θ1, θ2, θSa, σ1, σ2)=(-3.958 1,0.989 0,1.155 0,-2.227 8,0.086 7,0.382 2)和Θ =(θ0, θ1, θ2, θSa, σ1, σ2)=(-3.969 6,0.995 9,1.143 3,-2.222 9,0.085 7,0.346 1)。按式(1)得到的双线性需求模型如图 9所示。采用同上述相同的方法,得到的按两种规范(通则)设计的6层框架结构的易损性曲线及两者的对比情况如图 10、11所示。

|
Download:
|
| 图 9 6层结构的双线性地震需求模型 Fig. 9 Bilinear seismic demand model of six-layer structure | |

|
Download:
|
| 图 10 6层结构的地震易损性曲线 Fig. 10 Fragility curves of six-layer structure | |
|
Download:
|
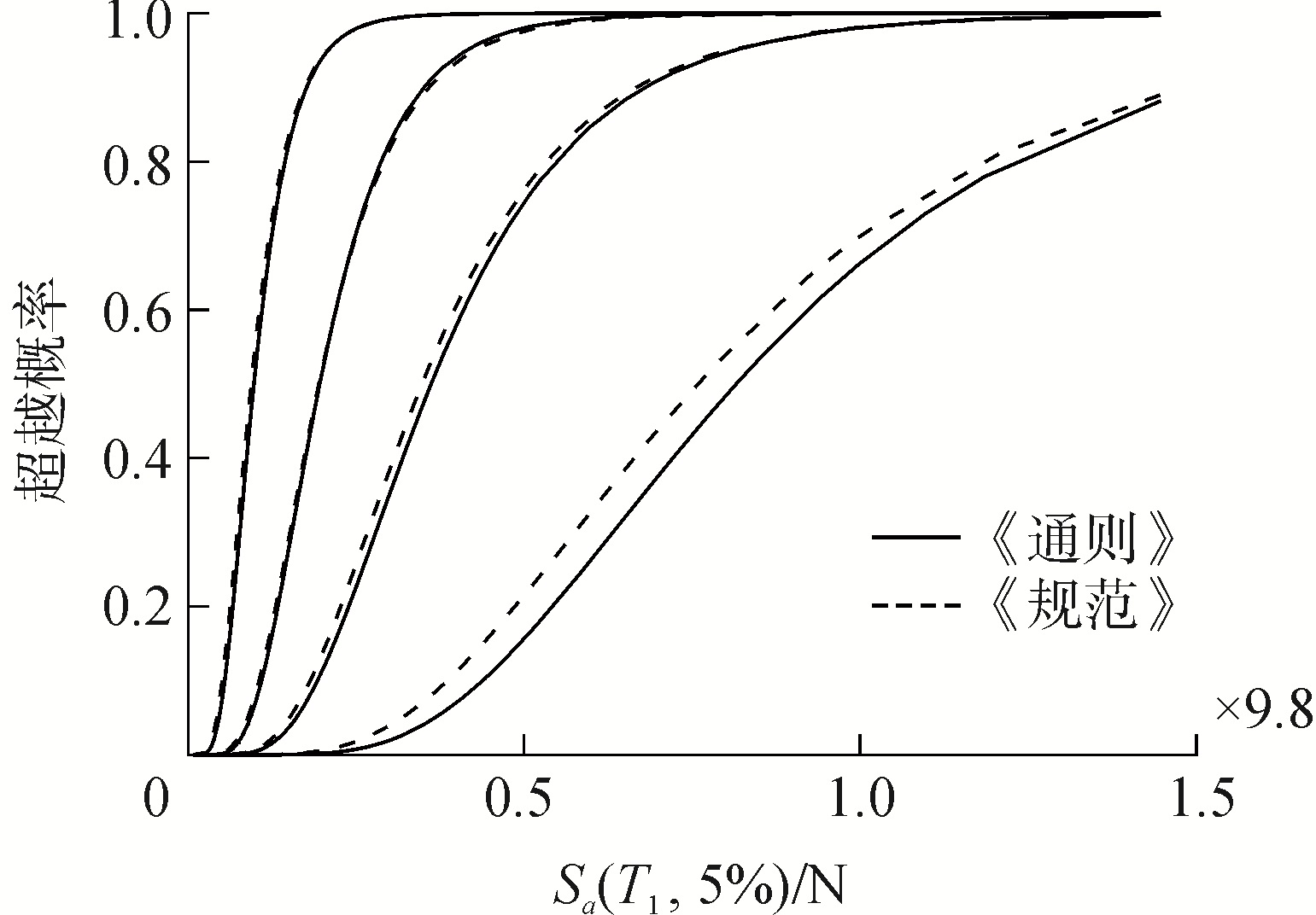
| 图 11 6层结构地震易损性曲线对比 Fig. 11 Comparison of seismic fragility curves of six-layer structures | |
通过对比不难发现,6层框架结构与4层框架结构在地震易损性方面具有类似的表现。综合6个框架结构来看:1)对于按照同一规范设计的框架结构,随着地震作用强度的增加,结构发生相应破坏的超越概率逐渐增大,并且曲线的置信区间也有所增大,结构反应的离散性增强;2)基于《通则》设计的框架结构发生程度较轻破坏的可能性与按照《规范》设计的结构相比,差距不大;而发生较为严重的破坏时,依照《通则》设计的结构的抗震表现则要优于《规范》结构,其中又以抗倒塌性能的差异最为显著,主要是因为两种结构产生层间位移较小时,即在弹性阶段,两者差异并不明显;而随着位移增大,结构进入塑性,破坏的程度也逐渐随之加重,性态结构的抗震优势逐步凸显,两者之间的抗震性能差异也便由此增大。
4 结论1) 按照同一种规范设计的结构,随着地震强度等级的增大,结构发生各级破坏的超越概率逐渐变大,随着结构逐渐进入弹塑性阶段,其响应会有更大的离散性和不确定性;
2) 基于《通则》设计的结构在相同强度等级的地震作用下,置信区间范围较小,抗震性能更为稳定;
3) 按照《通则》设计的结构相对于按《规范》设计的结构有更好的抵抗发生较严重破坏的能力,其中以抗倒塌性能最为明显,超越概率可相差10%左右。
| [1] |
POLAND C, HILL J, SHARPE R, et al. Performance based seismic engineering of buildings: final report[M]. Structural Engineers Association of California, [S.l.], 1995.
(  0) 0)
|
| [2] |
中国地震局工程力学研究所. CECS 160-2004, 建筑工程抗震性态设计通则(试用)[S].北京: 中国计划出版社, 2004. Institute of Engineering Mechanics, China Earthquake Administration. CECS 160-2004, General rule for performance-based seismic design of buildings[S]. Beijing: China Planning Press, 2004. (  0) 0)
|
| [3] |
王焕定. 关于《建筑工程抗震性态设计通则(试用)》的讨论[J]. 地震工程与工程振动, 2005, 25(5): 186-188. WANG Huanding. A discussion on "general rule for performance-based seismic design of buildings"[J]. Earthquake engineering and engineering vibration, 2005, 25(5): 186-188. (  0) 0)
|
| [4] |
PRIESTLEY M J N. Performance based seismic design[J]. Bulletin of the New Zealand society for earthquake engineering, 2000, 33(3): 325-346. (  0) 0)
|
| [5] |
蒋伟, 徐龙军, 张进国. 框架结构抗震性态设计分析[J]. 地震工程与工程振动, 2013, 33(5): 93-99. JIANG Wei, XU Longjun, ZHANG Jinguo. Analysis of performance-based seismic design of frame structures[J]. Journal of earthquake engineering and engineering vibration, 2013, 33(5): 93-99. (  0) 0)
|
| [6] |
肖建庄, 丁陶, 王长青, 等. 现浇与预制再生混凝土框架结构抗震性能对比分析[J]. 东南大学学报(自然科学版), 2014, 44(1): 194-198. XIAO Jianzhuang, DING Tao, WANG Changqing, et al. Contrastive analysis on seismic performances between cast-in-situ and precast frame structure made of recycled aggregate concrete[J]. Journal of Southeast University (natural science edition), 2014, 44(1): 194-198. (  0) 0)
|
| [7] |
施炜, 叶列平, 陆新征, 等. 不同抗震设防RC框架结构抗倒塌能力的研究[J]. 工程力学, 2005, 25(3): 41-48. SHI Wei, YE Lieping, LU Xinzheng, et al. Study on the collapse-resistant capacity RC frames with different seismic fortification levels[J]. Engineering mechanics, 2005, 25(3): 41-48. (  0) 0)
|
| [8] |
杨红, 高文生, 王志军. 空间框架简化为平面模型的抗震分析[J]. 重庆大学学报, 2008, 31(11): 1267-1272. YANG Hong, GAO Wensheng, WANG Zhijun. The rationality of plane model simplifying three-dimension frame in seismic response analysis[J]. Journal of Chongqing University, 2008, 31(11): 1267-1272. DOI:10.11835/j.issn.1000-582X.2008.11.012 (  0) 0)
|
| [9] |
POWELL G H, ROW D G. Influence of analysis and design assumptions on computed inelastic response of moderately tall frames. Report No. UBC/EERC76/11[R]. Berkeley: University of California, 1976.
(  0) 0)
|
| [10] |
Shome N, Cornell C A. Probabilistic seismic demand of nonlinear structures. Reliability of marine structures report No. RMS-35[R]. Stanford, California: Department of Civil and Environmental Engineering, Stanford University, 1999.
(  0) 0)
|
| [11] |
王亚勇. 关于设计反应谱、时程法和能量方法的探讨[J]. 建筑结构学报, 2000, 21(1): 21-28. WANG Yayong. A review of seismic response spectra, time history analysis and energy method[J]. Journal of building structures, 2000, 21(1): 21-28. DOI:10.3321/j.issn:1000-6869.2000.01.005 (  0) 0)
|
| [12] |
LUCO N, CORNELL C A. Effects of connection fractures on SMRF seismic drift demands[J]. Journal of structural engineering, 2000, 216(1): 127-136. (  0) 0)
|
| [13] |
VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis[J]. Earthquake engineering structure dynamics, 2002, 31(3): 491-514. DOI:10.1002/(ISSN)1096-9845 (  0) 0)
|
| [14] |
RAMAMOORTHY S K, GARDONI P, BRACCI J M. Probabilistic demand models and fragility curves for reinforced concrete frames[J]. Journal of structural engineering, 2006, 132(10): 1563-1572. DOI:10.1061/(ASCE)0733-9445(2006)132:10(1563) (  0) 0)
|
| [15] |
BOX G E P, TIAO G C. Bayesian inference in statistical analysis[M]. Hoboken: John Wiley & Sons, 2011.
(  0) 0)
|
| [16] |
杨成.结构动力分析在基于性能的抗震工程中的应用[D].成都: 西南交通大学, 2010. YANG Cheng. Structural dynamics analysis in performance-based earthquake engineering[D]. Chengdu: Southwest Jiaotong University, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1689229 (  0) 0)
|
| [17] |
中国建筑科学研究院. GB 50011-2010, 建筑抗震设计规范[S].北京: 中国建筑工业出版社, 2010. China Academy of Building Research. GB 50011-2010, Code for seismic design of buildings[S]. Beijing: China Architecture and Building Press, 2010. (  0) 0)
|
| [18] |
WEN Y K, ELLINGWOOD B R, BRACCI J M. Vulnerability functions. Technical Rep. DS-4[R]. Mid-America Earthquake Center, Univ of Illinois at Urbana Champaign, 2004.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


