随着高光谱成像技术及相关数据的不断发展,高光谱图像分类技术已成为遥感领域的研究热点问题[1-2]。相对于其他遥感图像,高光谱图像高维非线性、波段间相关性高以及训练样本标记难以获得等特点,给分类工作带来了巨大的挑战。因此,在已标记样本比较少的情况下,如何快速、准确地对高光谱遥感图像地物目标进行分类日益成为数据挖掘、机器学习和模式识别等领域的热点研究问题之一。针对此类问题,半监督分类[3-4]结合监督学习和无监督学习,同时运用已标记数据的信息和未标记数据的信息来提高分类器泛化性能,能够更好地反映出整个地物目标的样本集合的空间分布,从而使训练得到的分类器具有更好的性能。主动学习[5]也是从未标记样本中选取“有价值”的样本从而提高分类器性能,目前已经广泛应用于遥感图像处理[6-10]。因此,融合主动学习的半监督学习为解决高光谱遥感图像地物分类识别提供了新的研究思路。
1974年,Simon最早提出主动学习概念[11]。在主动学习中,主动学习算法作为构造有效训练集的方法,通过迭代抽样,分类器主动选择包含信息量大的未标记样本,更新训练集,在已标记样本少的前提下提高分类算法的效率。主动学习广泛应用于文本分类、语音识别、图像检索、遥感图像分类等领域。支持向量机是基于统计学习理论的常用的机器学习方法,具有较强的泛化能力,应用广泛。Simon较早地提出了SVMactive算法[12],该算法迭代选取距离超平面最近的样本,这些样本可能改变超平面位置,选取这类样本能够有效地改善分类器性能。主动学习与SVM相结合,能够得到更有价值的训练样本,提高分类性能的同时保持了SVM的泛化性。主动学习算法大致可以分为三类:1)基于边缘采样[13],2)基于后验概率估计,3)基于委员会[14]。主动学习通过特定的启发式选择函数随机选择置信度较低的样本增加了训练集的扰动性,这类样本信息量较高有利于增加基分类器间的差异性。而半监督分类通常选择高置信度的样本并对其标记,更新训练集。主动学习和半监督学习均是最大可能的挖掘有价值的无标记样本,因此利用主动学习和半监督学习的差异互补,可以在增加多分类器差异性的同时又提高学习模型分类精度。大量研究表明,融合主动学习和半监督学习的算法具有更好的鲁棒性和更快的学习能力[15-17]。
如何引入伪标记样本是融合半监督学习和主动学习的一个重要技巧[18]。如果加入了错误的伪标记样本,可能会降低学习模型的泛化能力。大部分的研究工作通过加入伪标记样本弥补带标签样本不足的概况,往往忽视伪标记样本正确性的问题,因而如何获取可信度高的伪标记样本也是一个值得研究的问题。
传统的半监督算法中,无标记训练样本错分带来的错误累积问题非但不会利用好无标记样本信息反而会导致分类器性能下降,针对此类问题进行改进,提出了一种新的融合主动学习和半监督学习的分类算法(semi-supervised and active learning framework based on DE algorithm, SemiALDE),该算法能够提高无标记样本标签的准确性,增强训练集可靠性。对Indian和Pavia高光谱数据集进行实验证明所提算法能够有效提高分类精度。
1 SVM基本理论支持向量机(support vector machine,SVM)是一种典型的监督分类模型,在解决小样本、非线性以及高维模式识别中表现出良好的泛化性能,已成为机器学习领域研究热点。SVM是一种基于结构风险最小化原则的机器学习方法,边缘采样策略(margin sampling, MS)是一种非常适合SVM模型的主动学习方法。SemiALDE算法采用SVM作为学习模型,边缘采样(MS)作为基本采样方法。
支持向量机的基本原理是寻找分类超平面使得两类样本点能够分开,实际上是求解一个凸优化问题。设
| $\min\left\{\frac 1 2{‖\mathit{\boldsymbol{w}}‖}^2+C\sum\limits^ n _{i=1}ξ_i\right\}\\ s.t.\\ y_i[(\mathit{\boldsymbol{w}}·\phi(x_i))+b]≥1-ξ_i\\ ξ_i≥0,i=1,2,\cdots ,n$ | (1) |
式中:
代入拉格朗日函数得到原始问题的对偶问题,求解对偶问题,得到判别函数为
| $f(x)=\text{sgn}\{(\mathit{\boldsymbol{w}}^*·\phi(x_i))+b^*\}=\\ \text{sgn}\{\sum\limits^ n _{i=1}α_i\ ^*y_iK(x_i,x)+b^*\}$ | (2) |
式中:b*可由Kuhn-Tucher定理推得,
| $K(x_i,x)=\text{exp}[-‖x_i-x‖^2/2σ^2]$ | (3) |
对于二分类问题的SVM算法,最优超平面位于两个不同的类的最大Margin中间。越靠近最优超平面的样本点越有可能作为一个支持向量。因此,选择这些样本点更有可能改进当前学习模型,MS算法更适合SVM学习模型。
MS算法可以描述为选择符合以下条件的样本:
| $x^*=\arg \min\limits_{x_i∈U}f(x_i)$ | (4) |
式中:
在SemiALDE算法中,首先利用伪标记技术选择信息量丰富的无标记样本,然后利用DE算法从伪标记样本中选择多样性的样本并对其进行标记,最终加入到有标记样本集中对SVM分类器训练。
在高光谱图像分类中,如何有效地从无标记样本中获取有价值的信息是样本选择的关键。为了尽可能地利用无标记样本信息,SemiALDE算法采取伪标记技术从无标记样本中筛选有价值的伪标记样本来扩充有限的带标记样本集。加入伪标记的优点在于在有标记样本很少的情况下,尽可能构造具有代表性的训练集,伪标记技术利用学习模型自动赋予置信度高的样本伪标记,极大减少了人工标记的成本。然而,伪标记技术比较依赖初始有标记样本的分布,训练样本的空间分布特性会对学习模型产生一定的影响。因此完全依赖伪标记技术筛选无标记样本会造成一定的错误累积。针对半监督学习作为伪标记技术的不足,SemiALDE算法使用DE算法进一步改善伪标记样本的准确度。在众多启发式优化方法中,差分进化是一种基于群体差异的启发式随机搜索算法,并且DE算法原理简单、受控参数少,表现出高可靠性、强鲁棒性和良好的优化性能。DE算法在伪标记策略筛选的基础上进一步筛选最优的伪标记样本,提高了伪标记样本的准确度和多样性,伪标记技术结合DE算法是本文算法的关键。
2.1 伪标记技术SemiALDE算法的关键是伪标记技术,该方法通过结合迭代验证技术改进伪标记的准确性。利用学习模型在迭代过程中的差异性来修正错误的伪标记样本提高伪标记的准确性,从而提升学习模型的学习能力。
主动学习过程中,SVM学习模型利用新加入的伪标记样本迭代改进,经过新一轮的采样,学习模型在改进过程中产生的差异性将会进一步修正伪标记样本集,提高了伪标记样本的可靠性。
半监督学习作为伪标记技术的不足通常体现在两点。1) 从未标记样本中选择伪标记样本的评估准则往往难以给出确定的方案。伪标记样本的数量和阈值选取总是和当前的学习模型密切相关,数量或阈值选取不当可能会导致大量错误标记样本的产生,无法提升算法性能。2) 初始带标记样本的空间分布特性也会对伪标记样本的选取产生影响,难以构造较好的学习模型。
本文采取迭代验证思想获得伪标记样本,首先基于有标记样本集和伪标记样本集来创建分类器h1。然后利用MS采样方法从无标记样本集中选择样本,并对其标记加入到有标记样本集中,更新有标记、无标记样本集。然后基于有标记样本集创建验证分类器h2。用分类器h1和h2给伪标记样本和无标记样本标记。在h1和h2中具有相同标记类别的无标记样本会被加入到伪标记样本集中同时更新伪标记样本集。
2.2 差分进化(DE)算法差分进化(differential evolution algorithm,DE)算法是一种基于群体进化的全局搜索优化算法, 根据父代个体间的差分矢量进行编译、交叉、选择操作探索整个种群空间, 并利用贪婪竞争机制选择下一代个体, 寻求最优解[19]。
设D问题维数,NP为种群规模,G为进化代数,第i个种群向量为
| $X_{i,G}=[x_{1,i,G}\ x_{2,i,G}\ \cdots \cdots\ x_{D,i,G}]\\ i=(1,2,\cdots ,\text{NP})$ | (5) |
1)差分变异:
基本的变异方式DE/rand/1的方程为
| $V_{i,G}=X_{r^i_{1,G}}+F(X_{r^i_{2,G}}-X_{r^i_{3,G}})$ | (6) |
式中:
2)交叉操作:
交叉操作通过随机选择,使得实验向量至少有一位是变异向量
| $u_{j,i,G}=\left\{\begin{align}v_{j,i,G},&\ \ \text{rand}_{i,j}[0,1]\le C_r\\ &\ \ 或者 j=j_\text{rand}\\ x_{j,i,G},&\ \ 其他\end{align}\right.$ | (7) |
式中:
3)选择:
DE采用“贪婪”搜索策略, 根据目标向量和实验向量的适应值选择最优个体为下一代目标:
| $u_{j,i,G}=\left\{\begin{align}U_{i,G}\ \ \text{if}\ f(U_{i,G})\le f(X_{i,G})\\ X_{i,G}\ \ \text{if}\ f(U_{i,G})>f(X_{i,G})\end{align}\right.$ | (8) |
式中
在DE算法中, 种群内个体的差分向量经过缩放后, 与种群内另外的相异个体相加得到变异向量,根据变异向量生成方法的不同, 形成了多种变异策略[20]。SemiALDE算法使用式(6) 的一种改进形式:
| $V_{i,G}=X_{i,G}+F(X_{r^i_{1,G}}-X_{i,G})+λ(X_{r^i_{2,G}}-X_{r^i_{3,G}})$ | (9) |
式中
对于多分类问题,通常对二分类模型的支持向量机进行组合使用,主要有一对多和一对一两种策略,本文通过“one-against-rest”转化为多个二分类问题。
2.3 算法流程给定有标记样本集
1)在有标记样本集
2)利用MS抽样从无标记样本中选择靠近SVM超平面边缘的r个样本并对其标记,组成集合
| $S_R=\{{x_k,y_k}\}^r_{k=1}$ |
3)更新有标记、无标记样本集:
4)利用更新后的有标记样本集训练验证SVM分类器h2;
5)分类器h1、h2分别对新的无标记样本进行标记,记为Label1和Label2;
6)更新伪标记样本,分类器h1、h2分类结果相同的无标记样本计入伪标记样本集:
| $U_p=\{(x_i,\text{Label}_1(x_i))|\text{Label}_1(x_i)=\text{Label}_2(x_i)\}$ |
7)重复步骤1~6直至满足迭代次数,获得最新的伪标记样本
8)利用改进的DE算法从
9)对
10)利用所得分类器开始对测试样本进行标记,测评分类精度。
3 实验数据与分析 3.1 实验数据为验证算法有效性,本文选取两个高光谱图像数据,印第安纳高光谱AVIRIS图像数据和Pavia工程学院高光谱数据,从中选取8个主要类别参与实验。两个数据集的地物图如图 1所示,图像大小均设为144×144,其中,印第安纳高光谱AVIRIS图像参与处理的图像波段数为200个,Pavia工程学院原始数据集包含125个波段,去除噪声后,参与实验的波段数为103。
|
图 1 监督信息图 Fig.1 Supervised information map |
本实验的仿真条件:电脑处理器为Intel(R)Core(TM)i3-2310M,6G的RAM,电脑系统为64位windows8操作系统,仿真软件为Matlab2015b。
评价准则:总体分类精度(overall accuracy, OA),平均分类精度(average accuracy, AA),Kappa系数。
设N是样本总数,m为类别数,mii是i类正确分类的样本数,Ai为第i类的分类精度。
总体分类精度OA为
| $\text{OA}=\frac 1 N\sum\limits^ n _{i=1}m_{ii}$ | (10) |
第i类分类精度Ai:
| $A_i=\frac{m_{ii}} {N_i}$ | (11) |
平均分类精度AA:
| $\text{AA}=\frac 1 N\sum\limits^ n _{i=1}A_i$ | (12) |
Kappa系数:
| $\text{Kappa}=\frac{N×\sum\limits^ n _{i=1}m_{ii}-\sum\limits^ n _{i=1}N_i×m_{ii}} {N^2-\sum\limits^ n _{i=1}N_i×m_{ii}}$ | (13) |
在实验中,伪标记部分迭代次数N设为5,差分进化算法的参数为
通过实验对比标准SVM、SVM_MS、所提算法三种分类算法的优劣。实验随机选取10%为训练样本,剩下的是测试样本。首先对印第安纳高光谱图像进行分类,表 1给出了平均分类精度(AA),总体分类精度(OA)、Kappa系数以及运行时间,从中可以看出SVM_MS算法的分类性能明显好于SVM,AA提高了5.16%,OA提高了6.52%,Kappa提高了0.069 9。对比SVM_MS算法,SemiALDE算法分类性能明显提升了,AA提高了1.87%,OA提高了1.97%,Kappa提高了0.028。SemiALDE算法通过融合主动学习半监督分类,产生富含信息且置信度较高的伪标记样本,DE算法又对其择优选出最优样本引入训练样本集,明显提高了分类精度。从时间上分析,本文算法的运行效率较低,算法采用迭代的方式选择训练样本造成一定的时间消耗。图 2为三种算法分类结果的灰度图表示,可以直观的观察到图 2(c)的错分样本数量明显少于图 2(a)和图 2(b),由图可知SemiALDE算法可以有效提高高光谱图像的分类精度。
| 表 1 印第安纳高光谱图像分类结果 Tab.1 Classification results for the AVIRIS data of Indian Pine |

|
图 2 印第安纳高光谱图像三种方法的分类结果图 Fig.2 Classification maps for the AVIRIS data of Indian Pine obtained by SVM, SVM_MS, SemiALDE |
对Pavia高光谱图像进行相同的实验,同样选取10%作为训练样本,剩余的为测试样本。表 2列出了标准SVM、SVM_MS和SemiALDE算法的仿真结果,从表 2可以看出SVM_MS算法的AA比SVM提高了1.94%,OA提高了0.29%,Kappa提高了0.0337。而所提出的SemiALDE算法比SVM_MS算法的分类结果有进一步的提高,其中AA、OA和Kappa分别提高1.19%,0.49%和0.017。针对Pavia数据集的实验结果,本文算法的时间消耗较大。标准SVM、SVM_MS和SemiALDE算法的仿真结果灰度图如图 3所示,图 3(c)所示的SemiALDE算法表现了明显的优越性。
| 表 2 Pavia工程学院高光谱图像分类结果 Tab.2 Classification results for the data of University of Pavia |

|
图 3 Pavia工程学院高光谱图像三种方法的分类结果图 Fig.3 Classification maps for the data of University of Pavia obtained by SVM, SVM_MS, SemiALDE |
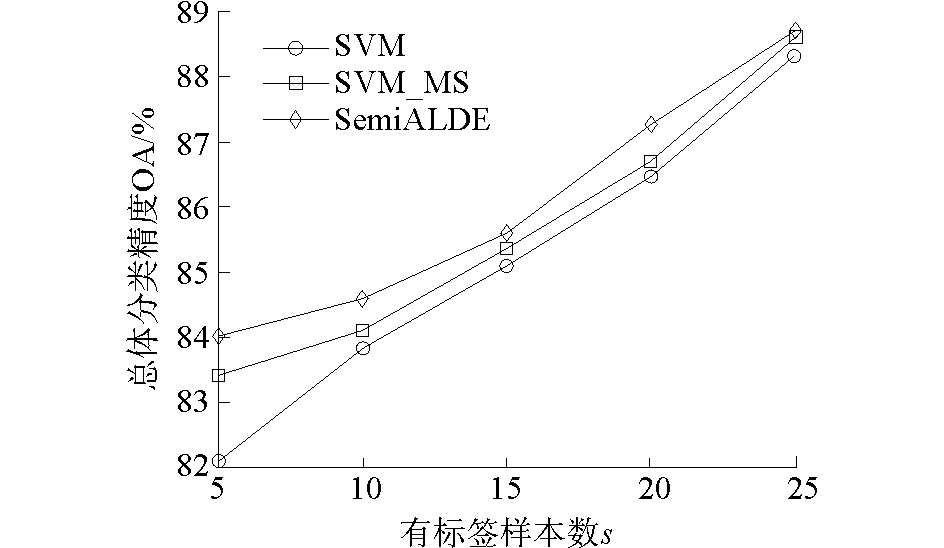
此外图 4、图 5分别展示了两个数据集带标签样本数目s与总体分类精度(OA)的关系曲线,带标签样本数目s分别取5、10、15、20、25、30。由曲线图可以看出,SemiALDE算法优于SVM和SVM_MS算法。在样本数目很少的情况下,SemiALDE算法加入新的伪标记样本扩充训练样本集,带来的优势更为明显。

|
图 4 带标签样本数s与OA的关系曲线印第安纳高光谱图像 Fig.4 Influence of s on the overall accuracy (OA) for the AVIRIS data of Indian Pine |
|
图 5 带标签样本数s与OA的关系曲线Pavia工程学院高光谱图像 Fig.5 Influence of s on the overall accuracy (OA) for the data of University of Pavia |
本文利用融合半监督学习的主动学习思想,提出了一种新的半监督算法(SemiALDE)。不同于其他传统的分类算法,SemiALDE算法优势体现在两个方面:
1)融合主动学习算法、半监督分类模型协同筛选富含信息量且置信度较高的样本;
2)伪标记技术结合DE算法构造具有差异性的训练样本集。综述过往研究可知,标记样本的可靠性及噪声问题是影响半监督学习性能的关键因素,错误的标记样本会使学习机性能显著下降,这里SemiALDE算法将伪标记策略与DE算法相结合,有效地减少错误标记样本对学习过程产生的不良影响。
为证明本章算法的有效性,对两个高光谱数据集分别进行了仿真实验,实验结果表明,SemiALDE算法的分类精度和Kappa系数都有明显提高。尤其是在带标记样本少的情况下,SemiALDE算法能够高效地选取准确性较高、具有代表性的样本扩充带标签样本,有效地提升了主动学习选择样本的效率和学习模型的性能,与标准SVM_MS算法相比具有明显的优势。研究表明,伪标记技术比较依赖初始有标记样本的分布,训练样本的空间分布特性会对学习模型产生一定的影响。
今后的研究工作将关注伪标记样本与标记样本分布性问题,提高伪标记样本对小样本学习性能的改善效果。另外,本文算法的复杂度较高,时间消耗较大,减少样本筛选环节的复杂度也是今后研究工作的重点。
| [1] |
MATHER P M, KOCH M. Computer processing of remotely-sensed images:an intruction[M]. New York: John Wiley & Sons, 2011: 229-285.
( 0) 0)
|
| [2] |
SHAHSHAHANI B M, LANGGREDE D A. The effect of unlabeled samples in reducing the small sample size problem and mitigating the hughes phenomenon[J]. IEEE transactions on geoscience and remote sensing, 1994, 32(5): 1087-1095. DOI:10.1109/36.312897 ( 0) 0)
|
| [3] |
MILLER D J, UYAR H S. A mixture of experts classifier with learning based on both labeled and unlabeled data[J]. Journals of processing systems, 1997, 12(9): 571-577. ( 0) 0)
|
| [4] |
CHAPELLE O, ZENT A. Semi-supervised classification by low density separation[C]//Proceeding of the tenth international workshop on artificial intelligence and statistics, Barbados, 2005:57-64.
( 0) 0)
|
| [5] |
SETTLES B. Active learning literature survey[J]. University of Wisconsin Madison, 2010, 39(2): 127-131. ( 0) 0)
|
| [6] |
CAMPBELL N, CRISTIANINI A S. Query learning with large margin classifiers[C]//Proc 17th ICML, 2000:111-118.
( 0) 0)
|
| [7] |
SCHOHN D A C. Less is more:active learning with support vector machines[C]//In Proc 17th ICML, 2000:839-846.
( 0) 0)
|
| [8] |
LUO T, KRAMER K, GOLDGOF D B, et al. Active learning to recognize multiple types of plankton[C]//J Mach Learn Res, [S.l.], 2005:589-613.
( 0) 0)
|
| [9] |
MITRA P, SHANKAR B U, PAL S K. Segmentation of multispectral remote sensing images using active support vector machines[J]. Pattern recognition letters, 2004, 25(9): 1067-1074. DOI:10.1016/j.patrec.2004.03.004 ( 0) 0)
|
| [10] |
XU Z, YU K, TRESP V, et al. Representative sampling for text classification using support vector machines[C]//Proc 25th Eur Conf Inf Retrieval Res, [S.l.], 2003:393-407.
( 0) 0)
|
| [11] |
SIMON H A, LEA G. Problem solving and rule education:A unified view knowledge and organization[J]. Erbuam, 1974, 15(2): 63-73. ( 0) 0)
|
| [12] |
SIMON T. Active learning:theory and application[M]. Stanford University, 2001: 24-31.
( 0) 0)
|
| [13] |
SCHOHN G, COHN D. Less is more:active learning with support vectors machines[C]//Proc 17th ICML, Stanford, 2000:839-846.
( 0) 0)
|
| [14] |
FREUND Y, SEUNG H S, SHAMIR E, et al. Selective sampling using the query by committee algorithm[J]. Machine learning, 1997, 28(2/3): 133-168. DOI:10.1023/A:1007330508534 ( 0) 0)
|
| [15] |
MING Li, ZHANG Hongyu, WU Rongxin, et al. Sample based software defect prediction with active and semi-supervised learning[J]. Automated software engineering, 2012, 19(2): 201-230. DOI:10.1007/s10515-011-0092-1 ( 0) 0)
|
| [16] |
DING Ni, MA Hongbing. Active learning for hyperspectral image classification using sparse code histogram and graph-based spatial refinement[J]. International journal of remote sensing, 2017(3). ( 0) 0)
|
| [17] |
JUN Xu, HANG Renlong, LIU Qingshan. Patch-based active learning (PTAL) for spectral-spatial classification on hyperspectral data[J]. International journal of remote sensing, 2014, 35(5): 1846-1875. DOI:10.1080/01431161.2013.879349 ( 0) 0)
|
| [18] |
LI M, WANG R, TANG K.Combining semi-supervised and active learning for hyperspectral image classification[C]//Proceedings of Computational Intelligence and Data Mining(CIDM).[S.l.], 2013.
( 0) 0)
|
| [19] |
STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 ( 0) 0)
|
| [20] |
BREST J, MAU EC M S. Population size reduction for the differential evolution algorithm[J]. Applied intelligence, 2008, 29(3): 228-247. DOI:10.1007/s10489-007-0091-x ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


