2. 中国通信服务杭州公司, 浙江 杭州 310050;
3. 浙江工业大学 艺术学院, 浙江 杭州 310023
2. China Comservice Hangzhou Construction Co., Ltd., Hangzhou 310050, China;
3. College of Art, Zhejiang University of Technology, Hangzhou 310023, China
室内定位是实现基于位置服务的关键技术之一,已经受到越来越多的理论研究和工程应用关注。GPS[1]在室外环境中获得了广泛应用,但其信号无法穿过厚重的水泥墙,而且室内环境要比室外复杂的多,因此GPS不适合应用于室内定位。目前几种主要的室内定位技术包括红外线、超宽带(ultra-wide band, UWB)、射频识别(radio frequency identification, RFID)和超声波等,大部分都要求主动定位和性价比低等缺点。随着无线局域网(wireless local area network, WLAN)[2]的发展,无线热点已经广泛部署于各种室内场合,如学校、医院、餐厅、超市等。如果能有效利用这些现有的设备实现室内定位,将大大降低系统成本;同时随着无线局域网传输速率的不断提高,如未来的802.11ac将具有更高的工作频带,这为进一步精确的室内定位提供了可能性。
目前已经出现了一些基于WLAN的室内定位方案。根据被定位目标是否携带有源设备参与到定位过程,可以将基于WLAN的定位方法分成有源和无源两种[3]。在很多情况下,目标不一定会携带定位设备,一个典型的场景就是应用在安防领域的入侵检测。在这种情况下,入侵者并不希望自己的位置被检测到。传统无源定位利用的是RSSI(received signal strength indicator),该物理量是多条路径信号的强度叠加。一种典型的利用RSSI实现无源定位的方法是指纹库方法[4]。与传统的强度-距离模型不同,指纹库在训练阶段建立不同位置的不同RSSI模式,在测试阶段则与库中RSSI的相似度进行位置匹配。RSSI强度易于获得,但由于室内普遍存在着多径效应使得基于RSSI的定位方法存在波动性大且不够稳定的缺点[5]。
虽然基于RSSI仍然是WLAN定位的主流技术之一,但已经出现了一些利用物理层更稳定的信道状态信息(channel state information, CSI)来进行定位的研究。特别是近几年随着CSI的获取更加容易[6],对CSI的研究也越来越多[7]。在所采用的定位算法方面,Li B等利用概率方法即贝叶斯公式[8]实现了定位,但其物理量仍然是RSSI,具有进一步改进的空间。文献[9]中引入了CSI和RSSI并利用贝叶斯算法进行滤波处理,提高了不同房间位置的分类效果。然而,总体上说该方法在精度上仍然有很大的改进空间。
本文针对无源室内定位,提出了一种将信道状态信息和朴素贝叶斯分类结合的定位算法,同时引入了置信度方法,从而进一步提高了室内定位中位置分类的正确率。
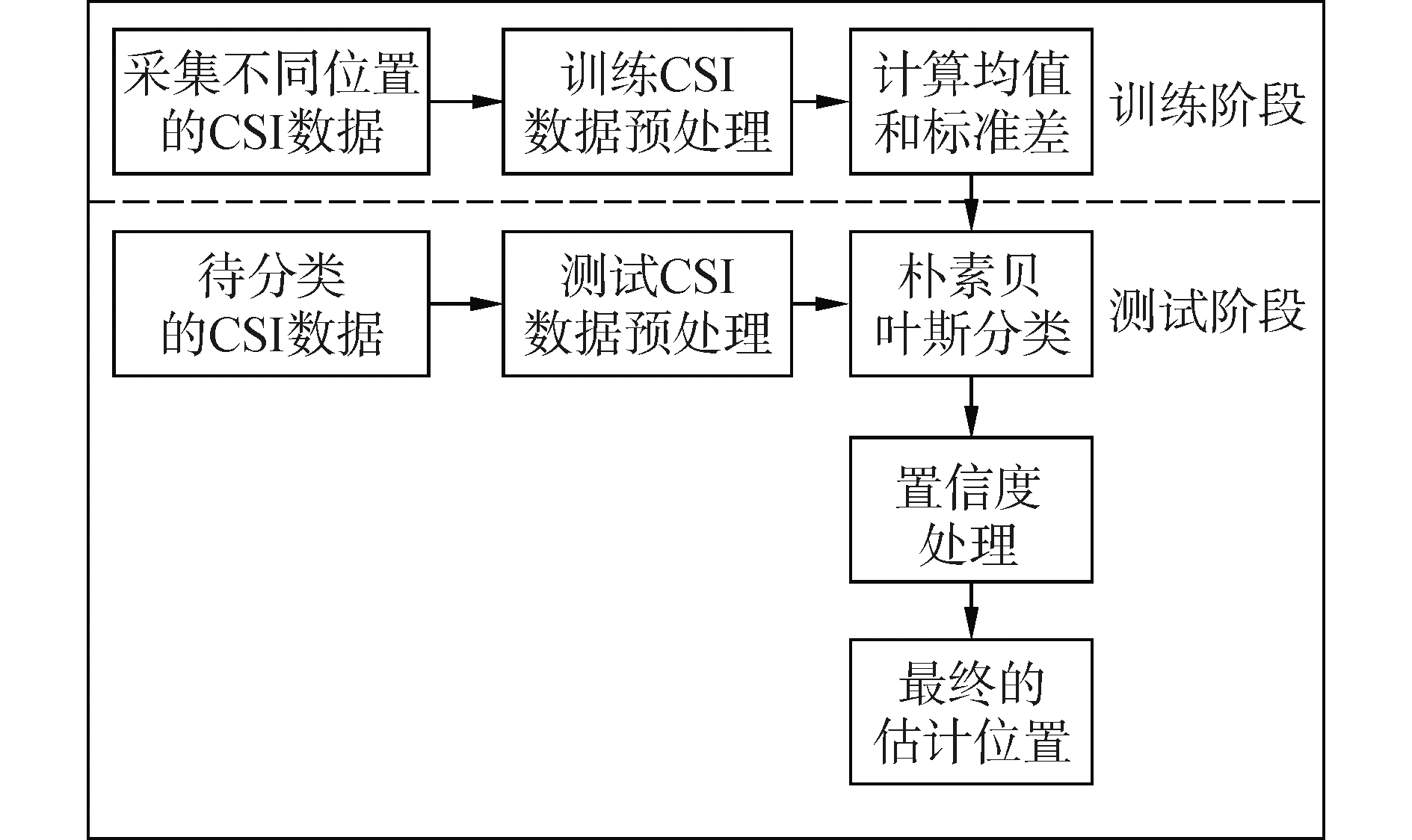
1 无源室内定位系统结构本文实现方法的总体结构如图 1所示。
|
图 1 总体结构框图 Fig.1 Overall structure diagram |
系统首先基于不同的训练位置采集了该位置的信道状态信息数据。在训练阶段,系统采集每根天线对上的子载波数据作为一个样本特征,并进行数据异常值去除和归一化处理。通过对每个位置的所有训练样本求出平均值和标准差,作为该位置的一个指纹。在测试阶段,系统利用朴素贝叶斯方法对数据进行指纹比对和位置分类。同时,为了进一步提高分类准确率,系统还引入了置信度指标,综合不同天线对上的分类结果并通过置信度进行联合判断,从而得到最终的估计位置。
2 信道状态信息及朴素贝叶斯分类方法 2.1 信道状态信息传统基于WLAN的无源定位方法主要是基于RSSI,但RSSI存在信号不够稳定、可靠性差和定位精度低等不足。信道状态信息可以有效克服RSSI这些缺点,通过更细粒度的信道分布感知和采集物理层信息来实现室内定位。
在一个典型的室内环境中,发送信号经过多条路径到达接收端,每条路径都会引入不同的时延、幅度衰减和相移。为了区分每条不同的路径,可以将无线信道建模为空间线性滤波器,从而得到信道冲激响应(channel impulsive response, CIR):
| $h(τ)=\sum\limits^ N _{i=1}|a_i|\text{exp}(-\text jθ_i)δ(τ-τ_i)$ | (1) |
式中:
进一步的,通过FFT将CIR转换到频域,得到信道频率响应(channel frequency response, CFR):
| $H(f)=\text{FFT}[h(τ)]$ | (2) |
目前WLAN的协议,如802.11n等都将正交频分复用(orthogonal frequency division multiplexing, OFDM)技术和多入多出(multiple-input multiple-output, MIMO)[10]技术作为其标准技术。这两种技术在CSI数据形成中起到了重要作用。
OFDM对信道频率响应以一定的频率间隔进行抽样,得到抽样后的信道频率响应为
| $H(f)=[H(f_1),H(f_2),\cdots,H(f_K)]$ | (3) |
式中:
MIMO技术则实现了信号的分集发送与接收。假设发送天线数为T,接收天线数为R,则最多可得到T×R条链路。如果通过提取每条链路上的CSI数据进行分析,每个样本可得到T×R×30个子载波,其中30为子载波数。
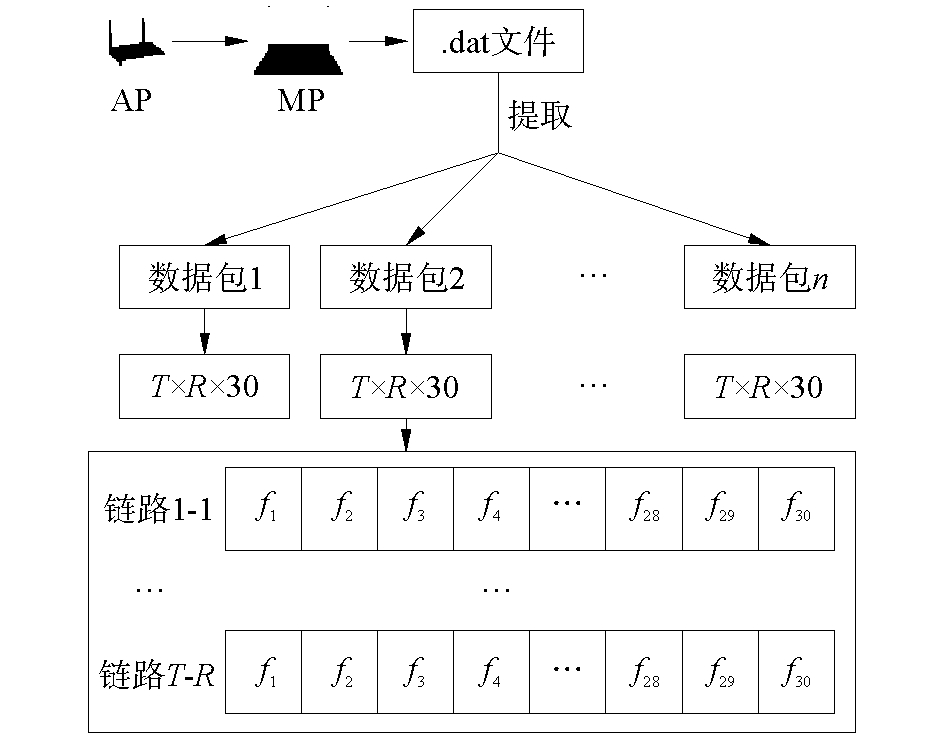
在实际测量中,CSI数据的采集过程和数据格式如图 2所示。监控点(monitor point, MP)接收从接入点(access point, AP)发来的数据包分组,同时将信道状态信息数据记录到一个dat文件中。dat文件中的数据由多个数据包构成,而每个数据包又由T×R个包含30个子载波的CSI数据组成。
|
图 2 CSI数据格式 Fig.2 Format of CSI data |
无源室内定位实现的关键在于:室内人员处于不同位置时会引起环境的不同变化,并对无线信号的信道状态产生不同影响。因此,有效定位所采用的物理量需要满足以下两个条件:1)在同一个位置具有稳定性;2)在不同位置具有一定的区分度。
为验证以上两个条件,实验首先在真实的场景中进行了3次CSI数据采集。第1次,人体静止于室内某个点,采集到数据样本1;第2次,间隔一段时间后,再次采集人体位于该点时的CSI,得到样本2;第3次,人体静止于室内另一个位置得到样本3。
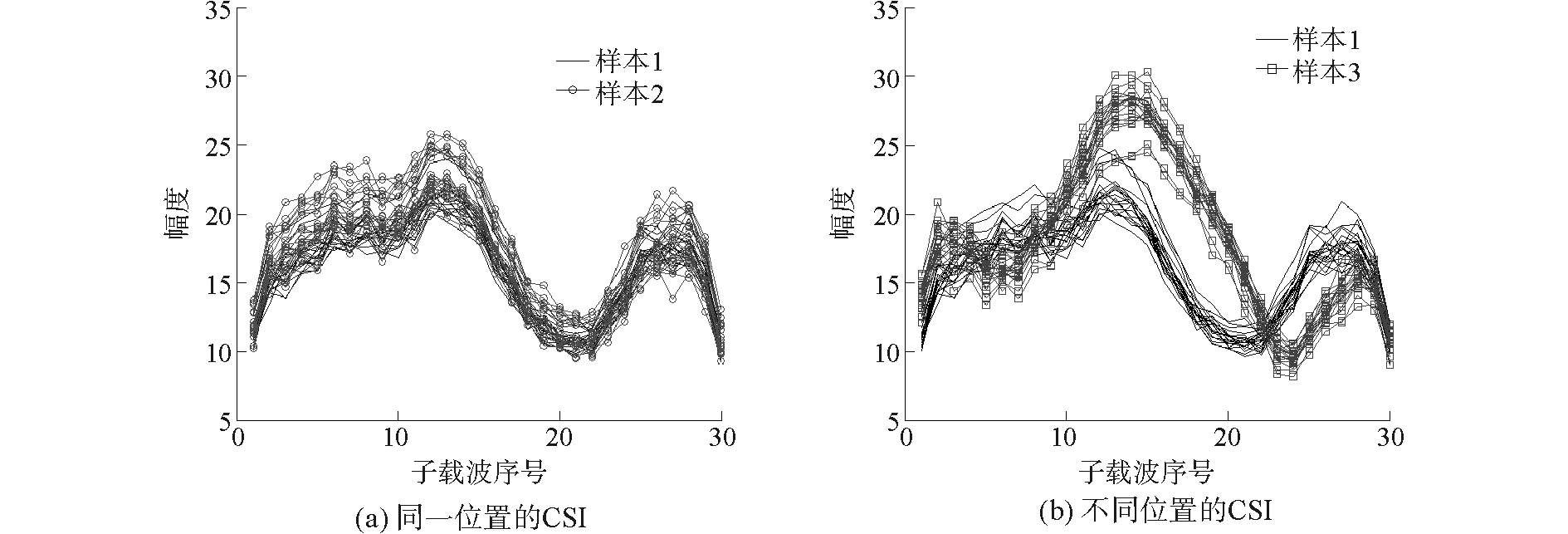
图 3分别为人体位于同一个位置(数据样本1和数据样本2)和位于不同位置(数据样本1和数据样本3)时采集到的CSI幅度,统一选取天线链路1-1来进行说明。其中横坐标表示1~30个子载波序列,纵坐标表示CSI幅度值。需要说明的是,由于CSI幅度是一个相对值,因此这里的信号幅度没有单位。
|
图 3 同一位置的CSI和不同位置的CSI Fig.3 CSI from the same and different location |
可以看到图 3(a)两次数据的曲线基本上重合,说明人体位于同一个位置时信道状态的特征是非常类似的,因此具有稳定性;图 3(b)表示两个位置采集到的CSI数据,具有一定的区分度,可以分辨出两个位置。
满足条件1)、2),意味着信道状态信息可以通过人体位于每个位置时产生的不同信号特征来表征这个位置,并能与其他的位置进行区分,相当于一条“信号特征-位置”的指纹,从而可以实现对室内目标的无源定位。
2.2 CSI数据预处理在对CSI数据进行朴素贝叶斯分类前,需要对其进行预处理。训练数据的预处理主要包括异常值处理和归一化两部分。
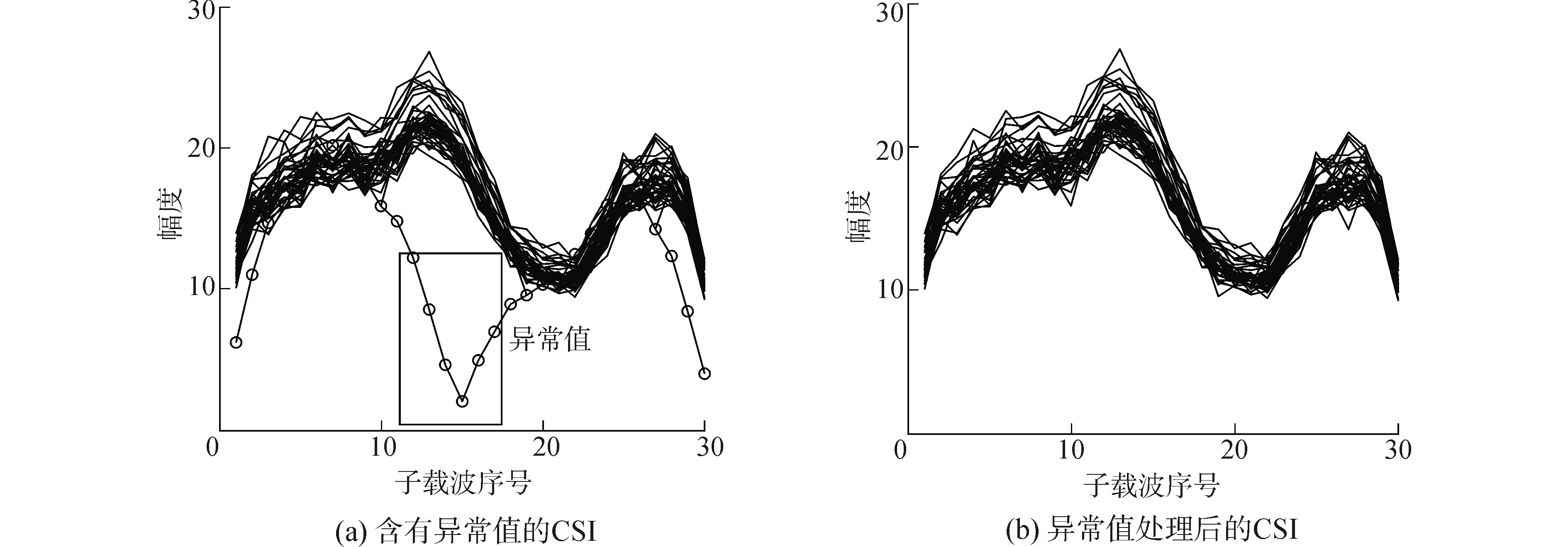
异常值是指明显偏离平均值的CSI幅度值。如图 4(a)所示,在第15号子载波上,某个样本的幅度出现了明显的不同,因此可判断为一个异常值。异常值的存在仅仅是对于数量来讲。在室内环境中,往往会出现多个比较强的多径,其表现为CSI幅度也会呈现出多个“簇”。图 4(a)中的“异常值”极有可能是另一条多径形成的簇。在实验环境中,发现大部分位置的分组集中在一个簇中,而另一簇的分组数量较少,因此在实际应用中将这一部分的数据视为异常值。
|
图 4 异常值和异常值处理后的CSI Fig.4 Abnormal value and CSI after processed |
本文采用了拉依达方法检测异常值并将异常值代替为样本的均值。拉依达方法通过将某个数据与同一特征的均值进行比较,若差值大于3倍的标准差,则判断该值为异常值。异常值处理过程的伪代码如下:
输入:原始数据
1 for each feature
2 for each sample
3 if
4
5 end if
6 end for
7 end for
输出:去除异常值后的数据X
其中,
数据预处理的第二部分是归一化。归一化是指将每一维度的数据转换到0~1的范围内,这可以有效防止某些取值过大的特征对其他特征产生影响,使得特征间更具有可比性。采用如下方法对数据进行归一化:
| $X_\text{new}=(X_\text{old}-X_{\min})/(X_{\max}-X_{\min})$ | (4) |
式中:
另外,值得注意的是,通常训练阶段的样本数远多于测试阶段的样本数。当样本数较少时,去除异常值的方法可能会失效。因此测试阶段的数据预处理仅进行归一化即可。
2.3 朴素贝叶斯分类利用CSI进行无源室内定位最终可以归结为分类的问题。本文采用了机器学习中一个经典的分类算法——朴素贝叶斯分类[11]。朴素贝叶斯分类的理论基础是贝叶斯公式:
| $P(A|B)=\frac{P(B|A)·P(A)} {P(B)}$ | (5) |
式中:P(A)表示事件A发生的概率,P(B)表示事件B发生的概率,P(A|B)表示事件B发生的情况下,A发生的概率,P(B|A)表示事件A发生的情况下,B发生的概率。
朴素贝叶斯分类的核心思想是:对于一个待分类项,通过计算该项出现的条件下各个分类出现的概率,并选取概率最大的类别作为待分类项的类别。朴素贝叶斯分类需要基于两个假设:1)特征之间相互独立;2)每个特征同等重要。
本文采用的朴素贝叶斯分类过程可以概括如下:
1)待分类项:
| $x=\{f_1,f_2,\cdots,f_m\}$ | (6) |
式中
2)类别集合:
| $C=\{L_1,L_2,\cdots,L_n\}$ | (7) |
式中
3)计算待分类数据在各个位置类别下出现的概率:
| $P(L_i|x),i=1,2,\cdots ,n$ | (8) |
4)选择概率最大的所在类为待分类数据的类
| $P(L_k|x)=\max\{P(L_i|x)\}\Rightarrow x∈L_k$ | (9) |
根据贝叶斯公式,式(9)可化为
| $\max(P(L_i|f))=\max \left(\frac{P(f|L_i)·P(L_i)} {P(f)}\right)$ | (10) |
这里假设所有位置都是等概率出现的,则有
| $P(L_i)=\frac{1} {n}$ | (11) |
而
| $\max(P(f|L_i))$ | (12) |
根据特征之间相互独立的假设,得到
| $P(f|L_i)=P(f_1|L_i)·P(f_2|L_i)\cdots P(f_m|L_i)$ | (13) |
当特征值不是离散值时,式(13) 需建模为高斯分布:
| $P(f_j|L_i)=\frac{1} {\sqrt{2π}D_i}\text{exp} \left(\frac{-(f_j-M_i)^2} {2D_i^2}\right)$ | (14) |
式中:
根据上面的推导,不难发现要实现朴素贝叶斯分类,需要求出每个位置类别的均值和标准差,这一过程可视为朴素贝叶斯分类的训练过程。
与其他分类算法相似的是,确定数据的特征值是算法中非常重要的环节。本文将每个子载波的幅度作为分类的特征值,即式(6) 中的每个特征对应着一个子载波幅度。
3 置信度方法为了进一步提高位置估计的正确度,本文提出了置信度的方法。
3.1 置信度的定义假设待分类的测试数据为
| $S=\{s_1,s_2,\cdots ,s_p\}$ | (15) |
式中:记
| $L_j=\text{Bayes}(M,D,s_j),j=1,2,\cdots ,p$ | (16) |
式中:
| $\text{belief}=\frac{\text{count}(\text{mode}(L_j))}{p}$ | (17) |
式中:mode(Lj)表示所有分类结果中出现次数最多的分类位置,而count(mode(Lj))表示该位置的出现次数,p代表该测试数据中总的样本数。举例说明如下,如测试数据中有20个样本,判断为位置1的有15个,剩余5个样本判断为其他位置。这样,得到出现次数最多的分类为位置1,其出现的次数为15次,又因为样本总数为20个,得到置信度15/20=0.75。
3.2 利用置信度来提高分类的正确率不同天线对上的位置分类结果有以下几种情况,如表 1所示。
| 表 1 天线对分类结果 Tab.1 Classification Results |
单纯选择某对天线对的分类结果会使另一对天线对上的信息丢失,需要尽可能利用每对天线对上的分类结果,做出更加可靠的分类结果。
置信度正是为了用于衡量分类的可信度而提出的。当可信度低于一定水平时,分类结果的可靠性就比较低。需要综合其他天线对的分类结果进行判断。具体而言,利用置信度来提高分类准确度的过程为:通过对某个位置CSI数据中的所有测试样本进行朴素贝叶斯分类后,得到估计的位置和置信度,而最终位置为置信度最大的天线对所对应的估计位置。
4 实验设计 4.1 实验平台实验平台主要分成接入点(AP)和监控点(MP)两部分。AP使用普通的无线路由器,型号为TP-LINK WR842 N,其有两根天线。MP为安装了Intel 5300无线网卡的Compaq笔记本,其操作系统为Ubuntu 10.04 LTS。
根据AP和MP的天线数,理论上最多可以产生2×3=6条天线对链路,但在实际中MP仅有2条天线接入,因此最多的链路数为4。此外,由于受到环境波动、设备工作状态等因素影响,能够稳定提取到的链路数在2~4。为避免数据格式不一致对算法造成的影响,本文选取了天线对1-1和1-2进行研究。
在数据采集时,人体静止于房间内某个位置,MP接收来自AP的数据包,并从中提取出CSI数据。CSI数据中包含了人体的位置信息。
4.2 实验环境及参数设置选择两种不同的室内环境进行实验。第一种环境是在实验室中,如图 5(a),这种环境相对具有较多的多径。第二种环境是在一个相对空旷的教室里,如图 5(b),对应于受到多径效应较少的环境。

|
图 5 实验环境 Fig.5 Experiment environment |
如图 6(a)所示的环境1中,房间大小为7.2 m×7.2 m,选取19个数据采集点;如图 6(b)所示的环境2中,房间大小为5 m×15 m,数据点数量为30个且均匀分布于测试区域中。在两种环境中,位置点之间的距离均在1~1.2 m,每个点的采集时间均为80 s。AP高度为20 cm,MP高度为38 cm。在每个采集点,人体的朝向与姿势保持一致。另外,为了证明本文方法同样适用于环境中没有目标的情况,本文增加了对室内无人时的CSI数据采集,并同样将其视为一个位置分类。

|
图 6 数据采集点分布 Fig.6 Distribution of data collecting points |
对于每个点采集到的CSI数据,选取其中的20个分组用于对算法的性能进行测试,其余分组则用于算法训练。
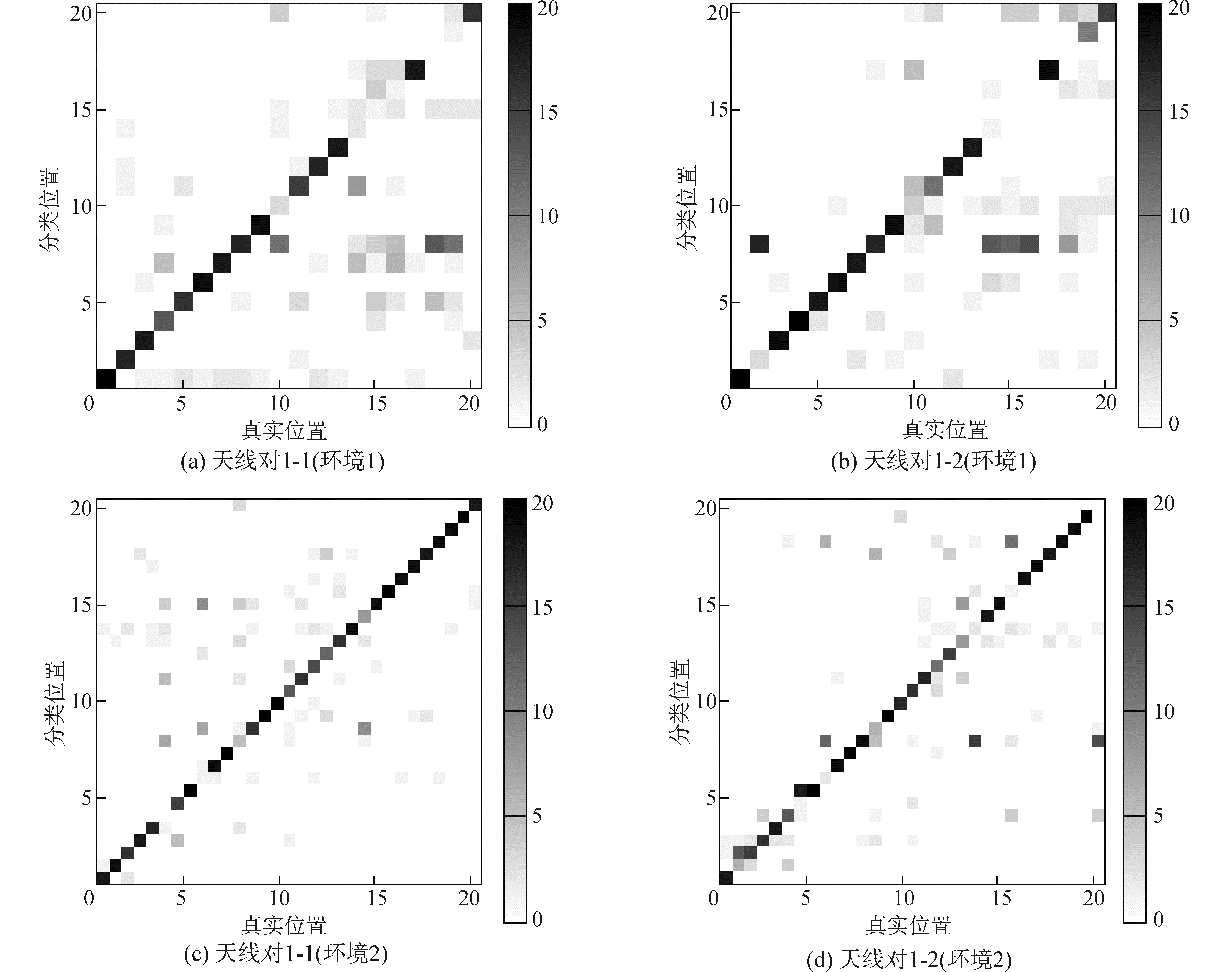
5 实验结果 5.1 朴素贝叶斯算法的性能利用朴素贝叶斯方法对位置进行分类,实验选取两种环境下的1-1和1-2天线对数据,同时将无人环境的数据分别记为第20个位置和第31个位置。记录每个位置20次测试分组的分类结果,画出其混淆矩阵,如图 7所示,其中,颜色条表示分类效果,颜色越深表明分类效果越好。每个色块的颜色深浅表示该位置分类到某个位置的数量。对角线的颜色越深,表明该位置的分类效果越好。
|
图 7 贝叶斯分类效果 Fig.7 Performance of naive Bayes |
总体来看,大部分的结果集中于对角线上,即获得了正确的位置分类。图 7(a)和(b)中的位置14和位置16、位置19等,由于处于室内的墙角,人体位于这些位置时对环境造成的影响较小,因此分类效果变差。图 7(c)和(d)是环境2下的分类效果。环境2由于受到较少的多径效应,其总体分类效果比环境1好。同时,位置20和位置31,即无人环境时,也得到了较好的分类效果,这说明本文方法同样适用于环境中没有目标的情况。
另外,还可以发现,同一环境下的同一个位置,不同的天线对上的分类效果是存在差异的,如环境1中的位置2、环境2的位置24等,虽然其中的一对天线对分类效果较差,但另一对则可能获得较好的分类效果。
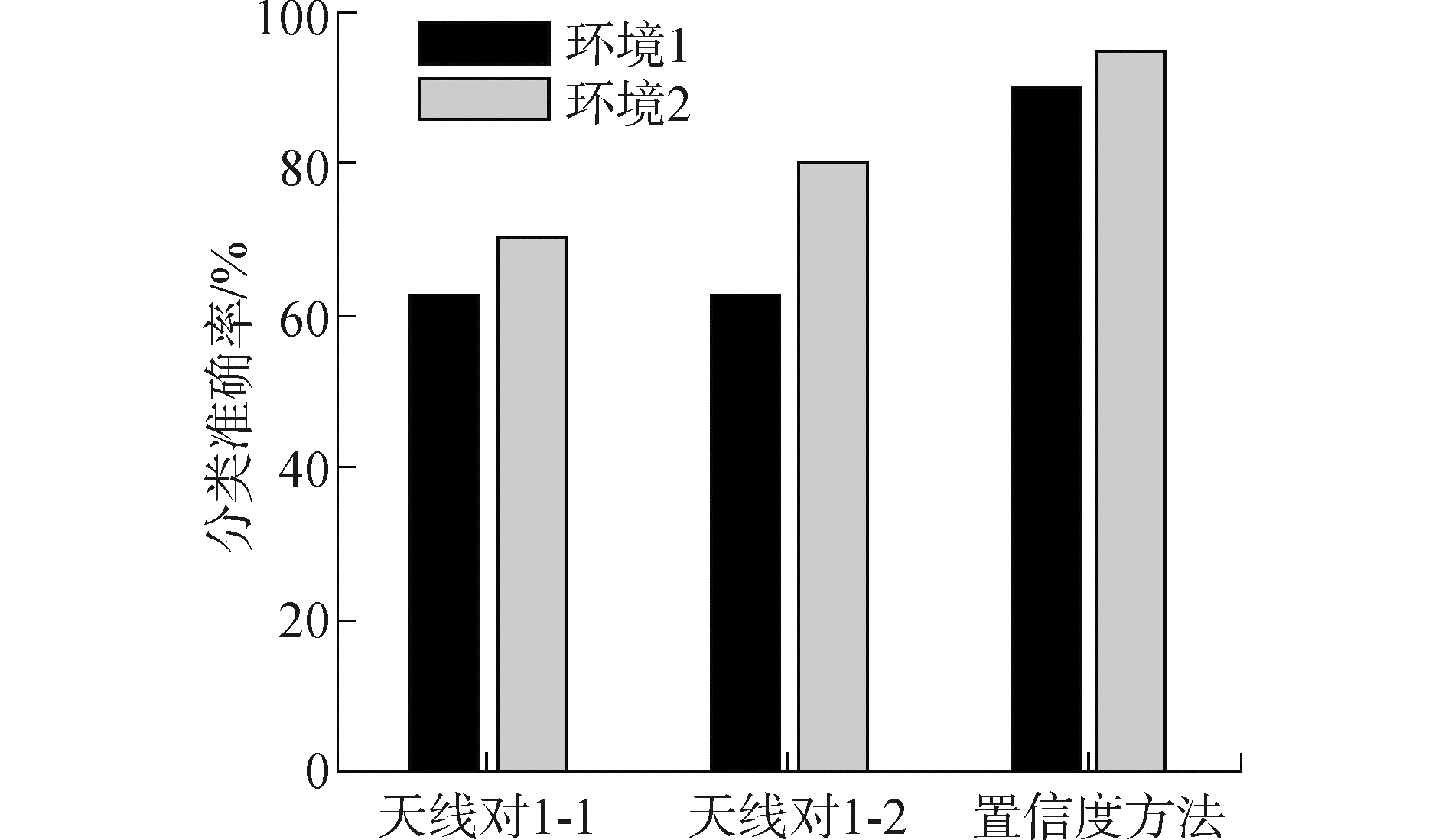
5.2 置信度方法的性能在5.1节的基础上,引入了置信度的方法,观察置信度方法对性能的影响。图 8为两种环境下不同方法的分类正确率。分别用朴素贝叶斯方法对天线对1-1和1-2进行位置分类,并与置信度方法进行比较。
|
图 8 置信度方法的性能 Fig.8 Performance of the confidence method |
从图 8中可以看到,环境1中两对天线对的性能非常接近,正确率都在62.5%;而在环境2中,天线对1-1的性能比1-2好10%左右。由于受到较少的多径干扰,环境2的分类正确率要比环境1高。在采用置信度的方法后,在两种环境下的定位准确率都比单纯采用朴素贝叶斯得到了提升。本文提出的置信度方法利用了不同天线对上的信息,起到了分集的作用,最终的分类正确率在90%以上。
6 结论1)利用了普通笔记本和Intel 5300网卡不需要其他的特殊设备实现了室内人体无源定位。在准确率和稳定性方面相比传统的方法具有较大的优势,同时系统实现的成本较低,有利于普及;
2)将信道状态信息与机器学习中的朴素贝叶斯分类方法结合来完成室内定位方案。实验结果表明,本文方法具有较高的准确率;
3)引入了置信度的指标,综合多条天线对的结果,进一步提高了分类准确度。置信度方法可在原来基础上提升20%左右的性能,对定位精度具有较大改善。
本文方法在某些方面仍然具有改进空间,如增
加可用天线链路的数量等。针对多目标及运动目标定位等更复杂的情况则需要进一步的深入研究,本文的无人环境和静止单目标定位工作可为以后深入研究提供技术基础。
| [1] |
徐定杰, 吕东泽, 沈锋. GPS辐射源的无源雷达两级干扰抑制方法[J]. 哈尔滨工程大学学报, 2012, 33(3): 336-341. XU Dingjie, LYU Dongze, SHEN Feng. A two-stage disturbance cancellation method for GPS based passive radar[J]. Journal of Harbin Engineering University, 2012, 33(3): 336-341. (  0) 0)
|
| [2] |
CROW B P, WIDJAJA I, KIM J G, et al. IEEE 802.11 wireless local area networks[J]. IEEE communications magazine, 1997, 35(9): 116-126. DOI:10.1109/35.620533 ( 0) 0)
|
| [3] |
LI Z, BRAUN T, DIMITROVA D C. A passive WiFisource localization system based on fine-grained power based trilateration.[C]//World of Wireless, Mobile and Multimedia Networks, 2015:1-9.
( 0) 0)
|
| [4] |
LIU H, DARABI H, BANERJEE P, et al. Survey of wireless indoor positioning techniques and systems[J]. IEEE transactions on systems man & cybernetics part C, 2007, 37(6): 1067-1080. ( 0) 0)
|
| [5] |
ELNAHRAWY E, LI X, MARTIN R P. The limits of localization using signal strength:a comparative study[C]//IEEE Secon First IEEE Communications Society Conference on Sensor & Ad Hoc Communications & Networks, 2004:406-414.
( 0) 0)
|
| [6] |
HALPERIN D, HU W, SHETH A, et al. Predictable 802.11packet delivery from wireless channel measurements[J]. ACM sigcomm computer communication review, 2010, 40(4): 159-170. DOI:10.1145/1851275 ( 0) 0)
|
| [7] |
ZHOU Z, YANG Z, WU C, et al. Towards omnidirectio-nal passive Human Detection[J]. Proceedings of IEEE INFOCOM, 2013, 12(11): 3057-3065. ( 0) 0)
|
| [8] |
LI B, SALTER J, DEMPSTER A G, et al. Indoor positioning techniques based on wireless LAN[C]//IEEE International Conference on Lan, 2007:13-16.
( 0) 0)
|
| [9] |
朱荣, 白光伟, 沈航, 等. 基于贝叶斯过滤法的CSI室内定位方法[J]. 计算机工程与设计, 2015, 36(3): 567-571. ZHU Rong, BAI Guangwei, SHEN Hang, et al. Bayesian filtering based CSI indoor localization method[J]. Computer engineering and design, 2015, 36(3): 567-571. (  0) 0)
|
| [10] |
毕晓君, 夏晓蕾. 基于自适应匹配追踪的MIMO-OFD-M窄带干扰检测[J]. 哈尔滨工程大学学报, 2015(9): 1287-1291. BI Xiaojun, XIA Xiaolei. Narrow band interference detection forMIMO-OFDM systems based on sparsityadaptive matching pursuit[J]. Journal of Harbin Engineering University, 2015(9): 1287-1291. (  0) 0)
|
| [11] |
WU X, KUMAR V, QUINLAN J R, et al. Top 10 algorithms in data mining[J]. Knowledge & information systems, 2007, 14(1): 1-37. ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


