2. 长沙理工大学 水利工程学院, 湖南 长沙 410114;
3. 天津城建大学 天津市软土特性与工程环境重点实验室, 天津 300384
2. School of Hydraulic Engineering, Changsha University of Science and Technology, Changsha 410114, China;
3. Tianjin Key Laboratory of Soft Soil Characteristics & Engineering Environment, Tianjin Chengjian University, Tianjin 300384, China
在数值模拟自由表面流的过程中,需要实时捕捉自由表面的位置,以确定N-S方程的求解范围。level set是一种常用的自由表面捕捉方法,通过捕捉符号距离函数φ的零等值线(面)实现对自由表面的追踪[1]。此外,为确保level set方程的求解结果满足符号距离函数条件(|∇φ|=1),需要周期性地对其进行重构[2]。与其他捕捉方法比较,level set方法的优点在于其能够有效处理自由表面的拓扑变化,缺点是很难保证质量守恒。为了克服这一点,除了采用高精度的计算格式[3-4]外,Enright提出了快速粒子level set法,借助无质量粒子校正level set函数的计算值,使其结果几乎无质量损失[5]。后来的研究表明,该粒子level set法只需采用一阶精度的半拉格朗日格式求解level set方程以及快速步进法重构level set函数,既可获得高精度的结果,又能有效减少计算时间[6-7]。鉴于粒子level set方法快速准确的特点,笔者已成功将其引入数值波浪水槽模型中,并获得了高质量的自由表面追踪效果[10-12]。然而,随着模型推广至三维,原有的粒子level set串行算法已无法满足计算需求,势必需要借助并行技术来提高数值模拟的效率。
分区并行计算是将整个计算区域分割成多个子区域,并将各子区域的计算分配给不同线程执行。作为粒子level set法的重要环节,level set函数并行重构的实现是粒子level set法并行化的关键。在这方面,笔者曾提出过一种level set函数分区并行重构算法[13],有效地缩短了计算时间。本文的主要工作是在该算法的基础上优化并行同步方案,以进一步提高重构效率,建立基于OpenMP多线程技术的并行计算新模型,并通过圆球、圆环管和哑铃三个等值面重构算例,分析和讨论并行计算新模型的精度和效率。
1 快速步进法快速步进法用于求解方程|∇φ|=1的边值问题,采用下列一阶迎风格式进行离散:
| $\begin{array}{l} \left| {\nabla \phi } \right| = [{\rm{max}}{(D_{ijk}^{ - x}\phi , - D_{ijk}^{ + x}\phi ,{\rm{ }}0)^2} + \\ \quad \quad \;\;\;{\rm{max}}{(D_{ijk}^{ - y}\phi ,{\rm{ }} - D_{ijk}^{ + y}\phi ,{\rm{ }}0)^2} + \\ \quad \quad \;\;\;{\rm{max}}{(D_{ijk}^{ - z}\phi ,{\rm{ }} - D_{ijk}^{ + z}\phi ,{\rm{ }}0)^2}{]^{1/2}} = 1 \end{array}$ | (1) |
式中:
上述格式的特点是网格节点的选择依赖于节点φ值大小,φ值较小的节点决定φ值较大的节点。即当确定紧邻交界面网格节点的φ值后,便可从边界开始逐步向外构造出φ>0区域内其他网格节点的φ值。若改变区域内网格节点上φ值的符号,亦可构造出φ<0区域内网格节点上的φ值。具体算法如下:
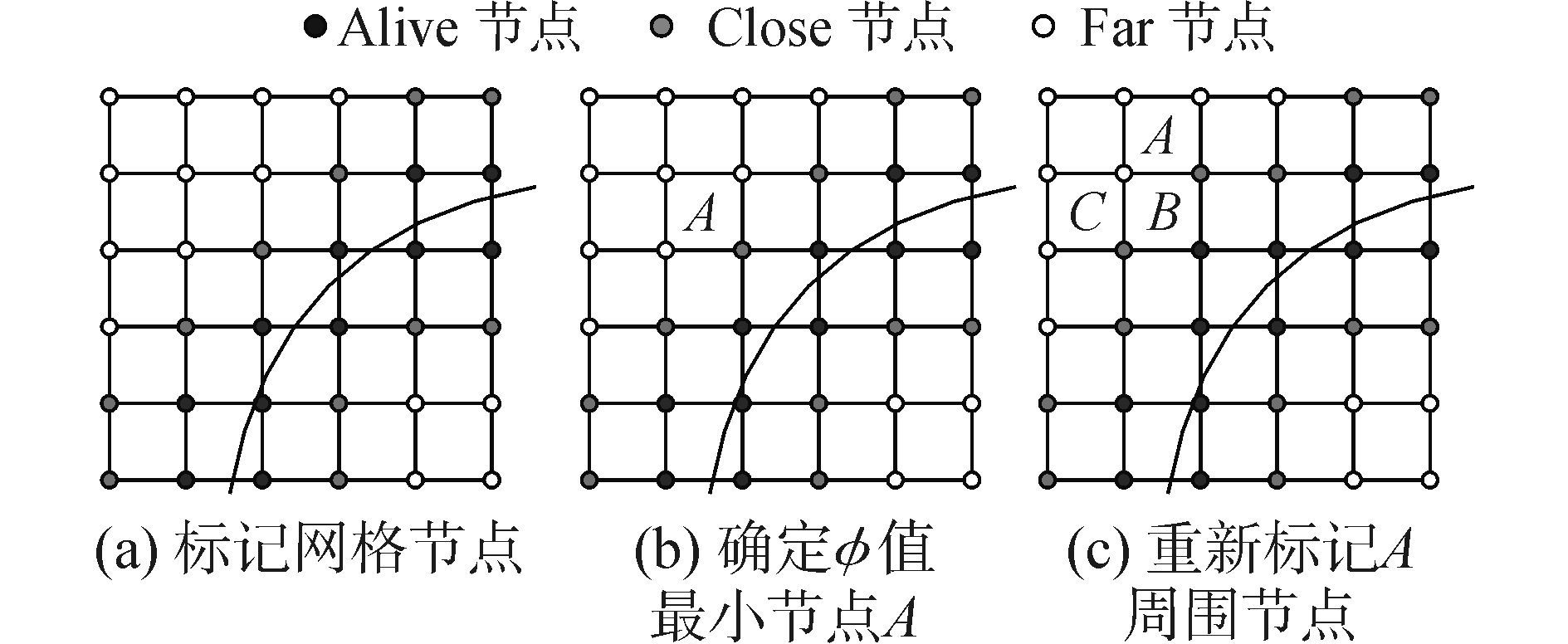
1) 标记交界面周围的已知φ值的网格节点为Alive节点,与Alive节点相邻的其他节点为Close节点,剩余节点为Far节点,如图 1(a)所示;
|
图 1 快速步进法构造φ值的过程 Fig.1 Construction of φ value by fast marching method |
2) 按式(1) 计算Close节点上的φ值;
3) 在Close节点集中找到φ值最小的节点A,标记该节点为Alive节点,如图 1(b)所示;
4) 重新计算与节点A相邻的所有节点的φ值,并将其中的Far节点B和C标记为Close节点,如图 1(c)所示;
5) 从Close节点集中删除节点A;
6) 若Close节点集为空,计算结束,否则返回步骤3。
2 并行快速步进法的改进 2.1 计算区域划分与网格布置要发挥并行计算的优势,通常将计算区域划分成多个大小一致的子区域,以保证每个线程分配的计算量接近。为了方便相邻区域间交换数据,各子区域外需要布置虚拟网格。例如图 2,整个计算区域平均分成2个子区域,子区域1在右边界外布置一排虚拟网格,用于备份子区域2左边界网格上的函数值,同理,子区域2在左边界外布置一排虚拟网格,用于备份子区域1右边界网格上的函数值;节点A、C和虚拟网格节点C′的坐标位置一致,子区域1的虚拟节点C′用于接收子区域2上节点A的信息,同样,子区域2的虚拟节点也将接收子区域1右边界节点的信息。

|
图 2 计算区域划分与虚拟网格布置 Fig.2 Subdivision of computation domain and arrangement of ghost mesh |
原有的分区并行的基本算法[13]如下:
1) 对于任一子区域,运用快速步进法构造交界面外所有非Alive节点的φ值;
2) 同步子区域;
3) 满足收敛条件,计算结束,否则,返回步骤1。
在子区域同步过程中,本区域的虚拟网格节点首先接收从相邻区域边界节点传递来的φ值,再检查虚拟网格节点的φ值是否小于边界节点的φ值,若成立,将虚拟网格节点的φ值赋给边界节点,并定义所有赋予值中最小者为φmin,最后,重新计算本区域内所有大于φmin的网格节点上φ值。由于要重新计算所有大于φmin的网格节点,这使得步骤1中部分非Alive节点上的φ值构造可能是无用的。因此,可将同步过程嵌入到快速步进法循环中,通过及时传递边界节点信息,减少网格节点φ值的无效计算次数,提高计算效率。
2.3 改进的并行算法在改进的并行化快速步进法中,一方面将新标记为Alive边界节点的函数值及时传递到相邻子区域的虚拟网格节点上;另一方面在每次循环中判断相邻子区域计算结果是否对本子区域计算产生影响,即每次循环都检查子区域虚拟网格节点φ值是否被更新,且小于对应的边界节点φ值。具体算法如下:
1) 执行串行快速步进法中步骤1和2;
2) 检查是否存在新标记为Alive的虚拟网格节点,且该节点上φ值小于位置重合的边界节点上的φ值;若这种虚拟节点存在,则对应边界节点标记为Close,同时将虚拟网格节点上φ值赋给该边界节点,然后将本子区域内所有不小于该φ值的Alive节点重新标记为Close,与交界面相邻的节点除外;
3) 若Close节点集非空,执行串行快速步进法中步骤3)~5)。在步骤4中,若重新计算节点为边界节点,其φ值应取计算值和原值中的较小者;
4) 若上一步中删除的Close节点为边界节点,将该边界节点的φ值传递给相邻子区域的虚拟网格节点,并将虚拟网格节点标记为Alive;
5) 若Close节点集非空,返回步骤2;
6) 若所有子区域Close节点集皆为空,计算结束;若存在新标记为Alive的虚拟网格节点,则返回步骤2。
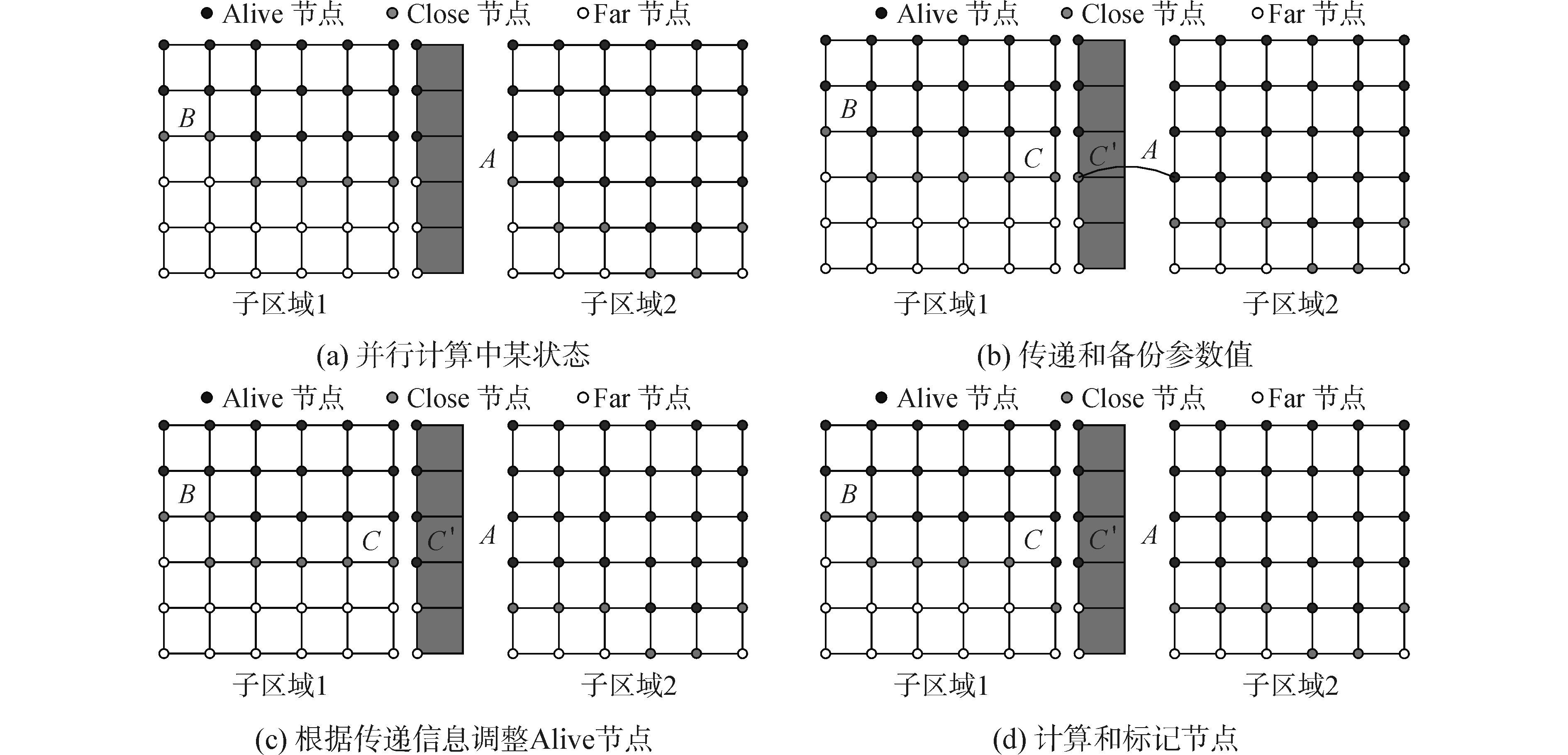
图 3给出了子区域间的同步过程。图 3(a)中,节点A和B分别是子区域2和1中φ值最小的Close节点;当节点A被标记成Alive节点后,该节点的相关信息被传递给子区域1,并备份到虚拟节点C′上,同时节点B被标记为Alive(图 3(b));图 3(c)中,子区域1的网格节点将根据虚拟节点C′上φ值进行重新标记,节点B又被标记回Close。由于节点C是子区域1中φ值最小的Close节点,C节点将被标记成Alive节点,并重新计算与C相邻的非Alive节点上的φ值,同时标记相邻的Far节点为Close(图 3(d))。
|
图 3 子区域间同步过程 Fig.3 Synchronization between sub-domains |
计算区域为100×100×100,圆球位于整个区域中心,球体半径为25,如图 4(a)所示。计算过程中,整个计算区域均分成8个大小相等的子区域。图 4(b)给出了φ=-10和φ=10等值面的并行计算结果。表 1给出了φ=10等值面所包围体积的数值结果以及整个区域φ值的计算误差,其中L1误差按照文献[14]计算,即

|
图 4 圆球等值面重构 Fig.4 Isosurface reconstruction of sphere |
| 表 1 圆球等值面并行重构的计算损失和误差 Tab.1 Computational loss and error of the parallel isosurface reconstruction of sphere |
| $\sum\limits_{ijk = 1}^N {\left| {\phi _{ijk}^{{\rm{compute}}} - \phi _{ijk}^{{\rm{actual}}}} \right|} /N$ | (2) |
在粒子level set方法中,level set方程求解和level set函数重构过程只需在交界面周围一定范围内执行,即可保证交界面捕捉的准确性。图 5(a)比较了全局和局部(|φ|<3) 并行化快速步进法的加速比。可以看出,无论全局还是局部操作,并行计算模型均获得良好的加速比,8线程下全局计算的加速比接近6,而局部计算的加速比也大于5。

|
图 5 圆球等值面重构的加速比 Fig.5 Speedup of isosurface reconstruction of sphere |
在并行计算过程中,分区并行所需子区域间信息交换和节点重新计算等额外开销是影响并行计算效率的关键。定义并行信息传递参数Fc和并行节点重演参数Fr分别为
| ${F_c} = \frac{{{N_t}}}{M}$ | (3) |
| ${F_r} = \frac{{{M_r}}}{M}$ | (4) |
式中:Nt为子区域间信息传递总次数,M为计算区域内总节点数, Mr为节点重新计算总次数。
图 6比较了不同线程数下的Fc和Fr值(球心位置[50, 50, 50])。可以看出:Fc和Fr都随着线程数的增加而变大,说明加速比的增长幅度不是恒定的,而是随线程数增加呈减小的趋势;Fc和Fr值小于0.2,表明该并行状态的额外开销对加速比的影响较小;相比全局并行重构,局部并行重构的Fc和Fr值更大,表明其额外开销所占的比例更高,使得加速比的增长幅度低于全局并行重构。

|
图 6 圆球等值面重构的Fc和Fr(球心位置[50, 50, 50]) Fig.6 Fc and Fr for isosurface reconstruction of sphere(centre located at [50, 50, 50]) |
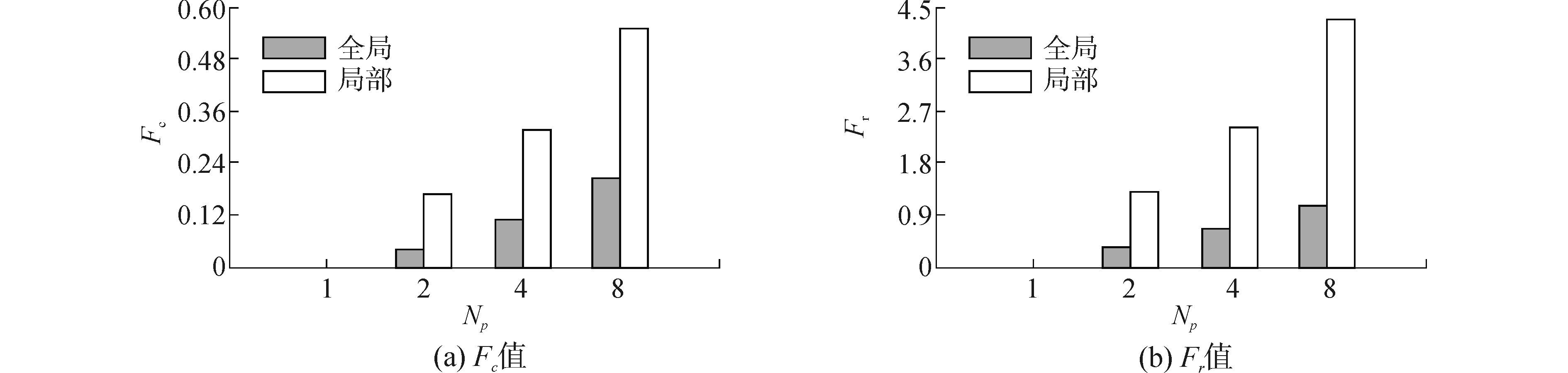
图 5(b)给出了位于[25, 25, 25]的圆球在不同线程下全局和局部level set函数重构的加速比,此时,8线程下全局计算的加速比只达到2,而局部操作甚至不到1。图 7比较了此状态下的Fc和Fr值。可以看出,该状态下的额外计算开销远远高于球心位于[50, 50, 50]的情况。尤其是Fr值,8线程下局部重构的Fr值甚至超过4,这是导致其加速比随线程数增加反而减小的主要原因。
|
图 7 圆球等值面重构的Fc和Fr值(球心位置[25, 25, 25]) Fig.7 Fc and Fr for isosurface reconstruction of sphere (center located at [25, 25, 25]) |
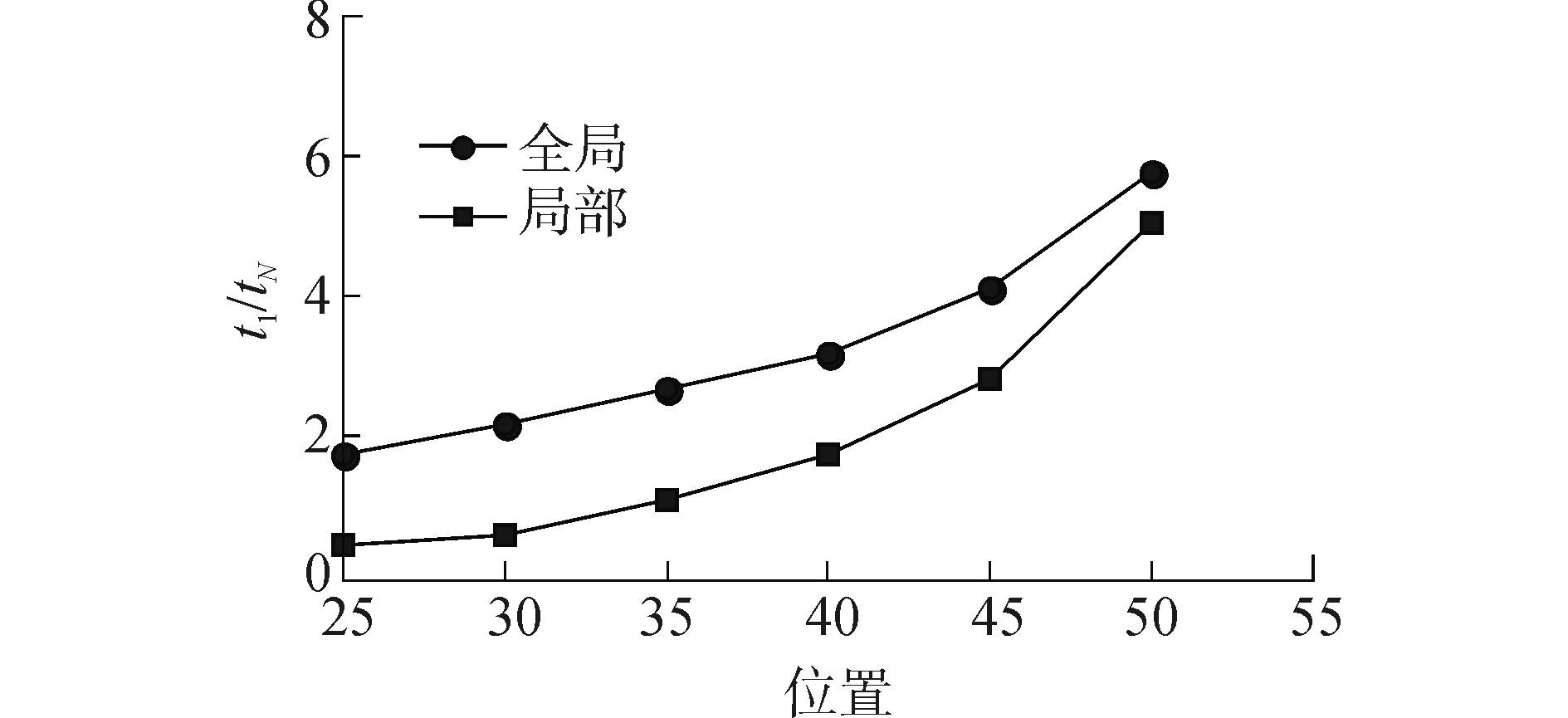
图 8比较了8线程下圆球在不同位置的加速比。当球心位置位于[25, 25, 25]时,整个球体完全落入一个子分区中,过量的信息交换与节点重演带来巨大的额外开销,所获得的加速比最小;当圆球向区域中心逐渐靠近时,各子区域所获得初始表面面积趋于相等,所获得的加速比随之增加,直至最大。
|
图 8 8线程下不同位置圆球等值面重构的加速比 Fig.8 Speedup of isosurface reconstruction of sphere located at different positions under eight threads |
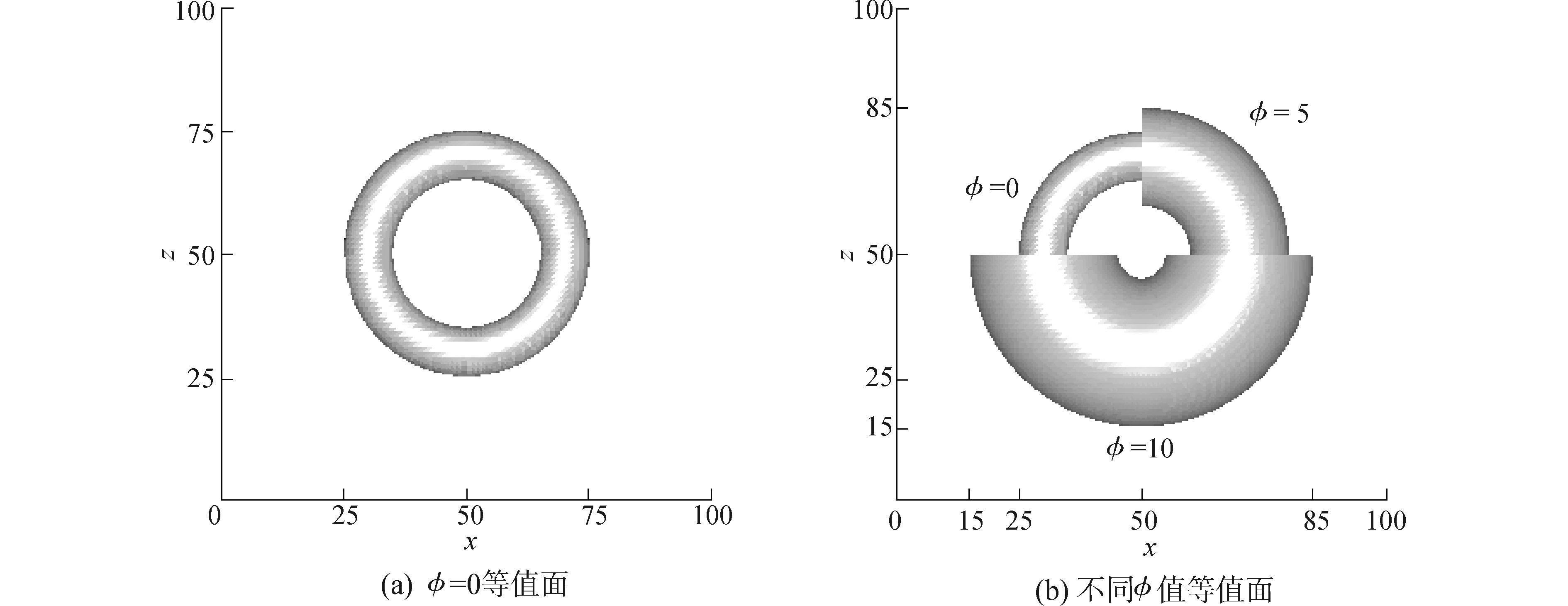
计算区域为100×100×100,圆环管放置在计算区域中心(图 9(a)),其表达式如下
|
图 9 圆环管等值面重构 Fig.9 Isosurface reconstruction of circular cube |
| $\left\{ {\begin{array}{*{20}{l}} {x = (R + r{\rm{cos}}\;t){\rm{sin}}\;\theta + 50}\\ {y = r{\rm{sin}}\;t + 50}\\ {z = (R + r{\rm{cos}}\;t){\rm{cos}}\;\theta + 50} \end{array}} \right.$ | (5) |
其中,外径R=20,内径r=5。计算过程中,整个计算区域可分成8个大小相等的区域。图 9(b)给出了φ=5和φ=10等值面的计算结果。表 2则比较了不同网格分辨率下φ=10等值面所包围体积的数值结果及φ值重构的计算误差。
| 表 2 圆环管等值面并行重构的计算损失和误差 Tab.2 Computational loss and error of parallel isosurface reconstruction of circular cube |
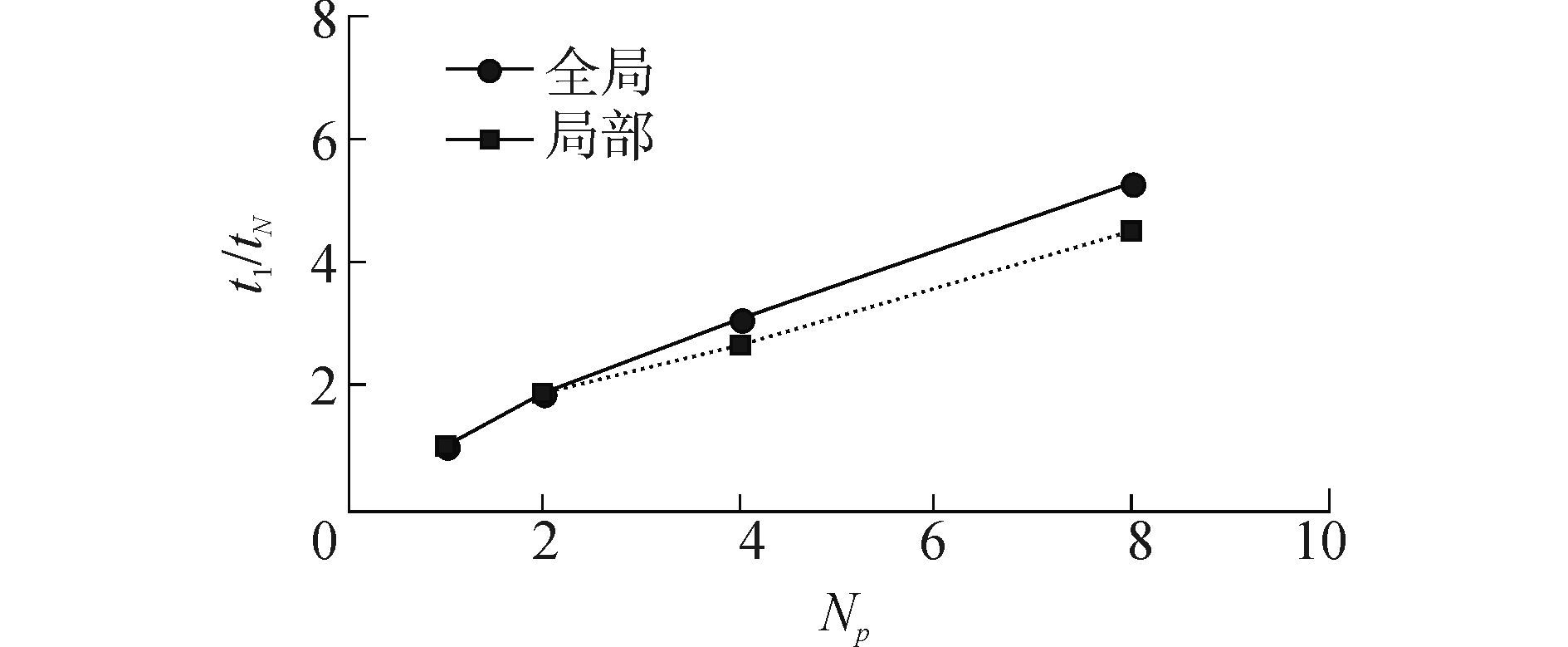
图 10比较了全局和局部(|φ|<3) 重构下并行模型的加速比,其中2线程和4线程的局部并行重构加速比取三种计算区域均分方案的平均。这是因为采用2线程和4线程进行局部并行重构时,边界上需要信息传递的边界节点总数随计算区域均分方式不同而有所差异。例如,在线程数为2的条件下,若按y方向均分计算区域,所要计算的边界节点总数要大于其他两种情况,从表 3可以看出,按y方向均分计算区域的Fc和Fr值大于其他两种均分方式,这也使得其加速比略小于其他两种方式。
|
图 10 圆环管等值面重构的加速比 Fig.10 Speedup of isosurface reconstruction of circular cube |
| 表 3 2线程下不同区域划分对的等值面局部并行重构效率的影响 Tab.3 Effect of domain division on the efficiency of the local parallel isosurface reconstructions under two threads |
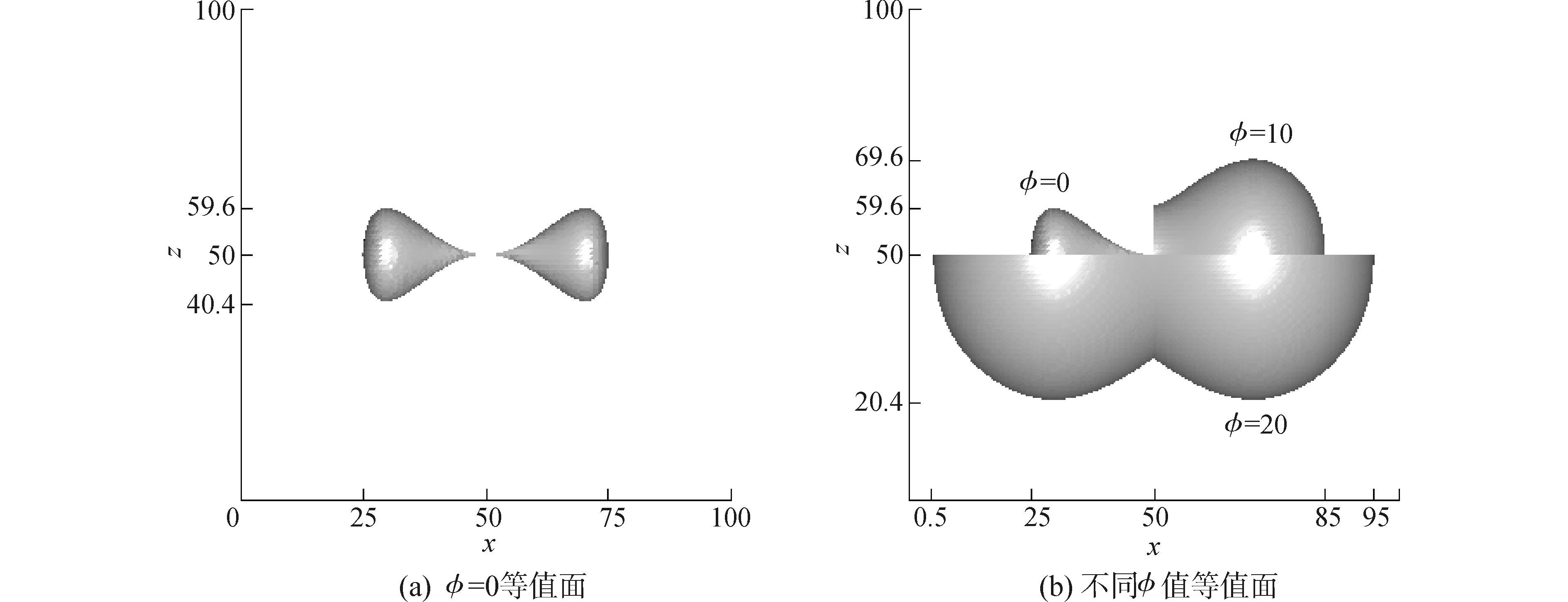
计算区域为100×100×100,哑铃曲面的具体表达式如下
| $\left\{ {\begin{array}{*{20}{l}} {x = at + 50}\\ {y = a{t^2}\sqrt {1 - {t^2}} {\rm{sin}}\;\theta + 50}\\ {z = a{t^2}\sqrt {1 - {t^2}} {\rm{cos}}\;\theta + 50} \end{array}} \right.$ | (6) |
其中,a=25(见图 11(a))。整个计算区域被平均分成8个子区域。图 11(b)为φ=10和φ=20等值面的计算结果。表 4比较了不同网格分辨率下φ=10等值面所包围体积的数值结果及φ值重构的计算误差。
|
图 11 哑铃等值面重构 Fig.11 Isosurface reconstruction of dumbbell |
| 表 4 不同网格分辨率下计算损失和误差(哑铃曲面) Tab.4 Computational loss and error of parallel isosurface reconstruction of dumbbell |
在本算例中,按x方向均分计算区域时需要信息传递的边界节点数最少,因此,其2线程下的加速比要略高于其他两种情况(表 3)。图 12为全局和局部(|f|<3) 并行计算的加速比, 同样,2线程和4线程下局部并行重构的加速比取三种计算区域均分方案的平均。可以看出,8线程的加速比仍大于4。

|
图 12 哑铃等值面重构的加速比 Fig.12 Speedup of isosurface reconstruction of dumbbell |
1) 改进的快速步进并行重构方法能够显著缩短计算时间,且基本保持1阶精度,在8线程的条件下,最大加速比能够接近6;
2) 相同线程数下,子区域对初始表面边界的划分将影响并行重构的加速比,均分表面可获得较高的加速比;
3) 局部分区并行重构应尽量减少子区域边界上需要计算的节点数目,这样子区域间信息传递次数和节点重新计算的次数将相应地减少,而计算效率也随之提高。
| [1] |
OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed:algorithms based on Hamilton-Jacobi formulations[J]. Journal of computational physics, 1988, 79(1): 12-49. DOI:10.1016/0021-9991(88)90002-2 ( 0) 0)
|
| [2] |
SUSSMAN M, SMEREKA P, OSHER S. A level set approach for computing solutions to incompressible two-phase flow[J]. Journal of computational physics, 1994, 114(2): 146-159. ( 0) 0)
|
| [3] |
JIANG G S, SHU C W. Efficient implement of weighted ENO schemes[J]. Journal of computational physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 ( 0) 0)
|
| [4] |
JIANG G S, PENG D P. Weighted ENO schemes for Ham-ilton-Jacobi equations[J]. SIAM journal on scientific computing, 2000, 21(6): 2126-2143. DOI:10.1137/S106482759732455X ( 0) 0)
|
| [5] |
ENRIGHT D, FEDKIW R. A hybrid particle level set method for improved interface capturing[J]. Journal of computational physics, 2002, 183(1): 83-116. DOI:10.1006/jcph.2002.7166 ( 0) 0)
|
| [6] |
ENRIGHT D, LOSASSOM F. A fast and accurate semi-Lagrangian particle level set method[J]. Computers and structure, 2005, 83(6): 479-490. ( 0) 0)
|
| [7] |
JIANG L, LIU F B, CHEN D R. A fast particle level set method with optimized particle correction procedure for interface capturing[J]. Journal of computational physics, 2015, 299: 804-819. DOI:10.1016/j.jcp.2015.06.039 ( 0) 0)
|
| [8] |
SETHAIN J. Fast marching methods[J]. SIAM review, 1999, 41(2): 199-235. DOI:10.1137/S0036144598347059 ( 0) 0)
|
| [9] |
STRAIN J. Semi-Lagrangian methods for level set equations[J]. Journal of computational physics, 1999, 151(2): 498-533. DOI:10.1006/jcph.1999.6194 ( 0) 0)
|
| [10] |
黄筱云, 李绍武, 夏波. 一种新型三维水流数值模型[J]. 海洋学报, 2010, 32(6): 167-173. HUANG Xiaoyun, LI Shaowu, XIA Bo. A new three dimensional numerical model for stream[J]. Acta oceanologica sinica, 2010, 32(6): 167-173. (  0) 0)
|
| [11] |
HUANG X Y, LI S W. A two-dimensional numerical wave flume based on SA-MPLS method[J]. Acta oceanologica sinica, 2012, 31(3): 18-30. DOI:10.1007/s13131-012-0203-2 ( 0) 0)
|
| [12] |
LI S W, ZHUANG Q, HUANG X Y, et al. 3D simulation of flow with free surface based on adaptive octree mesh system[J]. Transactions of Tianjin University, 2015, 21(1): 32-40. DOI:10.1007/s12209-015-2314-2 ( 0) 0)
|
| [13] |
黄筱云, 董国海, 赵利平, 等. Level set函数重新初始化的并行快速步进方法[J]. 哈尔滨工程大学学报, 2016, 37(5): 666-671. HUANG Xiaoyun, DONG Guohai, ZHAO Liping, et al. A parallelized fast marching method for reinitialization of level set function[J]. Journal of Harbin Engineering University, 2016, 37(5): 666-671. (  0) 0)
|
| [14] |
SUSSMAN M, FATEMI E. An efficient, interface-preserving level set redistancing algorithm and its application to interfacial incompressible fluid flow[J]. SIAM journal on scientific computing, 1999, 20(4): 1165-1191. DOI:10.1137/S1064827596298245 ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


