生命线工程对维护城市功能系统和国计民生具有重要意义，众多地下复杂结构均含有缺陷，缺陷使生命线工程的动应力集中问题更加复杂。弹性波动理论是研究含有凸起、裂纹等缺陷的复杂地下结构的弹性动力学问题的重要方法，被广泛应用于地下衬砌结构这一生命线工程的抗震与抗爆设计中，如供水、排水、石油输送管道以及地下隧道工程等，而复杂地形中坡度较缓的山丘，可以简化为半圆凸起。众多学者对裂纹缺陷与凸起问题进行研究并取得大量成果^[1-12]。齐辉等对直角域或半空间中圆形凸起与裂纹的动力问题进行了分析^[1-8]。南景富等对脱胶衬砌与裂纹的动力响应问题给出了数值解^[9]。梁建文等研究了衬砌和地下球形结构的动应力集中问题^[10-11]。杨在林等研究了非均匀介质的动力学问题^[12-14]。

本文采用“分区”思想，将含半圆凸起的直角域进行分区，分成圆形凸起和含半圆凹陷的两个区域。利用“镜像法”，构造出满足水平、垂直边界应力自由的波函数。通过衬砌与凸起周边连续性条件建立方程组，利用裂纹切割法和坐标转换法得到了衬砌周边动应力集中系数和裂纹尖端动应力因子的解析表达式。文章最后给出具体算例和数值结果，讨论了入射角度、入射波数、裂纹长度、裂纹角度、圆形衬砌位置、圆形衬砌厚度比等对动应力集中系数、动应力强度因子与地表位移的影响。

1 直角域中凸起和衬砌模型的描述

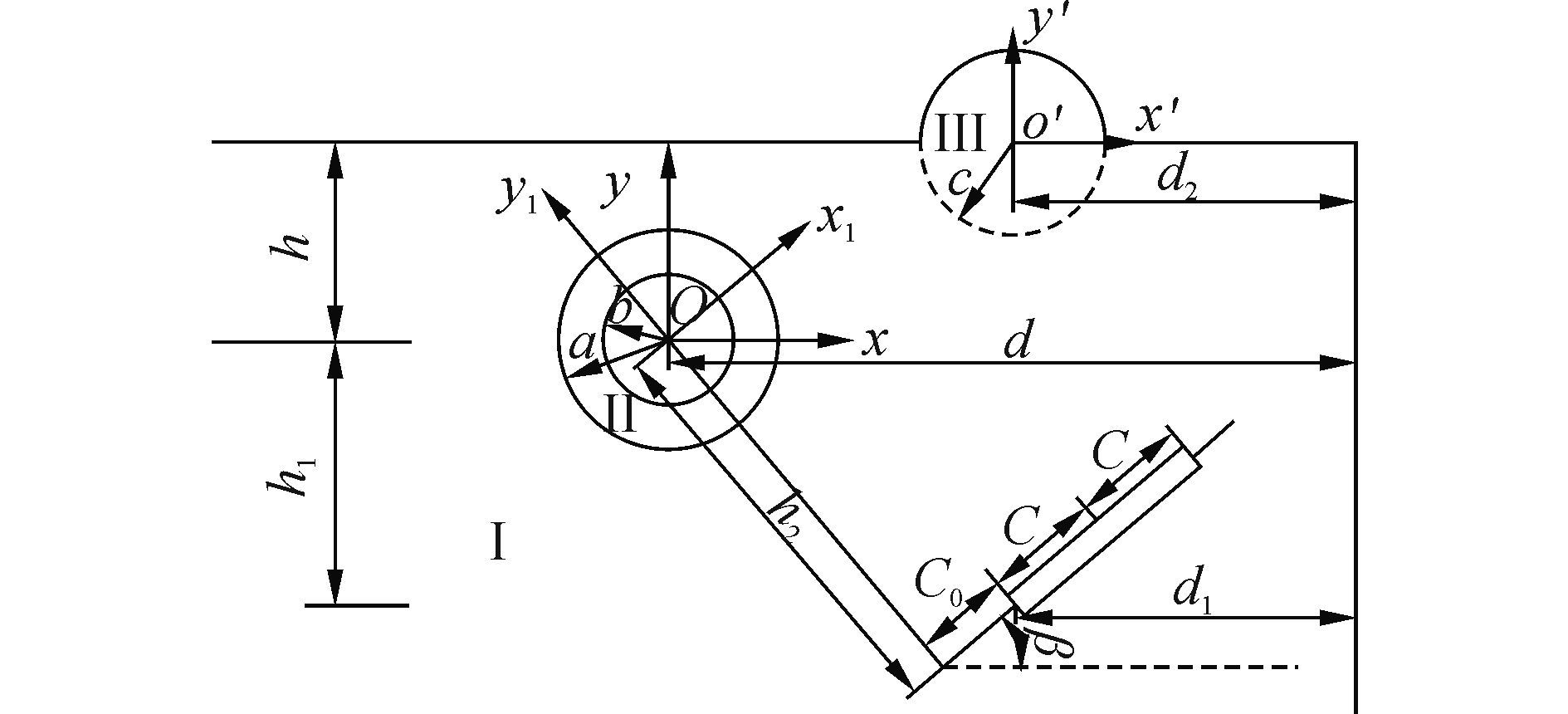
天然介质中有很多复杂的地形，这些地形在地震波作用下会出现动应力集中问题。本文模型是直角域地形结构中地下衬砌与坡度缓和的山丘凸起在SH波作用下动应力响应问题的简化。如图 1，介质Ⅰ为含圆形衬砌和直线裂纹的直角域，其水平、垂直边界分别为Γ_H、Γ_V；介质Ⅱ为圆形衬砌，其质量密度与剪切模量分别为ρ₂、μ₂，中心位置与垂直边界Γ_V距离为d，与水平边界Γ_H距离为h，内、外半径分别为b、a，其内边界、外边界分别为Γ_B、Γ_A；介质Ⅲ为圆形凸起，其半径为c，边界为Γ_C，中心位置与垂直边界Γ_V距离为d₂。介质Ⅰ与介质Ⅲ质量密度与剪切模量分别为ρ₁、μ₁。裂纹长度为2C，角度为β，裂纹尖端与垂直边界Γ_V距离为d₁，与衬砌圆点o垂直距离为h₁，坐标系x₁oy₁中x₁方向与裂纹方向平行，裂纹尖端与y₁的垂直距离为c₀。本文采用坐标变换法，建立坐标系xoy、x₁oy₁与x′o′y′，所对应的复坐标系分别为：η=x+yi=re^iθ、η₁=x₁+y₁ i =r₁ e ^iθ₁与η′=x′+y′ i =r′e^iθ′，各坐标系关系为

$ \left\{ \begin{array}{l} {x_1} = x\cos \beta + y\sin \beta \\ {y_1} = y\cos \beta - x\sin \beta \\ x' = x + {d_2} - d\\ y' = y - h\\ {h_2} = \left( {{h_1} + {c_0}\sin \beta } \right)/\cos \beta \\ {d_1} = d - {c_0}\cos \beta - {h_2}\sin \beta \end{array} \right. $

(1)

2 直角域中位移场的基本控制方程

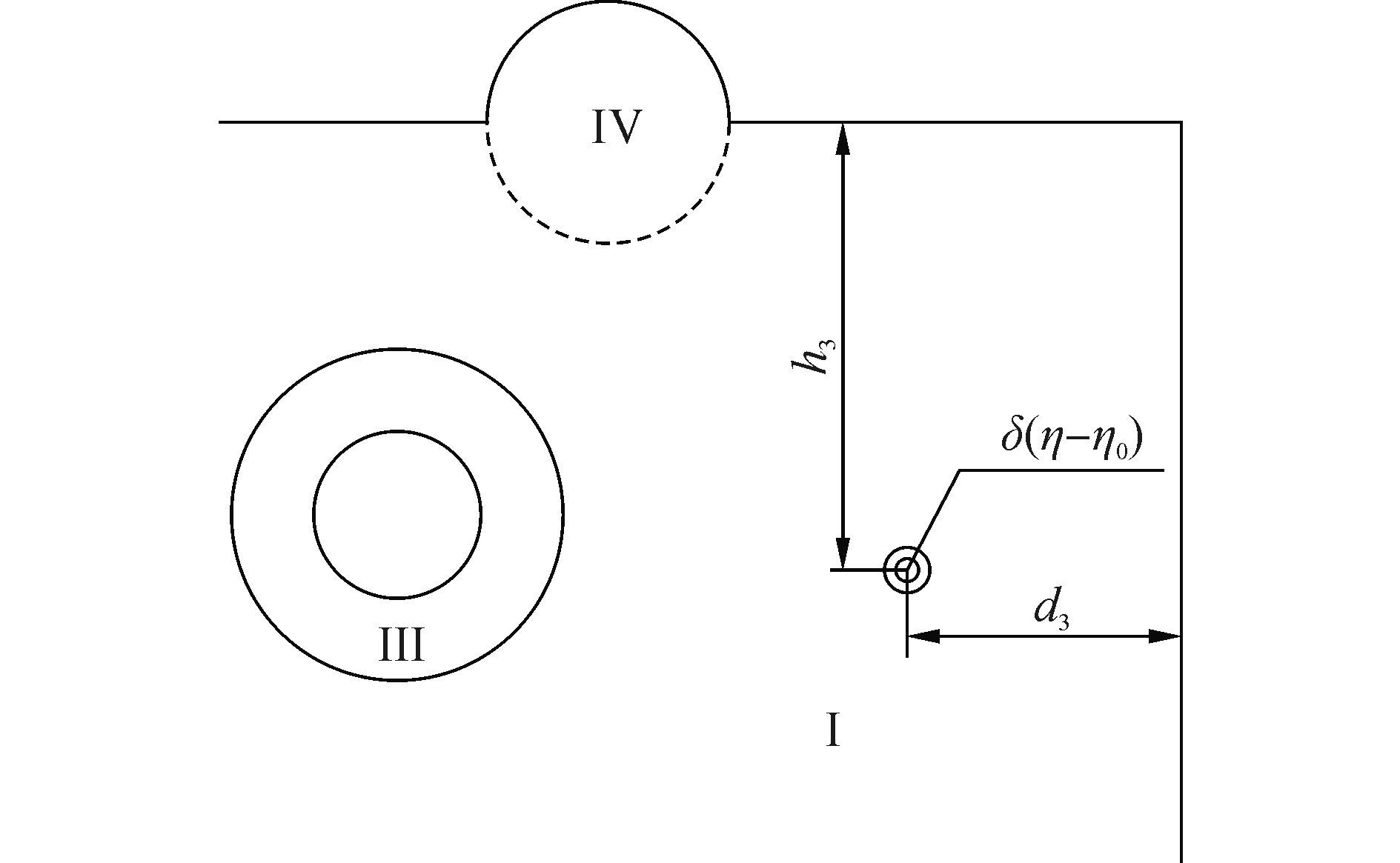
如图 2所示，本节采用Green函数法对含圆形衬砌和半圆凸起的直角域进行分析，研究直角域介质Ⅰ在线源荷载δ(η-η₀)作用下的动应力响应问题。其中η₀=d-d₃+(h-h₃) i，表示位于介质Ⅰ内部的点。

直角域中由线源荷载引起的位移必然满足控制方程。引入复变量η=x+y i, η=x-y i，在复平面(η, η)中位移控制方程为

$ \frac{{{\partial ^2}G}}{{\partial \eta \partial \bar \eta }} + \frac{1}{4}{k^2}G = 0 $

(2)

式中：k=ω/c_s是入射波数，ω为波函数圆频率，${c_s} = \sqrt {\mu /\rho } $为介质的剪切波速。

在复平面令η=re^iθ, η=re^-iθ上，本构关系为

$ \left\{ \begin{array}{l} {\tau _{rz}} = \mu \left( {\frac{{\partial G}}{{\partial \eta }}{{\rm{e}}^{{\rm{i}}\theta }} + \frac{{\partial G}}{{\partial \bar \eta }}{{\rm{e}}^{ - {\rm{i}}\theta }}} \right)\\ {\tau _{\theta z}} = i\mu \left( {\frac{{\partial G}}{{\partial \eta }}{{\rm{e}}^{{\rm{i}}\theta }} - \frac{{\partial G}}{{\partial \bar \eta }}{{\rm{e}}^{ - {\rm{i}}\theta }}} \right) \end{array} \right. $

(3)

本节研究的直角域的边界条件可以表示为

$ \left\{ \begin{array}{l} {\Gamma _H}:\tau _{yz}^{\rm{I}} = 0\\ {\Gamma _V}:\tau _{xz}^{\rm{I}} = 0\\ {\Gamma _A}:{G^{\rm{I}}}\left| {_{r = a, - {\rm{\pi }} \le \theta \le {\rm{\pi }}}} \right. = {G^{{\rm{II}}}}\left| {_{r = a, - {\rm{\pi }} \le \theta \le {\rm{\pi }}}} \right.\\ {\Gamma _A}:\tau _{rz}^{\rm{I}}\left| {_{r = a, - {\rm{\pi }} \le \theta \le {\rm{\pi }}}} \right. = \tau _{rz}^{{\rm{II}}}\left| {_{r = a, - {\rm{\pi }} \le \theta \le {\rm{\pi }}}} \right.\\ {\Gamma _B}:\tau _{rz}^{{\rm{II}}}\left| {_{r = b, - {\rm{\pi }} \le \theta \le {\rm{\pi }}}} \right. = 0\\ {\Gamma _C}:\tau _{rz}^{{\rm{III}}}\left| {_{r = c,0 \le \theta \le {\rm{\pi }}}} \right. = 0\\ {\Gamma _C}:{G^{\rm{I}}}\left| {_{r = c, - {\rm{\pi }} \le \theta \le {\rm{0}}}} \right. = {G^{{\rm{III}}}}\left| {_{r = c, - {\rm{\pi }} \le \theta \le {\rm{0}}}} \right.\\ {\Gamma _C}:\tau _{rz}^{\rm{I}}\left| {_{r = c, - {\rm{\pi }} \le \theta \le {\rm{0}}}} \right. = \tau _{rz}^{{\rm{III}}}\left| {_{r = c, - {\rm{\pi }} \le \theta \le {\rm{0}}}} \right. \end{array} \right. $

(4)

式中：τ_rz^Ⅰ、τ_rz^Ⅱ、τ_rz^Ⅲ分别为介质Ⅰ、介质Ⅱ、介质Ⅲ中径向剪切应力，G^Ⅰ、G^Ⅱ、G^Ⅲ分别为介质Ⅰ、介质Ⅱ、介质Ⅲ中位移。

由线源荷载δ(η-η₀)产生的扰动，可视为已知的入射波Gⁱ与反射波G^r，应满足直角域水平边界Γ_H和垂直边界Γ_V上应力自由，本文利用“镜像法”，构造其表达式：

$ {G^i} = \frac{{\rm{i}}}{{2{\mu _1}}}\left[ {{\rm{H}}_0^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {\eta _0}} \right|} \right) + {\rm{H}}_0^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {{\eta '}_0}} \right|} \right)} \right] $

(5)

$ \begin{array}{*{20}{c}} {{G^r} = \frac{{\rm{i}}}{{2{\mu _1}}}\left[ {{\rm{H}}_0^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {{\bar \eta }_0} - 2{\rm{i}}h} \right|} \right) + } \right.}\\ {\left. {{\rm{H}}_0^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {{\bar \eta '}_0} - 2{\rm{i}}h} \right|} \right)} \right]} \end{array} $

(6)

式中η′₀=η₀-2d。

对于介质Ⅲ圆形凸起形成的散射波G^s1和介质Ⅱ圆形衬砌所形成的散射波G^s2，均满足直角域中直线边界应力自由, 利用“镜像法”，构造出其表示式：

$ \begin{array}{l} {G^{s1}} = \sum\limits_{m = - \infty }^{ + \infty } {{A_m}\left\{ {{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {\eta '} \right|} \right)\left( {{{\left[ {\frac{{\eta '}}{{\left| {\eta '} \right|}}} \right]}^m} + {{\left[ {\frac{{\eta '}}{{\left| {\eta '} \right|}}} \right]}^{ - m}}} \right) + } \right.} \\ \;\;\;\;\;\;\;\;\;\;{\left( { - 1} \right)^m}{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {\eta ' - 2{d_2}} \right|} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\left. {\left( {{{\left[ {\frac{{\eta ' - 2{d_2}}}{{\left| {\eta ' - 2{d_2}} \right|}}} \right]}^m} + {{\left[ {\frac{{\eta ' - 2{d_2}}}{{\left| {\eta ' - 2{d_2}} \right|}}} \right]}^{ - m}}} \right)} \right\} \end{array} $

(7)

$ \begin{array}{l} {G^{s2}} = \sum\limits_{m = - \infty }^{ + \infty } {{B_m}\left\{ {{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| \eta \right|} \right){{\left[ {\frac{\eta }{{\left| \eta \right|}}} \right]}^m} + {\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _2}} \right|} \right) \times } \right.} \\ \;\;\;\;\;\;\;\;\;\;{\left[ {\frac{{{\eta _2}}}{{\left| {{\eta _2}} \right|}}} \right]^m} + {\left( { - 1} \right)^m}{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _3}} \right|} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\left. {{{\left[ {\frac{{{\eta _3}}}{{\left| {{\eta _3}} \right|}}} \right]}^m} + {{\left( { - 1} \right)}^m}{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _4}} \right|} \right){{\left[ {\frac{{{\eta _4}}}{{\left| {{\eta _4}} \right|}}} \right]}^{ - m}}} \right\} \end{array} $

(8)

式中：η=x+y i，η₂=η-2hi，η₃=η₂-2d，η₄=η-2d

对于介质Ⅱ中的驻波G^st1，满足边界Γ_C上半圆上应力自由条件，按文献[6]中思路，利用坐标系x′o′y′，构造其表达式如下

$ {G^{st1}} = \sum\limits_{n = - \infty }^{ + \infty } {\sum\limits_{m = - \infty }^{ + \infty } {{C_m}{a_{mn}}{K_{mn}}{J_n}\left( {{k_1}\left| {\eta '} \right|} \right){{\left[ {\frac{{\eta '}}{{\left| {\eta '} \right|}}} \right]}^n}} } $

(9)

其中：

$ \begin{array}{l} {a_{mn}} = \left\{ \begin{array}{l} \frac{1}{2}\\ \frac{{1 - {{\rm{e}}^{ - {\rm{i}}{{\left( {m - n} \right)}^{\rm{\pi }}}}}}}{{2{\rm{\pi i}}\left( {m - n} \right)}} \end{array} \right.\\ {K_{mn}} = \frac{{{J_{m - 1}}\left( {{k_1}a} \right) - {J_{m + 1}}\left( {{k_1}a} \right)}}{{{J_{n - 1}}\left( {{k_1}a} \right) - {J_{n + 1}}\left( {{k_1}a} \right)}},\\ \eta ' = \eta + {d_2} - d - h{\rm{i}} \end{array} $

对于介质Ⅲ内所形成的驻波G^st2，根据文献[5]中思路，构造其表达式如下：

$ {G^{st2}} = \sum\limits_{n = - \infty }^{ + \infty } {\left[ {{D_m}H_m^{\left( 1 \right)}\left( {{k_2}\left| \eta \right|} \right) + {E_m}H_m^{\left( 2 \right)}\left( {{k_2}\left| \eta \right|} \right)} \right] \times {{\left[ {\frac{\eta }{{\left| \eta \right|}}} \right]}^m}} $

(10)

由推导可知：

$ \begin{array}{l} {G^{\rm{I}}} = {G^i} + {G^r} + {G^{s1}} + {G^{s2}},\tau _{rz}^{\rm{I}} = \tau _{rz}^i + \tau _{rz}^r + \tau _{rz}^{s1} + \tau _{rz}^{s2};\\ {G^{{\rm{II}}}} = {G^{st1}},\tau _{rz}^{{\rm{II}}} = \tau _{rz}^{st1};{G^{{\rm{III}}}} = {G^{st2}},\tau _{rz}^{{\rm{III}}} = \tau _{rz}^{st2} \end{array} $

(11)

根据边界条件(4) 列方程，并将方程中等式两边同时乘以exp(-inθ)或exp(-inθ₁)，(n=0, ±1, ±2, ±3…)，在相应的区间(-π, π)或(0, π)上进行积分，截取有限项得到方程组：

$ \begin{array}{*{20}{c}} {\sum\limits_{m = - \infty }^{ + \infty } {{A_m}\xi _{mn}^{\left( {11} \right)}} + \sum\limits_{m = - \infty }^{ + \infty } {{B_m}\xi _{mn}^{\left( {12} \right)}} + \sum\limits_{m = - \infty }^{ + \infty } {{D_m}\xi _{mn}^{\left( {14} \right)}} + }\\ {\sum\limits_{m = - \infty }^{ + \infty } {{E_m}\xi _{mn}^{\left( {15} \right)}} = \xi _n^{\left( 1 \right)}}\\ {\sum\limits_{m = - \infty }^{ + \infty } {{A_m}\xi _{mn}^{\left( {21} \right)}} + \sum\limits_{m = - \infty }^{ + \infty } {{B_m}\xi _{mn}^{\left( {22} \right)}} + \sum\limits_{m = - \infty }^{ + \infty } {{D_m}\xi _{mn}^{\left( {24} \right)}} + }\\ {\sum\limits_{m = - \infty }^{ + \infty } {{E_m}\xi _{mn}^{\left( {25} \right)}} = \xi _n^{\left( 2 \right)}}\\ {\sum\limits_{m = - \infty }^{ + \infty } {{D_m}\xi _{mn}^{\left( {34} \right)}} + \sum\limits_{m = - \infty }^{ + \infty } {{E_m}\xi _{mn}^{\left( {35} \right)}} = \xi _n^{\left( 3 \right)}}\\ {\sum\limits_{m = - \infty }^{ + \infty } {{A_m}\xi _{mn}^{\left( {41} \right)}} + \sum\limits_{m = - \infty }^{ + \infty } {{B_m}\xi _{mn}^{\left( {42} \right)}} - }\\ {\sum\limits_{l = - \infty }^{ + \infty } {\sum\limits_{m = - \infty }^{ + \infty } {{C_m}{a_{ml}}{a_{\mathit{ln}}}{K_{ml}}{J_l}\left( {{k_1}c} \right)} } = \xi _n^{\left( 4 \right)}}\\ {\sum\limits_{m = - \infty }^{ + \infty } {{A_m}\xi _{mn}^{\left( {51} \right)}} + \sum\limits_{m = - \infty }^{ + \infty } {{B_m}\xi _{mn}^{\left( {52} \right)}} - }\\ {\frac{{{k_1}{\mu _1}}}{2}\sum\limits_{l = - \infty }^{ + \infty } {\sum\limits_{m = - \infty }^{ + \infty } {{C_m}{a_{ml}}{a_{\mathit{ln}}}\left( {{J_{m - l}}\left( {{k_1}c} \right)} \right.} } - }\\ {\left. {{J_{m + l}}\left( {{k_1}c} \right)} \right) = \xi _n^{\left( 5 \right)}} \end{array} $

(12)

式中：

$ \begin{array}{*{20}{c}} {\xi _{mn}^{\left( {11} \right)} = \int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {\left\{ {{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {\eta '} \right|} \right)\left( {{{\left[ {\eta '/\left| {\eta '} \right|} \right]}^m} + {{\left[ {\eta '/\left| {\eta '} \right|} \right]}^{ - m}}} \right) \times } \right.} }\\ {\left( { - 1} \right)m{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {\eta ' - 2{d_2}} \right|} \right) \times }\\ {{{\left[ {\left( {\eta ' - 2{d_2}} \right)/\left| {\eta ' - 2{d_2}} \right|} \right]}^m} \times }\\ {{{\left( { - 1} \right)}^m}{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {\eta ' - 2{d_2}} \right|} \right) \times }\\ {\left. {{{\left[ {\left( {\eta ' - 2{d_2}} \right)/\left| {\eta ' - 2{d_2}} \right|} \right]}^{ - m}}} \right\}{{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } \end{array} $

$ \xi _{mn}^{\left( {12} \right)} = \int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {\left( {\sum\limits_{j = 1}^4 {S_m^{\left( j \right)}} } \right){{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } $

$ \xi _{mn}^{\left( {14} \right)} = - \int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {{\rm{H}}_m^{\left( 1 \right)}\left( {{k_2}\left| \eta \right|} \right){{\left[ {\eta /\left| \eta \right|} \right]}^m}{{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } $

$ \xi _{mn}^{\left( {15} \right)} = - \int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {{\rm{H}}_m^{\left( 2 \right)}\left( {{k_2}\left| \eta \right|} \right){{\left[ {\eta /\left| \eta \right|} \right]}^m}{{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } $

$ \xi _{mn}^{\left( {21} \right)} = \frac{{{k_1}{\mu _1}}}{2}\int\limits_{ - {\rm{\pi }}}^{ - {\rm{\pi }}} {\left[ {\sum\limits_{j = 1}^4 {v_m^{\left( j \right)}{{\rm{e}}^{{\rm{i}}\theta }}} + \sum\limits_{j = 1}^4 {\psi _m^{\left( j \right)}{{\rm{e}}^{ - {\rm{i}}\theta }}} } \right]{{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } , $

$ \xi _{mn}^{\left( {22} \right)} = \frac{{{k_1}{\mu _1}}}{2}\int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {\left[ {\sum\limits_{j = 1}^4 {\chi _m^{\left( j \right)}{{\rm{e}}^{{\rm{i}}\theta }}} + \sum\limits_{j = 1}^4 {\gamma _m^{\left( j \right)}{{\rm{e}}^{ - {\rm{i}}\theta }}} } \right]{{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } , $

$ \xi _{mn}^{\left( {24} \right)} = - \frac{{{k_2}{\mu _2}}}{2}\int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {\left[ {\zeta {{\rm{e}}^{i\theta }} + \vartheta {{\rm{e}}^{ - i\theta }}} \right]{{\rm{e}}^{ - {\rm{i}}n\theta '}}{\rm{d}}\theta } , $

$ \xi _{mn}^{\left( {25} \right)} = - \frac{{{k_2}{\mu _2}}}{2}\int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {\left[ {\delta {{\rm{e}}^{i\theta }} + \zeta {{\rm{e}}^{ - i\theta }}} \right]{{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } , $

$ \xi _{mn}^{\left( {34} \right)} = \int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {\left[ {\zeta {{\rm{e}}^{i\theta }} + \vartheta {{\rm{e}}^{ - i\theta }}} \right]{{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } , $

$ \xi _{mn}^{\left( {35} \right)} = \int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {\left[ {\delta {{\rm{e}}^{i\theta }} + \zeta {{\rm{e}}^{ - i\theta }}} \right]{{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } , $

$ \begin{array}{*{20}{c}} {\xi _{mn}^{\left( {41} \right)} = \int\limits_{ - {\rm{\pi }}}^{\rm{0}} {\left\{ {{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {\eta '} \right|} \right)\left( {{{\left[ {\eta '/\left| {\eta '} \right|} \right]}^m} + {{\left[ {\eta '/\left| {\eta '} \right|} \right]}^{ - m}}} \right) \times } \right.} }\\ {\left( { - 1} \right)m{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {\eta ' - 2{d_2}} \right|} \right) \times }\\ {{{\left[ {\left( {\eta ' - 2{d_2}} \right)/\left| {\eta ' - 2{d_2}} \right|} \right]}^m} \times }\\ {{{\left( { - 1} \right)}^m}{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {\eta ' - 2{d_2}} \right|} \right) \times }\\ {\left. {{{\left[ {\left( {\eta ' - 2{d_2}} \right)/\left| {\eta ' - 2{d_2}} \right|} \right]}^{ - m}}} \right\}{{\rm{e}}^{ - {\rm{i}}n{\theta _1}}}{\rm{d}}{\theta _1}} \end{array} $

$ \xi _{mn}^{\left( {42} \right)} = \int\limits_{ - {\rm{\pi }}}^0 {\left( {\sum\limits_{j = 1}^4 {S_m^{\left( j \right)}} } \right){{\rm{e}}^{ - {\rm{i}}n{\theta _1}}}{\rm{d}}{\theta _1}} $

$ \xi _{mn}^{\left( {51} \right)} = \frac{{{k_1}{\mu _1}}}{2}\int\limits_{ - {\rm{\pi }}}^0 {\left[ {\sum\limits_{j = 1}^4 {v_m^{\left( j \right)}{{\rm{e}}^{{\rm{i}}{\theta _1}}}} + \sum\limits_{j = 1}^4 {\psi _m^{\left( j \right)}{{\rm{e}}^{ - {\rm{i}}{\theta _1}}}} } \right]{{\rm{e}}^{ - {\rm{i}}n{\theta _1}}}{\rm{d}}{\theta _1}} , $

$ \xi _{mn}^{\left( {52} \right)} = \frac{{{k_1}{\mu _1}}}{2}\int\limits_{ - {\rm{\pi }}}^{\rm{0}} {\left[ {\sum\limits_{j = 1}^4 {\chi _m^{\left( j \right)}{{\rm{e}}^{{\rm{i}}{\theta _1}}}} + \sum\limits_{j = 1}^4 {\gamma _m^{\left( j \right)}{{\rm{e}}^{ - {\rm{i}}{\theta _1}}}} } \right]{{\rm{e}}^{ - {\rm{i}}n{\theta _1}}}{\rm{d}}{\theta _1}} , $

$ \xi _n^{\left( 1 \right)} = - \int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {\left( {{G^i} + {G^\tau }} \right){{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } , $

$ \xi _n^{\left( 2 \right)} = - \frac{{{\rm{i}}{k_1}}}{4}\int\limits_{ - {\rm{\pi }}}^{\rm{\pi }} {\left[ {\sum\limits_{j = 1}^4 {{\varphi ^{\left( j \right)}}{{\rm{e}}^{{\rm{i}}\theta }}} + \sum\limits_{j = 1}^4 {{\varphi ^{\left( j \right)}}{{\rm{e}}^{ - {\rm{i}}\theta }}} } \right]{{\rm{e}}^{ - {\rm{i}}n\theta }}{\rm{d}}\theta } $

$ \xi _n^{\left( 3 \right)} = 0 $

$ \xi _n^{\left( 4 \right)} = - \int\limits_{ - {\rm{\pi }}}^{\rm{0}} {\left( {{G^i} + {G^\tau }} \right){{\rm{e}}^{ - {\rm{i}}n{\theta _1}}}{\rm{d}}{\theta _1}} , $

$ \xi _n^{\left( 5 \right)} = - \frac{{{\rm{i}}{k_1}}}{4}\int\limits_{ - {\rm{\pi }}}^{\rm{0}} {\left[ {\sum\limits_{j = 1}^4 {{\varphi ^{\left( j \right)}}{{\rm{e}}^{{\rm{i}}{\theta _1}}}} + \sum\limits_{j = 1}^4 {{\varphi ^{\left( j \right)}}{{\rm{e}}^{ - {\rm{i}}{\theta _1}}}} } \right]{{\rm{e}}^{ - {\rm{i}}n{\theta _1}}}{\rm{d}}{\theta _1}} $

其中，

$ v_m^{\left( 1 \right)} = {\rm{H}}_{m - 1}^{\left( 1 \right)}\left( {{k_1}\left| \eta \right|} \right){\left[ {\eta /\left| \eta \right|} \right]^{m - 1}}, $

$ v_m^{\left( 2 \right)} = - {\rm{H}}_{m - 1}^{\left( 1 \right)}\left( {{k_1}\left| \eta \right|} \right){\left[ {\eta /\left| \eta \right|} \right]^{ - m - 1}} $

$ \begin{array}{*{20}{c}} {v_m^{\left( 3 \right)} = {{\left( { - 1} \right)}^m}{\rm{H}}_{m - 1}^{\left( 1 \right)}\left( {{k_1}\left| {n - 2d} \right|} \right) \times }\\ {{{\left[ {\left( {\eta - 2d} \right)/\left| {\eta - 2d} \right|} \right]}^{m - 1}}} \end{array} $

$ \begin{array}{*{20}{c}} {v_m^{\left( 4 \right)} = - {{\left( { - 1} \right)}^m}{\rm{H}}_{m + 1}^{\left( 1 \right)}\left( {{k_1}\left| {\eta - 2d} \right|} \right) \times }\\ {{{\left[ {\left( {\eta - 2d} \right)/\left| {\eta - 2d} \right|} \right]}^{ - m - 1}}} \end{array} $

$ \psi _m^{\left( 1 \right)} = - {\rm{H}}_{m + 1}^{\left( 1 \right)}\left( {{k_1}\left| \eta \right|} \right){\left[ {\eta /\left| \eta \right|} \right]^{m + 1}}, $

$ \psi _m^{\left( 2 \right)} = {\rm{H}}_{m - 1}^{\left( 1 \right)}\left( {{k_1}\left| \eta \right|} \right){\left[ {\eta /\left| \eta \right|} \right]^{ - m + 1}}, $

$ \begin{array}{*{20}{c}} {\psi _m^{\left( 3 \right)} = - {{\left( { - 1} \right)}^m}{\rm{H}}_{m + 1}^{\left( 1 \right)}\left( {{k_1}\left| {n - 2d} \right|} \right) \times }\\ {{{\left[ {\left( {\eta - 2d} \right)/\left| {\eta - 2d} \right|} \right]}^{m + 1}}} \end{array} $

$ \begin{array}{*{20}{c}} {\psi _m^{\left( 4 \right)} = {{\left( { - 1} \right)}^m}{\rm{H}}_{m - 1}^{\left( 1 \right)}\left( {{k_1}\left| {\eta - 2d} \right|} \right) \times }\\ {{{\left[ {\left( {\eta - 2d} \right)/\left| {\eta - 2d} \right|} \right]}^{ - m + 1}}} \end{array} $

$ \chi _m^{\left( 1 \right)} = {\rm{H}}_{m - 1}^{\left( 1 \right)}\left( {{k_1}\left| \eta \right|} \right){\left[ {\eta /\left| \eta \right|} \right]^{m - 1}}, $

$ \chi _m^{\left( 2 \right)} = - {\rm{H}}_{m + 1}^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _2}} \right|} \right){\left[ {{\eta _2}/\left| {{\eta _2}} \right|} \right]^{ - m - 1}} $

$ \chi _m^{\left( 3 \right)} = {\left( { - 1} \right)^m}{\rm{H}}_{m - 1}^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _3}} \right|} \right){\left[ {{\eta _3}/\left| {{\eta _3}} \right|} \right]^{m - 1}}, $

$ \chi _m^{\left( 4 \right)} = - {\left( { - 1} \right)^m}{\rm{H}}_{m + 1}^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _4}} \right|} \right){\left[ {{\eta _4}/\left| {{\eta _4}} \right|} \right]^{ - m - 1}}, $

$ \gamma _m^{\left( 1 \right)} = - {\rm{H}}_{m + 1}^{\left( 1 \right)}\left( {{k_1}\left| \eta \right|} \right){\left[ {\eta /\left| \eta \right|} \right]^{m + 1}} $

$ \gamma _m^{\left( 2 \right)} = - {\rm{H}}_{m - 1}^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _2}} \right|} \right){\left[ {{\eta _2}/\left| {{\eta _2}} \right|} \right]^{ - m + 1}}, $

$ \gamma _m^{\left( 3 \right)} = - {\left( { - 1} \right)^m}{\rm{H}}_{m + 1}^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _3}} \right|} \right){\left[ {{\eta _3}/\left| {{\eta _3}} \right|} \right]^{m + 1}}, $

$ \gamma _m^{\left( 4 \right)} = {\left( { - 1} \right)^m}{\rm{H}}_{m - 1}^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _4}} \right|} \right){\left[ {{\eta _4}/\left| {{\eta _4}} \right|} \right]^{ - m + 1}}, $

$ \zeta = {\rm{H}}_{m - 1}^{\left( 1 \right)}\left( {{k_2}\left| \eta \right|} \right){\left[ {\eta /\left| \eta \right|} \right]^{m - 1}}, $

$ \vartheta = - {\rm{H}}_{m + 1}^{\left( 1 \right)}\left( {{k_2}\left| \eta \right|} \right){\left[ {\eta /\left| \eta \right|} \right]^{m + 1}}, $

$ \delta = {\rm{H}}_{m - 1}^{\left( 2 \right)}\left( {{k_2}\left| \eta \right|} \right){\left[ {\eta /\left| \eta \right|} \right]^{m - 1}}, $

$ \zeta = - {\rm{H}}_{m - 1}^{\left( 2 \right)}\left( {{k_2}\left| \eta \right|} \right){\left[ {\eta /\left| \eta \right|} \right]^{m + 1}} $

$ {\varphi ^{\left( 1 \right)}} = {\rm{H}}_{ - 1}^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {\eta _0}} \right|} \right)\left[ {\left( {\bar \eta - {{\bar \eta }_0}} \right)/\left| {\eta - {\eta _0}} \right|} \right], $

$ {\varphi ^{\left( 2 \right)}} = {\rm{H}}_{ - 1}^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {{\eta '}_0}} \right|} \right)\left[ {\left( {\bar \eta - {{\bar \eta '}_0}} \right)/\left| {\eta - {{\eta '}_0}} \right|} \right], $

$ {\varphi ^{\left( 3 \right)}} = {\rm{H}}_{ - 1}^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {{\bar \eta }_0} - 2{\rm{i}}h} \right|} \right)\left[ {\frac{{\bar \eta - {\eta _0} + 2{\rm{i}}h}}{{\left| {\eta - {{\bar \eta }_0} - 2{\rm{i}}h} \right|}}} \right], $

$ {\varphi ^{\left( 4 \right)}} = {\rm{H}}_{ - 1}^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {{\bar \eta '}_0} - 2{\rm{i}}h} \right|} \right)\left[ {\frac{{\bar \eta - {{\eta '}_0} + 2{\rm{i}}h}}{{\left| {\eta - {{\bar \eta '}_0} - 2{\rm{i}}h} \right|}}} \right], $

$ {\varphi ^{\left( 1 \right)}} = {\rm{H}}_{ - 1}^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {\eta _0}} \right|} \right)\left[ {\left( {\eta - {\eta _0}} \right)/\left| {\eta - {\eta _0}} \right|} \right], $

$ {\varphi ^{\left( 2 \right)}} = {\rm{H}}_{ - 1}^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {{\eta '}_0}} \right|} \right)\left[ {\left( {\eta - {{\eta '}_0}} \right)/\left| {\eta - {{\eta '}_0}} \right|} \right], $

$ {\varphi ^{\left( 3 \right)}} = {\rm{H}}_{ - 1}^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {{\bar \eta }_0} - 2{\rm{i}}h} \right|} \right)\left[ {\frac{{\eta - {{\bar \eta }_0} + 2{\rm{i}}h}}{{\left| {\eta - {{\bar \eta }_0} - 2{\rm{i}}h} \right|}}} \right], $

$ {\varphi ^{\left( 4 \right)}} = {\rm{H}}_{ - 1}^{\left( 1 \right)}\left( {{k_1}\left| {\eta - {{\bar \eta }_0} - 2{\rm{i}}h} \right|} \right)\left[ {\frac{{\eta - {{\bar \eta }_0} - 2{\rm{i}}h}}{{\left| {\eta - {{\bar \eta }_0} - 2{\rm{i}}h} \right|}}} \right] $

式中：θ为坐标系xoy内辐角，θ₁为坐标系x₁oy₁内辐角。

3 直角域中SH波形成的位移场

入射波w^{(i, e)}、反射波w^{(r, e)}、散射波w^{(s1, e)}、w^{(s2, e)}均满足直角域中水平边界Γ_H和垂直边界Γ_V上应力自由条件，利用“镜像法”构造其表达：

$ \begin{array}{l} {w^{\left( {i,e} \right)}} = {w_0}\left\{ {\exp \left\{ {\frac{{{\rm{i}}{k_1}}}{2}\left[ {\eta {{\rm{e}}^{ - {\rm{i}}{\alpha _0}}} + \bar \eta {{\rm{e}}^{{\rm{i}}{\alpha _0}}}} \right]} \right\} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\exp \left\{ {\frac{{{\rm{i}}{k_1}}}{2}\left[ {\eta {{\rm{e}}^{{\rm{i}}{\alpha _0}}} + \bar \eta {{\rm{e}}^{ - {\rm{i}}{\alpha _0}}}} \right]} \right\}} \right\} \end{array} $

(13)

$ \begin{array}{l} {w^{\left( {r,e} \right)}} = {w_0}\left\{ {\exp \left\{ {\frac{{{\rm{i}}{k_1}}}{2}\left[ {\left( {\eta - 2d} \right){{\rm{e}}^{ - {\rm{i}}{\beta _0}}} + \left( {\bar \eta - 2d} \right){{\rm{e}}^{{\rm{i}}{\beta _0}}}} \right]} \right\} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\exp \left\{ {\frac{{{\rm{i}}{k_1}}}{2}\left[ {\left( {\eta - 2d} \right){{\rm{e}}^{{\rm{i}}{\beta _0}}} + \left( {\bar \eta - 2d} \right){{\rm{e}}^{ - {\rm{i}}{\beta _0}}}} \right]} \right\}} \right\} \end{array} $

(14)

式中：β₀=π-α₀，α₀为SH波入射角度，在SH波作用下产生的波场与上节中Green函数作用下产生的波场具有相同的形式：

$ \begin{array}{l} {w^{\left( {s1,e} \right)}} = \sum\limits_{m = - \infty }^{ + \infty } {{P_m}\left\{ {H_m^{\left( 1 \right)}\left( {{k_1}\left| {\eta '} \right|} \right)\left( {{{\left[ {\frac{{\eta '}}{{\left| {\eta '} \right|}}} \right]}^m} + {{\left[ {\frac{{\eta '}}{{\left| {\eta '} \right|}}} \right]}^{ - m}}} \right) + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left( { - 1} \right)^m}H_m^{\left( 1 \right)}\left( {{k_1}\left| {\eta ' - 2{d_2}} \right|} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {{{\left[ {\frac{{\eta ' - 2{d_2}}}{{\left| {\eta ' - 2{d_2}} \right|}}} \right]}^m} + {{\left[ {\frac{{\eta ' - 2{d_2}}}{{\left| {\eta ' - 2{d_2}} \right|}}} \right]}^{ - m}}} \right)} \right\} \end{array} $

$ \begin{array}{l} {w^{\left( {s2,e} \right)}} = \sum\limits_{m = - \infty }^{ + \infty } {{B_m}\left\{ {{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| \eta \right|} \right){{\left[ {\frac{\eta }{{\left| \eta \right|}}} \right]}^m} + {\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _2}} \right|} \right) \times } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left[ {\frac{{{\eta _2}}}{{\left| {{\eta _2}} \right|}}} \right]^{ - m}} + {\left( { - 1} \right)^m}{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _3}} \right|} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left[ {\frac{{{\eta _3}}}{{\left| {{\eta _3}} \right|}}} \right]}^m} + {{\left( { - 1} \right)}^m}{\rm{H}}_m^{\left( 1 \right)}\left( {{k_1}\left| {{\eta _4}} \right|} \right){{\left[ {\frac{{{\eta _4}}}{{\left| {{\eta _4}} \right|}}} \right]}^{ - m}}} \right\} \end{array} $

$ {w^{\left( {st1,e} \right)}} = \sum\limits_{n = - \infty }^{ + \infty } {\sum\limits_{m = - \infty }^{ + \infty } {{R_m}{a_{mn}}{K_{mn}}{J_n}\left( {{k_1}\left| {\eta '} \right|} \right){{\left[ {\frac{{\eta '}}{{\left| {\eta '} \right|}}} \right]}^n}} } $

$ \begin{array}{l} {w^{\left( {st2,e} \right)}} = \sum\limits_{n = - \infty }^{ + \infty } {\left[ {{S_m}H_m^{\left( 1 \right)}\left( {{k_2}\left| \eta \right|} \right) + {T_m}{\rm{H}}_m^{\left( 2 \right)}\left( {{k_2}\left| \eta \right|} \right)} \right] \times } \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left[ {\frac{\eta }{{\left| \eta \right|}}} \right]^m} \end{array} $

(15)

式中：w^{(s1, e)}、w^{(s2, e)}分别表示SH波作用下由凸起和衬砌形成散射波位移，w^{(st1, e)}、w^{(st12, e)}分别表示SH波作用下凸起和衬砌中的驻波位移，未知量P_m、Q_m、R_m、S_m、T_m根据边界条件(4) 确定，所列方程组中已知系数与求解Green函数所列方程组中已知系数相同，求解方法与求解Green函数中未知量的方法一致。

利用裂纹切割法，在欲出现裂纹的区域施加与剪应力τ_θz^Ⅰ对应的大小相等、方向相反的出平面荷载-τ_θz^Ⅰ，则裂纹区域内合应力均为零, 从而构造出裂纹。附加的载荷-τ_θz^Ⅰ作为新波源对区域内的波场产生影响，利用坐标系x₁oy₁，对应的复坐标系为η₁=r₁e^iθ₁，在圆形衬砌与直线裂纹共存的直角域中总波场可以表示为

$ \begin{array}{l} {w^{\rm{I}}} = {w^{\left( {i,e} \right)}} + {w^{\left( {r,e} \right)}} + {w^{\left( {s1,e} \right)}} + {w^{\left( {s2,e} \right)}} - \\ \;\;\;\;\;\;\;\;\int_{\left( {{c_0}, - {h_1}} \right)}^{\left( {{c_0} + 2C, - {h_1}} \right)} {\tau _{\theta z}^{\rm{I}}{G^{\rm{I}}}d{\eta _1}} \end{array} $

(16)

式中：τ_θz^Ⅰ(r₁, θ₁)=τ_θz^{(i, e)}(r₁, θ₁)+τ_θz^{(r, e)}(r₁, θ₁)+τ_θz^{(s1, e)}(r₁, θ₁)+τ_θz^{(s2, e)}(r₁, θ₁)，G^Ⅰ为格林函数。

利用坐标系x₁oy₁，在SH波作用下夹杂或圆孔周边的环向剪切应力可以表示为

$ \tau _{\theta z}^ * = \left| {\tau _{\theta z}^ \cdot {\tau _0}} \right| $

(17)

式中：τ₀=ikμw₀为入射应力最大幅值，$\tau _{\theta z}^ \cdot $为圆形衬砌周边的总应力：

$ \begin{array}{l} \tau _{\theta z}^ \cdot = \tau _{\theta z}^{\left( {i,e} \right)} + \tau _{\theta z}^{\left( {r,e} \right)} + \tau _{\theta z}^{\left( {s1,e} \right)} + \tau _{\theta z}^{\left( {s2,e} \right)} - \\ \;\;\;\;\;\;\;\;\int_{\left( {{c_0}, - {h_1}} \right)}^{\left( {{c_0} + 2C, - {h_1}} \right)} {\tau _{\theta z}^{\rm{I}}\left[ {{\rm{i}}\mu \left( {\frac{{\partial {G^{\rm{I}}}}}{{\partial {\eta _1}}}{{\rm{e}}^{{\rm{i}}{\theta _1}}} - \frac{{\partial {G^{\rm{I}}}}}{{\partial {{\bar \eta }_1}}}{{\rm{e}}^{ - {\rm{i}}{\theta _1}}}} \right)} \right]{\rm{d}}{\eta _1}} \end{array} $

(18)

裂纹尖端对应的值即为动应力强度因子。在计算中, 通常定义一个无量纲的动应力强度因子k₃：

$ {k_3} = \left| {\frac{{{\tau _{rz}}\left| {_{\bar r = {{\bar r}_0}}} \right.}}{{\left( {{\tau _0}Q} \right)}}} \right| $

(19)

式中：τ_rz|_r=r0表示裂纹尖端附近区域内微小距离处的名义应力；Q为具有长度平方根量纲的特征参数本文取$Q = \sqrt {{\rm{\pi }}C} $。

4 直角域中凸起和衬砌对SH波散射的计算

本节研究在SH波作用下含裂纹的直角域中衬砌和凸起的动应力集中问题和裂纹尖端动应力因子问题，并对计算结果图进行分析。根据以上理论推导，本文计算SH波由下方向上垂直入射即入射角α₀=π/2时直角域中衬砌与直线裂纹相互作用的模型，可视为地下复杂结构生命线工程的抗震问题。本文令k=k₁、b^*=b/a、h^*=h/a、b₁^*=b₁/a、h₁^*=h₁/a、d₁^*=d₁/a、C^*=C/a、c₀^*=c₀/a，无量纲化的地表位移|W^*|=|W|/a，衬砌厚度比为λ=1-b/a，讨论入射波数ka、基体与衬砌的波数比k^*=k₁/k₂，衬砌与基体的剪切模量比μ^*=μ₂/μ₁、衬砌中心与水平边界Γ _H 垂直距离h、裂纹尖端与衬砌中心垂直距离h₁等参数对衬砌周边动应力集中系数τ_θz^*、裂纹尖端动应力强度因子k₃以及水平地表位移|W^*|的影响。

本文分别取:1)k₁^*=0.5，μ₁^*=0.25；2)k₁^*=2，μ₁^*=4；3)k₁^*=4，μ₁^*=16，3种情况作为算例，分别表示夹杂与基体相对较硬、较软、更软。

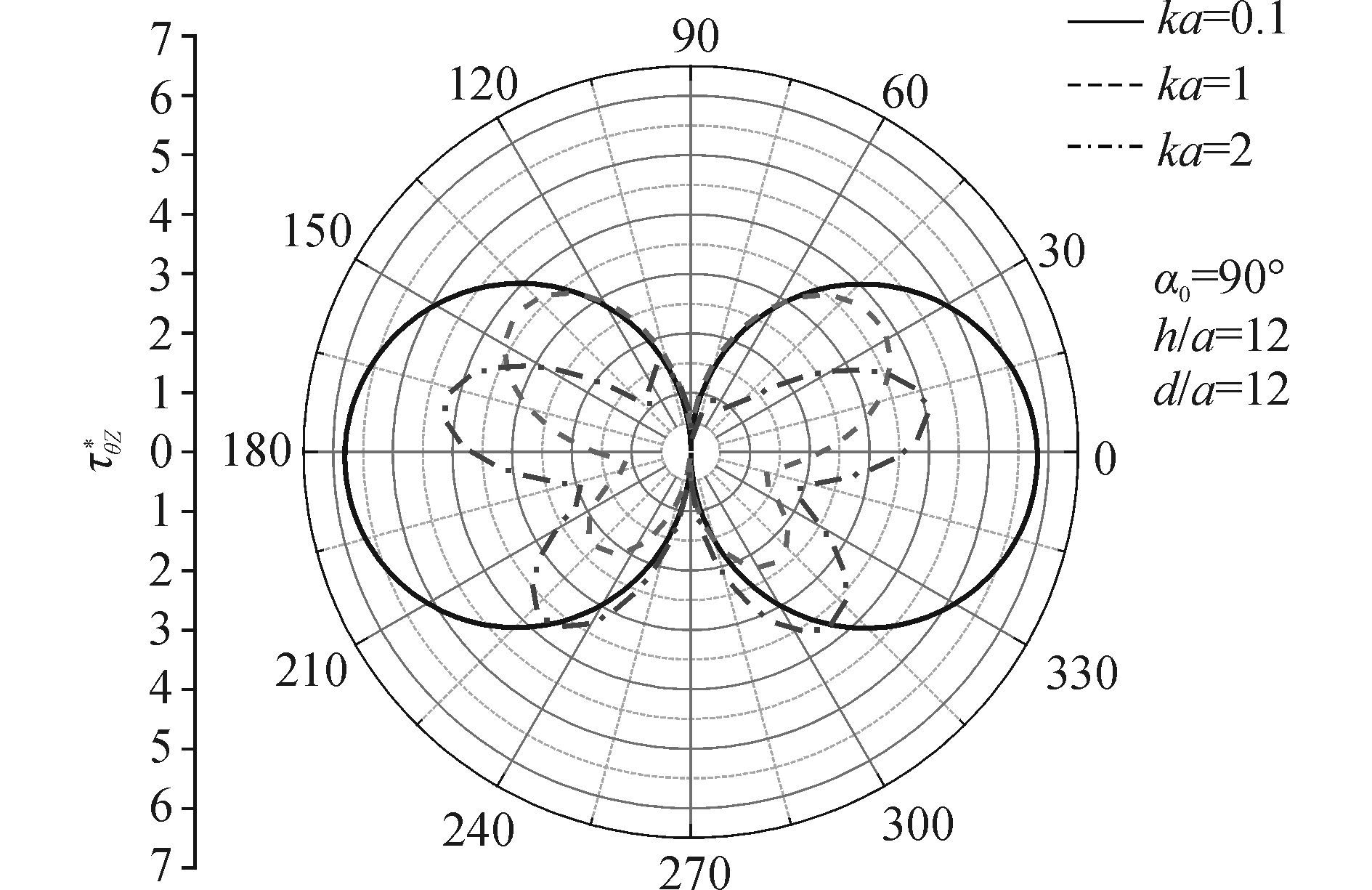
令μ₂=0，b=0，本文模型退化为含圆孔的直角域，取与文献[15]中相同参数，得到圆孔周边动应力系数如图 3所示，与文献[15]中结果吻合较好，证明了本文方法精确可行。

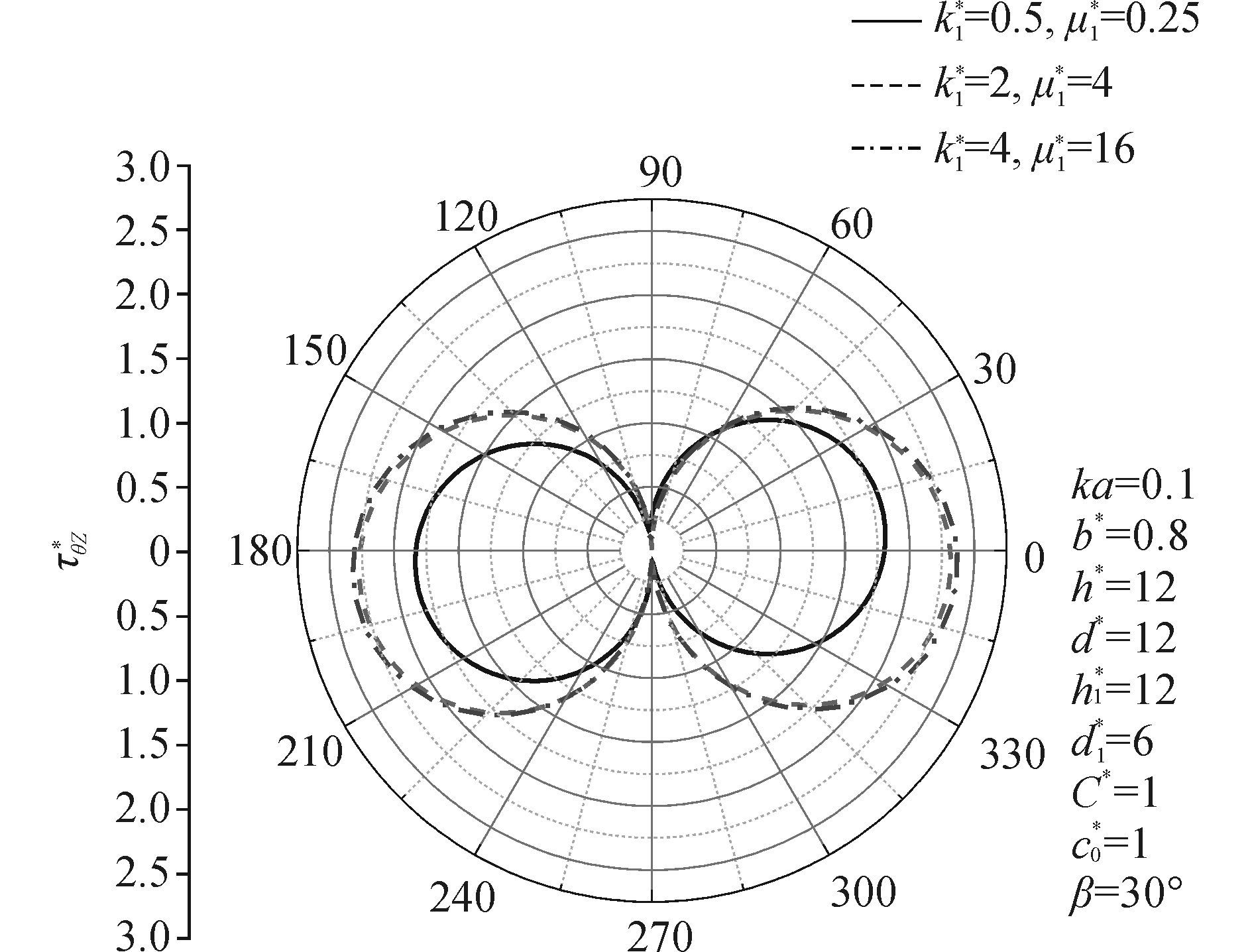
图 4、5给出了SH波低频和高频入射时衬砌周边动应力集中系数τ_θz^*随k^*与μ^*分布情况。图中τ_θz^*基本呈对称分布。由图 4可知，当SH波低频入射时，动应力集中系数最大值分布在衬砌两侧，k₁^*=4，μ₁^*=16时τ_θz^*达到最大值2.37(θ=0°)。在图 5(b)中k₁^*=4，μ₁^*=16时τ_θz^*达到最大值7.45(θ=17°)。所以衬砌相对于基体越软时，τ_θz^*越大。

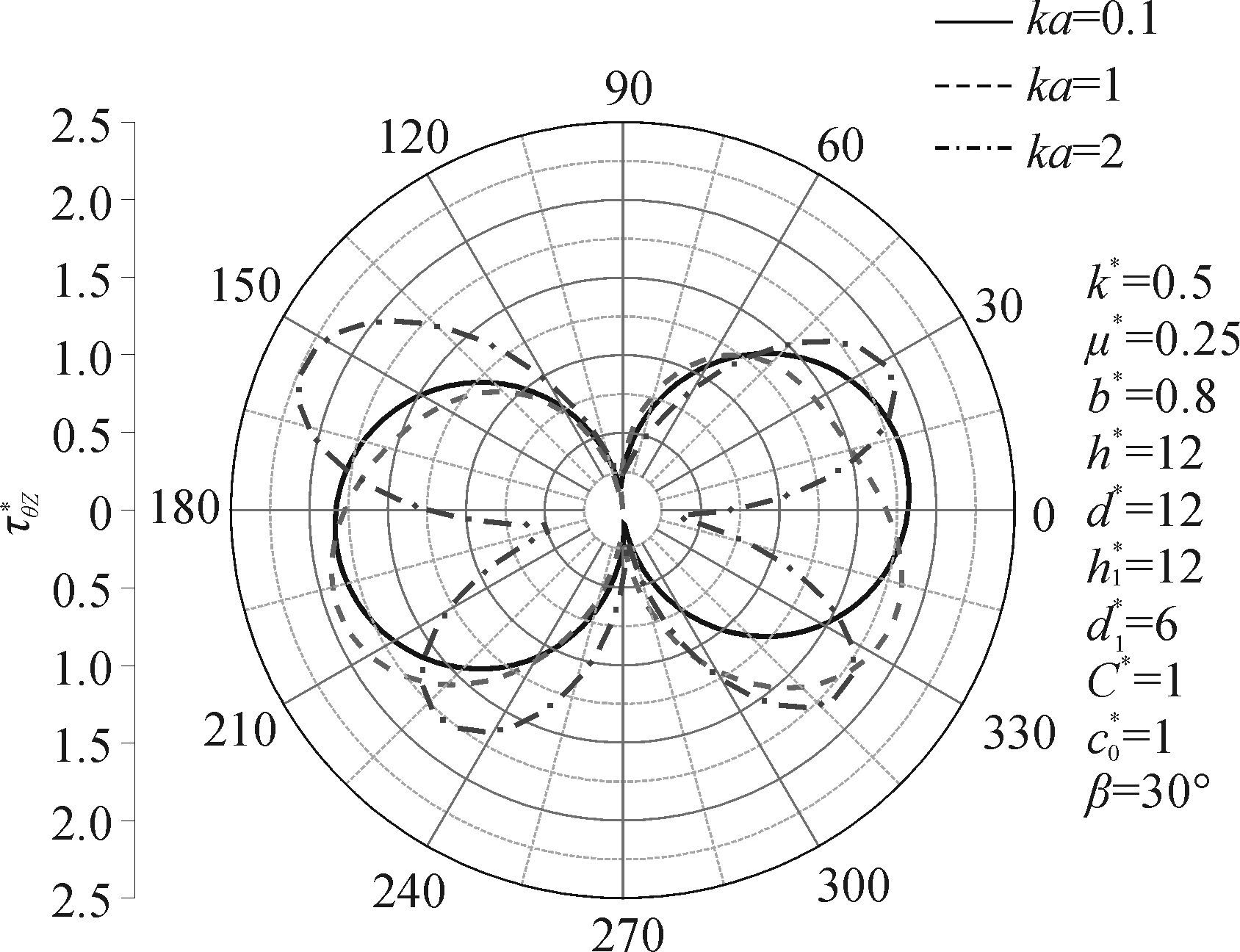
图 6给出衬砌周边DSCF随ka的分布情况。由图 6可知，当ka=2时τ_θz^*达到最大值2.22(θ=153°)。

由以上可知，当SH波高频入射时衬砌相对于基体越软危害越大。

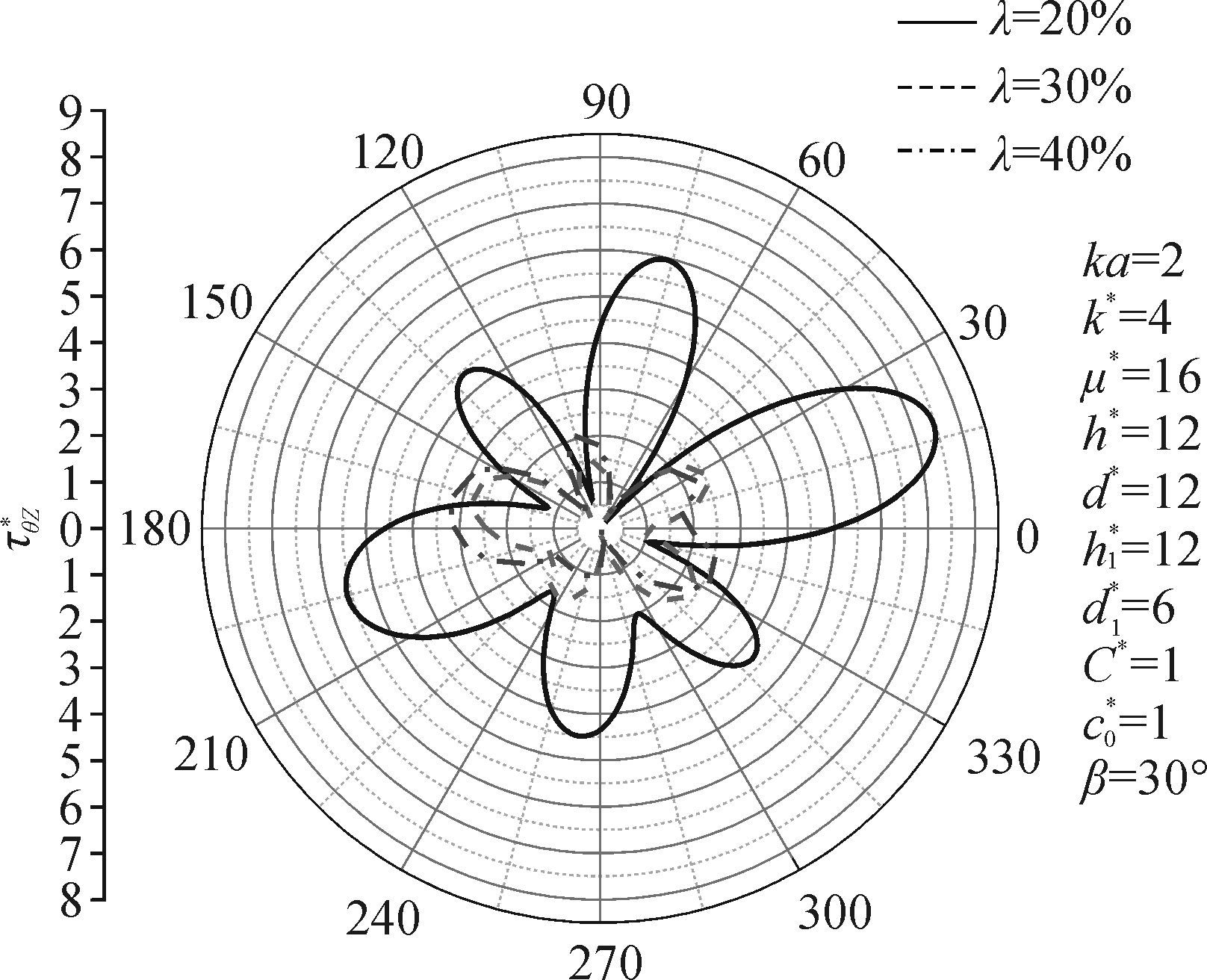
图 7给出了SH波高频入射时衬砌周边DSCF随厚度比λ变化情况。由图 7可知，当λ=30%时τ_θz^*最大值为2.76(θ=166°)，但λ=40%时τ_θz^*最大值为3.20(θ=172°)，因此增加衬砌的厚度比λ并不一定能使τ_θz^*减小。

图 8给出了衬砌周边动应力集中系数τ_θz^*随C^*的分布情况，由图 8可知，C^*=2时，τ_θz^*最大值为3.24(θ=-154°)，约为C^*=0.5时τ_θz^*最大值1.1(θ=-56°)的2.94倍，工程中对于裂纹过长的情况应引起注意。

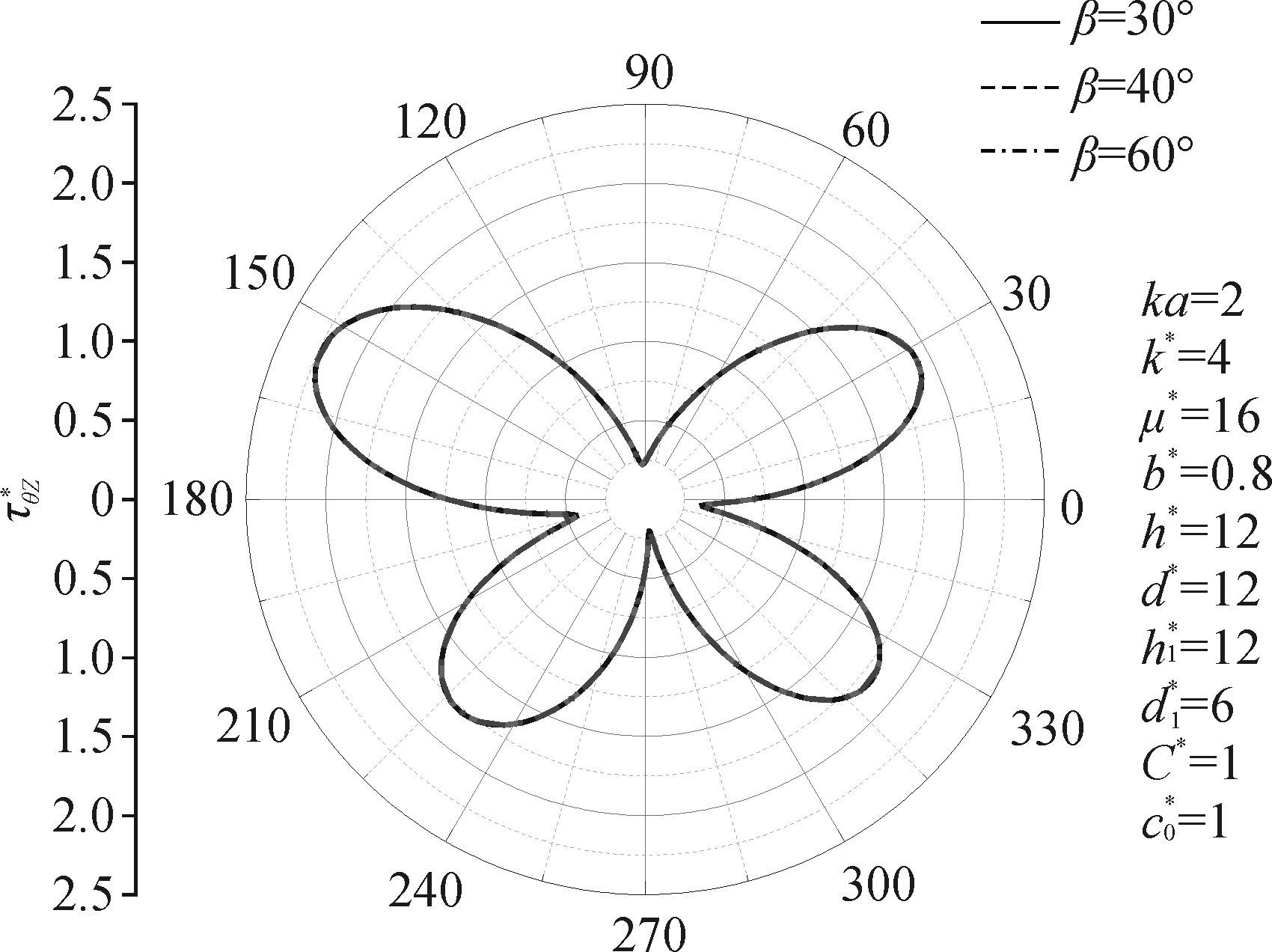
图 9给出了衬砌周边动应力集中系数τ_θz^*随β的分布情况，由图 9可知，τ_θz^*随β的分布基本一致，裂纹角度β对τ_θz^*影响较小。

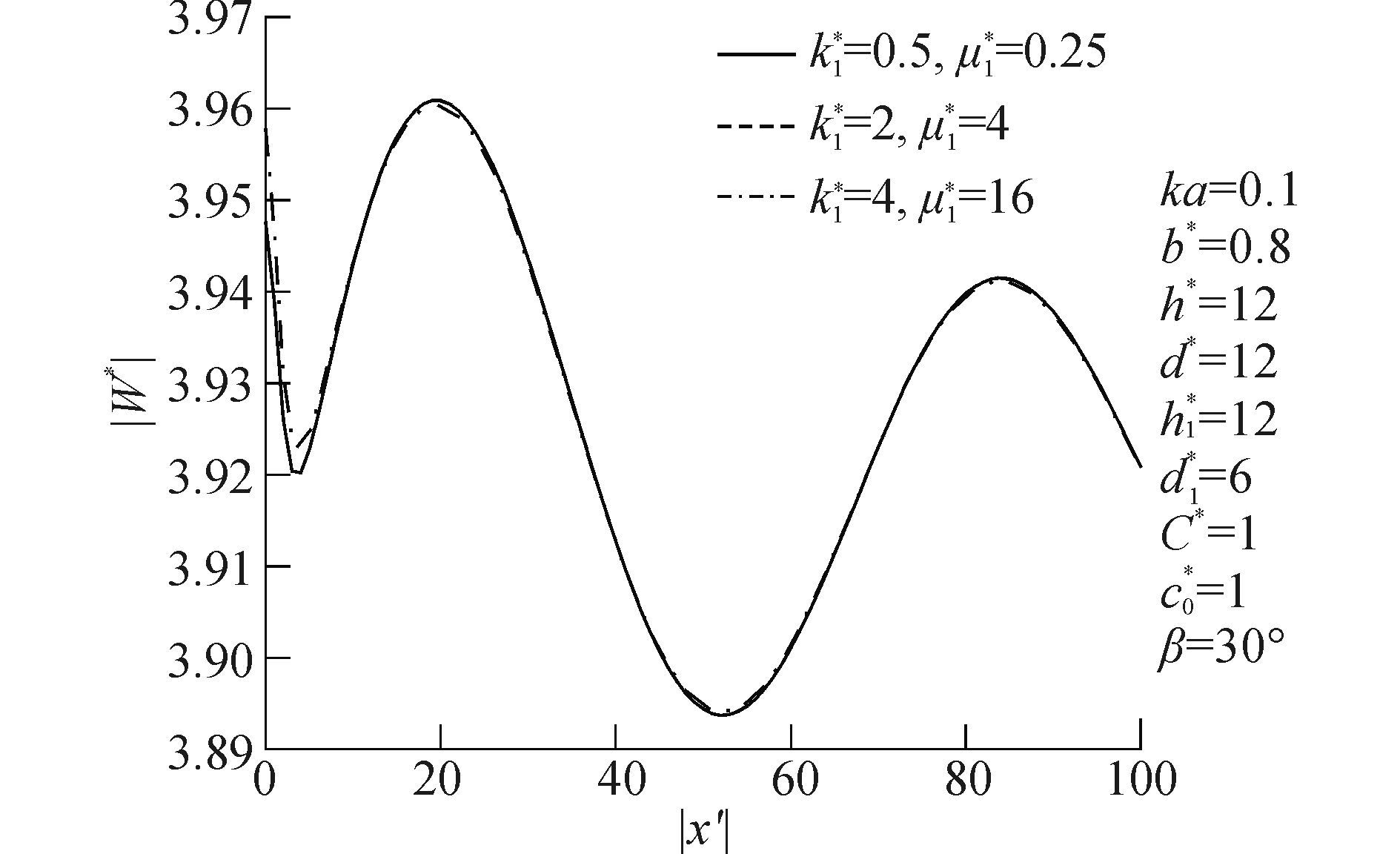
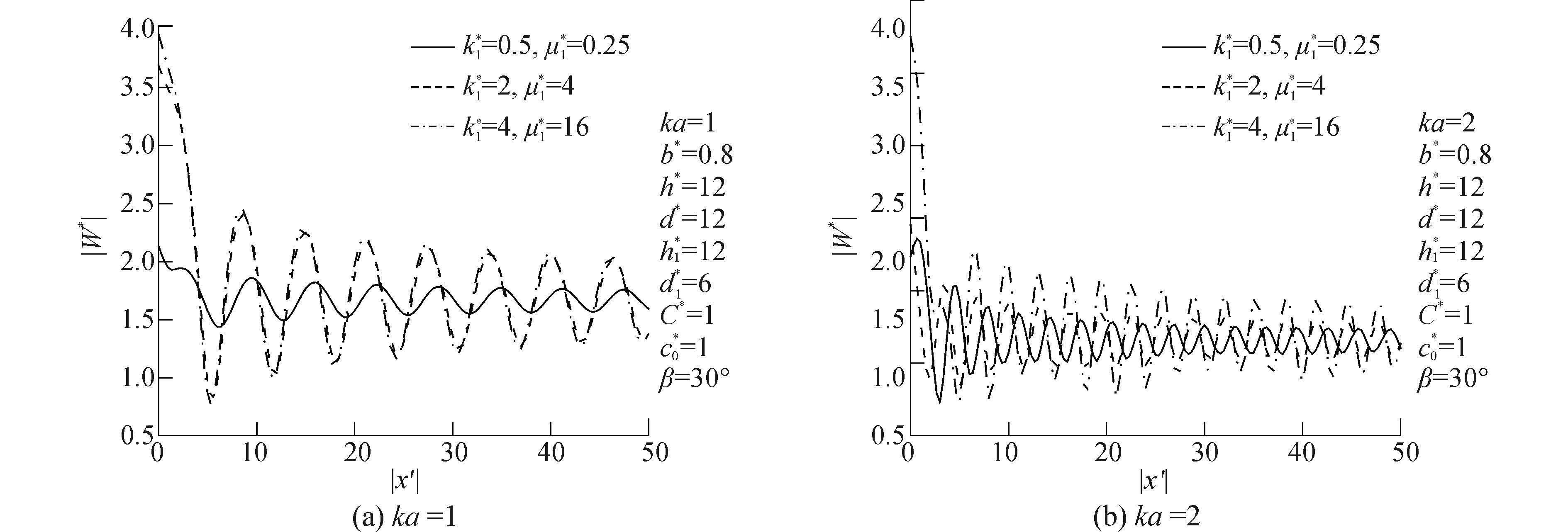
利用坐标系x′o′y′，令θ′=π，得到x′负方向上的地表位移值|W^*|，图 10、11分别给出了SH波低频与高频入射时地表位移|W^*|随k^*与μ^*变化图，横坐标用x′绝对值表示。由图 10可知，当SH波低频入射时，|W^*|随k^*与μ^*分布基本一致，当x=20时|W^*|达到最大值3.96。由图 11可知，当SH波高频入射时，地表位移|W^*|呈现出越来越明显的振荡特征，并沿x方向呈周期性变化，随着x增大振幅越来越小，最终趋于稳定。可见SH波高频入射时k^*与μ^*对|W^*|存在影响。

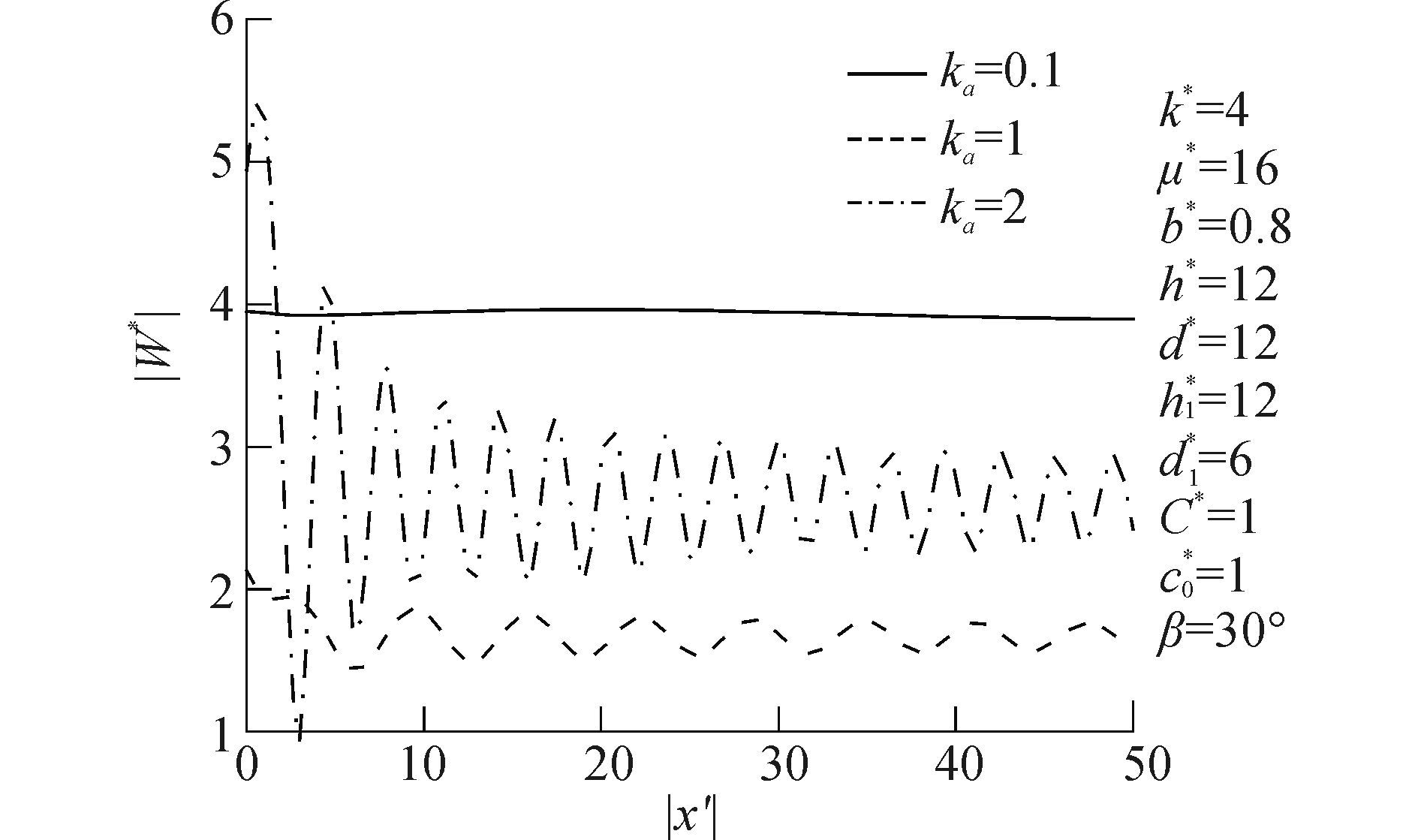
图 12给出了k₁^*=0.5，μ₁^*=|W^*|随ka变化图。由图 9可知，地表位移|W^*|受ka影响较大，当ka=2时，|W^*|在x=0处达到最大值5.3。

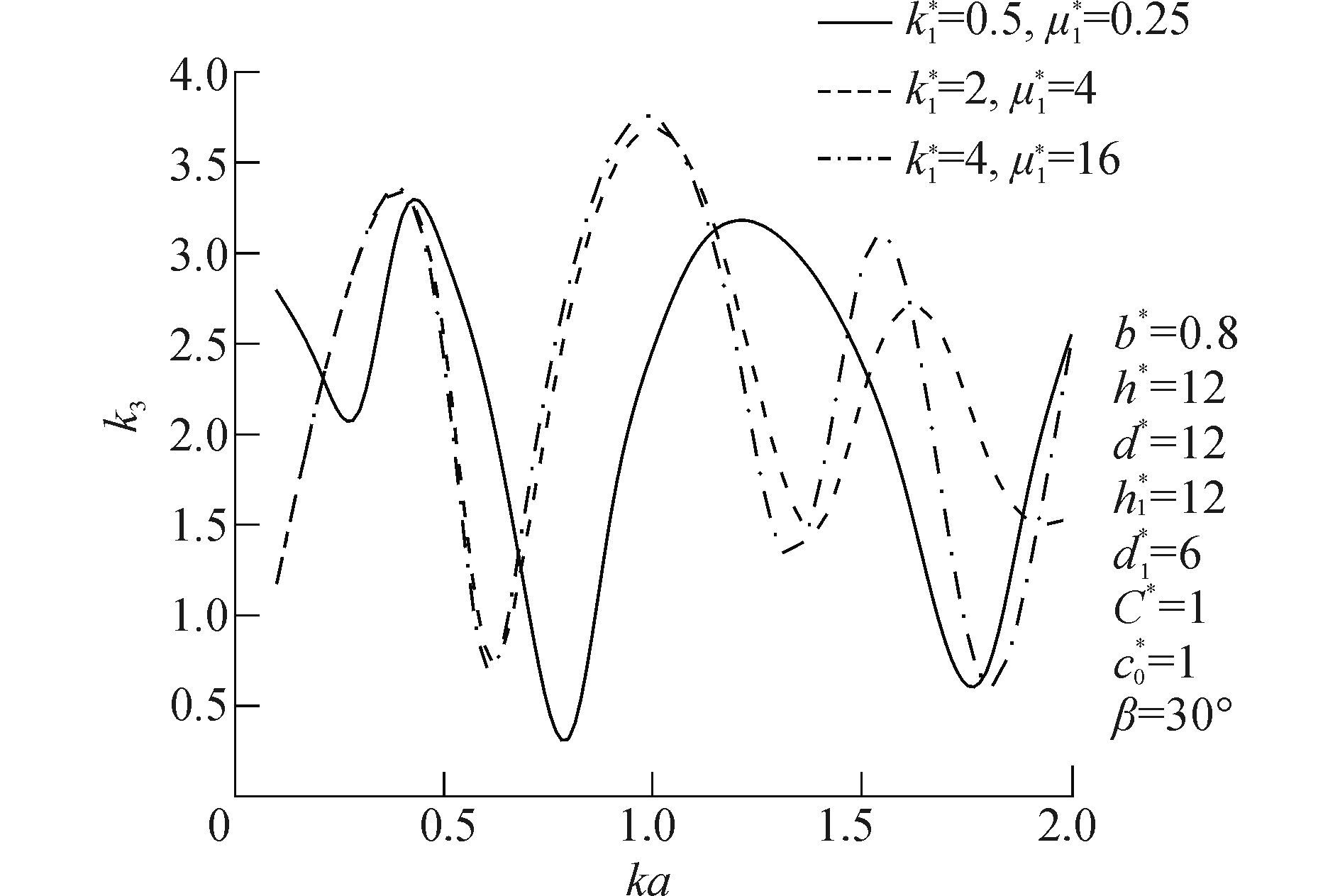
图 13给出了裂纹尖端动应力因子DSIF随ka变化图。在ka=1时k₃达到最大值3.75。

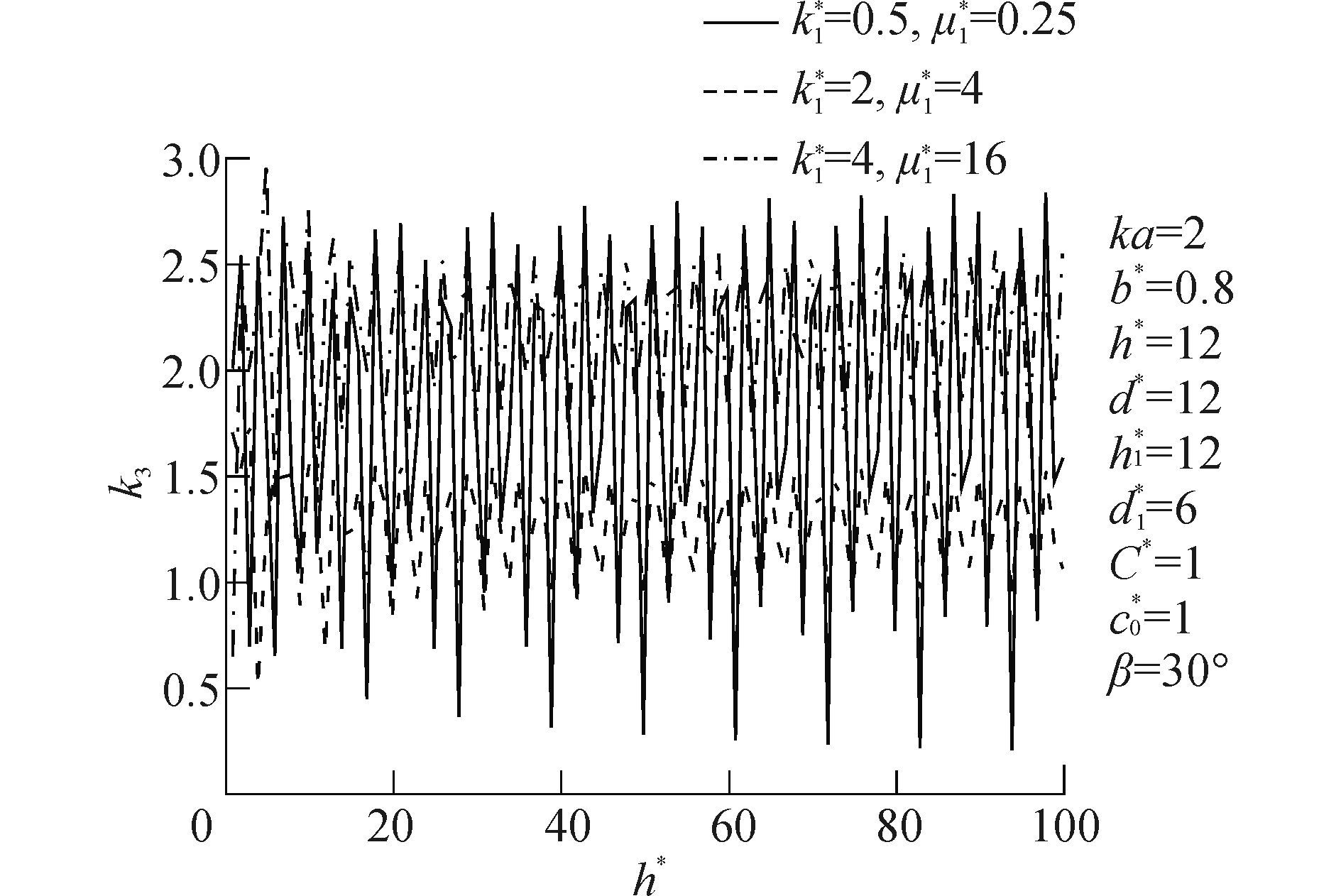
图 14、15分别给出了SH波低频与高频入射时裂纹尖端动应力因子DSIF随h^*变化情况。由图 14可知，SH波低频入射时，当k₁^*=0.5，μ₁^*=0.25衬砌相对基体较硬时在h^*=20、h^*=50、h^*=80处k₃达到最大值4.2。

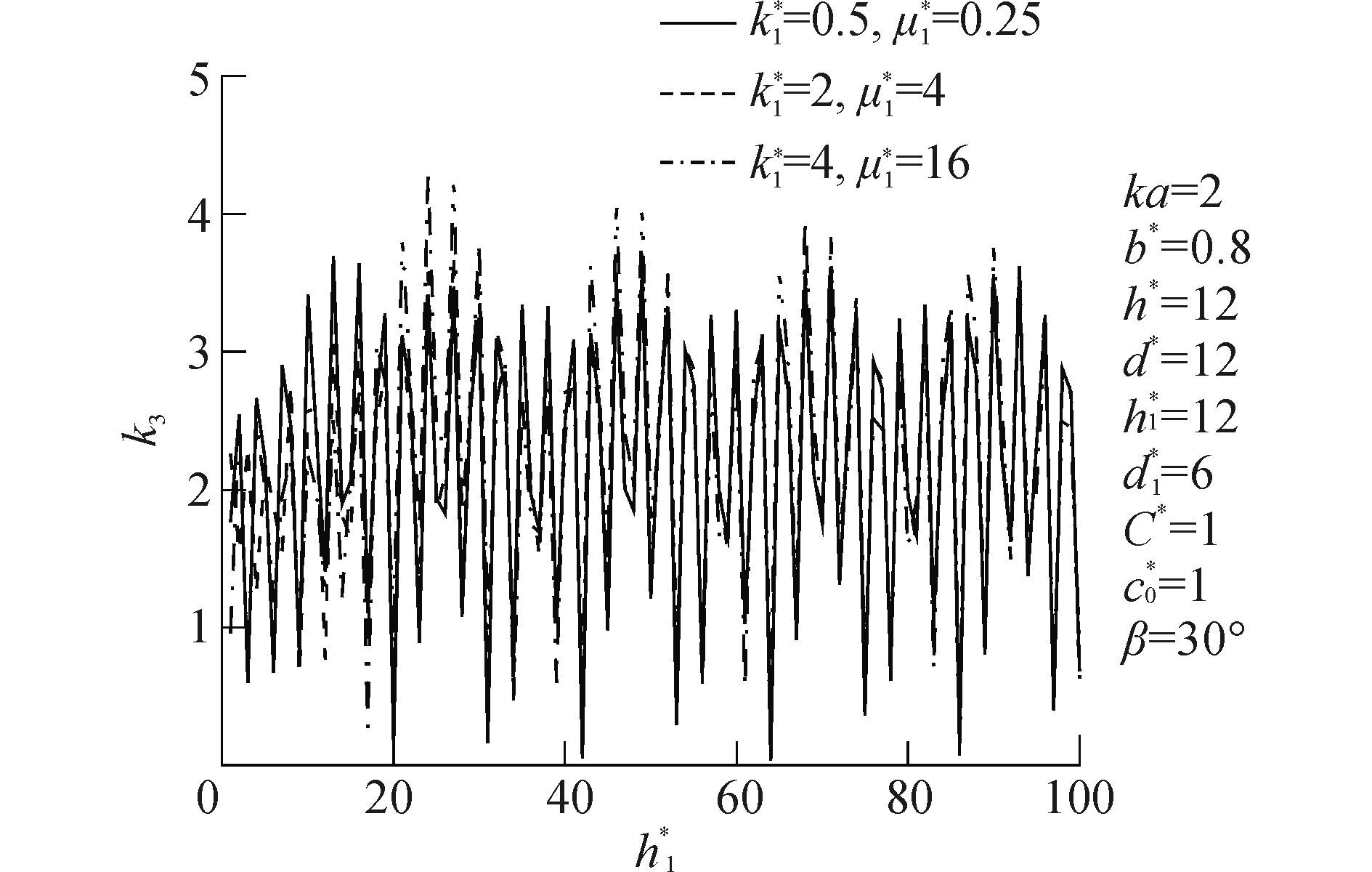
图 16、17分别给出了SH波低频与高频入射时裂纹尖端动应力因子DSIF随h₁^*变化情况。由图 16可知，SH波低频入射时，k₃随h₁^*出现周期性变化，由图 17可知，SH波高频入射时，k₃的振荡性加强，k₁^*=4，μ₁^*=16衬砌相对基体较软时k₃达到最大值4.2。

5 结论

1)ka、裂纹长度C对τ_θz^*影响显著；衬砌相对于基体越软时，τ_θz^*越大；裂纹角度β对τ_θz^*影响较小。增加衬砌的厚度比λ并不一定能使τ_θz^*减小以达到抗震的目的，这在工程中应该引起注意。

2)ka对地表位移|W^*|影响较大，当SH波高频入射时，|W^*|振荡性加强，逐渐趋于稳定。

3) 当SH波低频入射k₃随h^*变化时衬砌相对基体较硬对裂纹尖端危害较大。当SH波高频入射k₃随h₁^*变化时衬砌相对基体较软对k₃危害较大。