为了发挥硫氧镁水泥的优点、克服其强度不高、水化不充分的缺点,多年来学术界一直在致力于采用外加剂技术改善其性能,发现在掺加某些外加剂之后硫氧镁水泥出现了一种新的、未知的碱式硫酸镁结晶相,其力学性能大大提高,在相同条件下其抗压强度、抗折强度均高于氯氧镁水泥,显示了诱人的应用前景。为了区别于传统的硫氧镁水泥,按照水泥命名的规律,将这种形成以5·1·7相为主要水化产物的新型硫氧镁水泥命名为碱式硫酸镁水泥[1-3]。其优点如下:1) 力学强度,早强、高强、高抗折(抗折强度18.3~23.9 MPa)、抗压强度45.8~56.7 MPa、折压比1/2.1~1/3,其抗折强度是相同强度等级的硅酸盐水泥材料的2~3倍左右。2) 特殊的亲和性和高可塑性,利用该新型特种生态胶凝材料将国家亟待解决的工农业固体废弃物(粉煤灰、矿渣等)、农林三废(秸秆、木屑等)转变为新型建筑材料,广泛替代水泥、木材、砖瓦等建筑材料的同时,产品具有不含苯、甲醛等有毒物质,低碳、绿色、环保、抗震、无限可塑性等优点。3) 抗腐蚀性能,应用于耐腐蚀胶凝材料、海工水泥。在氯化镁溶液中浸泡180 d后抗压强度有81.3 MPa提高到97.0 MPa,增加幅度为19%,其抗腐蚀系数为1.19。碱式硫酸镁胶凝材料可用于盐渍土环境和海洋工程中的防腐蚀高性能混凝土。总之, 碱式硫酸镁水泥具有快凝、早强、高强、抗水、抗腐蚀等优点,而且其生产可大量使用工业三废、农业三废,其前景无疑是广阔的[4]。
碱镁水泥是新开发出来不久的胶凝材料, 在碱镁混凝土的研究中发现碱式硫酸镁混凝土具有超过同抗压强度普通混凝土一倍以上的抗拉强度,较大的刚度,且具有早强、抗腐蚀性能强等优点[4-5]。近期对碱式硫酸镁混凝土的开发大部分集中在外墙保温、室内装饰等非承重构件中,为了探讨碱式硫酸镁混凝土在承重结构中,特别是在框架结构中的实际应用,充分了解其在力学性能方面的优越性,拓展其在土木工程行业中的应用领域,那么对碱镁混凝土构件力学性能的研究是必不可少的一个环节。本文对碱镁混凝土大偏心受压柱的力学性能进行试验研究,并与普通混凝土大偏心受压柱试验结果进行对比。
1 大偏压柱试验 1.1 构件的制作本实验以碱式硫酸镁水泥(含粉煤灰)为胶凝材料制备混凝土(见表 1)。所使用的砂子为碱镁水泥所用砂为河砂,含水率为0.8%;碎石(石灰岩,强度较低)为10~30 mm单粒级,最大粒径为30 mm。其中氧化镁活性为50%,砂为中砂,粉煤灰为C级,水为自来水,砂、石含水率均为1%。筋混凝土构件取样浇注成型边长为100 mm的混凝土立方体试件。所制备混凝土的表观密度约为2 400 kg/m3,塌落度C40为90,C50为11。
| 表 1 碱镁混凝土构件混凝土配合比 Tab.1 Mix proportion of basic magnesium sulfate cement concrete |
碱式硫酸镁水泥混凝土的基本原料为:碱式硫酸镁水泥、砂、石子、粉煤灰、矿渣、水。试验所用粗骨料为5~25 mm连续级配的碎石。细骨料的细度模数为2.4。碱式硫酸镁水泥的强度等级为42.5, 普通混凝土柱所用水泥为金羚羊牌硅酸盐水泥,强度等级为42.5。
大偏压柱的详图见图 1,碱镁混凝土的配合比见表 1,普通混凝土配合比见表 2,钢筋性能参数满足国家标准。水泥为海螺425水泥,砂、石、减水剂等材料性能指标与碱镁混凝土所用材料相同。其中水泥为海螺425水泥,砂、石、减水剂等材料性能指标与碱镁混凝土所用材料相同。

|
图 1 大偏压柱配筋图 Fig.1 Details of the large eccentric compression column |
| 表 2 普通混凝土1 m3材料用量 Tab.2 Material dosage of portland cement concrete every cubic meter |
对普通混凝土柱和碱镁混凝土柱的同批取样试块进行28 d强度测试,结果是抗压强度分别达到C40和C50的强度要求;对碱镁混凝土进行抗拉强度测试,发现其强度为同标号普通混凝土抗拉强度的一倍。
试验前除按照混凝土构件测试规范的要求制作钢柱帽钢柱靴。偏心距为170 mm,柱帽加载点位置处粉笔标注。
1.3 碱式硫酸镁水泥钢筋混凝土偏心受压柱加载试验研究1) 仪表布置:
① 加荷用500 t长柱压力试验机;
② 测挠度用百分表支架固定百分表;
③ 测钢筋应力用电阻应变仪及平衡预调箱;
④ 测定混凝土应变用混凝土应变片。
测点及仪表布置如图 2所示。

|
图 2 试验中的大偏压柱加载装置 Fig.2 Schematic diagram of loading machine in the experiments |
本次实验在牛腿柱外平面(加载后的受拉侧)的跨中和距两个柱头300 mm处分别设置一个位移计(见图 2), 通过动态3817动态采集系统和计算机连续采集,测量柱的挠度沿柱高的变化。
布置了混凝土应变片的柱三个面为侧面、柱牛腿受拉平面(即牛腿柱外平面)、牛腿柱受压面(即牛腿柱内平面)。其中侧面粘贴3个等间距竖向应变片是为了测定大偏压柱是否满足平截面假定,其他两个面只在跨中区域分别粘贴横向应变片和竖向应变片。
钢筋应变片布置在四根主筋的跨中位置,试验中,电阻应变片的应变数值采集通过东华3815静态采集系统采集完成。
2) 试验步骤:临近开裂时,荷载减半,直至开裂,记下开裂荷载;开裂后,逐级加荷,直至破坏,记下破坏荷载。
3) 检查仪表,调整仪表初读数。
4) 分级加载,开裂前每级加载20 kN,开裂后,每级加载4 kN,纵向钢筋受力屈服后,每级加载2 kN。满载后分2级卸载。加卸载每级停歇时间5 min,并在前后两次加载的中间时间内读数并记录,数据填入记录。
5) 参照估算的试验柱开裂荷载值,分级缓慢加载,加载间隙注意观察裂缝是否出现。
6) 每级加载后,在间歇时间内测读并记录千分表和百分表以及压力机荷载读数。
7) 所加荷载约为试验柱估算的破坏荷载的60%~70%时,用读数放大镜测读试验柱上最大裂缝宽度、用直尺量测裂缝间距。
8) 加载至试验柱破坏, 记录压力机荷载读数。
2 试验过程与分析 2.1 大偏心受压破坏过程描述碱镁混凝土大偏压破坏始于受拉区钢筋屈服,然后受压区混凝土压碎,整个构件屈服破坏,有明显屈服过程,类似于延性破坏。
碱镁水泥混凝土柱开裂荷载为170 kN,裂缝在牛腿侧面跨中上侧出现,此时跨中挠度为1.17 mm;随着荷载的增加,裂缝逐渐对称出现在远离跨中的位置至柱顶和柱脚;随着荷载进一步增加至破坏荷载65%,裂缝逐渐变宽并向牛腿柱侧面延伸发展;随着荷载进一步增加至320 kN,牛腿柱侧面底部有裂缝出现,并向上延伸。
接近屈服荷载时,受压区(牛腿柱正面)开始起皮,出现细小裂缝;当受拉区裂缝宽度急剧增大,牛腿柱向加载方向明显侧弯时,受拉区钢筋应变片显示受拉钢筋屈服;此时没有进一步增加荷载,受压区混凝土表面仍然继续开裂并扩展、变宽,直至大片混凝土表面脱落,露出的压筋已经屈服变弯,此时数采仪荷载读数为450 kN,柱中挠度为3.4 mm。但直至构件屈服破坏,牛腿柱侧面裂缝都没有进一步延伸至牛腿柱正面, 且箍筋应变片读数显示箍筋远未屈服。此时碱镁水泥混凝土柱的破坏过程和破坏特征类似于普通硅酸盐混凝土柱,但破坏荷载明显高于普通砼柱(在相同混凝土强度等级条件下)。碱镁混凝土柱裂缝展开图如图 3所示。

|
图 3 大偏压柱三面裂缝展开图 Fig.3 Diagram of cracking expansion of the column |
图 4数据结果显示,相同荷载作用下,碱镁砼柱比普通砼柱的变形大,显示了较小的刚度;碱镁砼柱也比普通砼柱的极限变形大。

|
图 4 碱镁混凝土大偏压柱破坏形态 Fig.4 Failure modes of the large eccentric compression column of BMS |
试验过程中和试验结果还显示,柱在大偏心荷载作用下的最大位移一般不是发生在跨中,而是稍稍偏上或偏下,这与设计中的箍筋位置、施工过程产生的误差等因素有关。
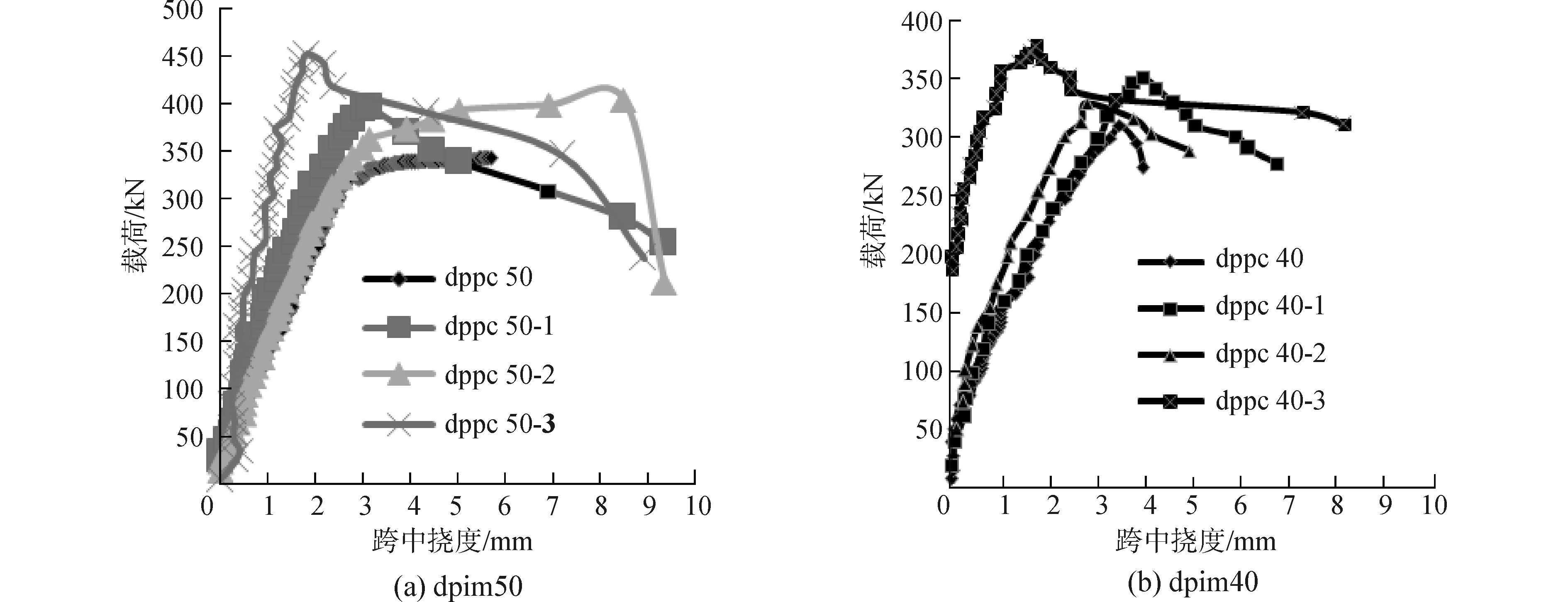
从图 5对比曲线可以看出,碱镁混凝土大偏压柱下降段较平缓,说明其延性好于普通砼。
|
图 5 大偏压构件荷载-跨中挠度对比曲线 Fig.5 Relation curves between the loading and the deflection of the large eccentric compression column at the midspan |
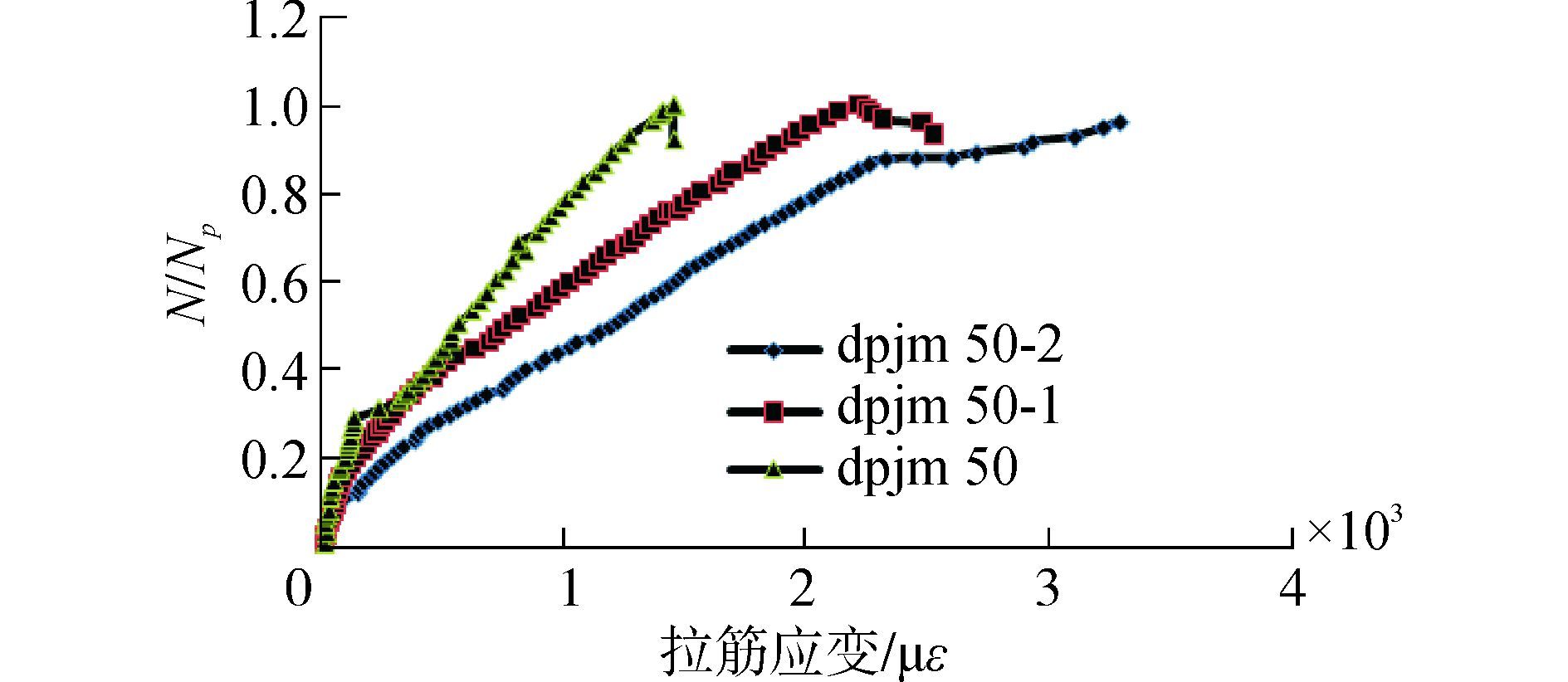
图 6中可见,无论普灰还是碱镁柱,随着荷载的增加,钢筋应变的增加开始时比较缓慢,以后逐渐加快,当应力到达屈服点后,钢筋应变急剧加快。
|
图 6 大偏压柱钢筋拉应变-相对荷载曲线 Fig.6 Relation curves between the relative loading and the relative deflection of the large eccentric compression column at the midspan |
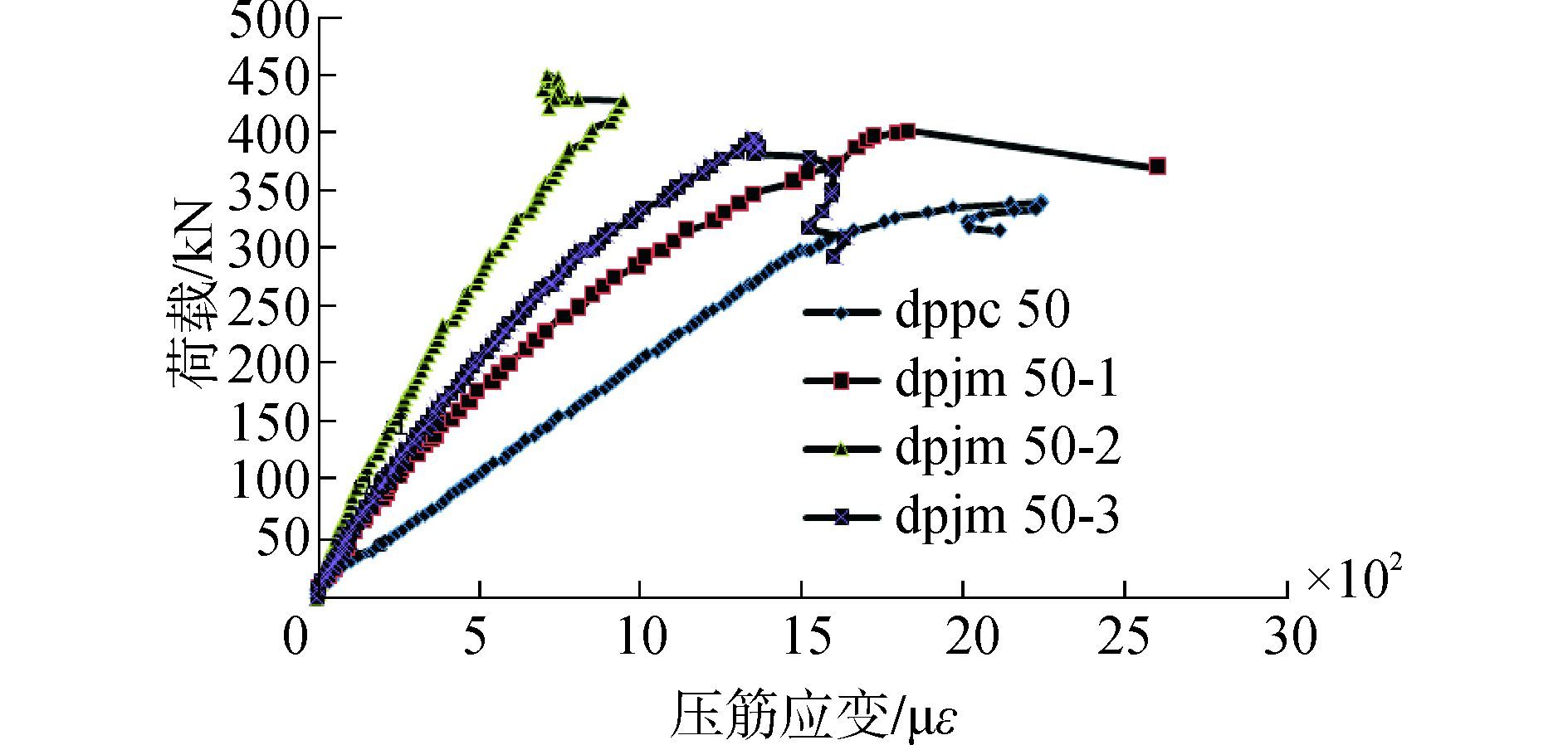
从图 7中可见,荷载作用下,加载至极限荷载80%以前,荷载-应变关系曲线接近直线;随着荷载的增加,应变发展加快,曲线开始非线性发展。
|
图 7 大偏压相对荷载-压筋应变对比曲线 Fig.7 Relation curves between the relative loading and the strain of compressive reinforcement of the large eccentric compression column at the midspan |
碱镁混凝土大偏压构件的正截面承载力计算与普通钢筋混凝土计算的主要不同之处,在于要考虑截面受拉区碱镁混凝土的抗拉作用。在分析碱镁混凝土柱正截面受力过程时,必须满足几何、物理和静力三方面的关系。
1) 变形协调几何关系-平截面假定。
从图 9可知,碱镁混凝土大偏压构件完全符合平截面假定。
2) 钢筋的应力-应变关系。
为了简化计算,正截面承载力计算时受力钢筋采用简化的理想弹塑性应力-应变关系,即钢筋的应力取等于钢筋应变与其弹性模量的乘积,但不大于钢筋的强度设计值。纵向钢筋的极限拉应变取0.01。
其应力-应变关系方程为
| ${\delta _s} = {E_s}{A_s} \le {f_y}$ |
3) 碱镁混凝土的应力-应变关系:
| $y = x + {x^2} + {x^3}\left( {0 \le x < 1} \right)$ |
| $y = \frac{x}{{6{{\left( {x - 1} \right)}^2} + x}}\left( {x \ge 1} \right)$ |
4) 关于截面拉区碱镁混凝土的贡献。
在普通混凝土大偏压构件正截面承载力计算时,一般不考虑截面拉区混凝土的贡献,经过以往分析发现,如果考虑了混凝土的抗拉强度,截面最终承载力的增加不会超过1.5%。因此其对破坏弯矩的影响非常微小可忽略不计。而对于碱镁混凝土受弯构件,混凝土具有较高的抗拉强度(尤其是较高强度的碱镁混凝土),经计算发现,拉区碱镁混凝土的拉力对柱截面承载力的贡献随着纵筋配筋率的变化约在10%~30%范围内变化,因此在正截面受弯承载力计算时应该考虑截面拉区碱镁混凝土拉力的贡献。
2.2 碱镁混凝土大偏压柱正截面计算公式从表 3中可以发现碱镁混凝土大偏压柱承载力比普通混凝土大偏压柱高约20%,需要对普通混凝土大偏压计算公式进行修订,须考虑受拉区碱镁混凝土对承载力的贡献。
| 表 3 大偏压柱承载力统计表 Tab.3 Statistical table of the capability of the large eccentric compression column |
仿照普通混凝土,将截面上的曲线应力图形等效为矩形应力图形的原则为
1) 等效矩形应力图形的面积与理论图形的面积相等,即拉应力和压应力的合力大小不变;
2) 等效矩形应力图的形心位置与理论应力图形的形心位置相同,即压应力和拉应力的合力作用点不变;
3) 不考虑主裂缝断面,考虑未开裂面和开裂面的平均效应。
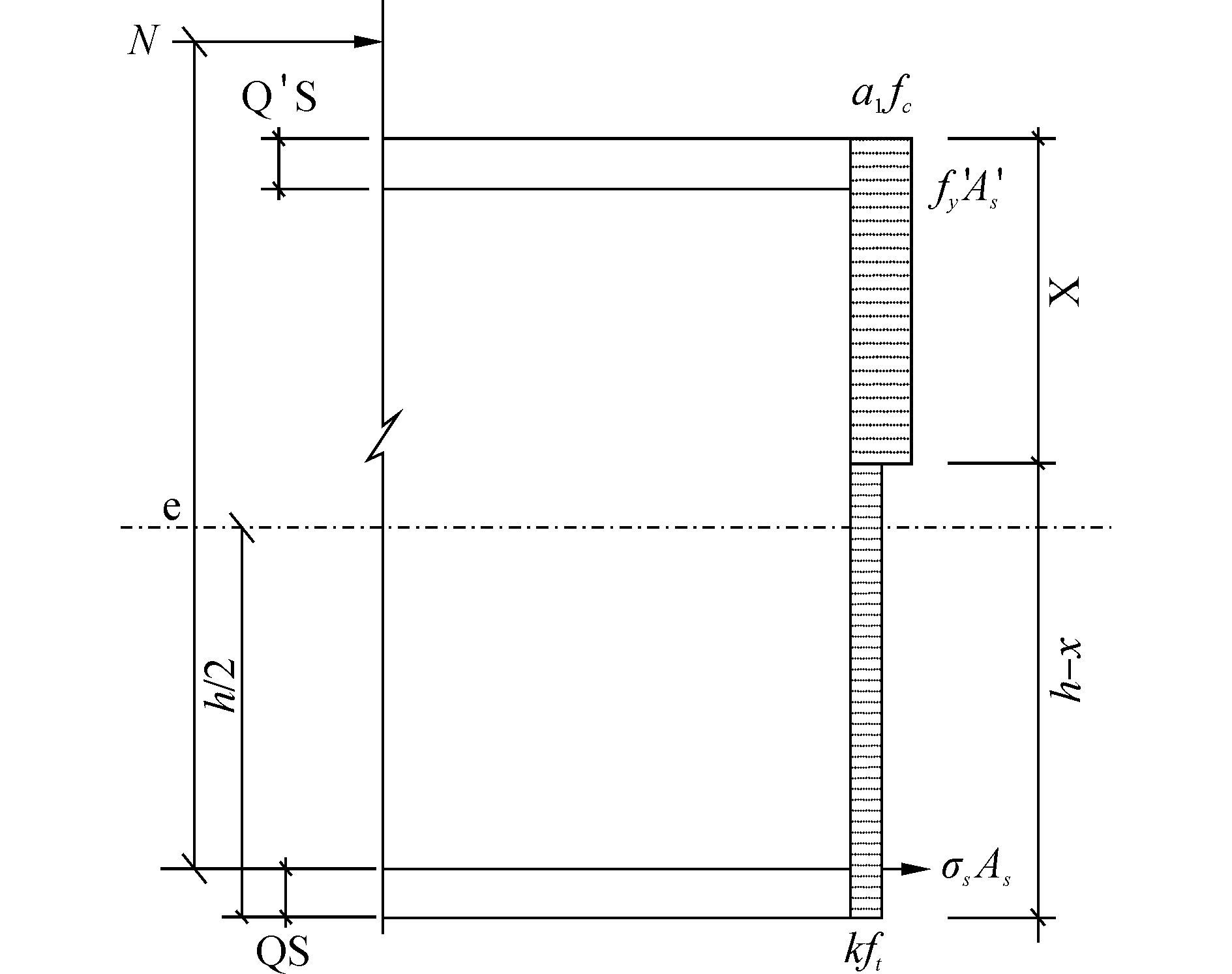
碱镁混凝土柱正截面破坏时的等效应力分布如图 8所示。
|
图 8 矩形截面大偏压构件正截面承载力计算简图 Fig.8 Stress distribution of rectangular section beam |
图 8中受压区高度x可取截面应变保持平面的假定所确定的中和轴高度乘以系数β1=0.78,压应力值可由碱镁混凝土轴心抗压强度设计值fc乘以系数ɑ1确定。当碱镁混凝土强度等级不超过C50时,ɑ1取为1.0。
2.2.2 碱镁混凝土矩形截面大偏压构件正截面受压承载力计算公式| $ Ne \le \alpha {f_c}bx\left( {{h_0} - \frac{x}{2}} \right) - k{f_t}b\left( {h - \frac{x}{\beta }} \right)\left[ {0.5\left( {h - \frac{x}{\beta }} \right) - {\alpha _s}} \right] $ | (1) |
混凝土受压区高度应按下列公式确定:
| $ 0.9{f_c}bx = 0.25{f_t}b\left( {h - x/0.77} \right) + {f_y}{A_s} + N $ | (2) |
| $ e = {e_i} + \frac{h}{2} - a $ | (3) |
| $ {e_i} = {e_0} + {e_a} $ | (4) |
式中:N为柱所受的纵向力;e为轴向压力作用点至纵向受拉普通钢筋的距离;ei为初始偏心距;a为纵向受拉普通钢筋至截面近边缘的距离;e0为轴向压力对截面重心的偏心距;ea为附加偏心距,其值应取20 mm和偏心方向截面最大尺寸的1/30两者中的较大值。
当偏心受压构件的长细比l0/i>34-12(M1/M2)时,控制截面的弯矩应按下式:
| $ M = {C_{\rm{m}}}{\eta _{{\rm{ns}}}}{M_2} $ | (5) |
| $ {\eta _{{\rm{ns}}}} = 1 + \frac{{0.12\left( {1.25{\varepsilon _{cu}} + {f_y}/{E_s}} \right)}}{{\left( {\frac{{{M^2}}}{N} + {e_a}} \right)/{h_0}}}{\left( {\frac{{{l_0}}}{h}} \right)^2} $ | (6) |
式中:Cm为偏心距调节系数;M1、M2为求得的柱端弯矩,绝对值较大端为M2,绝对值较小端为M1;ηns为弯矩增大系数,e0=M2/N; 当Cmηns<1时,取Cmηns=1;h0为截面有效高度。
2.2.3 混凝土受压区高度符合的条件| $ x \le {x_b} $ | (7) |
由于碱镁混凝土柱受拉区混凝土的抗拉作用不能忽略,故导致受压区混凝土等效高度x增大,使得极限弯矩提高,即相当于增加了受拉区钢筋的效果。但x增大到一定值,就会发生类似小偏压的破坏,即受压区混凝土压碎导致的柱破坏。
当x<2a′s时,受压区钢筋达不到受压屈服条件,则可直接以受拉区钢筋合力作用点取矩加上拉区碱镁混凝土产生的弯矩后直接求解。
2.2.4 柱的界限相对受压区高度以及配筋率限值通常认为,对非均匀受压构件,混凝土的极限压应变达到εcu或者受拉钢筋的极限拉应变达到0.01,即这两个极限应变中只要具备其中一个,就标志着构件达到了承载能力极限状态。
偏心受压柱的界限相对受压区高度是指:当构件达到极限承载力时,正截面受拉钢筋应力达到屈服强度时的应变值,同时受压区边缘碱镁混凝土也达到极限压应变值,此时构件处于适筋与超筋之间的界限状态而破坏,其界限状态换算受压区高度xb与截面有效高度h0的比值称为界限相对受压区高度,以ξb表示。
根据应变平截面假定以及界限相对受压区高度的定义,代入β=0.78值、本试验所用HRB400钢筋的fy实测值以及碱镁混凝土的εcu值,可求出本文试验中碱镁混凝土柱的ξb值为
| $ {\xi _{\rm{b}}} = \beta /\left( {1 + {f_y}/{\varepsilon _{cu}}{E_s}} \right) = 0.576 $ | (8) |
虽然碱镁混凝土柱截面的受压区等效系数β比普通混凝土柱小,但由于碱镁混凝土受压边缘的极限压应变εcu为5 100 με,使得碱镁混凝土柱的ξb比采用同种配筋的普通混凝土柱大。由式(1) 可以看出,当柱的实际配筋率大于界限状态破坏时的配筋率时,即实际的ξ>ξb时,则柱破坏时钢筋应力σs小于其相应的屈服强度fy , 属于小偏压破坏;反之,当ξ<ξb时,柱所配钢筋在受弯破坏时能够屈服,属于大偏压破坏。因此,ξb是衡量偏心受压柱破坏时钢筋强度能否充分利用的一个特征值。
当ξ=ξb时,柱相应的配筋梁为最大配筋率。
普通混凝土柱其他计算公式则适用于碱镁混凝土柱,如开裂荷载、挠度、刚度、裂缝平均间距、最大裂缝宽度等。
2.2.5 美国混凝土规范和欧洲规范的相关计算ACI318-99中:
| $ {P_n} = \gamma {{f'}_c}bx + {{f'}_s}{A_s} - {f_s}{A_s} $ | (9) |
| $ \begin{array}{*{20}{c}} {{M_n} = {P_n}e = \gamma {{f'}_c}bx\left( {\frac{h}{2} - \frac{x}{2}} \right) + {{f'}_s}{A_s}\left( {\frac{h}{2} - {{a'}_s}} \right) + }\\ {{f_s}{A_s}\left( {{h_0} - \frac{h}{2}} \right)} \end{array} $ | (10) |
公式中忽略了受压钢筋取代碱镁混凝土面积的情况,因此美国混凝土规范建议:配筋率较大时要考虑受压钢筋减少受压区碱镁混凝土面积的事实,即在受压钢筋作用点处作用一个大小为γf′cAs的拉力。
按美国规范的大偏压柱承载力计算结果:C40为319 kN, C50为341 kN。
欧洲规范对大偏压柱的计算相关规定:对称配筋条件下, 受拉钢筋屈服, 如果同时满足受压钢筋也屈服的条件, 在大偏心情况下有
| $ {N_{{\rm{Ed}}}} = \eta {f_{cd}}b\left( {\xi d} \right) $ | (11) |
| $ {M_{{\rm{Ed}}}} = \eta {f_{cd}}b\left( {\xi d} \right)\left( {\frac{h}{2} - \frac{{\xi d}}{2}} \right) + {f_{yd}}{A_s}\left( {d - {d_2}} \right) $ | (12) |
式中:d2为受压钢筋至受压区边缘的距离。若受压钢筋没有屈服, 则
| $ {N_{{\rm{Ed}}}} = \eta {f_{cd}}b\left( {\xi d} \right) + \frac{{d - {d_2}}}{d}{E_s}{\varepsilon _{cu}}{A_s} - {f_{yd}}{A_s} $ | (13) |
| $ \begin{array}{*{20}{c}} {{M_{{\rm{Ed}}}} = \eta {f_{cd}}b\left( {\xi d} \right)\left( {\frac{h}{2} - \xi d/2} \right) + {f_{yd}}{A_s}\left( {d - \frac{h}{2}} \right) + }\\ {\frac{{d - {d_2}}}{d}{E_s}{\varepsilon _{cu}}{A_s}\left( {\frac{h}{2} - {d_2}} \right)} \end{array} $ | (14) |
如果受压钢筋不能屈服, 则说明受压区高度较小, 受压钢筋发挥的作用也比较小。计算柱的弯矩承载力时, 当受压高度小于某个值时, 可以保守的取为受拉钢筋对受压钢筋点的力矩。为保证受压混凝土形心在受压钢筋形心之外, 中国规范将该受压高度值取为2d2。
因此, 当受压高度值小于2d2时, 欧洲规范指定的受压钢筋一定不会屈服, 可以直接使用规定临界受压高度值为2d2,即有
| $ {M_{{\rm{Ed}}}} = {f_{yd}}{A_s}\left( {d - {d_2}} \right) $ | (15) |
按欧洲规范的大偏压柱承载力计算结果如下:碱镁C40为237.9 kN, 碱镁C50为259.36 kN。
3 结论1) 碱镁混凝土大偏心受压柱与普通混凝土大偏压柱破坏形态类似,但极限承载力高30%左右;
2) 随着碱镁混凝土强度提高,大偏压柱的开裂荷载和极限承载力小幅提高,但延性有所下降;
3) 普通混凝土大偏压柱的承载力计算公式不适用于碱镁混凝土柱,需考虑受拉区碱镁混凝土的作用;普通混凝土柱的抗裂弯矩和挠度计算、最大裂缝宽度计算公式仍然适用于碱镁混凝土大偏压构件;
4) 碱镁混凝土大偏心受压柱比普通混凝土大偏压柱的延性好的多。
| [1] |
WEN Jing, YU Hongfa. Effects of H3PO4 and Ca(H2PO4)2 on mechanical properities and water-resistant properity of thermal decomposed magnesium oxychloride cement[J]. Journal of Central South University, 2013, 20(12): 3729-3735. DOI:10.1007/s11771-013-1901-4 ( 0) 0)
|
| [2] |
ASPDIN J. An improvement in the modes of producing an artificial stone [P].BP5022, 1824-10-21. http://www.academia.edu/8288873/Concrete_and_the_Engineered_Picturesque_The_Parc_des_Buttes_Chaumont_Paris_1867
( 0) 0)
|
| [3] |
WU Chengyou, YU Hongfa, ZHANG Huifang. Extraction of aluminum by pressure acid-leaching method from coal fly ash[J]. Transactions of nonferrous metals society of China, 2012, 22(9): 2282-2288. DOI:10.1016/S1003-6326(11)61461-1 ( 0) 0)
|
| [4] |
吴成友. 碱式硫酸镁水泥的基本理论及其在土木工程中的应用技术研究[D]. 西宁: 中国科学院青海盐湖研究所, 2014: 147-151. WU Chengyou. Fundamental theory and civil engineering application of basic magnesium sulfate cement [D].Xining:University of Chinese academy of sciences, 2014:147-151. http://cdmd.cnki.com.cn/Article/CDMD-80046-1015805248.htm (  0) 0)
|
| [5] |
HE Liang. Design method of concrete of basic magnesium Sulfate [D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2016:78-80.
( 0) 0)
|
| [6] |
WU Chengyou, YU Hongfa, DONG Jinmei, et al. Effects of phosphoric acid and phosphates on magnesium oxysulfate cement[J]. Materials and structures, 2013. DOI:10.1617/s11527-013-0202-6 ( 0) 0)
|
| [7] |
WU Chengyou, YU Hongfa, ZHANG Huifang. The effects of aluminum-leached coal fly ash residue on magnesium oxycloride cement[J]. Advances in cement research, 2013, 25(5): 254-261. DOI:10.1680/adcr.12.00019 ( 0) 0)
|
| [8] |
WU Chengyou, YU Hongfa, ZHANG Huifang. Extraction of aluminum by pressure acid-leaching method from coal fly ash[J]. Transactions of nonferrous metals society of China, 2012, 22(9): 2282-2288. DOI:10.1016/S1003-6326(11)61461-1 ( 0) 0)
|
| [9] |
KERMAN S, CAMPBELL B J, SATYAVARAPU K K, et al. The superstructure determination of displacive distortions via symmetry-mode analysis[J]. Acta crystallographica section A, 2012, 68(2): 222-234. ( 0) 0)
|
| [10] |
TOMCE R, WU Chenyou, YU Hongfa, et al. Dinnebier. Structural characterization of new magnesium oxysulfate hydrate cement phase and its surface reactions with atmospheric carbon dioxide[J]. Journal of the American ceramic society, 2013(9): 1-8. ( 0) 0)
|
| [11] |
中华人民共和国住房和城乡建设部. 混凝土结构设计规范[S]. 中国建筑工业出版社, 2010: 44-46. Ministry of Housing and Urban-Rural Construction of the People's Republic of China. Code for design of concrete structures [S]. China Building Industry Press, 2010:44-46. (  0) 0)
|
| [12] |
施岚青. 注册结构工程师专业考试应试指南[M]. 北京: 中国建筑工业出版社, 2015: 493-523. SHI Lanqing. Guide to professional examinations for registered structural engineers[M]. Beijing: China Building Industry Press, 2015: 493-523. (  0) 0)
|
| [13] |
胡小柱. 再生混凝土柱静力性能研究[D]. 南京: 南京航空航天大学, 2008: 26-27. HU Xiaozhu. Study on the behavior of recycled aggregate concrete columns under static loading[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2008:26-27. http://cdmd.cnki.com.cn/Article/CDMD-10287-2009053820.htm (  0) 0)
|
| [14] |
ZENG Xiangchao. Research on the beams and columns of basic magnesium sulfate cement concrete[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2016:140-145.
( 0) 0)
|
| [15] |
周志祥. 高等钢筋混凝土结构[M]. 北京: 人民交通出版社, 2012: 123-126. ZHOU Zhixiang. Advanced Reinforced Concrete Structures[M]. Beijing: China Communications Press, 2012: 123-126. (  0) 0)
|
| [16] |
FATHIFAZL G. Structural performance of steel reinforced recycled concrete members [D]. Ottawa:Carleton University, 2008:258-260.
( 0) 0)
|
| [17] |
ACI Committee 318. Building code requirements for structural concrete (ACI 318-05) and commentary (318R-05)[S]. American Concrete Institute, Farmington Hills, MI, 2005:430-432.
( 0) 0)
|
| [18] |
BRITISH STANDARDS. BS EN1990:2002 Basis of structural Design[S].London:British Standards Institution, 2002:100-1.
( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


