2. 沧州市华油飞达石油装备有限公司, 河北 沧州 061000
2. Cangzhou Huayou Feida Oil Equipment Limited Company, Cangzhou 061000, China
与陆地风电相比,海上风场具有风能资源丰富、干扰物少、噪声及视觉污染少、空间广阔等诸多优势。为了提高风机发电功率,需要更高的风速,促使海上风电不断向深水海域推进。风力机根据转动轴和风向相对位置分为水平轴风力机和垂直轴风力机。其中,垂直轴风力机不需对风装置,切割风流的噪音污染小,启动风速低,抗风能力强,叶片所需旋转空间小,机舱置于塔柱底部,安装、维护成本较低[1]。
随着单机发电功率的增加(从20世纪80年代的50 kW达到目前的5 MW以及计划中的10~20 MW),风力机的尺寸越来越大,垂直轴风力机的传动系统在风机底部,不会对风机塔架造成影响,这一特点使得垂直轴风力机在海上风电的大型化发展中具有更大的优势。Cahay等提出了安装在半潜式基础上的2 MW三叶片H型风力机的概念[2]。Borg等研究了5MW达里厄型风力机分别安装在Spar型和半潜型浮式基础上的运动响应[3]。Owens等编写了垂直轴风力机结构刚—柔耦合计算的程序包[4]。
有关垂直轴风力机的气动性能研究,目前主要采用数值方法和解析方法。数值法是基于N-S方程,采用CFD数值方法进行模拟,解析方法主要是基于动量理论的流管模型。Berthelsen在HAWC2软件中增加DLLS(动态数据链接库)使其适用于浮式垂直轴风力机气动载荷的计算[5]。韩非非等采用多流管模型和单流管模型分别研究了垂直轴风力机的气动性能,分析了风轮实度、雷诺数以及风剪效应对风机气动性能的影响[6]。叶忱等运用多流管理论和CFD方法分别计算了垂直轴风机的功率,两种方法所得结果吻合较好[7]。左薇等在多流管模型基础上添加附加阻力系数和动态失速修正,分析了流管数目、风轮实度和高径比对Φ型风机气动特性的影响[8]。惠万馨等研究了H型风机的流场分布特点,证明了稳定状态的流场变化具有周期性,尾流区域随风流动逐渐变窄,流场分布与风机相位角有关[9]。Mohamed等对比分析了CFD求解格式对不同网格划分软件的适用条件,并对不同翼型的H型风机气动性能进行了比较[10]。Bedon等对三叶片垂直轴风力机在纵倾条件下的气动性能进行了研究[11]。
本文综合采用双盘面多流管理论和CFD数值模拟方法,研究了Spar型浮式基础支撑的2.6MW-Φ型风力机的气动载荷特性,分析了浮式基础的运动对风力机气动性能的影响。
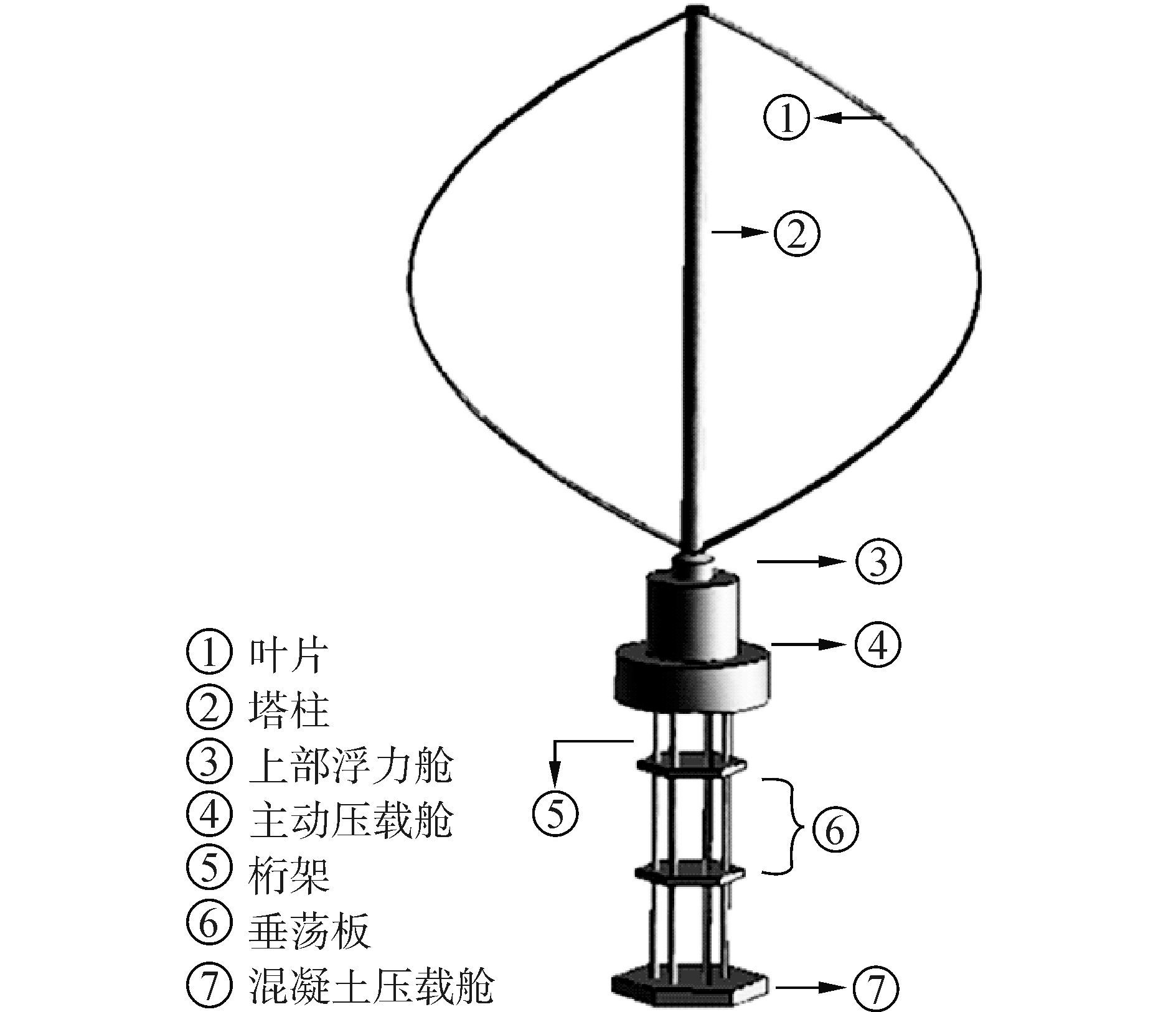
1 浮式风力机形式及参数本文采用的浮式风力机形式如图 1所示。风力机安装在桁架式Spar型浮式基础之上,叶片带动塔柱在风力作用下旋转,将风能转化为机械能,并通过安装在基础舱室内的传动机构与发电装置将塔柱旋转的机械能转化为电能,上部风力机和下部浮式基础的具体参数如表 1和表 2所示。
|
图 1 浮式风力机示意图 Fig.1 Diagram of wind turbine |
| 表 1 风力机参数 Tab.1 Parameters of wind turbine |
| 表 2 浮式基础参数 Tab.2 Parameters of floating foundation |
Strickland在单流管模型的基础上提出多流管模型,假定各个流管之间互不影响。这一理论更加全面可靠,但计算过程相对复杂。Paraschivoiu在多流管模型的基础上做了改进,提出双致动盘多流管模型,将流管分为上风区和下风区两部分。
上风区平均扭矩系数:
| ${\bar C_{Q1}} = \frac{{NcH}}{{2{\rm{ \mathsf{ π} }}{{\rm{V}}_\infty }^2}}S\int_{ - \frac{{\rm{ \mathsf{ π} }}}{2}}^{\frac{{\rm{ \mathsf{ π} }}}{2}} {\int_{ - 1}^1 {{C_T}} } {W^2}(\eta /{\rm{cos}}\delta ){\rm{d}}\xi {\rm{d}}\theta $ | (1) |
式中:N为叶片数量,c为弦长,H为转子半高,V∞为来流风速,S为扫风面积,CT为叶片截面切向力系数,W为上风区相对入流速度,η为转子局部与赤道半径之比,ξ为截面高与风轮半高之比,δ为叶片法向与赤道平面夹角,θ为相位角。
转子上风区功率系数为
| ${C_{P1}} = (R\omega /{V_\infty }){\bar C_{Q1}} = {X_{EQ}}{\bar C_{Q1}}$ | (2) |
式中:R为转子半径,ω为转子角速度,XEQ为风轮赤道处尖速比。
同理,可结合下风气动特性得到风力机整体功率系数。
2.2 计算结果及分析采用双致动盘多流管理论,利用Matlab软件编程,计算风机气动性能。利用循环迭代求解,流程如下:当给定转子几何型线、来流速度以及转速时,假定干扰因子初值为1,可得到局部尖速比,雷诺数等条件。根据已知翼型参数CL和CD进行差值得到新值,可求得CN和CT,再根据上风函数得到干扰因子新值,如此循环迭代,直到两次得到的干扰因子相差不到10-4即循环结束[12]。由干扰因子可求诱导速度,进而得到叶片受力情况。变换不同的风速和转速,得到一系列功率系数曲线,如图 2所示。

|
图 2 不同速度下的功率系数曲线 Fig.2 Power coefficient curves at different speeds |
由图 2可以看出,当风速一定时功率系数随转速的增加先增大后减小,不同风速条件下的最大功率系数不变,但所对应的转速随风速的增加而增加;当转速一定时,功率系数随风速的增加先增大后减小,不同转速条件下的最大功率系数保持不变,但所对应的风速随转速的增加而增加。给定尖速比定义如下
λ=ωR/V∞
式中:ω为风机转速,R为风机赤道截面半径,V∞为赤道截面无穷远处来流风速。根据上述计算结果,绘制CP-λ曲线,如图 3所示。综合以上两种情况,当风力机模型参数确定时,功率系数变化仅与尖速比λ有关。
|
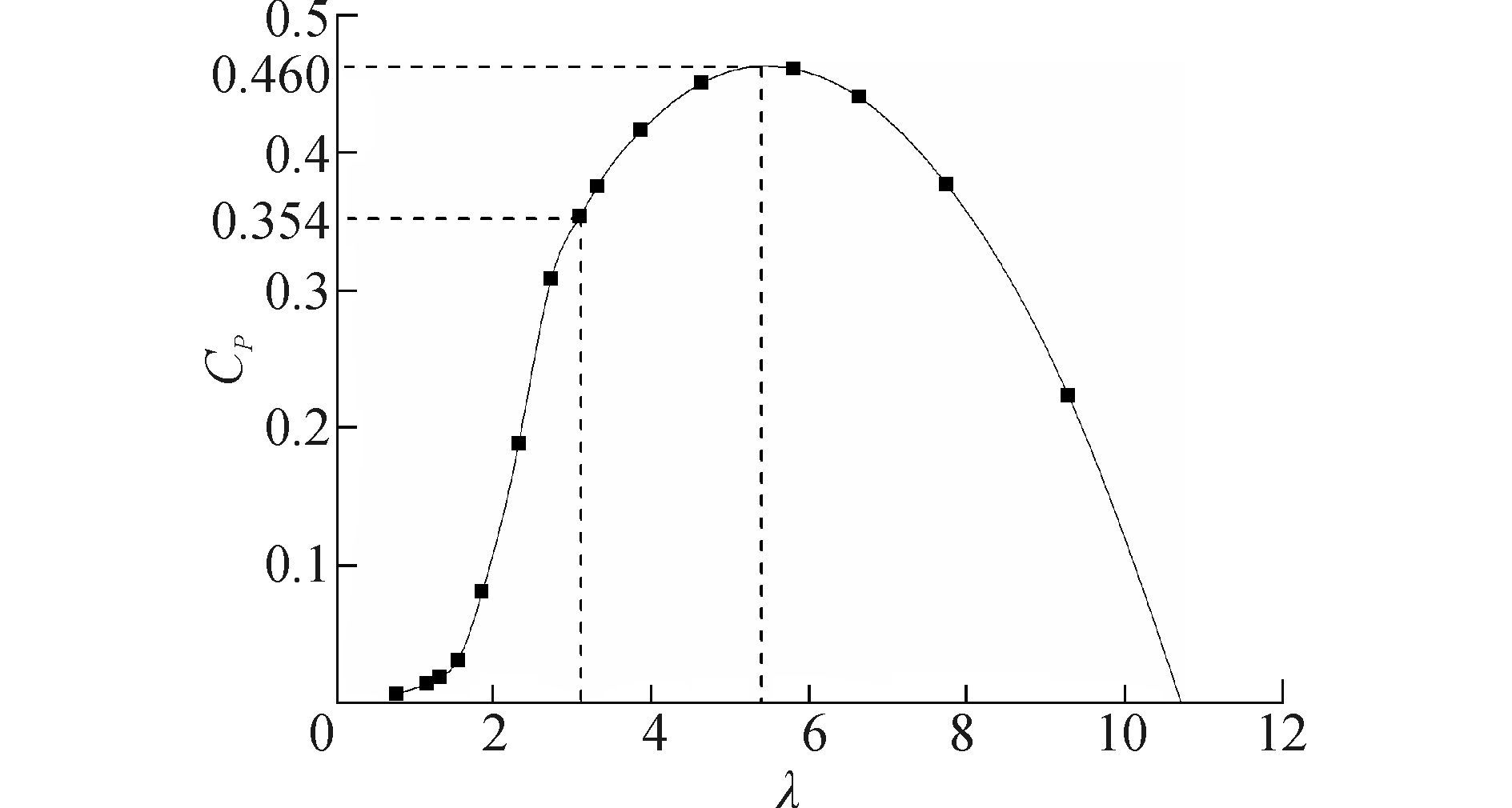
图 3 CP-λ曲线 Fig.3 CP-λ curve |
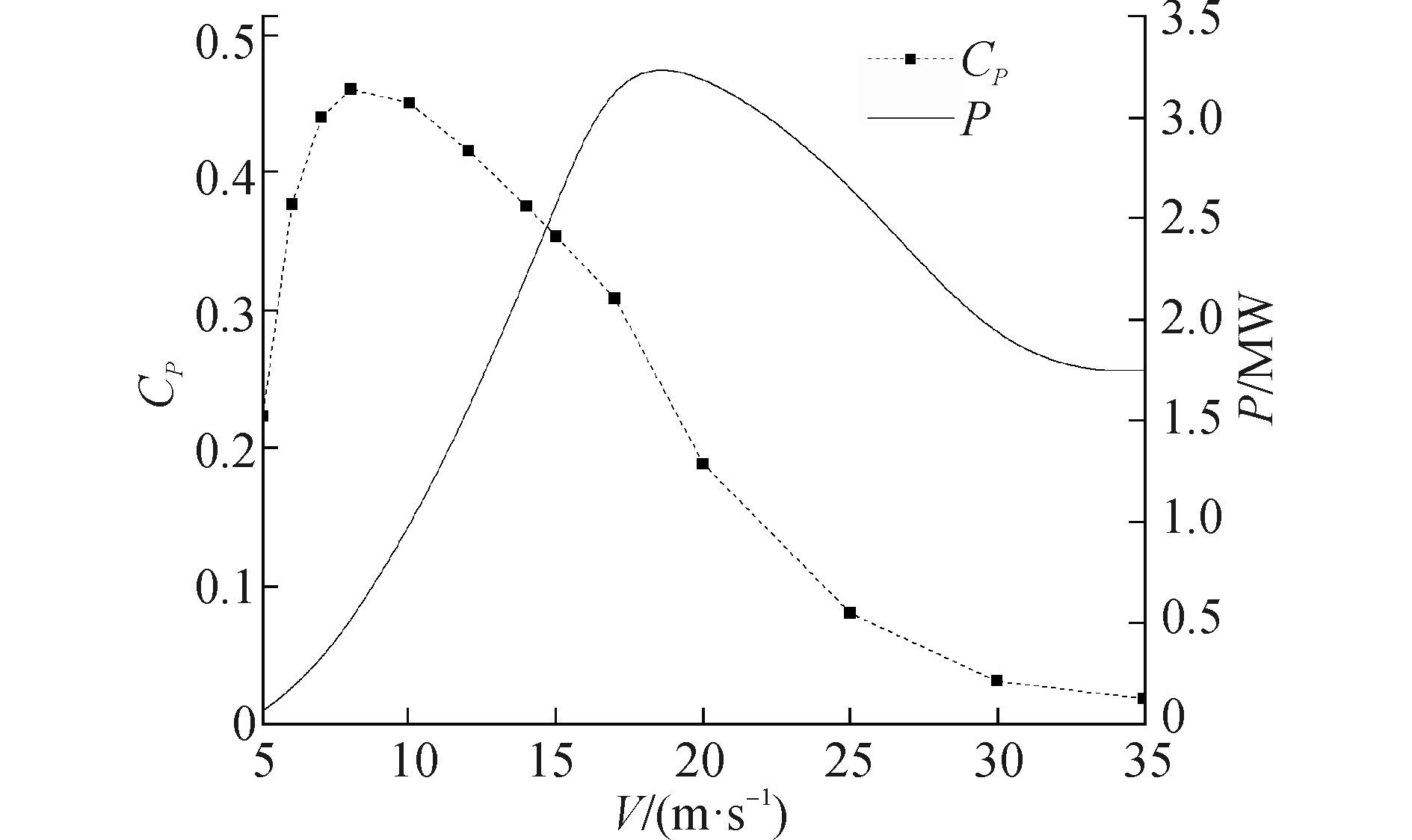
图 3表明,风机额定工况下功率系数CP为0.354,最大功率系数为0.46,对应最佳尖速比为5.4,适应尖速比最大为10.7。根据不同风速条件下的CP值可以求得风力机对应的功率P,绘制功率-风速曲线,如图 4所示。
|
图 4 风机功率曲线与CP曲线 Fig.4 Curves power of wind turbine and CP |
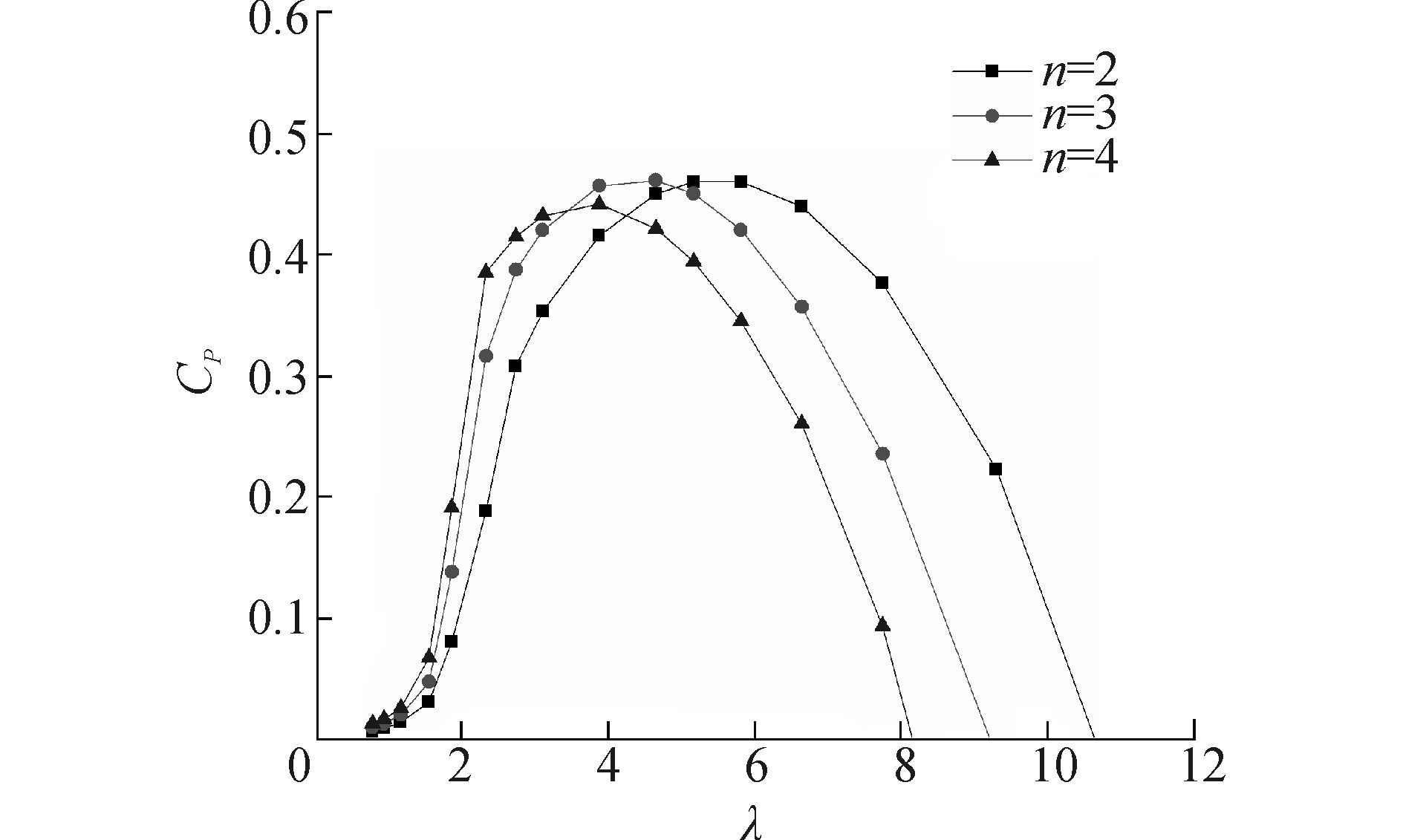
以下依次改变叶片数量n、叶片截面翼型、风轮实度δ和叶片形状,分别计算风机功率系数,分析风机结构参数对其功率系数的影响,结果如图 5~8所示。
|
图 5 叶片数量的影响 Fig.5 Effect of the number of blade |
|
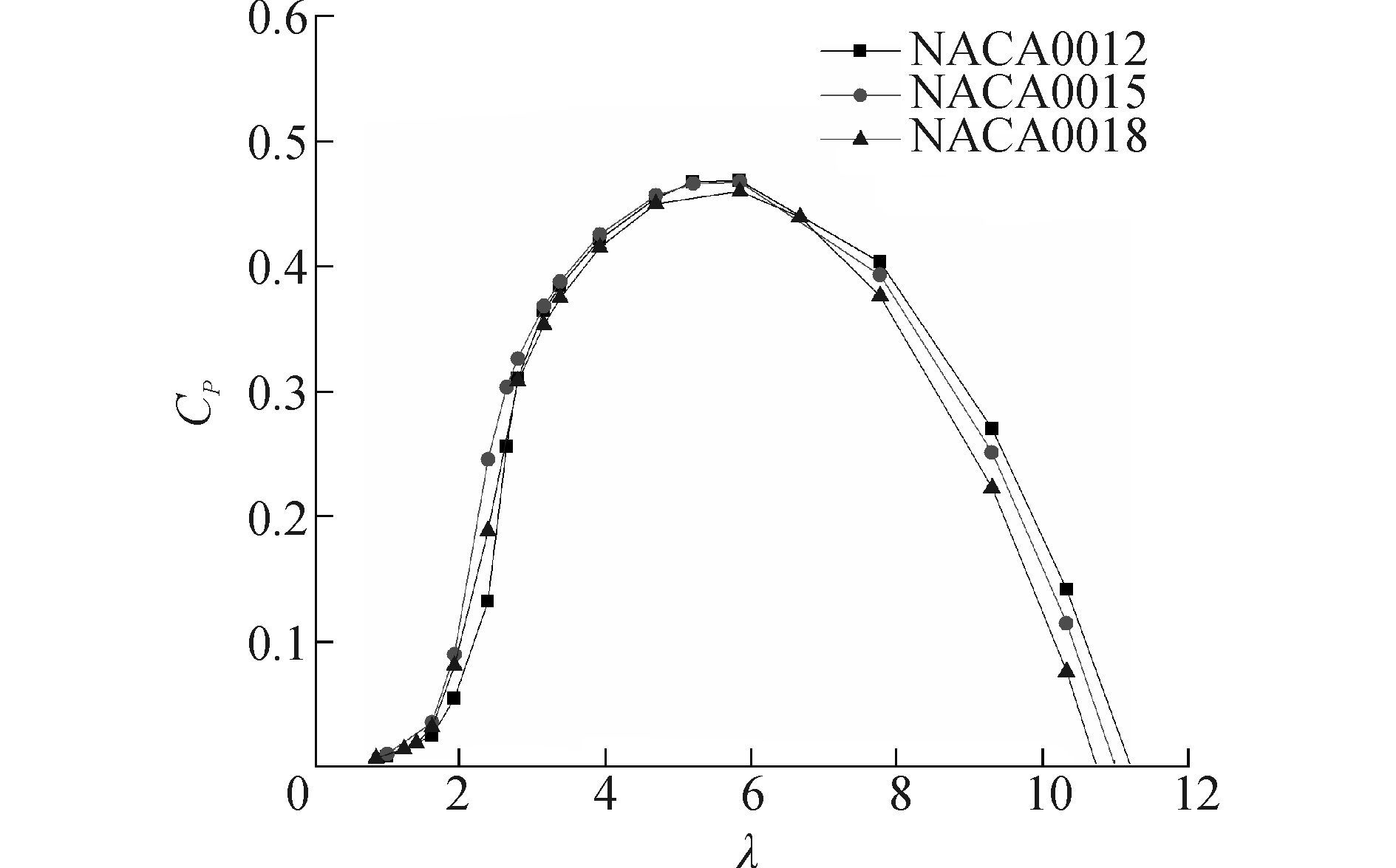
图 6 截面翼型的影响 Fig.6 Effect of airfoil section |

|
图 7 风轮实度的影响 Fig.7 Effect of rotor solidity |
|
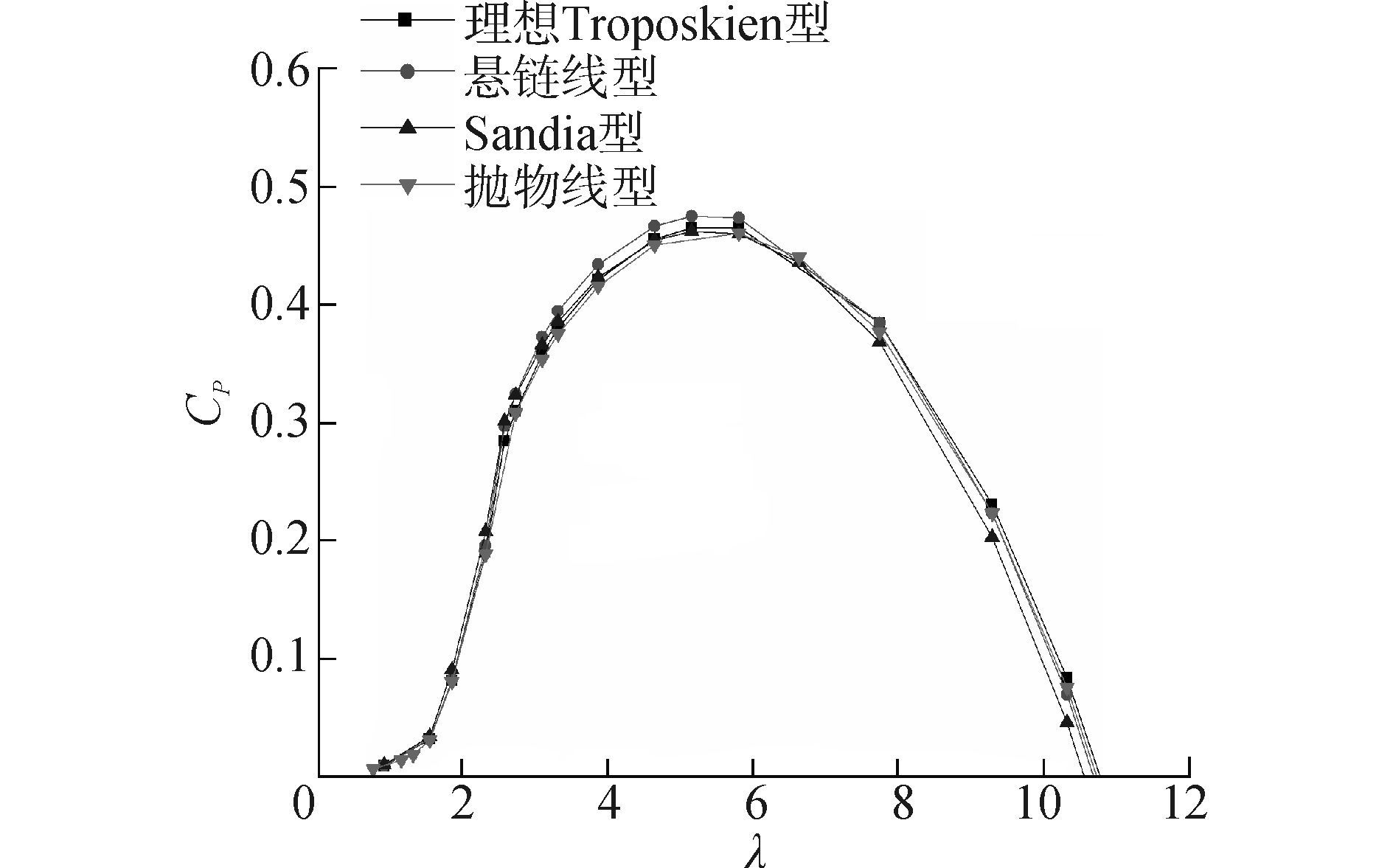
图 8 叶片形状的影响 Fig.8 Effect of the shape of blade |
分析图 5可知,不同叶片数量的风机尖速比范围有差别,叶片数量越少尖速比范围越大,即适应风速范围越大。三种工况的最佳尖速比不同,所对应的最大功率系数值略有差别,其中双叶片风机性能最优,三叶片次之,四叶片最低。
图 6给出了NACA0012、NACA0015和NACA0018三种不同翼型对风力机功率系数的影响,结果表明,三种翼型的最大功率系数值几乎相同,且对应的最佳尖速比相同,为5.5左右。在低尖速比情况下NACA0015性能最优,NACA0018次之。相反,在高尖速比情况下,NACA0012的转子具备高性能。考虑到结构强度因素并综合以上分析,本文选择NACA0018翼型。
图 7给出了风轮实度对风机功率系数的影响。大型Φ型风力机风轮实度在0.2左右,一般不小于0.1。本文通过改变翼型弦长得到不同实度情况下的CP-λ曲线,具体计算工况如表 3所示。从图 7可以看出实度越大的风机尖速比范围越小,适应风速的对应范围也就越小。最大功率系数值随着实度的增大而先增大后减小,实度为0.2时的最大功率系数值最优。图 8比较了不同叶片几何形状对风力机功率系数的影响。悬链线型的最大功率系数值最大,几种线型的最佳尖速比基本相同,适应尖速比范围也一致,总体来说并无太大区别。
| 表 3 不同实度计算工况 Tab.3 Conditions of different rotor solidity |
采用SST k-ω模型分析风力机周围流场的流动情况。该模型在近壁面区域使用k-ω模型,边界层外部区域使用k-ε模型,而在边界层内混合使用这两种模型,并用混合加权函数进行平均[13]。这种模型对于风力机模拟来说较为常用。
| $\frac{{\partial \left( {\rho k} \right)}}{{\partial {\rm{t}}}} + \frac{\partial }{{\partial {x_i}}}(\rho k{u_i}) = \frac{\partial }{{\partial {x_j}}}\left( {{\mathit{\Gamma }_k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {\bar G_k} - {Y_k} + {S_k}$ | (3) |
| $\frac{{\partial \left( {\rho \omega } \right)}}{{\partial {\rm{t}}}} + \frac{\partial }{{\partial {x_i}}}(\rho \omega {u_i}) = \frac{\partial }{{\partial {x_j}}}\left( {{\mathit{\Gamma }_\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {D_\omega } + {S_\omega }$ | (4) |
式中:k为湍流动能,ρ为空气密度,ω为湍流耗散率,Gk为由平均速度梯度产生的湍流动能,Gω为由ω产生的湍流耗散率,Γk、Γω分别表示k和ω的有效扩散率,Yk、Yω分别表示k和ω的耗散项,Sk、Sω表示用户自定义的源项,Dω为横向耗散导数项[14]。
文中数值计算部分采用FLUENT软件进行。
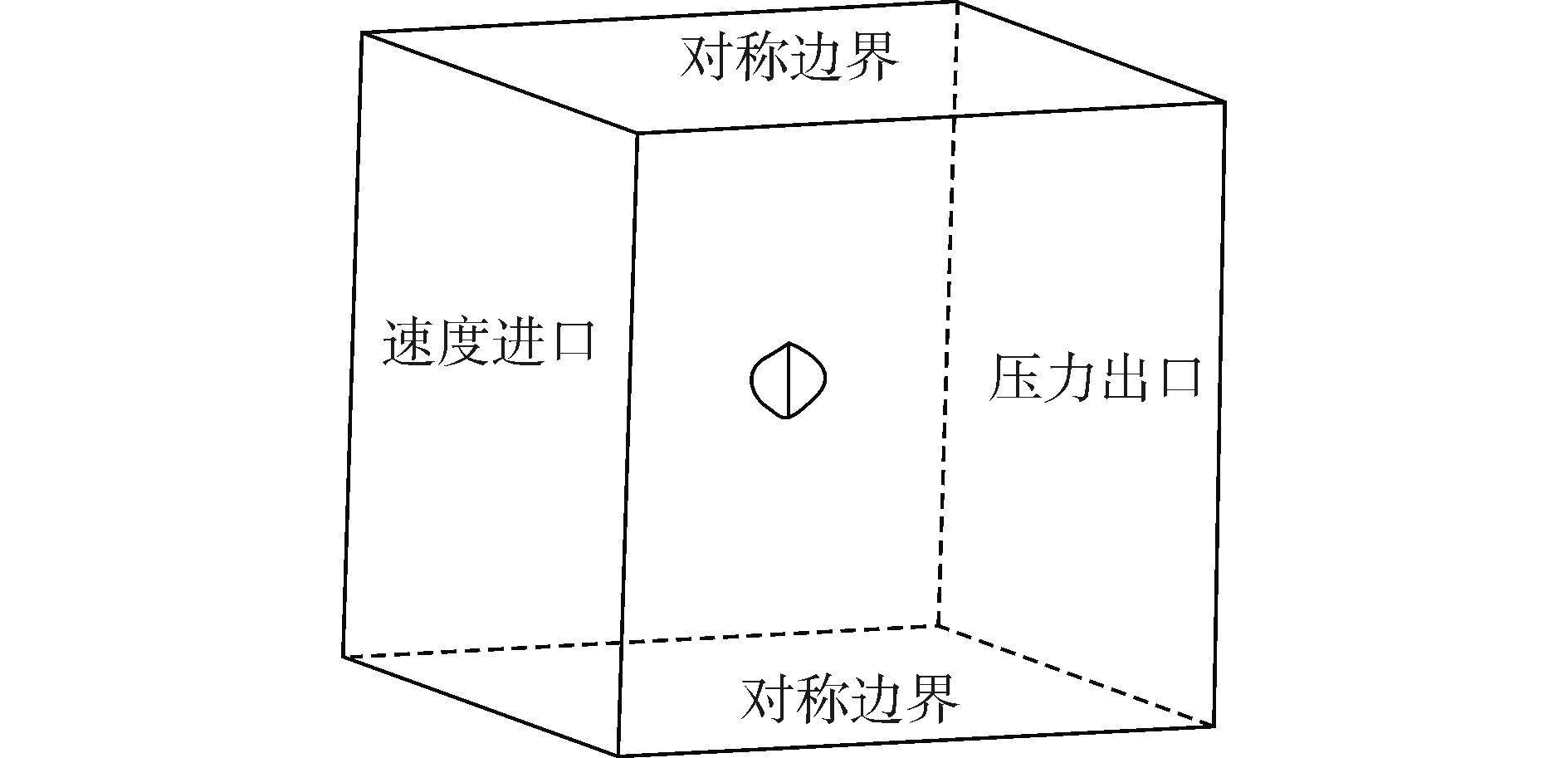
3.2 数值计算模型的建立采用GAMBIT软件建立风力机模型如图 9所示,包括风机叶片和塔柱两个部分。运用滑移网格技术,将整体计算域分为转动区域和静止区域,以此实现风机转动和流场信息的传递。为在精确求解的基础上节省资源,风机附近区域网格加密,边界渐疏。在对比分析风场尺寸对数值结果影响的基础上,最终采用风场尺寸为600 m×600 m×600 m,如图 10所示,风场的6个边界面到风轮中心距离均为4倍风轮直径。图 10同时给出了计算的边界条件,来流风方向为速度进口,去流风方向为压力出口,其他四面为对称边界条件。

|
图 9 风机模型示意图 Fig.9 Diagram of wind turbine model |
|
图 10 风场及边界条件 Fig.10 Wind field and boundary conditions |
为分析塔柱的影响,本文建立了两个模型,即考虑塔柱和不考虑塔柱两种情况。不考虑塔柱时,风场转动区域网格数量为2 354 766,内部静止区域网格数量为540 064,外部静止区域网格数557 519,网格总数为3 452 349;考虑塔柱时,转动区域网格数量为2 798 730,内部静止区域网格数为784 774,外部静止区域网格数为507 535,整体网格数为4091 039;两个模型的边界条件及参数设置相同。将模型导入FLUENT中,采用SST k-ω湍流模型,选用耦合式求解,时间步长为0.02 s。
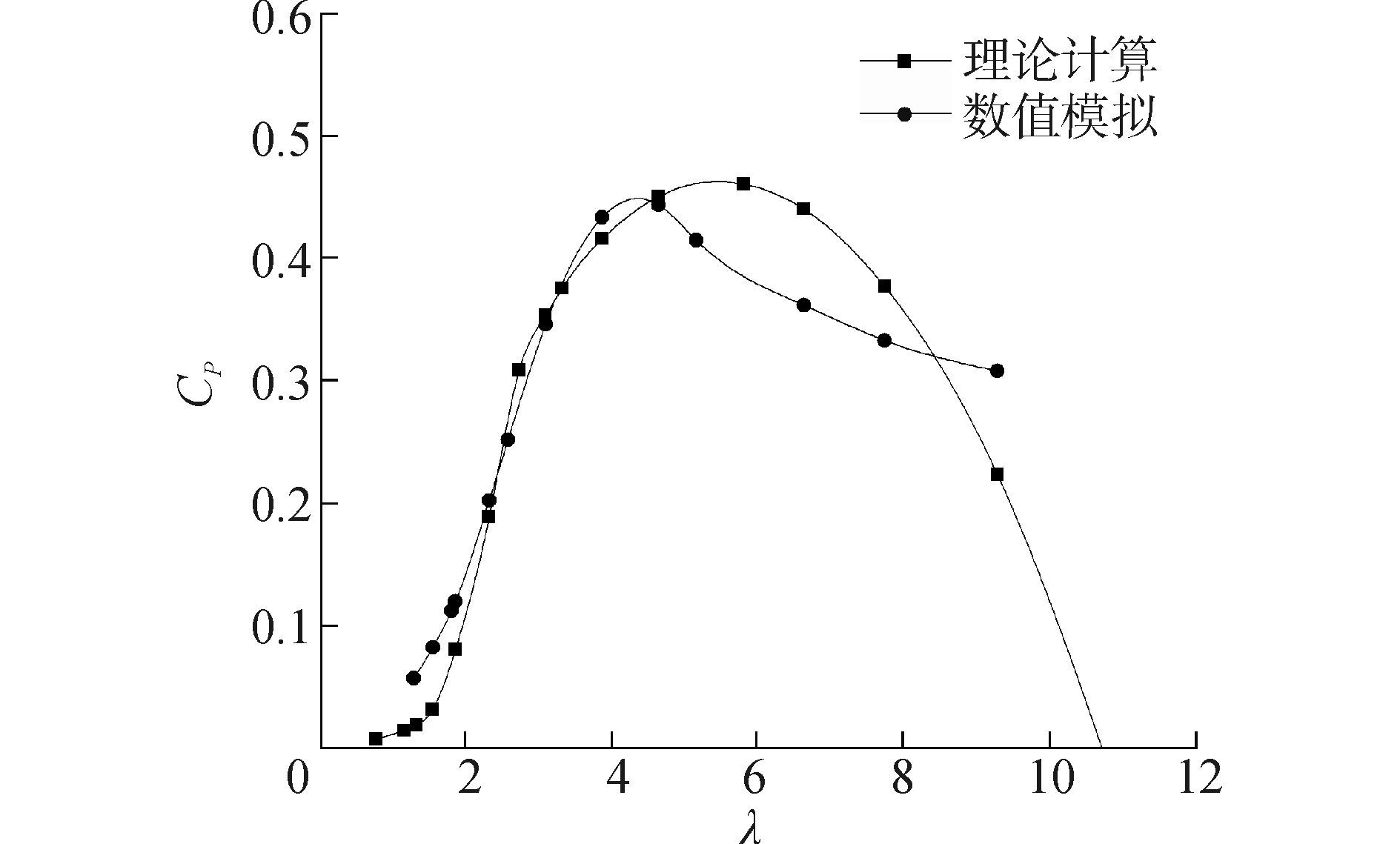
3.3 计算结果及分析 3.3.1 理论结果与数值结果的对比由于理论计算没有考虑塔柱的影响,为与理论结果进行对比,本节数值计算也将不考虑塔柱。针对不同的风速计算功率系数,绘制CP-λ曲线并与理论计算结果对比,如图 11所示。
|
图 11 Cp-λ曲线对比图 Fig.11 Comparison diagram of Cp-λ curves |
图 11表明,尖速比较小时理论结果与数值模拟结果吻合较好。对于额定工况,CP理论计算结果为0.354,数值模拟结果为0.346,两者相差2.3%。数值模拟的最佳尖速比为4.36,理论计算为5.4。
由于理论模型采用二维方法求解,再对叶片整体进行积分,忽略了三维效应和动态效应的影响。且随着尖速比的不断增高,阻力对风力机气动性能的影响增大,三维效应产生的诱导阻力对风力机的气动性能影响更加明显,这导致了在大尖速比时,数值模拟结果小于理论计算[15]。当尖速比在9左右时,数值模拟结果大于理论计算,这一现象出现的原因有待探究。
3.3.2 塔柱的影响分析针对不考虑塔柱和考虑塔柱两种模型,分别计算额定工况下不同时刻的风场速度分布情况,所得速度云图如图 12和图 13所示。

|
图 12 不考虑塔柱时风轮赤道处截面速度云图 Fig.12 Velocity contour at the equator section of wind turbine without considering tower |
|
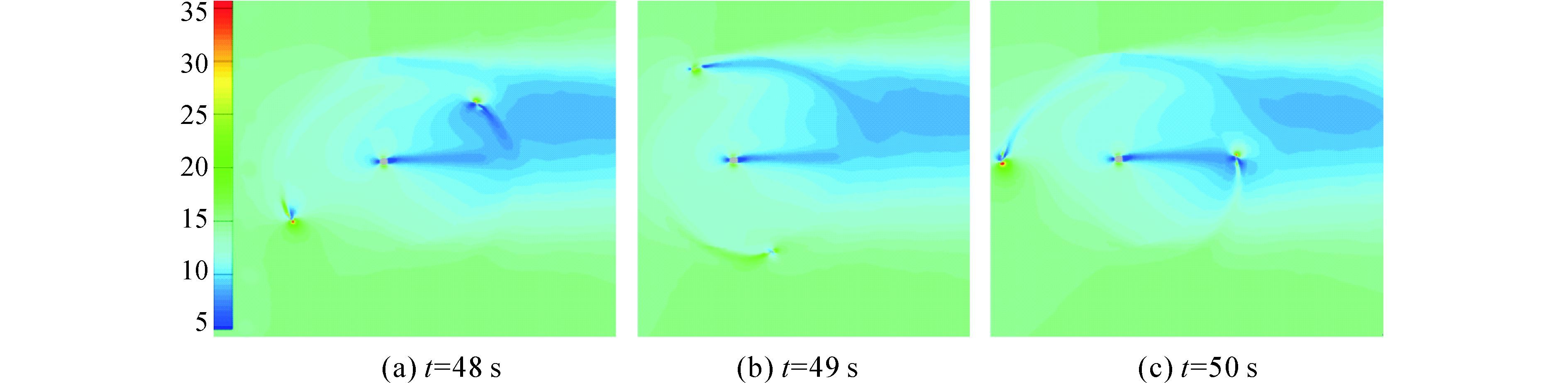
图 13 考虑塔柱时风轮赤道处截面速度云图 Fig.13 Velocity contour at the equator section of wind turbine when tower is considered |
图 12表明,风力机运转时会对周围流场产生扰动,上风区叶片扫过风场后尾迹向下游流动,对下风区叶片的气动特性影响较大。相比于上风区来说,下风区叶片所受来流风速较低。同样,下风区叶片产生的尾迹也会对风轮整体下游流场产生影响。叶片转动产生的尾迹随风流动到风轮下游,最终汇合形成低速尾流区,尾流随着流动的不断延伸逐渐变窄。图 13表明,塔柱的存在使塔柱后方风速降低,该影响沿风流动方向逐渐减小,最终形成低速区域与风轮整体低速区汇合。塔柱对于上风区叶片来说几乎没有干扰,仅当下风区叶片经过塔柱后方时会受到影响。
由上述分析可得,在额定工况下,塔柱对风机功率系数的影响并不大。考虑一般情况,变换不同风速对比风力机功率系数,结果如图 14所示。
|
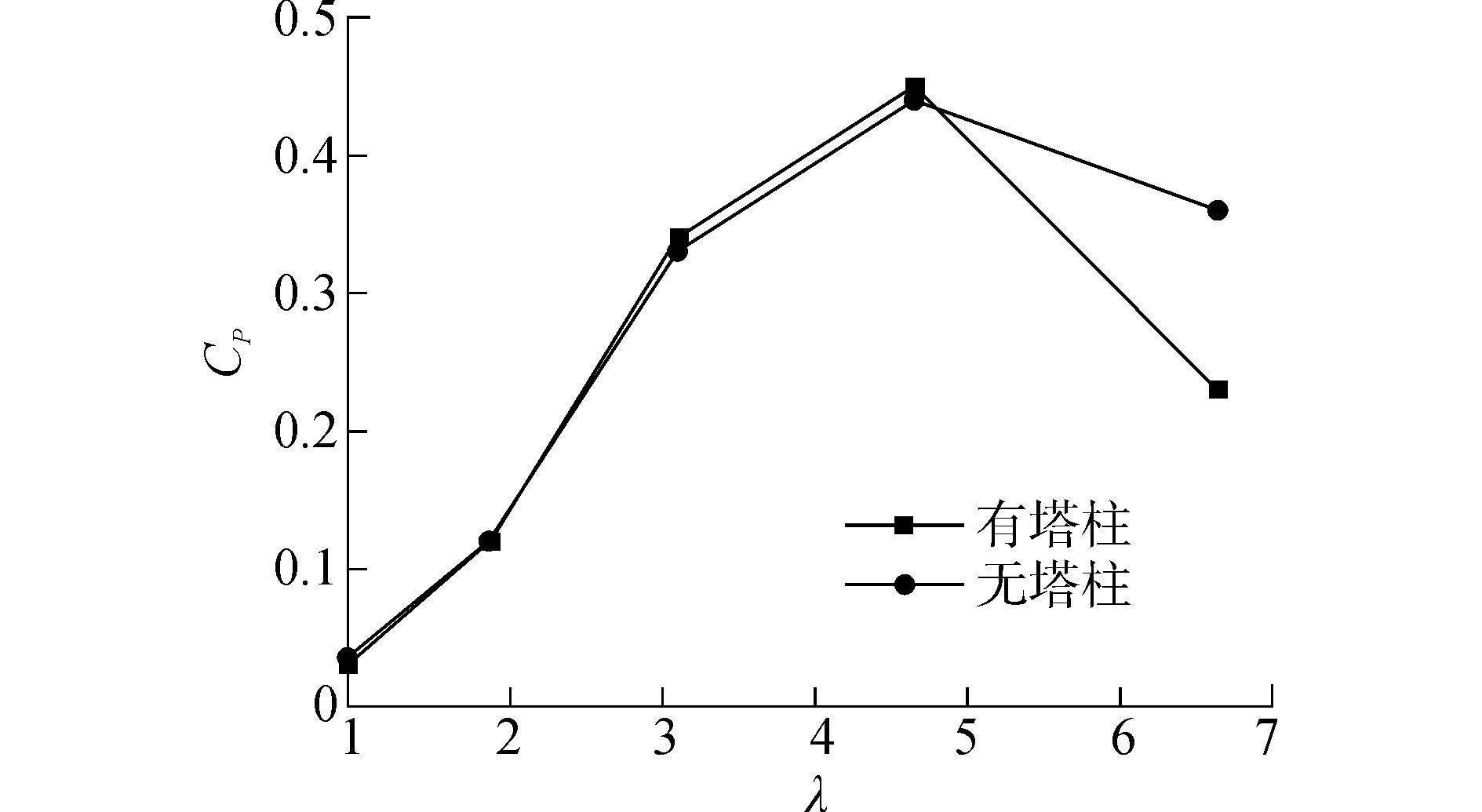
图 14 有塔柱、无塔柱风机模型CP-λ曲线对比 Fig.14 Comparison of CP-λ curves between wind turbine models with tower and without tower |
图 14表明,在尖速比较小时,两种模型的Cp-λ曲线很接近,塔柱对风机功率几乎没有影响。当尖速比大于5时,考虑塔柱的模型CP值较小,两者之间的差别比较明显。尖速比为6.64时,有塔柱模型CP值为0.23,无塔柱模型CP值为0.36,两者相差36%。综上可得,在小尖速比条件下,即风速相对风轮转速较大时,塔柱对风机功率性能影响不明显,而尖速比较大时塔柱的二次效应影响较大。
3.3.3 浮式基础运动对风力机气动性能的影响分析本节将研究Spar平台在波浪影响下做垂荡运动时风机的功率系数变化。假定平台运动幅值为3 m,分别做周期为20 s和10 s的简谐垂荡运动,计算不同风速下的风机功率系数,绘制曲线如图 15所示。
|
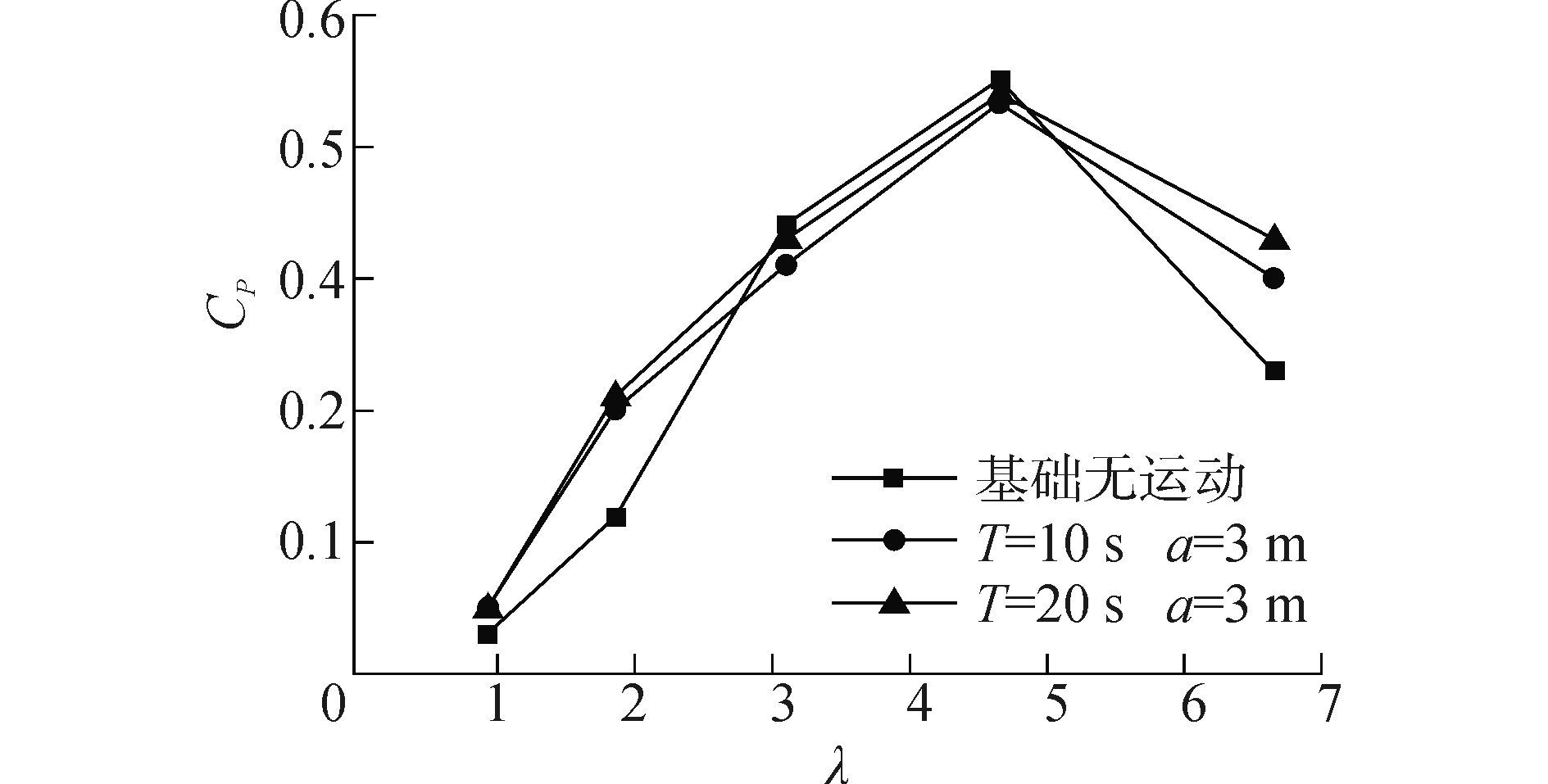
图 15 有、无基础运动影响的CP-λ曲线对比 Fig.15 Comparison of CP-λ curves with and without the influence of basic motion |
由图 15可知,对于不同垂荡运动状态,在小尖速比情况下,即风速较大时,垂荡运动速度相对为小量,所以不同垂荡周期的基础运动对风机CP影响相差较小;尖速比增大,风速减小,垂荡运动速度影响增强,不同垂荡周期的基础运动对风力机CP影响的差别逐渐显现。风机功率系数CP在基础运动的影响下有所改变,与基础无运动时对比,小尖速比情况下CP有所增加;尖速比增大CP降低;当尖速比继续增大,CP有增加的趋势,可见对于不同尖速比其影响也不尽相同。
由于CFD计算过程比较费时,所以本文只简单对比了两种垂荡运动工况下的风机CP变化,为了更加全面的分析海上浮式基础运动对风力机气动性能的影响,还应增加几种不同的运动形式进行对比分析,这也是本文后续研究的目标之一。
4 结论1) 分别采用理论方法和CFD数值模拟计算了风力机的功率系数,结果表明,在小尖速比时理论计算结果与数值模拟结果吻合较好,在大尖速比时有一定差别。变换模型尺度,综合考虑多种因素,最终选定风力机为双叶片抛物线型、风轮实度0.2、NACA0018翼型。
2) 对比了有无塔柱时的速度云图并分析了功率系数,计算表明,塔柱对上风区风速几乎没有影响,但使其后方风速降低,风通过塔柱后形成的尾迹与风轮整体低速区汇合。在小尖速比情况下,塔柱对风机功率几乎没有影响;尖速比较大时塔柱的影响变大。
3) 基础的垂荡运动会影响风机的功率系数,不同尖速比的影响结果不同;小尖速比情况下不同垂荡周期的风机CP相差较小,尖速比增大,不同垂荡周期的基础运动影响差别逐渐显现。
| [1] |
韩冬, 张慧芳, 陈欣, 等. 基于海上风场的垂直轴风力发电装置研究[C]//第十四届中国海洋(岸)工程学术讨论会论文集(下册), 2009: 1487-1489. HAN Dong, ZHANG Huifang, CHEN Xin, et al. Research on vertical axis wind power generator based on offshore wind farm[C]//Proceedings of the fourteenth China Marine (Offshore) Engineering Symposium, 2009:1487-1489. (  0) 0)
|
| [2] |
CAHAY M, LUQUIAU E, SMADJA C, et al. Use of a Vertical Wind Turbine in an Offshore Floating Wind Farm [C]//Offshore Technology Conference, Proceedings OTC2011 Houston, Texas, USA, 2011.
( 0) 0)
|
| [3] |
BORG M, COLLU M. Offshore floating vertical axis wind turbines, dynamics modeling state of the art. Part Ⅲ:Hydrodynamics and coupled modeling approaches[J]. Renewable and sustainable energy reviews, 2014, 39: 1226-1234. DOI:10.1016/j.rser.2014.07.122 ( 0) 0)
|
| [4] |
OWENS B C, GRIFFITH D T. Modal dynamics and stability of large multi-megawatt deepwater offshore vertical-axis wind turbines:initial support structure and rotor design impact studies [C]//32nd ASME Wind Energy Symposium. Maryland, USA, 2014, AIAA2014-0518.
( 0) 0)
|
| [5] |
BERTHELSEN P A, FYLLING I, VITA L, et al. Conceptual design of a floating support structure and mooring system for a vertical axis wind turbine[C]//ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers, 2012:259-268.
( 0) 0)
|
| [6] |
韩非非, 席德科, 任栋, 等. 用多流管模型预测达里厄型垂直轴风力机性能[J]. 太阳能学报, 2011, 32(9): 1309-1314. ( 0) 0)
|
| [7] |
叶忱, 赵旭, 王静静, 等. 垂直轴风力机气动性能分析与数值模拟研究[J]. 机械与电子, 2012(1): 20-24. YE Chen, ZHAO Xu, WANG Jingjing, et al. Vertical axis wind turbine aerodynamic performance analysis and numeri-cal simulation[J]. Machinery & electronics, 2012(1): 20-24. (  0) 0)
|
| [8] |
左薇, 康顺, 仇永兴. φ型风力机空气动力学特性研究[J]. 工程热物理学报, 2012, 05: 774-777. ZUO Wei, KANG Shun, QIU Yongxing. Study of aerodyne-mic performance of φ type wind turbine[J]. Journal of engineering thermophysics, 2012, 05: 774-777. (  0) 0)
|
| [9] |
惠万馨, 顾煜炯, 刘莎莎, 等. 垂直轴风力机三维气动性能的数值模拟及分析[J]. 现代电力, 2013, 01: 85-89. HUI Wanxin, GU Yujing, LIU Shasha, et al. Numerical research of 3D aerodynamic performance of vertical axis wind turbine[J]. Modern electric power, 2013, 01: 85-89. DOI:10.3969/j.issn.1007-2322.2013.01.018 (  0) 0)
|
| [10] |
MOHAMED M H, ALI A M, HAFIZ A A. CFD analysis for H-rotor Darrieus turbine as a low speed wind energy converter[J]. Engineering science & technology an international journal, 2014, 18(1): 1-13. ( 0) 0)
|
| [11] |
BEDON G, BETTA S D, BENINI E. A computational assessment of the aerodynamic performance of a tilted Darrieus wind turbine[J]. Journal of wind engineering & industrial aerodynamics, 2015, 145: 263-269. ( 0) 0)
|
| [12] |
伊恩·帕拉斯基沃尤(IonParaschivoiu). 垂直轴风力机原理与设计[M]. 上海: 上海科学技术出版社, 2013.
( 0) 0)
|
| [13] |
张惠. FLUENT 14流场分析自学手册[M]. 北京: 人民邮电出版社, 2014. ZHANG Hui. FLUENT 14 self-study manual of flow field analyzing[M]. Beijing: Posts & Telecom Press, 2014. (  0) 0)
|
| [14] |
任年鑫, 欧进萍. 大型风力机二维翼型气动性能数值模拟[J]. 太阳能学报, 2009, 08: 1087-1091. REN Nianxi, OU Jinping. Numerical simulation for pneumatic characteristics for two-dimensional airfoils large wind turbine[J]. Acta energiae solaris sinica, 2009, 08: 1087-1091. DOI:10.3321/j.issn:0254-0096.2009.08.017 (  0) 0)
|
| [15] |
施璐. Darrieus型垂直轴风力机自由尾迹模型评估及气动性能分析[D]. 武汉: 华中科技大学, 2013. SHI Lu. Assessment of free wake aerodynamic models on the analysis of Darrieus vertical axis wind turbines[D]. Wuhan:Huazhong University of Science and Technology, 2013. http://www.docin.com/p-1519409122.html (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


