随着21世纪的来临,科技的发展,在对水下航行器及海洋机电设备的供电中,传统的利用湿拔插接口和导线的电能传输越来越无法满足很多工程的要求,人们越来越需要一种更安全更方便的新型的非接触式电能传输技术[1-2]。2007年,MIT利用电磁谐振原理,自制无线传输装置点亮了2 m外的60 W灯泡,实现了长距离无线传输的突破[3-4]。磁谐振式电能传输运用电-磁-电的原理,避免了电能的直接传输,彻底解决了传输过程中的漏电隐患,因此非常适合运用在水下或者工作条件较恶劣的环境下。
海水作为电的良导体,具有较高的电导率,因而对高频电磁波具有强烈的衰减作用[5]。随着传输距离增加,系统效率同时受到了互感减小和电磁波振幅衰减两种效应的影响。同时,海水阻抗随着传输距离而改变,导致系统发射端和接收端的阻抗不匹配。对于接收端来说,阻抗不匹配使接收线圈将部分能量反射出去并且在海水中衰减掉,造成了效率的进一步降低。
为了提高电能传输效率,最大效率追踪法就成了解决问题的关键[6-8]。追踪方法的本质为阻抗匹配,即当输入阻抗和输出阻抗达到完全匹配时,发射端发出的能量将全部被接收端吸收,从而减小反射损耗。目前,最常用的追踪方法是最大功率点扰动观测法。其优点是算法简单,被测参数少,响应速度快,对传感器精度要求不高[9-10]。但无论传统的定步长的扰动观测法,还是变步长快速跟踪的扰动观测法都存在着缺陷:当输出功率逼近最大功率点附近时,由于两次测量的功率值不可能完全相等,导致系统会持续进行计算追踪,此时输出功率会在最大功率点两端持续震荡,导致输出不稳定并且造成一定的功率损失[11-12]。
为了提高整个系统的最大效率跟踪控制系统的性能,本文提出一种输出稳定型最大效率追踪方法,用于水下磁谐振耦合非接触能量传输系统。并通过仿真和试验验证所提方法的可行性和稳定性。
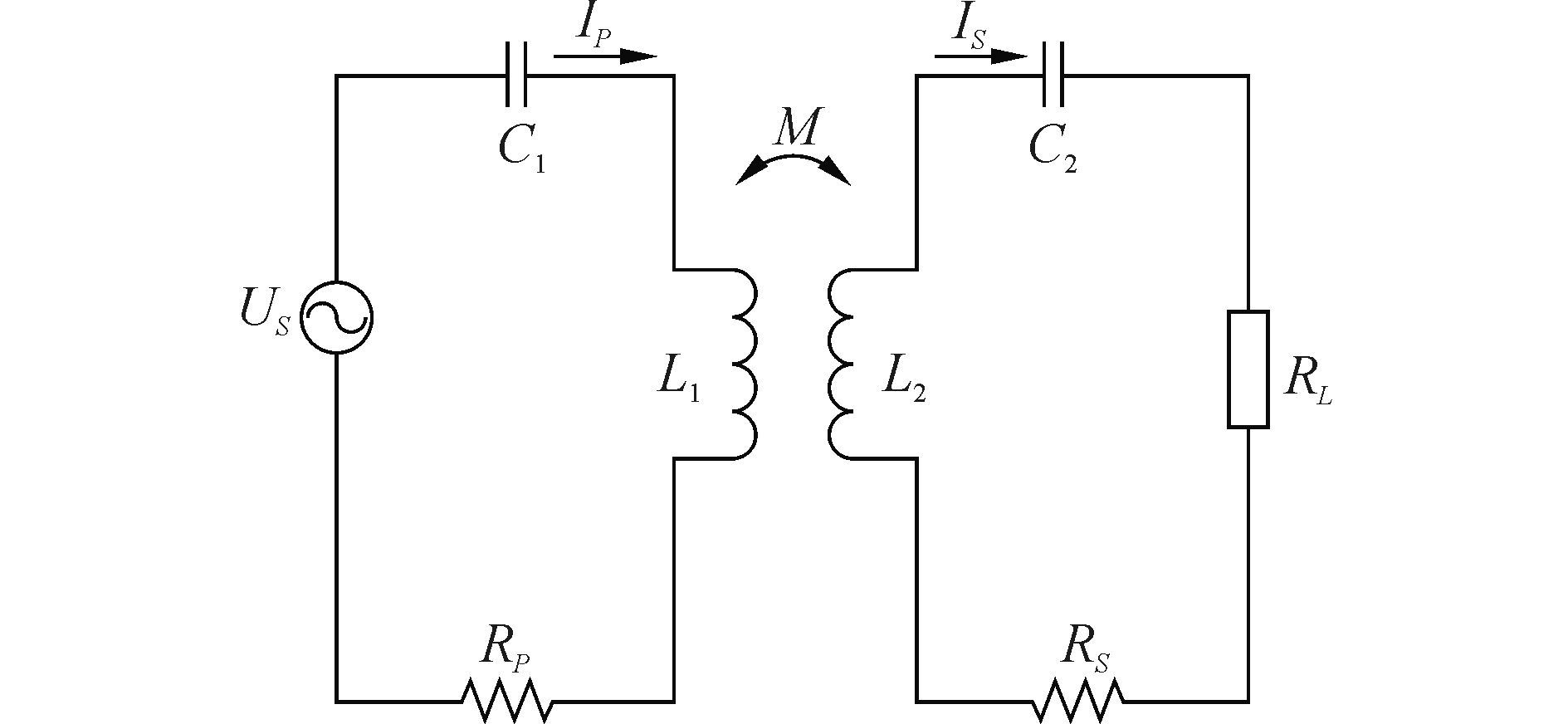
1 海水中磁谐振式无线电能传输模型本文采用两线圈结构系统[13]。两线圈耦合电路模型如图 1所示,其中US为正弦激励,RP、RS为电感等效串联电阻,L1、L2为线圈电感,C1、C2为谐振电容,RL为负载线圈反射的等效负载电阻,M为初、次级回路的互感。
|
图 1 两线圈磁谐振耦合能量传输系统 Fig.1 Two coils resonance coupling wireless energy transfer system |
当系统正常工作时,两线圈同时达到谐振状态,设谐振角频率为ω,则根据基尔霍夫定律可得
| $ \left[ {\begin{array}{*{20}{c}} {{U_S}}\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{Z_P}}&{ - {\rm{j}}\omega M}\\ { - {\rm{j}}\omega M}&{{Z_S}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_P}}\\ {{I_S}} \end{array}} \right] $ | (1) |
其中,
| $ \left\{ \begin{array}{l} {Z_P} = {R_P} + {\rm{j}}\omega {L_1} + \frac{1}{{{\rm{j}}\omega {C_1}}}\\ {Z_S} = {R_L} + {R_S} + {\rm{j}}\omega {L_2} + \frac{1}{{{\rm{j}}\omega {C_2}}} \end{array} \right. $ | (2) |
则系统的传输效率表达形式为
| $ \eta = \frac{{{{\left( {\omega M} \right)}^2}{R_L}}}{{{Z_S}\left[ {{Z_P}{Z_S} + {{\left( {\omega M} \right)}^2}} \right]}} $ | (3) |
由于本磁谐振无线电能传输系统应用于水下航行器的电能补给,而海水对高频电磁波有强烈的衰减作用,因此必须考虑电磁波在海水中传播的损耗[10]。
假设电磁波沿+Z轴方向传播。所以此均匀平面电磁波波的电场解和磁场解可以表示为
| $ E\left( z \right) = {e_x}{E_x} = {e_x}{E_{xm}}{{\rm{e}}^{ - rz}} = {{\rm{e}}_x}{E_{xm}}{{\rm{e}}^{ - \alpha z}}{{\rm{e}}^{ - {\rm{j}}\beta z}} $ | (4) |
| $ \begin{array}{l} H\left( z \right) = \frac{1}{{{\eta _c}}}{e_z} \times E\left( z \right) = {e_y}\frac{1}{{{\eta _c}}}{E_{xm}}{{\rm{e}}^{ - \alpha z}}{{\rm{e}}^{ - {\rm{j}}\beta z}} = \\ \;\;\;\;\;\;\;\;\;\;\;{e_y}\frac{1}{{{\eta _c}}}{E_{xm}}{{\rm{e}}^{ - \alpha z}}{{\rm{e}}^{ - {\rm{j}}\left( {\beta z + \varphi } \right)}} \end{array} $ | (5) |
其中
| $ {\eta _c} = \sqrt {\frac{\mu }{{{\varepsilon _c}}}} = \sqrt {\frac{\mu }{{\varepsilon - j\frac{\sigma }{\omega }}}} = \left| {{\eta _c}} \right|{e^{j\varphi }} $ | (6) |
式中:Exm为电磁场的初始电场强度,α和β分别为传播常数r=α+jβ的实部和虚部,它们都是实数,α为衰减常数,β称为相位常数。φ为相位角,ηc称为导电媒质的本征阻抗,它由媒质参数和电磁波频率确定。ηc是决定一段距离的海水对特定频率电磁波的阻抗大小,与距离的指数密呈正比,因此是电磁波能量衰减的决定因素,也是本文讨论的关键点。
所以,导电媒质中的平均功率密度可以写为
| $ \begin{array}{*{20}{c}} {{S_{{\rm{ave}}}} = \frac{1}{2}{R_e}\left[ {E\left( z \right) \times H\left( z \right)} \right] = }\\ {\frac{1}{2}{R_e}\left[ {{e_x}{E_{xm}}{{\rm{e}}^{ - \alpha z}}{{\rm{e}}^{ - {\rm{j}}\beta z}} \times {e_y}\frac{{{E_{xm}}}}{{\left| {{\eta _c}} \right|}}{{\rm{e}}^{ - \alpha z}}{{\rm{e}}^{ - {\rm{j}}\left( {\beta z + \varphi } \right)}}} \right] = }\\ {{e_z}\frac{1}{2}\frac{{E_{xm}^2}}{{\left| {{\eta _c}} \right|}}{{\rm{e}}^{ - 2\alpha z}}\cos \varphi } \end{array} $ | (7) |
其中,α和β的表达式为
| $ \alpha = \omega \sqrt {\frac{{\mu \varepsilon }}{2}\left[ {\sqrt {1 + {{\left( {\frac{\sigma }{{\omega \varepsilon }}} \right)}^2} - 1} } \right]} $ | (8) |
| $ \beta = \omega \sqrt {\frac{{\mu \varepsilon }}{2}\left[ {\sqrt {1 + {{\left( {\frac{\sigma }{{\omega \varepsilon }}} \right)}^2} + 1} } \right]} $ | (9) |
可见,由于导电媒质的导电率σ≠0而引起衰减常数α≠0,使得平面波传播过程中伴随着电磁能量的损耗,表现为电磁场量振幅的不断减小。平均功密度的减小速率为2α。
设δ为电磁波传播d m后剩余功率密度与初始功率密度的百分比,由式(7) 得δ的表达式为
| $ \delta = \frac{{{S_{{\rm{ave1}}}}}}{{{S_{{\rm{ave0}}}}}} = {{\rm{e}}^{ - 2\alpha d}} \times 100\% $ | (10) |
在海水中,σ=4 s/m,相对介电常数εr=81,相对磁导率μr=1,真空磁导率为μ0=4π×10-7, 当f=100 kHz时,设电磁波初始场强为Exm,由(7) 和(10) 可计算得到
| $ \begin{array}{l} {S_{{\rm{ave}}}} = {e_z}\frac{1}{2}\frac{{E_{xm}^2}}{{\left| {{\eta _c}} \right|}}{{\rm{e}}^{ - 2\alpha z}}\cos \varphi = {e_z}\frac{{E_{xm}^2}}{{2 \times 0.44{\rm{W/}}{{\rm{m}}^2}}}{{\rm{e}}^{ - 2.52z}}\cos {45^ \circ } = \\ \;\;\;\;\;\;\;\;\;{e_z}0.8{\left( {{E_{xm}}} \right)^2}{{\rm{e}}^{ - 2.52z}}\\ \delta = \frac{{{S_{{\rm{aved}}}}}}{{{S_{{\rm{ave0}}}}}} = {{\rm{e}}^{ - 2.52d}} \times 100\% \end{array} $ |
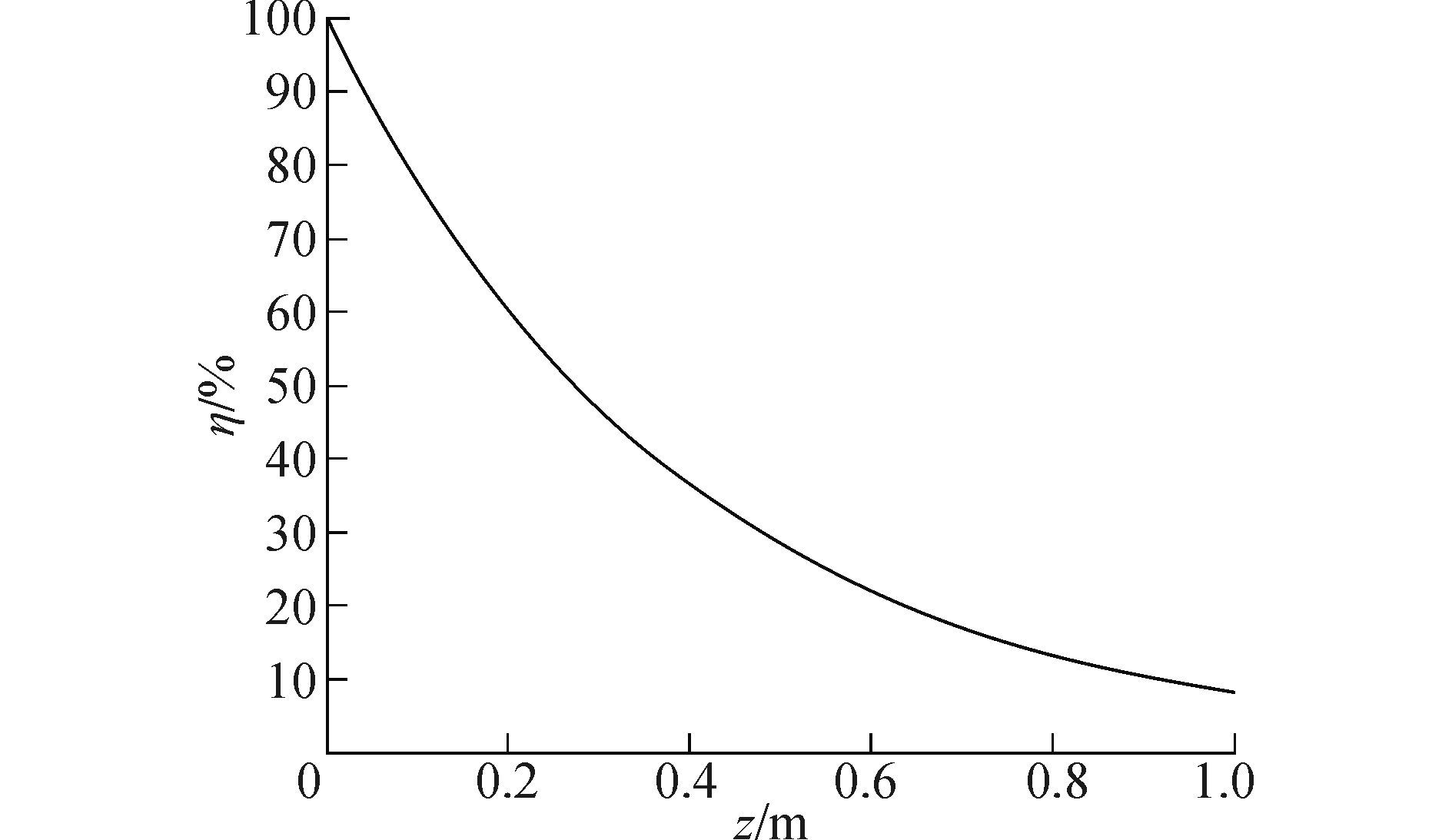
图 2所示为当f=100 kHz时电磁能量在海水中的衰减率。可以看到,水中能量衰减是随传输距离以指数速率下降,当z=0.2m时,能量衰减已经达到40%。
|
图 2 f=100 kHz时电磁能量在海水中的衰减率 Fig.2 Attenuation rate of electromagnetic wave in seawater when f=100 kHz |
引入电磁波损耗后,传输距离为d m电能传输系统的效率可以改写为
| $ \begin{array}{*{20}{c}} {{\eta _{sea}} = \eta \times \delta = }\\ {\frac{{{{\left( {\omega M} \right)}^2}{R_L}}}{{{Z_S}\left[ {{Z_P}{Z_S} + {{\left( {\omega M} \right)}^2}} \right]}} \times {{\rm{e}}^{ - 2.52d}} \times 100\% } \end{array} $ | (11) |
由于互感M与传输距离d的三次方成反比,同时海水中电磁波强度也以距离的指数密速率递减。两种因素叠加,导致在海水中如何提高磁谐振系统的效率成为了必须要解决的问题。
2 最大效率的追踪根据传输理论,当输入端的阻抗等于输出端的阻抗时,效率达到最大。对该系统而言,即从接收端看去,当接收端阻抗等于发射端阻抗与海水阻抗之和时,获得最大传输效率。当系统设计完成后,发射端的阻抗也随之确定,此时变化的只有海水的阻抗与接收端的充电电池组的内阻阻抗。由于运动的海水影响,发射端与接收端的相对位置不可避免地发生变化,导致两端之间的海水阻抗也随之变化。式(11) 表明,即使微小的距离变化也会造成传输效率的大幅偏移,系统偏离最大效率工作点,引起效率大幅降低。另外,本文使用的5串5并的18 650锂电池组,单体电池由3.7 V充电至约4.1 V的内阻变化范围是30~40 mΩ,因此电池组在充电过程中的总变化范围为30~40 mΩ。如果可以调节接收端的阻抗值,使得接收端阻抗时刻等于发射端和海水阻抗之和,那么系统将时刻保持在最佳传输效率处[13]。
2.1 最大效率追踪控制电路本文提出了一种适合水下谐振耦合能量传输最大效率追踪系统,用于实时将匹配接收端阻抗和输入阻抗,原理图如图 3所示。
|
图 3 最大效率追踪系统原理 Fig.3 Schematic of maximum efficiency tracking system |
理论上,改变发射端或者接收端阻抗都可以达到阻抗匹配的目的。然而,发射端通常装在水中平台上,接收端装载在水下设备中,希望发射端可以为更多种类不同阻抗的水下设备充电。因此采用较小阻抗的发射端并将其制作成标准设备,同时将阻抗匹配部分装载在接收端是更为合理的设计。
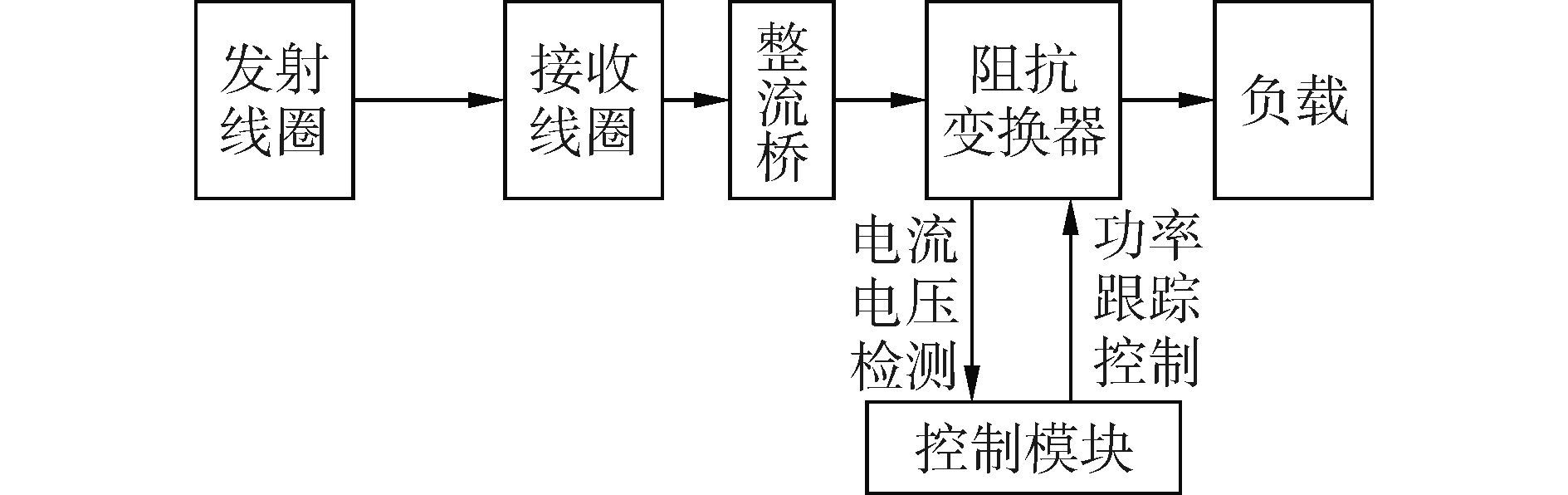
图 4所示为最大效率跟踪系统结构图,高频交流电通过电磁谐振耦合被接收线圈接收并进行整流后,通过阻抗变换器。在阻抗变换器中,电压电流检测器采集实时电压与电流并反馈给控制单元,控制单元计算后输出经过调制的PWM信号,通过驱动电路控制阻抗变换器中的开关管Q,调节占空比D,调节接收端的阻抗从而达到匹配状态。

|
图 4 最大效率追踪系统结构 Fig.4 structure chart of maximum efficiency tracking system |
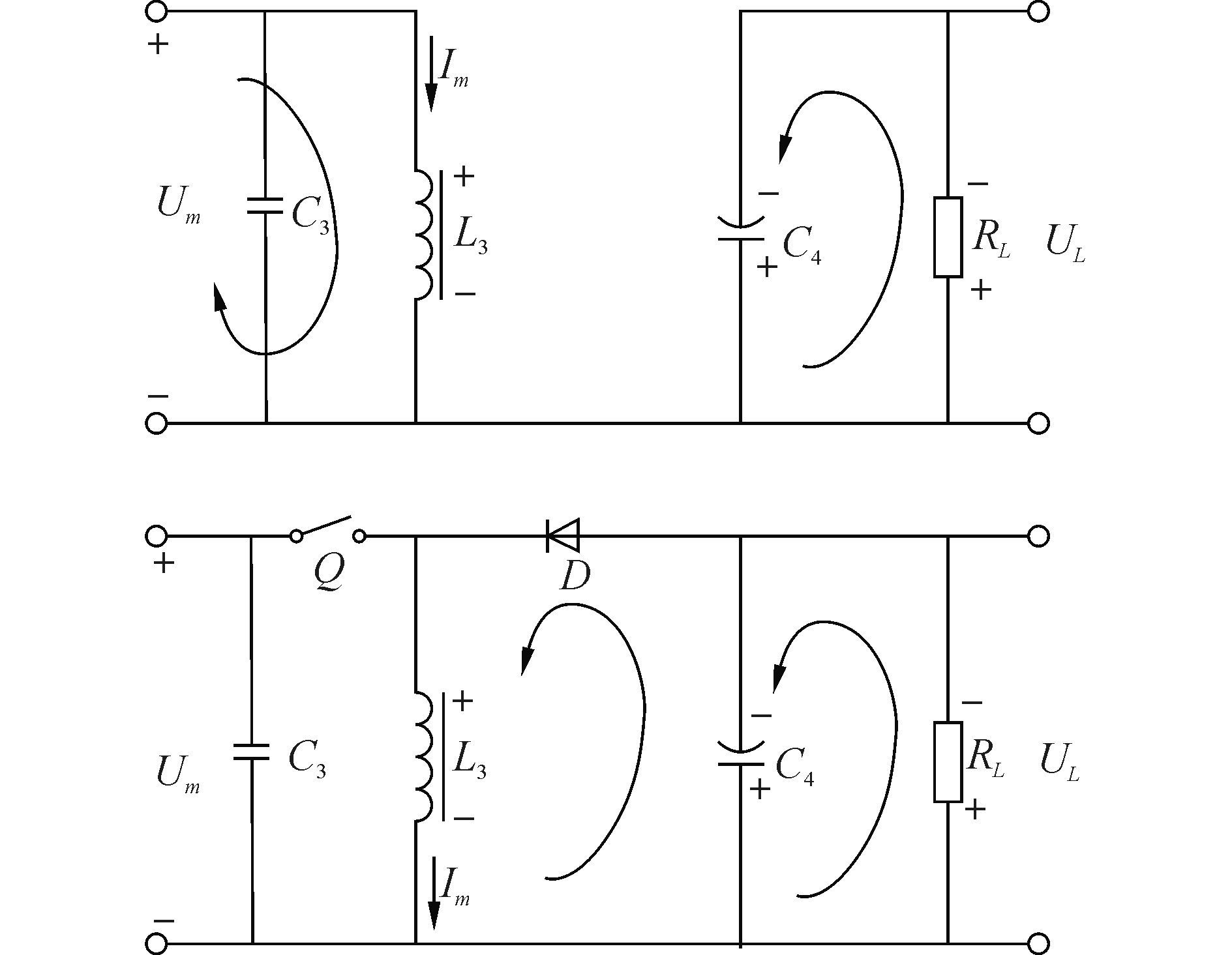
本文选取Buck-Boost变换器[13]作为阻抗变换电路,工作原理图如图 5所示。
|
图 5 Buck-Boost电路工作原理,分别为开通和关断状态 Fig.5 Working principle of Buck-Boost circuit |
设电路工作占空比为D,周期为Ts。可以得到当Buck-Boost电路在稳态工作时:
| $ \left\{ \begin{array}{l} \frac{{{U_m}}}{{{U_L}}} = \frac{D}{{1 - D}}\\ \frac{{{I_m}}}{{{I_L}}} = \frac{{1 - D}}{D} \end{array} \right. $ | (12) |
则Buck-Boost电路的输入阻抗Rm可表示为
| $ {R_m} = \frac{{{U_m}}}{{{I_m}}} = \frac{{{U_L}}}{{{I_L}}} \cdot \frac{{{{\left( {1 - D} \right)}^2}}}{{{D^2}}} = \frac{{{R_L}{{\left( {1 - D} \right)}^2}}}{{{D^2}}} $ | (13) |
式(13) 表明,当负载大小RL确定后,通过改变占空比D就可以改变Buck-Boost电路输入端阻抗Rm的大小,Rm的理论调节域为0~+∞。结合图 4可以看出,Rm即是系统接收端的实际阻抗。当调节接收端Rm与发射端与海水阻抗和实时匹配,即可达到实时最大效率传输状态。
2.2 控制策略在众多算法中,扰动观察法由于结构简单,测量参数较少,运算量较小等优点被广泛运用在多种电力系统中。无论是固定扰动步长法还是变步长法,它的原理是引入一个微小的扰动变化改变占空比,然后观察占空比D变化前后输出功率的变化,再将占空比调整至功率较大的那个点,经过一次次的比较,最终输出功率将趋近于最大输出功率。由于发射端的输入功率恒定,此时传输效率也达到最大值,系统达到阻抗匹配状态。
对于水下磁谐振式能量传输系统来说,在海水中,两线圈的相对位置时刻受到潮汐洋流等影响而产生微小的变化,意味着最佳效率点时刻都在变化,系统将一直不停地追踪变化的最佳功率点,震荡不仅影响负载寿命,还会损失一部分功率从而降低效率。综合考虑,如图 6所示,本文提出了一种新的输出稳定型最大效率追踪控制策略。

|
图 6 控制策略 Fig.6 Control strategy |
在k+1时刻,控制器发出一个微小的扰动T改变占空比D,采样电路采样得到(k+1) 时刻电压和电流值Um(k+1) 和Im(k+1),并输入控制单元中。控制单元中的乘法器计算出实时功率P(k+1),并与k时刻的功率P(k)和电压Um(k)进行比较得到差值ΔP和ΔUm。
此时,将得到的ΔP进行有效性判定,判定的方法为:引入一个功率变化的参考值ΔPref,若|ΔP|>ΔPref,此时系统将占空比D向功率增加的方向改变T,即将占空比移动至采样功率较大的点;若|ΔP|≤ΔPref,则表示两次功率的变化量较小,测量点此时在最大功率点附近,系统保持上一时刻的状态,保持稳定。当完成一轮比较后,进入下一次循环。占空比D的变化方向由ΔP和ΔUm的正负共同决定,判定逻辑为“同或门”:
参考值ΔPref是本控制算法的核心参数,其值选取需要结合实际应用的环境状况,充电电池组的抗波动能力等。通过实验表明,经验上ΔPref要大于电池组的抗电压波动的范围值。
3 仿真和结果为了进一步验证该输出稳定型最大效率追踪策略的可行性,根据图 4,本文使用仿真软件建立了该系统的仿真模型。图 7为控制策略部分的算法仿真模型图。

|
图 7 最大效率追踪算法仿真 Fig.7 Simulation of maximum efficiency tracking system |
仿真模型中Buck-Boost电路电感为78 μH,电容1 300 μF,负载电阻2.88 Ω。当输入功率为12 W,初始输入端等效阻抗为4 Ω,开关管频率20 kHz,采用变步长的ode12tb进行仿真。在仿真中,设置在t=0.025 s时,输入端等效阻抗由4 Ω变为2 Ω,用于模拟海水阻抗发生变化的情况。同时将参考值ΔPref设置为0.6 W。
当输入端电阻变化时,发射端的阻抗发生改变,系统最大效率传输点偏移。此时追踪系统开始工作,通过调整占空比D改变接收端阻抗Rm,使之重新达到匹配状态。
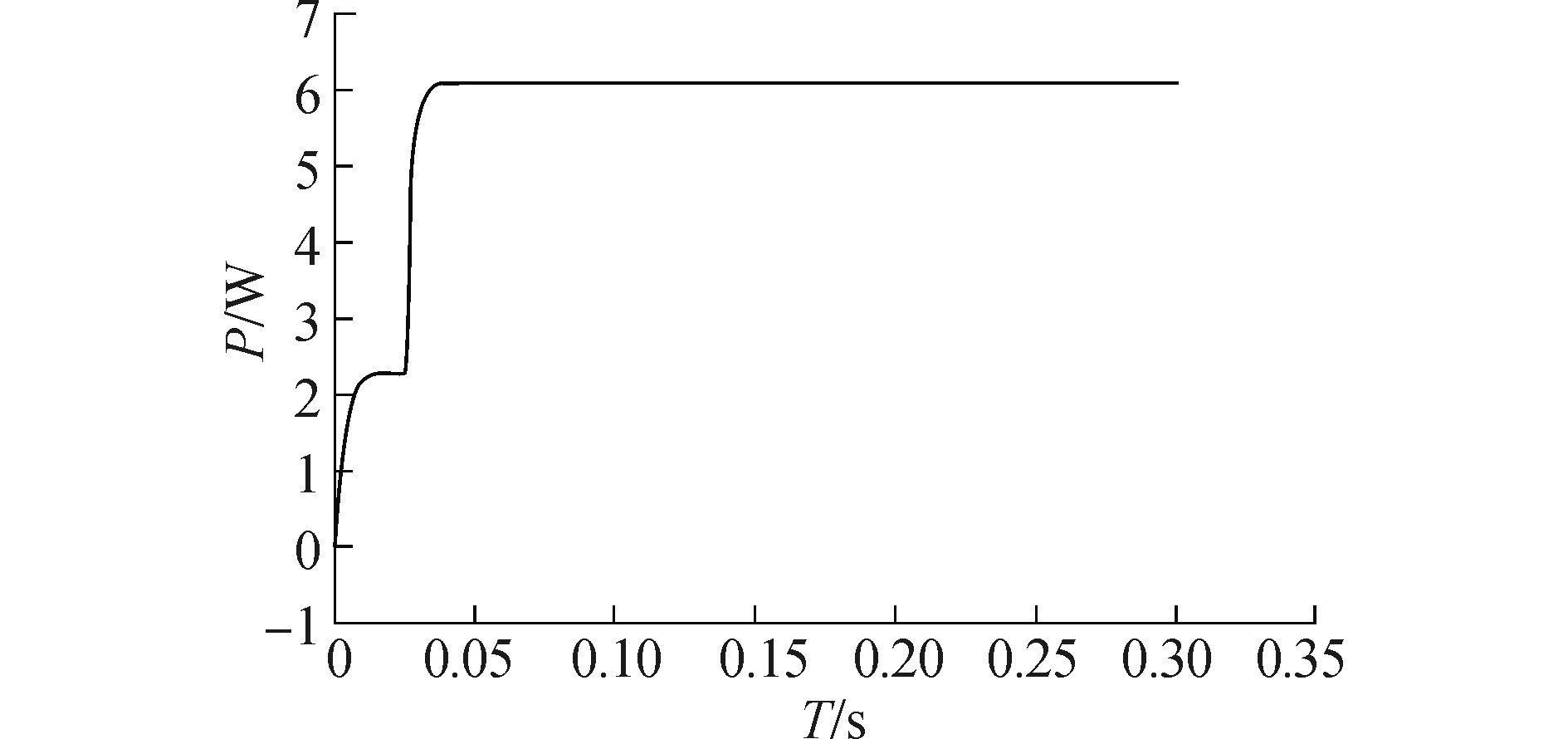
图 8和图 9分别为在此仿真条件下应用传统的最大效率追踪策略以及输出稳定型策略的输出功率仿真。可以看出,t=0.025 s时输入阻抗改变,控制器开始运行,在约0.012 s后,两种方法重新达到阻抗匹配点附近。传统方法下系统在5.5 W处产生振幅约为1 W的震荡。而与此同时,输出稳定型方法则输出平顺,达到6 W。这是由于当系统的功率变化小于预设的参考值ΔPref时,扰动停止,从而输出一个固定占空比的PWM波,不仅消除了震荡,并且减少了功率损失。

|
图 8 传统最大效率追踪的输出功率波形 Fig.8 Output power with traditional maximum efficiency tracking |
|
图 9 输出稳定型最大效率追踪的输出功率波形 Fig.9 Output power with stable and maximum efficiency tracking |
为了进一步验证该控制系统和算法的可行性,本文搭建了一个水下无线能量传输试验台,部分装置如图 10所示。控制芯片使用的是TI公司推出的TMS320F2812的32位高性能DSP。实验装置各参数如表 1和表 2所示。系统中耦合线圈由直径为r=0.8 mm铜芯漆包线绕制而成,实验开始时发射线圈和接收线圈的距离为15 cm;负载为5 Ω;水箱中为模拟海水环境的食盐水,浓度约为3%。

|
图 10 部分实验装置 Fig.10 Picture of part experimental device |
| 表 1 线圈参数 Tab.1 Parameters of three coils |
| 表 2 实验装置参数 Tab.2 Parameters of experimental device |
为了检验算法的可行性,分别测量了使用输出稳定型最大效率追踪算法、使用传统最大效率追踪算法(定步长扰动观察法)和不使用任何算法三种情况下的输出功率。实验分为两个阶段:第一阶段,设置阻抗盒的初始输入阻抗为10 Ω,测量三种情况下效率的大小;第二阶段,将阻抗盒的输入阻抗改变为5 Ω,测量使用和不使用该算法下的效率大小。实验结果如表 3所示(结果为输出平均效率)。
| 表 3 三种情况下的传输效率 Tab.3 Transfer efficiency of three conditions |
由实验结果可得,在输入阻抗变化前,未使用最大效率追踪算法的效率仅为26%,而使用了两种最大功率追踪算法的效率均为47%和45%,表明了最大功率算法可以显著提高水下磁谐振能量传输系统的效率。
当输入阻抗由10 Ω变为5 Ω,由于输入端阻抗的下降,三种情况下系统效率均有不同程度的提高。而加入最大功率算法的两种情况下,效率的提高明显,增幅都达到了7%,效率显著提高至52%。同时,输出稳定型算法在最佳效率点稳定住了输出功率,从而减小了功率波动造成系统损耗,相比传统最大功率算法效率又提高了约3%。
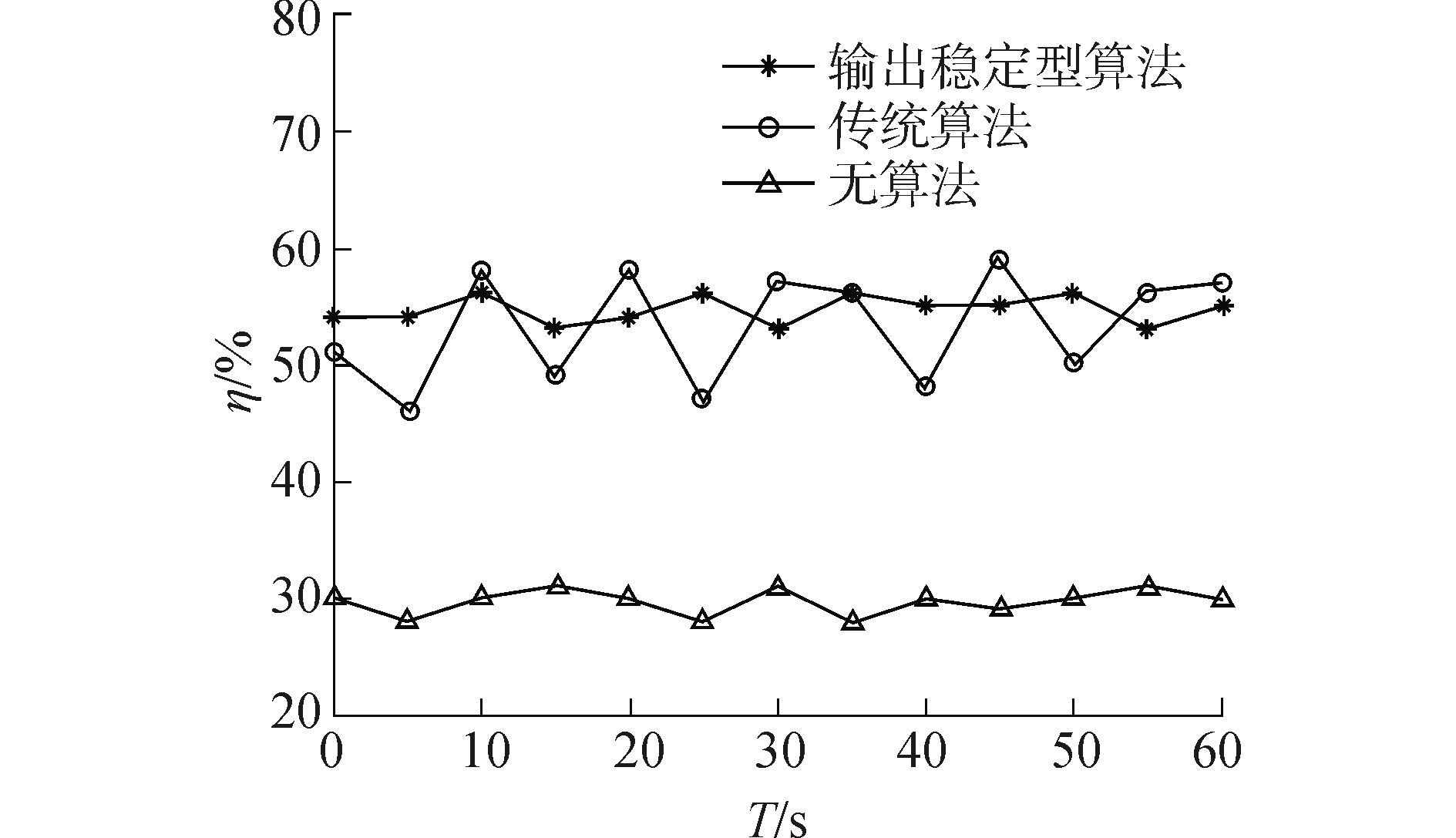
为了验证本文提出的有效性判定对稳定输出的效果,在上述实验情况下,测量了输出阻抗为5 Ω时输出稳定型最大效率追踪算法、传统最大效率追踪算法的输出功率以及不加入任何追踪算法时的效率值,实验结果如图 11所示。
|
图 11 三种情况下的传输效率 Fig.11 Transfer efficiency chart of three conditions |
对比三条曲线可知,传统最大效率追踪算法,输出效率波动较大,幅度约为13%。而本文提出的算法法在稳定输出上具有明显的改善,波动幅度小于4%,并且相对于传统算法平均效率也有所提高。而在不采用任何算法的情况中,由于两端阻抗严重不匹配,大量能量被反射到水中,因此效率明显低于前两种情况。
5 结论1) 该方法解决了水下磁谐振式电能传输系统在工作时输出功率偏低的问题,以及传统最大效率追踪方法输出功率在最大效率处震荡的问题,提高了传输效率。
2) 运用改进的输出稳定控制算法稳定输出电压,抑制了输出震荡,进一步减小了损耗,延长负载寿命。
3) 输出稳定型最大效率追踪系统具有良好的动态和静态性能,在水下磁谐振式电能传输系统中具有较好的应用前景。
| [1] |
PAINTER H F.Current and future wet-mate connector technology developments forscientific scabed observatory applications[C]//OCEANS 2006, Boston, USA, 2006:881-886.
( 0) 0)
|
| [2] |
BARLOW S. The ruggedization of hybrid wet-mate connectors[J]. Sea technology, 1997, 38(7): 17-21. ( 0) 0)
|
| [3] |
SOIJAČIĆ M, KURS A, KARALIS A, et al. Wireless power transfer via strongly coupled magnetic resonances[J]. Science, 2007, 317: 83-86. DOI:10.1126/science.1143254 ( 0) 0)
|
| [4] |
KARALIS A, JOANNOPOULOS J D, SOIJAČIĆ M. Efficient wireless non-radiative mid-range energy transfer[J]. Annals of physics, 2008, 323: 34-48. DOI:10.1016/j.aop.2007.04.017 ( 0) 0)
|
| [5] |
陈聪, 周骏, 龚沈光. 海水中电磁波传播特性的研究[J]. 海军工程大学学报, 2004, 16(2): 61-64. CHEN Cong, ZHOU Jun, GONG Shenguang. Propagation properties of electromagnetic wave in sea water[J]. Journal of Maval University of engineering, 2004, 16(2): 61-64. (  0) 0)
|
| [6] |
CHEN Y M, LIU Y C, WU F Y. Multi input converter with power factor correction, maximum power tracking and ripple-free input currents[J]. IEEE Trans on power electr, 2004, 19(3): 631-639. DOI:10.1109/TPEL.2004.829777 ( 0) 0)
|
| [7] |
BEUKES H J, ENSLIN J H R.Analysis of a new compound converter as MPPT, battery regulator and bus regulator for satellite power wystem [C]//Proc of 24th annual Power Electronics Specialists Conference(PESC).1993:846-852.
( 0) 0)
|
| [8] |
KIM T Y, AHN H G, PARK E K, et al. A novel maximum power point tracking control for photovoltaic power system under rapidly changing solar radiation[C]//Proc IEEE Conf International Symposium on Industrial Electronics, 2011.
( 0) 0)
|
| [9] |
CHEON S, KIM Y H, KANG S Y. Circuit-model-based analysis of a wireless energy-transfer system via coupled magnetic resonances[J]. IEEE transactions on industrial electronics, 2010, 58(7): 2906-2914. ( 0) 0)
|
| [10] |
SHAHRZAD J M, ALIREZA M, BOZENA K. Mid-range wireless energy transfer using inductive resonance for wireless sensors[J]. IEEE international conference on computer Design, 2009: 517-522. ( 0) 0)
|
| [11] |
田龙. 天线自适应阻抗匹配系统设计与实现[D]. 苏州: 苏州大学, . 2013 TIAN Long. Design and realization of adaptive impedance matching system[D].Suzhou:Soochow University, 2013. http://www.docin.com/p-1379140681.html (  0) 0)
|
| [12] |
李宇. Buck-Boost变换器的研究[D]. 南京: 南京航空航天大学, . 2006 LI Yu. Research on Buck-Boost converter[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10287-2006119118.htm (  0) 0)
|
| [13] |
傅文珍, 张波, 丘东元, 等. 自谐振线圈耦合式电能无线传输的最大效率分析与设计[J]. 中国电机工程学报, 2009, 29(18): 21-26. FU Wenzhen, ZHANG Bo, QIU Dongyuan, et al. Maximum efficiency analysis and design of self-resonance coupling coils for wireless power transmission system[J]. Proceedings of the CSEE, 2009, 29(18): 21-26. DOI:10.3321/j.issn:0258-8013.2009.18.004 (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


